Как найти тепло зная работу

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 апреля 2021 года; проверки требует 1 правка.

Тепловой эквивалент работы  — коэффициент пропорциональности между механической работой , затрачиваемой при выделении теплоты, и количеством выделившейся теплоты .

.

Этот коэффициент всегда сохраняет одно и то же значение независимо от способа получение теплоты, вида работы, температуры тела и т.д.
Тепловой эквивалент работы является величиной, обратной механическому эквиваленту тепла :

.

В системе МКГСС тепловой эквивалент работы равен 0,002345 ккал/кгс·м, в Международной системе единиц (СИ) .

Понятие теплоты. Эквивалентность теплоты и работы[править | править код]

В основе закона сохранения и превращения энергии лежит принцип эквивалентности различных форм движения материи (видов энергии). Было установлено, что различные формы движения материи (тепловая, механическая, электрическая, химическая и т. п.), количественными мерами которых являются количества соответствующих видов работ и теплоты, могут переходить в другие формы в строго опредёленных эквивалентных количествах, не зависящих ни от характера процесса преобразования, ни от условий протекания этого процесса^[1].

Различие между теплотой и работой состоит в том, что они являются различными формами передачи энергии. Теплота представляет собой такую форму передачи энергии, которая определяется либо непосредственным контактом между телами (см. теплопроводность, конвекция), либо лучистым переносом энергии. Работа представляет собой иной механизм передачи энергии, при котором обязательно имеет место изменение объёма тела^[2].

В ходе развития науки представления о теплоте изменялись. Во времена Аристотеля было распространено представление о том, что теплота является одним из «первичных качеств», присущих материи, причём каждому из тел это «первичное качество» присуще в различной мере. В XVII в. в трудах Декарта и Бэкона содержатся попытки связать представление о теплоте с движением частиц, из которых состоит тело. В связи с широким развитием калориметрии в XVIII в. в науке прочно укрепилось понятие теплорода, или флогистона — особой невязкой и невидимой жидкости, переходящей от более нагретых тел к менее нагретым при их соприкосновении.

В конце XVIII в. появляются научные работы, опровергающие теорию теплорода. В 1798 г. английский ученый Румфорд провел эксперимент, в котором к внутренней поверхности орудийного ствола был прижат тупой резец. Румфорд обнаружил, что в результате трения резца о ствол температура ствола возрастала вследствие выделения тепла. При этом было установлено, что тепло в этом опыте может выделяться столь долго, сколь долго вращается орудийный ствол, из чего ученый сделал вывод о том, что «если изолированное тело или система тел способны без ограничения производить теплоту, то эта теплота не может быть метериальной субстанцией» и что «только движение в состоянии обеспечить непрерывное возбуждение и распространение тепла в наших опытах».

Опыт Джоуля[править | править код]

В 1843—1850 гг. английский физик Джеймс Джоуль провел опыты, целью которых было установление соотношения между работой, затрачиваемой при выделении тепла, и количеством выделившегося тепла. В теплоизолированный медный сосуд, заполненный водой, Джоуль поместил мешалку, снабжённую лопастями. К стенкам сосуда также были прикреплены лопатки, затрудняющие свободное движение воды при вращении мешалки. Мешалка приводится во вращение за счёт опускания связанного с ней тросом через блок груза весом . При опускании на высоту работа, производимая грузом (и, следовательно, мешалкой), равняется убыли потенциальной энергии груза . Тепло, выделившееся в сосуде с водой, вычисляется по повышению температуры воды, измеряемой термометром.

В результате серии опытов Джоуль установил, что при затрате одного и того же количества работы выделяется одно и то же количество тепла. Таким образом, было показано, что количество полученного тепла эквивалентно количеству затраченной работы. Это соотношение было справедливо и при совершении работы за счёт затраты тепла.

Вскоре после опытов Джоуля была разработана молекулярно-кинетическая теория вещества, в соответствии с которой теплота является энергией хаотического теплового движения микрочастиц, составляющих тепло.

Соотношение между единицами работы и теплоты[править | править код]

Соотношения между единицами работы и теплоты, выраженных в разных системах единиц измерения, представлены в таблице.

	кгс·м	Дж	эрг	ккал	кВт⋅ч
1 килограмм-сила-метр	1	9,80665	98,0665⋅106	2,34228⋅10−3	2,72407⋅10−6
1 Джоуль	0,101972	1	107	0,238846⋅10−3	0,27778⋅10−6
1 эрг	10,1972⋅10−9	10-7	1	23,8846⋅10−12	27,778⋅10−15
1 килокалория	426,935	4186,8	41,868⋅109	1	1,163⋅10−3
1 киловатт-час	367098	3,6⋅106	36⋅1012	859,845	1

См. также[править | править код]

• Закон сохранения энергии.
• Механический эквивалент теплоты.

Примечания[править | править код]

^[1]
[2]

Первый закон термодинамики

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.

Начнём с обсуждения работы газа.

Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где — давление газа, — площадь поршня. Если при этом поршень перемещается, то газ совершает работу.

При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).

к оглавлению ▴

Работа газа в изобарном процессе

Предположим, что газ расширяется при постоянном давлении . Тогда сила , с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние (рис. 1).

Рис. 1.

Работа газа равна:

Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:

(1)

Если и — начальный и конечный объём газа, то для работы газа имеем: . Изобразив данный процесс на -диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).

Рис. 2. Работа газа как площадь

Пусть теперь газ изобарно сжимается от объёма до объёма . С помощью аналогичных рассуждений приходим к формуле:

Но , и снова получается формула (1).

Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.

Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.

к оглавлению ▴

Работа газа в произвольном процессе

Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.

Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление будет оставаться приблизительно постоянным. Газ совершит малую работу . Тогда работа газа во всём процессе найдётся суммированием этих малых работ:

Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):

Рис. 3. Работа газа как площадь

к оглавлению ▴

Работа, совершаемая над газом

Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу , которую поршень совершает над газом.

Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой , равной силе по модулю и противоположной по направлению: (рис. 4).

Рис. 4. Внешняя сила , действующая на газ

Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:

Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна . Наоборот, при сжатии работа газа отрицательна , а работа, совершаемая поршнем над газом, положительна 0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.

Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .

Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.

Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа , то изменение внутренней энергии тела будет равно:

(2)

Нас больше всего интересует случай, когда тело является газом. Тогда (где , как всегда, есть работа самого газа). Формула (2) принимает вид: , или

(3)

Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.

Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.

к оглавлению ▴

Применение первого закона термодинамики к изопроцессам

Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.

1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:

Всё подведённое к газу тепло идёт на совершение газом работы.

2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:

Всё тепло, переданное газу, идёт на изменение его внутренней энергии.

3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:

к оглавлению ▴

Адиабатный процесс

Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.

Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.

Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.

При адиабатном процессе . Из первого закона термодинамики получаем: , или .

В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.

Наоборот, в процессе адиабатного сжатия будет , поэтому : газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.

Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).

Рис. 5. Сравнительный ход изотермы и адиабаты

В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?

При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.

А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.

Содержание:

1. Теплота и работа
2. Энергия движения и взаимодействия молекул. Внутренняя энергия тел
3. Изменение внутренней энергии тела
4. Единица количества теплоты
5. Понятие о теплоёмкости тела. Удельная теплоёмкость вещества
6. Измерение удельной теплоёмкости
7. Развитие взглядов на природу теплоты
8. Механический эквивалент теплоты
9. Закон сохранения и превращения энергии

Теплота представляет собой такую форму передачи энергии, которая определяется либо непосредственным контактом между телами (см. теплопроводность, конвекция), либо лучистым переносом энергии. Работа представляет собой иной механизм передачи энергии, при котором обязательно имеет место изменение объёма тела.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Теплота и работа

Работа – путем упорядоченного движения молекул. Внутренняя энергия – энергия взаимодействия всех частиц. Все величины являются энергией и измеряются в джоулях. Первый закон термодинамики. Теплота, подведенная к системе, расходуется на изменение внутренней энергии и совершение работы.

Энергия движения и взаимодействия молекул. Внутренняя энергия тел

Мы теперь знаем, что молекулы, из которых состоят тела, находятся в движении. Молекулы газа движутся поступательно с разными скоростями и в разных направлениях. Для газа характерна хаотичность движения молекул. В жидкостях молекулы могут колебаться, вращаться и поступательно перемещаться относительно друг друга. В твёрдых телах молекулы и атомы колеблются около некоторых средних положений.

Как и всякие движущиеся тела, молекулы обладают кинетической энергией.

Мы знаем также, что молекулы в теле связаны между собой силами сцепления, в газах слабо, в жидкостях и твёрдых телах очень сильно. Поэтому молекулы обладают также потенциальной энергией, зависящей от их взаимного расположения.

Кинетическая энергия движения частиц, из которых состоит тело, вместе с потенциальной энергией взаимодействия этих частиц составляют внутреннюю энергию тела.

Имея всегда какой-то запас внутренней энергии, тело одновременно может обладать механической энергией. Например, снаряд движущийся на некоторой высоте, кроме внутренней энергии, обладает ещё механической энергией — потенциальной и кинетической.

Изменение внутренней энергии тела

Внутренняя энергия тела не является какой-то постоянной величиной: у одного и того же тела она может изменяться. При повышении температуры, например, внутренняя энергия тела увеличивается, так как увеличивается средняя кинетическая энергия движения молекул этого тела. С понижением же температуры, наоборот, внутренняя энергия тела уменьшается.

Внутренняя энергия меняется также при переходе тела из одного агрегатного состояния в другое, при деформации тела, при раздроблении тела на более мелкие части, так как во всех этих случаях меняется взаимное расположение частиц, а значит, и их потенциальная энергия.

Из всего сказанного следует, что внутренняя энергия тела зависит от состояния этого тела. С изменением состояния тела меняется и его внутренняя энергия.

Рассмотрим теперь, в результате каких процессов происходит изменение внутренней энергии тела.

Если движущееся тело производит работу против сил трения, то его механическая энергия уменьшается; одновременно меняется и состояние тела. При трении тела нагреваются, дробятся на части и даже могут переходить из одного агрегатного состояния в другое (например, при трении плавятся кусочки льда). Следовательно, в процессе совершения работы внутренняя энергия тела изменяется.

Внутреннюю энергию тела можно изменять и иным путём. Вода в чайнике, поставленном на плиту, закипает, её внутренняя энергия изменяется. Воздух и различные предметы в комнате нагреваются от печки; следовательно, их внутренняя энергия увеличивается, так как увеличивается кинетическая энергия молекул.

Но при этом работа не совершается. Значит, изменение внутренней энергии может происходить не только в результате совершения работы, но и при различных тепловых процессах.

Процесс изменения внутренней энергии тела без совершения работы называется теплопередачей. Теплопередача осуществляется и при непосредственном контакте тел (чайник на плите) и если тела разделены расстоянием (нагревание предметов от печки или от солнца).

Итак, внутреннюю энергию тела можно изменять двумя путями: путём совершения работы и путём теплопередачи.

Когда тело увеличивает запас своей внутренней энергии, то это значит, что оно получает какое-то количество энергии извне; наоборот, уменьшение запаса внутренней энергии означает, что тело отдаёт часть своей энергии.

Мерой энергии, получаемой или отдаваемой телом в процессе теплопередачи, служит особая величина, называемая количеством теплоты.

Единица количества теплоты

В те времена, когда впервые стали производить измерения количества теплоты (вторая половина XVIII в.), понятиями работы и энергии в науке ещё не пользовались (они были введены в XIX в.).

Для измерения количества теплоты была введена особая единица. За единицу количества теплоты принято то количество теплоты, которое необходимо для нагревания 1 г воды на 1°С. Эта единица называется калорией ¹ (сокращённое обозначение: кал). Употребляют также и единицу, в 1000 раз большую — килокалорию ккал).

¹ Калория — от латинского слова калор — жар.

Рихман Георг (1711—1753) — замечательный русский учёный. Родился в 1711 г., в один год с  Ломоносовым. Учился в Петербургской Академии наук. В 1741 г. был назначен профессором академии. Его работы касались главным образом исследования теплоты и электричества. В области теплоты он заложил основы калориметрии. Совместно с  Ломоносовым впервые в России начал изучение электрических явлений. Рихман впервые применил электроскоп для исследования электрических зарядов на телах.

Тщательные измерения показывают, что для нагревания 1 г воды на 1°С требуется несколько большее или меньшее количество теплоты, в зависимости от исходной температуры.

Так, для нагревания 1 г воды от 1 до 2° требуется приблизительно на 1% больше количества теплоты, чем для нагревания от 31 до 32°. При точных измерениях принято считать за 1 калорию количество теплоты, необходимое для нагревания 1 г чистой воды от 19,5 до 20,5°С.

Понятие о теплоёмкости тела. Удельная теплоёмкость вещества

Нагревая тела с одинаковой массой, но состоящие из различных веществ (железа, дерева, кирпича и т. д.), можно обнаружить, что для повышения их температуры на данное число градусов требуются различные количества теплоты.

Количество теплоты, необходимое для нагревания тела на 1°, называется теплоёмкостью этого тела.

Опыт показывает, что для нагревания тела не на 1° С, а на t° требуется в t раз большее количество теплоты. При остывании на t° тело отдаёт такое же количество теплоты, которое поглощает при нагревании на t°.

Чем больше масса тела, тем больше его теплоёмкость, т. е. тем большее количество теплоты требуется для нагревания его на 1° С.

Теплоёмкость однородного тела пропорциональна его массе и зависит от вещества, из которого оно состоит.

Сравнивать между собой можно теплоёмкости различных веществ, имеющих одинаковую массу, равную, например, единице массы.

Количество теплоты, необходимое для нагревания 1 г вещества на 1° С, называется удельной теплоёмкостью вещества.

Пусть Q — количество теплоты, которое надо передать телу, масса которого m, чтобы повысить температуру его от до  Чтобы определить удельную теплоёмкость вещества с, надо количество теплоты Q разделить на массу тела m и на разность температур Таким образом,

Удельные теплоёмкости обычно выражают в  или в 

Удельная теплоёмкость воды при нагревании от 19,5°С до 20,5°С равна 1  При других температурах она отличается от 1 но это отличие очень незначительно, и мы его в дальнейшем учитывать не будем. Вообще удельная теплоёмкость любого вещества с изменением температуры хотя и незначительно, но меняется.

Во многих случаях при расчётах пользуются средним значением удельной теплоёмкости. Для некоторых веществ такие значения удельной теплоемкости приведены в следующей таблице:

• Водород……..3,41
• Гелий……..1,26
• Спирт……..0,58
• Эфир……..0,56
• Керосин……..0,51
• Лёд……..0,48
• Воздух……..0,24
• Алюминий……..0,22
• Стекло……..0,19
• Алмаз……..0,12
• Железо……..0,11
• Медь……..0,09
• Серебро……..0,05
• Ртуть……..0,03
• Олово……..0,05
• Свинец……..0,03

Зная удельную теплоёмкость вещества, по формуле 

можно рассчитать количество теплоты, идущее на нагревание тела.

Измерение удельной теплоёмкости

Для измерения удельной теплоёмкости твёрдых, жидких и газообразных веществ существуют различные способы. Мы рассмотрим наиболее простой способ измерения теплоёмкости твёрдых веществ.

Испытуемое тело нагревают до определенной температуры и затем погружают его в особый прибор — калориметр, в который налито определённое количество воды (рис. 129).

Рис. 129. Схема установки по определению удельной теплоёмкости вещества с помощью калориметра.

Если вода в калориметре имеет температуру ниже, чем температура опущенного в неё тела, то она нагревается, а тело охлаждается до тех пор, пока их температуры не сравняются. Количество теплоты, отданное телом, равно количеству теплоты, полученному калориметром и водой. Этот опытный факт и даёт возможность определить удельную теплоёмкость тела.

Пусть масса калориметра равна m₁ его удельная теплоёмкость c₁ , масса воды в калориметре m₂, удельная теплоёмкость воды с, начальная температура воды и калориметра t⁰₁ , масса испытуемого тела m, его удельная теплоёмкость с_х и начальная температура общая температура калориметра и тела (греч. «тэта»). Тогда результат указанного опыта можно выразить уравнением:

    (1)

Это уравнение  теплового баланса. Оно показывает, что при теплообмене между испытуемым телом и калориметром количество теплоты, отданное телом, равно количеству теплоты, полученному калориметром.

Из уравнения (1) определяется искомая удельная теплоёмкость:

Надо иметь в виду, что, кроме обмена энергией между внесённым телом и калориметром, такой обмен возможен между телом и окружающими калориметр предметами. При точных измерениях необходимо по возможности уменьшать потери энергии и_вводить в вычисления поправки, учитывающие ту часть энергии, которая передаётся в процессе опыта окружающей среде.

Развитие взглядов на природу теплоты

В XVIII в. господствовало мнение, что теплота есть особая невидимая и невесомая жидкость, способная переходить из одного тела в другое. Такая жидкость, называвшаяся  теплородом, находилась, по мнению сторонников этой гипотезы, во всех телах.

Гипотезы теплорода в своё время придерживались знаменитые учёные — Ньютон, Лавуазе Лаплас, Гей-Люссак  и др. Само название «теплоёмкость» введено было потому, что оно указывало на содержание теплорода.

В то время как большинство учёных XVIII в. принимали гипотезу теплорода, против неё выступил М. В. Ломоносов.

В 1745 г. М. В. Ломоносов опубликовал работу «Размышления о причине теплоты и холода», начинавшуюся так: «Весьма известно, что тепло возбуждается движением: руки от взаимного трения согреваются, дерево загорается, искры вылетают при ударе кремнём о сталь, железо накаливается при ковании его частыми, сильными ударами; по прекращению их тепло уменьшается, и полученный огонь потухает… Из всего этого совершенно очевидно, что имеется достаточное основание теплоты в движении. А так как никакое движение без материи происходить не может, то необходимо,чтобы достаточное основание теплоты состояло в движении какой-либо материи».

По Ломоносову, теплота возникает в телах в результате сообщения им движения; следовательно, сущность теплоты — в движении частиц, образующих тело.

Учение Ломоносова о природе теплоты нашло признание среди ряда крупнейших учёных его времени. Так, например, знаменитый математик и физик Эйлер в письме, адресованном Ломоносову, писал: «Всякий знает, что появившиеся до сих пор трактаты о причинах теплоты ещё не разъяснили вполне этого предмета, и занимающиеся его исследованием заслуживают величайшей похвалы. Вас нельзя не поблагодарить за то, что вы рассеяли мрак, покрывавший доселе этот вопрос».

Знал о работах Ломоносова и известный итальянский физик Вольта. В 1786 г. он отметил «то чрезвычайное остроумие, с которым господин Ломоносов в своё время опроверг теплород».

Дальнейшее развитие и опытное обоснование учение о природе теплоты нашло в работах английских учёных  Румфорда и Дэви.

В 1798 г. Румфорд писал: «Когда я присутствовал в мюнхенском арсенале при сверлении пушек, меня поразила высокая температура, которую металл быстро принимал при сверлении, и ещё более высокая температура металлических стружек, которая превышала температуру кипения воды».

Желая убедиться, существует ли теплород, Румфорд произвёл ряд опытов, при которых тщательно изолировал испытуемый предмет от нагревания какими-либо другими предметами. Он сверлил металлический цилиндр, поместив его в ящик, наполненный холодной водой, и убедился, что через короткое время вода начинает кипеть. «Трудно описать недоумение и удивление, отразившееся на лицах присутствующих, когда они увидели, что столь большое количество воды было доведено до кипения без помощи огня».

Румфорд заметил, что чем дольше работает лошадь, приводящая в движение сверло, тем больше выделяется теплоты. На основании этого наблюдения он сделал вывод, что «нельзя считать веществом то, что можно получить в неограниченном количестве из изолированного тела, и нельзя представить себе теплоту иначе, чем некоторым движением».

В 1802 г. Дэви показал на опыте, что при трении двух кусков льда образуется вода, теплоёмкость которой в два раза больше, чем теплоёмкость льда. Этот опыт Дэви повторяет, помещая кусок льда под колокол воздушного насоса. И в этом случае, хотя лёд не мог ниоткуда получить «теплорода», он обращается в воду, на что затрачивается теплота.

Несмотря на убедительность доводов Ломоносова, Румфорда, Дэви, опровергавших существование теплорода, гипотеза теплорода ещё довольно долго существовала в науке. Для доказательства её несостоятельности потребовались новые опыты, новые научные исследования.

Механический эквивалент теплоты

В начале XIX в. в промышленность и транспорт широко внедряются паровые двигатели. Одновременно изыскиваются возможности повышения их экономичности. В связи с этим перед физикой и техникой ставится вопрос большой практической важности: как при наименьшей затрате топлива в машине совершить возможно больше работы.

Первый шаг в решении этой задачи сделал французский инженер Сади Карпов  1824 г., изучая вопрос о коэффициенте полезного действия паровых машин.

В 1842 г. немецкий учёный Роберт Майер теоретически определил, какое количество механической работы можно получить при затрате одной килокалории теплоты.

В основу своих расчётов Майер положил различие в теплоёмкостях газа.

У газов различают две теплоёмкости: теплоёмкость при постоянном давлении (с_р) и теплоёмкость при постоянном объёме (c_v).

Теплоёмкость газа при постоянном давлении измеряется количеством теплоты, которое идёт на нагревание данной массы газа на 1°С без изменения его давления.

Теплоёмкость же при постоянном объёме численно равна количеству теплоты, идущей на нагревание данной массы газа на 1°С без изменения объёма, занимаемого газом.

У всякого газа теплоёмкость при постоянном давлении больше теплоёмкости при постоянном объёме. Так, например, для воздуха удельные теплоёмкости с_р и c_v имеют следующие значения:

Объясняется это различие в теплоёмкостях газа следующим образом. При нагревании газа при постоянном объёме увеличивается только внутренняя энергия газа.

При нагревании же газа при постоянном давлении увеличивается, как и в первом случае, внутренняя энергия газа, но, кроме того, газ при расширении совершает работу. Проследим ход рассуждений Майера.

Рис. 130. Рисунок, поясняющий теоретический расчёт Майера механического эквивалента теплоты.

Допустим, что в сосуде (рис. 130), площадь основания которого 1 м², заключён при температуре 0° и давлении 760 мм рт. ст. 1 м³ воздуха. Воздух, заключённый в сосуде, закрыт поршнем АВ, который Майер в своих рассуждениях считал невесомым.

Масса 1 м³ воздуха равна 1,293 кг. Если нагреть этот воздух на 1°С, то он расширится и

поднимет поршень на (в положение А₁В₁).

Перемещая поршень, воздух в сосуде производит работу по преодолению силы атмосферного давления Гак как атмосферное давление равно 1,0332 то сила, действующая на поршень сверху, равна:

Работа, совершаемая расширяющимся воздухом по преодолению этой силы, равна:

Количество теплоты, идущей на нагревание воздуха в сосуде при постоянном давлении, равно:

Для нагревания же этого количества воздуха при постоянном объёме требуется:

За счёт количества теплоты  газ совершил работу, равную 37,82 кГм.

Из этих расчётов вытекает, что 0,0886 ккал эквивалентны 37,82 кГм. Отсюда количество механической работы, эквивалентное 1 ккал теплоты, равно:

Внутреннюю энергию тела, как было установлено в § 71, можно изменять двумя путями: путём совершения работы и путём теплопередачи.

Количество механической работы, которое вызывает такое же изменение внутренней энергии тела, как и сообщение ему единицы количества теплоты, называется механическим эквивалентом теплоты.

Рис. 131. Схема опыта Джоуля по определению механического эквивалента теплоты. Чтобы вода не увлекалась движением лопаточек, калориметр был разделён перегородками с вырезами в них для прохождения лопаточек.

Опытные определения механического эквивалента теплоты впервые были произведены Джоулем в период с 1840 по 1849 г. Один из наиболее известных его способов определения механического эквивалента теплоты состоял в следующем.

В калориметр А (разрез его показан на рис. 131) наливалась вода. Падающие грузы W и W’  приводили во вращение ось К с лопаточками L. Калориметр имел перегородки N; он был устроен так для того, чтобы увеличить трение подвижной части прибора о воду. Вследствие трения лопаточек о воду последняя нагревалась (температура внутри калориметра измерялась термометром).

Джемс Прескотт Джоуль (1818— 1889) — выдающийся английский физик, сыграл большую роль в опытном обосновании закона сохранения и превращения энергии.

Он впервые точно определил на опыте механический эквивалент теплоты. Одновременно с русским физиком Э. X. Ленцем открыл закон, который определяет количество теплоты, выделяемое электрическим током при прохождении по проводнику. Совместно с В. Томсоном открыл явление понижения температуры газа при его расширении.

Именем Джоуля названа единица работы джоуль.

По высоте падения h и массе грузов m подсчитывалась произведённая работа А = mgh. По повышению температуры в калориметре подсчитывалось количество теплоты Q, выделенное при трении подвижной части калориметра о воду. На эту величину увеличивалась внутренняя энергия воды.

Многочисленные измерения показали, что отношение работы А к количеству теплоты Q, на которое увеличивалась внутренняя энергия воды, в результате совершения этой работы, представляет постоянную величину. Эта величина и является механическим эквивалентом теплоты. Механический эквивалент обозначается буквой J:

Джоуль заменял воду ртутью и получал тот же результат. Наконец, вместо работы трения лопаточек о воду Джоуль измерял в калориметре работу трения двух кусков металла. Измерения дали ту же величину механического эквивалента теплоты.

Зная механический эквивалент теплоты, легко выразить единицу измерения количества теплоты через единицы работы:

Закон сохранения и превращения энергии

Рассмотрим более подробно описанный выше опыт Джоуля. В этом опыте потенциальная энергия падающих грузов превращалась в кинетическую энергию вращающихся лопаток; благодаря работе против сил трения кинетическая энергия лопаток превращалась во внутреннюю энергию воды. Мы сталкиваемся здесь со случаем превращения одного вида энергии в другой. Потенциальная энергия падающих грузов превращается во внутреннюю энергию воды, количество теплоты Q является мерой превращенной энергии. Таким образом, количество энергии сохраняется при её превращениях в другие виды энергии.

Естественно поставить вопрос: сохраняются ли при превращениях количества других видов энергии, например кинетической, электрической и т. д.? Допустим, что летит пуля массой  со скоростью Ее кинетическая энергия равна  Пуля попала в какой-либо предмет и застряла в нём. Кинетическая энергия пули превращается при этом во внутреннюю энергию пули и предмета, измеряемую количеством теплоты Q, которая вычисляется по известной формуле (§ 73). Если кинетическая энергия при превращении во внутреннюю энергию не теряется, то должно иметь место равенство:

Опыт подтверждает это заключение. Количество энергии сохраняется.

При прохождении электрического тока проводник нагревается: электрическая энергия превращается во внутреннюю энергию проводника. Опыт показывает, что при работе электрического тока в 1 получается всегда количество теплоты, равное 860 ккал. Таким образом, сохраняется общее количество энергии. Этот вывод относится ко всем видам энергии.

Тысячелетняя практика показала, что ни один из видов энергии никогда не возникает из ничего. Это положение подтверждается фактом невозможности осуществления вечного двигателя (см. ч. 1, § 78). Большой опытный материал показал также, что энергия и не исчезает при всех своих превращениях. Все явления природы происходят в соответствии с законом сохранения и превращения энергии, который формулируется так:

Во всех процессах, происходящих в природе, энергия не возникает и не исчезает, она только превращается из одного вида в другой в эквивалентных количествах.

Все формы энергии: кинетическая, потенциальная, электромагнитная, химическая, внутриатомная и др. — способны превращаться друг в друга.

Именно возможность взаимного превращения всех форм энергии обусловливает богатство и разнообразие явлений природы.

Для иллюстрации этого великого закона природы рассмотрим несколько примеров.

Солнечные лучи несут определённый запас энергии. Падая на поверхность Земли, лучи нагревают её. Энергия солнечных лучей при этом превращается во внутреннюю энергию почвы и тел, находящихся на поверхности Земли. Последняя передаётся окружающему Землю воздуху; воздушные массы приходят в движение, появляется ветер — происходит превращение в механическую (кинетическую) энергию. Часть энергии солнечных лучей поглощается на поверхности Земли листьями растений; при этом в растениях происходят сложные химические реакции, в результате которых образуются органические соединения — происходит превращение в химическую энергию.

В § 57 и 58 говорилось об использовании энергии движущейся воды; последняя возникает также в результате превращения энергии солнечного излучения.

Наконец, в настоящее время наука овладевает возможностями превращения внутриатомной энергии в другие, нужные для практики виды энергии.

Закон сохранения и превращения энергии широко используется при исследовании явлений природы. Этот закон представляет научную основу для разнообразных расчётов во всех областях техники.

Услуги по физике:

1. Заказать физику
2. Заказать контрольную работу по физике
3. Помощь по физике

Лекции по физике:

1. Физические величины и их измерение
2. Основные законы механики
3. Прямолинейное равномерное движение
4. Прямолинейное равнопеременное движение
5. Сила
6. Масса
7. Взаимодействия тел
8. Механическая энергия
9. Импульс
10. Вращение твердого тела
11. Криволинейное движение тел
12. Колебания
13. Колебания и волны
14. Механические колебания и волны
15. Бегущая волна
16. Стоячие волны
17. Акустика
18. Звук
19. Звук и ультразвук
20. Движение жидкости и газа
21. Молекулярно-кинетическая теория
22. Молекулярно-кинетическая теория строения вещества
23. Молекулярно – кинетическая теория газообразного состояния вещества
24. Температура и теплота
25. Термодинамические процессы
26. Идеальный газ
27. Уравнение состояния идеального газа
28. Изменение внутренней энергии
29. Переход вещества из жидкого состояния в газообразное и обратно
30. Кипение, свойства паров, критическое состояние вещества
31. Водяной пар в атмосфере
32. Плавление и кристаллизация
33. Тепловое расширение тел
34. Энтропия
35. Процессы перехода из одного агрегатного состояния в другое
36. Тепловое расширение твердых и жидких тел
37. Свойства газов
38. Свойства жидкостей
39. Свойства твёрдых тел
40. Изменение агрегатного состояния вещества
41. Тепловые двигатели
42. Электрическое поле
43. Постоянный ток
44. Переменный ток
45. Магнитное поле
46. Электромагнитное поле
47. Электромагнитное излучение
48. Электрический заряд (Закон Кулона)
49. Электрический ток в металлах
50. Электрический ток в электролитах
51. Электрический ток в газах и в вакууме
52. Электрический ток в полупроводниках
53. Электромагнитная индукция
54. Работа, мощность и тепловое действие электрического тока
55. Термоэлектрические явления
56. Распространение электромагнитных волн
57. Интерференционные явления
58. Рассеяние
59. Дифракция рентгеновских лучей на кристалле
60. Двойное лучепреломление
61. Магнитное поле и электромагнитная индукция
62. Электромагнитные колебания и волны
63. Природа света
64. Распространение света
65. Отражение и преломление света
66. Оптические приборы и зрение
67. Волновые свойства света
68. Действия света
69. Линзы и получение изображений с помощью линз
70. Оптические приборы и глаз
71. Фотометрия
72. Излучение и спектры
73. Квантовые свойства излучения
74. Специальная теория относительности в физике
75. Теория относительности
76. Квантовая теория и природа поля
77. Строение и свойства вещества
78. Физика атомного ядра
79. Строение атома

Вы находитесь на странице вопроса Как найти кол – во теплоты, если известна полезная работа и КПД? из категории Физика.
Уровень сложности вопроса рассчитан на учащихся 5 – 9 классов. На странице
можно узнать правильный ответ, сверить его со своим вариантом и обсудить
возможные версии с другими пользователями сайта посредством обратной связи.
Если ответ вызывает сомнения или покажется вам неполным, для проверки
найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте
новый вопрос, используя ключевые слова: введите вопрос в поисковую строку,
нажав кнопку в верхней части страницы.

На этой странице вы узнаете

• В чем прелесть фазовых переходов?
• Что лучше выбрать: Mercedes или BMW?

Люди научились летать в космос, покорять недра Земли и погружаться в глубины океана. Эти и другие достижения возможны благодаря способности извлекать максимум пользы из имеющихся ресурсов,а именно получать тепловую энергию различными доступными способами. Сегодня мы разберем задачи, которые заставят тепловые процессы играть на нашей стороне. 

Тепловые машины и их КПД

Рекомендация: перед тем как приступить к выполнению задач неплохо было бы повторить тему «Уравнение состояния идеального газа» . Но ключевую теорию, на которой основано решение задач, сейчас разберем вместе.

Мы не почувствуем, как испарится капелька у нас на руке, потому что это не требует много тепла от нашего тела. Но мы можем наблюдать, как горят дрова в мангале, когда мы жарим шашлык, потому что выделяется огромное количество теплоты. А зачем мы вообще рассматриваем эти фазовые переходы? Все дело в том, что именно фазовые переходы являются ключевым звеном во всех процессах, где нас просят посчитать КПД, от них нашему рабочему телу и подводится теплота нагревателя.

Человечество придумало такие устройства, которые могут переработать тепловую энергию в механическую.

Тепловые двигатели, или тепловые машины, — устройства, способные преобразовывать внутреннюю энергию в механическую. 

Их устройство довольно просто: они на входе получают какую-то энергию (в основном — энергию сгорания топлива), а затем часть этой теплоты расходуется на совершение работы механизмом. Например, в автомобилях часть энергии от сгоревшего бензина идет на движение. Схематично можно изобразить так:

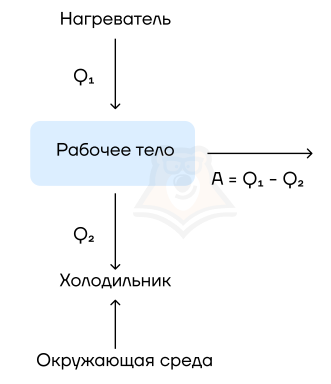
Рабочее тело — то, что совершает работу — принимает от нагревателя количество теплоты Q₁, из которой A уходит на работу механизма. Остаток теплоты Q₂ рабочее тело отдает холодильнику, по сути — это потеря энергии.

Физика не была бы такой загадочной, если б все в ней было идеально. Как и в любом процессе или преобразовании, здесь возможны потери, зачастую очень большие. Поэтому «индикатором качества» машины является КПД, с которым мы уже сталкивались в механике:

Коэффициент полезного действия (КПД) тепловой машины — это отношение полезной работы двигателя к энергии, полученной от нагревателя.

Мы должны понимать, что КПД на практике никогда не получится больше 1, поскольку всегда будут тепловые потери. 

Полезную работу можно расписать как Q₁ — Q₂ (по закону сохранения энергии). Тогда формула примет вид:

(eta = frac{Q_1 — Q_2}{Q_1} = 1 — frac{Q_2}{Q_1})

Цикл Карно

Мы знаем, что потери — это плохо, поэтому должны предотвращать их. Как это сделать? Нам ничего делать не нужно, за нас уже все сделал Сади Карно, французский физик, разработавший цикл, в котором машины достигают наивысшего КПД. Этот цикл носит его имя и состоит из двух изотерм и двух адиабат. Рассмотрим, как этот цикл выглядит в координатах p(V).

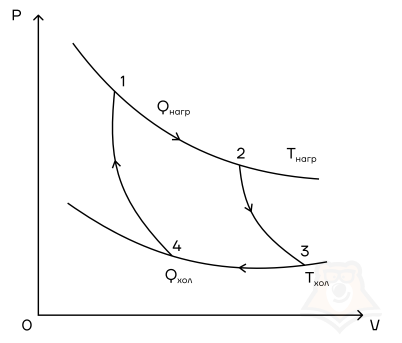
• Температура верхней изотермы 1-2 — температура нагревателя (так как теплота в данном процессе подводится).
• Температура нижней изотермы 3-4 — температура холодильника (так как теплота в данном процессе отводится).
• 2-3 и 4-1 — это адиабатические расширение и сжатие соответственно, в них газ не обменивается теплом с окружающей средой.

Цикл Карно — цикл идеальной тепловой машины, которая достигает наивысшего КПД. 

Формула, по которой можно рассчитать ее КПД выражается через температуры:

Приступим к задачам

Задачи на данную тему достаточно часто встречаются в задании 27 из КИМа ЕГЭ. Давайте разберем некоторые примеры.

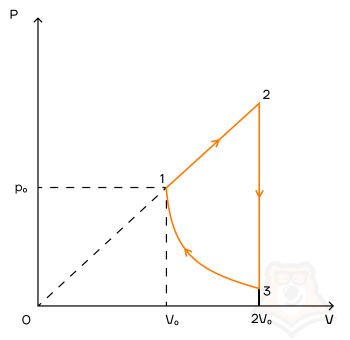
Задание 1. Одноатомный газ совершает циклический процесс, как показано на рисунке. На участке 1–2 газ совершает работу A₁₂ = 1520 Дж. Участок 3–1 представляет собой адиабатный процесс. Количество теплоты, отданное газом за цикл холодильнику, равно |Q_хол| = 4780 Дж. Найдите работу газа |A₁₃| на адиабате, если количество вещества постоянно.

Решение:

Шаг 1. Первое, с чего лучше начинать задачи по термодинамике — исследование процессов. 

Посмотрим на участок 1-2 графика: продолжение прямой проходит через начало координат, поэтому график функционально можно записать, как p = aV, где a — какое-то число, константа. Графиком является не изотерма, поскольку график изотермы в координатах p-V — гипербола. Из уравнения Менделеева-Клапейрона следует: (frac{pV}{T} = const). Отсюда можно сделать вывод, что возрастает температура, так как растут давление и объем.  Температура и объем растут, значит, увеличивается и внутренняя энергия и объем соответственно.

Участок 2-3: процесс изохорный, поскольку объем постоянен, следовательно, работа газом не совершается. Рассмотрим закон Шарля: (frac{p}{T} = const). Давление в этом процессе растет, тогда растет и температура, поскольку дробь не должна менять свое значение. Делаем вывод, что внутренняя энергия тоже увеличивается.

Участок 3-1: адиабата по условию, то есть количество теплоты в этом переходе равна нулю из определения адиабатного процесса. Работа газа отрицательна, так как газ уменьшает объем. 

Оформим все данные в таблицу. 

Определим знаки Q, используя первый закон термодинамики: Q = ΔU + A.

Из этих данных сразу видно, что количество теплоты, отданное холодильнику — это количество теплоты в процессе 2-3.

Шаг 2. Первый закон термодинамики для процесса 1-2 запишется в виде: 

Q₁₂ = ΔU₁₂ + A₁₂. 

Работа A12 — площадь фигуры под графиком процесса, то есть площадь трапеции: 

(A_{12} = frac{p_0 + 2p_0}{2} * V0 =frac{3p_0V_0}{2}). 

Запишем изменение внутренней энергии для этого процесса через давление и объем. Мы выводили эту формулу в статье «Первое начало термодинамики»:

(Delta U_{12} = frac{3}{2}(2p_0 * 2V_0 — p_0V_0) = frac{9p_0V_0}{2}). 

Заметим, что это в 3 раза больше работы газа на этом участке: 

(Delta U_{12} = 3A_{12} rightarrow Q_{12} = 4A_{12}).

Шаг 3. Работа цикла — площадь фигуры, которую замыкает график, тогда . A = A₁₂ — |A₃₁|. С другой стороны, работа цикла вычисляется как разность между энергиями нагревателя и холодильника: A = Q₁₂ — |Q₃₁|.

 Сравним эти формулы:

Q₁₂ -|Q₃₁| = A₁₂ — |A₃₁|,

подставим выражения из предыдущего пункта:

4A₁₂ — |Q₃₁| = A₁₂ — |A₃₁| (rightarrow) |A₃₁| = -3A₁₂ + |Q₃₁| = -31520 + 4780 = 220 Дж.

Ответ: 220 Дж

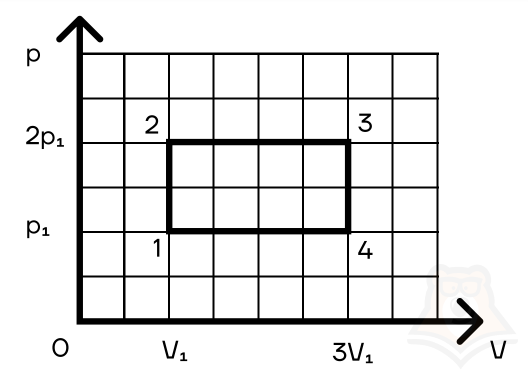
Задание 2. Найти КПД цикла для идеального одноатомного газа.

Решение:

Шаг 1. КПД цикла определим по формуле: (eta = frac{A}{Q}), где Q — количество теплоты от нагревателя, а А — работа газа за цикл. Найдем А как площадь замкнутой фигуры: A = (2p₁ — p₁)(3V₁ — V₁) = 2p₁V₁.

Шаг 2. Найдем процесс, который соответствует получению тепла от нагревателя. Воспользуемся теми же приемами, что и в прошлой задаче:

Посмотрим на участок 1-2 графика: давление растет, объем не меняется. По закону Шарля (frac{p}{T} = const) температура тоже растет. Работа газа равна 0 при изохорном процессе, а изменение внутренней энергии положительное.

2-3: давление не меняется, растет объем, а значит, работа газа положительна. По закону Гей-Люссака (frac{V}{T} = const) температура тоже растет, растет и внутренняя энергия.

3-4: давление уменьшается, следовательно, и температура уменьшается. При этом процесс изохорный и работа газа равна 0.

4-1: давление не меняется, объем и температура уменьшаются — работа газа отрицательна и внутренняя энергия уменьшается.

Оформим данные в таблицу: 

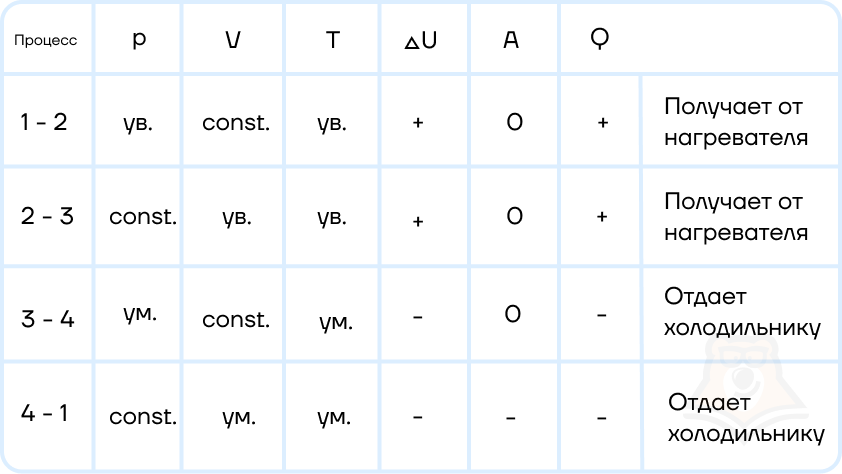
Отметим, что  необходимое Q = Q₁₂ + Q₂₃.

Шаг 3. Запишем первый закон термодинамики для процессов 1-2 и 2-3:

(Q_{12} = U_{12} + A_{12} = Delta U_{12} = frac{3}{2}(2p_1V_1 -p_1V_1) = frac{3}{2}p_1V_1).
(Q_{23} = Delta U_{23} + A_{23}), работу газа найдем как площадь под графиком: A₂₃ = 2p₁(3V₁ — V₁) = 4p₁V₁.
(Delta U_{12} = frac{3}{2}(2p_1 * 3V_1 — 2p_1V_1) = 6p_1V_1).
(Q_{23} = Delta U_{23} + A_{23} = 10p_1V_1).

Шаг 4. Мы готовы считать КПД: (eta = frac{A}{Q} = frac{A}{Q_{12} + Q_{23}} = frac{2p_1V_1}{frac{3}{2}p_1V_1 + 10p_1V_1} = frac{4}{23} approx 0,17).

Ответ: 17%

Теперь вас не должно настораживать наличие графиков в условиях задач на расчет КПД тепловых машин. Продолжить обучение решению задач экзамена вы можете в статьях «Применение законов Ньютона» и «Движение точки по окружности».

Фактчек

• Тепловые двигатели — устройства, способные преобразовывать внутреннюю энергию в механическую. 
• Тепловая машина принимает тепло от нагревателя, отдает холодильнику, а рабочим телом совершает работу.
• Коэффициент полезного действия (КПД) тепловой машины — это отношение полезной работы двигателя к энергии, полученной от нагревателя.
  (eta = frac{A}{Q_1} = frac{Q_1 — Q_2}{Q_1} = 1 — frac{Q_2}{Q_1})  
• Цикл Карно — цикл с максимально возможным КПД: (eta = frac{T_1 — T_2}{T_1} = 1 — frac{T_2}{T_1})
• Не забываем, что работа считается, как площадь фигуры под графиком.

Проверь себя

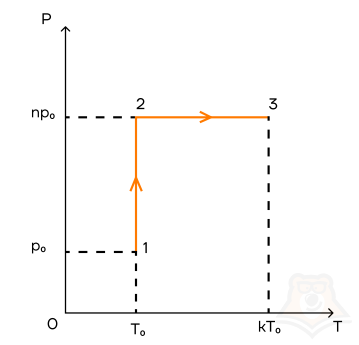
Задание 1. 
1 моль идеального газа переходит из состояния 1 в состояние 2, а потом — в состояние 3 так, как это показано графике. Начальная температура газа равна T₀ = 350 К. Определите работу газа при переходе из состояния 2 в состояние 3, если k = 3, а n = 2.

1. 5672 Дж
2. 4731 Дж
3. 5817 Дж
4. 6393 Дж

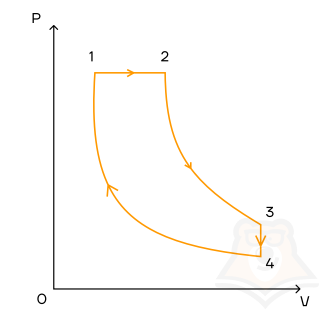
Задание 2. 
1 моль идеального одноатомного газа совершает цикл, который изображен на pV-диаграмме и состоит из двух адиабат, изохоры, изобары. Модуль отношения изменения температуры газа при изобарном процессе ΔT₁₂ к изменению его температуры ΔT₃₄ при изохорном процессе равен 1,5. Определите КПД цикла.

1. 0,6
2. 0,5
3. 0,8
4. 1

Задание 3.
В топке паровой машины сгорело 50 кг каменного угля, удельная теплота сгорания которого равна 30 МДж/кг. При этом машиной была совершена полезная механическая работа 135 МДж. Чему равен КПД этой тепловой машины? Ответ дайте в процентах.

1. 6%
2. 100%
3. 22%
4. 9%

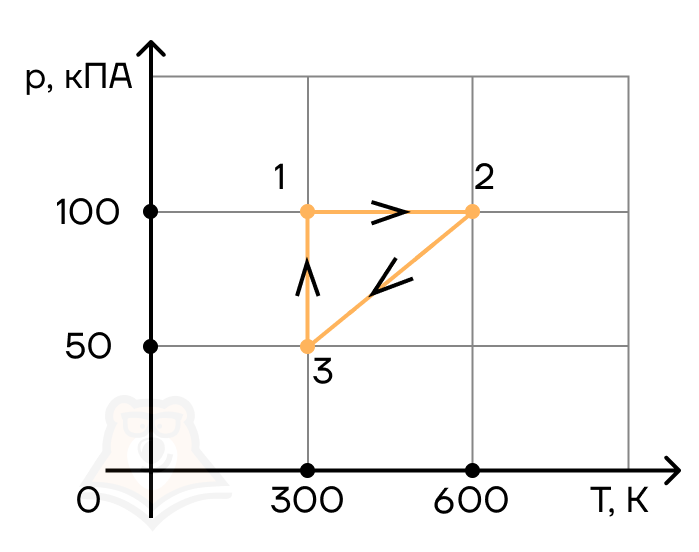
Задание 4.
С двумя молями одноатомного идеального газа совершают циклический процесс 1–2–3–1 (см. рис.). Чему равна работа, совершаемая газом на участке 1–2 в этом циклическом процессе?

1. 4444 Дж
2. 2891 Дж
3. 4986 Дж
4. 9355 Дж

Ответы:1 — 3; 2 — 1; 3 — 4; 4 — 3.