Как найти теплоемкость для двухатомного газа

Как найти теплоемкость для двухатомного газа

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 ноября 2020 года; проверки требует 1 правка.

Теплоёмкость определяется суммой поступательных, вращательных и удвоенным числом колебательных степеней свободы.

Теплоёмкость идеального газа — отношение количества теплоты, сообщённой газу delta Q, к изменению температуры dT, которое при этом произошло {displaystyle C={frac {delta Q}{dT}}} [1].

Удельная и молярная теплоёмкость[править | править код]

Молярная теплоёмкость — теплоёмкость 1 моля вещества [2]:

{displaystyle C_{M}={frac {C}{nu }}={frac {1}{nu }}{frac {delta Q}{Delta T}},}

где {displaystyle nu =m/M,} m — масса, M — молярная масса вещества.

Теплоёмкость единичной массы вещества называется удельной теплоёмкостью и, в системе СИ, измеряется в Дж/(кг·К)[1].

Формула расчёта удельной теплоёмкости[1][2]:

{displaystyle c={frac {C_{M}}{M}}={frac {delta Q}{mdT}},}

где c — удельная теплоёмкость, m — масса нагреваемого (охлаждающегося) вещества.

Теплоёмкость идеального газа в изопроцессах[править | править код]

Адиабатический[править | править код]

В адиабатическом процессе теплообмена с окружающей средой не происходит, то есть {displaystyle dQ=0}. Однако, объём, давление и температура меняются, то есть {displaystyle dTneq 0}[3].

Следовательно, теплоёмкость идеального газа в адиабатическом процессе равна нулю: C = {0 over dT} = 0.

Изотермический[править | править код]

В изотермическом процессе постоянна температура, то есть {displaystyle dT=0}. При изменении объёма газу передаётся (или отбирается) некоторое количество тепла[3]. Следовательно, теплоёмкость идеального газа равна плюс-минус бесконечности: {displaystyle Cto pm infty }

Изохорный[править | править код]

В изохорном процессе постоянен объём, то есть {displaystyle delta V=0} и, следовательно газ не совершает работы. Первое Начало Термодинамики для изохорного процесса имеет вид[1]:

{displaystyle dU=delta Q=nu C_{V}dT.qquad (1)}

А для идеального газа

{displaystyle dU={frac {i}{2}}nu RDelta T.}

Таким образом,

C_V=frac i2 R,

где i — число степеней свободы частиц газа.

Другая формула:

{displaystyle C_{V}={frac {R}{gamma -1}},}

где gamma  — показатель адиабаты, R — газовая постоянная газа.

Изобарный[править | править код]

Молярная теплоёмкость при постоянном давлении обозначается как C_p. В идеальном газе она связана с теплоёмкостью при постоянном объёме соотношением Майера C_p = C_v + R[1].
Уравнение Майера вытекает из первого начала термодинамики[4]:

{displaystyle delta Q=mathrm {d} U+delta A,qquad (2)}.

В рассматриваемом случае, согласно определению теплоёмкости:

{displaystyle delta Q=C_{p}mathrm {d} T,}

Учитываем, что работа газа равна [4]:

{displaystyle delta A=mathrm {d} (pV)=nRmathrm {d} Tqquad =pmathrm {d} Vqquad +Vmathrm {d} pqquad =pmathrm {d} Vqquad ,(Vmathrm {d} pqquad =0)(3)}

Согласно уравнению Менделеева-Клапейрона для одного моля газа[1]:

{displaystyle pmathrm {d} V=Rmathrm {d} T.qquad (4)}

Подставляя уравнение (4) в (3) получаем:

{displaystyle delta A=Rmathrm {d} Tqquad (5)}

Так как энергия одной молекулы равна {displaystyle <e>={frac {i}{2}}kT} (6)[Комм 1][5], то и внутренняя энергия в целом и при изобарном процессе будет определяться по соотношению (1). Следовательно, подставляя уравнения (1) и (5) в (2) получаем соотношение Майера.

Молекулярно-кинетическая теория позволяет вычислить значения молярной теплоёмкости для классического идеального газа газов через значение универсальной газовой постоянной исходя из уравнения (6) и предположения, что молекулы газа не взаимодействуют между собой[5]:

Теплоёмкости можно также определить исходя из уравнения Майера, если известен показатель адиабаты, который можно измерить экспериментально (например, с помощью измерения скорости звука в газе или используя метод Клемана — Дезорма).

Теплоёмкость реального газа может значительно отклонятся от теплоёмкости идеального газа. Так при температуре в 25 °С и атмосферном давлении атомарный водород имеет теплоёмкость 2,50R , а атомарный кислород — 2,63R. Также теплоёмкость реального газа зависит от температуры[5].

См. также[править | править код]

  • Идеальный газ
  • Первое начало термодинамики
  • Теплоёмкость

Комментарии[править | править код]

  1. ↑ i — сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы
  2. ↑ 1 2 При жёсткой связи между атомами, то есть колебательные степени свободы исключены из рассмотрения. Примером трёхатомной линейной молекулы служит цианистый водород HCN.

Примечания[править | править код]

  1. ↑ 1 2 3 4 5 6 Савельев, 2001, с. 26—30.
  2. ↑ 1 2 Базаров И. П., Термодинамика, 2010, с. 41.
  3. ↑ 1 2 Савельев, 2001, с. 30—31.
  4. ↑ 1 2 Савельев, 2001, с. 18-20.
  5. ↑ 1 2 3 Савельев, 2001, с. 61-63.

Литература[править | править код]

  • Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.— Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
  • Белоконь Н. И. Основные принципы термодинамики. — М.: Недра, 1968. — 110 с.
  • Савельев И. В. Курс общей физики:Молекулярная физика и термодинамика. — М.: Астрель, 2001. — Т. 3. — 208 с. — 7000 экз. — ISBN 5-17-004585-9.
Источник

Теплоемкостью
системы
тел
(тела)
называется физическая величина, равная
отношению количества теплоты dQ,
которое нужно затратить для нагревания
системы тел (тела), к изменению температуры
dТ,
характеризующей
это нагревание:

.
[C]=Дж/К.

Удельной
теплоемкостью
вещества с
называется скалярная величина, равная
отношению теплоемкости однородного
тела С
к его массе:


.
[c]=
Дж/(кг.К)

Молярной
теплоемкостью
называется физическая величина, численно
равная отношению теплоемкости системы
С
к количеству вещества n,
содержащегося в ней:

.
[Cm]=Дж/(моль.К)

Различают
молярные теплоемкости при постоянном
объеме и постоянном давлении:

;


.

Уравнение,
связывающее молярные теплоемкости при
постоянном давлении и постоянном объеме
имеет вид (уравнение Майера):

Cp
– CV=
R.

Подробно
это уравнение, его вывод мы обсудим в
следующем параграфе.

Учитывая
распределение энергии по степеням
свободы и уравнение Майера, получим
распределение теплоемкостей Cp
и CV
по степеням свободы:


,


.


.

При
рассмотрении термодинамических процессов
удобно пользоваться соотношением:


.

Величина g
определяется числом и характером
степеней свободы молекулы.

Молекула

Характер
связи между атомами

Число

поступ

степеней

вращат.

свободы

i

CV

Cp

g

Одно-атомная

–

3

–

3

1,67

Двух-атомная

жесткая

3

2

5

1,40

Трех-атомная

жесткая

3

3

6

3R

4R

1,33


Обратимся
к двухатомной молекуле. Если связь между
атомами жесткая, то число степеней
свободы равна 5 (три поступательных и
две вращательных). Теперь предположим,
что связь упругая, то есть атомы могут
совершать колебания друг относительно
друга. Тогда требуется еще одна координата
для определения конфигурации молекулы,
это расстояние между атомами. Следовательно,
у двухатомной молекулы в общем случае
шесть степеней свободы. Во многих случаях
колебательное движение атомов не
возбуждается. Но если колебания
совершаются и их амплитуды малы (по
сравнению с расстоянием между атомами),
то такие колебания можно считать
гармоническими. Атомы в этом случае
являются гармоническими осцилляторами.
Но осциллятор обладает как кинетической,
так и потенциальной энергией. Для
гармонического
осциллятора, как известно из механики,
средние значения кинетической и
потенциальной энергии равны между
собой. Тогда по закону равнораспределения
на каждую колебательную степень свободы
приходится kT/2
в виде кинетической энергии и kT/2
в виде потенциальной энергии. Энергия,
приходящаяся на одну колебательную
степень свободы равна не kT/2,
а 2.
kT/2=
kT.
Поэтому при подсчете степеней свободы
надо число колебательных степеней
свободы удвоить. Для двухатомного газа


,

причем
СV
не зависит от температуры. Что же
наблюдалось на опыте?

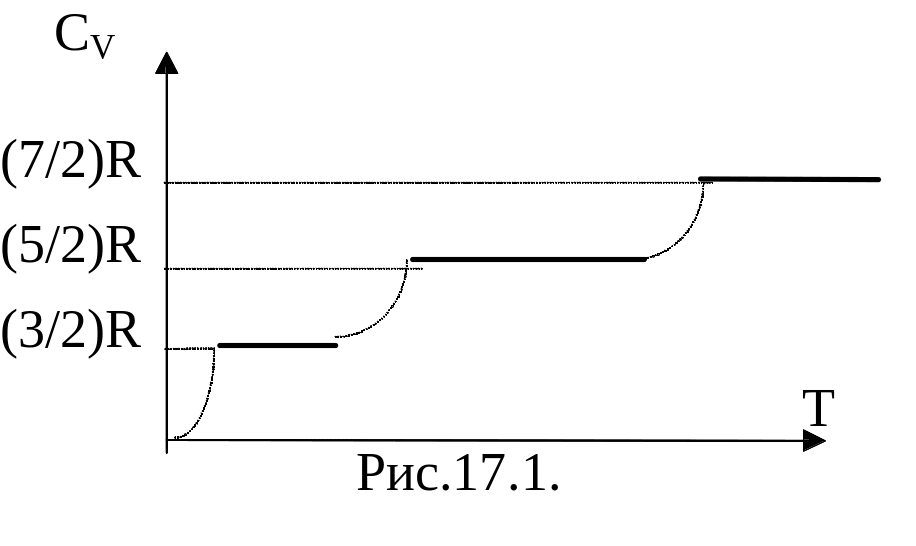
Опыт
показал (рис.17.1), что в определенном
интервале температур эта теплоемкость
составляет всего (5/2)R, при очень низких
температурах она уменьшалась до (3/2)R, а
при высоких становится больше 3R. Это
означает, что при низких температурах
молекулы участвуют только в поступательном
движении. По мере повышения Т молекулы
начинают совершать и вращательные
движения. И лишь при высоких температурах
она совершает все три вида движения
(добавляется колебательное).

Классическая
теория такое поведение объяснить не
может. Объяснение было получено в рамках
квантовой теории. В зависимости
теплоемкости от температуры проявляются
квантовомеханические свойства молекул
– энергия вращательного и колебательного
движения у них меняется скачками на
величину h,
где –
частота вращения или колебания, h
– постоянная Планка. Так как получить
такой прирост энергии молекула может
лишь при соударении с другой, движущейся
с большей поступательной скоростью, то
при низких температурах колебания и
вращения не происходят (соответствующие
степени свободы «вымораживаются»). При
более высокой температуре средняя
энергия, приходящаяся на каждую из этих
степеней, зависит от соотношения между
hn
и kT.

Итак, при
низких температурах происходит только
поступательное движение, нет молекул,
которые обладали бы вращательными, тем
более колебательными движениями. При
средних температурах все молекулы
участвуют как в поступательном, так и
во вращательном движении, но не участвуют
в колебательном. При высоких температурах
все молекулы вовлечены и в колебательное
движение. При охлаждении теплоемкость
понижается с (7/2)R до (5/2)R. Это объясняется
тем, что колебательная степень свободы
«вымораживается». При последующем
понижении вымораживаются вращательные
степени свободы.

Выходит, что
классическая теория о равнораспределении
энергии по степеням свободы при низких
температурах практически не применима.
Оно верно только для высоких температур.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

В случае, если результатом теплообмена становится передача телу некоего количества теплоты Q, то его температура и внутренняя энергия претерпевают изменения.

Определение 1

Необходимое для нагревания 1 кг вещества на 1 К количество теплоты Q носит название удельной теплоемкости вещества c, а ее формула выглядит следующим образом: 

c=Qm∆T.

В большом количестве ситуаций удобной для использования является молярная теплоемкость C: 

C=M·c, где M представляет собой молярную массу вещества.

Теплоемкость, полученная таким способом, не является однозначной характеристикой вещества. Исходя из первого закона термодинамики, можно сказать, что изменение внутренней энергии тела зависимо не только от количества полученной теплоты, но и от величины совершенной телом работы. В разных условиях осуществления процесса теплопередачи тело может совершать различную работу. Таким образом, переданное телу одинаковое количество теплоты способно провоцировать изменения его внутренней энергии и, соответственно, температуры.

Подобной неоднозначностью при определении теплоемкости характеризуются только газообразные вещества. Объем в процессе нагрева практически не меняет своей величины, что сводит работу расширения к нулю. По этой причине вся полученная телом теплота уходит на изменение его внутренней энергии. Газ в процессе теплопередачи может значительно менять свой объем и совершать работу, чем отличается от твердых тел и жидкостей. Таким образом, теплоемкость газообразного вещества имеет зависимость от характера термодинамического процесса.

Изопроцессы в газах

Определение 2

Чаще всего рассматриваются два значения теплоемкости газов: 

  • CV являющаяся молярной теплоемкостью в изохорном процессе (V=const);
  • Cp представляющая собой молярную теплоемкость в изобарном процессе (p=const).

При условии постоянного объема газ не совершает работы: A=0. Исходя из первого закона термодинамики для 1 моля газа, можно сказать, что справедливым является следующее выражение: 

QV=CV∆T=∆U.

Изменение величины ΔU внутренней энергии газа прямо пропорционально изменению значения ΔT его температуры.

В условиях процесса при постоянном давлении первый закон термодинамики дает такую формулу: 

Qp=∆U+p(V2-V1)=CV∆T+pV.

В котором ΔV является изменением объема 1 моля идеального газа при изменении его температуры на ΔT. Таким образом, можно заявить, что: 

Cp=Qp∆T=CV+p∆V∆T.

Из уравнения состояния идеального газа, записанного для 1 моля, может выражаться отношение ΔVΔT: 

pV=R.

В котором R представляет собой универсальную газовую постоянную. При условии постоянства давления p=const, можно записать следующее:p∆V=R∆T или ∆V∆T=Rp.

Определение 3

Из этого следует, что выражающее связь между молярными теплоемкостями Cp и CV соотношение имеет вид (формула Майера): 

Cp=CV+R.

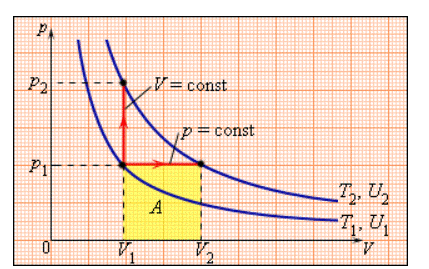
В процессе с неизменным давлением молярная теплоемкость Cp газа всегда превышает молярную теплоемкость CV в процессе с не подверженным изменениям объемом, что демонстрируется на рисунке 3.10.1.

Изопроцессы в газах

Рисунок 3.10.1. Два возможных процесса нагревания газа на ΔT=T2 –T1. При p=const газ совершает работу A=p1(V2 – V1). Поэтому Cp>CV.

Определение 4

Отношение теплоемкостей в процессах с постоянным давлением и постоянным объемом занимает важное место в термодинамике и обозначается в виде греческой буквы γ. 

γ=CpCV.

Данное отношение включено в формулу для адиабатического процесса.

Между двумя изотермами, обладающими температурами T1 и T2 на диаграмме (p, V) реальны различные варианты перехода. Так как для всех подобных переходов изменение величины температуры ΔT=T2 –T1 является одним и тем же, выходит, что изменение значения
ΔU внутренней энергии тоже одинаково. С другой стороны, совершенные при этом работы A и количества теплоты Q, полученные в результате теплообмена, выйдут разными для различных путей перехода. Из этого следует, что газа имеет относительно приближенное к бесконечности число теплоемкостей. Cp и CV представляют собой частные, однако, очень важные для теории газов, значения теплоемкостей.

Изопроцессы в газах

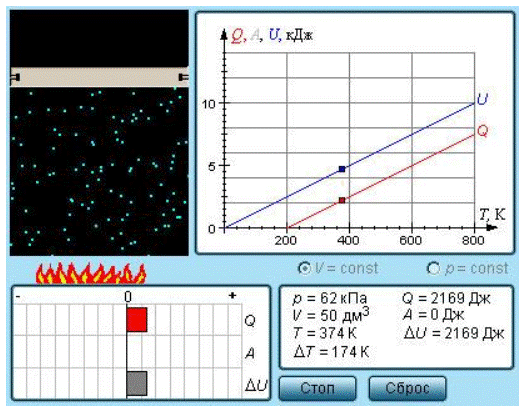
Рисунок 3.10.2. Модель теплоемкости идеального газа.

Определение 5

Термодинамические процессы, в которых теплоемкость газа не подвергается изменениям, носят название политропических.

Каждый изопроцесс являются политропическим. В изотермическом процессе ΔT=0, из-за чего CT=∞. В адиабатическом процессе ΔQ=0, выходит, что Cад=0.

Замечание 1

Стоит обратить внимание на то, что «теплоемкость» и «количество теплоты» являются крайне неудачными терминами, доставшимися современной науке в качестве наследства теории теплорода, которая господствовала в XVIII веке.

Данная теория представляла теплоту в виде содержащегося в телах особого невесомого вещества. Считалось, что оно не подвержено уничтожению и не может быть созданным. Явление нагрева объясняли повышением, а охлаждение – понижением содержания в телах теплорода. Однако теория теплорода оказалась несостоятельной, так как не смогла дать ответа на вопрос, почему одинаковое изменение внутренней энергии тела возможно получить, приводя ему разное количество теплоты в зависимости от совершаемой им работы. По этой причине утверждение, что в данном теле содержится некоторый запас теплорода лишено смысла.

Молекулярно-кинетическая теория

В молекулярно-кинетической теории устанавливается следующее соотношение между средней кинетической энергией E→ поступательного движения молекул и абсолютной температурой T: 

E→=32kT.

Внутренняя энергия 1 моля идеального газа эквивалентна произведению E→ на число АвогадроNА: 

U=32kNAT=32RT.

При условии изменения температуры на величину ΔT внутренняя энергия изменяется на величину:

U=32R∆T=CV∆T.

Коэффициент пропорциональности между ΔU и ΔT эквивалентен теплоемкости CV в условиях постоянного давления: 

CV=32R=12,47 ДЖ/моль·К.

Данное выражение подтверждается экспериментами с газами, которые состоят из одноатомных молекул вроде гелия, неона или аргона. При этом для двухатомных (водород, азот) и многоатомных (углекислый газ) газов такое соотношение не согласуется с полученными в результате опытов данными. Причина этого расхождения заключается в том, что для двух- и многоатомных молекул средняя кинетическая энергия должна включать энергию как поступательного, так и вращательного их движения.

Молекулярно-кинетическая теория

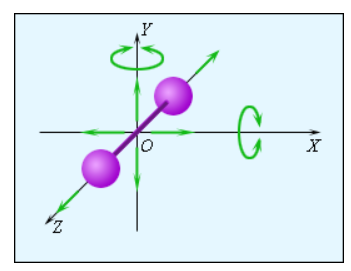
Рисунок 3.10.3. Модель двухатомной молекулы. Точка O совпадает с центром масс молекулы.

Рисунок 3.10.3 иллюстрирует модель двухатомной молекулы. Молекула имеет возможность производить пять независимых типов движений: три поступательных движения вдоль осей X, Y, Z и два вращения относительно осей X и Y.

Опытным путем выяснено, что вращение относительно оси Z, на которой лежат центры обоих атомов, может быть возбуждено только при очень высоких значениях температуры. В условиях обычных температур вращение вокруг оси Z не происходит.

Определение 6

Каждое независимое движение в молекуле носит название степени свободы.

Выходит, что одноатомная молекула обладает 3 поступательными степенями свободы, «жесткая» двухатомная молекула 5 степенями, то есть 3 поступательными и 2 вращательными, а многоатомная молекула 6 степенями свободы, из которых 3 приходятся на поступательные и 3 на вращательные.

Теорема 1

В классической статистической физике доказывается теорема о равномерном распределении энергии по степеням свободы:

Если система молекул находится в тепловом равновесии при температуре T, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой степени свободы молекулы она равна 12kT.

Из данной теоремы следует, что для молярных теплоемкостей газа Cp и CV и их отношения
γ справедлива запись в следующем виде: 

CV=i2R, Cp=Cv+R=i+22R, γ=CpCV=i+2i,

где i представляет собой количество степеней свободы газа.

Для газа, состоящего из одноатомных молекул (i=3)

CV=32R, Cp=Cv+R=52R, γ=CpCV=53=1,66.

Для газа, состоящего из двухатомных молекул (i=5)

CV=52R, Cp=Cv+R=72R, γ=CpCV=75=1,4.

Для газа, состоящего из многоатомных молекул (i=6)

CV=3R, Cp=Cv+R=4R, γ=CpCV=43=1,33.

В обычных условиях экспериментально измеренные теплоемкости многих газов неплохо согласуются с приведенными выражениями, но в целом классическая теория теплоемкости газов вполне удовлетворительной не является. Существует колоссальное число примеров со значительной разницей между результатами эксперимента и теорией. Данный факт объясняется тем, что классическая теория не может полностью учесть, связанную с внутренними движениями в молекуле энергию.

Теорема о равномерном распределении энергии по степеням свободы может быть применена и по отношению к тепловому движению частиц в твердом теле. Входящие в состав кристаллической решетки атомы колеблются около положений равновесия. Энергия данных колебаний представляет собой внутреннюю энергию твердого тела. Каждый конкретный атом может колебаться в кристаллической решетке в трех взаимно перпендикулярных направлениях. Выходит, что каждый атом имеет 3 колебательные степени свободы. При условии гармонических колебаний средняя кинетическая энергия эквивалентна средней потенциальной энергии. По этой причине в соответствии с теоремой о равномерном распределении на каждую колебательную степень свободы приходится средняя энергия kT, а на один атом – 3kT. 

Определение 7

Внутренняя энергия 1 моля твердого вещества равна следующему выражению:

U=3RNAkt=3Rt.

Следовательно, молярная теплоемкость вещества в твердом состоянии равняется: 

С=3R=25,12 Дж/моль·К.

Данное выражение носит название закона Дюлонга–Пти. Для твердых тел почти нет различия между Cp и CV по причине пренебрежительно малой работы при сжатии или расширении.

Опыт показывает, что молярная теплоемкость у многих твердых тел (химических элементов) при обычных температурах на самом деле близка к 3R. При этом, в условиях низких температур заметны довольно сильные расхождения между теорией и экспериментом. Таким образом, гипотеза о равномерном распределении энергии по степеням свободы может считаться лишь приближением. Заметная в опыте зависимость теплоемкости от температуры объясняется только при условии использования квантовых представлений.

Источник

Макеты страниц

Измерения, проведенные на неодноатомных газах, показали, что их молярные теплоемкости превосходят теплоемкости одноатомных газов. Это видно из табл. 6, в которой для ряда многоатомных газов приведены значения тех же величин, что и в предыдущей таблице.

Таблица 6 (см. скан) Теплоемкость многоатомных газов

Из таблицы видно, что газы, молекулы которых содержат два и более атомов, отличаются от одноатомных газов значениями величин (а значит, и Значение же выражения у всех газов одно и то же. Это значит, что независимо от числа атомов в молекуле разность молярных теплоемкостей неизменно равна т. е. моль любого идеального газа, расширяясь при повышении его температуры на 1 К в условиях постоянного давления, совершает одну и ту же работу, равную

Из таблицы видно, что перечисленные в ней газы отчетливо разделяются на две группы: газы двухатомные, у которых близко к к 1,4, и газы, молекулы которых содержат три и более атомов. У этих газов значения близки к 3, а — к 1,3.

Это значит, что для газов первой группы (двухатомных) значения молярных теплоемкостей близки друг к другу и равны

Следовательно,

Для газов, молекулы которых состоят из трех или более атомов, теплоемкости, как это видно из табл. 6, имеют следующие численные значения:

отсюда

Приведенные экспериментальные данные о теплоемкости относятся к газам при сравнительно небольших давлениях (порядка атмосферы и ниже) и к температурам, близким к комнатным. В этих условиях газы мало отличаются от идеальных.

Чем же объяснить такие закономерности, относящиеся к величинам теплоемкости двух- и многоатомных газов? Ответ на этот вопрос дает так называемый закон равнораспределения.

Закон равнораспределения и теплоемкость многоатомных газов. В предыдущем параграфе, при рассмотрении теплоемкости одноатомного газа, было обращено внимание на то, что средняя кинетическая энергия молекулы, приходящаяся на одну степень свободы, равна Естественно было предположить, что если бы молекула газа обладала еще какими-нибудь степенями свободы, то и на каждую из них пришлась бы кинетическая энергия

Действительно, в классической статистической физике (классической — значит не квантовой) такая теорема доказывается (Больцман). Эту теорему можно сформулировать так: если система молекул находится в тепловом равновесии при температуре то средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой степени свободы молекулы она равна

(Другая формулировка этого же закона гласит: если какая-либо составляющая энергии системы пропорциональна квадрату координаты или компоненты скорости, то в состоянии теплового равновесия системы при температуре среднее значение этой части энергии равно

Эта теорема называется законом равномерного распределения кинетической энергии по степеням свободы, или, коротко, законом равнораспределения.

Этот закон позволяет ответить на поставленный выше вопрос.

В отношении своей внутренней энергии двух- и многоатомные газы отличаются от одноатомных числом степеней свободы своих молекул. Значит, для вычисления внутренней энергии газа и, следовательно, теплоемкости надо уметь определять число степеней свободы молекул газа.

Рассмотрим сначалзпростейший случай — двухатомной молекулы. Ее можно себе представить в виде системы, состоящей из двух атомов, расположенных на некотором расстоянии друг от друга (рис. 34). Если расстояние между этими атомами не меняется (такие молекулы мы будем называть жесткими), то такая система, вообще говоря, имеет шесть степеней свободы.

Действительно, положение и конфигурация такой молекулы определяются: тремя координатами ее центра масс, которыми определяется поступательное движение молекулы как целого, и тремя координатами, определяющими возможные вращения молекулы около взаимно перпендикулярных осей.

Рис. 34.

Однако опыт и теория показывают, что вращение молекул около оси X (см. рис. 34), на которой лежат центры обоих атомов, может быть возбуждено лишь при очень высоких температурах. При обычных температурах вращение около оси X не происходит, так же как не вращается отдельный атом. Поэтому для описания возможных вращений нашей молекулы достаточно двух координат.

Следовательно, число степеней свободы жесткой двухатомной молекулы равно 5, из них три поступательные (как принято говорить) и две вращательные степени свободы.

Но атомы в молекуле не всегда жестко связаны друг с другом; они могут совершать колебания друг относительно друга. Тогда, очевидно, требуется еще одна координата для определения конфигурации молекулы, это — расстояние между атомами.

Рис. 35.

Следовательно, в общем случае двухатомная молекула обладает шестью степенями свободы: тремя поступательными, двумя вращательными и одной колебательной.

Если молекула состоит из атомов, нежестко связанных, то она имеет степеней свободы (каждый атом имеет три степени свободы). Из этого числа три степени свободы поступательные и три вращательные, за исключением случая, когда атомы расположены на одной прямой, — тогда вращательных степеней свободы только две (как у двух-, атомной молекулы).

Для примера на рис. 35 приведена модель трехатомной молекулы и показаны оси вдоль которых может быть разложен

вектор угловой скорости молекулы. Таким образом, нелинейная n-атомная молекула в общем случае может иметь колебательных степеней свободы, а линейная

Во многих случаях колебательное движение атомов вовсе не возбуждается. Но если колебания атомов в молекуле совершаются и если их амплитуды достаточно малы (по сравнению с расстоянием между ними), то такие колебания можно считать гармоническими; атомы в этом случае являются гармоническими осцилляторами.

Но осциллятор обладает не только кинетической, но и потенциальной энергией (последняя обусловлена силами, возвращающими атом в положение равновесия). Для гармонического осциллятора, как известно из механики, средние значения кинетической и потенциальной энергии равны между собой. Следовательно, если в молекуле возбуждены гармонические колебания атомов, то по закону равнораспределения на каждую колебательную степень свободы преходится в виде кинетической энергии и в виде потенциальной. Для ангармоничных (не гармонических) колебаний это неверно.

Другими словами: энергия, приходящаяся на каждую колебательную степень свободы, равна не

После этого нетрудно вычислить теплоемкость многоатомных газов.

Если число степеней свободы молекулы газа равно то ее средняя энергия равна

а внутренняя энергия одного моля такого газа

Соответственно этому молярные теплоемкости газа

и

При подсчете числа степеней свободы надо число колебательных степеней свободы удвоить. Этого можно не делать, если дать несколько другое определение числу степеней свободы именно, если это число определить как число независимых квадратичных переменных, которым и определяется энергия системы.

В самом деле, кинетическая энергия поступательного и вращательного движений молекулы пропорциональна сумме квадратов соответствующих (независимых) компонент скоростей (линейных и угловых).

Что касается энергии колебаний атомов внутри молекулы, совершаемых, например, вдоль оси X, то она равна сумме кинетической энергии, пропорциональной квадрату скорости и потенциальной, которая, как известно, пропорциональна квадрату смещения х относительно положения равновесия. Таким образом, согласно новому определению числа степеней свободы, колебательному движению атома вдоль данной оси следует приписать две степени свободы, и формула (27.1) применима без оговорок (сравните вторую формулировку закона равнораспределения).

Изложенные только что соображения о возможном числе степеней свободы молекул позволяют истолковать приведенные выше экспериментальные данные о теплоемкости многоатомных газов.

Так, например, из того факта, что теплоемкость водорода, азота, кислорода и некоторых других двухатомных газов довольно точно равна следует, что число степеней свободы молекул этих газов равно 5. Это значит, что молекулы этих газов можно считать жесткими (колебательные степени свободы – не возбуждены). То же относится и к некоторым трехатомным газам. Но здесь экспериментальные результаты обнаруживают существенные отклонения от теоретически ожидаемых. Из формулы (27.2) следует, что теплоемкость для «жестких» трехатомных молекул должна равняться

Между тем теплоемкости всех трехатомных газов, перечисленных в табл. 6, оказываются несколько больше этого значения (на величину, которую нельзя объяснить погрешностями измерения).

На трудности наталкивается и попытка объяснить с точки зрения изложенной теории найденные значения теплоемкости хлора. Приведенное в табл. 6 значение теплоемкости хлора соответствует шести степеням свободы для молекулы хлора. Но молекула хлора, как двухатомная, может иметь либо пять степеней свободы, если два его атома жестко связаны между собой (тогда либо семь степеней свободы (согласно второму определению числа если атомы внутри молекулы могут совершать колебания (тогда

Как видно, и в этом случае теория теплоемкости не может считаться удовлетворительной. Это объясняется тем, что наша теория не в состоянии должным образом учесть энергию, связанную с внутренними движениями в молекуле, к которым закон равнораспределения не всегда применим.

Особенно важным отклонением от результатов теории является тот факт, что теплоемкость оказывается зависящей от температуры, в то время как, согласно уравнению (27.2), она должна быть для данного газа с данным значением величиной постоянной. Опыт

показывает, что теплоемкость с понижением температуры уменьшается.

Эту зависимость можно было бы объяснить тем, что с изменением температуры изменяется число «действующих» степеней свободы молекул, т. е. какие-то движения молекул, происходящие в одной области температур, прекращаются в другой. Однако такое предположение требует, чтобы теплоемкость изменялась с температурой скачками. Ведь то или иное движение может или происходить, или не происходить; в нервом случае ему соответствует энергия во втором эта энергия и связанный с ней вклад в теплоемкость отсутствуют. Возможно, конечно, не внезапное прекращение или возникновение того или иного вида движения молекулы, а постепенное изменение его интенсивности. Но закон равнораспределения не различает этого; с любой степенью свободы связана одна и та же энергия. Между тем температурная зависимость теплоемкости, как показывает опыт, имеет плавный ход — теплоемкость изменяется постепенно. Это свидетельствует о том, что закон равномерного распределения энергии по степеням свободы не может считаться вполне верным и имеет ограниченную применимость.

Теплоемкость водорода. Водород обладает той особенностью, что температурная зависимость теплоемкости у него особенно резко выражена. Если при комнатной температуре теплоемкость водорода при постоянном объеме равна то при температуре около 50 К (-223°С) она становится равной т. е. водород ведет себя как одноатомный газ, обладающий тремя степенями свободы.

Рис. 36.

Кривая зависимости теплоемкости водорода от температуры представлена на рис. 36, из которого видно, что теплоемкость с понижением температуры падает постепенно, что, вообще говоря, необъяснимо с точки зрения классической теории теплоемкости. Можно, правда, предположить, что с понижением температуры постепенно уменьшается число молекул, совершающих вращательное движение, но и в этом случае остается неясным, почему именно одна часть молекул совершает такие движения, в то время как у другой эти степени свободы «выключены».

Здесь мы встречаемся с одним из многих случаев, когда классическая физика оказывается не в состоянии объяснить опытные

факты. В нашем случае расхождение теории и опыта свидетельствует, очевидно, о том, что представление о молекулах как о твердых шариках, движения которых происходят по законам механики, не вполне соответствует действительности. Теперь хорошо известно, что молекулы состоят из взаимодействующих между собой атомов, а атомы имеют сложное строение и состоят из многих еще меньших частиц, которые также движутся сложным образом. Движение же атомных частиц не подчиняется классической механике, а управляется особым «сводом законов» — квантовой механикой. Поэтому, пока идет речь о теплоемкости одноатомных газов, на которую не влияют внутриатомные движения и связанная с ними энергия, изложенная выше теория теплоемкости оказывается в превосходном согласии с опытом. Но во многоатомных молекулах существенную роль играют уже внутренние процессы в молекулах и атомах, с которыми несомненно связаны, например, колебательные степени свободы. Естественно, что наша, теория, не учитывающая особых квантовых свойств атомных систем, в этом случае дает лишь приблизительно верные результаты. Квантовая же теория дает полное объяснение всем опытным данным о теплоемкости.

В частности, в случае атома-водорода квантовая теория показывает, что молекулы водорода могут находиться в двух разных состояниях — в состоянии параводорода и ортоводорода, теплоемкости которых должны отличаться друг от друга. Различие между этими состояниями состоит в следующем.

Из квантовой теории следует, что атомы (точнее, атомные ядра) обладают некоторым моментом количества движения (моментом импульса). Когда из двух атомов водорода образуется молекула, эти моменты ядер (они, как и всякие другие моменты, являются векторными величинами) могут расположиться либо параллельно либо антипараллельно друг другу. Как само существование ядерных моментов, так и их возможные ориентации являются следствием квантовой механики и из обычной механики не могут быть получены. Водород, молекулы которого состоят из атомов с параллельно ориентированными моментами ядер, называется ортоводородом, в отличие от водорода с антипараллельными моментами ядер атомов в молекуле, который называется параводородом.

В обычном водороде содержатся оба вида молекул, причем их относительное содержание зависит от температуры. При комнатной температуре в нормальном водороде содержится около 25% параводорода, а с понижением температуры содержание параводорода возрастает, так что при 20 К водород почти целиком состоит из параводорода (99,8%).

Орто- и парасостояиию водорода соответствуют разные значения энергии вращательного движения, чем и объясняется различное значение теплоемкости водорода в этих двух состояниях. Но при низких температурах (около 50 К) теплоемкость, зависящая от вращательного движения молекул, в обоих состояниях становится равной нулю. Этим и объясняется то, что теплоемкость водорода становится такой же, как у одноатомного газа.

Теплоемкость других многоатомных газов, так же как у водорода, падает с понижением температуры, стремясь к значению теплоемкости одноатомных газов но происходит это в области очень низких температур, когда непосредственное измерение теплоемкости газов встречает большие трудности.

Измерения теплоемкости позволяют, таким образом, сделать важные заключения о строении молекул. Поэтому такие измерения, особенно при низких температурах, имеют большое значение. Кроме того, знание величины теплоемкости и ее температурной зависимости необходимо при решении многих технических проблем.

1

Оглавление

  • ПРЕДИСЛОВИЕ
  • ВВЕДЕНИЕ
  • Глава I. КИНЕТИЧЕСКАЯ ТЕОРИЯ ИДЕАЛЬНЫХ ГАЗОВ
  • § 1. Идеальный газ
  • § 2. Давление газа
  • § 3. Температура
  • § 4. Уравнение состояния идеального газа
  • § 5. Законы идеального газа
  • § 6. Скорости газовых молекул
  • § 7. Броуновское движение
  • § 8. Барометрическая формула
  • § 9. Закон Больцмана
  • § 10. Понятие о вероятности
  • § 11. Понятие о распределении. Функция распределения
  • § 12. Распределение молекул по компонентам скорости
  • § 13. Распределение молекул по скоростям
  • § 14. Средние скорости молекул
  • § 15. Наивероятнейшая скорость молекул
  • § 16. Формула Максвелла для относительных скоростей
  • § 17. Закон распределения молекул по скоростям и атмосферы планет
  • § 18. Экспериментальная проверка закона распределения
  • § 19. Измерение параметров состояния
  • Глава II. КИНЕТИЧЕСКАЯ ТЕОРИЯ ТЕПЛОТЫ. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
  • § 20. Внутренняя энергия идеального газа
  • § 21. Количество теплоты
  • § 22. Механический эквивалент теплоты
  • § 23. Первое начало термодинамики
  • § 24. Теплоемкость идеальных газов
  • § 25. Теплоемкость одноатомных газов
  • § 26. Теплоемкость газов и число степеней свободы молекул
  • § 27. Теплоемкость двухатомных и многоатомных газов
  • § 28. Изменение состояния при изменении объема газа
  • § 29. Работа при изотермическом изменении объема идеального газа
  • § 30. Адиабатное изменение объема идеального газа
  • § 31. Работа при адиабатном изменении объема газа
  • § 32. Политропический процесс
  • § 33. Расширение газа в пустоту
  • § 34. Измерение количества теплоты и теплоемкости
  • Глава III. СТОЛКНОВЕНИЯ МОЛЕКУЛ И ЯВЛЕНИЯ ПЕРЕНОСА
  • § 35. Молекулярные движения и явления переноса
  • § 36. Среднее число столкновений в единицу времени и средняя длина свободного пробега молекул
  • § 37. Эффективное поперечное сечение частицы и вероятность
  • § 38. Рассеяние молекулярного пучка в газе
  • § 39. Экспериментальное определение длины свободного пробега
  • § 40. Диффузия в газах
  • § 41. Нестационарная диффузия
  • § 42. Стационарная диффузия. Вычисление коэффициента диффузии
  • § 43. Коэффициент взаимной диффузии
  • § 44. Термическая диффузия
  • § 45. Теплопроводность газов
  • § 46. Нестационарная теплопроводность
  • § 47. Стационарная теплопроводность. Вычисление коэффициента теплопроводности
  • § 48. Вязкость газов (внутреннее трение)
  • § 49. Измерение коэффициента вязкости (вискозиметрия)
  • § 50. Соотношения между коэффициентами переноса
  • Глава IV. ФИЗИЧЕСКИЕ ЯВЛЕНИЯ В РАЗРЕЖЕННЫХ ГАЗАХ (ВАКУУМЕ)
  • § 51. Теплопередача в газах при малых давлениях
  • § 52. Течение газов при малых давлениях (молекулярное течение)
  • § 53. Молекулярное течение газа в цилиндрической трубе
  • § 54. Молекулярное течение смеси газов. Разделение газовых смесей
  • § 55. Диффузия газов в вакууме
  • § 56. Разность давлений между различно нагретыми частями газа (тепловая транспирация)
  • § 57. Элементы вакуумной техники
  • § 58. Измерение малых давлений
  • § 59. Вакуумная установка
  • Глава V. НЕИДЕАЛЬНЫЕ (РЕАЛЬНЫЕ) ГАЗЫ. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
  • § 60. Отклонения свойств газов от идеальности
  • § 61. Сжижение газов (конденсация)
  • § 62. Фазовый переход
  • § 63. Фазовые диаграммы
  • § 64. Методы определения критических параметров
  • § 65. Уравнение Ван-дер-Ваальса
  • § 66. Изотермы Ван-дер-Ваальса
  • § 67. Критическая температура и критическое состояние
  • § 68. Экспериментальное определение констант уравнения Ван-дер-Ваальса
  • § 69. Сравнение уравнения Ван-дер-Ваальса с данными опыта
  • § 70. Приведенное уравнение Ван-дер-Ваальса. Закон соответственных состояний
  • § 71. Межмолекулярные силы взаимодействия в реальном газе
  • § 72. Теплоемкость неидеальных газов
  • Глава VI. ЭЛЕМЕНТЫ ТЕРМОДИНАМИКИ
  • § 73. Равновесные состояния
  • § 74. Обратимые и необратимые процессы
  • § 75. Квазистатические процессы
  • § 76. Необратимость и вервятность
  • § 77. Взаимные превращения механической и тепловой энергии
  • § 78. Первое начало термодинамики
  • § 79. Преобразование теплоты в механическую работу
  • § 80. Цикл Карно
  • § 81. Холодильная машина
  • § 82. Доказательство теорем Карно
  • § 83. Свободная энергия
  • § 84. Энтропия
  • § 85. Некоторые термодинамические соотношения
  • § 86. Энтропия при обратимых процессах в замкнутой системе
  • § 87. Энтропия при необратимых процессах в замкнутой системе, акон возрастания энтропии
  • § 88. Второе начало термодинамики и превращение теплоты в работу
  • § 89. Физический смысл энтропии. Энтропия и вероятность
  • § 90. Энтропия и беспорядок
  • § 91. «Демон» Максвелла
  • § 92. Термодинамическая шкала температур
  • § 93. Третье начало термодинамики
  • § 94. Отрицательные температуры
  • Глава VII. СВОЙСТВА ЖИДКОСТЕЙ
  • § 95. Объемные свойства жидкостей
  • § 96. Теплоемкость жидкостей
  • § 97. Явления переноса в жидкостях
  • § 98. Явления на границе жидкости
  • § 99. Условия равновесия на границе двух сред. Краевой угол
  • § 100. Силы, возникающие на кривой поверхности жидкости
  • § 101. Капиллярные явления
  • § 102. Некоторые методы измерения коэффициента поверхностного натяжения
  • § 103. Зависимость коэффициента поверхностного натяжения от температуры
  • § 104. Испарение и кипение жидкостей
  • § 105. Температурная зависимость упругости насыщенных паров
  • § 106. Упругость насыщенного пара над кривой поверхностью жидкости
  • § 107. Кипение жидкостей
  • § 108. Жидкие растворы
  • § 109. Осмотическое давление
  • Глава VIII. НИЗКИЕ ТЕМПЕРАТУРЫ
  • § 110. Сжижение газов
  • § 111. Эффект Джоуля-Томсона
  • § 112. Адиабатное расширение газа с совершением внешней работы
  • § 113. Сжижение газов с использованием эффекта Джоуля — Томсона (метод Линде)
  • § 114. Сжижение газов методом адиабатного расширения в детандерах (метод Клода)
  • § 115. Некоторые свойства сжиженных газов
  • § 116. Сверхнизкие температуры
  • § 117. Свойства вещества при низких температурах
  • § 118. Жидкий гелий
  • Глава IX. ТВЕРДОЕ ТЕЛО
  • § 120. Кристаллическая решетка
  • § 121. Дефекты в кристаллах
  • § 122. Механические свойства твердых тел. Деформации
  • § 123. Деформация растяжения и сжатия. Сдвиг
  • § 124. Связь между модулями упругости
  • § 125. Упругая деформация и тепловое расширение
  • § 126. Зависимость деформации от напряжения
  • § 127. Механизм пластической деформации
  • § 128. Дислокации в кристаллах
  • § 129. Переход в твердое состояние
  • § 130. Диаграмма состояния. Тройная точка
  • § 131. Фазовые переходы первого и второго рода
  • § 132. Твердый гелий
  • § 133. Растворение и кристаллизация из раствора
  • § 134. Сплавы. Диаграммы плавкости
  • § 135. Зонная очистка металлов
  • § 136. Опытное определение температуры плавления
  • § 137. Тепловые свойства твердых тел
  • § 138. Измерение теплоемкости
  • § 139. Тепловое расширение твердых тел
  • § 140. Теплопроводность
  • § 141. Диффузия в твердых телах
Источник

Добавить комментарий