Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 ноября 2020 года; проверки требует 1 правка.
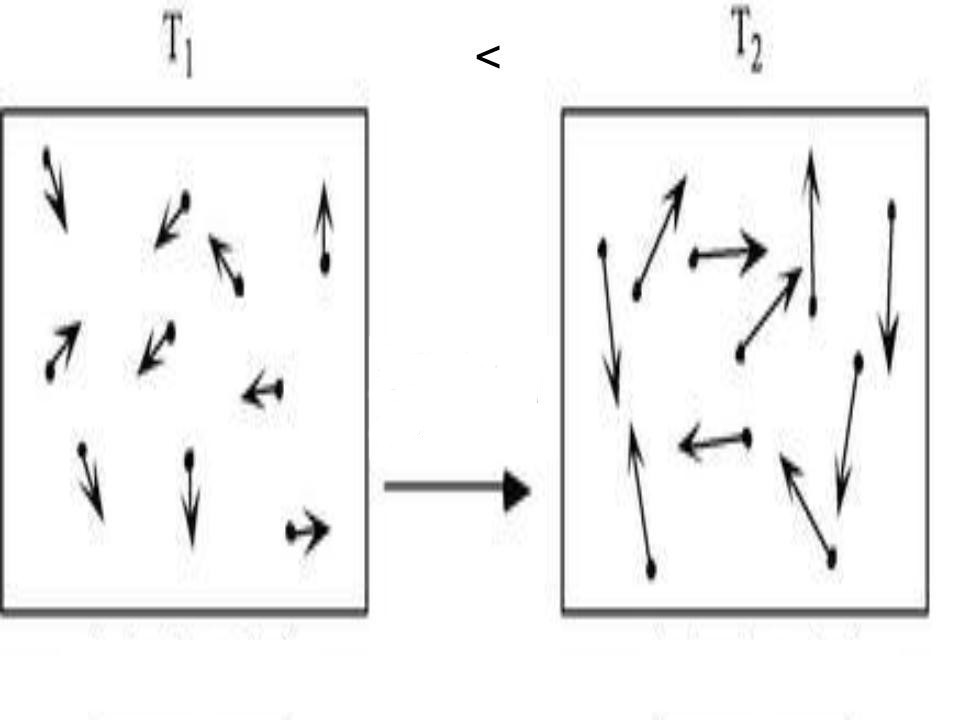
Теплоёмкость определяется суммой поступательных, вращательных и удвоенным числом колебательных степеней свободы.
Теплоёмкость идеального газа — отношение количества теплоты, сообщённой газу 
, к изменению температуры 
, которое при этом произошло 
[1].
Удельная и молярная теплоёмкость[править | править код]
Молярная теплоёмкость — теплоёмкость 1 моля вещества [2]:
где 
— масса, 
— молярная масса вещества.
Теплоёмкость единичной массы вещества называется удельной теплоёмкостью и, в системе СИ, измеряется в Дж/(кг·К)[1].
Формула расчёта удельной теплоёмкости[1][2]:
- где c — удельная теплоёмкость, m — масса нагреваемого (охлаждающегося) вещества.
Теплоёмкость идеального газа в изопроцессах[править | править код]
Адиабатический[править | править код]
В адиабатическом процессе теплообмена с окружающей средой не происходит, то есть 
. Однако, объём, давление и температура меняются, то есть 
[3].
Следовательно, теплоёмкость идеального газа в адиабатическом процессе равна нулю: 
.
Изотермический[править | править код]
В изотермическом процессе постоянна температура, то есть 
. При изменении объёма газу передаётся (или отбирается) некоторое количество тепла[3]. Следовательно, теплоёмкость идеального газа равна плюс-минус бесконечности: 
Изохорный[править | править код]
В изохорном процессе постоянен объём, то есть 
и, следовательно газ не совершает работы. Первое Начало Термодинамики для изохорного процесса имеет вид[1]:
А для идеального газа
Таким образом,
где 
— число степеней свободы частиц газа.
Другая формула:
где 
— показатель адиабаты, 
— газовая постоянная газа.
Изобарный[править | править код]
Молярная теплоёмкость при постоянном давлении обозначается как 
. В идеальном газе она связана с теплоёмкостью при постоянном объёме соотношением Майера 
[1].
Уравнение Майера вытекает из первого начала термодинамики[4]:
.
В рассматриваемом случае, согласно определению теплоёмкости:
Учитываем, что работа газа равна [4]:
Согласно уравнению Менделеева-Клапейрона для одного моля газа[1]:
Подставляя уравнение (4) в (3) получаем:
Так как энергия одной молекулы равна 
(6)[Комм 1][5], то и внутренняя энергия в целом и при изобарном процессе будет определяться по соотношению (1). Следовательно, подставляя уравнения (1) и (5) в (2) получаем соотношение Майера.
Молекулярно-кинетическая теория позволяет вычислить значения молярной теплоёмкости для классического идеального газа газов через значение универсальной газовой постоянной исходя из уравнения (6) и предположения, что молекулы газа не взаимодействуют между собой[5]:
Теплоёмкости можно также определить исходя из уравнения Майера, если известен показатель адиабаты, который можно измерить экспериментально (например, с помощью измерения скорости звука в газе или используя метод Клемана — Дезорма).
Теплоёмкость реального газа может значительно отклонятся от теплоёмкости идеального газа. Так при температуре в 25 °С и атмосферном давлении атомарный водород имеет теплоёмкость 2,50R , а атомарный кислород — 2,63R. Также теплоёмкость реального газа зависит от температуры[5].
См. также[править | править код]
- Идеальный газ
- Первое начало термодинамики
- Теплоёмкость
Комментарии[править | править код]
- ↑ i — сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы
- ↑ 1 2 При жёсткой связи между атомами, то есть колебательные степени свободы исключены из рассмотрения. Примером трёхатомной линейной молекулы служит цианистый водород HCN.
Примечания[править | править код]
- ↑ 1 2 3 4 5 6 Савельев, 2001, с. 26—30.
- ↑ 1 2 Базаров И. П., Термодинамика, 2010, с. 41.
- ↑ 1 2 Савельев, 2001, с. 30—31.
- ↑ 1 2 Савельев, 2001, с. 18-20.
- ↑ 1 2 3 Савельев, 2001, с. 61-63.
Литература[править | править код]
- Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.— Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
- Белоконь Н. И. Основные принципы термодинамики. — М.: Недра, 1968. — 110 с.
- Савельев И. В. Курс общей физики:Молекулярная физика и термодинамика. — М.: Астрель, 2001. — Т. 3. — 208 с. — 7000 экз. — ISBN 5-17-004585-9.
Теплоемкостью
тела называется
величина, равная количеству теплоты,
которое нужно сообщить телу, чтобы
повысить его температуру на 1
К.
Удельная
теплоемкость вещества
– величина, равная количеству теплоты,
необходимому для нагревания 1
кг
вещества на 1
К:
.
Молярная
теплоемкость вещества –
величина, равная количеству теплоты,
необходимому для нагревания 1
моля
вещества на 1
К:
, откуда
.
Различают
теплоемкости газа при изохорном и
изобарном процессах.
1. Молярная
теплоемкость газа при изохорном процессе
.
Для изохорного
процесса первое начало термодинамики:
.
Следовательно
,
откуда
.
2. Молярная
теплоемкость газа при изобарном процессе
.
Для изобарного
процесса первое начало термодинамики:
.
Так как для
изобарного процесса
,
то
,
откуда
.
Уравнение Майера.
Сравнение между
собой Ср
и СV
приводит к уравнению
Майера:
.
Это уравнение
показывает, что Ср
больше, чем СV
на величину универсальной газовой
постоянной R.
Это объясняется тем, что при изобарном
нагревании газа, в отличие от изохорного
нагревания, требуется дополнительное
количество теплоты на совершение работы
расширения газа.
Таким образом,
молярная теплоемкость газа определяется
лишь числом степеней свободы и не зависит
от температуры. Это утверждение
справедливо в довольно широком интервале
температур лишь для одноатомных газов.
Уже у
двухатомных газов число степеней
свободы, проявляющееся в теплоемкости,
зависит от температуры.
Тема 9. Адиабатический процесс.
Адиабатическим
называется процесс, при котором
отсутствует теплообмен между системой
и окружающей средой. При адиабатическом
процессе изменяются все термодинамические
параметры (р,
V,
Т)
в соответствии с уравнением
Пуассона:
,
где
–коэффициент
Пуассона,
равный отношению молярных теплоемкостей
.
Полученное выражение
есть уравнение
адиабатического процесса
в переменных р
и V
.
Для перехода от
переменных р
и V
к переменным V,
Т
или p,
Т
при описании адиабатического процесса
используется уравнение Клапейрона —
Менделеева:
.
В результате
соответствующие уравнения адиабатического
процесса:
в переменных
V
и Т
,
в переменных
р
и
Т .
Работа газа при
адиабатическом процессе.
Из первого начала
термодинамики (
)
для адиабатического процесса (
)
следует, что
.
Если газ адиабатически
расширяется от объема V1
до объема V2
, то его
температура уменьшается от T1
до T2
и работа расширения идеального газа:
.
Используя уравнение
адиабатического процесса в переменных
V
и Т
, то
есть
полученное выражение для работыА
при адиабатическом расширении газа
можно преобразовать к иному виду,
отражающему адиабатическое изменение
объема газа от величины V1
до величины
V2
:
.
Тема 10. Обратимый и необратимый процессы. Круговой процесс. Тепловая машина и цикл Карно.
Термодинамический
процесс называется обратимым,
если он может проходить как в прямом,
так и в обратном направлении, причем
если такой процесс проходит сначала в
прямом, а затем в обратном направлении,
и система возвращается в исходное
состояние, то в окружающей среде и в
этой системе не происходит никаких
изменений. Всякий процесс, не удовлетворяющий
этим условиям, является необратимым.
Круговым процессом
(или циклом)
называется процесс, при котором система,
пройдя через ряд состояний, возвращается
в исходное состояние.
Тепловая машина
– это устройство для преобразования
теплоты в работу.
Принцип действия
тепловой машины приведен на рис. 5. От
термостата с более высокой температурой
Т1
,
называемого нагревателем,
за цикл отнимается количество теплоты
Q1
,
а термостату с более низкой температурой
Т2
,
называемому холодильником,
за цикл передается количество теплоты
Q2
,
при этом совершается работа: А
= Q1
– Q2.
Французский физик
Карно рассмотрел обратимый циклический
процесс, состоящий из чередования двух
изотермических и двух адиабатических
процессов (рис. 6). В цикле Карно в качестве
рабочего тела используется идеальный
газ, находящийся в цилиндре с подвижным
поршнем.
Рис. 5
Рис. 6
График цикла Карно
в координатах р
и V
изображен на рис. 6, где изотермическим
расширению и сжатию соответствуют
кривые 1–2
и 3–4,
а адиабатическим расширению и сжатию
– кривые 2–3
и 4–1.
При изотермическом процессе U=const,
поэтому количество теплоты Q1,
полученное газом от нагревателя, равно
работе расширения А12,
совершаемой газом при переходе из
состояния 1
в состояние
2:
.
При адиабатическом
расширении 2–3
работа А23
совершается за счет изменения внутренней
энергии:
.
Количество
теплоты Q2
,
отданное газом холодильнику при
изотермическом сжатии, равно работе
сжатия А34
:
.
Работа адиабатического
сжатия:
.
Работа, совершаемая
в результате кругового процесса:
,
Термический
коэффициент полезного действия цикла
Карно можно определить по формуле:
или
,
то есть
к.п.д. тепловой
машины, работающей по циклу Карно,
определяется только температурами
нагревателя
Т1
и холодильника
Т2
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В термодинамике при изучении переходов из начального в конечное состояние некоторой системы важно знать тепловой эффект процесса. С этим эффектом тесно связано понятие теплоемкости. В данной статье рассмотрим вопрос, что понимают под изохорной теплоемкостью газа.
Идеальный газ
Идеальным называется такой газ, частицы которого считаются материальными точками, то есть не имеют размеров, но обладают массой, и у которого вся внутренняя энергия состоит исключительно из кинетической энергии движения молекул и атомов.
Любой реальный газ в идеале никогда не будет удовлетворять описанной модели, поскольку его частицы все же имеют некоторые линейные размеры и взаимодействуют между собой с помощью слабых ван-дер-ваальсовых связей или химических связей другого типа. Однако при низких давлениях и высоких температурах расстояния между молекулами велики, а их кинетическая энергия превышает потенциальную в десятки раз. Все это позволяет применять с высокой степенью точности идеальную модель для реальных газов.
Внутренняя энергия газа
Внутренняя энергия любой системы – это физическая характеристика, которая равна сумме потенциальной и кинетической энергии. Поскольку в идеальных газах можно пренебречь потенциальной энергией, то для них можно записать равенство:
U = Ek.
Где Ek – энергия кинетическая системы. Используя молекулярно-кинетическую теорию и применяя универсальное уравнение состояния Клапейрона-Менделеева, несложно получить выражение для U. Оно записано ниже:
U = z/2*n*R*T.
Здесь T, R и n – абсолютная температура, газовая постоянная и количество вещества соответственно. Величина z – это целое число, показывающее количество степеней свободы, которыми обладает молекула газа.
Изобарная и изохорная теплоемкость
В физике теплоемкостью называется количество теплоты, которое необходимо предоставить изучаемой системе, чтобы нагреть ее на один кельвин. Справедливо также и обратное определение, то есть теплоемкость – это количество теплоты, которое система выделяет при охлаждении на один кельвин.
Проще всего для системы определить изохорную теплоемкость. Под ней понимают теплоемкость при постоянном объеме. Поскольку система в таких условиях работу не совершает, то вся энергия расходуется на повышение внутренних энергетических запасов. Обозначим изохорную теплоемкость символом CV, тогда можно записать:
dU = CV*dT.
То есть изменение внутренней энергии системы прямо пропорционально изменению ее температуры. Если сравнить это выражение, с записанным в предыдущем пункте равенством, то приходим к формуле для CV в идеальном газе:
СV = z/2*n*R.
Данной величиной на практике неудобно пользоваться, поскольку она зависит от количества вещества в системе. Поэтому было введено понятие удельной изохорной теплоемкости, то есть величины, которую рассчитывают либо на 1 моль газа, либо на 1 кг. Обозначим первую величину символом CVn, вторую – символом CVm. Для них можно записать такие формулы:
CVn = z/2*R;
CVm = z/2*R/M.
Здесь M – молярная масса.
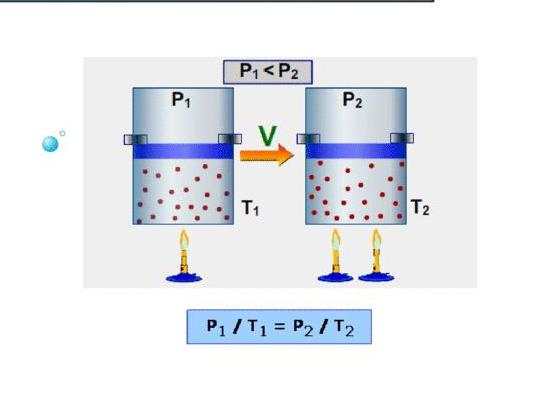
Изобарной называется теплоемкость при поддержании постоянного давления в системе. Примером такого процесса является расширение газа в цилиндре под поршнем при его нагревании. В отличие от изохорного, во время изобарного процесса подводимое к системе тепло расходуется на повышение внутренней энергии и на выполнение механической работы, то есть:
H = dU + P*dV.
Энтальпия изобарного процесса представляет собой произведение изобарной теплоемкости на изменение температуры в системе, то есть:
H = CP*dT.
Если рассмотреть расширение при постоянном давлении 1 моль газа, то первое начало термодинамики запишется в виде:
CPn*dT = CVn*dT + R*dT.
Последнее слагаемое получено из уравнения Клапейрона-Менделеева. Из этого равенства следует связь между изобарной и изохорной теплоемкостями:
CPn = CVn + R.
Для идеального газа удельная молярная теплоемкость при постоянном давлении всегда больше соответствующей изохорной характеристики на величину R=8,314 Дж/(моль*К).
Степени свободы молекул и теплоемкость
Выпишем еще раз формулу для удельной молярной изохорной теплоемкости:
CVn = z/2*R.
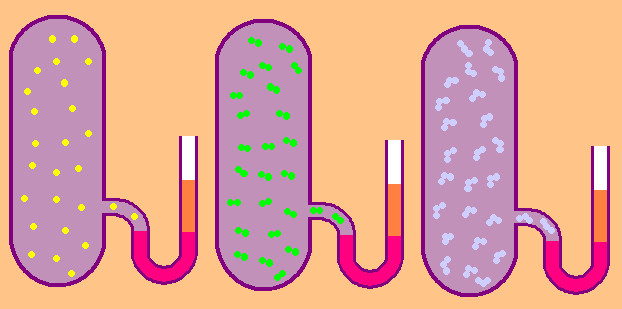
В случае газа одноатомного величина z = 3, поскольку атомы в пространстве могут перемещаться лишь в трех независимых направлениях.
Если же речь идет о газе, состоящем из двухатомных молекул, например, кислород O2 или водород H2, то, помимо поступательного движения, эти молекулы могут еще вращаться вокруг двух взаимно перпендикулярных осей, то есть z будет равно 5.
В случае более сложных молекул для определения CVn следует использовать z=6.
В случае, если результатом теплообмена становится передача телу некоего количества теплоты Q, то его температура и внутренняя энергия претерпевают изменения.
Необходимое для нагревания 1 кг вещества на 1 К количество теплоты Q носит название удельной теплоемкости вещества c, а ее формула выглядит следующим образом:
c=Qm∆T.
В большом количестве ситуаций удобной для использования является молярная теплоемкость C:
C=M·c, где M представляет собой молярную массу вещества.
Теплоемкость, полученная таким способом, не является однозначной характеристикой вещества. Исходя из первого закона термодинамики, можно сказать, что изменение внутренней энергии тела зависимо не только от количества полученной теплоты, но и от величины совершенной телом работы. В разных условиях осуществления процесса теплопередачи тело может совершать различную работу. Таким образом, переданное телу одинаковое количество теплоты способно провоцировать изменения его внутренней энергии и, соответственно, температуры.
Подобной неоднозначностью при определении теплоемкости характеризуются только газообразные вещества. Объем в процессе нагрева практически не меняет своей величины, что сводит работу расширения к нулю. По этой причине вся полученная телом теплота уходит на изменение его внутренней энергии. Газ в процессе теплопередачи может значительно менять свой объем и совершать работу, чем отличается от твердых тел и жидкостей. Таким образом, теплоемкость газообразного вещества имеет зависимость от характера термодинамического процесса.
Изопроцессы в газах
Чаще всего рассматриваются два значения теплоемкости газов:
- CV являющаяся молярной теплоемкостью в изохорном процессе (V=const);
- Cp представляющая собой молярную теплоемкость в изобарном процессе (p=const).
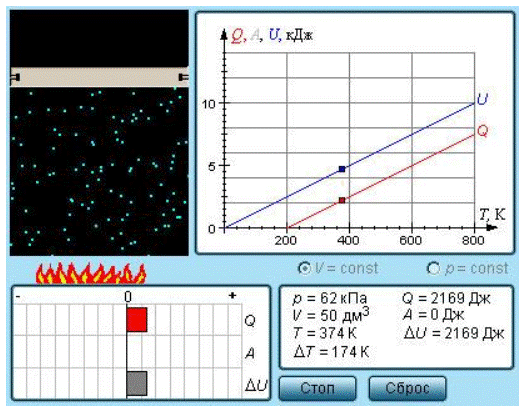
При условии постоянного объема газ не совершает работы: A=0. Исходя из первого закона термодинамики для 1 моля газа, можно сказать, что справедливым является следующее выражение:
QV=CV∆T=∆U.
Изменение величины ΔU внутренней энергии газа прямо пропорционально изменению значения ΔT его температуры.
В условиях процесса при постоянном давлении первый закон термодинамики дает такую формулу:
Qp=∆U+p(V2-V1)=CV∆T+pV.
В котором ΔV является изменением объема 1 моля идеального газа при изменении его температуры на ΔT. Таким образом, можно заявить, что:
Cp=Qp∆T=CV+p∆V∆T.
Из уравнения состояния идеального газа, записанного для 1 моля, может выражаться отношение ΔVΔT:
pV=R.
В котором R представляет собой универсальную газовую постоянную. При условии постоянства давления p=const, можно записать следующее:p∆V=R∆T или ∆V∆T=Rp.
Из этого следует, что выражающее связь между молярными теплоемкостями Cp и CV соотношение имеет вид (формула Майера):
Cp=CV+R.
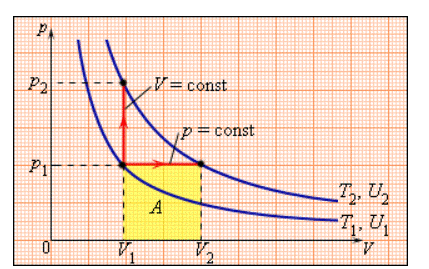
В процессе с неизменным давлением молярная теплоемкость Cp газа всегда превышает молярную теплоемкость CV в процессе с не подверженным изменениям объемом, что демонстрируется на рисунке 3.10.1.
Рисунок 3.10.1. Два возможных процесса нагревания газа на ΔT=T2 –T1. При p=const газ совершает работу A=p1(V2 – V1). Поэтому Cp>CV.
Отношение теплоемкостей в процессах с постоянным давлением и постоянным объемом занимает важное место в термодинамике и обозначается в виде греческой буквы γ.
γ=CpCV.
Данное отношение включено в формулу для адиабатического процесса.
Между двумя изотермами, обладающими температурами T1 и T2 на диаграмме (p, V) реальны различные варианты перехода. Так как для всех подобных переходов изменение величины температуры ΔT=T2 –T1 является одним и тем же, выходит, что изменение значения
ΔU внутренней энергии тоже одинаково. С другой стороны, совершенные при этом работы A и количества теплоты Q, полученные в результате теплообмена, выйдут разными для различных путей перехода. Из этого следует, что газа имеет относительно приближенное к бесконечности число теплоемкостей. Cp и CV представляют собой частные, однако, очень важные для теории газов, значения теплоемкостей.
Рисунок 3.10.2. Модель теплоемкости идеального газа.
Термодинамические процессы, в которых теплоемкость газа не подвергается изменениям, носят название политропических.
Каждый изопроцесс являются политропическим. В изотермическом процессе ΔT=0, из-за чего CT=∞. В адиабатическом процессе ΔQ=0, выходит, что Cад=0.
Стоит обратить внимание на то, что «теплоемкость» и «количество теплоты» являются крайне неудачными терминами, доставшимися современной науке в качестве наследства теории теплорода, которая господствовала в XVIII веке.
Данная теория представляла теплоту в виде содержащегося в телах особого невесомого вещества. Считалось, что оно не подвержено уничтожению и не может быть созданным. Явление нагрева объясняли повышением, а охлаждение – понижением содержания в телах теплорода. Однако теория теплорода оказалась несостоятельной, так как не смогла дать ответа на вопрос, почему одинаковое изменение внутренней энергии тела возможно получить, приводя ему разное количество теплоты в зависимости от совершаемой им работы. По этой причине утверждение, что в данном теле содержится некоторый запас теплорода лишено смысла.
Молекулярно-кинетическая теория
В молекулярно-кинетической теории устанавливается следующее соотношение между средней кинетической энергией E→ поступательного движения молекул и абсолютной температурой T:
E→=32kT.
Внутренняя энергия 1 моля идеального газа эквивалентна произведению E→ на число АвогадроNА:
U=32kNAT=32RT.
При условии изменения температуры на величину ΔT внутренняя энергия изменяется на величину:
U=32R∆T=CV∆T.
Коэффициент пропорциональности между ΔU и ΔT эквивалентен теплоемкости CV в условиях постоянного давления:
CV=32R=12,47 ДЖ/моль·К.
Данное выражение подтверждается экспериментами с газами, которые состоят из одноатомных молекул вроде гелия, неона или аргона. При этом для двухатомных (водород, азот) и многоатомных (углекислый газ) газов такое соотношение не согласуется с полученными в результате опытов данными. Причина этого расхождения заключается в том, что для двух- и многоатомных молекул средняя кинетическая энергия должна включать энергию как поступательного, так и вращательного их движения.
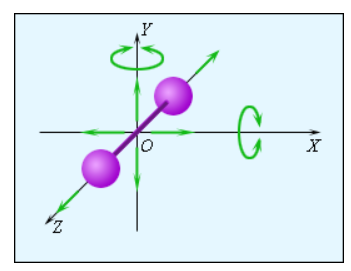
Рисунок 3.10.3. Модель двухатомной молекулы. Точка O совпадает с центром масс молекулы.
Рисунок 3.10.3 иллюстрирует модель двухатомной молекулы. Молекула имеет возможность производить пять независимых типов движений: три поступательных движения вдоль осей X, Y, Z и два вращения относительно осей X и Y.
Опытным путем выяснено, что вращение относительно оси Z, на которой лежат центры обоих атомов, может быть возбуждено только при очень высоких значениях температуры. В условиях обычных температур вращение вокруг оси Z не происходит.
Каждое независимое движение в молекуле носит название степени свободы.
Выходит, что одноатомная молекула обладает 3 поступательными степенями свободы, «жесткая» двухатомная молекула 5 степенями, то есть 3 поступательными и 2 вращательными, а многоатомная молекула 6 степенями свободы, из которых 3 приходятся на поступательные и 3 на вращательные.
В классической статистической физике доказывается теорема о равномерном распределении энергии по степеням свободы:
Если система молекул находится в тепловом равновесии при температуре T, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой степени свободы молекулы она равна 12kT.
Из данной теоремы следует, что для молярных теплоемкостей газа Cp и CV и их отношения
γ справедлива запись в следующем виде:
CV=i2R, Cp=Cv+R=i+22R, γ=CpCV=i+2i,
где i представляет собой количество степеней свободы газа.
Для газа, состоящего из одноатомных молекул (i=3)
CV=32R, Cp=Cv+R=52R, γ=CpCV=53=1,66.
Для газа, состоящего из двухатомных молекул (i=5)
CV=52R, Cp=Cv+R=72R, γ=CpCV=75=1,4.
Для газа, состоящего из многоатомных молекул (i=6)
CV=3R, Cp=Cv+R=4R, γ=CpCV=43=1,33.
В обычных условиях экспериментально измеренные теплоемкости многих газов неплохо согласуются с приведенными выражениями, но в целом классическая теория теплоемкости газов вполне удовлетворительной не является. Существует колоссальное число примеров со значительной разницей между результатами эксперимента и теорией. Данный факт объясняется тем, что классическая теория не может полностью учесть, связанную с внутренними движениями в молекуле энергию.
Теорема о равномерном распределении энергии по степеням свободы может быть применена и по отношению к тепловому движению частиц в твердом теле. Входящие в состав кристаллической решетки атомы колеблются около положений равновесия. Энергия данных колебаний представляет собой внутреннюю энергию твердого тела. Каждый конкретный атом может колебаться в кристаллической решетке в трех взаимно перпендикулярных направлениях. Выходит, что каждый атом имеет 3 колебательные степени свободы. При условии гармонических колебаний средняя кинетическая энергия эквивалентна средней потенциальной энергии. По этой причине в соответствии с теоремой о равномерном распределении на каждую колебательную степень свободы приходится средняя энергия kT, а на один атом – 3kT.
Внутренняя энергия 1 моля твердого вещества равна следующему выражению:
U=3RNAkt=3Rt.
Следовательно, молярная теплоемкость вещества в твердом состоянии равняется:
С=3R=25,12 Дж/моль·К.
Данное выражение носит название закона Дюлонга–Пти. Для твердых тел почти нет различия между Cp и CV по причине пренебрежительно малой работы при сжатии или расширении.
Опыт показывает, что молярная теплоемкость у многих твердых тел (химических элементов) при обычных температурах на самом деле близка к 3R. При этом, в условиях низких температур заметны довольно сильные расхождения между теорией и экспериментом. Таким образом, гипотеза о равномерном распределении энергии по степеням свободы может считаться лишь приближением. Заметная в опыте зависимость теплоемкости от температуры объясняется только при условии использования квантовых представлений.
Перевод термодинамической системы (например, порции идеального газа) из состояния `1` в состояние `2` можно осуществить разными способами. На рис. 12 показаны графики двух возможных процессов (`1-“а”-2` и `1-“в”-2`), позволяющих осуществить такой перевод. Изменение внутренней энергии системы в том и в другом случае одинаково (оно определяется положениями точек `1` и `2` на -диаграмме), а работа, совершённая системой над окружающими телами, различна (площадь фигур под графиками процессов `1-“а”-2` и `1-“в”-2` разная, площадь под графиком процесса `1-“в”-2` больше).
Следовательно, и количество теплоты, затраченное на перевод системы из состояния `1` в `2` ( $$ Q=Delta U+{A}^{text{‘}}$$ ), будет разным.
Теплоёмкостью $$ C$$ термодинамической системы (тела) называют отношение бесконечно малого количества теплоты $$ Delta Q$$, переданного системе, к изменению $$ Delta T$$ его температуры, вызванного этим количеством теплоты.
$$ C={displaystyle frac{Delta Q}{Delta T}}$$ — теплоёмкость тела (системы).
Единицей измерения этой величины будет $$ left[Cright]={displaystyle frac{1mathrm{Дж}}{mathrm{К}}}$$.
Численное значение теплоёмкости тела показывает, какое количество теплоты потребуется для изменения температуры всего тела на `1` градус по шкале Цельсия (Кельвина).
При расчётах чаще пользуются удельной теплоёмкостью (теплоёмкостью `1` кг вещества).
называют отношение теплоёмкости тела (системы) к массе этого тела (системы):
| $$ {c}_{mathrm{уд}}={displaystyle frac{C}{m}}={displaystyle frac{Delta Q}{m· Delta T}}$$ — удельная теплоёмкость тела (системы). | (1) |
Единицей измерения этой величины будет $$ left[cright]={displaystyle frac{1mathrm{Дж}}{mathrm{кг}·mathrm{К}}}$$.
называют отношение теплоёмкости тела (системы) к количеству вещества в этом теле (системе):
| $$ {c}_{mathrm{мол}}={displaystyle frac{C}{nu }}={displaystyle frac{Delta Q}{ Delta T·nu }}$$ — молярная теплоёмкость тела (системы). | (2) |
Единицей измерения этой величины будет $$ left[{c}_{mathrm{мол}}right]={displaystyle frac{1mathrm{Дж}}{mathrm{моль}·mathrm{К}}}$$.
Получим соотношение между удельной и молярной теплоёмкостями:
| $$ {c}_{mathrm{мол}}={displaystyle frac{Q}{ Delta T·frac{m}{M}}}={displaystyle frac{Q·M}{ Delta T·m}}={c}_{mathrm{уд}}·M$$ — соотношение между молярной и удельной теплоёмкостями | (3) |
Теперь найдём молярную теплоёмкость идеального газа при изобарном и при изохорном процессах.
При изобарном процессе присутствуют и $$ Delta U$$, и $$ {A}^{text{‘}}$$, следовательно:
$$ {c}_{p}={displaystyle frac{Q}{nu · Delta T}}={displaystyle frac{Delta U+Atext{‘}}{nu · Delta T}}={displaystyle frac{Delta U}{nu Delta T}}+{displaystyle frac{Atext{‘}}{nu Delta T}}={displaystyle frac{frac{i}{2}nu R Delta T}{nu Delta T}}+{displaystyle frac{nu R Delta T}{nu Delta T}}={displaystyle frac{iR}{2}}+R=R{displaystyle frac{i+2}{2}}$$,
$${c}_{p}=R{displaystyle frac{i+2}{2}}$$ — молярная теплоёмкость газа при изобарном процессе.
При изохорном процессе работа не совершается, $$ {A}^{text{‘}}=0$$, следовательно:
$$ {c}_{V}={displaystyle frac{Q}{nu Delta T}}={displaystyle frac{Delta U+{A}^{text{‘}}}{nu Delta T}}={displaystyle frac{Delta U}{nu Delta T}}={displaystyle frac{frac{i}{2}nu R Delta T}{nu Delta T}}={displaystyle frac{iR}{2}}$$
$$ {c}_{V}=R{displaystyle frac{i}{2}}$$ — молярная теплоёмкость газа при изохорном процессе.
Соотношение между $$ {c}_{V}$$ и $$ {c}_{р}$$ можно записать в двух формах:
1) $$ {c}_{p}={c}_{V}+R$$ — закон Майера, и
2) $$ gamma ={displaystyle frac{{c}_{p}}{{c}_{V}}}$$ — коэффициент Пуассона.
Т. к. мы уже знаем, чему равно число степеней свободы у разных молекул, то можем вычислить и значения $$ {с}_{р}$$ и $$ gamma $$:
|
формула |
Одноатомные `(i = 3)` |
Двухатомные `(i = 5)` |
|||
| `c_p` |
`R((i+2)/2)` |
`5/2 R` |
`20,775 “Дж”/(“моль”*”К”)` | `7/2 R` | `29,085 “Дж”/(“моль”*”К”)` |
|
`gamma` |
`(i+2)/i` |
`5/3` |
`1,66667` |
`7/5` |
`1,4` |
Воздух представляет собой смесь газов, преимущественно двухатомных азота и кислорода, потому для него эксперименты дают значение $$ gamma approx mathrm{1,4}$$.
Для твёрдых тел теплоёмкости $$ {с}_{р}$$ и $$ {c}_{V}$$ будут почти одинаковыми. Это можно показать следующим образом. По определению $$ C={displaystyle frac{Delta Q}{ Delta T}}$$, но $$ Delta Q= Delta U+pDelta V$$, тогда
$$ {C}_{p}={displaystyle frac{Delta U+pDelta V}{ Delta T}}={displaystyle frac{Delta U}{ Delta T}}+{displaystyle frac{pDelta V}{ Delta T}}={C}_{V}+{displaystyle frac{pDelta V}{ Delta T}}$$.
При нагревании твёрдых или жидких тел изменение объёма составляет около $$ {10}^{-6}$$ первоначального объёма, поэтому вторым слагаемым можно пренебречь по сравнению с первым, что и позволяет говорить о равенстве $$ {c}_{p}={c}_{V}$$.
Для газов $$ frac{ Delta V}{V}$$ на два порядка больше, чем для твёрдых или жидких тел, потому пренебрегать вторым слагаемым нельзя, более того, оно будет составлять заметную долю теплоёмкости $$ {c}_{p}$$.
