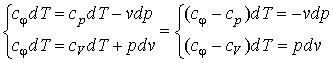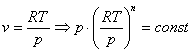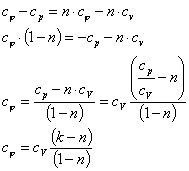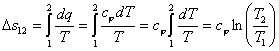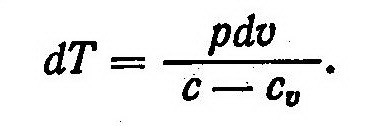Как найти теплоемкость при политропном процессе

Как найти теплоемкость при политропном процессе

До сих
пор рассматривались процессы, у которых
имелись вполне определенные признаки:
изохорный процесс осуществлял­ся при
постоянном объеме; изобарный — при
постоянном давле­нии; изотермический
— при постоянной температуре;
адиабат­ный— при
отсутствии теплообмена между рабочим
телом и внеш­ней средой. Наряду с этими
процессами можно представить еще
бесконечное множество процессов, у
которых имеются другие постоянные
признаки.

Условились всякий
процесс идеального газа, в котором
удель­ная теплоемкость является
постоянной величиной, называть политропным
процессом, а линию процесса — политропой.

Из определения
политропного процесса следует, что
основные термодинамические процессы
— изохорный, изобарный, изотерми­ческий
и адиабатный,— если они протекают при
постоянной удель­ной теплоемкости,
являются частными случаями политропного
процесса. Итак, политропный процесс
проходит при постоянной теплоемкости.

Если теплоемкость
зависит от температуры, то нужно найти
среднюю теплоемкость, чтобы процесс
стал политропным.

Уравнение процесса

Для исследования
процесса и расчета слагаемых I закона
термодинамики нужно установить связь
между параметрами состояния в политропном
процессе. Эта функция называется
уравнением политропы. Запишем уравнение
I закона термодинамики, преобразуем

и поделим почленно

Так
как  = const в
процессе, то левая часть  = const и
называется показатель политропы:

n = ,   

При
этом, каждому
значению n соответствует
некоторый конкретный процесс.

Получили
дифференциальное уравнение:

n=

Разделяем переменные

и интегрируем в
пределах процесса

Потенцируем

  или   

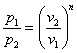
Это
выражение выполняется не только для
крайних точек процесса, но и для всех
промежуточных. Оно называется  уравнением
политропы:

Запишем
это уравнение через другие параметры
P-T   и  V-T:

Теплоемкость политропных процессов

Теплоемкость
политропного процесса  можно
определить из выражения

 = n

где k –
показатель адиабаты.

Найдем
значение   и  n  для
изопроцессов определения  сведем
результаты в таблицу

процесс

n

T=const

1

p=const

0

v=const

q=const

0

k

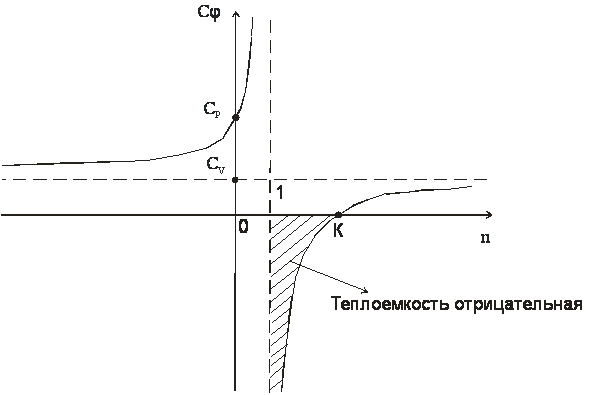
Изобразим
зависимость (n)
графически

В
деапазоне 1<n<k теплоемкость
процессов отрицательная, т.е. с подводом
теплоты температура системы уменьшается,
а с отводом теплоты – увеличивается.

Смысл отрицательной
теплоемкости заключается в том, что вся
подведенная теплота расходуется на
работу и, кроме этого, на работу
затрачивается еще и часть внутренней
энергии системы

 

dq=du+dl        подвод
тепла

dq=du+dl      отвод
тепла

Энергетические характеристики политропных процессов Изменение энтропии

По аналогии с
интегралом работы было получено выражение
для подсчета количества теплоты в ТДП.
Для этого был введен параметр состояния
системы – энтропия.

Энтропия
является функцией состояния. Ее изменение
в пределах процесса определяется как
разность конечного и начального значений.
Также как внутренняя энергия она
определяется с точностью до произвольной
постоянной. В ТДП нужно знать только ее
изменение. Энтропия, и ее изменение не
поддается физическому определению и
измерению, а является расчетной величиной.

                        

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 апреля 2022 года; проверки требуют 3 правки.

Статья является частью одноименной серии.
Тепловые процессы
Thermodynamics navigation image.svg
  • Адиабатический процесс
  • Изохорный процесс
  • Изобарный процесс
  • Изотермический процесс
  • Изоэнтропийный процесс
  • Изоэнтальпийный процесс
  • Политропный процесс
См. также «Физический портал»

Политро́пный процесс, политропи́ческий процесс — термодинамический процесс, во время которого теплоёмкость газа остаётся неизменной.

В соответствии с сущностью понятия теплоёмкости C={delta Q over delta T}, предельными частными явлениями политропного процесса являются изотермический процесс, теплоёмкость которого бесконечна (delta T=0), и адиабатный процесс, который протекает без подвода теплоты, и, следовательно, теплоёмкость которого равна нулю (delta Q=0).

В случае идеального газа, изобарный процесс и изохорный процесс также являются политропными (удельные теплоёмкости идеального газа при постоянном объёме и постоянном давлении соответственно равны iR/(2M) и (i+2)R/(2M), (где R — универсальная газовая постоянная, M — молярная масса, i — число степеней свободы) и не меняются при изменении термодинамических параметров).

Показатель политропы[править | править код]

Кривая на термодинамических диаграммах, изображающая политропный процесс, называется «политропа». Для идеального газа уравнение политропы может быть записано в виде:

{displaystyle PV^{n}=const,}

где P — давление, V — объём газа, n — «показатель политропы», причём

{displaystyle n={c-c_{P} over c-c_{V}}.}

Здесь c — теплоёмкость газа в данном процессе, {displaystyle c_{P}} и c_{V} — теплоёмкости того же газа, соответственно, при постоянном давлении и объёме.

В зависимости от вида процесса, можно определить значение n:

Различные значения показателя политропы n

Значение
показателя политропы 		Уравнение Описание процесса
n<0 — Хотя этот случай не имеет практического значения для наиболее распространённых технических приложений, показатель политропы может принимать отрицательные значения в некоторых специальных случаях, рассматриваемых, например, в некоторых состояниях плазмы в астрофизике.[1]
n=0 {displaystyle PV^{0}=P=const} Изобарный процесс (протекающий при постоянном давлении). Происходит как изменение внутренней энергии, так и совершение работы
n=1 {displaystyle PV=NkT} Изотермический процесс (протекающий при постоянной температуре). Следуя из основного уравнения МКТ для идеального газа и первого начала термодинамики, внутренняя энергия идеального газа в данном процессе не меняется, и вся подведённая теплота затрачивается на совершение работы. Однако, это не справедливо для реальных газов, внутренняя энергия которых зависит и от температуры, и от объёма
1<n<gamma — Квазиадиабатические процессы, протекающие, например, в двигателях внутреннего сгорания во время расширения газа.
n=gamma {displaystyle PV^{gamma }=const} gamma ={displaystyle {frac {C_{P}}{C_{V}}}} — показатель адиабаты, используемый при описании адиабатического процесса (происходит без теплообмена газа с окружающей средой. Обмен энергией термодинамической системы с окружающей средой исключительно за счёт совершения работы).
n=infty — Изохорный процесс (протекающий при постоянном объёме. Газ работы не совершает, обмен энергией с окружающей средой только посредством теплообмена).

Когда показатель n лежит в пределах между любыми двумя значениями из указанных выше (0, 1, gamma , или infty ), это означает, что график политропного процесса заключён между графиками соответствующих двух процессов.

Заметим, что 1<gamma <2, так как {displaystyle gamma ={frac {C_{P}}{C_{V}}}={frac {C_{V}+R}{C_{V}}}=1+{frac {R}{C_{V}}}={frac {C_{P}}{C_{P}-R}}.}

Примечания[править | править код]

  1. ↑ Horedt G. P. Polytropes: Applications In Astrophysics And Related Fields Архивная копия от 15 декабря 2018 на Wayback Machine, Springer, 10/08/2004, pp.24.
Источник
Автор статьи

Сергей Феликсович Савельев

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Что такое политропический процесс

Определение

Политропическим или политропным процессом называют процесс, который происходит при неизменной теплоемкости. Все уравнения изо процессов и адиабатный процесс можно легко получить изменяя показатель политропы. Так, при изохорном процессе молярная теплоемкость равна ${(c}_{mu V})$:

[c_{mu V}=frac{i}{2}R left(1right).]

При изобарном ($c_{mu p}$):

[c_{mu p}=frac{i+2}{2}R left(2right).]

При изотермическом процессе теплоемкость равна $pm infty $. При адиабатическом процессе теплоемкость равна нулю.

Уравнение политропы для идеального газа

Получим уравнение политропы для идеального газа, следуя тому, что теплоемкость должна быть постоянна.

Запишем первое начало термодинамики в виде:

[СdT=C_VdT+pdV (3)]

Из уравнения Менделеева — Клайперона для идеального газа:

[pV=nu RTto T=frac{pV}{nu R}left(4right).]

Из соотношения Майера:

[C_p-C_V=nu R left(5right).]

Подставим (5) в (4), получим:

[T=frac{pV}{C_p-C_V}to p=frac{T(C_p-C_V)}{V} left(6right).]

Разделим уравнение (3) $T $, получим:

[frac{С-C_V}{T}dT=frac{(C_p-C_V)}{V}dVto frac{dT}{T}=frac{(C_p-C_V)}{(С-C_V)}frac{dV}{V} (7)]

Очевидно, что если теплоемкость процесса постоянная, то

[frac{(C_p-C_V)}{(С-C_V)}-постоянная величина.]

Уравнение интегрируем, потенцируем, получаем:

[TV^{n-1}=const (8),]

где $frac{left(C_p-C_Vright)}{left(C_V-Сright)}=n-1$.

Уравнение (8) — уравнение политропы в переменных T, V. Используя уравнение Менделеева – Клайперона легко получить политропу в параметрах $p,V$ или $p,T$.

При $С=0$, $n=𝛾$. При $C=infty , n=1$ получаем уравнение Бойля — Мариотта ($T=const$). При С=$C_p$, n=0 — уравнение для $p=const$, при С=$C_V, n=pm infty $- уравнение для $V=const$.

Пример 1

Задание: Идеальный газ совершает политропный процесс. Найти молярную теплоемкость в этом процессе $с_{mu n}$, если $i$ — число степеней свободы для этого газа.

Решение:

Запишем первое начало термодинамики:

[CdT=frac{i}{2}nu RdT+pdV left(1.1right).]

Разделим уравнение на $dT$, получим:

[C=frac{i}{2}nu R+pfrac{dV}{dT} left(1.2right).]

Запишем уравнение процесса:

[TV^{n-1}=const=Bto V=BT^{frac{1}{1-n}}left(1.3right).]

Продифференцируем (1.3):

[frac{dV}{dT}=Bfrac{1}{1-n}T^{frac{n}{1-n}}left(1.4right).]

Используем уравнение Менделеева – Клайперона:

[pV=nu RTto pcdot BT^{frac{1}{1-n}}=nu RTto p=frac{nu R}{B}T^{frac{n}{n-1}}left(1.5right).]

Подставим в (1.2) результаты преобразований (1.4) и (1.5), получим:

[C=frac{i}{2}nu R+frac{nu R}{B}T^{frac{n}{n-1}}Bfrac{1}{1-n}T^{frac{n}{1-n}}=frac{i}{2}nu R+frac{nu R}{1-n}left(1.6right).]

[с_{mu n}=frac{С}{nu }=frac{i}{2}+frac{1}{1-n} left(1.7right).]

Ответ: Выражение для молярной теплоемкости в политропном процессе: $с_{mu n}$=$frac{i}{2}+frac{1}{1-n}$.

«Политропический процесс» 👇

Пример 2

Задание: Можно ли вычислить работу газа по формуле:

[A=frac{p_1V_1}{n-1}left[1-{left(frac{V_1}{V_2}right)}^{n-1}right] (2.1)]

для адиабатного, изотермического и изобарного процессов?

Решение:

Основанием для решения задачи является уравнение политропы в параметрах $p,V$ (можно и в других):

[pV^n=const left(2.2right).]

Все перечисленные в условиях задачи процессы являются частными случаями политропического процесса. Рассмотрим адиабатный процесс. Для него $n=gamma$. Подставим показатель адиабаты в (2.1) вместо n, получим:

[A_1=frac{p_1V_1}{gamma -1}left[1-{left(frac{V_1}{V_2}right)}^{gamma -1}right] (2.3)]

Сравним с уравнением работы для адиабатного процесса, которое было рассмотрено в разделе, посвященном этому процессу, имеем:

[A=frac{nu RT_1}{gamma -1}left[1-{left(frac{V_1}{V_2}right)}^{gamma -1}right] left(2.4right).]

Если учесть, что из уравнения Менделеева-Клайперона:

[p_1V_1=нRT_1 left(2.5right),]

то получаем, что выражения (2.3) и (2.4) эквивалентны.

Рассмотрим изотермический процесс. Для него $n=1$, соответственно, уравнение политропы имеет вид:

[pV=const left(2.6right).]

Уравнение (2.6) известный закон Бойля — Мариотта. Подставим $n=1$ в (2.1), получим:

[A=frac{p_1V_1}{1-1}left[1-{left(frac{V_1}{V_2}right)}^{1-1}right] left(2.7right).]

Мы получили, что работа стремится к $infty $. Следовательно, приведенная формула (2.1) для вычисления работы в изотермическом процессе не подходит.

Рассмотри изобарный процесс. Для него $n=0$. Уравнение политропы примет вид:

[pV^0=const to p=const left(2.8right).]

Подставим $n=0$ в выражение для работы (2.1), получим:

[A=frac{p_1V_1}{0-1}left[1-{left(frac{V_1}{V_2}right)}^{0-1}right]=p_1left(frac{V_2}{V_1}-1right)=pleft(V_2-V_1right)left(2.9right).]

Выражение (2.9) соответствует формуле вычисления работы для изобарного процесса.

Ответ: Данная формула подходит для вычисления работы в процессах: адиабатном и изобарном, не подходит для вычисления работы в изотермическом процессе.

Пример 3

Задание: Газ участвует в политропическом процессе. Пусть уравнение процесса задано в параметрах $p,V$ при каких значениях $n$

  1. Температура растет при расширении газа?
  2. Температура падает при увеличении объема?
  3. T=const при увеличении объема?

Решение:

Уравнение политропы имеет вид:

[{pV}^n=const left(3.1right).]

Рассматривая уравнение (3.1), сразу можно дать ответ на третий вопрос: температура постоянна при n=0, так как в таком случае мы получаем закон Бойля – Мариотта:

[pV=const left(3.2right).]

Если перейти от (3.1) в уравнение политропы в параметрах T, V, то ответим и на два первых вопроса. Для перехода используем уравнение Менделеева — Клайперона (возьмем его для одного моля, что не нарушит общности рассуждений):

[pV=to p=frac{RT}{V}left(3.3right).]

Подставим (3.3) вместо p (3.2), получим:

[TV^{n-1}=const’to T=B’V^{1-n}left(3.4right).]

Для того, чтобы определить, что происходит с температурой согласно уравнению (3.4), необходимо сравнить $1-n$ с нулем. Если $1-n>0$, то с ростом $V$ растет и $T$. И наоборот.

  1. $1-n>0, to n
  2. $1-n1$ при таком n, если $Vuparrow , то Tdownarrow$.

Ответ: Температура растет при расширении газа если $n1$. $T=const$ при увеличении объема, если $n=0$.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

      Здравствуйте! В процессах изменения состояния газа переменными часто являются все параметры состояния (температура, давление, удельный объем), причем в некоторых процессах может изменяться и теплоемкость. Для того чтобы рассчитать такой процесс, необходимо знать зависимость теплоемкости от параметров процесса. Расчет значительно упрощается, если теплоемкость считать постоянной.Политропным называют процесс, происходящий при постоянной теплоемкости и вызываемый подводом тепла к рабочему телу или отводом тепла от него (название происходит от греческих слов «поли» — много и «тропос» — путь). В политропном процессе в общем случае могут изменяться все параметры и функции состояния.

     Для вывода уравнения политропного процесса продифференцируем уравнение Клапейрона :

ф1(1)

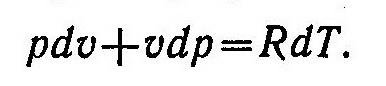
Из выражений dq=du+pdυ и du=cudT найдем

ф2(2)

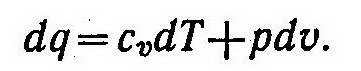
Подставив в это соотношение равенство dq = cdT, будем иметь

ф3(3)

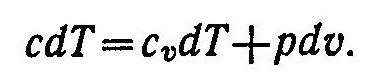
Из выражения (3) найдем

ф4

После подстановки этого равенства в выражение (1) получим

ф5(4)

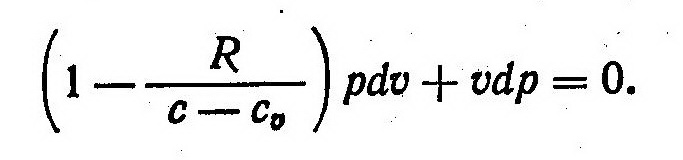
Величину газовой постоянной определим из уравнения Майера cp = cυ + R.

R = cp — cυ

Подставив величину R в выражение (4), и выполнив некоторые преобразования, найдем

ф6(5)

рис 1

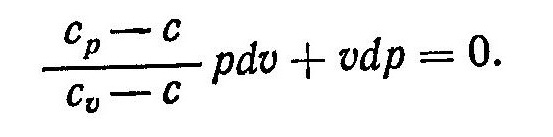
Разделив уравнение (5) на pυ и введя обозначение

ф7(6)

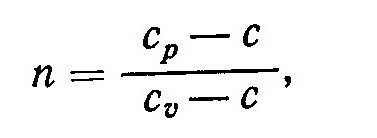
получим

ф8(7)

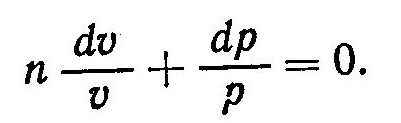
Интегрирование этого выражения возможно при условии n = const, то есть c=const. После интегрирования уравнения (7) получим

фор 9(8)

      Выражение (8) называют уравнением политропы. Оно определяет связь между параметрами состояния p и υ в политропном процессе. Величина n, которая находится из соотношения (6), называется показателем политропы. Показатель n является функцией теплоемкости и, как и теплоемкость зависит от характера процесса. Для анализа частных случаев процесса требуется знать соответствующий показатель политропы n.

     При изохорном процессе (c=cυ) функция (6) претерпевает бесконечный разрыв, изменяясь от n = +∞ до n — ∞. При изобарном процессе (с = ср) показатель n = 0. Следовательно, показатель политропы n в зависимости от характера процесса может изменяться в широких пределах, принимая любые значения от —∞ до +∞.
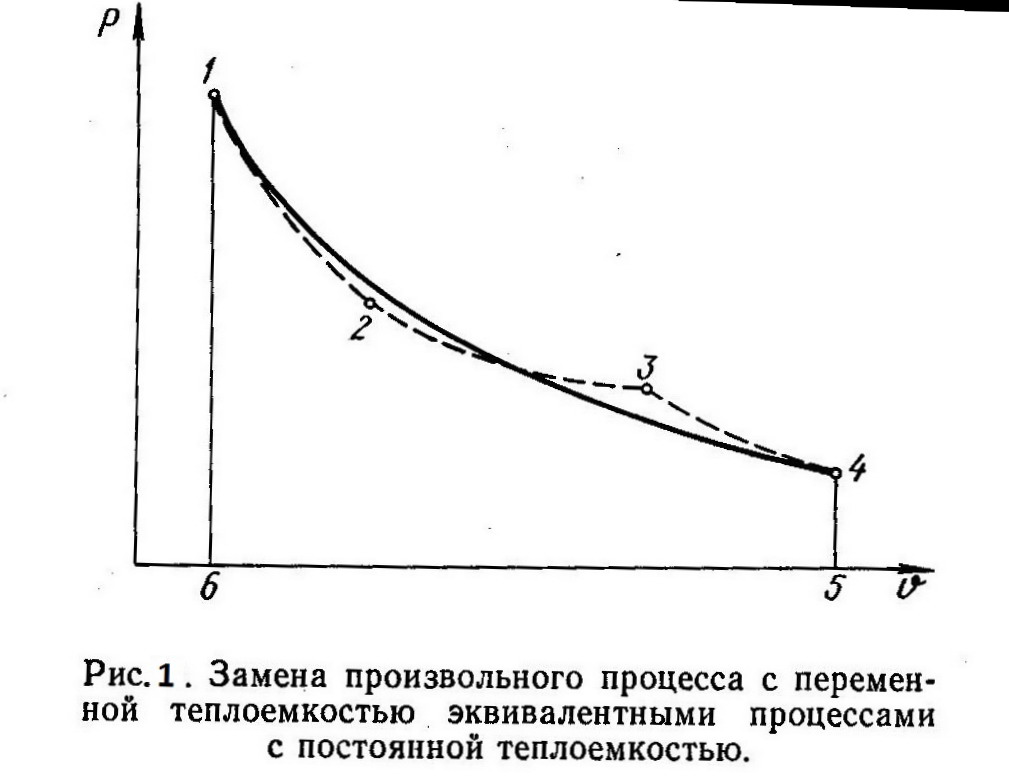
С помощью политропного процесса можно приближенно описать и рассчитать любой процесс изменения состояния 1—4 (рис. 1), для которого теплоемкость является переменной величиной. При этом произвольный процесс 1—4 необходимо заменить несколькими эквивалентными политропными процессами (процессы 1—2, 2—3 и 3—4), которые отличаются друг от друга постоянными значениями теплоемкости.

      Замена должна производиться таким образом, чтобы работа в процессе 1—4 была равна работе на пути 1—2 — 3—4, то есть, чтобы были равны площади, ограниченные соответствующими кривыми процессов и ординатами 1—6 и 4—5. Так как изменение внутренней энергии ∆u на участке 1—4 не зависит от пути процесса (∆u=const), то, согласно уравнению q = ∆u + l первого закона термодинамики, количество теплоты в обоих случаях будет также одинаково. Погрешности, обусловленные такой заменой, окажутся тем меньшими, чем большим числом эквивалентных политропных участков будет заменен произвольный процесс 1—4, протекающий при переменной теплоемкости. Исп. литература: 1) Теплотехника, под общей ред. И.Н. Сушкина, Москва, «Металлургия», 1973. 2) Теплотехника, Бондарев В.А., Процкий А.Е., Гринкевич Р.Н. Минск, изд. 2-е,”Вышейшая школа”, 1976.

Источник

Добавить комментарий