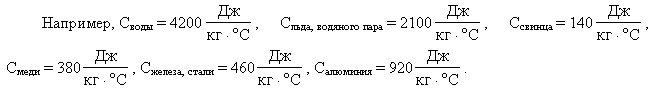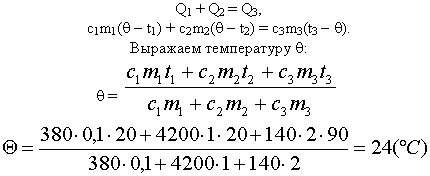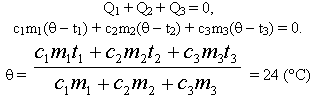Как найти теплообмен формула - Сайт, где вы сможете решить свои вопросы

Heat is a measure of thermal energy that can be transferred from one point to another. Heat is the transfer of kinetic energy from an energy source to a medium or from one medium or object to another medium or object.

Heat is one of the important components of phase changes associated with work and energy. Heat is also the measure of kinetic energy possessed by the particles in a system. The kinetic energy of the particles in the system increases with the increase in the temperature of the system. Hence heat measure changes with time.

Heat Transfer

When a system at a higher temperature is brought in contact with a system at a lower temperature, energy is transferred from the particles in the first system to the particles in the second. Therefore, heat transfer can be defined as the process of transfer of heat from an object (or a system) at a higher temperature to another object (or a system) at a lower temperature.

Heat Transfer Formula

The heat transfer formula determines the amount of heat transferred from one system to another.

Q = c × m × ΔT

Where,

Q is the heat supplied to the system

m is the mass of the system

c is the specific heat capacity of the system

ΔT is the change in temperature of the system

The specific heat capacity (c) is defined as the quantity of heat (in Joules) absorbed per unit mass (kg) of the material when its temperature increases by 1 K (or 1 °C). Its units are J/kg/K or J/kg/°C.

Derivation of the Formula

Let m be the mass of the system and c be the specific heat capacity of the system. Let ΔT be the change in temperature of the system.

Then the amount of heat supplied (Q) is the product of the mass m, specific heat capacity c and change in temperature ΔT and is given by,

Q = c × m × ΔT

Types of Heat Transfer

There are three types of heat transfer:

Conduction
Convection
Radiation

Conduction

The transfer of heat through solid materials is called conduction. The formula for heat transferred by the process of conduction is expressed as:

Q = kA(T_Hot-T_Cold)t/d

Where,

Q is heat transferred through conduction

k is thermal conductivity of the material

A is the area of the surface

T_Hotis the temperature of the hot surface

T_Cold is the temperature of the cold surface

t is time

d is the thickness of the material

Convection

The transfer of heat through liquids and gases is called convection. The formula for heat transferred by the process of convection is expressed as:

Q = H_cA(T_Hot-T_Cold)

Where,

Q is heat transferred through convection

H_c is the heat transfer coefficient

A is the area of the surface

T_Hotis the temperature of the hot system

T_Cold is the temperature of the cold system

Radiation

The transfer of heat through electromagnetic waves is called radiation. The formula for heat transferred by the process of radiation is expressed as:

Q = σ (T_Hot– T_Cold)⁴A

Where,

Q is heat transferred through radiation

σ is Stefan Boltzmann Constant

T_Hotis the temperature of the hot system

T_Cold is the temperature of the cold system

A is the area of the surface

Stefan Boltzmann Constant (σ) is calculated as:

σ = 2.π⁵ K_B⁴ / 15 h³ c² = 5.670367(13) × 10^-8 J . m^-2. S^-1 . K^-4

Where,

σ is Stefan Boltzmann Constant

pi(π) ∼= 3.14

k_Bis Boltzmann constant

h is Planck’s constant

c is speed of light in vacuum

Sample Problems

Problem 1: A system with a mass of 10 kg and an initial temperature of 200 K is heated to 450 K. Specific heat capacity of the system is 0.91 KJ/kg K. Calculate the heat gained by the system in this process.

Solution:

According to question,

Mass, m = 10 kg

Specific heat capacity, c = 0.91 KJ/kg K

Initial temperature, T_i=200 K

Final temperature, T_f = 450 K

Change in temperature, ΔT = 450K – 200K = 250K

Using the heat transfer formula,

Q = c × m × ΔT

Q = 0.91 x 10 x 250

Q = 2275 KJ

Therefore the total heat gained by the system is 2275 KJ.

Problem 2: The specific heat of iron is 0.45 J/g°C. What mass of iron is required for a heat transfer of 1200 Joules if the temperature change is 40°C?

Solution:

According to question,

Specific heat of iron, c = 0.45 J/g°C

Change in temperature, ΔT = 40°C

Amount of heat transferred, Q = 1200 J

Using the heat transfer formula,

Q = c × m × ΔT

m = Q /(c x ΔT)

m = 1200 /(0.45 x 40)

m = 66.667 g

Therefore required mass of iron for a heat transfer of 1200 Joules is 66.667 grams.

Problem 3: Consider two water columns at different temperatures separated by a glass wall of length 3m and width 1.5m and a thickness of 0.005m. One water column is at 380K and the other is at 120K. Calculate the amount of heat transferred if the thermal conductivity of glass is 1.4 W/mK.

Solution:

According to question,

Thermal Conductivity of glass, k = 1.4 W/mK.

Temperature of first water column, T_{Hot= 380K}

Temperature of second water column, T_{Cold = 120K}

Area of the glass wall separating two columns, A = length x width = 3m x 1.5m = 4.5m²

Thickness of the glass, d = 0.005m

Using the heat transfer formula for conduction,

Q = kA(T_Hot-T_Cold)t / d

Q = 1.4 x 4.5 (380-120) / 0.005

Q = 327600 W

Therefore, amount of heat transferred is 327600 Watts.

Problem 4: Calculate heat transfer through convection if the heat transfer coefficient of a medium is 8 W/(m² K) and the area is 25 m² and the temperature difference is 20K.

Solution:

According to question,

Heat transfer coefficient, H_c = 8 W/(m² K)

Area, A = 25m²

Change in temperature, (T_Hot – T_Cold)= 20K

Using the heat transfer formula for convection,

Q = H_cA(T_Hot-T_Cold)

Q = 8 x 25 x 20

Q = 4000 W

Therefore, amount of heat transferred through convection is 4000 Watts.

Problem 5: Calculate the heat transferred through radiation between two black bodies at temperatures 300K and 430K and the area of the medium is 48 m². (Given Stefan Boltzmann Constant, σ = 5.67 x 10^-8 W/(m²K⁴) ).

Solution:

According to question,

Temperature of hot body, T_Hot= 430K

Temperature of cold body, T_Cold = 300K

Change in temperature, (T_Hot– T_Cold) = 430K – 300K = 130K

Area, A = 48 m²

Stefan Boltzmann Constant, σ = 5.67 x 10^-8W/(m²K⁴)

Using the heat transfer formula for radiation,

Q = σ (T_Hot-T_Cold)⁴A

Q = 5.67 x 10^-8x 130⁴ x 48

Q = 777.3 W

Therefore, amount of heat transferred through radiation is 777.3 Watts.

Last Updated :
08 Mar, 2022

Like Article

Save Article

Источник

Определение

Термодинамика — это одна из основных частей физики. Она применяется в таких отраслях как: гидродинамика, аэродинамика, оптика, физическая химия и другие прикладные разработки.

Возникновение термодинамики относят к 19 веку, ведь именно в этот момент начала развиваться теплотехника. А термодинамика является ее теоретической основой.

Содержание современное термодинамики:

Изучение законов тепловой формы движения материи и все связанные с этим явления.

Цель термодинамики — это изучение общих закономерностей преобразования энергии.

При этом обязательно учитывается внутренняя энергия тел (Q ) , а именно ее изменение.

При этом меняться она может двумя способами:

Совершение работы над системой. То есть преобразования механической энергии во внутреннюю энергию.
Передача тепла — теплообмен.

Количество теплоты, которая была получена телом

В процессе теплообмена изменение внутренней энергии тела, это ни что иное как результат работы внешних сил. Однако это не та работа, которая связана со сменой внешних параметров системы, а работа производится благодаря молекулярным силам.

Пример 1

Соприкосновение тела и горячего газа. При таком взаимодействии через столкновение молекул тела с молекулами газа происходит передача энергии газа.

Мера измерения, которая применяется в процессе теплообмена при изменении внутренней энергии тела выступает количество тепла (Q).

Виды теплообмена:

теплопроводность;
конвекция (конвективный теплообмен);
излучение (теплообмен при помощи излучения).

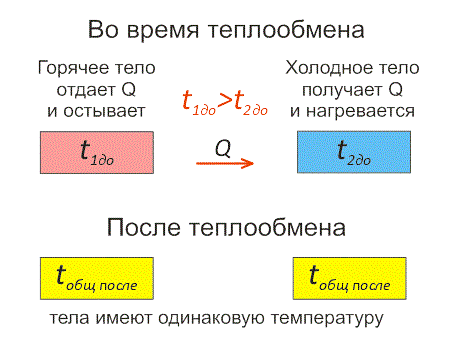
Рассмотрим пример с помощью рисунка теплообмена ниже.

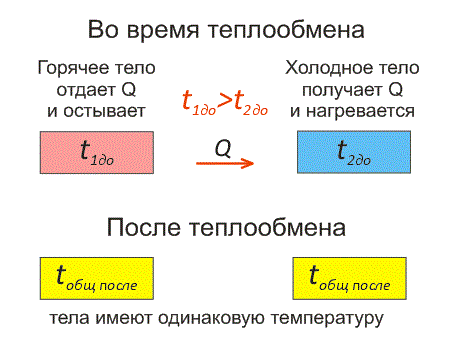
Пример 2

Есть два тела:

Одно имеет более высокую температуру и второе — низкую температуру.

Первое будет остывать и отдавать тепловую энергию до тех пор, когда температура двух тел не станет идентичной. Это будет называться тепловым равновесием взаимодействующих тел.

Когда работ в системе не совершается, но при этом к ней проводится тепло. При таком раскладе в соответствии с законом сохранения энергии (первым началом термодинамики) все тепло, которое будет передано системе, идет на увеличение внутренней энергии системы:

[Delta Q=Delta U text { (№1) }]

В этом случае, [triangle U] каждого тела при нагревании будет равняться массе тела (m) умноженной на удельную теплоемкость вещества (c) и умноженное на изменение температуры тела [(triangle T)].

[Delta U=m c Delta T(text { №2) }]

При плавлении и кристаллизации для расчета [triangle U] будет использована следующая формула:

[Delta U=pm lambda m text { (№3) }]

[lambda-] удельная теплота плавления или кристаллизации вещества.
m — масса тела.
Для определения при конденсации или парообразования применяем:

[Delta U=pm r m text { (№4) }]

r — удельная теплота конденсации или парообразования.
m — масса тела.

При этом не следует забывать, что все вышеупомянутые процессы: плавление, кристаллизация, конденсация, парообразование происходят без изменения температуры, то есть при постоянной температуре.

По изложению формул под номерами три и четыре, мы можем ясно увидеть, что изменение внутренней энергии системы не зависит от температуры.
Когда топливо полностью подлежит сгоранию выделяется теплота, которую можно определить с помощью следующей формуле:

[Delta Q=Delta U=q m text { (№5) }]

q — удельная теплота сгорания топлива.
m — масса тела.

Сохранение тепловой энергии и уравнение теплового баланса

При остывании одного тела, происходит отдача тепловой энергии, то есть теплообмен с окружающей средой. Утерянная теплота Q будет иметь знак “минус”.

При нагревании тела — оно получает тепловую энергию. И та приобретенная теплота Q будет иметь знак “плюс”.

Формулы

В изолированной системе может происходить только теплообмен. Один из главных законов в физике, а именно в термодинамике, является закон сохранения и превращения энергии.

В том случае, когда в системе, которая изолирована, не происходит никаких процессов превращений кроме теплообмена, количество теплоты, которая будет отдана телами (их внутренняя энергия будет уменьшаться) будет равна количеству тепла полученного телами (их внутренняя энергия будет увеличиваться). Но не смотря на процесс теплообмена, общая -суммарная энергия системы будет неизменна и мы сможем записать первое начало термодинамики с помощью формулы:

[Delta U=sum_{i=1}^{n} Delta U_{i}=0(mathrm{№} 6)]

Это и является уравнением теплового баланса.
Также можно его выразить иначе. Общее количество тепла, которое выделилось в изолированной системе будет равное суммарному количеству тепла, которое было поглощено в системе. Записать это можно в следующем виде:

[Q_{1}+Q_{2}+Q_{2}+ldots+Q_{n}=Q_{1}^{prime}+Q_{2}^{prime}+Q_{2}^{prime}+ldots Q_{k}^{prime} text { (№7). }]

Если брать смысл теплового баланса, он заключается в сохранении энергии для процессов, связанных с теплообменом в термоизолированных системах.

Нет времени решать самому?

Наши эксперты помогут!

Пример теплообмена между холодным и горячим телом

Пример 3

В горячую воду с температурой +80 градусов Цельсия, которая имеет массу двести грамм, добавили охлажденную воду, имеющею температуру +15 градусов Цельсия с массой сто грамм.

Вопрос:

Какая температура будет у смешанной воды после того, как произойдет тепловое равновесия?

Примечание: не учитывать теплообмен с окружающей средой.

В данном случае, мы с вами рассмотрим упрощенную задачу, для лучшего понимания закона сохранения энергии. В данной задаче, мы не будем учитывать осуществляемый теплообмен с емкостью, которая наполнена водой.

Решение:

Считаем систему изолированной, так как в условии было сказано, что окружающая среда не будет участвовать в теплообмене.

Из-за того, что теплообмен с окружающей средой и воздухом происходить не будет, вся тепловая энергия, которую получит холодная вода, будет отдана горячей водой

Записываем уравнение теплового баланса:
[Q_{text {остывания горячей воды }}+Q_{text {нагревания холодной воды }}]
Записываем формулу для каждого количества теплоты:
[Q_{text {остывания горячей воды }}=mathrm{C}_{text {воды }}^{*} m_{text {горячей воды }} *left(t_{text {общ }}-t_{text {горячей воды }}right)]
[Q_{text {нагревания холодной воды }}=mathrm{C}_{text {воды }}^{*} m_{text {холодной воды }}^{*}left(t_{text {общ }}-t_{text {холодной воды }}right)]

Примечания:

[c_{воды}] — берем из справочника
Массу воды обязательно переводим в килограммы
Разность [left(t_{text {общ }}-t_{text {горячей воды }}right)] будет с отрицательным знаком, потому что ее окончательная температура будет меньше ее изначальной.

Подставляем выражения и выводим окончательную формулу:
[c_{text {воды }} * m_{text {горячей воды }} *left(t_{text {общ }}-t_{text {горячей воды }}right)+c_{text {воды }} * m_{text {холодной воды }} * left(t_{о б щ}-t_{text {холодной воды }}right)]
Заменяем символы числами:
[begin{aligned}
&4200 * 0,2 *left(t_{text {общ }}-80right)+4200 * 0,1 *left(t_{text {общ }}-15right)=0 \
&840 *left(t_{text {общ }}-80right)+420 *left(t_{text {общ }}-15right)=0
end{aligned}]
Раскрываем скобки и получаем ответ [t_{text {общ }}=58,33]

Ответ: Температура смешанной воды будет равна 58,33 градуса Цельсия.

Пример на определение массы пара

Пример 4

В латунный калориметр, который имеет массу [m_{k}=0.1] килограмм со льдом, который имеет массу [m_{i}=1] килограмм , которые имеют общую температуру [T_{k i}=200 mathrm{~K}], начали пускать пар, который имеет температуру [T_{p}=400 mathrm{~K}]. После этого, в калориметре изменилась температура и стала постоянной [Theta=300 K].

Вопрос:

Какую массу имел пар?

Примечание:

Считать, что система, состоящая из льда, колориметра и пара — изолирована. Следовательно, теплообмена с окружающей средой нет.

Решение:

Исходя из условия задачи, мы можем сделать вывод, что все процессы теплообмена, которые будут происходить в системе, можно описать с помощью уравнения теплового баланса, учитывая агрегатные превращения.

В результате того, что лед плавится при помощи пара, калориметр наполняется водой ( если делать выводы по температуре, которая установилась в калориметре [Theta=300 K=27] градусов Цельсия). Происходит теплообмен сред: пар отдает свою теплоту, а калориметр со льдом её получают.

К исходным данным добавляем справочные:

Удельная теплоемкость пара [c_{p}=1,7 * 10^{3} frac{text { Дж }}{кгК}]
Удельная теплоемкость воды [c_{v}=4,2 * 10^{3}frac{text{ Дж }}{кгК}]
Удельная теплоемкость льда [c_{i}=2,1 * 10^{3} frac{text { Дж }}{кгK}]
Удельная теплоемкость латуни [c_{k}=0,386 * 10^{3} frac{ text { Дж }}{кгК}]
Удельная теплотапарообразования воды [r=2,1 * 10^{6} frac{text { Дж }}{кг}]
Удельная теплотапри плавлении льда [lambda=3,3 * 10^{5} frac{text { Дж }}{кг}]

Чтобы решить данную задачу, мы должны описывать каждую стадию изменения внутренней энергии.

Пар, когда отдает теплоту, начинает остывать от своей температуры [T_{p}] до конденсированной [T_{k o n d}], которая равняется 373 К.
Пар будет конденсироваться при постоянной температуре
Вода, которая была получена из пара будет остывать до температуры [Theta].
Как результат внутренняя энергия пара становится меньше [Delta U_{1}=Q_{o t d}=m_{p} c_{p}left(T_{p}-T_{c o n d}right)+m_{p} r+m_{p} c_{v}left(T_{k o n d}-Thetaright)].
Происходит нагревания льда благодаря тому, что он получает теплоту от пара и он от [T_{k i}] доходит до [T_{text {plav }}] и равняется 273 K.
Плавление льда
Нагревание воды до температуры [Theta].
Как результат, внутренняя энергия льда будет увеличена.
[Delta U_{1}=Q_{text {poluch }}=m_{i} c_{i}left(T_{text {plav }}-T_{k i}right)+m_{i} lambda+m_{i} c_{v}(Theta-T_{text {plav }})]
Происходит теплообмен с калориметром и он нагревается до [Theta].

Составляем уравнение теплового баланса:

[Delta U_{1}=Delta U_{2}+Delta U_{3}]

Для описания всего процесса составим уравнение теплового баланса:

[begin{aligned}
&m_{p} c_{p}left(T_{p}-T_{text {cond }}right)+m_{p} r+m_{p} c_{v}left(T_{text {kond }}-Thetaright)= \
&m_{i} c_{i}left(T_{text {plav }}-T_{k i}right)+m_{i} lambda+m_{i} c_{v}left(Theta-T_{text {plav }}right)+ \
&m_{k} c_{k}left(Theta-T_{k i}right)
end{aligned}]

[m_{p}=frac{m_{i} c_{i}left(T_{p l a v}-T_{k i}right)+m_{i} lambda+m_{i} c_{V}left(Theta-T_{text {plav }}right) m_{k} c_{k}left(Theta-T_{k i}right)}{c_{p}left(T_{p}-T_{text {cond }}right)+r+c_{V}left(T_{text {kond }}-Thetaright)}]

Заменяем символы на цифры:

[begin{aligned}
&m_{p}= \
&frac{1 * 2,1 * 10^{3} *(273-200)+1 * 3,3 * 10^{5}+1 * 4,2 * 10^{3} *(300-273)+0.1 * 3,9 * 10^{3} *}{1.7 * 10^{3} *(400-373)+2,1 * 10^{6}+4,2 * 10^{3} *(373-300)} \
&=frac{9,8 * 10^{5}}{2.5 * 10^{6}}=0.392(кг)
end{aligned}]

Ответ: Масса пара будет равна примерно 392 грамма.

Источник

Теплопередача

Процессы
теплообмена и их показатели

Теплопроводность
(кондукция)
– распространение тепла вследствие
теплового движения частиц вещества.

Конвекция
– процесс распространения тепла в
результате теплопроводности и перемещения
среды; конвективный перенос тепла имеет
место в движущихся жидкостях, газах,
сыпучих телах.

Тепловое
излучение
– превращение тепловой энергии тела в
лучистую и её передача в пространство,
окружающее тело. Процесс передачи тепла,
обусловленный взаимным излучением и
поглощением тепловой энергии между
двумя или несколькими телами, имеющими
разную температуру, называется
теплообменным
излучением.

Теплоотдача
– теплообмен между твёрдой стенкой
(телом) и обтекающей её средой (жидкой,
газообразной или сыпучей).

Теплопередача
– процесс теплообмена между двумя
средами (см. рис. 32), разделёнными
перегородкой (обычно твёрдой, состоящей
из одного или нескольких слоёв).

Формулы
для расчёта стационарных процессов
теплоотдачи
и теплопередачи:

Q=α₁
(t_ж1-t_с1)F₁;

Q=α₂
(t_с2-t_ж2)F₂;

Q=kΔtF;

Где
Q
– количество тепла, ккал/ч:

F₁
и F₂
– наружные поверхности, м²;

t_ж1
и t_ж2
– средние температуры соответственно
греющей и нагреваемой среды ºС;

t_с1
и t_с2
– средние температуры стенки соответственно
воспринимающей и отдающей тепло ºС;

α₁
и α₂
– коэффициенты теплоотдачи соответственно
от греющей среды к стенке и от стенки к
нагреваемой среде, ккал/м²
·ч· ºС,
в системе СИ: α
(вт/м²
·град)=1,163 α (ккал/м²
·ч· ºС);

k
– коэффициент теплопередачи от одной
среды к другой, отнесённый к F,
ккал/м²
·ч· ºС.

Термическое
сопротивление
– величина обратная коэффициентам
теплоотдачи и теплопередачи, (м²
·ч· ºС/ккал):

R₁=[(t_ж1-t_с1)F₁]/Q=1/
α₁;

R₂=[(t_с2-t_ж2)F₂]/Q=1/
α₂;

R=ΔtF/Q=1/
k.

Термическое
сопротивление сложной системы равно
сумме термических сопротивлений её
частей.

Средняя
разность температур или температурный
напор,
Δt
– усреднённая
по поверхности F
нагрева (или охлаждения) разность
температур сред участвующих в теплообмене.
Если
температура одной среды в пределах
поверхности нагрева (охлаждения) не
изменяется, то температурный напор не
зависит от взаимного направления
движения сред.

Среднелогарифмическая
разность температур
дляобеих схем движения теплообменивающихся
сред:

Δt_ср=
(Δt_б–
Δt_м)/[2,3lg(Δt_б
/Δt_м)],
ºС,

Где
Δt_б
– наибольшая разность температур
теплообменивающихся сред, ºС;

Δt_м
– наименьшая разность температур
теплообменивающихся сред, ºС.

Для
вычисления можно пользоваться
номограммой, приведённой на рис. 33.

В
тех случаях, когда Δt_б
/
Δt_м
<1,7, температурный
напор с достаточной точностью определяется
как среднеарифметическая разность
температур:

Δt_ср=
(Δt_б–
Δt_м)/2.

При
любых конечных температурах наибольший
возможный температурный напор достигается
при противотоке, наименьший – при
прямотоке. Все другие схемы течения
приводят к промежуточным значениям
температурного напора.

Плотность
теплового потока:

q=Q/
F=k Δt_ср
ккал/(м²
·ч)

В
системе СИ q
[вт/ м²]=
q 1,163 [ккал/(м²
·ч)].

Характеристика
накипи и коэффициент её теплопроводности
(λ=0,05…0,1γ³
ккал/м²
·ч· ºС,
где γ
– объёмный вес накипи, г/см³)
приведены в таблице 9.1.

Таблица
9.1

Вид накипи	Характеристика накипи	Коэффициент её теплопроводности λ
Загрязнённая маслом	Твёрдая	0,1
Cиликатная CaSiO₃	Твёрдая	0,05 – 0,2
Карбонатная (аморфная) CaСO₃	Мягкая	0,2 – 1
Гипсовая (сульфатная) CaSO₄	Твёрдая	0,5 – 2
Карбонатная (кристаллическая)	От аморфного порошка до твёрдого котельного камня	0,5 – 2
Смешанная	Твёрдая плотная	0,7

Коэффициент
теплопроводности нагара (в цилиндрах
ДВС):

λ_наг=0,116
вт/(м · ºК).

То
же для накипи:

λ_нак=0,
696…2,32 вт/(м · ºК).

Загрязнённая
поверхность теплообмена, особенно со
стороны охлаждения, вызывает повышение
температуры стенок и теплонапряжённости
(слой накипи толщиной 1мм по термическому
сопротивлению эквивалентен 40мм стальной
стенки). Образование на поверхности
поршня лаковой плёнки значительно
ухудшает теплоотдачу ( лаковая плёнка
толщиной 0,15мм уменьшает теплоотдачу
на 40%).

Коэффициент
теплопроводности λ
некоторых сталей и сплавов приведён в
таблице 9.2.

Таблица
9.2

Стали и сплавы	Температура, ºС	λ Вт/м·ºС (ккал/м ·ч· ºС)
Стали	Углеродистые	20 – 500	46 – 35 (40 – 30)
Низкоуглеродистые	20 – 500	27 – 35 (23,5 – 30)
Хромистые нержавеющие	20 – 500	24 -28 (21 – 24)
Хромоникелевые	20 – 500	12 – 22 (10 – 19)
Высоколегированные	100 – 500	15 – 20 (13 – 17)

Алюминиевая бронза	20	82 (71)
Бронза	20	22 – 46 (22 – 40)
Сплавы	Магниевые	20 – 200	58 – 133 (50 – 114)
Медные	20 – 100	13 – 76 (11 – 65)

Коэффициент
теплопроводности мазутов (ккал/м
·ч· ºС)
приведён в таблице 9.3.

Таблица
9.3

Марка мазута	Температура, ºС
30	40	50	60	70
20	0,103	0,102	0,101	0,099	0,098
40	0,116	0,115	0,114	0,113	0,112

Поверхностное
натяжение мазутов в
пределах температур 50 -100ºС
составляет 0,003
– 0,0025кгс/см.

Теплоотдача
через плоскую стенку.

Тепловой
поток между наружными стенками при F=
F₁=
F₂
(смотри рис. 32):

Q=λ
(t_с1-t_с2)F/δ
ккал/ч,

Где
λ
– коэффициент теплопроводности материала
стенки, ккал/м·ч·ºС;

δ
– толщина стенки, м.

Термическое
сопротивление стенки:

R_δ=(t_с1-t_с2)F/Q=
δ/ λ
м²·ч·ºС/ккал.

Коэффициент
теплопередачи через однослойную стенку
(смотри
рис. 32):

k
= 1/(1/ α₁+
δ/ λ +1/ α₂)
ккал/м²
·ч· ºС.

Коэффициент
теплопередачи через многослойную
плоскую стенку (смотри
рис. 32[7]):

k
= 1/(1/ α₁+Σ(
δ_i/
λ_i)
+1/ α₂)
Вт/
м²
· ºС
(ккал/м²
·ч· ºС).

Температура
на внешних поверхностях одно – или
многослойной стенки, ºС:

t_с1
= t_ж1–
Q/( F α₁)
=( t_ж1–
t_ж2
)/ α₁
= t_ж1-q/
α₁;

t_с2
= t_ж2–
Q/( F α₂)
=( t_ж1–
t_ж2
)/ α₂
= t_ж3+q/
α₂.

Теплоотдача
через цилиндрическую стенку.

Условный
коэффициент теплопередачи (для 1 погонного
м) через многослойную цилиндрическую
стенку (смотри
рис. 32[7]):

k_l
= 1/(1/ α₁d₁
+Σ
[2,3lg(d_i+1/
d_i)/2
λ_i]
+1/ α₂
d_т+1)
кВт/м²ч·ºС
(ккал/м²
ч· ºС).

Тепловой
поток через цилиндрический трубопровод:

Q=
k_l
πd₁lΔ
t ккал/ч,
или
Q=
k₂
lπd₂
Δ t,

Где

k_l

и k₂
– коэффициент теплопередачи, отнесённые
соответственно к внутренней и наружной
поверхности цилиндрической стенки; k_l
= k_l/
πd₁
и k₂
= k_l/
πd_2.

При
послойной цилиндрической стенке, у
которой d₂/d₁
<1,25
и при α₁=
α₂
, коэффициент теплопередачи можно
рассчитать как для плоской стенки.

Поверхность
нагрева в этом случае рассчитывается
по среднему диаметру:

F
=0,5π(d₂+d₁)l.

Для
однослойной цилиндрической стенки при
d₂/d₁
<1,25
и при α₁>>α₂
, или α₁<<α₂
коэффициент теплопередачи определяется
как для плоской стенки. При этом
поверхность нагрева (охлаждения)
рассчитывают по тому диаметру, при
котором имеет место наименьшее значение
коэффициента теплопередачи.

Теплоотдача
через оребрённую поверхность.

Оребрение
повышает эффективность теплопередачи,
если рёбра сделаны на стороне стенки,
где коэффициент теплоотдачи значительно
ниже, чем на дугой, теплопроводность
стенки высокая.

Тепловой
поток:

Q=k(t_ж1-t_ж2)F.

Коэффициент
теплопередачи через
оребрённую поверхность :

k
= 1/[1/ α₁+
δ_ст/
λ_ст
+ F /( F_ор
α₂)]
ккал/м²
·ч· ºС,

где
α₂
– средняя величина коэффициента
теплопередачи со стороны оребрённой
поверхности, ккал/м²
·ч· ºС;

δ_ст
– толщина стенки, м;

F
– теплообменная поверхность гладкой
стенки, м;

F_ор
– полная теплообменная поверхность
оребрённой стенки, м².

Тепловая
изоляция трубопроводов.

При
цилиндрической изоляции трубопроводов
тепловые потери трубы уменьшаются,
когда:

δ/
d₂<[d_изα₂2,3lg(d_из/
d₂)]/2
λ_из,

где
α₂
– коэффициент теплопередачи от поверхности
изоляции в окружающую среду, ккал/м²
·ч· ºС;

δ
– толщина изоляции, м;

d₂
– наружный диаметр изолируемого
трубопровода, м;

d_из
– наружный диаметр изоляции, м;

λ_из
– коэффициент теплопроводности изоляции,
ккал/м
·ч· ºС.

Предельная
толщина изоляции в зависимости от
диаметра трубопровода приведена в
таблице 9.4.

Таблица
9.4

Диаметр трубопровода, мм	Толщина изоляции, мм	Примечание
57	65	Для цилиндрических и плоских поверхностей толщина изоляции составляет 150мм
108	110
159	120
267	130
376	140
427	145

Наибольшие
тепловые потери изолированного
трубопровода имеют место при d_из
=2
λ_из
/α₂,
в связи с чем у однослойной изоляции
λ_из
<0,5d_изα₂.

Максимально
допустимые потери тепла через изоляцию
(ккал/м²
·ч)
приведены в таблице 9.5.

Таблица
9.5

Наружный диаметр изолированной цилиндрической поверхности, мм	Температура теплоносителя, ºС
100	150	200	250	300	350	400	450
С 1 погонного м изолированного трубопровода
57	60	80	90	–	–	–	–	–
108	85	110	130	165	180	210	220	245
159	105	135	165	195	215	250	265	290
216	120	160	195	235	260	285	315	345
267	135	185	220	265	295	330	365	395
325	155	210	245	300	335	365	410	445
376	170	230	280	330	365	400	445	490
427	185	255	305	355	395	430	475	525
С 1 м² наружной поверхности изоляции
Цилиндрические поверхности	100	130	150	170	185	200	215	230
Плоские поверхности	100	130	150	180	200	225	250	280

Теплопотери
1
пог. м
можно определить по формуле:

q_l=0,01n
q₀
Δt
ккал/(м·ч),

где
q₀
– тепловые потери (см. таблицу 9.6);

n
– поправочный коэффициент (см. таблицу
9.7).

Δt
– температурный напор, ºС.

Таблица
9.6

Тепловые потери q₀ для трубопровода диаметром 107мм при (t_ж1-t_ж2)=100 ºС
λ_из, ккал/м·ч·ºС	Толщина изоляции, мм
30	40	50	60	70	80	90	100	110	120	130
0,06	72	60	53	47	43	40	37	35	33	31	30
0,07	82	68	61	54	50	45	43	40	39	36	34
0,08	93	78	68	61	55	52	48	45	43	41	39
0,09	103	86	75	67	62	57	54	51	48	46	44
0,10	112	94	83	74	68	63	58	56	53	50	48
0,11	121	102	90	81	74	69	65	61	58	55	53
0,12	130	110	97	88	81	74	70	66	63	60	57
0,13	135	118	104	94	87	80	75	71	68	65	62
0,14	146	125	111	100	92	85	81	77	73	69	67
0,15	154	132	118	106	98	91	86	82	78	71	69

Таблица
9.7

Поправочный коэффициент п
Диаметр трубопро-вода, мм	Толщина изоляции, мм
30	40	50	60	70	80	90	100	110	120	130	140
32	0,44	0,47	0,48	0,49	–	–	–	–	–	–	–	–
57	0,65	0,66	0,66	0,66	0,67	0,70	0,70	0,70	–	–	–	–
76	0,78	0,79	0,80	0,80	0,80	0,81	0,81	0,81	0,82	0,83	–	–
89	0,87	0,87	0,88	0,88	0,89	0,89	0,89	0,89	0,89	0,91	0,91	–
133	1,18	1,18	1,16	1,15	1,14	1,14	1,14	1,13	1,12	1,12	1,12	1,12
159	1,36	1,34	1,34	1,32	1,30	1,30	1,26	1,26	1,26	1,26	1,26	1,26
219	1,78	1,76	1,72	1,67	1,64	1,62	1,60	1,56	1,56	1,56	1,56	1,54
273	2,15	2,08	2,04	1,96	1,92	1,92	1,87	1,82	1,82	1,82	1,82	1,78
325	2,55	2,48	2,40	2,32	2,27	2,25	2,16	2,13	2,10	2,10	2,10	2,05
376	2,90	2,80	2,72	2,60	2,58	2,53	2,45	2,37	2,35	2,33	2,32	2,28

Таблица9.8

Коэффициент теплопроводности, объёмный вес и температура применения теплоизоляционных и огнеупорных материалов
Наименование материала	Объёмный вес, кг/м³	Коэффициент теплопроводности, ккал/м ·ч· ºС	При температуре, ºС	Предельная температура, ºС
Алюминиевая фольга	120-130	0,055	20	550
Асбест	1200	0,25	100	100
Асбестовый картон	1000-1400	0,135+0,00016 t_ср	–	600
Асбестовая ткань: АТ-7, АТ-8, АТ-9	–	0,106+0,000159 t_ср	–	450 450 200
Асбестовый шнур	–	0,12+0,0002 t_ср	–	220
Асбозурит Д	650	0,16	100	900
Асбозурит Т	850	0,20	100	900
Асбослюда	580	0,12-0,118-0,125	0-50-100	600
Асботермит марки 500	500	0,10-0,115	30-100	600
Вата стеклянная	130	0,034+0,0003 t_ср	–	450
Войлок отеплительный	90	0,04-0,05	20	90
Вулканит	400	0,078-0,087	50-100	600
Древесноволкнистые плиты изоляционные	400	0.047	20	100
Изделия из ньювеля	275-300	0,09	200	375
Изделия из совелита	360-380	0,10	200	500
Изделия теплоизоляционные диатомовые	500	0.10-0,16	50-350	900
Магнезиальная мастика	1000	0,2	20	100
Минеральные плиты	350	0.065	30	60
Минеральная вата	200	0,045-0,055	30-100	600
Минеральный войлок	200	0,055	30	60-200
Новоасбозурит марки 600	350	0,12-0,135	30-100	600
Ньювель	350	0,70	50	350
Полихлорвинил	100	0,05	20	70
Пробковые плиты	260	0.05	20	120
Совелит	500	0,085	50	450
Стекловолокно (порошок)	590	0,075	30	–
Шамотные огнеупорные изделия	1900	0,6+0,00055 t_ср	–	1670

КОНВЕНТИВНЫЙ
ТЕПЛОБМЕН.

По
характеру движения теплоносителя
(жидкость, газ) различают конвекцию
вынужденную
под действием внешних сил и свободную,
при которой движение теплоносителя
обусловлено неравномерным распределением
его плотности в потоке в связи с
протеканием процесса теплообмена.
Передача тепла происходит через
пограничный
слой (ламинарный, турбулентный),
и коэффициент теплоотдачи зависит от
физических свойств самого слоя.

В
случаях конвективного теплообмена
различают две задачи:

Внутреннюю,
когда жидкость (газ) движутся внутри
канала;
Внешнюю,
когда жидкость извне омывает поверхность
тела.

Коэффициент
теплоотдачи от среды к стенке и наоборот
определяется через безразмерный критерий
Nu
Нуссельда,
который находится в зависимости от
критериев, определяющих характер
движения (Re
Рейнольдса) и
изменения физических свойств (Pr
Прандтля
и др.).

Для
определения критериев Nu
и Re
можно пользоваться номограммой (рис.
34). На ней сплошные линии используются
для определения α_к
и Nu,
а пунктирные – для определения Re.

Критерии
теплообмена.

Критерии
Рейнольдса

Re=wd/ν,

Где
w
– средняя по сечению скорость потока,
м/сек;

d
–
диаметр цилиндрической поверхности
трубы, смачиваемый потоком, м;
для некруглых каналов применяется
эквивалентный диаметр, м,
для щелей – толщина щели, для пластин
– длина, м;

–
коэффициент кинематической вязкости
среды, м²/сек.

Критерии
Прандтля

Pr=
ν/α=αсγ/λ,

Где
α=λ
/
сγ
– коэффициент температуропроводности,
м²/сек;

с
– истинная изобарная теплоёмкость,
ккал/кг·
ºС;

λ
– коэффициент теплопроводности, ккал/м·ч·
ºС;

γ
– удельный вес, кг/м³.

Критерий
состоит из физических величин, которые
относятся к одной из температур: средней
потока, стенки или пограничного слоя
(среднеарифмитическая между температурами
потока и потока и стенки).

Критерии
Нуссельда

Nu=
α d/λ,

Где
α
–
коэффициент теплоотдачи от среды к
стенке и от стенки к среде, ккал/м²·ч·
ºС;

λ
– коэффициент теплопроводности,
определяемый по средней температуре
потока и температуре стенки, ккал/м·ч·
ºС.

Критерии
Грасгофа

Gr=gl³βΔt
/ν²,

Где
l
– геометрический размер (диаметр трубы
при горизонтальном течении среды или
высота стенки при вертикальном движении
среды), м;

β
– объёмный коэффициент расширения среды;

Δt
– разность температур между средней
температурой потока и температурой
стенки, ºС.

В
случаях внутренней задачи за определяющий
размер принимается эквивалентный
диаметр:

d_эев
=АF/u,

Где
F
– площадь поперечного сечения канала,
м²;

u
– периметр сечения, по которому происходит
передача тепла, м.

Для
круглых труб d_эев
= d_вн.

Зависимости
критерии Нуссельда
дляпроцессов теплообмена определяют
из опыта и представляют в виде эмпирических
формул, при которых указывают диапазон
опытных значений определяющих критериев
и температур. Коэффициент теплоотдачи
находят по критерию Нуссельда:

α=λ
Nu / l=( Re, Pr, Gr, l/ d).

Теплоотдача
от газов к стенке.

Коэффициент
теплоотдачи конвекцией от продуктов
сгорания или воздуха к поверхности
нагрева или от поверхности нагрева к
воздуху можно определить по номограмме
(см. рис. 34[7]).

Номограмма
построена для шахматного и коридорного
пучка труб (рис. 35) при поперечном омывании
их продуктами сгорания, для трубного
пучка при продольном омывании его
воздухом и среднего состава продуктов
сгорания (r_Н₂_О=0,11).

ОБОЗНАЧЕНИЯ:

s₁/d
и s₂/d
– относительные шаги шахматного пучка:
продольный и поперечный;

d
– диаметр трубы, м;

w
– скорость потока, м/сек;

t
– средняя температура потока, ºС;

с_s
– коэффициент, зависящий от s₁/d
и s₂/d;

Z_ш
– число рядов шахматного пучка;

Z_к
– число рядов коридорного пучка;

l/d
– 0тношение длины трубы к диаметру.

ОРДИНАТЫ
НОМОГРАММЫ:

I
– значение Re
для шахматного пучка,

I
I
– значение Re
для коридорного пучка,

I
I I
– значение Re
для пучка при продольном омывании
воздухом.

Пунктирные
линии в правой нижней четверти номограммы
используются для определения Re,
а сплошные – Nu
и коэффициента теплоотдачи.

Пунктирными
стрелками показан ключ и порядок
определения коэффициента теплоотдачи
по номограмме.

Пример
определения коэффициента теплоотдачи.

Предварительно
по заданным значениям s₁/d
и s₂/d
находим коэффициент с_s
(см. график в верхней левой четверти).
При заданных w=5,45м/сек,
d
=50мм и t₂
=300ºС
находим Re
= 6,2 ·10³
на ординате I;
при Z_ш
=20 рядам и с_s=1,3
определяем Nu
=72,5; и перемещаясь по направлению
пунктирной линии ключа, находим α_к
=59
ккал/м²·ч·
ºС.

Максимально
возможная ошибка в определении из-за
изменения состава продуктов сгорания
для нефтяных топлив не превышает 1%.

Теплофизические
параметры сухого воздуха при 760 мм. рт.
ст. приведены в таблице 9.10, а для дымовых
газов – в таблице 9.11.

Таблица
9.10

Теплофизические параметры сухого воздуха при 760 мм. рт. ст
t, ºС	γ, кг/м³	с_р, ккал/кг· ºС	λ ·10², ккал/м·ч·ºС	α, ·10² м²/ч	μ·10⁶, кг·сек/м²	ν ·10⁶, м²/сек	рz
-30	1,543	0,242	1,89	5,37	1,60	10,80	0,723
-20	1,395	0,241	1,96	5,83	1,65	12,79	0,716
-10	1,342	0,241	2,03	6,28	1,70	12,43	0,712
0	1,293	0,240	2,10	6,77	1,75	13,28	0,707
10	1,247	0,240	2,16	7,22	1,80	14,16	0,705
20	1,205	0,240	2,23	7,71	1,85	15,06	0,703
30	1,165	0,240	2,30	8,23	1,90	16,00	0,701
40	1,128	0,240	2,37	8,75	1,95	16,96	0,699
50	1,093	0,240	2,43	9,26	2,00	17,95	0,698
60	1,060	0,240	2,49	9,79	2,05	18,97	0,696
80	1,000	0,241	2,62	10,87	2,15	21,09	0,692
100	0,946	0,241	2,76	12,11	2,23	23,13	0,688
120	0,898	0,241	2,87	13,26	2,33	25,45	0,686
140	0,854	0,242	3,00	14,52	2,42	27,80	0,684
160	0,815	0,243	3,13	15,80	2,50	30,09	0,682
180	0,779	0,244	3,25	17,10	2,58	32,48	0,681
200	0,746	0,245	3,38	18,49	2,65	34,85	0,680
250	0,674	0,248	3,67	21,96	2,79	40,61	0,677
300	0,615	0,250	3, 96	25,76	3,03	48,33	0,674
400	0,524	0,255	4,48	33,52	3,37	63,09	0,678
500	0,456	0,261	4,94	41,51	3,69	79,38	0,687
600	0,404	0,266	5,35	49,78	3,99	96,89	0,699
700	0,362	0,271	5,77	58,82	4.26	115,4	0,706
800	0,329	0,276	6,17	67,95	4,52	134,8	0,713
1000	0,277	0,283	6,94	88,53	5,00	177,1	0,719

Таблица
9.11

Теплофизические параметры дымовых газов при 760 мм. рт. ст
t, ºС	γ, кг/м³	с_р, ккал/кг· ºС	λ ·10², ккал/м·ч·ºС	α, ·10² м²/ч	μ·10⁶, кг·сек/м²	ν ·10⁶, м²/сек	рz
0	1,295	0,240	1,96	6,08	1,609	12,20	0,72
100	0,950	0,255	2,69	11,10	2,079	21,54	0,69
200	0,748	0,262	3,45	17,60	2,497	32,80	0,67
300	0,617	0,268	4,16	35,16	2,878	45,81	0,65
400	0,525	0,275	4,90	33,94	3,230	60,38	0,64
500	0,457	0,283	5,64	43,61	3,553	76,30	0,63
600	0,405	0,290	6,38	54,32	3,860	93,61	0,62
700	0,363	0,296	7,11	66,17	4,148	112,1	0,61
800	0,330	0,302	7,87	79,09	4,422	131,8	0,60
900	0,301	0,308	8,61	92,87	4,680	152,5	0,59
1000	0,275	0,312	9,37	109,21	4,930	174,3	0,58
1100	0,257	0,316	10,10	124,37	5,169	197,1	0,57
1200	0,240	0,320	10,85	141,27	5,402	221,0	0,56
Примечание: данные приведены для дымовых газов среднего состава: СО₂=13%, Н₂О= 11%, N₂=76%

Теплоотдача
от газа к поверхности внутренних стенок
цилиндров ДВС.

Колебания
температуры в стенках цилиндра
распространяются на незначительную
глубину от поверхности (не более
0,001…0,002м).
Количество тепла, передаваемого газом
в цилиндре путём конвекции, составляет
примерно82% всего количества тепла (18%
на лучевое испускание). Для определения
коэффициента теплоотдачи α_Г
в цилиндрах различных типов двигателей
используют опытные
зависимости
(Нуссельда,
Брилинга, Эйхельберга, Иноземцева,
Пфлаума, Семёнова
и др.)

Формула
Эйхельберга
(судовые
двухтактные дизели):

α_Г
=2,1 (с_т)^0,33(Р_ГТ_Г)^0,5
(Р_к)^0,25ккал/м²·ч·
ºС,

Здесь:
с_т
– средняя
скорость поршня, м/с;

Р_Г
, Т_Г
– давление
(кгс/см²)
и температура газа (ºК)
в цилиндре;

Р_к
– абсолютное давление наддува, кгс/см².

Ориентировочные
значения среднего
коэффициента от газа к стенкам камеры
сгорания:

α_Г^ср
=270…320
ккал/м²·ч·
ºС
– для двухтактных малооборотных дизелей;

α_Г^ср
=260…280
ккал/м²·ч·
ºС
– для четырёхтактных дизелей.

Коэффициент
теплоотдачи от газа к боковой поверхности
головки поршня, расположенной над
поршневыми кольцами:

α_Г^П
=280…300
ккал/м²·ч·
ºС.

Теплоотдача
от стенки к воде.

Коэффициент
теплоотдачи от стенки к воде для
турбулентного потока (Re
>10)
и гладких прямых трубок при нагревании
воды:

α₂
=[bw_в^0,8
(l/d)^-0,054]/d_в^0,2
ккал/м²·ч·
ºС,

где
b
=
152+24t_ср;

d_в
– внутренний диаметр трубки, м.

Для
приближённых расчетов при (l/d)=100…400
можно пользоваться формулой:

α₂
=0,75bw_в^0,8
/d_в^0,2
ккал/м²·ч·
ºС.

На
рисунке 36[7] приведены зависимости
физических параметров γ, ν. λ морской
воды от её средней температуры и
солёности. Там же даны графики b= f(t_ср)
для солёности 30. 35 и 40%_о.

Зависимость
между солёностью морской воды (в градусах
Брандта) и содержанием в ней хлора
(связанного с натрием) определяется по
формуле:

S
=
0,3+1,805Cl%_о.

Теплоотдача
в изогнутых трубах
выше, чем на прямых участках.

Коэффициент
теплоотдачи для винтовых змеевиков
при

Re>
Re_кр=2300+10500(d/R)
рассчитывается как для прямой трубы с
введением множителя ε=1+1,8(d/R),
где d
– диаметр трубки, м; R
– радиус сгиба, м.

Для
втулок и крышек судовых двигателей
(табл. 9.12):

α₂
=300+1800(w_в)^0,5
ккал/м²·ч·
ºС,

где
w_в
– скорость воды относительно стенок
(для верхних поясов втулки –(0,25…1,5)м/сек,
для крышки – (0,5…1,5)м/сек).

Теплоотдача
от стенки к пару.

Коэффициент
теплоотдачи от стенки к перегретому
пару α₂можно
определить с помощью номограммы (рис.
4-42 [7]), где дан её ключ. Разность температур
стенок и пара:

Δt=q(d_н/
d_вн)/
α₂+0,575
q(d_н/λ)lg(d_н/
d_вн),

Где
q
– тепловая нагрузка, ккал/м²·ч.

Для
пароперегревателя:

q
=[D_пп(i_пп-i_н)]/H_пп,

Где
q
– расход перегретого пара, кг/ч;

i_пп,
i_н
– энтальпия соответственно перегретого
пара и насыщенного пара, ккал/кг;

H_пп
– поверхность пароперегревателя, м².

Надёжность
работы трубок оценивается по сопоставлению
действительного значения t_ст
с допустимой температурой для данной
марки котельной стали.

Таблица
9.12

Средняя величина α₂, ккал/м²·ч· ºС
Детали ЦПГ	α₂
Втулки и крышки	1000 -2000
Поршни	с водяным охлаждением	~4000
с масляным охлаждением	~5000
Примечание: α₂ [квт/м²· ºС]=1,16·10^-3 α₂ [ккал/м²·ч· ºС]

Теплоотдача
при кипении воды в трубах.

Кипение
начинается после того, как температура
поверхности нагрева t_с
станет выше температуры насыщения пара
t_н
при данном давлении.

Пузырьковый
режим
наблюдается до критических значений
тепловой нагрузки поверхности (плотности
теплового потока) q_кр
или Δt_кр=(t_с
– t_н)_кр,
которые зависят от физических свойств
жидкости, а также от состояния поверхности.
При кипении воды в
условиях естественной конвекции
и р=1ата:

q_кр
=(1,2…1,3)
·10⁶
ккал/м²·ч,
Δt_кр=25
ºС.

Режим
плёночного кипения
и резкое падение коэффициента теплоотдачи
наступают при q>
q_кр

или Δt>
Δt_кр.
В области развитого плёночного кипения
α
почти не зависит от Δt,
а q
возрастает приблизительно пропорционально
Δt.

В
случае парового обогрева при
переходе через критическую точку
вместе с α
падает также и q,
что
приводит снижению производительности
теплообменного аппарата. При
кипении в большом объёме
(в том числе на наружной поверхности
пучка труб) в условиях естественной
конвекции коэффициент теплоотдачи α
можно определить по приближённой
формуле:

α
=(С_р)^0,4
q^-0,7

ккал/м²·ч·
ºС.

Эта
формула справедлива в пределах тепловой
нагрузки 5000<q<(0,2…0,4)
q_кр

и давлении от 0,2
до 10ата.
Здесь С – коэффициент, зависящий от
свойства жидкости и поверхности нагрева.
Для воды, кипящей в трубах из цветных
сплавов С=2,6

Для
холодильных агентов
при температуре кипения от -40 до 0
ºС:

Аммиак
α₀
=92 q^0,25

Фреон-12
α₀
=66 q^0,25

Фреонт-11
α₀
=30 q^0,25

Здесь
q
– удельный тепловой поток, ккал/м²·ч.

При
кипении фреонов растворённоё в них
масло существенно ухудшает теплоотдачу.
При концентрации масла во фреоне в
пределах 0…10% α
=φ α₀,
где φ=1…0,7.

Теплоотдача
при конденсации водяного пара.

Для
одиночной горизонтальной трубы и первого
ряда пучка горизонтальных трубок,
обтекаемых сверху вниз водяным паром
(без примеси воздуха), коэффициент
теплоотдачи вычисляют по формуле:

α
=(В w_П^0,16)/(
d_н
^0,705Δt^0,125)
ккал/м²·ч·
ºС,

Где
w_П
– скорость набегающего потока, м/сек;

d_н
– наружный диаметр трубки, м;

Δt
– температурный напор;

t_н
– температура насыщенного пара при
давлении конденсации, ºС;

t_с
– средняя температура стенки, ºС;

В
=549+7,05(-30)^0,9.

В
зависимости от состояния поверхности
теплообмена на ней может происходить
капельная
или плёночная конденсация
пара.

Стекающая
плёнка конденсата обладает термическим
сопротивлением,
величина которого зависти от характера
течения (ламинарное, турбулентное)
и толщины плёнки.

При
плёночной конденсации: α_П
=6000…10000
ккал/м²·ч·
ºС.

При
капельной конденсации в условиях
неподвижного пара: α_П=30000
ккал/м²·ч·
ºС.

При
движущемся паре и повышенных давлениях
значение α_П
доходит
до
125000
ккал/м²·ч·
ºС
и выше.

Интенсивность
конденсации пара на охлаждающей
поверхности определяется характером
двух процессов, протекающих одновременно:
отвода тепла от поверхности и притока
к ней частиц пара (массообмен). При
конденсации пара содержащего
неконденсирующие газы, интенсивность
процесса определяется, главным образом,
скоростью переноса частиц пара к
охлаждающей поверхности (конвекция,
диффузия).

Окисная
плёнка на поверхности металла обладает
дополнительным термическим сопротивлением
и оказывает тормозящее действие на
течение плёнки конденсата. Для
окислённых, но не загрязнённых
труб коэффициент теплоотдачи снижается
на15-20% по сравнению с чистыми гладкими
поверхностями.

Конденсаторы.

Для
приближённых расчетов пользуются
графиком (рис. 4-43 [7]); Нижние кривые
определяют средний коэффициент
теплопередачи k₀
для латунных трубок с наружными диаметрами
19, 22, 25мм при d_к
=40кг/ м²·ч
и t₁=21ºС.
По верхним кривым устанавливают значения
поправочных коэффициентов β_t
и
β_d
для заданного режима работы конденсатора.

Средний
коэффициент теплопередачи вычисляют
по формуле:

k
=k₀
β_t
β_d
β_s
.

Значения
, полученные по графикам (рис. 38), несколько
завышены, особенно для низких температур
(<15
ºС)
забортной воды.

Зависимости
среднего коэффициента теплопередачи
в главном конденсаторе ГТЗА типа ТС-1
показаны на рис.39.

Подогреватели
питательной воды (ППВ).

В
паровых ППВ коэффициент
теплопередачи k
определяется в зависимости от скорости
воды в трубах w₁
и её средней температуры. Графики (рис.
4.45[7])
построены для подогревателей с латунными
трубками d_н=19мм
(при d_н
=16мм k
увеличивается на 21%, а при d_н
=25мм уменьшается на 3%). На рис. 4.46[7]
показана зависимость вида k=f(G_В,δt);
δt
– ТЕМПЕРАТУРНЫЙ НАПОР на выходе воды.

Теплоотдача
при конденсации холодильных агентов.

Коэффициент
теплоотдачи от фреона к стенке трубы
α_ф
зависит от температурного напора Δt
(см. рис. 4.47[7]). Уменьшение α_ф
с увеличением Δt
объясняется образованием плёнки
конденсата на трубах.

Коэффициент
теплоотдачи от масла к стенке
для судовых маслоохладителей (с трубками
диаметром 16/14мм) определяется по формуле:

α=2,6β₁β₂
t_м^0,9w_м^0,6,
где β₁=0,97+0,055
w_в
– поправка на скорость движения охлаждающей
воды в трубках;

w_в
–
средняя скорость движения охлаждающей
воды в трубках, м/сек;

β₂=
(14,4+ t _в)
^0,5
– поправка на температуру охлаждающей
воды;

t_в–
средняя температура охлаждающей воды
в охладителе, °С;

t_м–
средняя температура охлаждаемого масла
в охладителе, °С;

w_м
– средняя скорость масла, м/сек.

Зависимости
коэффициента теплопередачи
k=f(G_В,t_В)
в маслоохладителях (практически чистых,
типов МО-220 и МО-260) показаны на рис.
4.48[7]. В условиях постоянного расхода
масла и заданной температуры забортной
воды k
изменяется приблизительно прямо
пропорционально расходу охлаждающей
воды G_В.

Зависимости
коэффициента теплопередачи
k_Т=f(G_Т,t_Т1)
для практически чистых поверхностей
нагрева паровых топливоподогревателей
типа ПН-40 (при t_Т2
=95°С) приведены на рис. 4.49[7].

ПОВЕРОЧНЫЕ
РАСЧЁТЫ ТЕПЛООБМЕННИКОВ И ИХ ХАРАКТЕРИСТИК

Уравнение
теплового баланса:

Q=G₁(i₁‘
– i₁“)η_пот=
G₂(i₂”
-i₂‘)
,

где
Q – количество тепла, передаваемого от
первичного теплоносителя ко вторичному
(тепловая мощность аппарата), ккал/ч;

G
– весовой расход, кг/ч;

i
– энтальпия теплоносителей, ккал/кг;

η_пот
=0,97…0,99 – коэффициент тепловых потерь.

Индекс
«1» относится к первичному (греющему),
а индекс «2» – ко вторичному теплоносителю;
одним штрихом обозначено состояние
теплоносителя при входе, а двумя штрихами
– при выходе.

Для
аппаратов с первичным теплоносителем
– конденсирующимся паром, а вторичным
– нагреваемой водой (паровые теплообменники,
конденсаторы):

Q=G₁(i₁‘
– t₁“)η_пот=
с₂
G₂(t₂”
– t₂‘),

где
t₁“
– температура конденсата греющего
пара.

Если
оба теплоносителя – жидкости или
конденсирующиеся газы (водяные
подогреватели, маслоохладители и т.
п.), то:

Q=
с₁G₁(t₁‘
– t₁“)η_пот=
с₂
G₂(t₂”
– t₂‘).

Водяной
тепловой эквивалент:

W=
с G
– количество тепла, необходимое для
нагрева G
кг теплоносителя на 1°С

Уравнение
теплопередачи:

Q=kFΔt_ср,

Где
k
– коэффициент теплопередачи, Дж/м²·с·
ºС
(ккал/м²·ч·
ºС);

F–
поверхность теплообмена, м²;

Δt_ср
– средняя разность температур, °С.

Тепловая
мощность аппарата:

Q=kFΔt_ср
=
(с G)_бδt_м=
(с G)_мδt_б,

Где
(с
G)_б;
(с
G)_м
– больший и меньший тепловые (водяные)
эквиваленты теплоносителей, Дж/°С
(ккал/°С);

δt_б;
δt_м
= больший и меньший перепады температур
теплоносителей, °С (см. рис. 45).

Уравнение
характеристики теплообменного аппарата:

q=Q/Δ=1/[а/(с
G)_б+в/(с
G)_м+1/kF],

Где
Q
– тепловая производительность
аппарата,Дж/с (ккал/ч);

q
– тепловая производительность аппарата
на 1°С максимальной разности температур
между греющим и нагреваемым теплоносителями,
Вт/°С
(ккал/ч· ºС);

Δ
– максимальная разность между греющим
и нагреваемым теплоносителями;

а
и в
– постоянные коэффициенты, зависящие
от схемы движения теплоносителя в
аппарате приведены в таблице 9.13.

Таблица
9.13

Значение коэффициентов а и в
Схема движения теплоносителя	Условное изображение процесса (рис. 4-50[7])	а	в
Противоток	I и I I	0,35	0,65
Прямоток	I I I и IV	0,65	0,65
Перекрёстный ток	–	0,50	0,65

При
изменении фазового состояния одного
теплоносителя:

q=Q/Δ=1/[0,65/(с
G)+1/kF],
ккал/
ч· ºС,

где
(с
G)
– тепловой эквивалент неменяющегося
теплоносителя.

При
изменении фазового состояния обоих
теплоносителей:

q=Q/Δ=kF.

Тепловая
производительность аппарата пропорциональна
максимальной разности температур
греющего и нагреваемого теплоносителей
().

По
характеристике теплообменного аппарата
(см. рис. 4-51[7]) оценивают изменение
теплопроизводительности и конечных
параметров теплоносителей при изменении
расхода одного из них.

Для
конкретных условий теплообмена величина
kF
может быть выражена следующим образом:

для
водяных и газовых теплообменников при
турбулентном движении обеих сред:
kF=Ф₀(G_П
G_В)^0,5;

для
пароводяных и паровоздушных теплообменников,
в которых пар конденсируется, а вода
или воздух движутся в турбулентном
режиме:
kF=Ф₀(G_В)^0,5,

где
Ф₀
– тепловая производительность аппарата,
отнесённая к 1°С средней разности
температур и единице расхода нагреваемой
воды (газа); Ф₀
– постоянный параметр аппарата, зависящий
от его конструктивных особенностей,
чистоты поверхности и воздушной полости
(определяется опытным путём – см. главу
« теплообменные установки и аппараты»).

Температурный
напор на выходе
воды (конечный) в пароводяном подогревателе
(конденсаторе):

δt=Δt_р·l⁽^kF/Gс)
°С,
где Δt_р
– разность между температурой насыщения
греющего пара и температурой воды на
входе в подогреватель;

G
– расход питательной воды через
подогреватель, кг/ч; – поверхность
подогревателя, м²;

с–
средняя теплоёмкость питательной воды,
ккал/кг °С.

ТЕПЛОБМЕН
ИЗЛУЧЕНИЕМ

Основные
понятия и законы теплового излучения.

Тепловое
излучение происходит как в видимой
(0,4…0,76мкн), так и в невидимой (инфракрасной
– 0,76…420мкн) областях спектра. Основная
часть лучистой энергии приходится на
волны длиной от 0,76мкн до 15 мкн.

В
общем случае тепловой поток телами
поглощается (Q_А),
отражается (Q_R)
и пропускается (Q_D):

Q=
Q_А+
Q_R+
Q_D,
при
этом:

А=Q_А
/
Q
– коэффициент поглощения;

D=
Q_R
/
Q
– коэффициент отражения;

R=
Q_D
/
Q
– коэффициент пропускания.

Для
прозрачных тел: D=0
и А+
R=1;

Для
абсолютно чёрного тела
D=R=0
и А=1;

Для
абсолютно белого тела А+
D =0
и R=1.

Абсолютно
чёрное тело
обладает наибольшей излучающей
способностью по сравнению с любыми
реальными телами при одинаковой
температуре. Спектральная интенсивность
излучения абсолютно чёрного тела зависит
от длины волны и температуры (см.
рис.4-53[7[).

Максимум
спектральной интенсивности отвечает
длине волны:

λ_тах=0,2897/Т,
см.

Максимум
интенсивности излучения абсолютно
чёрного тела
с увеличением температуры перемещается
в сторону более коротких волн (закон
Вина).

Тепловое
излучение
относят к заданному направлению или к
полусфере. Его характеризуют следующие
величины:

а)
энергия полусферического излучения,
или плотность излучения

Е,
кВт/ м²
(ккал/м²·ч);

б)
интенсивность
полусферического излучения
I_λ,
кВт/ м³
(ккал/м³·ч)
–
энергия излучения в узком интервале
длин волн;

в)
угловая
плотность излучения
i,
, кВт/ стер (ккал/стер·ч) –
отношение лучистого потока кВт
(ккал/ч),
посылаемого в данном направлении
элементарной площадкой ΔF
в пределах телесного угла Δω,
к величине этого угла;

г)
калорическая
яркость
кВт/
стер м²
(ккал/стер·м²·ч)
–
отношение угловой плотности излучения
к проекции площадки на плоскость,
перпендикулярную направлению излучения
(см. рис. 4-54[7]).

Плотность
излучения чёрного тела
во всём диапазоне длин волн пропорциональна
четвёртой степени его абсолютной
температуры (закон
Стефана- Больцмана):

Е₀=С₀
(Т/100)⁴,
кВт/ м²
(ккал/ м²·ч),

Где
С₀=5,70кВт/
м²°К
(4,90
ккал/(
м²·ч·
°К))–
коэффициент
излучения абсолютно чёрного тела ,

Т
– температура тела, °К.

Серое
тело
поглощает одну и ту же долю падающего
на него излучения во всём интервале
длин волн. К серым телам могут быть
отнесены все твёрдые тела, имеющие
шероховатые или окисленные поверхности
со сравнительно высокими поглотительными
свойствами. Для серых тел А>1
и не зависит от температуры. Плотность
излучения серого тела:

Е=АЕ₀
=ε Е₀=σ(Т/100)⁴,
кВт/ м²
(ккал/ м²·ч),

Где
А=
ε=Е/ Е₀
–
степень
черноты,
зависящая от природы тела, характера
его поверхности и температуры (см. табл.
9.14);

σ=4,9
ε
кВт/(
м²·ч·
°К⁴)
[ккал/( м²·ч·
°К⁴)]–
коэффициент излучения серого тела.

Серое
тело излучает энергии тем больше, чем
выше его коэффициент поглощения (закон
Киргофа).
При этом всякое тело может
излучать только
в
тех областях спектра, в которых оно
обладает способностью поглощения
лучистой энергии.

Для
абсолютно
чёрного тела калорическая яркость
излучения,
т. е. величина лучистого потока в
направлении (см. рис. 4-54[7]), отнесённая
к единице телесного угла Δω
и единице поверхности ΔF
,перпендикулярной к направлению
излучения, одинакова
для всех направлений (закон Ламберта).

Таблица
9.14

Степень черноты нормального излучения для различных материалов
Материал	t,°С	ε
Алюминий шероховатый	26	0,055
Сталь	Листовая шлифованная	940-1100	0,55-0,61
Окисленная при 600°С	200-600	0,80
Листовая с плотным блестящим слоем окиси	26	0,82
Латунь	Прокатная	22	0,06
С тусклой поверхностью	50-350	0,22
Медь	Полированная	80-115	0,018-0,023
Окисленная при 600°С	200-600	0,57-0,87
Олово, листовое лужённое железо	25	0,043-0,064
Цинк полированный	225-325	0,045-0,053
Оцинкованное листовое железо	28	0,128
Оцинкованное листовое железо окисленное	24	0,276
Асбестовый картон	24	0,96
Кирпич	Шамотный	1100	0,75
Огнеупорный	–	0,8-0,9
Лак чёрный матовый	40-95	0,96-0,98
Масляные краски различных цветов	100	0,92-0,96
Сажа	95-270	0,952

Теплообмен
излучением между двумя плоскими
параллельными поверхностями (F=F₁=F₂)
серых тел с температурами Т₁
и Т₂
(Т₁
> Т₂)
рассчитывают по формуле:

Q_1,2=4,9
ε_пр
· F ·[(Т₁/100)⁴–
(Т₂/100)⁴]
кВт (ккал/ч),

Где
ε_пр
– приведённая степень черноты системы
тел;

F
– площадь поверхности тела.

Для
двух неограниченных параллельных
плоскостей:

ε_пр
=1/(1/ε₁+1/ε₂
-1),

Где
ε₁
и ε₂–
степени черноты теплообменивающихся
поверхностей.

Коэффициент
теплоотдачи
при теплообмене между двумя серыми
поверхностями:

α_л^“=4,9·10^-8·
ε_пр
·[( Т₁⁴–
Т₂⁴)/(
Т₁–
Т₂)]=А
ε_пр
ккал/( м²·ч·°С),

Где
А=4,9·10^-8·
[( Т₁⁴–
Т₂⁴)/(
Т₁–
Т₂)]
(см. табл.9.15).

Если
одно тело с поверхностью F₁
со всех сторон окружено поверхностью
F₂
второго серого тела и F₂
>>
F₁
, то ε_пр
= ε₁.
количество переданного тепла определяется
по формуле, приведённой выше. Для снижения
теплопотерь нагретыми поверхностями
их закрывают отражательными листами
(экранами).

Таблица
9.15

Коэффициент А=4,9·10^-8· [( Т₁⁴– Т₂⁴)/( Т₁– Т₂)]
t₁, °С	t₂, °С
10	20	30	40	50	60	70	80	90	100	200
10	0	–	–	–	–	–	–	–	–	–	–
20	4,9	0	–	–	–	–	–	–	–	–	–
30	5	5,2	0	–	–	–	–	–	–	–	–
40	5,2	5,5	5,8	0	–	–	–	–	–	–	–
50	5,6	5,8	6,05	6,5	0	–	–	–	–	–	–
60	5,9	6,1	6,44	6,75	7	0	–	–	–	–	–
70	6,2	6,4	6,75	7,1	7,5	7,5	0	–	–	–	–
80	6,5	6,8	7,1	7,5	7,7	8	8	0	–	–	–
90	6,95	7,1	7,45	7,7	8	8,3	8,5	9	0	–	–
100	7,15	7,45	7,75	8,1	8,4	8,75	9	9,5	10	0	–
200	11,4	11,7	12,1	12,5	12,9	13,4	13,7	14,2	14,7	15,2	0
300	17,3	17,8	18,3	18,7	19,2	19,6	20,6	20,8	21,3	21,9	28,6
400	25,2	25,8	26,3	26,9	27,5	28	28,6	29,4	30	32,7	38,3
500	35,5	36,1	36,5	37,4	38,1	38,9	39,6	40,3	41,1	41,8	50,6
600	48,3	48,8	49,1	50,5	51,3	52,4	53	53,9	54,8	55,6	65,7

Теплообмен
излучением в топочном объёме.

Для
анализа процесса горения и теплообмена
в топочном объёме определяют действительную
температуре газа на выходе из топки –
t_Т
(номограмма,
рис. 4-55[7]). По этой температуре, используя
диаграмму i-t,
можно найти значение теплосодержания
продуктов сгорания и количество тепла,
переданного поверхностями нагрева,
расположенными в топочном пространстве.
На номограмме (см. рис. 50) между правыми
(верхней и нижней) четвертями нанесена
i-t–диаграмма
(жидкое топливо) при коэффициенте избытка
воздуха α=1,15
(нижний ряд цифр – теплосодержание
газа, над ним теоретическая температура
газов t_а).

Для
определения температуры газов необходимо
знать следующие исходные величины:

р
– давление в топке, ата;

V_Т
– объём топки, м³;

F
– суммарную поверхность стен топки, м²;

Н_л
– суммарную радиационную поверхность
нагрева м²;

β
– коэффициент, зависящий от типа сжигаемого
топлива (β=0,75
для жидких топлив и твёрдых с выходом
летучих более 18%);

В_р
– расход топлива, кг/ч;

Q_Т
– количество тепла, выделяющегося при
сгорании 1кг топлива, ккал/кг;

ξ
–
коэффициент, характеризующий степень
загрязнения поверхностей нагрева (при
сжигании жидких топлив ξ
=0,9,
при зашипованных экранах – 0,2, закрытых
шамотным кирпичом – 0,1).

Радиационная
поверхность нагрева:

Н_л
=Σ
F_i
х_i
и
F
=Σ
F_i,

Где
F_i
– площадь стены, закрытая экраном или
котельным пучком с угловым коэффициентом
х_i
(см. рис. 51[7]).

Порядок
определения t_Т.

Предварительно
определяют следующие величины:

V_Т
р/F; ψ=Н_л
/F; В_р
Q_Т
/ξ Н_л
и
t_а
(по
диаграмме i-t).
Задаются значением – и откладывают его
на правой нижней четверти номограммы
(см. рис. 50[7]), а затем следуют, как показано
пунктиром, до пересечения с вертикальной
линией t_а
в правой верхней четверти. Точка
пересечения этих линий указывает
действительную температуру t_Т
на выходе из топки. Если принятое
предварительно и найденное значение
не совпадают, указанные операции
повторяют до полного совпадения обоих
значений t_Т.

Задачи.

Бетонная
отопительная панель представляет собой
плиту, в которой имеются нагревательные
элементы — каналы змеевиковой или
колончатой формы с теплоносителем.

Для
изготовления панелей используют тяжелый
бетон, обладающий достаточно высокой
теплопроводностью [например,
теплопроводность λ_б=1,51
Вт/(м·К) или 1,3 ккал/(ч·м·°С) при 0°С и
плотности в сухом состоянии 2400 кг/м³]
и коэффициентом линейного расширения

Чаще
всего каналы для теплоносителя образуют
стальные трубы, коэффициент линейного
расширения которых весьма близок к
коэффициенту расширения бетона
(коэффициенты равны при температуре
около 55° С).

Заделка
труб в бетон дает существенный
теплотехнический эффект — увеличивается
теплопередача труб по сравнению с
открыто проложенными. Это явление
основано на известной закономерности:
теплопередача трубы, изолированной
теплопроводным материалом, возрастает
с увеличением толщины слоя покрытия.
Возрастание происходит до некоторого
«критического» значения внешнего
диаметра d_Kp
изолированной трубы, полученного из
уравнения, если считать α_н
не изменяющимся.

Для
бетонного цилиндра вокруг трубы при
коэффициенте наружного теплообмена
около 11,6 Вт/(м²·К)
или 10 ккал/(ч·м²·°С)
«критический» диаметр равен приблизительно
220 мм.

Возрастание
теплопередачи обетонированной трубы
объясняется увеличением
внешней теплоотдающей поверхности,
которая с ростом, диаметра развивается
быстрее, чем сопротивление теплопроводности
слоя бетона.

Теплопередача
не одной, а ряда труб в бетонной панели,
приведенная к 1 м, несколько ниже
теплопередачи одиночной трубы в бетоне
и зависит от расстояния между трубами
(шага труб, обозначенного буквой s) и их
положения в панели.

Общая
задача-1. Определить,
как изменится теплоотдача стальной
трубы (длина L_тр=2м)
диаметром d_тр=32мм
с толщиной стенки δ=3мм после бетонирования
её (при диаметре бетонного цилиндра
d_бт)?
Коэффициенте наружного теплообмена
считать постоянным и равным α_н
=11,6 Вт/(м²·К).
Коэффициенте внутреннего теплообмена
от воды к стенке считать постоянным и
равным α_вн=1000Вт/(м²·К).
Теплопроводность бетона считать
постоянной и равной λ_б=1,51
Вт/(м·К). Теплопроводность стали считать
постоянной и равной λ_ст=70
Вт/(м·К) Температура теплоносителя
t_в=60°С.
Температура воздуха в помещении
t_воз=18°С.
Формулы для расчёта на стр. 69.

Вариант	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
d_бт ,мм	50	60	70	80	90	100	110	120	130	140	150	160	170	180	190

Вариант	16	17	18	19	20	21	22	23	24	25
d_бт ,мм	250	260	270	280	290	400	510	620	730	840

Общая
задача-2.
Для уменьшения тепловых потерь через
стены здания и повышения температуры
внутренней поверхности кирпичной стены
толщиной δ_стприменена
изоляция слоем минеральной ваты толщиной
δ_изв
двух вариантах (установка снаружи и
установка внутри). Требуется определить
теплопотери ΔQ (1м²
площади стены) в обоих вариантах и
температуру стены со стороны помещения
и выбрать наивыгоднейший из них. Формулы
для расчёта на стр. 68. Для решения принять:

Температуру
воздуха внутри помещения 20°С;
Температуру
наружного воздуха -20°С;
Теплопроводность
минеральной ваты считать постоянной
и равной λ_из=0,05
Вт/(м·К);
Теплопроводность
кирпичной кладки считать постоянной
и равной λ_ст=0,93
Вт/(м·К);
Коэффициенте
наружного теплообмена считать постоянным
и равным α_н
=6 Вт/(м²·К);
Коэффициенте
внутреннеготеплообмена считать
постоянным и равным α_н
=12Вт/(м²·К).

Вариант	1	2	3	4	5	6	7	8	9	10	11	12
δ_ст ,мм	600	600	600	600	500	500	500	500	400	400	400	400
δ_из ,мм	50	75	100	125	50	75	100	125	50	75	100	125

Вариант	13	14	15	16	17	18	19	20	21	22	23	24	25
δ_ст ,мм	300	300	300	300	700	700	700	700	800	700	700	700	700
δ_из ,мм	50	75	100	125	50	75	100	125	50	75	100	125	25

Контрольные
вопросы.

Назовите
и опишите все виды теплообмена.
Что
называется сложным теплообменом?
Что
называется градиентом температур?
Что
такое теплопроводность?
Что
называется конвективным теплообменом?
Какие
режимы теплоносителей бывают на
практике?
Перечислите
основные факторы, влияющие на интенсивность
конвективного теплообмена.
Объясните
механизм передачи тепла излучением.
Приведите
примеры сложного теплообмена
применительно к жилым и и производственным
зданиям.

Источник

Пособие рекомендовано учащимся, желающим
получить практические навыки в решении задач на
теплообмен, и может быть полезным для учителей и
абитуриентов.

При соприкосновении тел, имеющих разные
температуры, между этими телами происходит
теплообмен. С точки зрения
молекулярно-кинетической теории, это
объясняется так: молекулы более нагретого тела
имеют большую кинетическую энергию, чем молекулы
тела, менее нагретого. При “столкновениях”
молекул соприкасающихся тел происходит процесс
выравнивания их средних кинетических энергий.
Молекулы более нагретого тела теряют часть своей
кинетической энергии, при этом нагретое тело
будет остывать. Кинетическая энергия молекул
холодного тела возрастает, поэтому температура
этого тела будет увеличиваться. В конечном итоге
кинетические энергии молекул обоих тел
сравняются, и температуры тел станут
одинаковыми. На этом теплообмен прекращается.

Энергию, которую тело получает или отдаёт в
процессе теплообмена, называют количеством
теплоты (Q).

Количество теплоты, как и все другие виды
энергии, измеряется в системе СИ в Джоулях: [Q] = Дж.
(Здесь и в дальнейшем единицы измеряются в
системе СИ.)

Нагревание или охлаждение

При нагревании или охлаждении тела количество
теплоты, поглощаемое или выделяемое им,
рассчитывается по формуле:

Q = сm(t₂– t₁), (1)

где m – масса тела, кг;

(t₂– t₁) – разность температур
тела,° С (или К);

с – удельная теплоёмкость вещества, из
которого состоит тело,

Удельная теплоёмкость вещества – это
количество теплоты, которое нужно сообщить
одному килограмму данного вещества, чтобы
увеличить его температуру на 1° С (или это
количество теплоты, которое выделяет один
килограмм данного вещества, остывая на 1° С).

Значения удельных теплоемкостей других
веществ можно найти в справочниках, а также в
школьном учебнике или задачнике.

При нагревании тела его внутренняя энергия
увеличивается. Это требует притока энергии к
телу от других тел. Значит, оно поглощает
некоторое количество теплоты, принимая его от
других тел, участвующих в теплообмене.

При охлаждении тела его внутренняя энергия
уменьшается. Поэтому остывающее тело отдаёт
кому-либо некоторое количество теплоты.

Обычно конечную температуру, установившуюся в
результате теплообмена, обозначают греческой
буквой (тэта).

В формуле (1) произведение cm для каждого
конкретного тела есть величина постоянная. Её
называют теплоёмкостью тела и обозначают С:

C = c m.(2)

Размерность теплоемкости: Теплоемкость тела показывает,
сколько энергии нужно подвести к данному телу,
чтобы нагреть его на 1° С (или сколько энергии
выделяет это тело, остывая на 1° С).

Теплообмен между телами, имеющими одинаковые
температуры, не происходит, даже если
контактируют вещества, находящиеся в разных
агрегатных состояниях. Например, при температуре
плавления (0° С) лёд и вода могут находиться
бесконечно долго, при этом количество льда и
количество воды останутся неизменными.
Аналогично ведут себя пар и жидкость,
находящиеся при температуре кипения. Теплообмен
между ними не происходит.

Плавление или кристаллизация

Если при нагревании тела его температура
достигнет температуры плавления, то начинает
происходить процесс перехода этого вещества из
твердого состояния в жидкое. При этом идут
изменения в расположении и характере
взаимодействия молекул. Температура при
плавлении не изменяется. Это означает, что
средние кинетические энергии молекул жидкости и
твердого тела при температуре плавления
одинаковы. Однако внутренняя энергия тела при
плавлении возрастает за счет увеличения энергии
взаимодействия молекул. Количество теплоты,
поглощаемое телом при плавлении, рассчитывается
по формуле

(3)

где m – масса тела, кг;

–
удельная теплота плавления,

При кристаллизации, наоборот, внутренняя
энергия тела уменьшается на величину и эта теплота данным
телом выделяется. Она поглощается другими
телами, участвующими в теплообмене.

Удельная теплота плавления показывает,
сколько энергии нужно сообщить одному
килограмму данного вещества, взятого при
температуре плавления, чтобы полностью
превратить его при этой температуре в жидкость
(или сколько энергии выделяет 1 кг жидкости,
взятой при температуре кристаллизации, если вся
она при этой температуре полностью превратится в
твёрдое тело).

Удельную теплоту плавления любого вещества
можно найти в справочниках. Для льда же

Температура плавления у каждого вещества своя.
Её также можно найти в справочниках. Важно
подчеркнуть, что температура плавления вещества
равна температуре кристаллизации этого же
вещества. У льда t_пл = 0° С.

Кипение или конденсация

При достижении жидкостью температуры кипения
начинает происходить другой фазовый переход –
кипение, при котором расстояния между молекулами
значительно увеличиваются, а силы
взаимодействия молекул уменьшаются. Вся
подводимая к жидкости теплота идет на разрыв
связей между молекулами. При конденсации пара в
жидкость, наоборот, расстояния между молекулами
значительно сокращаются, а силы взаимодействия
молекул увеличиваются. Для кипения жидкости
энергию к жидкости нужно подводить, при
конденсации пара энергия выделяется. Количество
теплоты, поглощаемое при кипении или выделяемое
при конденсации, рассчитывается по формуле:

где m – масса тела, кг; L – удельная
теплота парообразования,

Удельная теплота парообразования
показывает, сколько энергии нужно сообщить
одному килограмму жидкости, взятой при
температуре кипения, чтобы при этой температуре
полностью превратить её в пар (для конденсации:
сколько энергии выделяет один килограмм пара,
взятого при температуре конденсации, полностью
превращаясь в жидкость).

При одинаковом давлении температура кипения и
температура конденсации одного и того же
вещества одинаковы.

Температуры кипения и удельные теплоты
парообразования также можно найти в
справочниках. Для воды же они соответственно
равны: рис. 9 (при нормальном атмосферном
давлении).

Уравнение теплового баланса

Тела, участвующие в теплообмене, представляют
собой термодинамическую систему.
Термодинамическая система называется теплоизолированной,
если она не получает энергию извне и не отдаёт её;
теплообмен происходит только между телами,
входящими в эту систему. Для любой
теплоизолированной системы тел справедливо
следующее утверждение: количество теплоты,
отданное одними телами, равно количеству
теплоты, принимаемому другими телами.

Q_отд.= Q_получ. (5)

Это утверждение описывает частный случай
закона сохранения и превращения энергии в
применении к процессу теплообмена. А формула (5)
является одним из видов уравнения теплового
баланса.

При решении задач с помощью данного вида
уравнения теплового баланса в формуле (1) в
качестве t₂ следует брать большую
температуру, а в качестве t₁ – меньшую.
Тогда разность (t₂– t₁) будет
положительна и всё произведение cm(t₂–t₁)
также будет положительным. Все теплоты, отданные
и полученные, будут положительными.

Уравнение теплового баланса можно записать и в
таком виде:

Q₁+ Q₂+…+ Q_n= 0, (6)

где n – количество тел системы.

Алгебраическая сумма всех количеств теплоты
(поглощенных и выделенных) в теплоизолированной
системе равна нулю.

Q₁, Q₂, …, Q_n – это теплоты,
поглощаемые или выделяемые участниками
теплообмена. Очевидно, что в этом случае какие-то
теплоты должны быть положительны, а какие-то –
отрицательны. При записи уравнения теплового
баланса в виде (6) всегда t₂ – конечная
температура, а t₁ – начальная.

Если тело нагревается, то разность (t₂ – t₁)положительна и все произведение cm(t₂– t₁)
положительно. То есть Q > 0 тогда, когда теплота к
данному телу подводится.

А если t₂< t₁ (тело остывает), то
разность (t₂ – t₁) отрицательна, то есть
Q < 0. В этом случае тело энергию выделяет.

Если при фазовом переходе энергия к телу
подводится (плавление, кипение), то Q > 0; если
тело выделяет энергию (кристаллизация,
конденсация), то Q < 0.

В принципе уравнения (5) и (6) равносильны.
Результат решения задачи не зависит от того,
каким видом уравнения пользуемся. Выбор способа
решения – за читателем.

Применим уравнение теплового баланса для
решения ряда задач (здесь приводим лишь одну
задачу, остальные материалы можно найти по
адресу http:// kirov-festival.nm.ru).

Задача 1

В медном калориметре массой 100 г находится 1 кг
воды при температуре 20° С. В воду опускают
свинцовую деталь массой 2 кг, имеющую температуру
90° С. До какой температуры нагреется вода? (В этой
и последующих задачах потерями теплоты в
калориметре пренебречь.)

Решение

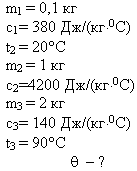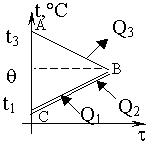	Проведём анализ: Вода и калориметр находились в тепловом равновесии, поэтому они имели одинаковую температуру: t₁= t₂= 20° С. При опускании в воду с температурой 20° С свинцового тела с температурой 90° С между водой и свинцом будет происходить теплообмен. Свинец будет остывать, а вода – нагреваться. В этом же процессе участвует и калориметр, который, как и вода, будет тоже нагреваться.
	Изменение температур тел с течением времени удобно изображать на графике зависимости t(t ). Отрезок АВ соответствует графику изменения температуры свинцового тела. Стрелка, идущая от него, показывает, что, остывая, свинец выделяет энергию Q₃.
	Два параллельных отрезка СВ соответствуют графикам изменения температур калориметра и воды. Стрелки, идущие к ним, показывают, что для нагревания калориметра и воды требуется энергия Q₁ и Q₂, которую они поглощают.
Решим задачу с использованием уравнения теплового баланса в виде (5):

Решим задачу с использованием уравнения
теплового баланса в виде (6):

Ответ: Вода нагреется до 24° С.

Предлагаю читателю самостоятельно сделать
проверку размерности.

Напомним, остальной материал (полноценную
версию пособия) можно найти по адресу http:// kirov-festival.nm.ru.

Источник

Тела, температура которых отличается, могут обмениваться тепловой энергией. То есть, между телами будет происходить теплообмен. Самостоятельно тепловая энергия переходит от более нагретых тел к менее нагретым.

Что такое теплообмен и при каких условиях он происходит

Тела, имеющие различные температуры, будут обмениваться тепловой энергией. Этот процесс называется теплообменом.

Теплообмен – процесс обмена тепловой энергией между телами, имеющими различные температуры.

Рассмотрим два тела, имеющие различные температуры (рис. 1).

Тело, имеющее более высокую температуру, будет остывать и отдавать тепловую энергию телу, имеющему низкую температуру. А тело с низкой температурой будет получать количество теплоты и нагреваться.

Рис.1. Два тела во время теплообмена и после

На рисунке, горячее тело имеет розовый оттенок, а холодное изображено голубым цветом.

Когда температуры тел выравниваются, теплообмен прекращается.

Чтобы теплообмен происходил, нужно, чтобы тела имели различные температуры.

Когда температура тел выравняется, теплообмен прекратится.

Тепловое равновесие — это состояние, при котором тела имеют одинаковую температуру.

Уравнение теплового баланса и сохранение тепловой энергии

Когда тело остывает, оно отдает тепловую энергию (теплоту). Утерянное количество теплоты Q имеет знак «минус».

А когда тело нагревается – оно получает тепловую энергию. Приобретенное количество теплоты Q имеет знак «плюс».

Эти факты отражены на рисунке 2.

Рис. 2. Полученное количество теплоты имеет знак «+», а отданное Q – знак «-»

Закон сохранения тепловой энергии: Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом.

Примечание: Существует и другая формулировка закона сохранения энергии: Энергия не появляется сама собой и не исчезает бесследно. Она переходит из одного вида в другой.

Уравнение теплового баланса

Тот факт, что тепловая энергия сохраняется, можно записать с помощью математики в виде уравнения. Такую запись называют уравнением теплового баланса.

Запишем уравнение теплового баланса для двух тел, обменивающихся тепловой энергией:

[large boxed{ Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 }]

(large Q_{text{остывания горяч}} left( text{Дж} right) ) – это количество теплоты горячее тело теряет.

(large Q_{text{нагревания холод}} left( text{Дж} right) ) – это количество теплоты холодное тело получает.

В левой части уравнения складываем количество теплоты каждого из тел, участвующих в теплообмене.

Записываем ноль в правой части уравнения, когда теплообмен с окружающей средой отсутствует. То есть, теплообмен происходит только между рассматриваемыми телами.

В некоторых учебниках применяют сокращения:

[large Q_{1} + Q_{2} = 0 ]

Примечание: Складывая два числа мы получим ноль, когда эти числа будут:

равными по модулю и
имеют различные знаки (одно число — знак «плюс», а второе – знак «минус»).

Если несколько тел участвуют в процессе теплообмена

Иногда в процессе теплообмена участвуют несколько тел. Тогда, для каждого тела нужно записать формулу количества теплоты Q. А потом все количества теплоты подставить в уравнение для теплового баланса:

[large boxed{ Q_{1} + Q_{2} + Q_{3} + ldots + Q_{n} = 0 } ]

При этом:

Q для каждого нагреваемого тела будет обладать знаком «+»,
Q для каждого охлаждаемого тела — знаком «-».

Пример расчетов для теплообмена между холодным и горячим телом

К горячей воде, массой 200 грамм, имеющей температуру +80 градусов Цельсия, добавили холодную воду, в количестве 100 грамм при температуре +15 градусов Цельсия. Какую температуру будет иметь смесь после установления теплового равновесия? Считать, что окружающая среда в теплообмене не участвует.

Примечание: Здесь мы рассматриваем упрощенную задачу, для того, чтобы облегчить понимание закона сохранения энергии. Мы не учитываем в этой задаче, что вода содержится в емкости. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.

При решении других задач обязательно учитывайте, что емкость, в которой будет содержаться вещество, имеет массу. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.

Решение:

В условии сказано, что окружающая среда в теплообмене не участвует. Поэтому, будем считать рассматриваемую систему замкнутой. А в замкнутых системах выполняются законы сохранения. Например, закон сохранения энергии.

Иными словами, с сосудом и окружающим воздухом теплообмен не происходит и, все тепловая энергия, отданная горячей водой, будет получена холодной водой.

1). Запишем уравнение теплового баланса, в правой части которого можно записать ноль:

[large Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 ]

2). Теперь запишем формулу для каждого количества теплоты:

[large Q_{text{остывания горяч}} = c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) ]

[large Q_{text{нагревания холодн}} = c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) ]

Примечания:

(large c_{text{воды}} ) – удельную теплоемкость воды находим в справочнике;
Массу воды переводим в килограммы;
Горячая вода остывает и отдает тепловую энергию. Поэтому, разность (large (t_{text{общ}} — t_{text{горяч}} ) ) будет иметь знак «минус», потому, что конечная температура горячей воды меньше ее начальной температуры;
Холодная вода получает тепловую энергию и нагревается. Из-за этого, разность (large (t_{text{общ}} — t_{text{холодн}} ) ) будет иметь знак «плюс», потому, что конечная температура холодной воды больше ее начальной температуры;

3). Подставим выражения для каждого Q в уравнение баланса:

[large c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) + c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) = 0 ]

4). Для удобства, заменим символы числами:

[large 4200 cdot 0,2 cdot (t_{text{общ}} — 80 ) + 4200 cdot 0,1 cdot (t_{text{общ}} — 15 ) = 0 ]

Проведем упрощение:

[large 840 cdot (t_{text{общ}} — 80 ) + 420 cdot (t_{text{общ}} — 15 ) = 0 ]

Раскрыв скобки и решив это уравнение, получим ответ:

[large t_{text{общ}} = 58,33 ]

Ответ: Температура смеси после прекращения теплообмена будет равна 58,33 градуса Цельсия.

Задача для самостоятельного решения:

В алюминиевом калориметре массой 100 грамм находится керосин массой 250 грамм при температуре +80 градусов Цельсия. В керосин поместили свинцовый шарик, массой 300 грамм. Начальная температура шарика +20 градусов Цельсия. Найдите температуру тел после установления теплового равновесия. Внешняя среда в теплообмене не участвует.

Примечание к решению: В левой части уравнения теплового баланса теперь будут находиться три слагаемых. Потому, что мы учитываем три количества теплоты:

(large Q_{1} ) – охлаждение алюминия от температуры +80 градусов до конечной температуры;
(large Q_{2} ) – охлаждение керосина от температуры +80 градусов до конечной температуры;
(large Q_{3} ) – нагревание свинца от температуры +20 градусов до конечной температуры;

А справа в уравнение теплового баланса запишем ноль. Так как внешняя среда в теплообмене не участвует.

Выводы

Если тела имеют различную температуру, то между ними возможен обмен тепловой энергией, т. е. теплообмен;
Когда тела будут иметь равную температуру, теплообмен прекратится;
Тело с высокой температурой, отдает тепловую энергию (теплоту) и остывает. Отданное количество теплоты Q имеет знак «минус»;
А тело с низкой температурой получает тепловую энергию и нагревается. Полученное количество теплоты Q имеет знак «плюс»;
Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом. Это – закон сохранения тепловой энергии;
Сохранение тепловой энергии можно записать в виде уравнения теплового баланса;
В левой части уравнения складываем количества теплоты (всех тел, участвующих в теплообмене);
В правой части уравнения записываем ноль, когда теплообмен с окружающей средой отсутствует.

Источник

Heat Transfer

Heat Transfer Formula

Derivation of the Formula

Types of Heat Transfer

Sample Problems

Количество теплоты, которая была получена телом

[Delta Q=Delta U text { (№1) }]

[Delta U=m c Delta T(text { №2) }]

[Delta U=pm lambda m text { (№3) }]

[Delta U=pm r m text { (№4) }]

[Delta Q=Delta U=q m text { (№5) }]

Сохранение тепловой энергии и уравнение теплового баланса

[Delta U=sum_{i=1}^{n} Delta U_{i}=0(mathrm{№} 6)]

[Q_{1}+Q_{2}+Q_{2}+ldots+Q_{n}=Q_{1}^{prime}+Q_{2}^{prime}+Q_{2}^{prime}+ldots Q_{k}^{prime} text { (№7). }]

Пример теплообмена между холодным и горячим телом

Пример на определение массы пара

[Delta U_{1}=Delta U_{2}+Delta U_{3}]

Теплопередача

Плавление или кристаллизация

Кипение или конденсация

Что такое теплообмен и при каких условиях он происходит

Уравнение теплового баланса и сохранение тепловой энергии

Уравнение теплового баланса

Если несколько тел участвуют в процессе теплообмена

Пример расчетов для теплообмена между холодным и горячим телом

Задача для самостоятельного решения:

Выводы

Вам также может понравиться

Как правильно воспитателю детского сада составить план

Selenium python как найти элемент по тексту

Как найти большую сторону параллелограмма формула

Добавить комментарий Отменить ответ