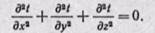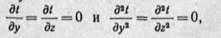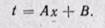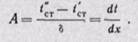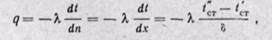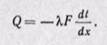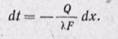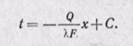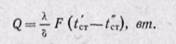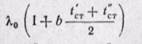Для
многослойной стенки плотность теплового
потока одинакова для всех слоёв

где i – порядковый
номер стенки;
n – количество
слоёв.
Эквивалентный
коэффициент теплопроводности многослойной
стенки определяется из выражения:

Температура
на границе раздела слоёв определяется
из следующего выражения:
, (3.8)
где
берётся из справочника.
Так
как тепловая изоляция многослойная,
первичный слой – огнеупорный, второй
и третий – теплопроводный, следовательно
потери теплоты в окружающую среду
определяются из уравнения (3.6)
Пример: Один
слой 250 мм,
,
.
Определить температуру в центре стенки,
если коэффициент теплопроводности
равен
.
Решение: ;
.
3.3 Теплопередача через плоскую однослойную стенку при граничных условиях III-рода
Теплопередача
– процесс теплообмена между двумя
средами (теплоносителями), разделёнными
стенкой (перегородкой). В этом случае
при граничных условиях III-рода
задаются температуры сред теплоносителей,
коэффициенты теплоотдачи
между горячей средой и стенкой и
между стенкой и холодной средой, т.е.
задаётся закон теплообмена. Также
задаётся коэффициент теплопроводности
и
толщина стенки δ.
Требуется
найти плотность теплового потока,
тепловой поток и температуру поверхности
стенки.
Согласно
закону Ньютона-Рихмана плотность
теплового потока между горячей средой
и поверхностью стенки:
. (3.9)
По
закону Фурье этот же поток передаётся
теплопроводностью:
. (3.9)
Этот
же тепловой поток согласно закону
Ньютона-Рихмана от наружной поверхности
стенки отдаётся холодной среде:
. (3.9)
Выражая
из этих уравнений разности температур
и складывая между собой, мы окончательно
получаем выражение для плотности
теплового потока q:

. (3.10)
Обозначим
величину

(3.11)
К
– коэффициент теплопередачи через
плоскую однослойную однородную стенку.
Он представляет собой количество
теплоты, передаваемое в единицу времени
через единицу поверхности при разности
температур между средами в один градус.
Значения коэффициентов теплопередачи
для различных видов теплообмена будут
даны в таблице в разделе конвективного
теплообмена. Коэффициент теплопередачи
всегда меньше меньшего α. Для того чтобы
увеличить теплопередачу, нужно увеличить
меньшее α.
. (3.12)
Тепловой
поток
. (3.13)
Величина
обратная коэффициенту теплопередачи
– полное термическое сопротивление
теплопередачи:
, (3.14)
где – термическое
сопротивление теплоотдачи со стороны
горячей жидкости;
– термическое
сопротивление стенки (чем меньше ,
тем выше
);
– термическое
сопротивление теплоотдачи от стенки к
холодной среде.
.
Полное
количество теплоты, передаваемое через
стенку за время τ
,
Дж.
Коэффициента
теплопередачи не является термофизическим
коэффициентом, его нет в справочниках.
Он рассчитывается по формуле (3.11).
Из
(3.9) легко найти температуры горячей и
холодной стенок:
, (3.15)
.
3.4 Теплопередача через многослойную плоскую стенку при граничных условиях III-рода
Пусть
заданы температуры сред
и
,
коэффициенты теплоотдачи
и
(закон теплообмена), коэффициенты
теплопроводности
,
и
,
толщина слоёв стенки
,
и
.
Аналогично
формуле (3.9) записывают уравнение
сохранения плотности теплового потока
q,
выражая разность температур и складывая
почленно полученные выражения плотности
теплового потока

, (3.16)

. (3.17)
Коэффициент
теплопередачи:
(3.18)
(3.19)
Из
уравнения (3.16), определяя плотность
теплового потока, находим температуры
на поверхностях стенки
,
и температуры на границах слоёв
,
.
Соседние файлы в папке ТМО. Конспект лекций
- #
- #
- #
Теплопроводность через стенку
Под теплопередачей через стенку понимают процесс передачи теплоты между двумя средами через непроницаемую стенку любой геометрической формы в стационарном и нестационарном режимах теплообмена. Стенка может быть многослойной.
Рассмотрим стационарный режим теплопередачи через плоскую, цилиндрическую и сферическую стенки при котором теплопередача – величина постоянная и температурное поле не изменяется во времени и зависит только от координаты. В этом случае при условии постоянства теплофизических свойств тела температура в плоской стенке изменяется линейно, а в цилиндрической – по логарифмическому закону, т.е.
Q = const и T = f(x) – линейная (при плоской стенке) или логарифмическая функция (при круглой стенке).
Согласно второму закону термодинамики процесс теплопередачи идет от среды с большей температурой к среде с меньшей температурой.
Теплопередача через непроницаемую стенку включает в себя следующие процессы:
- теплоотдачу от горячей среды к стенке;
- теплопроводность внутри стенки;
- теплоотдачу от стенки к холодной среде.
Теплопередача через плоскую стенку (граничные условия первого рода)
Теплопроводность – первое элементарное тепловое явление переноса теплоты посредством теплового движения микрочастиц в сплошной среде, обусловленное неоднородным распределением температуры.
Совокупность значений температуры для всех точек пространства в данный момент времени называется температурным полем.
Если температурное поле не изменяется во времени, то мы имеем дело со стационарным тепловым режимом.
Тепловой поток Q [Вт] – это количество теплоты, передаваемой в единицу времени (1 Дж/с=1 Вт).
Поверхностная плотность теплового потока рассчитывается по формуле:
где Q – тепловой поток [Вт]; F – площадь стенки [м 2 ].
На основании закона Фурье q=-λdT/dx, значение плотности теплового потока для однослойной стенки будет определяться по формуле:
где δ = dx – толщина стенки, λ
λ/δ; [Вт/м 2 *К] – коэфициент тепловой проводности стенки.
а обратная величина –
R = δ/λ; [м 2. К/Вт] – термическое сопротивление стенки.
Для теплового потока формулу так же можно представить в виде:
Общее количество теплоты проходящее через площадь стены S за время t можно представить как:
Распределение температуры в плоской стенке
Рассмотрим изменение температуры в нашей стене. Так как у нас тепловой поток постоянный, то dT/dx = const=C1; T=C1х+С2 (1). Определим С1 и С2 через граничные условия.
При х=0 T=T1, подставим в уравнение (1) и получим T1=С2.
При х=δ T=T2, подставим в уравнение (1) и получим T2=С1*δ+С2, T2=С1*δ+T1, получим: С1=(Т2-T1)/δ. Теперь подставим в уравнение (1) найденные С1 и С2, получим следующее распределение температуры в нашей стене:
Если нам нужно узнать на какой глубине стены Т=То, то формула преобразуется в следующий вид:
Теплопроводность через многослойную стенку
Если у нас есть стенка из нескольких (n) слоев с разными коэффициентами теплопроводности λi и разной толщиной δi.
Термическое сопротивление стенки считается так:
Для теплового потока формула будет иметь вид:
Температура на границе слоя вычисляется по следующей формуле:
Например, если нужно вычислить температуру между 3-м и 4-м слоем, формула будет такая:
Эквивалентная теплопроводность многослойной стенки:
Теплопередача через плоскую стенку в граничащую среду (граничные условия третьего рода)
Теплопередача – это более сложный процесс теплообмена между жидкими и газообразными средами, разделенными твердой стенкой. Теплопередача включает в себя и процесс теплопроводности, и процесс теплоотдачи.
Коэффициент теплоотдачи α, Вт/(м 2 ·К) – это количество теплоты, отдаваемое в единицу времени единицей поверхности при разности температур между поверхностью и окружающей средой, равной одному градусу.
Коэффициент теплопередачи k, Вт/(м 2 ·К), характеризует тепловой поток, проходящий через единицу площади поверхности стенки при разности температуры сред, равной одному градусу:
q = k * (Tвозд.внутри – Tвозд.снаружи); Вт/м 2
Коэффициент теплопередачи для n слойной стенки:
Термические сопротивления теплоотдаче на внешних поверхностях стенки будут равны:
Тогда общее термическое сопротивление теплопередаче будет равно:
Температуры на поверхности стенки можно определить по формулам:
Теплопроводность через цилиндрическую стенку (граничные условия первого рода)
Теплообменные аппараты в большинстве случаев имеют не плоские, а цилиндрические поверхности, например рекуператоры типа “труба в трубе”, кожухотрубные водонагреватели и т.д. Поэтому возникает необходимость рассмотрения основных принципов расчета цилиндрических поверхностей.
Согласно закону Фурье, количество теплоты, проходящее в единицу времени через этот слой, равно:
Подставим значения граничные значение и вспомним, что разность логарифмов равна логарифму отношению аргументов, получим:
Распределение температур внутри однородной цилиндрической стенки подчиняется логарифмическому закону, и уравнение температурной кривой имеет вид:
Количество теплоты, проходящее через стенку трубы, может быть отнесено либо к единице длины трубы L, либо к единице внутренней F1 или внешней F2 поверхности трубы. При этом расчетные формулы принимают следующий вид:
Все материалы, представленные на сайте, носят исключительно справочный и ознакомительный характер и не могут считаться прямой инструкцией к применению. Каждая ситуация является индивидуальной и требует своих расчетов, после которых нужно выбирать нужные технологии.
Не принимайте необдуманных решений. Имейте ввиду, что то что сработало у других, в ваших условиях может не сработать.
Администрация сайта и авторы статей не несут ответственности за любые убытки и последствия, которые могут возникнуть при использовании материалов сайта.
Сайт может содержать контент, запрещенный для просмотра лицам до 18 лет.
Теплопроводность через однослойную плоскую стенку
Дифференциальное уравнение теплопроводности позволяет определить температуру в зависимости от времени и координат в любой точке поля.
Для любого конкретного случая к нему надо присоединить необходимые краевые условия.
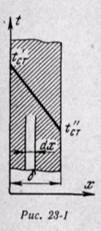
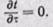
Но при принятых условиях первые и вторые производные от ( по y иz также равны нулю:
поэтому уравнение теплопроводности можно написать в следующем виде:
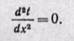
Интегрируя уравнение (23-1), находим
После вторичного интегрирования получаем
При постоянном коэффициенте теплопроводности это уравнение прямой линии. Следовательно, закон изменения температуры при прохождении теплоты через плоскую стенку будет линейным.
Найдем постоянные интегрирования А и В.
При х = 0 температура t = t’cr — B; при х = δ температура t = t”cr — Аδ +tст, откуда
Плотность теплового потока найдем из уравнения Фурье (22-7)
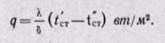
Зная удельный тепловой поток, можно вычислить общее количество теплоты, которое передается через поверхность стенки F за время τ:
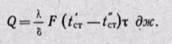
Количество теплоты, которое передается теплопроводностью через плоскую стенку, прямо пропорционально коэффициенту теплопроводности стенки К, ее площади F, промежутку времени т, разности температур на наружных поверхностях стенки (t’ст — t”ст) и обратно пропорционально толщине стенки δ. Тепловой поток зависит не от абсолютного значения температур, а от их разности
t’ст — t”ст = Δt наtзываемой температурным напором.
Полученное уравнение (23-2) является справедливым для случая, когда коэффициент теплопроводности является постоянной величиной. В действительности коэффициент теплопроводности реальных тел зависит от температуры и закон изменения температур будет выражаться кривой линией. Если коэффициент теплопроводности зависит от температуры в незначительной степени, то на практике закон изменения температур считают линейным.
Уравнение (23-2) можно получить непосредственно из закона Фурье (22-6), считая, что температура изменяется только в направлении оси х:
Разделив переменные, получаем
Интегрируя последнее уравнение при условии Q = const, находим
Постоянную интегрирования С найдем из граничных условий:
при х = 0 температура
при х = δ температура 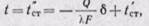
Введем в уравнение (23-2) поправки па зависимость λ от t, считая эту зависимость линейной:

В этом случае, подставив в уравнение Фурье вместо К его значение из формулы (а), получаем

Разделив переменные и интегрируя в пределах от х = 0 до x = δ и в интервале температур от t’ст до t”ст, получаем
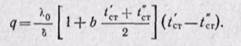
Полученное уравнение (23-4) позволяет определить плотность теплового потока при переменном коэффициенте теплопроводности. В этом уравнении множитель
является среднеинтегралыюй величиной коэффициента теплопроводности.
В уравнении (23-2) было принято λ,=const и равным среднему значению λср. Поэтому, сравнивая уравнения (23-2) и (23-4), получаем

Следовательно, если λср определяется при среднеинтегральной температуре то формулы (23-2) и (23-4) равнозначны.
При этом плотность теплового потока может определяться из уравнения
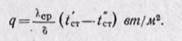
Интегрируя уравнение (б) в пределах от х — О до любой текущей координаты х и в интервале температур от t’ст ДО tx, получим уравнение температурного поля
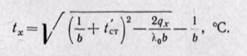
Из этого уравнения следует, что температура внутри стенки изменяется по кривой. Если коэффициент b отрицателен, то кривая будет направлена выпуклостью вниз; если b положителен, то выпуклостью вверх.
Теплопроводность плоской однослойной стенки
Теплопроводность плоской однослойной стенки
- Рис. 11. 3. Плоские стены. Рассмотрим однородную стенку толщиной b, выполненную из материала, теплопроводность которого l не зависит от температуры. Поверхность левой стороны стены поддерживается при постоянной постоянной температуре l, по высоте стены, а правой-низкой, но при постоянной температуре 1 г.
Давление р определяется отношением суммы нормальных к поверхности составляющих сил образующихся вследствие ударов о стенку хаотически движущихся микрочастиц рабочего тела, к площади поверхности А. Людмила Фирмаль
Температура стены изменяется только по ее толщине, направлению оси x рис. 11. 3. То есть температурное поле является 1-мерным, а температурный градиент равен d1 dx. Найти плотность теплового потока через заданную стенку и установить характер изменения температуры вдоль толщины стенки.
- Уравнение Фурье одномерного температурного поля. Чтобы интегрировать это уравнение, разделите переменные 11 — х- После интеграции 11. 2 Чтобы найти интегральную постоянную, используйте известные температуры x-0, −6 и x-1 2. Таким образом, c f таким образом, уравнение k. 2 будет иметь следующий формат АГ.
Термодинамической системой называется совокупность макроскопических тел, которые могут взаимодействовать между собой и с другими телами, составляющими внешнюю среду, в виде обмена энергией или веществом. Людмила Фирмаль
Когда вы решаете уравнение Хорошо О Плотность теплового потока плоской стенки прямо пропорциональна теплопроводности, перепаду температур и обратно пропорциональна толщине стенки. Изменение температуры по отношению к толщине стенки выражается формулой 11. 2.

Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
[spoiler title=”источники:”]
http://helpiks.org/3-16578.html
http://lfirmal.com/teploprovodnost-ploskoj-odnoslojnoj-stenki/
[/spoiler]
9.2. Стационарная теплопроводность через плоскую стенку
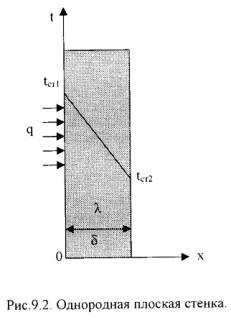
1).Однородная
плоская стенка (Рис.9.2.).
Температуры поверхностей стенки –tст1 и tст2.
Плотность теплового потока:
q
= -λ∙ ∂t/∂n = – λ∙ ∂t/∂x = –
λ∙ (tcт2 – tcт1)/(xcт2 – xcт1)∙
или
q = λ∙ (tcт2 – tcт1)/(xcт2 – xcт1)∙
Dt/Dx (9.13)
Тогда
q
= λ/δ∙(tст1 – tст2) =
λ/δ∙Δt, (9.14)
Если R =δ/λ -термическое сопротивление теплопроводности
стенки [(м2∙К)/Вт], то плотность теплового потока:
q
= (tст1 – tст2)/R . (9.15)
Общее количество теплоты, которое передается через поверхность F за
время τ определяется:
Q
= q∙F∙τ = (tст1 – tст2)/R·F∙τ
. (9.16)
Температура тела в точке с координатой х
находится по формуле:
tx
= tст1 – (tст1 – tст2)∙x/ δ . (9.17)
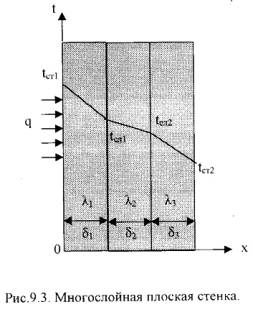
2).
Многослойная плоская стенка.
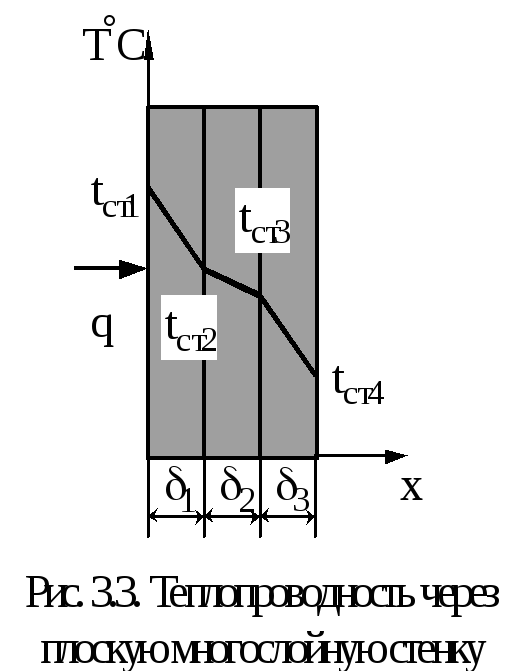
Рассмотрим 3-х слойную стенку (Рис.9.3). Температура наружных
поверхностей стенокtст1 и tст2, коэффициенты
теплопроводности слоевλ1, λ2, λ3,
толщина слоевδ1, δ2, δ3.
Плотности тепловых потокок через каждый слой стенки:
q
= λ1/δ1∙(tст1 – tсл1)
, (9.18)
q = λ2/δ2∙(tсл1 – tсл2)
, (9.19)
q = λ3/δ3∙(tсл2 – tст2)
, (9.20)
Решая эти уравнения, относительно разности температур и складывая,
получаем:
q
= (t1 – t4)/(δ1/λ1 +
δ2/λ2 + δ3/λ3)
= (tст1 – tст4)/Ro , (9.21)
где: Ro = (δ1/λ1 + δ2/λ2
+ δ3/λ3) – общее термическое
сопротивление теплопроводности многослойной стенки.
Температура слоев определяется по следующим формулам:
tсл1
= tст1 – q∙(δ1/λ1). (9.22)
tсл2 = tсл1 – q·δ2/λ2).
(9.23)
|
|
Макеты страниц
Из этих уравнений определяются частные температурные напоры, а именно:

Складывая их, получаем полный температурный напор:

из которого определяется значение плотности теплового потока

и значение коэффициента теплопередачи


Рис. 6-2. Теплопередача через однослойную плоскую стенку; характер изменения температуры в теплоносителях и разделяющей их стенке.
Таким образом, чтобы вычислить значение коэффициента теплопередачи k для плоской стенки, необходимо знать толщину этой стенки 


Величина, обратная коэффициенту теплопередачи, называется общим термическим сопротивлением теплопередачи. Из уравнения (6-5) эта величина равна:

Из этого соотношения следует, что общее термическое сопротивление равно сумме частных:

где 


2. Многослойная плоская стенка. Рассматривается стенка, состоящая из нескольких, например двух, слоев (рис. 6-3).
Толщины слоев 






При установившемся тепловом состоянии системы плотность теплового потока постоянна и поэтому можно написать:

Из этих уравнений определяются частные температурные напоры:

Складывая раздельно левые и правые части уравнений, получаем полный температурный напор

из которого определяется значение плотности теплового потока

и значение коэффициента теплопередачи для двухслойной плоской стенки

Распределение температур при теплопередаче через плоскую одно- и многослойную стенки представлено соответственно на рис. 6-2 и 6-3.
Неизвестные температуры 

Если стенка состоит из нескольких слоев толщиной 


или

В этом случае уравнение (6-5) принимает вид:

или


Рис. 6-3. Теплопередача через многослойную плоскую стенку.
Температуры стенки можно определить и графически. Один из таких способов был описан в гл. 1. Поэтому мы здесь рассмотрим второй, который основан на замене термического сопротивления горячей и холодной среды термическим сопротивлением твердой стенки с таким же коэффициентом теплопроводности, как и действительная стенка.
Пусть температуры наружных поверхностей воображаемой стенки соответственно равны температурам горячей и холодной среды 


откуда

Здесь величины 






Рис. 6-4. Графический способ определения температур на поверхности стенки.

Рис. 6-5. Графическое определение температуры на поверхности и в плоскости соприкосновения слоев двухслойной стенки.
Действительно, из подобия треугольников АВС и ADE имеем, что 

Согласно уравнению (б) 


Если стенка многослойная и требуется определить лишь температуру наружных поверхностей, то построение производят точно таким же образом, как и для однослойной стенки, имея дело лишь со средним коэффициентом теплопроводности 
Температура же между слоями в точке А определяется по пересечению двух лучей (способ построения виден из рис. 6-5).
Пример 6-1. Определить потерю теплоты через 1 м2 кирпичной обмуровки котла толщиной 






Согласно уравнению (6-5)

Подставляя это значение в уравнение (6-4), имеем:

Наконец, из уравнения (б)

3. Однородная цилиндрическая стенка. Пусть имеется цилиндрическая стенка (труба) с внутренним диаметром 







При установившемся тепловом состоянии системы количество теплоты, отданное горячей и воспринятое холодной средой, одно и то же. Следовательно, можно написать:

Из этих соотношений определяем частные температурные напоры:

Складывая уравнения системы (к), получаем полный температурный напор


Рис. 6-6. Теплопередача через однослойную цилиндрическую стенку.

Рис. 6-7. Теплопередача через многослойную цилиндрическую стенку.
Из уравнения (л) определяется значение линейной плотности теплового потока 

откуда линейный коэффициент теплопередачи (на 

Величина, обратная линейному коэффициенту теплопередачи, 
Из уравнения (6-9) имеем:

Последнее означает, что общее термическое сопротивление равно сумме частных — термического сопротивления теплопроводности стенки 


4. Многослойная цилиндрическая стенка. В этом случае рассматривается передача теплоты через многослойную, например двухслойную, цилиндрическую стенку. Диаметры и коэффициенты теплопроводности отдельных слоев известны (рис. 6-7). Температура горячей среды 





При установившемся тепловом состоянии системы можно записать:

Определяем частные температурные напоры:

Складывая левые и правые части уравнений (н), получаем полный температурный напор

и значение линеинои плотности теплового потока

Распределение температур при теплопередаче через однослойную и многослойную цилиндрические стенки показано на рис. 6-6 и 6-7 соответственно.
Линейный коэффициент теплопередачи для двухслойной стенки

а общее термическое сопротивление 
Для многослойной стенки трубы

и

Чтобы определить неизвестные температуры стенки 



Способ определения температуры между слоями описан в гл. 1. Расчетные формулы теплопередачи для труб довольно громоздки, поэтому при практических расчетах применяются некоторые упрощения. Если толщина стенки не очень велика, то вместо формулы (6-8) в расчетах применяется формула для плоской стенки (6-4), которая в этом случае (в применении к трубе длиной 1 м) принимает вид:

где k — коэффициент теплопередачи для плоской стенки, рассчитанный по формуле (6-5), dx — средний диаметр стенки; 
При этом если 


т. е. при расчете теплопередачи по формуле (6-12) вместо 




Пример 6-2. Паропровод диаметром 200/216 мм покрыт слоем совелитовой изоляции толщиной 120 мм, коэффициент теплопроводности которой 



Согласно условию задачи 

Первые два члена общего термического сопротивления по сравнению с остальными малы, при расчетах ими можно было бы пренебречь. На основании формулы (5-8)

И, наконец, согласно формуле (н):

5. Шар. Пусть внутренний диаметр шара равен 






При стационарном тепловом состоянии системы количество теплоты, переданное от горячей жидкости к холодной, можно выразить тремя уравнениями:

Из этих уравнений определяется значение 

Следовательно, коэффициент теплопередачи для шаровой стенки определяется оотношением

Обратная величина 


Рис. 6-8. Теплопередача через шаровую стенку.
При практических расчетах надо проверять соотношение термических сопротивлений; относительно малыми из них всегда можно пренебречь.
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА ПЕРВАЯ. ТЕПЛОПРОВОДНОСТЬ
- 1-1. ОСНОВНОЙ ЗАКОН ТЕПЛОПРОВОДНОСТИ
- 1-2. ТЕПЛОПРОВОДНОСТЬ ПЛОСКОЙ СТЕНКИ
- 1-3. ТЕПЛОПРОВОДНОСТЬ ЦИЛИНДРИЧЕСКОЙ СТЕНКИ
- 1-4. ТЕПЛОПРОВОДНОСТЬ ШАРОВОЙ СТЕНКИ И ТЕЛ НЕПРАВИЛЬНОЙ ФОРМЫ
- 1-5. ТЕПЛОПРОВОДНОСТЬ ТЕЛ С ВНУТРЕННИМИ ИСТОЧНИКАМИ ТЕПЛОТЫ
- ГЛАВА ВТОРАЯ. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН
- 2-1. ОБЩИЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 2-2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ТЕПЛООБМЕНА
- 2-3. ОСНОВЫ ТЕОРИИ ПОДОБИЯ
- 2-4. ПОДОБИЕ ПРОЦЕССОВ КОНВЕКТИВНОГО ТЕПЛООБМЕНА
- 2-5. ОБОБЩЕНИЕ ОПЫТНЫХ ДАННЫХ НА ОСНОВЕ ТЕОРИИ ПОДОБИЯ
- ГЛАВА ТРЕТЬЯ. ТЕПЛООБМЕН В ЖИДКОСТЯХ И ГАЗАХ
- 3-1. ТЕПЛООТДАЧА ПРИ ОБТЕКАНИИ ПЛОСКОЙ ПОВЕРХНОСТИ (ПЛАСТИНЫ)
- 3-2. ТЕПЛООТДАЧА ПРИ ТЕЧЕНИИ ЖИДКОСТИ В ТРУБАХ
- 3-3. ТЕПЛООТДАЧА ПРИ СВОБОДНОЙ КОНВЕКЦИИ
- 3-4. ТЕПЛООТДАЧА ПРИ ПОПЕРЕЧНОМ ОБТЕКАНИИ ТРУБ
- ГЛАВА ЧЕТВЕРТАЯ. ТЕПЛООБМЕН ПРИ КИПЕНИИ И КОНДЕНСАЦИИ
- 4-1. ТЕПЛООБМЕН ПРИ КИПЕНИИ
- 4-2. ТЕПЛООБМЕН ПРИ КОНДЕНСАЦИИ ПАРА
- ГЛАВА ПЯТАЯ. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
- 5-1. ЗАКОНЫ ТЕПЛОВОГО ИЗЛУЧЕНИЯ
- 5-2. ЛУЧИСТЫЙ ТЕПЛООБМЕН МЕЖДУ ТЕЛАМИ
- 5-3. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ ГАЗОВ
- ГЛАВА ШЕСТАЯ. ПРОЦЕССЫ ТЕПЛОПЕРЕДАЧИ
- 6-1. СЛОЖНЫЙ ТЕПЛООБМЕН И ТЕПЛОПЕРЕДАЧА
- 6-2. ТЕПЛОПЕРЕДАЧА ЧЕРЕЗ СТЕНКИ
- 6-3. ТЕПЛОПЕРЕДАЧА ЧЕРЕЗ СЛОЖНЫЕ СТЕНКИ
- 6-4. ИНТЕНСИФИКАЦИЯ ПРОЦЕССОВ ТЕПЛОПЕРЕДАЧИ
- 6-5. ТЕПЛОВАЯ ИЗОЛЯЦИЯ
- ГЛАВА СЕДЬМАЯ. НЕСТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ
- 7-1. ОПИСАНИЕ ПРОЦЕССА
- 7-2. АНАЛИТИЧЕСКОЕ РЕШЕНИЕ
- 7-3. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ
- 7-4. РЕГУЛЯРНЫЙ ТЕПЛОВОЙ РЕЖИМ
- ГЛАВА ВОСЬМАЯ. ТЕПЛООБМЕННЫЕ АППАРАТЫ
- 8-2. РЕКУПЕРАТИВНЫЕ АППАРАТЫ
- 8-3. ТЕПЛООБМЕННЫЕ РЕГЕНЕРАТИВНЫЕ И СМЕСИТЕЛЬНЫЕ АППАРАТЫ
- 8-4. ГИДРОМЕХАНИЧЕСКИЙ РАСЧЕТ ТЕПЛООБМЕННЫХ АППАРАТОВ
- ГЛАВА ДЕВЯТАЯ. МОДЕЛИРОВАНИЕ ТЕПЛОВЫХ УСТРОЙСТВ
- 9-2. УСЛОВИЯ МОДЕЛИРОВАНИЯ
- 9-3. ПРИМЕРЫ МОДЕЛИРОВАНИЯ
- ГЛАВА ДЕСЯТАЯ. ОТДЕЛЬНЫЕ ЗАДАЧИ ТЕПЛООБМЕНА
- 10-1. ГИДРОДИНАМИЧЕСКАЯ ТЕОРИЯ ТЕПЛООБМЕНА
- 10-2. ТЕПЛООБМЕН ПРИ ВЫСОКИХ СКОРОСТЯХ
- 10-3. ТЕПЛООБМЕН ПОВЕРХНОСТЕЙ С ИСКУССТВЕННОЙ ШЕРОХОВАТОСТЬЮ
- 10-4. ТЕПЛООТДАЧА РАСПЛАВЛЕННЫХ МЕТАЛЛОВ
- 10-5. ПЕРЕДАЧА ТЕПЛОТЫ ЧЕРЕЗ СТЕРЖЕНЬ
- 10-6. ПЕРЕДАЧА ТЕПЛОТЫ ЧЕРЕЗ РЕБРА
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ
1.4. Теплопроводность плоской однослойной и многослойной стенки
Теплопроводность плоской однослойной стенки
|
Рис. 1.8. Плоская однослойная стенка |
Задача решается для плоской однородной стенки толщиной δ, выполненной из материала, коэффициент теплопроводности которого λ не зависит от температуры. Левая поверхность стенки поддерживается при заданной постоянной по высоте стенки температуре t1 правая — при более низкой, постоянной температуре t2. Температура стенки меняется только по ее толщине, в направлении оси х (рис. 1.8), т. е. температурное поле будет одномерным, а градиент температуры будет равен dt/dx. Определим плотность теплового потока через заданную стенку и установим характер изменения температуры по толщине стенки. Уравнение Фурье для одномерного температурного поля: |
q = -λ
Чтобы проинтегрировать это уравнение, разделим переменные:
dt =-(q/ λ)*dx 1.6
После интегрирования от t1 до t2 и и х от 0 до d получено:
Рекомендуемые материалы
t=t1 –(q/ λ)*dx, q= (t1-t2)/(d/l)= (t1-t2)/rt 1.7
где: rt= d/l – удельное термическое сопротивление плоской стенки.
Плотность теплового потока в плоской стенке прямо пропорциональна коэффициенту теплопроводности, перепаду температур и обратно пропорциональна толщине стенки.
Суммарный тепловой поток Q через поверхность F плоскуой пластины равен Q=q*F
Теплопроводность плоской однослойной и многослойной стенки
|
Рис.1.9 |
В технических расчетах часто встречаются многослойные плоские стенки. При условии плотного прилегания отдельных слоев решение задачи теплопроводности, полученное для однослойной плоской стенки, можно распространить и на многослойную стенку (Рис.1.9). ). Предполагается, что температуры соприкасающихся поверхностей в зоне контакта одинаковы (idem), т.е. контактное термическое сопротивление равно нулю (0). Каждый из слоев состоит из однородного материала с коэффициентами теплопроводности каждого слоя l1 , l2, l3. Известны температуры наружных поверхностей многослойной стенки t1 и t4 и толщина каждого слоя d1 , d2, d3 . Принято, что температуры t1 и t4 постоянны, т. е. рассматривается одномерная стационарная задача. |
При этом плотность теплового потока для всех слоев в направлении х будет постоянной и одинаковой Необходимо определить величину q и температуры t2 , t3 соприкасающихся поверхностей слоев, которые по условиям задачи неизвестны.
Согласно решению для плоской однослойной пластины q= (t1–t2)/(d1/l1)= (t2–t3)/(d2/l2)= (t3–t4)/(d3/l3)
Эту зависимость можно записать в следующем виде
(t1–t2)= q (d1/l1)
(t2–t3)= q (d2/l2)
(t3–t4)= q (d3/l3)
После сложения левые и правые частей получено: (t1–t4)= q *( (d1/l1)+ (d2/l2)+ (d3/l3) ) или: q= (t1–t4)/ ( (d1/l1)+ (d2/l2)+ (d3/l3) )
Люди также интересуются этой лекцией: Оформление самодержавия (Роль опричнины).
Аналогичное решение можно получить для многослойной стенки из n cлоев:
q= (t1-tn)/ 

Величину rti = (di/li) называют термическим сопротивлением теплопроводности i слоя, а Rt= 
Температура в каждом слое стенки при q=const меняется линейно. Следовательно, для многослойной стенки температурная кривая представляет собой ломаную линию.
Тангенс угла наклона каждого отрезка равен градиенту температуры в пределах данного слоя, значение которого можно найти из уравнения 1.5 если его продифференцировать:
tga=gradt= (dt/dx)=-q/l1