Как найти теплоту через импульс

Как найти кол-во теплоты, выделяемое при неупругом столкновении двух тел? Известны обе массы и обе скорости

Наталия Дмитриева

Ученик

(98),
закрыт

8 лет назад

ВиталийГорностаев

Мастер

(2365)

10 лет назад

Обозначим скорости тел до столкновения V1 V2
Общая скорость после столкновения U
Закон сохранения импульса m1*V1+m2*V2=U*(m1+m2)
Отсюда U=(m1*V1+m2*V2)/(m1+m2)
Кинетическая энергия до столкновения Ek1=m1*(V1)^2+m2*(V2)^2
Кинетическая энергия после столкновения Ek2=(m1+m2)*(U)^2
Количество теплоты Q=Ek2-Ek1

Источник

Условие задачи:

Найти количество теплоты, выделившееся при лобовом абсолютно неупругом ударе двух свинцовых шаров массой 1 кг каждый, скользящих без вращения по абсолютно гладкой поверхности. До удара шары двигались по одной прямой в одном направлении. Скорость первого шара равна 10 см/с, скорость второго – 20 см/с.

Задача №2.10.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(m=1) кг, (upsilon_1=10) см/с, (upsilon_2=20) см/с, (Q-?)

Решение задачи:

Запишем два закона:

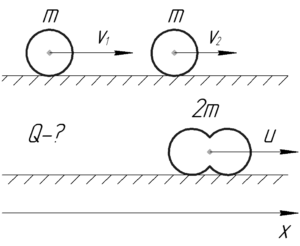
закон сохранения импульса (ЗСИ) в проекции на ось (x), поскольку система, состоящая из двух шаров замкнута в этом направлении;
закон сохранения энергии (ЗСЭ), но учтем, что часть начальной кинетической энергии шаров при абсолютно неупругом ударе переходит в теплоту (Q).

[left{ begin{gathered}
m{upsilon _1} + m{upsilon _2} = 2mu hfill \
frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m{u^2}}}{2} + Q hfill \
end{gathered} right.]

Из ЗСИ выразим скорость шаров после удара:

[u = frac{{{upsilon _1} + {upsilon _2}}}{2}]

Полученное выражение подставим в ЗСЭ:

[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m}}{2}{left( {frac{{{upsilon _1} + {upsilon _2}}}{2}} right)^2} + Q]

Раскроем квадрат суммы в правой части уравнения:

[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m}}{2}left( {frac{{upsilon _1^2 + 2{upsilon _1}{upsilon _2} + upsilon _2^2}}{4}} right) + Q]

Откроем скобки:

[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{mupsilon _1^2}}{4} + frac{{m{upsilon _1}{upsilon _2}}}{2} + frac{{mupsilon _2^2}}{4} + Q]

[Q = frac{{mupsilon _1^2}}{4} – frac{{m{upsilon _1}{upsilon _2}}}{2} + frac{{mupsilon _2^2}}{4} = frac{m}{4}left( {upsilon _1^2 – 2{upsilon _1}{upsilon _2} + upsilon _2^2} right)]

[Q = frac{m}{4}{left( {{upsilon _1} – {upsilon _2}} right)^2}]

Получилась “красивая” формула для расчета ответа. Переведем скорости в единицы системы СИ.

[10; см/с = frac{{10}}{{100}}; м/с = 0,1; м/с]

[20; см/с = frac{{20}}{{100}}; м/с = 0,2; м/с]

Считаем ответ:

[Q = frac{1}{4}{left( {0,1 – 0,2} right)^2} = 2,5 cdot 10^{-3}; Дж = 2,5; мДж]

Ответ: 2,5 мДж.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.10.2 Тележка массой 100 кг движется со скоростью 2 м/с. Когда она проезжает мимо
2.10.4 Охотник стреляет из ружья. Определить силу отдачи, если масса дроби 35 г
2.10.5 Шары массами 1 и 2 кг движутся навстречу друг другу. Скорость первого шара 5 м/с

Источник

§6. Задачи на столкновения и законы сохранения импульса и энергии

В физике под столкновениями понимают процессы взаимодействия между телами (частицами) в широком смысле слова, а не только в буквальном – как соприкосновение тел. Сталкивающиеся тела на большом расстоянии являются свободными. Проходя друг мимо друга, тела взаимодействуют между собой, в результате могут происходить различные процессы – тела могут соединиться в одно тело (абсолютно неупругий удар), могут возникать новые тела и, наконец, может иметь место упругое столкновение, при котором тела после некоторого сближения вновь расходятся без изменения своего внутреннего состояния. Столкновения, сопровождающиеся изменением внутреннего состояния тел, называются неупругими. Тела (частицы), участвующие в столкновении, характеризуются (до и после столкновения) импульсами и энергиями. Процесс столкновения сводится к изменению этих величин в результате взаимодействия. Законы сохранения энергии и импульса позволяют достаточно просто устанавливать соотношения между различными физическими величинами при столкновении тел. Особенно ценным здесь является то обстоятельство, что зачастую законы сохранения могут быть использованы даже в тех случаях, когда действующие силы неизвестны. Так обстоит дело, например, в физике элементарных частиц.

Происходящие в обычных условиях столкновения макроскопических тел почти всегда бывают в той или иной степени неупругими – уже хотя бы потому, что они сопровождаются некоторым нагреванием тел, т. е. переходом части их кинетической энергии в тепло. Тем не менее, в физике понятие об упругих столкновениях играет важную роль. С такими столкновениями часто приходится иметь дело в физическом эксперименте в области атомных явлений, да и обычные столкновения можно часто с достаточной степенью точности считать упругими.

Сохранение импульса тел (частиц) при столкновении обусловлено тем, что совокупность тел, участвующих в столкновении, составляет либо изолированную систему, т. е. на тела, входящие в систему, не действуют внешние силы, либо замкнутую: внешние силы отличны от нуля, а сумма внешних сил равна нулю. Несколько сложнее обстоит дело с применением закона сохранения энергии при столкновениях. Обращение к сохранению энергии требует порой учёта различных форм внутренней энергии.

Можно сказать, что действие законов сохранения импульса и энергии в процессах столкновения подтверждено широким спектром опытных данных.

Неупругие столкновения

Два куска пластилина массами `m_1` и `m_2`, летящие со скоростями `vecv_1` и `vecv_2` слипаются. Найдите наибольшее `Q_max` и наименьшее количество `Q_min` теплоты, которое может выделиться в результате абсолютно неупругого соударения.

Рассмотрим абсолютно неупругое соударение («слипание») тел, движущихся в ЛСО скоростями `vecv_1` и `vecv_2` соответственно. В процессе абсолютно неупругого соударения импульс системы сохраняется.

`m_1vecv_1+m_2vecv_2=(m_1+m_2)vecv`.

Отсюда находим скорость составного тела

`vecv=(m_1vecv_1+m_2vecv_2)/(m_1+m_2)`.

Закон сохранения энергии принимает вид

`(m_1vecv_1^2)/2+(m_2vecv_2^2)/2=((m_1+m_2)*vecv)/2+Q`.

Из приведенных соотношений находим убыль кинетической энергии

`Q=(m_1*m_2*(vecv_2-vecv_1)^2)/(2(m_1+m_2))=1/2 mu(vecv_2-vecv_1)^2`,

здесь `mu=(m_1m_2)/(m_1+m_2)` – приведенная масса системы тел.

Итак, при абсолютно неупругом соударении во внутреннюю энергию переходит кинетическая энергия тела приведенной массы, движущегося с относительной скоростью.

Убыль механической энергии достигает наибольшей величины

`Q_max=(m_1*m_2*(vecv_2-vecv_1)^2)/(2(m_1+m_2))=1/2 mu(v_1+v_2)^2`

при `vecv_1 uarr darr vecv_2`.

Убыль механической энергии будет наименьшей

`Q_min=(m_1*m_2*(vecv_2-vecv_1)^2)/(2(m_1+m_2))=1/2 mu(v_2-v_1)^2`

при `vecv_1 uarr uarr vecv_2`.

Упругие столкновения

На гладкой горизонтальной поверхности лежит гладкая шайба массой `M`. На него налетает гладкая шайба массой `m`, движущийся со скоростью `vec v`. Происходит упругий центральный удар шайб. Найдите скорости `vecv_1` и `vecv_2` шайб после соударения. При каком условии налетающая шайба будет двигаться после соударения в прежнем направлении?

Задачу рассмотрим в ЛСО, ось `Ox` которой направим по линии центров шайб в момент соударения. Внешние силы, действующие на шайбы в процессе соударения, это силы тяжести и силы нормальной реакции опоры. Их сумма равна нулю. Следовательно, импульс системы шайб в процессе взаимодействия не изменяется. По закону сохранения импульса `m vec v = m vecv_1 + M vecv_2`.

Переходя к проекциям на ось `Ox`, получаем `mv = mv_(1x) + Mv_2`, здесь учтено, что направление скорости `vecv_1` налетающей шайбы после соударения не известно. По закону сохранения энергии

`(mv^2)/2 = (mv_(1x)^2)/2 + (Mv_2^2)/2`.

Полученные соотношения перепишем в виде

`m(v – v_(1x)) = Mv_2`,

`m(v^2 – v_(1x)^2) = Mv_2^2`.

Разделив второе равенство на первое `(v != v_(1x))`, приходим к линейной системе `v_2 = v + v_(1x)`, `m(v – v_(1x)) = Mv_2`, решение которой имеет вид

`v_(1x) = (m – M)/(m + M) v`, `v_2 = (2m)/(m + M) v`.

Налетающая шайба будет двигаться после соударения в прежнем направлении `(v_(1x) > 0)` при `m > M`, т. е. если масса налетающей шайбы больше массы покоящейся шайбы.

Две гладкие упругие круглые шайбы движутся поступательно по гладкой горизонтальной поверхности со скоростями `vecv_1` и `vecv_2`. Найдите скорости `vecv_1^’` и `vecv_2^’` шайб после абсолютно упругого нецентрального соударения. Массы шайб `m_1` и `m_2`.

Задачу рассмотрим в ИСО, оси координат `Ox` и `Oy` которой лежат в горизонтальной плоскости, при этом ось `Ox` направлена по линии центров шайб в момент соударения (рис. 16).

В течение времени соударения на систему шайб действуют только вертикальные внешние силы: это силы тяжести и силы нормальной реакции. Их сумма равна нулю. Тогда импульс системы шайб в процессе взаимодействия сохраняется

`vecp_1 + vecp_2 = vecp_1^’ + vecp_2^’`,

здесь `vecp_1 = m_1 vecv_1`, `vecp_2 = m_2 vecv_2`, `vecp_1^’ = m_1 vecv_1^’`, `vecp_2^’ = m_2 vecv_2^’` – импульсы шайб до и после соударения.

Так как шайбы идеально гладкие, то в процессе соударения внутренние силы -силы упругого взаимодействия – направлены только по оси `Ox`. Эти силы не изменяют `y`-составляющие импульсов шайб. Тогда из `p_(1y) = p_(1y)^’`, `p_(2y) = p_(2y)^’` находим `y`-составляющие скоростей шайб после соударения

`vecv_(1y)^’ = v_(1y)`, `v_(2y)^’ = v_(2y)`,

т. е. в проекции на ось `Oy` скорости шайб в результате соударения не изменились.

Найдём `x`-составляющие скоростей шайб после упругого соударения. При таком соударении сохраняется кинетическая энергия

`(m_1 (v_(1x)^2 + v_(1y)^2))/2 + (m_2 (v_(2x)^2 + v_(2y)^2))/2 = (m_1 ((v_(1x)^’)^2 + (v_(1y)^’)^2))/2 + (m_2 ((v_(2x)^’)^2 + (v_(2y)^’)^2))/2`.

С учётом равенства `y`-составляющих скоростей шайб до и после соударения последнее равенство принимает вид

`(m_1 v_(1x)^2)/2 + (m_2 v_(2x)^2)/2 = (m_1 (v_(1x)^’)^2)/2 + (m_2 (v_(2x)^’)^2)/2`.

Обратимся к закону сохранения импульса и перейдём к проекциям импульсов шайб на ось `Ox`

`m_1 v_(1x) + m_2 v_(2x) = m_1 v_(1x)^’ + m_2 v_(2x)^’`.

Таким образом, исходная задача сведена к задаче об абсолютно упругом центральном ударе: именно такой вид приняли бы законы сохранения энергии и импульса, если бы скорости шайб были направлены по линии центров. Полученную нелинейную систему уравнений можно свести к линейной. Для этого следует (как и в предыдущей задаче) в обоих уравнениях по одну сторону знака равенства объединить слагаемые, относящиеся к первой шайбе, а по другую – ко второй, и разделить `(v_(1x) != v_(1x)^’)` полученные соотношения. Это приводит к линейному уравнению

`v_(1x) + v_(1x)^’ = v_(2x) + v_(2x)^’`.

Решая систему из двух последних уравнений, находим

`v_(1x)^’ = ((m_1 – m_2) v_(1x) + 2m_2 v_(2x))/(m_1 + m_2)`,

`v_(2x)^’ = (2m_1 v_(1x) + (m_2 – m_1) v_(2x))/(m_1 + m_2)`.

Полученные соотношения для `v_(1x)^’`, `v_(1y)^’` и `v_(2x)^’`, `v_(2y)^’` решают вопрос о проекциях и величинах скоростей шайб после соударения

`v_1^’ = sqrt((v_(1x)^’)^2 + (v_(1y)^’)^2)`, `v_2^’ = sqrt((v_(2x)^’)^2 + (v_(2y)^’)^2)`,

а также об углах `alpha_1` и `alpha_2`, которые векторы скорости `vecv_1^’` и `vecv_2^’` образуют с положительным направлением оси `Ox`:

`bbb”tg” alpha_1 = (v_(1y)^’)/(v_(1x)^’)`, `bbb”tg” alpha_2 = (v_(2y)^’)/(v_(2x)^’)`.

Построенное в общем виде решение задач упругого центрального и нецентрального соударений открывает дорогу к анализу целого ряда задач, для которых рассмотренная модель соответствует характеру взаимодействия тел (частиц).

Источник

Начиная с определений импульса и объяснения законов сохранения, в статье показывается способ решения ряда задач, в которых важно только начальное и конечное состояние (но, например, ничего нельзя сказать про время движения), в частности, задач на столкновение тел.

Введение

С помощью законов сохранения многие механические задачи решаются намного проще, чем при использовании динамических уравнений движений. С другой стороны, законами сохранения можно пользоваться только в тех случаях, когда необходимо, зная начальное состояние тела, найти конечное. При данном описании системы невозможно узнать время движения тела и все промежуточные состояния.

Для лучшего понимания темы различных соударений давайте еще раз повторим теорию по законам сохранения в механике.

Самыми распространенными законами сохранения является закон сохранения импульса и энергии.

Импульс

Определение. Импульсом p тела (материальной точки) называется векторная физическая величина, равная произведению массы m на скорость (здесь и далее жирным шрифтом выделены векторные величины).

p = mv.

Изменение импульса можно представить через второй закон Ньютона:

Δp = mΔv = FΔt

Если рассмотреть систему материальных точек, которые движутся с разными скоростями, то импульс задается следующим выражением:

p = m₁v₁+ m₂v₂ + …

Закон сохранения импульса

При отсутствии внешних сил импульс системы материальных точек сохраняется.

Замечание 1. Отсутствие внешних сил означает, что система замкнута.

Замечание 2. Часто в задачах есть внешние силы, но при этом законом сохранения импульса в каком-то виде пользоваться можно.

Внешние силы есть, но они взаимно скомпенсированы (например сила тяжести и сила нормальной реакции опоры при движении по гладкой поверхности).
Внешние силы не имеют проекции на какую-то заданную ось (например, ось ОX), тогда импульс может сохраняться вдоль этого направления.
Если в некоторый момент времени внутренние силы много больше внешних, тогда импульс системы сохраняется (например, разрыв снаряда)

Так как задачи только на закон сохранения достаточно однообразные, то рассмотрим и закон сохранения энергии.

Работа и энергия

Любая механическая система характеризуется скалярной величиной E — энергией, которая однозначно определяет состояние системы. Зная энергию системы в двух состояниях, можно найти работу внешних сил, совершенную над системой:

ΔE = E₂ – E₁ = A.

Механическая работа

Определение. Если на тело, движущееся по прямой, действует постоянная сила F, то механической работой A этой силы на перемещение s называется скалярное произведение

A = (F, s) = |F||s| · cos(α) = Fs · cos(α),

где α — угол между векторами F и s.

Определение. Средняя мощность <P> силы F — это отношение работы А, совершенной силой F за время t, к интервалу времени t.

<P> = A / t.

Мощность также можно переписать так: <P> = Fv · cos(α).

Консервативные и диссипативные силы

Определение.Консервативные силы (потенциальные силы) —это силы, работа которых при перемещении из состояния 1 в состояние 2 не зависит от траектории, а зависит только от начального и конечного положения точек 1 и 2.

Примеры.Работа силы тяжести или электростатических сил не зависит от траектории, следовательно, это консервативные силы.

К диссипативным силам относятся различные виды силы трения.

Замечание. Работа диссипативных сил всегда отрицательна. Следовательно, они уменьшают механическую энергию тела, переводя ее в тепло.

Кинетическая и потенциальная энергия

Определение. Кинетическая энергия тела равна произведению массы тела на квадрат скорости, деленное на два:

Eкин = mv² / 2.

Так как работа консервативных сил зависит только от начального и конечного положения, то для нее можно определить потенциальную энергию.

Потенциальная энергия для силы тяжести определяется следующим выражением:

Eпот = mgh.

Замечание. Для силы тяжести можно легко вывести потенциальную энергию, зная работу силы притяжения.

Другие примеры.Зная силу растяжения или сжатия пружины, легко посчитать потенциальную энергию сжатой (растянутой) пружины:

Eпот = k(x₂ – x₁)² / 2.

Закон сохранения и изменения энергии

Формулировка. Механическая энергия в замкнутой системе сохраняется при отсутствии диссипативных сил:

ΔE = 0

Замечание 1. Механической энергией называется сумма потенциальной и кинетической энергии.

E = Eкин + Епот.

Замечание 2.При наличии консервативных сил может меняться скорость тела (системы тел) и их общая кинетическая энергия, но это будет происходить за счет перехода кинетической энергии в потенциальную.

Формулировка. Изменение механической энергии под действием внешних и внутренних неконсервативных сил равно суммарной работе этих сил А:

ΔE = A.

Теорема об изменении кинетической энергии

Формулировка. Работа всех сил (консервативных и диссипативных) равна изменению кинетической энергии системы.

∑A = ΔEкин.

Замечание. С помощью этой теоремы легко решать многие задачи. Например, рассмотрим задачу о нахождении тормозного пути автомобиля, движущегося со скоростью v = 60 км/ч по дороге с коэффициетом трения μ = 0,5.

Работа силы трения:

A = –μN = –μmgS,

где N — сила нормальной реакции, S — тормозной путь автомобиля.

Изменение кинетической энергии:

ΔE = –mv² / 2.

По теореме о изменении кинетической энергии:

–mv² / 2 = –μmgS.

S = v² / 2gμ = 29 м

Замечание.Скорость необходимо перевести в СИ.

Соударения

Определение. Центральный удар — это соударение 2 тел , при котором скорости каждого из тел направлены вдоль линии, соединяющей центры обоих тел.

Замечание. Если один из шаров покоится, то скорость второго тела должна быть направлена вдоль линии, соединяющей центры тел.

При решении задач на столкновение двух и более тел надо привыкнуть к следующим формулировкам:

Абсолютно упругий удар (упругий удар) — это тип соударения, при котором выполняется закон сохранения энергии и закон сохранения импульса. Часто этот тип соударения применим к железным шарикам.
Неупругий удар — это удар, при котором выполняется закон сохранения импульса и закон изменения механической энергии (так как теряется часть энергии при ударе).
Абсолютно неупругий удар — это удар, при котором два тела продолжают двигаться как единое целое. При этом столкновении выполняется закон сохранения импульса и закон изменения механической энергии.

Замечание. Как мы видим, для решения задач нужно сначала записать соответствующие законы сохранения энергии и импульса или изменения энергии. Далее необходимо решить получившуюся систему уравнений.

Задача 1

Железный шар массы m = 500 г движется по гладкой горизонтальной поверхности со скоростью 10 м/с и сталкивается с неподвижным восковым шаром, имеющим массу М = 200 г, после чего оба шара движутся вместе. Найдите количество теплоты, выделившееся при ударе.

Решение. В этой задаче удар абсолютно неупругий, поэтому выполняется закон сохранения импульса (ЗСИ) и изменения энергии.

Запишем ЗСИ на ось OX:

mv = (m + M)V. (1)

Для того, чтобы найти выделившуюся энергию при соударении, необходимо записать закон изменения энергии (ЗИЭ)

ΔE = mv² / 2 — (m + M)V² / 2. (2)

Далее остается только математическая часть задачи — решить систему уравнений (1) и (2). Из (1) найдем V:

V = mv / (M + m).

Подставив в (2), получим:

Замечание. Такую задачу невозможно решить для неупругого удара, при котором тела не слипаются друг с другом, так как нам будет неизвестны скорости двух разлетевшихся тел.

Список литературы

Белолипецкий С. Н., Еркович О. С., Казаковцева В. А., Цвецинская Т. С. Задачник по физике. М., 2005.
Черноуцан А. Учебно-справочное пособие для старшеклассников и абитуриентов. М., 2000.

Источник

Закон сохранения импульса

Произведение массы тела на его скорость называется импульсом тела (другое название – количество движения). Так как скорость – вектор, то и импульс является векторной величиной. Разумеется, направление импульса совпадает с направлением скорости движения тела.

При помощи нового понятия закон Ньютона F = ma может быть выражен иначе. Так как a = (v₂ ? v₁)/t, то F = (mv₂ ? mv₁)/t, или Ft = mv₂ ? mv₁. Произведение силы на время ее действия равно изменению импульса тела.

Вернемся к явлению отдачи.

Наш результат рассмотрения отдачи орудия можно теперь сформулировать короче: сумма импульсов орудия и снаряда после выстрела остается равной нулю. Очевидно, такой же она была и до выстрела, когда орудие и снаряд находились в состоянии покоя.

Скорости, входящие в уравнение m₁v₁ + m₂v₂ = 0, – это скорости непосредственно после выстрела. При дальнейшем движении снаряда и орудия на них начнут действовать силы тяжести, сопротивление воздуха, а на пушку дополнительно – и сила трения о землю. Вот если бы выстрел был произведен в безвоздушном пространстве из орудия, висящего в пустоте, тогда движение со скоростями v₁ и v₂ продолжалось бы сколь угодно долго. Орудие двигалось бы в одну сторону, а снаряд – в противоположную.

В артиллерийской практике в настоящее время широко применяются орудия, установленные на платформе и стреляющие на ходу. Как же изменить выведенное уравнение, чтобы оно было применимо к выстрелу из такого орудия? Мы можем записать:

m₁u₁ + m₂u₂ = 0,

где u₁ и u₂ – скорости снаряда и орудия по отношению к движущейся платформе. Если скорость платформы V, то скорости орудия и снаряда по отношению к покоящемуся наблюдателю будут v₁ = u₁ + V и v₂ = u₂ + V.

Подставляя значения u₁ и u₂ в последнее уравнение, получим:

(m₁ + m₂)V = m₁v₁ + m₂v₂.

В правой части равенства у нас стоит сумма импульсов снаряда и орудия после выстрела. А в левой? До выстрела орудие и снаряд с общей массой m₁ + m₂ движутся вместе со скоростью V. Значит, и в левой части равенства стоит общий импульс снаряда и орудия, но до выстрела.

Мы доказали очень важный закон природы, который называется законом сохранения импульса. Доказали мы его для двух тел, но можно легко показать, что такой же результат имеет место и для любого числа тел. Каково же содержание закона? Закон сохранения импульса говорит, что сумма импульсов нескольких тел, находящихся во взаимодействии, не меняется в результате этого взаимодействия.

Ясно, что закон сохранения импульса будет справедлив лишь тогда, когда на ту группу тел, которую мы рассматриваем, не действуют силы со стороны. Такая группа тел называется в физике замкнутой.

Ружье и пуля во время выстрела ведут себя, как замкнутая группа двух тел, несмотря на то, что испытывают действие силы земного притяжения. Вес пули мал по сравнению с силой пороховых газов и явление отдачи произойдет по одним и тем же законам, независимо от того, где будет произведен выстрел, – на Земле или в ракете, летящей в межпланетном пространстве.

Закон сохранения импульса позволяет легко решать различные задачи, относящиеся к столкновениям тел. Попробуем одним глиняным шариком попасть в другой – они слипнутся и будут продолжать движение вместе; если выстрелить из ружья в деревянный шар, он покатится вместе с застрявшей в нем пулей; стоявшая вагонетка покатится, если человек с разбегу прыгнет в нее. Все приведенные примеры с точки зрения физика весьма похожи. Правило, связывающее скорости тел при столкновениях такого типа, сразу же получается из закона сохранения импульса.

Импульсы тел до встречи были m₁v₁ и m₂v₂, после столкновения тела объединились, их общая масса равна m₁ + m₂. Обозначив скорость объединившихся тел через V, получим:

m₁v₁ + m₂v₂ = (m₁ + m₂)V,

или

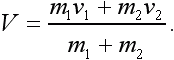
Напомним о векторном характере закона сохранения импульса. Импульсы mv, стоящие в числителе формулы, надо складывать как векторы.

«Объединяющий» удар при встрече движущихся под углом тел показан на рис. 31. Для того чтобы найти величину скорости, надо длину диагонали параллелограмма, построенного на векторах импульсов встречающихся тел, разделить на сумму их масс.

Как найти кол-во теплоты, выделяемое при неупругом столкновении двух тел? Известны обе массы и обе скорости

Условие задачи:

Дано:

Решение задачи: