Испарение сопровождается остыванием жидкости. Чем она холоднее, тем менее интенсивно происходит образование пара. Но скорость процесса можно поддерживать, если жидкость подогревать, то есть подводить к ней тепло.
Так возникает понятие удельной теплоты парообразования. У каждого жидкости и даже твердого тела (ведь и его можно превратить в пар) эта величина своя. Рассмотрим, как найти удельную теплоту парообразования.
Содержание
- Единица измерения
- Формула для величины
- Какие данные нужны, чтобы рассчитать значение?
- Алгоритм и правила расчета
- Несколько примеров нахождения
- Таблица для ряда веществ
- Видео по теме статьи
- Заключение
Единица измерения
Удельная теплота парообразования – это величина, которая показывает, сколько теплоты необходимо сообщить веществу массой 1 кг, чтобы превратить его в пар. При этом температура вещества должна быть постоянной.
Обычно рассматриваемую величину обозначают латинскими буквами L, r или греческой λ (лямбда). Теплота в системе СИ измеряется в Джоулях (Дж), масса – в килограммах (кг). Таким образом, L измеряется в Дж/кг.
Так как теплота в джоулях принимает зачастую большие значения, может встречаться обозначения кДж (килоджоули) – Дж*1000, или МДж (мегаджоули) – Дж*1000 000.
Формула для величины

- Q – теплота,
- m – масса.
Ее часто используют для расчетов энергетических затрат на выпаривание воды из растворов: Q= L* m.
L определяют в лабораториях и заносят в таблицы, составляют справочники, которыми можно пользоваться любому желающему. При этом всегда указывают температуру и давление, при которых находилось L.
С ростом температуры L уменьшается, так как жидкость расширяется, взаимодействие между ее частицами уменьшается, и ее легче превратить в пар. Когда плотность пара и жидкости сравниваются, наступает критическое состояние.
Оно характеризуется определенным давлением и температурой. Для воды — это 374 ℃ и 218,5 атм. В таком состоянии L=0.
Какие данные нужны, чтобы рассчитать значение?
Чтобы вычислить искомую величину, применяют знания о том, что теплота испарения равна теплоте конденсации со знаком «минус». Это значит, что когда пар конденсируется (превращается в воду), он охлаждается и отдает свое тепло окружающей среде. Можно применить формулу: Q= L* m.
Для расчетов необходимы следующие данные:
- Q – теплота, отданная паром, Дж,
- m – масса образовавшейся в процессе конденсации воды, кг;
- L – удельная теплота парообразования, Дж/кг – собственно то, что нужно определить.
Применяют также закон сохранения энергии и понятие теплоемкости: Qв=С*Mв*(T2-T1), где:
- С – удельная теплоемкость воды, которая нагревается под действием сконденсированного пара, Дж/(кг*К), – считается известной и берется из таблицы,
- Mв – ее масса;
- T2-T1 – изменение температуры в Кельвинах или градусах Цельсия.
Алгоритм и правила расчета

- Анализируют, как проходит процесс, какое вещество отдает, а какое получает тепло.
- Переводят все единицы измерения в одну систему.
- Записывают необходимые формулы.
- Решают уравнение с одним неизвестным.
При проведении расчетов надо следить за размерностью величин. В системе СИ масса измеряется в кг, теплота в Дж, а температура в градусах Кельвина. Разность температур можно считать в градусах Цельсия.
Часто бывает нужно найти удельную теплоту парообразования при условиях кипения жидкости и нормальном атмосферном давлении (760 мм рт. ст.). В таких условиях получают чистую воду из растворов или выделяют из смеси веществ ее части.
Процесс используется в химической и пищевой промышленности и даже на бытовом уровне.
Несколько примеров нахождения
Задача №1. Сколько необходимо энергии для превращения в пар следующих кипящих веществ:
- 2 кг этилового спирта;
- 2 кг воды;
- 2 кг расплавленного свинца.
Необходимо воспользоваться формулой Q= L* m и взять значение L из таблицы. Получится:
- 0,84*МДж*2 кг = 1,68 МДж;
- 2,3 МДж*2 кг = 4,6 МДж;
- 8,6 МДж *2 кг = 17,2 МДж.
Как видно, превратить в пар воду сложнее, чем этанол, но легче, чем металл. На первый взгляд, это очевидно, но когда дело касается веществ, близких по температуре кипения, то разница становится менее заметна, ее невозможно угадать. Тем не менее, она имеет особое значение.
Задача №2. Как вычислить, сколько энергии необходимо, чтобы превратить 1 тонну воды при 20 ℃ в пар при 100 ℃?
Решение: 1 т = 1000 кг.

- Q1 – тепло, ушедшее на нагревание воды с 20 до 100 градусов,
- Q2 – тепло, необходимое для образования пара (процесс происходит без изменения температуры).
Q1 = С*M* (T2-T1), С воды = 4200 Дж/(кг*К), Q2 = L*M, L воды при обычном кипении = 2,3 МДж/кг, T2-T1 = 100-20 = 80.
Подставляя известные величины, находят искомую энергию: Q = 4200*1000*80+2,3 *106*1000 = 4,2*80*106+2300*106=2636 (МДж)
Задача №3. Сколько надо затратить электроэнергии, чтобы превратить 1 л воды в пар?
Решение: Q= Lводы*m. Масса 1 литра обычной водопроводной воды равна 1 кг. Q=2260 кДж/кг *1 кг=2260 кДж=2,3 МДж.
1 кВт*ч = 3,6 МДж. Из простой пропорции следует, что надо затратить 0,64 кВт*ч. Для 2-х литров величина возрастет в 2 раза, для 3-х – в три, и так далее.
Зная тарифы на электроэнергию, несложно посчитать стоимость, во сколько рублей обойдется такое кипячение. Надо также учитывать, что частично энергия уйдет в воздух и на нагрев сосуда, частей плиты, поэтому реальный расход будет выше.
Таблица для ряда веществ
Удельная теплота парообразования при нормальном атмосферном давлении (1 атм = 760 мм рт. ст.) и температуре кипения (для каждого вещества она своя).
| Вещество | L, МДж/кг | T кипения, ℃ |
| Вода | 2,3 | 100 |
| Этиловый спирт | 0,84 | 78,4 |
| Метиловый спирт | 1,1 | 64,1 |
| Ртуть | 0,28 | 357 |
| Жидкий азот | 0,2 | -195,8 |
| Аммиак | 1,4 | -33,4 |
| Фреон 12 | 0,16 | -24,9 |
| Расплавленный алюминий | 10,9 | 2450 |
Для воды при 20 ℃ L=2,45МДж/кг.
Видео по теме статьи
Об удельной теплоте парообразования расскажет видео:
Заключение
Единица измерения удельной теплоты парообразования – Дж/кг. Она показывает, сколько при заданной температуре надо подвести тепла, чтобы преобразовать 1 кг вещества в пар. Величина определяется путем проведения экспериментов.
Для воды при 100 ℃ ее значение 2260 кДж/кг. Эта величина довольно большая в сравнении с характеристиками других веществ. С ростом температуры значение удельной теплоты образования пара уменьшается.
На этой странице вы можете рассчитать количество теплоты, необходимое для превращение жидкости в пар с помощью калькулятора онлайн. Для этого необходимо ввести массу жидкости и ее удельную теплоту парообразования (см. таблицу).
Удельная теплота парообразования – физическая величина, показывающая, какое количество теплоты потребуется для превращения жидкости массой 1кг в пар без изменения температуры. Обозначается буквой L и измеряется в Дж/кг.
Содержание:
- калькулятор количества теплоты для превращения в пар
- формула количества теплоты для превращения в пар
- таблица “Удельная теплота парообразования”
- примеры задач
Формула количества теплоты для превращения в пар
{Q = L cdot m}
Q – необходимое количество теплоты для превращения жидкости, находящейся при температуре кипения в пар
L – удельная теплота парообразования (см. таблицу)
m – масса жидкости, находящейся при температуре кипения.
Удельная теплота парообразования жидкостей и расплавленных металлов при температуре кипения и нормальном атмосферном давлении
| Жидкость | Удельная теплота парообразования, кДж/кг |
|---|---|
| Азот жидкий | 201 |
| Аллюминий | 9200 |
| Аммиак | 1370 |
| Бензин | 230 – 310 |
| Висмут | 840 |
| Вода (при 0°С) | 2500 |
| Вода (при 20°С) | 2450 |
| Вода (при 100°С) | 2260 |
| Вода (при 370°С) | 440 |
| Вода (при 374,15°С) | 0 |
| Водород жидкий | 450 |
| Воздух | 197 |
| Гелий жидкий | 23 |
| Железо | 6300 |
| Золото | 1650 |
| Керосин | 209 – 230 |
| Кислород жидкий | 214 |
| Магний | 5440 |
| Медь | 4800 |
| Никель | 6480 |
| Олово | 3010 |
| Ртуть | 293 |
| Свинец | 860 |
| Спирт этиловый | 906 |
| Эфир этиловый | 356 |
| Цинк | 1755 |
Примеры задач на нахождение количества теплоты
Задача 1
Какое количество теплоты требуется для обращения в пар воды массой 0.2 кг при температуре 100°C?
Решение
Подставим значения из условия в формулу и рассчитаем результат. Удельную теплоту парообразования для воды при температуре 100°C возьмем из таблицы: L = 2260 кДж/кг.
Q = L cdot m = 2260 cdot 0.2 = 452 Дж
Ответ: 452 Дж
Проверим ответ с помощью калькулятора .
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 сентября 2021 года; проверки требуют 13 правок.
Уде́льная теплота́ парообразова́ния и конденса́ции — физическая величина, показывающая, какое количество теплоты необходимо, чтобы обратить количество жидкости с единичной массой в пар, при данной температуре жидкости и без её изменения (температуры) в процессе испарения. Равна удельной теплоте конденсации единичной массы пара в жидкость.
Расчёт[править | править код]
Удельная теплота парообразования и конденсации обозначается буквой 
где Q — теплота, истраченная на превращение жидкости в пар или пара в жидкость, m — масса.
Наименьшее значение удельной теплоты парообразования будет при температуре кипения жидкости.
Размерность удельной теплоты парообразования в СИ — Дж/кг. Устаревшие, но иногда применяемые единицы для теплоты парообразования — ккал/кг и кал/кг.
В химии теплота парообразования обычно приводится к молю вещества. Эта величина называется молярной теплотой испарения (конденсации); единица её измерения — Дж/моль. Также используются устаревшие единицы: ккал/моль, кал/моль.
Значения для некоторых веществ[править | править код]
Удельная теплота парообразования некоторых веществ при нормальном атмосферном давлении (760 мм. рт. ст. = 101,325 кПа) и температуре, равной температуре кипения вещества[1]:
| Вещество | Температура кипения, °C |
Удельная теплота парообразования/ конденсации, кДж/кг |
|---|---|---|
| Азот | −195,8 | 199 |
| Ртуть | 357 | 282 |
| Диэтиловый эфир | 34,6 | 380 |
| Водород | −252,6 | 448 |
| Этиловый спирт | 78,4 | 837 |
| Свинец | 1 740 | 855 |
| Аммиак | −33,4 | 1 370 |
| Вода | 100 | 2300 |
| Медь | 2 600 | 4 820 |
| Железо | 3 200 | 6 120 |
| Алюминий | 2 450 | 10 900 |
| Литий | 1 340 | 21 000 |
| Графит | 4 200 | 29 700 |
| Бериллий | 2 469 | 32 500 |
| Бор | 3 865 | 45 300 |
См. также[править | править код]
- Удельная теплоёмкость
- Удельная теплота плавления
- Сублимация
Примечания[править | править код]
- ↑ Теплота испарения // БСЭ, 3 изд.
Определение теплоты испарения жидкости
Испарением называется переход вещества из жидкого в газообразное состояние. Оно происходит на свободной поверхности жидкости. Для выходы из жидкости молекулы должны преодолеть силы молекулярного сцепления. Кроме того, при испарении совершается работа против внешнего давления Р, поскольку объём жидкости меньше давления пара. Переход части молекул в пар приводит к обеднению жидкости быстрыми молекулами, то есть, к её охдаждению. Количество теплоты, необходимое для изотермического испарения одного моля жидкости при внешнем давлении, равном упругости её насыщенных паров, называется молярной теплотой испарения (парообразования).
Теплоту парообразования жидкости можно измерить непосредственно при помощи калориметра. такой метод, однако, не позволяет получить точных результатов. В натоящей работе для определения теплоты испарения применён косвенный метод, основанный на формуле Клапейрона-Клаузиуса:
dP/dT = L/(T(V2 – V1))
P – давление насыщенного пара жидкости, L – теплота испарения. V2 – объём пара, V1 – объём жидкости. Найдя из опыта dP/dT, T, V2 и V1 можно определить L путём расчёта. Измерения производятся при давлениях ниже атмосферного. V1 не превосходит 0,5 процентов от V2. При нажей точности опыта величиной V1 можно пренебречь. Объём V (V2) связан с давлением и температурой уравнение Ван-дер-Ваальса, в котором величиной б следует пренебречь, так как б одного порядка с V1. Пренебрежение членом a/V^2 по сравнению с Р вносит ошибку менее трёх процентов (и меньше при пониженном давлении). Положим поэтому V = RT/P. Найдём L = RT^2/P dP/dT = -R d(ln P)/d(1/T).
В нашем опыте температура жидкости измеряется термометром, давление пара – манометром, а производная находится графически как угловой коэффициент.

Расчет теплот испарения и возгонки
Уравнение Клапейрона – Клаузиуса дает возможность определить тепловой эффект фазового перехода (в данном случае – испарения или возгонки) на основании экспериментальных данных о зависимости давления насыщенного пара (жидкой или твердой фаз) от температуры.
Расчет средней теплоты испарения или возгонки
|
Средней теплотой испарения или возгонки называется величина |
∆ |
, получаемая из |
|||
|
уравнения Клапейрона-Клаузиуса в приближении её постоянства( |
∆ф.п. = |
) в нешироком |
|||
|
интервале температур ( |
20 – 50 К). |
||||
|
Для расчета |
средней теплоты фазового перехода используются интегральные формы |
||||
|
∆ = |
уравнения Клапейрона-Клаузиуса, полученные в результате приближенного интегрирования: ln = ∆ф.п.
|
Принимаем ∆ = |
ln |
= |
∆ф.п. |
|||||||||||
|
и выносим за знак интеграла: |
||||||||||||||
|
ln |
= |
∆ф.п. |
||||||||||||
|
Далее возможны два варианта интегрирования: |
||||||||||||||
|
1) Аналитический расчет |
||||||||||||||
|
Проводим определенное интегрирование указанного выражения: |
||||||||||||||
|
ln |
= |
∆ф.п. |
||||||||||||
|
В результате получаем расчетную формулу: |
||||||||||||||
|
ln |
= − |
∆ф.п. |
1 |
− |
1 |
|||||||||
|
где |
и – давления насыщенного пара соответственно при температурах |
и . |
||||||||||||
|
Таким |
образом, |
можно приближённо |
рассчитать среднюю теплоту |
испарения |
(возгонки) если известны хотя бы два равновесных давления пара при двух температурах.
Вместо давлений при двух температурах могут быть известны другие параметры, через которые давление можно выразить. Например, параметры состояния идеального газа: T, V, n.
1

2) Графический расчет Проводим неопределенное интегрирование уравнения и получаем уравнение прямой, не
проходящей через начало координат:
ln = − ∆ ∙ 1 +
|
Строим график в координатах |
и по тангенсу угла наклона прямой определяем |
||||||||||||||
|
или возгонки: |
|||||||||||||||
|
среднюю энтальпию испаренияln − |
= − |
∆ф.п. |
|||||||||||||
|
ф.п. |
|||||||||||||||
|
l |
− |
∆ф.п. |
= −2,303 ∙ |
∙ |
|||||||||||
|
координатах |
, то |
||||||||||||||
|
Если график построен в |
∆ |
= − |
∙ |
||||||||||||
|
Кроме того, уравнение прямой может быть представлено в виде |
|||||||||||||||
|
ln |
= + , где А и В |
||||||||||||||
|
– некоторые числовые коэффициенты. Тогда |
∆ф.п. |
= − ∙ |
. |
||||||||||||
Расчет истинной теплоты испарения или возгонки
При расчете истинного теплового эффекта испарения или возгонки (т.е. энтальпии фазового перехода при заданной конкретной температуре) используют дифференциальную форму уравнения Клапейрона-Клаузиуса.
ln = ∆ф.п.
или
= ∆ф.п.
Выражаем:
ln
∆ф.п. =
2

И далее задача сводится к нахождению производной, которую можно найти
аналитически или графически. 1) Аналитический расчет
Аналитический расчет возможен, если имеется функциональная зависимость вида
|
= |
( ) |
||||||||||||
|
. |
|||||||||||||
|
Например: |
|||||||||||||
|
где A, B, C, D – постоянныеlnкоэффициенты= + |
+ уравненияln + . |
||||||||||||
|
Дифференцируем данное выражение по температуре: |
|||||||||||||
|
ln |
|||||||||||||
|
Далее, |
умножаем на |
и |
получаем= − |
зависимость+ + |
теплоты фазового превращения от |
||||||||
|
температуры: |
ln |
||||||||||||
|
ф.п. |
ф.п. . |
||||||||||||
|
Подставляя в полученное∆уравнение= |
заданную температуру= − + , рассчитываем+ |
значение |
|||||||||||
|
Если имеется функциональная зависимость вида |
, то расчет |
теплового эффекта |
|||||||||||
|
∆ |
|||||||||||||
|
проводят по такому же принципу, с той лишь разницей, что=его( |
выражают из уравнения |
||||||||||||
|
) |
= ∆ф.п.
∆ф.п. =
2)Графический расчет
Взависимости от координат, в которых представлена графическая зависимость, расчет
∆проводится по соответствующему уравнению:
|
а) график в координатах |
∆ |
. |
|||||
|
В этом случае определение |
основано на уравнении: |
||||||
|
= ( |
) |
∆ф.п. |
|||||
|
ln |
= |
= |
|||||
|
Тангенс угла наклона касательной к графику в этих координатах равен: |
|||||||
|
Значит, |
= ∆ф.п.
3

Отсюда расчетная формула, связывающая тепловой эффект с тангенсом угла наклона касательной
∆ф.п. =
|
Если график построен в координатах l |
− |
, то |
|
∆ф.п. = 2,3
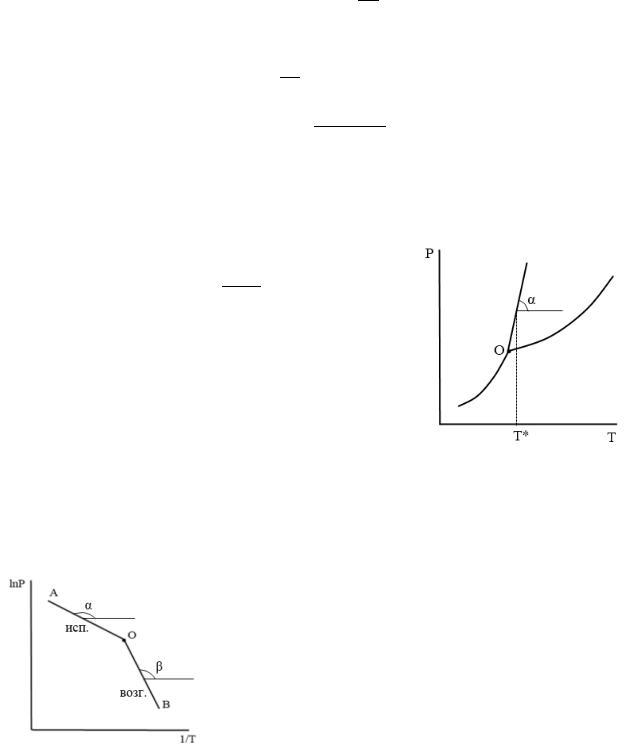
б) график в координатах = ( ).
Определение ∆ф.п. основано на уравнении:
= ∆ф.п.
Тангенс угла наклона касательной к графику в этих координатах равен:
=
= ∆ф.п.
Отсюда расчетная формула, связывающая тепловой эффект с тангенсом угла наклона касательной:
∆ф.п. =
Подставляя в это выражение найденный тангенс угла наклона касательной и конкретные значения Р* и Т*, находим тепловой эффект.
4
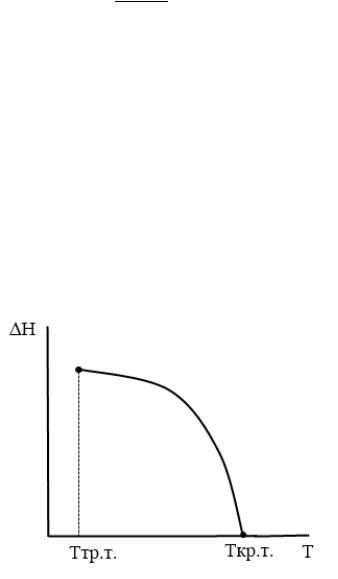
Зависимость теплоты испарения от температуры
Характер зависимости теплоты испарения от температуры определяется уравнением Кирхгофа:
∆исп. = ∆исп. . = ,пар − ,ж < 0
Следовательно, теплота испарения уменьшается с ростом температуры. В уравнении Кирхгофа записана производная функции одной переменной – температуры. В данной форме оно справедливо в той области температур и давлений, в которой пар можно считать идеальным газом и энтальпия испарения практически не зависит от давления. С приближением к критической точке для многих веществ пар становится неидеальным газом (например, у воды давление критической точки 218 атм и пар нельзя считать идеальным газом), но характер температурной зависимости энтальпии испарения сохраняется.
Графически эту зависимость в области температур существования жидкости (вдоль линии насыщенного пара) можно представить следующим образом:
График зависимости теплоты испарения от температуры начинается от температуры
тройной точки.
При низких и средних температурах теплота испарения убывает незначительно, от температуры практически не зависит.
По мере приближения к критической точке, эта зависимость становится все более ярко выраженной, наклон линии резко возрастает, и при критической температуре теплота испарения обращается в ноль:
|
∆исп. кр.т. = |
||||
|
Т.о. в области высоких температур зависимость |
||||
|
ln − будет отклоняться от прямолиней- |
||||
|
ной: |
||||
|
5 |

Правило Трутона
Теплоты испарения различных жидкостей закономерно связаны с их нормальными
температурами кипения.
Существует эмпирическое правило, которое носит название правила Трутона: Мольные
энтропии испарения неполярных неассоциированных жидкостей при нормальной
температуре кипения примерно одинаковы и в среднем составляют:
|
∆исп. = |
∆исп. |
≈ |
± |
Дж |
|
н.т.к. |
моль ∙ К |
В справочнике, на стр. 109 правило Трутона приведено в следующем виде:
|
∆исп. |
≈ , |
Дж |
|
н.т.к. |
моль ∙ К |
Это правило выполняется только для неполярных, неассоциированных в паровой фазе жидкостей и только при нормальной температуре кипения, которая у каждого вещества
единственная.
Интегрирование уравнения Клапейрона для процесса плавления
Т.к. мольные (удельные) объемы твердой и жидкой фаз очень близки друг другу по величине ( ж ≈ тв), уравнение Клапейрона для процесса плавления (а равно как и для процессов полиморфного превращения) преобразовать нельзя, и оно используется только в
таком виде:
= ∆пл.
∆
Или, что больше отвечает физическому смыслу процесса:
= ∆
∆пл.
Величина , определяющая наклон линии плавления к оси температур, хоть и является,
в свою очередь, функцией давления и температуры, но изменяется незначительно при
6

достаточно большом увеличении давления. Поэтому при изменении давления до 10 атм (иногда
|
и более) в хорошем приближении можно считать, что |
= |
, и линия плавления является |
||||||||
|
прямой линией. |
||||||||||
|
Соответственно, интегрирование уравнения Клапейрона-Клаузиуса для процесса |
||||||||||
|
плавления проводится следующим образом: |
∆пл. |
|||||||||
|
= |
||||||||||
|
приблизительно постоянная величина, рассчитанная, |
||||||||||
|
Cоотношение |
∆ |
берется как |
∆ |
|||||||
|
∆ |
||||||||||
|
например, при температуре , и выносится за знак интеграла: |
||||||||||
|
= |
∆пл. |
|||||||||
|
∆ |
∆
Другими словами, заменяем на ∆ .
|
∆ |
= |
∆пл. |
|
∆ |
||
|
− |
= |
∆пл. |
|
∆ |
||
|
= |
+ |
∆пл. |
|
∆ |
Так можно рассчитать, при каком давлении температура плавления станет равной ,
если известна при ,
или рассчитать температуру плавления при заданном давлении:
Расчет теплоты плавления
В основе – уравнение Клапейрона:
= ∆пл.
∆
1) Аналитический расчет Проводится по известной зависимости = ( ).
Пусть эта зависимость имеет вид:
=+ +
где А, В, С – постоянные коэффициенты уравнения.
Выразим теплоту плавления из уравнения Клапейрона:
7
∆пл. = ∆
Продифференцируем зависимость = ( ) по давлению:
=+ 2
∆
∆ = ( + 2 )
Подставляя в полученное выражение необходимые значения p и Т, находим ∆Н.
2) Графический расчет По наклону линии плавления:
|
= |
= |
∆пл. |
||
|
∆ |
||||
|
Отсюда выражаем ∆ |
: |
∆пл. = ∆
Подставляя сюда значение Т* и тангенса угла наклона линии плавления, получаем значение теплоты плавления.
3) Расчет теплоты плавления в тройной точке по теплотам испарения и возгонки
Находим теплоты испарения и возгонки по тангенсу угла наклона соответствующих прямых:
∆исп. = − ∙
∆возг. = − ∙
Затем находим теплоту плавления по соотношению:
∆пл. = ∆возг. − ∆исп.
ОА – линия испарения, ОВ – линия возгонки, т. О – тройная точка.
8
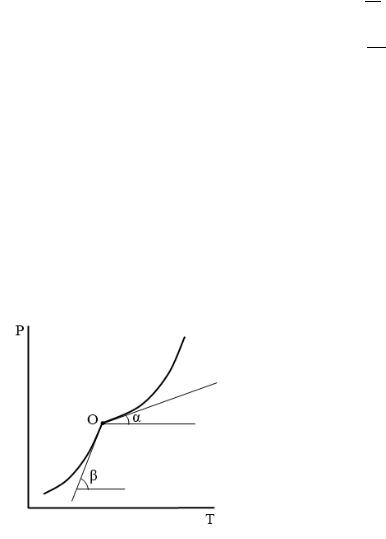
Если известны уравнения линий испарения и возгонки:
то можно найти теплоты испарения и возгонки через коэффициенты уравнений:
∆исп. = − ∙ и ∆возг. = − ∙ ′′
Теплоту плавления находим по разности теплот испарения и возгонки.
∆пл. = ( − )
Теплота плавления:
∆пл. = ∆возг. − ∆исп.
б) по графику − .
Проводим касательные к кривым испарения и возгонки в тройной точке:
|
∆исп. |
= |
|||||||||
|
∆возг. |
= |
|||||||||
|
В этих формулах Т и Р соответствуют температуре и |
||||||||||
|
давлению тройной точки. |
= ∆возг. − ∆исп. или: |
|||||||||
|
Теплота плавления: |
∆пл. |
|||||||||
|
∆пл. = |
− |
= |
( |
− |
) |
|||||
Расчет изменения внутренней энергии и энтропии при фазовых превращениях
|
Расчет изменения внутренней энергии |
и энтропии |
∆ |
для фазового перехода осуще- |
||
|
ствляется после того, как найдено значение |
теплового эффекта |
. |
|||
|
∆ |
∆ |
Изменение внутренней энергии
Рассчитывается по соотношению:
∆ф.п. = ∆ф.п. − ∆ф.п.
а) Плавление
∆пл. = 0
Следовательно
∆пл. = ∆пл.
9

б) Испарение, возгонка
∆исп.(возг.). = 1 ∆исп.(возг.) = ∆исп.(возг.) −
Для обратного перехода (конденсации):
∆конд = −1
∆конд. = −∆исп.(возг.)
Изменение энтропии
∆ф.п. = ∆ф.п.
Для конденсации:
∆конд. = −∆исп.(возг.)
10
Соседние файлы в предмете Физическая химия
- #
20.05.2020168.33 Кб3кр.png
- #
- #
20.05.2020933.47 Кб3лекции 1-5 фх
- #
- #
- #
- #
20.05.2020452.73 Кб2лекция 6
- #
20.05.2020596.4 Кб2лекция 7
- #
20.05.2020484.98 Кб1лекция 8
- #
- #
20.05.2020412.29 Кб1семинар 1


