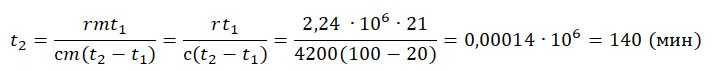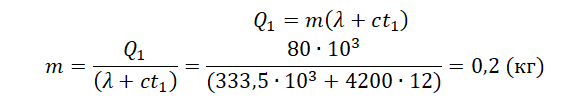Как твердые тела переходят в жидкое состояние посредством плавления, так и жидкости переходят в газообразное состояние посредством парообразования. Для осуществления этого процесса, жидкости необходимо сообщить определенное количество теплоты. Рассчитать эту энергию мы можем, используя такую величину, как удельная теплота парообразования.
На данном уроке вы познакомитесь с подробным решением задач на парообразование и конденсацию. Ниже приведены формулы из пройденных уроков, которые мы будем использовать:
- $Q = Lm$
- $Q = cm(t_2 — t_1)$
- $Q = qm$
- $Q = lambda m$
- $eta = frac{A_п}{A_з}$
Табличные значения величин, которые вам понадобятся:
- Удельная теплота парообразования
- Удельная теплоемкость
- Удельная теплота плавления
- Удельная теплота сгорания
Задача №1
Какое количество теплоты требуется для обращения в пар воды массой $0.2 space кг$ при температуре $100 degree C$?
Дано:
$m = 0.2 space кг$
$t = 100 degree C$
$L = 2.3 cdot 10^6 frac{Дж}{кг}$
$Q — ?$
Показать решение и ответ
Скрыть
Решение:
Температура, равная $100 degree C$ — это температура кипения воды. Значит, мы можем использовать формулу для расчета количества теплоты, необходимого для превращения жидкости в пар:
$Q = Lm$.
Рассчитаем:
$Q = 2.3 cdot 10^6 frac{Дж}{кг} cdot 0.2 space кг = 0.46 cdot 10^6 space Дж = 460 space кДж$.
Ответ: $Q = 460 space кДж$.
Задача №2
Какое количество энергии необходимо, чтобы $5 space л$ воды при $0 degree C$ довести до кипения и затем ее всю испарить?
Дано:
$V = 5 space л$
$t_1 = 0 degree C$
$t_2 = 100 degree C$
$L = 2.3 cdot 10^6 frac{Дж}{кг}$
$c = 4200 frac{Дж}{кг cdot degree C}$
$rho = 1000 frac{кг}{м^3}$
СИ:
$5 cdot 10^{-3} space м^3$
$Q — ?$
Показать решение и ответ
Скрыть
Решение:
Чтобы довести воду до кипения и испарить ее, нам нужно затратить некоторое количество теплоты на ее нагревание и некоторое количество теплоты на парообразование: $Q = Q_1 + Q_2$.
Изначально нам потребуется сообщить воде количество теплоты, необходимое для ее нагревания от $0 degree C$ до ее температуры кипения $100 degree C$. Это количество теплоты будет равно:
$Q_1 = cm(t_2 — t_1)$.
Выразим массу воды через плотность и объем и подставим в формулу:
$m = rho V$,
$Q_1 = c rho V(t_2 — t_1)$.
Рассчитаем:
$Q_1 = 4200 frac{Дж}{кг cdot degree C} cdot 1000 frac{кг}{м^3} cdot 5 cdot 10^{-3} space м^3 cdot (100 degree C — 0 degree C) = 21 space 000 frac{Дж}{degree C} cdot 100 degree C = 2.1 cdot 10^6 space = 2.1 space МДж$.
Теперь рассчитаем количество теплоты, которое необходимо сообщить жидкости, взятой при температуре кипения, для парообразования:
$Q_2 = Lm = L rho V$.
Рассчитаем эту энергию:
$Q_2 = 2.3 cdot 10^6 frac{Дж}{кг} cdot 1000 frac{кг}{м^3} cdot 5 cdot 10^{-3} space м^3 = 11.5 cdot 10^6 space Дж = 11.5 space МДж$.
Теперь мы можем рассчитать всю понадобившуюся энергию:
$Q = Q_1 +Q_2 = 2.1 space МДж + 11.5 space МДж = 13.6 space МДж$.
Ответ: $Q = 13.6 space МДж$.
Задача №3
Сколько теплоты выделится при конденсации $100 space г$ водяного пара, имеющего температуру $100 degree C$, и при охлаждении полученной воды до $20 degree C$?
Дано:
$m = 100 space г$
$t_1 = 100 degree C$
$t_2 = 20 degree C$
$L = 2.3 cdot 10^6 frac{Дж}{кг}$
$c = 4200 frac{Дж}{кг cdot degree C}$
СИ:
$m = 0.1 space кг$
$Q — ?$
Показать решение и ответ
Скрыть
Решение:
Общее количество теплоты будет складываться из энергии, которая выделится при конденсации (превращения пара в жидкость), и энергии, которая выделится при остывании жидкости: $Q = Q_1 + Q_2$.
Сначала рассчитаем количество теплоты, выделившееся при конденсации:
$Q_1 = Lm$,
$Q_1 = 2.3 cdot 10^6 frac{Дж}{кг} cdot 0.1 space кг = 0.23 cdot 10^6 space Дж = 230 space кДж$.
Теперь рассчитаем количество теплоты, которое выделится при охлаждении воды от $100 degree C$ до $20 degree C$. В задаче нужно затратить какую-то энергию, нам важно численное значение энергии, а не ее знак — ведь мы и так знаем, что энергия будет выделяться, а не поглощаться. Поэтому мы можем записать разницу температур как $t_1 — t_2$, чтобы избавиться от знака “минус”:
$Q_2 = cm(t_1 — t_2)$,
$Q_2 = 4200 frac{Дж}{кг cdot degree C} cdot 0.1 space кг cdot (100 degree C — 20 degree C) = 420 frac{Дж}{degree C} cdot 80 degree C = 33 space 600 space Дж = 33.6 space кДж$.
Определим общее выделившееся количество теплоты:
$Q = Q_1 + + Q_2 = 230 space кДж + 33.6 space кДж = 263.6 space кДж$.
Ответ: $Q = 263.6 space кДж$.
Задача №4
В сосуд, содержащий $30 space кг$ воды при $0 degree C$, вводится $1.85 space кг$ водяного пара, имеющего температуру $100 degree C$, вследствие чего температура воды становится равной $37 degree C$. Найдите удельную теплоту парообразования воды.
Дано:
$m_1 = 30 space кг$
$t_1 = 0 degree C$
$m_2 = 1.85 space кг$
$t_2 = 100 degree C$
$t = 37 degree C$
$c = 4200 frac{Дж}{кг cdot degree C}$
$L — ?$
Показать решение и ответ
Скрыть
Решение:
Когда в сосуд с водой одной температуры добавили пар с другой температурой, между этими двумя телами начинается теплообмен. Пар сначала конденсируется с выделением энергии и уже в виде воды будет охлаждаться также с выделением энергии. Эта энергия будет идти на нагревание воды.
Значит, мы можем записать следующее:
$Q_1 = Q_{2кон} + Q_2$,
где $Q_1$ — это количество энергии, необходимое для нагревания воды, $Q_{2кон}$ — количество теплоты, выделившееся при конденсации пара, $Q_2$ — количество теплоты, выделившееся при охлаждении сконденсированного пара в виде воды.
Удельная теплота парообразования, которую мы ищем, связана с величиной $Q_{2кон}$, которая по определению равна:
$Q_{2кон} = Lm_2$
Подставим в формулу для теплообмена между водой и паром:
$Q_1 = Lm_2 + Q_2$.
Выразим отсюда удельную теплоту парообразования:
$Lm = Q_1 — Q_2$,
$L = frac{Q_1 — Q_2}{m_2}$.
Рассчитаем количество теплоты, которое потребовалось на нагревание воды от $0 degree C$ до $37 degree$:
$Q_1 = cm_1(t — t_1)$,
$Q_1 = 4200 frac{Дж}{кг cdot degree C} cdot 30 space кг cdot (37 degree C — 0 degree C) = 126 space 000 frac{Дж}{degree C} cdot 37 degree C = 4662 cdot 10^3 space Дж$.
Теперь рассчитаем количество теплоты, которое выделилось при охлаждении воды (сконденсированного пара) от $100 degree C$ до $37 degree C$. Обратите внимание, что, составляя уравнение для энергообмена, мы уже учли, какая энергия выделяется, а какая — потребляется. Поэтому разница температур здесь запишется как $(t_2 — t)$, ведь знак “минус” мы уже учли выше.
$Q_2 = cm_2 (t_2 — t)$,
$Q_2 = 4200 frac{Дж}{кг cdot degree C} cdot 1.85 space кг cdot (100 degree C — 37 degree C) = 7770 frac{Дж}{degree C} cdot 63 degree C = 489 space 510 space Дж approx 490 cdot 10^3 space Дж$.
Теперь мы можем рассчитать удельную теплоту парообразования воды:
$L = frac{4662 cdot 10^3 space Дж — 490 cdot 10^3 space Дж}{1.85 space кг} approx 2255 cdot 10^3 frac{Дж}{кг} approx 2.3 cdot 10^6 frac{Дж}{кг}$.
Полученное значение удельной теплоты парообразования воды совпадает с табличным. Значит, расчеты выполнены верно.
Ответ: $L approx 2.3 cdot 10^6 frac{Дж}{кг}$.
Задача №5
Используя график зависимости количества теплоты, необходимого для перевода жидкости при температуре кипения в газообразное состояние, от массы (рисунок 1), определите для какой жидкости построен график, и вычислите количество теплоты, выделяющееся при конденсации пара этой жидкости массой $8 space кг$.
Для того, чтоб определить вид жидкости, нам нужно будет рассчитать ее удельную теплоту парообразования и сравнить с табличными данными.
Для этого из графика (рисунок 1) нам нужно взять какое-то значение количества теплоты и массы. Выберем удобные для нас и точные значения: при массе $2.5 space кг$ этой жидкости необходимо сообщить энергию в $1 space МДж$, чтобы превратить ее в пар.
Дано:
$Q_1 = 1 cdot МДж$
$m_1 = 2.5 space кг$
$m = 8 space кг$
СИ:
$Q_1 = 1 cdot 10^6 space Дж$
$L — ?$
$Q — ?$
Показать решение и ответ
Скрыть
Решение:
Используя данные графика, рассчитаем удельную теплоту парообразования:
$Q = Lm$,
$L = frac{Q}{m} = frac{1 cdot 10^6 space Дж}{2.5 space кг} = 0.4 cdot 10^6 frac{Дж}{кг}$.
Полученное значение удельной теплоты парообразования соответствует эфиру.
Вычислим, какое количество теплоты выделится при конденсации паров эфира массой $8 space кг$:
$Q = Lm$.
$Q = 0.4 cdot 10^6 frac{Дж}{кг} cdot 8 space кг = 3.2 cdot 10^6 space Дж = 3.2 space МДж$.
Ответ: эфир, $Q = 3.2 space МДж$.
Задача №6
Какое количество теплоты необходимо, чтобы превратить $1 space кг$ льда при $0 degree C$ в пар при $100 degree C$?
Дано:
$m = 1 space кг$
$t_1 = 0 degree C$
$t_2 = 100 degree C$
$lambda = 3.4 cdot 10^5 frac{Дж}{кг}$
$L = 2.3 cdot 10^6 frac{Дж}{кг}$
$c = 4200 frac{Дж}{кг cdot degree C}$
$Q — ?$
Показать решение и ответ
Скрыть
Решение:
Для того чтобы превратить лед в пар, сначала нам нужно его расплавить, затем нагреть получившуюся воду до температуры кипения и только потом сообщить еще какое-то количество теплоты, чтобы произошло парообразование: $Q = Q_1 + Q_2 + Q_3$.
Рассчитаем количество теплоты, которое необходимо сообщить льду, чтобы полностью расплавить его:
$Q_1 = lambda m$,
$Q_1 = 3.4 cdot 10^5 frac{Дж}{кг} cdot 1 space кг = 3.4 cdot 10^5 space Дж$.
Рассчитаем количество теплоты, которое необходимо сообщить воде, чтобы нагреть ее от $0 degree C$ до $100 degree C$:
$Q_2 = cm(t_2 — t_1)$,
$Q_2 = 4200 frac{Дж}{кг cdot degree C} cdot 1 space кг cdot (100 degree C — 0 degree C) = 4.2 cdot 10^5 space Дж$.
Рассчитаем количество теплоты, которое надо сообщить воде, чтобы полностью превратить ее в пар:
$Q_3 = Lm$,
$Q_3 = 2.3 cdot 10^6 frac{Дж}{кг} cdot 1 space кг = 23 cdot 10^5 space Дж$.
Просуммируем полученные энергии, чтобы узнать общее количество теплоты, которое потребовалось, чтобы превратить лед в пар:
$Q = Q_1 + Q_2 + Q_3 = 3.4 cdot 10^5 space Дж + 4.2 cdot 10^5 space Дж + 23 cdot 10^5 space Дж = 30.6 cdot 10^5 space Дж = 3060 space кДж$.
Ответ: $Q = 3060 space кДж$.
Задача №7
Какое количество пара при температуре $100 degree C$ требуется обратить в воду, чтобы нагреть железный радиатор массой $10 space кг$ от $10 degree C$ до $90 degree C$?
Дано:
$t = 100 degree C$
$L = 2.3 cdot 10^6 frac{Дж}{кг}$
$m_1 = 10 space кг$
$t_1 = 10 degree C$
$t_2 = 90 degree C$
$c = 460 frac{Дж}{кг cdot degree C}$
$m — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем количество теплоты, необходимое для нагревания железного радиатора:
$Q = cm_1 (t_2 — t_1)$,
$Q = 460 frac{Дж}{кг cdot degree C} cdot 10 space кг cdot (90 degree C — 10 degree C) = 4600 frac{Дж}{degree C} cdot 80 degree C = 368 space 000 Дж = 0,368 cdot 10^6 space Дж$.
Это же количество теплоты должно выделится при конденсации некоторой массы пара:
$Q = Lm$.
Выразими отсюда массу пара и рассчитаем ее:
$m = frac{Q}{L}$,
$m = frac{0,368 cdot 10^6 space Дж}{2.3 cdot 10^6 frac{Дж}{кг}} = 0.16 space кг = 160 space г$.
Ответ: $m = 160 space г$.
Воду, имеющую температуру $10 degree C$, нагревают до $90 degree C$, пропуская через нее водяной пар, температура которого $100 degree C$. Во сколько раз увеличится масса воды? Потерями теплоты пренебречь.
Дано:
$t_в = 10 degree C$
$t = 90 degree C$
$t_п = 100 degree C$
$L = 2.3 cdot 10^6 frac{Дж}{кг}$
$c = 4200 frac{Дж}{кг cdot degree C}$
$frac{m_в + m_п}{m_в} — ?$
Показать решение и ответ
Скрыть
Решение:
Водяной пар будет конденсироваться и выделять энергию. Эта энергия пойдет на нагревание воды.
При этом сконденсированный водяной пар в виде жидкости остается там же, смешиваясь с изначальной водой. В итоге, масса воды будет увеличиваться:
$m = m_в + m_п$.
Обратите внимание, что после того, как пар превратится в жидкость, ее температура все еще будет равна $100 degree C$. Она будет охлаждаться, передавая энергию изначальной массе воды для ее нагревания.
Итак, энергия выделившаяся при конденсации пара и дальнейшем охлаждении жидкости пойдет на нагревание изначальной массы воды. Тогда уравнение для теплообмена, происходящего между водой и паром можно записать в следующем виде:
$Q_1 + Q_2 = Q_3$.
Энергия, выделившаяся при конденсации пара:
$Q_1 = Lm_п$.
Энергия, выделившаяся при остывании воды:
$Q_2 = cm_п (t_п — t)$.
Энергия, которую необходимо затратить на нагревание изначальной массы воды:
$Q_3 = cm_в (t — t_в)$.
Обратите внимание, что, составляя уравнение для теплообмена, мы уже учли, какая энергия выделяется, а какая — потребляется. Поэтому разница температур здесь запишется как $t_в — t$, ведь знак “минус” мы уже учли выше.
Подставим эти в формулы в уравнение теплообмена:
$Lm_п + cm_п (t_п — t) = cm_в (t — t_в)$.
Отделим множители $m_п$ и $m_в$:
$m_п (L + c(t_п — t)) = cm_в (t — t_в)$,
$frac{m_п}{m_в} cdot (L + c(t_п — t)) = c(t — t_в)$,
$frac{m_п}{m_в} = frac{c(t — t_в)}{L + c(t_п — t)}$.
Теперь используем простой математический прием. Добавим единицу к левой и правой части нашего уравнения:
$1 + frac{m_п}{m_в} = 1 + frac{c(t — t_в)}{L + c(t_п — t)}$.
Выполним сложение в левой части уравнения:
$frac{m_в + m_п}{m_в} = 1 + frac{c(t — t_в)}{L + c(t_п — t)}$.
У нас получилось соотношение, которое показывает во сколько раз увеличилась масса воды. Рассчитаем его:
$frac{m_в + m_п}{m_в} = 1 + frac{4200 frac{Дж}{кг cdot degree C} cdot (100 degree C — 90 degree C)}{2.3 cdot 10^6 frac{Дж}{кг} + 4200 frac{Дж}{кг cdot degree C} cdot (100 degree C — 90 degree C)} = 1+ frac{42 cdot 10^3 frac{Дж}{кг}}{2.3 cdot 10^6 frac{Дж}{кг} + 0.042 cdot 10^6 frac{Дж}{кг}} = 1 + frac{42 cdot 10^3 frac{Дж}{кг}}{2.342 cdot 10^6 frac{Дж}{кг}} approx 1 + 0.02 approx 1.2$.
Т.е. масса воды после нагревания ее паром, увеличилась в 1.2 раза.
Ответ: $frac{m_в + m_п}{m_в} approx 1.2$.
Задача №9
В калориметр, содержащий воду при температуре кипения, бросили медный шар массой $0.5 space кг$ с температурой $500 degree C$. Вычислите массу испарившейся воды. Теплоемкостью калориметра пренебречь.
Дано:
$m = 0.5 space кг$
$t_1 = 500 degree C$
$t_2 = 100 degree C$
$L = 2.3 cdot 10^6 frac{Дж}{кг}$
$c = 400 frac{Дж}{кг cdot degree C}$
$m_1 — ?$
Показать решение и ответ
Скрыть
Решение:
Когда медный шар бросили в воду, между этими телами начался теплообмен. Медный шар начал охлаждаться и выделять энергию, которая пошла парообразование воды. Теплообмен прекратится, когда температура медного шара и воды выровняется — станет равна $100 degree C$. Обратите внимание, что парообразование тоже прекратится, так как воде перестанет сообщаться энергия.
Рассчитаем количество теплоты, которое выделится при остывании медного шара с $500 degree C$ до $100 degree$. При этом мы уже учли, какая энергия выделяется, а какая — потребляется. Поэтому разница температур здесь запишется как $t_1 — t_2$, ведь знак “минус” мы уже учли выше.
$Q = cm(t_1 — t_2)$,
$Q = 400 frac{Дж}{кг cdot degree C} cdot 0.5 space кг cdot (500 degree C — 100 degree C) = 200 frac{Дж}{degree C} cdot 400 degree C = 8 cdot 10^4 space Дж$.
Эта энергия будет израсходована на парообразование определенной массы воды:
$Q = Lm_1$.
Выразим отсюда массу испарившейся воды и рассчитаем ее:
$m_1 = frac{Q}{L}$,
$m_1 = frac{8 cdot 10^4 space Дж}{2.3 cdot 10^6 frac{Дж}{кг}} approx 0.035 space кг approx 35 space г$.
Ответ: $m_1 approx 35 space г$.
Задача №10
На примусе в медном чайнике массой $0.2 space кг$ вскипятили воду массой $1 space кг$, взятую при температуре $20 degree C$. В процессе кипячения $50 space г$ воды выкипело. Сколько в примусе сгорело бензина, если КПД примуса $30 %$?
Дано:
$m_ч = 0.2 space кг$
$m_в = 1 space кг$
$t_1 = 20 degree C$
$t_2 = 100 degree C$
$m_3 = 50 space г$
$eta = 30 % = 0.3$
$L = 2.3 cdot 10^6 frac{Дж}{кг}$
$c_ч = 400 frac{Дж}{кг cdot degree C}$
$c_в = 4200 frac{Дж}{кг cdot degree C}$
$q = 4.6 cdot 10^7 frac{Дж}{кг}$
СИ:
$m_3 = 0.05 space кг$
$m_б — ?$
Показать решение и ответ
Скрыть
Решение:
Из условий задачи ясно, что температура воды и чайника изначально была одинаковой. Потом чайник и воду стали нагревать до температуры кипения воды. Какое-то время после этого этим телам сообщалось еще какое-то количество теплоты, которое пошло на парообразование воды:
$Q = Q_1 + Q_2 + Q_3$.
Рассчитаем количество теплоты, которое необходимо сообщить медному чайнику, чтобы нагреть его:
$Q_1 = c_ч m_ч (t_2 — t_1)$,
$Q_1 = 400 frac{Дж}{кг cdot degree C} cdot 0.2 space кг cdot (100 degree C — 20 degree C) = 80 frac{Дж}{degree C} cdot 80 degree C = 6400 space Дж$.
Рассчитаем количество теплоты, которое необходимо сообщить воде, чтобы нагреть ее до температуры кипения:
$Q_2 = c_в m_в (t_2 — t_1)$,
$Q_2 = 4200 frac{Дж}{кг cdot degree C} cdot 1 space кг cdot (100 degree C — 20 degree C) = 4200 frac{Дж}{degree C} cdot 80 degree C = 336 space 000 space Дж$.
Рассчитаем количество теплоты, необходимое для превращения воды в пар:
$Q_3 = Lm_3$,
$Q_3 = 2.3 cdot 10^6 frac{Дж}{кг} cdot 0.05 space кг = 115 space 000 space Дж$.
Рассчитаем общее потребовавшееся количество теплоты:
$Q = Q_1 + Q_2 + Q_3 = 6400 space Дж + 336 space 000 space Дж + 115 space 000 space Дж = 457 space 400 Дж$.
Запишем формулу КПД для примуса:
$eta = frac{A_п}{A_з} = frac{Q}{Q_б}$.
Выразим отсюда количество теплоты, которое было выделено при сжигании спирта:
$Q_б = frac{Q}{eta}$.
С другой стороны, количество бензина, выделившееся при сгорании топлива, вычисляется по формуле:
$Q_б = qm_б$.
Подставим это выражение в формулу выше:
$qm_б = frac{Q}{eta}$.
Выразим отсюда массу сгоревшего бензина и рассчитаем ее:
$m_б = frac{Q}{eta cdot q}$,
$m_б = frac{457 space 400 Дж}{0.3 cdot 4.6 cdot 10^7 frac{Дж}{кг}} = frac{0.4574 cdot 10^6 space Дж}{1.38 cdot 10^6 frac{Дж}{кг}} approx 0.33 space кг approx 33 space г$.
Ответ: $m_б approx 33 space г$.
Фазовые переходы
-
Темы кодификатора ЕГЭ: изменение агрегатных состояний вещества, плавление и кристаллизация, испарение и конденсация, кипение жидкости, изменение энергии в фазовых переходах.
-
Плавление и кристаллизация
-
График плавления
-
Удельная теплота плавления
-
График кристаллизации
-
Парообразование и конденсация
-
Кипение
-
График кипения
-
График конденсации
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: изменение агрегатных состояний вещества, плавление и кристаллизация, испарение и конденсация, кипение жидкости, изменение энергии в фазовых переходах.
Лёд, вода и водяной пар — примеры трёх агрегатных состояний вещества: твёрдого, жидкого и газообразного. В каком именно агрегатном состоянии находится данное вещество — зависит от его температуры и других внешних условий, в которых оно находится.
При изменении внешних условий (например, если внутренняя энергия тела увеличивается или уменьшается в результате нагревания или охлаждения) могут происходить фазовые переходы — изменения агрегатных состояний вещества тела. Нас будут интересовать следующие фазовые переходы.
• Плавление (твёрдое тело жидкость) и кристаллизация (жидкость
твёрдое тело).
• Парообразование (жидкость пар) и конденсация (пар
жидкость).
к оглавлению ▴
Плавление и кристаллизация
Большинство твёрдых тел являются кристаллическими, т.е. имеют кристаллическую решётку — строго определённое, периодически повторяющееся в пространстве расположение своих частиц.
Частицы (атомы или молекулы) кристаллического твёрдого тела совершают тепловые колебания вблизи фиксированных положений равновесия — узлов кристаллической решётки.
Например, узлы кристаллической решётки поваренной соли — это вершины кубических клеток «трёхмерной клетчатой бумаги» (см. рис. 1, на котором шарики большего размера обозначают атомы хлора (изображение с сайта en.wikipedia.org.)); если дать испариться воде из раствора соли, то оставшаяся соль будет нагромождением маленьких кубиков.
Рис. 1. Кристаллическая решётка
Плавлением называется превращение кристаллического твёрдого тела в жидкость. Расплавить можно любое тело — для этого нужно нагреть его до температуры плавления, которая зависит лишь от вещества тела, но не от его формы или размеров. Температуру плавления данного вещества можно определить из таблиц.
Наоборот, если охлаждать жидкость, то рано или поздно она перейдёт в твёрдое состояние. Превращение жидкости в кристаллическое твёрдое тело называется кристаллизацией или отвердеванием. Таким образом, плавление и кристаллизация являются взаимно обратными процессами.
Температура, при которой жикость кристаллизуется, называется температурой кристаллизации. Оказывается, что температура кристаллизации равна температуре плавления: при данной температуре могут протекать оба процесса. Так, при лёд плавится, а вода кристаллизуется; что именно происходит в каждом конкретном случае — зависит от внешних условий (например, подводится ли тепло к веществу или отводится от него).
Как происходят плавление и кристаллизация? Каков их механизм? Для уяснения сути этих процессов рассмотрим графики зависимости температуры тела от времени при его нагревании и охлаждении — так называемые графики плавления и кристаллизации.
к оглавлению ▴
График плавления
Начнём с графика плавления (рис. 2). Пусть в начальный момент времени (точка на графике) тело является кристаллическим и имеет некоторую температуру
.
Рис. 2. График плавления
Затем к телу начинает подводиться тепло (скажем, тело поместили в плавильную печь), и температура тела повышается до величины — температуры плавления данного вещества. Это участок
графика.
На участке тело получает количество теплоты
где — удельная теплоёмкость вещества твёрдого тела,
— масса тела.
При достижении температуры плавления (в точке ) ситуация качественно меняется. Несмотря на то, что тепло продолжает подводиться, температура тела остаётся неизменной. На участке
происходит плавление тела — его постепенный переход из твёрдого состояния в жидкое. Внутри участка
мы имеем смесь твёрдого вещества и жидкости, и чем ближе к точке
, тем меньше остаётся твёрдого вещества и тем больше появляется жидкости. Наконец, в точке
от исходного твёрдого тела не осталось ничего: оно полностью превратилось в жидкость.
Участок соответствует дальнейшему нагреванию жидкости (или, как говорят, расплава). На этом участке жидкость поглощает количество теплоты
где — удельная теплоёмкость жидкости.
Но нас сейчас больше всего интересует — участок фазового перехода. Почему не меняется температура смеси на этом участке? Тепло-то подводится!
Вернёмся назад, к началу процесса нагревания. Повышение температуры твёрдого тела на участке есть результат возрастания интенсивности колебаний его частиц в узлах кристаллической решётки: подводимое тепло идёт на увеличение кинетической энергии частиц тела (на самом деле некоторая часть подводимого тепла расходуется на совершение работы по увеличению средних расстояний между частицами — как мы знаем, тела при нагревании расширяются. Однако эта часть столь мала, что её можно не принимать во внимание.).
Кристаллическая решётка расшатывается всё сильнее и сильнее, и при температуре плавления размах колебаний достигает той предельной величины, при которой силы притяжения между частицами ещё способны обеспечивать их упорядоченное расположение друг относительно друга. Твёрдое тело начинает «трещать по швам», и дальнейшее нагревание разрушает кристаллическую решётку — так начинается плавление на участке .
С этого момента всё подводимое тепло идёт на совершение работы по разрыву связей, удерживающих частицы в узлах кристаллической решётки, т.е. на увеличение потенциальной энергии частиц. Кинетическая энергия частиц при этом остаётся прежней, так что температура тела не меняется. В точке кристаллическая структура исчезает полностью, разрушать больше нечего, и подводимое тепло снова идёт на увеличение кинетической энергии частиц — на нагревание расплава.
к оглавлению ▴
Удельная теплота плавления
Итак, для превращения твёрдого тела в жидкость мало довести его до температуры плавления. Необходимо дополнительно (уже при температуре плавления) сообщить телу некоторое количество теплоты для полного разрушения кристаллической решётки (т.е. для прохождения участка
).
Это количество теплоты идёт на увеличение потенциальной энергии взаимодействия частиц. Следовательно, внутренняя энергия расплава в точке больше внутренней энергии твёрдого тела в точке
на величину
.
Опыт показывает, что величина прямо пропорциональна массе тела:
Коэффициент пропорциональности не зависит от формы и размеров тела и является характеристикой вещества. Он называется удельной теплотой плавления вещества. Удельную теплоту плавления данного вещества можно найти в таблицах.
Удельная теплота плавления численно равна количеству теплоты, необходимому для превращения в жидкость одного килограмма данного кристаллического вещества, доведённого до температуры плавления.
Так, удельная теплота плавления льда равна кДж/кг, свинца —
кДж/кг. Мы видим, что для разрушения кристаллической решётки льда требуется почти в
раз больше энергии! Лёд относится к веществам с большой удельной теплотой плавления и поэтому весной тает не сразу (природа приняла свои меры: обладай лёд такой же удельной теплотой плавления, как и свинец, вся масса льда и снега таяла бы с первыми оттепелями, затопляя всё вокруг).
к оглавлению ▴
График кристаллизации
Теперь перейдём к рассмотрению кристаллизации — процесса, обратного плавлению. Начинаем с точки предыдущего рисунка. Предположим, что в точке
нагревание расплава прекратилось (печку выключили и расплав выставили на воздух). Дальнейшее изменение температуры расплава представлено на рис. (3).
Рис. 3. График кристаллизации
Жидкость остывает (участок ), пока её температура не достигнет температуры кристаллизации, которая совпадает с температурой плавления
.
С этого момента температура расплава меняться перестаёт, хотя тепло по-прежнему уходит от него в окружающую среду. На участке происходит кристаллизация расплава — его постепенный переход в твёрдое состояние. Внутри участка
мы снова имеем смесь твёрдой и жидкой фаз, и чем ближе к точке
, тем больше становится твёрдого вещества и тем меньше — жидкости.Наконец,вточке
жидкостинеостаётсявовсе—онаполностьюкристаллизовалась.
Следующий участок соответствует дальнейшему остыванию твёрдого тела, возникшего в результате кристаллизации.
Нас опять-таки интересует участок фазового перехода : почему температура остаётся неизменной, несмотря на уход тепла?
Снова вернёмся в точку . После прекращения подачи тепла температура расплава понижается, так как его частицы постепенно теряют кинетическую энергию в результате соударений с молекулами окружающей среды и излучения электромагнитных волн.
Когда температура расплава понизится до температуры кристаллизации (точка ), его частицы замедлятся настолько, что силы притяжения окажутся в состоянии «развернуть» их должным образом и придать им строго определённую взаимную ориентацию в пространстве. Так возникнут условия для зарождения кристаллической решётки, и она действительно начнёт формироваться благодаря дальнейшему уходу энергии из расплава в окружающее пространство.
Одновременно начнётся встречный процесс выделения энергии: когда частицы занимают свои места в узлах кристаллической решётки, их потенциальная энергия резко уменьшается, за счёт чего увеличивается их кинетическая энергия — кристаллизующаяся жидкость является источником тепла (часто у проруби можно увидеть сидящих птиц. Они там греются!). Выделяющееся в ходе кристаллизации тепло в точности компенсирует потерю тепла в окружающую среду, и потому температура на участке не меняется.
В точке расплав исчезает, а вместе с завершением кристаллизации исчезает и этот внутренний «генератор» тепла. Вследствие продолжающегося рассеяния энергии во внешнюю среду понижение температуры возобновится, но только остывать уже будет образовавшееся твёрдое тело (участок
).
Как показывает опыт, при кристаллизации на участке выделяется ровно то же самое количество теплоты
, которое было поглощено при плавлении на участке
.
к оглавлению ▴
Парообразование и конденсация
Парообразование — это переход жидкости в газообразное состояние (в пар). Существует два способа парообразования: испарение и кипение.
Испарением называется парообразование, которое происходит при любой температуре со свободной поверхности жидкости. Как вы помните из листка «Насыщенный пар», причиной испарения является вылет из жидкости наиболее быстрых молекул, которые способны преодолеть силы межмолекулярного притяжения. Эти молекулы и образуют пар над поверхностью жидкости.
Разные жидкости испаряются с разными скоростями: чем больше силы притяжения молекул друг к другу — тем меньшее число молекул в единицу времени окажутся в состоянии их преодолеть и вылететь наружу, и тем меньше скорость испарения. Быстро испаряются эфир, ацетон, спирт (их иногда называют летучими жидкостями), медленнее — вода, намного медленнее воды испаряются масло и ртуть.
Скорость испарения растёт с повышением температуры (в жару бельё высохнет скорее), поскольку увеличивается средняя кинетическая энергия молекул жидкости, и тем самым возрастает число быстрых молекул, способных покинуть её пределы.
Скорость испарения зависит от площади поверхности жидкости: чем больше площадь, тем большее число молекул получают доступ к поверхности, и испарение идёт быстрее (вот почему при развешивании белья его тщательно расправляют).
Одновременно с испарением наблюдается и обратный процесс: молекулы пара, совершая беспорядочное движение над поверхностью жидкости, частично возвращаются обратно в жидкость. Превращение пара в жидкость называется конденсацией.
Конденсация замедляет испарение жидкости. Так, в сухом воздухе бельё высохнет быстрее, чем во влажном. Быстрее оно высохнет и на ветру: пар сносится ветром, и испарение идёт более интенсивно
В некоторых ситуациях скорость конденсации может оказаться равной скорости испарения. Тогда оба процесса компенсируют друг друга и наступает динамическое равновесие: из плотно закупоренной бутылки жидкость не улетучивается годами, а над поверхностью жидкости в этом случае находится насыщенный пар.
Конденсацию водяного пара в атмосфере мы постоянно наблюдаем в виде облаков, дождей и выпадающей по утрам росы; именно испарение и конденсация обеспечивают круговорот воды в природе, поддерживая жизнь на Земле.
Поскольку испарение — это уход из жидкости самых быстрых молекул, в процессе испарения средняя кинетическая энергия молекул жидкости уменьшается, т.е. жидкость остывает. Вам хорошо знакомо ощущение прохлады и порой даже зябкости (особенно при ветре), когда выходишь из воды: вода, испаряясь по всей поверхности тела, уносит тепло, ветер же ускоряет процесс испарения (nеперь понятно, зачем мы дуем на горячий чай. Кстати сказать, ещё лучше при этом втягивать воздух в себя, поскольку на поверхность чая тогда приходит сухой окружающий воздух, а не влажный воздух из наших лёгких ;-)).
Ту же прохладу можно почувствовать, если провести по руке кусочком ваты, смоченным в летучем растворителе (скажем, в ацетоне или жидкости для снятия лака). В сорокаградусную жару благодаря усиленному испарению влаги через поры нашего тела мы сохраняем свою температуру на уровне нормальной; не будь этого терморегулирующего механизма, в такую жару мы бы попросту погибли.
Наоборот, в процессе конденсации жидкость нагревается: молекулы пара при возвращении в жидкость разгоняются силами притяжения со стороны находящихся поблизости молекул жидкости, в результате чего средняя кинетическая энергия молекул жидкости увеличивается (сравните это явление с выделением энергии при кристаллизации расплава!).
к оглавлению ▴
Кипение
Кипение — это парообразование, происходящее по всему объёму жидкости.
Кипение оказывается возможным потому, что в жидкости всегда растворено какое-то количество воздуха, попавшего туда в результате диффузии. При нагревании жидкости этот воздух расширяется, пузырьки воздуха постепенно увеличиваются в размерах и становятся видимы невооружённым глазом (в кастрюле с водой они осаждают дно и стенки). Внутри воздушных пузырьков находится насыщенный пар, давление которого, как вы помните, быстро растёт с повышением температуры.
Чем крупнее становятся пузырьки, тем большая действует на них архимедова сила, и определённого момента начинается отрыв и всплытие пузырьков. Поднимаясь вверх, пузырьки попадают в менее нагретые слои жидкости; пар в них конденсируется, и пузырьки сжимаются опять. Схлопывание пузырьков вызывает знакомый нам шум, предшествующий закипанию чайника. Наконец, с течением времени вся жидкость равномерно прогревается, пузырьки достигают поверхности и лопаются, выбрасывая наружу воздух и пар — шум сменяется бульканьем, жидкость кипит.
Пузырьки, таким образом, служат «проводниками» пара изнутри жидкости на её поверхность. При кипении наряду с обычным испарением идёт превращение жидкости в пар по всему объёму — испарение внутрь воздушных пузырьков с последующим выводом пара наружу. Вот почему кипящая жидкость улетучивается очень быстро: чайник, из которого вода испарялась бы много дней, выкипит за полчаса.
В отличие от испарения, происходящего при любой температуре, жидкость начинает кипеть только при достижении температуры кипения — именно той температуры, при которой пузырьки воздуха оказываются в состоянии всплыть и добраться до поверхности. При температуре кипения давление насыщенного пара становится равно внешнему давлению на жидкость (в частности, атмосферному давлению). Соответственно, чем больше внешнее давление, тем при более высокой температуре начнётся кипение.
При нормальном атмосферном давлении ( атм или
Па) температура кипения воды равна
. Поэтому давление насыщенного водяного пара при температуре
равно
Па. Этот факт необходимо знать для решения задач — часто он считается известным по умолчанию.
На вершине Эльбруса атмосферное давление равно атм, и вода там закипит при температуре
. А под давлением
атм вода начнёт кипеть только при
.
Температура кипения (при нормальном атмосферном давлении) является строго определённой для данной жидкости величиной (температуры кипения, приводимые в таблицах учебников и справочников — это температуры кипения химически чистых жидкостей. Наличие в жидкости примесей может изменять температуру кипения. Скажем, водопроводная вода содержит растворённый хлор и некоторые соли, поэтому её температура кипения при нормальном атмосферном давлении может несколько отличаться от ). Так, спирт кипит при
, эфир — при
, ртуть — при
. Обратите внимание: чем более летучей является жидкость, тем ниже её температура кипения. В таблице температур кипения мы видим также, что кислород кипит при
. Значит, при обычных температурах кислород — это газ!
Мы знаем, что если чайник снять с огня, то кипение тут же прекратится — процесс кипения требует непрерывного подвода тепла. Вместе с тем, температура воды в чайнике после закипания перестаёт меняться, всё время оставаясь равной . Куда же при этом девается подводимое тепло?
Ситуация аналогична процессу плавления: тепло идёт на увеличение потенциальной энергии молекул. В данном случае — на совершение работы по удалению молекул на такие расстояния, что силы притяжения окажутся неспособными удерживать молекулы неподалёку друг от друга, и жидкость будет переходить в газообразное состояние.
к оглавлению ▴
График кипения
Рассмотрим графическое представление процесса нагревания жидкости — так называемый график кипения (рис. 4).
Рис. 4. График кипения
Участок предшествует началу кипения. На участке
жидкость кипит, её масса уменьшается. В точке
жидкость выкипает полностью.
Чтобы пройти участок , т.е. чтобы жидкость, доведённую до температуры кипения, полностью превратить в пар, к ней нужно подвести некоторое количество теплоты
. Опыт показывает, что данное количество теплоты прямо пропорционально массе жидкости:
Коэффициент пропорциональности называется удельной теплотой парообразования жидкости (при температуре кипения). Удельная теплота парообразования численно равна количеству теплоты, которое нужно подвести к 1 кг жидкости, взятой при температуре кипения, чтобы полностью превратить её в пар.
Так, при удельная теплота парообразования воды равна
кДж/кг. Интересно сравнить её с удельной теплотой плавления льда (
кДж/кг) — удельная теплота парообразования почти в семь раз больше! Это и не удивительно: ведь для плавления льда нужно лишь разрушить упорядоченное расположение молекул воды в узлах кристаллической решётки; при этом расстояния между молекулами остаются примерно теми же. А вот для превращения воды в пар нужно совершить куда большую работу по разрыву всех связей между молекулами и удалению молекул на значительные расстояния друг от друга.
к оглавлению ▴
График конденсации
Процесс конденсации пара и последующего остывания жидкости выглядит на графике симметрично процессу нагревания и кипения. Вот соответствующий график конденсации для случая стоградусного водяного пара, наиболее часто встречающегося в задачах (рис. 5).
Рис. 5. График конденсации
В точке имеем водяной пар при
. На участке
идёт конденсация; внутри этого участка — смесь пара и воды при
. В точке
пара больше нет, имеется лишь вода при
. Участок
— остывание этой воды.
Опыт показывает, что при конденсации пара массы (т. е. при прохождении участка
) выделяется ровно то же самое количество теплоты
, которое было потрачено на превращение в пар жидкости массы
при данной температуре.
Давайте ради интереса сравним следующие количества теплоты:
• , которое выделяется при конденсации
г водяного пара;
• , которое выделяется при остывании получившейся стоградусной воды до температуры, скажем,
.
Имеем:
Дж;
Дж.
Эти числа наглядно показывают, что ожог паром гораздо страшнее ожога кипятком. При попадании на кожу кипятка выделяется «всего лишь» (кипяток остывает). А вот при ожоге паром сначала выделится на порядок большее количество теплоты
(пар конденсируется), образуется стоградусная вода, после чего добавится та же величина
при остывании этой воды.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Фазовые переходы» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
Жидкость может переходить в парообразное состояние двумя способами – испарением и кипением. Испаряются жидкости во всем температурном диапазоне, в то время, как кипение происходит при строго определенной температуре для каждой конкретной жидкости.
Что такое кипение
Кипение – это:
- бурный переход жидкости в пар. Во всем объеме жидкости образуются пузырьки, пар в этих пузырьках насыщенный;
- эндотермический процесс, он происходит с поглощением энергии.
Образование пара во всем объеме жидкости называют кипением.
Примечание: Интересен тот факт, что перед началом кипения от чайника с водой доносится специфический шум.
Различия между испарением и кипением
Характерным проявлением кипения может служить образование пузырьков пара внутри жидкости (рис. 1):
Рис. 1. Во время испарения пар образуется только на поверхности, а во время кипения – во всем объеме жидкости
На следующем рисунке 2 представлены отличия процессов испарения и кипения подробнее:
Рис. 2. Есть два процесса образования пара – испарение и кипение, рисунок поясняет их основные отличия
Образование пара (парообразование):
- на поверхности – это испарение,
- во всем объеме – это кипение.
Испарение происходит при любой температуре с поверхности, а кипение – только при одной конкретной температуре, но во всем объеме жидкости.
Процессы кипения и конденсации на графиках
Пусть небольшое количество воды находится в просторном закупоренном сосуде.
Разберем, как выглядят на температурных графиках процессы кипения и конденсации. Для начала рассмотрим график нагревания и кипения (рис. 3).
Вначале вода имела температуру +20 градусов Цельсия. Будем нагревать эту воду. Поначалу ее температура будет расти. На графике это показано наклонной синей линией, находящейся в левой части рисунка.
Рис. 3. График нагревания воды, ее кипения и нагревания полученного пара
До бесконечности температура подниматься не будет. Как только температура достигнет некоторого предела, вода закипит. Из рисунка следует, когда температура воды достигла отметки +100 градусов Цельсия и начался процесс кипения. Этот процесс на рисунке схематично обозначен горизонтальной красной линией.
Горизонтальное положение линии кипения означает, что во время кипения температура воды не изменяется. Температура будет оставаться неизменной до тех пор, пока вся вода не превратится в газообразное состояние — пар. Для компактности рисунка я укоротил эту линию, на самом деле, длину этой линии нужно увеличить.
Уже после того, как вся вода превратилась в пар, температура пара начала повышаться. Это изображено на рисунке наклонной синей линией, находящейся правее красной линии.
Будем теперь отбирать тепловую энергию у молекул. Предположим, что мы охлаждаем горячий водяной пар, находящийся в закупоренном сосуде. Процессы его охлаждения и конденсации представлены на графике (рис. 4). Этот график можно получить, зеркально отразив вокруг вертикальной оси график, связанный с нагреванием, рассмотренный ранее.
Рис. 4. График охлаждения пара, его конденсации и охлаждения полученной воды
Из графика следует:
Вначале температура пара уменьшается от +180 градусов Цельсия до +100 градусов. Это наклонная синяя линия, расположенная в левой части рисунка.
Затем, происходит конденсация пара. Молекулы пара собираются в капли жидкости. При этом, температура пара не изменяется и остается равной +100 градусам Цельсия.
Как только весь пар конденсируется, образовавшаяся жидкая вода начинает охлаждаться до конечной температуры + 20 градусов Цельсия. На графике охлаждение воды – это синяя наклонная линия, находящаяся справа от красной линии конденсации.
Температура кипения и как ее найти на графике
Чтобы жидкость закипела, ее нужно нагреть до температуры кипения.
На рисунке 5 представлен температурный график нагревания воды. Температуру кипения можно определить по горизонтальной линии, обозначающую процесс кипения. Нужно продолжить эту линию пунктиром по направлению к вертикальной оси температур. Точка, в которой пунктир упрется в ось и будет температурой кипения жидкости.
Рис. 5. Если на графике температуры найти горизонтальную линию кипения, а потом провести пунктир к оси температуры, мы найдем температуру кипения
Температура кипения – это температура, при которой пар образуется во всем объеме жидкости. Такая температура у каждой жидкости своя, ее можно найти в справочнике физики.
Температуры кипения некоторых веществ
Сравним для наглядности значения температуры кипения некоторых веществ.
Нам известно, что температура кипения питьевой воды равна 100 градусам на шкале Цельсия.
При комнатной температуре некоторые вещества пребывают в газообразном состоянии, но при более низких температурах они превращаются в жидкости. Например, кислород превращается в кипящую жидкость при минус 183 градусах Цельсия.
В противоположность этому, вещества, которые мы привыкли видеть твердыми при комнатной температуре, в кипящую жидкость превратятся при более высоких температурах. К примеру, медь станет кипящей жидкостью при 2567 град. Цельсия, а железо – при 2500 град. Цельсия
На рисунке 6 представлен список некоторых веществ и указана температура, при которой эти вещества кипят.
Рис. 6. Таблица — температура кипения некоторых веществ
Расширенный список жидкостей и их температуру кипения можно найти в справочнике физики.
Почему температура жидкости при кипении не изменяется
Тепловая энергия, которую получает жидкость во время кипения, тратится на образование пара во всем объеме жидкости. Поэтому во время кипения температура жидкости не изменяется.
Разберем подробнее, что происходит, когда мы сообщаем тепловую энергию какой-либо жидкости.
Получаемая от источника тепловая энергия передается молекулам жидкости. Скорость движения молекул увеличивается, а значит, растет их кинетическая энергия. Чем выше температура, тем быстрее будут двигаться молекулы.
Находясь в жидкости, каждая молекула притягиваются к соседним молекулам. То есть, молекулы удерживаются в жидкости силами притяжения соседних молекул. Если есть взаимодействие молекул – их взаимное притяжение, значит, есть потенциальная энергия такого взаимодействия.
По мере нагревания, энергия движения некоторых молекул увеличится настолько, что они преодолеют притяжение соседних молекул и, покинут жидкость. Чем выше температура, тем большее число молекул сможет покинуть жидкость.
Мы помним, что при испарении жидкость покидают молекулы, находящиеся только на ее поверхности. А во время кипения энергию, достаточную для того, чтобы вылететь из жидкости, получают не только молекулы на поверхности, но и молекулы, находящиеся внутри жидкости.
Примечания:
- Наблюдая за кипящей жидкостью, можно заметить, что пар образуется внутри жидкости во всем ее объеме. Пузырьки пара буду образовываться даже у дна. Они будут подниматься к поверхности, при этом расширяясь. Внутри пузырьков находятся молекулы, энергия которых достаточна для того, чтобы покинуть жидкость.
- Вместо слов «Внутри жидкости», физики говорят — «Во всем объеме жидкости».
Как давление влияет на температуру кипения
Мы можем влиять на температуру кипения жидкостей, изменяя давление. Если давление воздуха увеличить, то температура кипения, так же, возрастет. К примеру, вода при давлении 220 атмосфер (это 21,6 миллионов Паскалей) закипит только тогда, когда ее температура поднимется до 370 градусов Цельсия.
А уменьшая давление, мы наоборот, температуру кипения жидкостей понизим. Именно из-за пониженного давления, температура кипения воды в высокогорных районах ниже, чем, на равнинной местности, которая ближе к уровню мирового океана. В горах вода закипает при температуре 90 градусов Цельсия. Из-за этого, некоторые продукты высоко в горах сварить не получится.
Чем выше давление, тем выше температура кипения жидкости. Уменьшив давление, мы понизим температуру кипения.
Что такое удельная теплота парообразования
Возьмем какую-либо жидкость массой 1 кг, предварительно нагретую до температуры кипения. Будем сообщать ей тепловую энергию, чтобы испарить эту жидкость полностью.
Та энергия (теплота), которую мы затратим, чтобы испарить с помощью кипения 1 кг жидкости, называется удельной теплотой парообразования. Удельной величиной эту теплоту называют потому, что она приходится на 1 кг жидкости.
Удельная теплота парообразования — это энергия, которую нужно затратить, чтобы испарить 1 кг жидкости, предварительно нагретой до температуры кипения.
(large L left( frac{text{Дж}}{text{кг}}right)) – удельная теплота парообразования (конденсации).
На рисунке 7 представлена таблица, в которой содержится удельная теплота парообразования (конденсации) при температуре кипения для некоторых жидкостей и металлов в расплавленном состоянии.
Рис. 7. Таблица – удельная теплота парообразования (конденсации) некоторых веществ при температуре кипения
Что происходит с энергией во время кипения и конденсации
Кипение: жидкость получает тепловую энергию (количество теплоты), из нее вырываются молекулы. Полученная энергия тратится на преодоление притяжения соседних молекул и на расширение образовавшегося пара.
Конденсация: молекулы пара отдают тепловую энергию в окружающее пространство, собираясь в капельки — превращаясь в жидкость.
Выполняется закон сохранения энергии. Именно поэтому теплота парообразования и теплота конденсации совпадают. Процессы кипения и конденсации протекают при одной и той же температуре. Различие кроется в том, что кипение происходит с поглощением энергии, а конденсация связана с выделением энергии.
Как удельная теплота парообразования связана с количеством теплоты — формула
Пусть жидкость предварительно нагрета до температуры кипения, и нам известны:
- ее масса (количество килограммов) и
- удельная теплота парообразования;
Мы можем посчитать общее количество теплоты, требуемое для перевода всей жидкости в пар. Расчеты нужно вести по формуле:
[large boxed{ Q = L cdot m }]
(large m left( text{кг} right) ) – масса вещества;
(large L left( frac{text{Дж}}{text{кг}} right) ) – удельная теплота парообразования (конденсации);
(large Q left( text{Дж} right) ) – количество теплоты, поглощенное жидкостью во время кипения, т. е. общая тепловая энергия для перевода всей жидкости в пар;
Формулу можно применять так же, чтобы рассчитать количество теплоты, выделяемое в окружающую среду молекулами пара при их конденсации.
Для процесса конденсации величина (large Q ) – это количество теплоты, выделенное молекулами пара в окружающую среду;
Чем удельная теплота парообразования отличается от количества теплоты
Отличия удельной теплоты парообразования от количества теплоты, приведены на рисунке 8:
Рис. 8. Если жидкость находится при температуре кипения, то удельная теплота парообразования — это энергия для перевода в пар одного кг жидкости, а количество теплоты – это энергия перевода в пар нескольких кг жидкости
В любом случае, жидкость предварительно нужно нагреть до температуры кипения.
Количество теплоты – это энергия, необходимая для конденсации или образования пара при температуре кипения для нескольких килограммов жидкости.
Удельная теплота парообразования – это энергия, необходимая для перевода в пар 1-го килограмма жидкости.
Выводы
- Жидкость может переходить в парообразное состояние двумя способами: испарением или кипением.
- Образование пара (парообразование) на поверхности – это испарение, а во всем объеме – это кипение.
- Кипение – это эндотермический процесс, который происходит с поглощением энергии. Во всем объеме жидкости образуются пузырьки, пар в этих пузырьках насыщенный;
- Чтобы жидкость начала кипеть, ее нужно нагреть до температуры кипения. Каждая жидкость кипит при строго определенной для нее температуре.
- Удельная теплота парообразования — это энергия, которую нужно затратить, чтобы испарить 1 кг жидкости, предварительно нагретой до температуры кипения.
- На графике температур процессы кипения и конденсации изображаются горизонтальными линиями.
- Умножив удельную теплоту парообразования (large L ) на количество килограммов m кипящей жидкости, получим общее количество теплоты (large Q ), затраченной на перевод всей жидкости в пар во время ее кипения.

Расчет теплот испарения и возгонки
Уравнение Клапейрона – Клаузиуса дает возможность определить тепловой эффект фазового перехода (в данном случае – испарения или возгонки) на основании экспериментальных данных о зависимости давления насыщенного пара (жидкой или твердой фаз) от температуры.
Расчет средней теплоты испарения или возгонки
|
Средней теплотой испарения или возгонки называется величина |
∆ |
, получаемая из |
|||
|
уравнения Клапейрона-Клаузиуса в приближении её постоянства( |
∆ф.п. = |
) в нешироком |
|||
|
интервале температур ( |
20 – 50 К). |
||||
|
Для расчета |
средней теплоты фазового перехода используются интегральные формы |
||||
|
∆ = |
уравнения Клапейрона-Клаузиуса, полученные в результате приближенного интегрирования: ln = ∆ф.п.
|
Принимаем ∆ = |
ln |
= |
∆ф.п. |
|||||||||||
|
и выносим за знак интеграла: |
||||||||||||||
|
ln |
= |
∆ф.п. |
||||||||||||
|
Далее возможны два варианта интегрирования: |
||||||||||||||
|
1) Аналитический расчет |
||||||||||||||
|
Проводим определенное интегрирование указанного выражения: |
||||||||||||||
|
ln |
= |
∆ф.п. |
||||||||||||
|
В результате получаем расчетную формулу: |
||||||||||||||
|
ln |
= − |
∆ф.п. |
1 |
− |
1 |
|||||||||
|
где |
и – давления насыщенного пара соответственно при температурах |
и . |
||||||||||||
|
Таким |
образом, |
можно приближённо |
рассчитать среднюю теплоту |
испарения |
(возгонки) если известны хотя бы два равновесных давления пара при двух температурах.
Вместо давлений при двух температурах могут быть известны другие параметры, через которые давление можно выразить. Например, параметры состояния идеального газа: T, V, n.
1

2) Графический расчет Проводим неопределенное интегрирование уравнения и получаем уравнение прямой, не
проходящей через начало координат:
ln = − ∆ ∙ 1 +
|
Строим график в координатах |
и по тангенсу угла наклона прямой определяем |
||||||||||||||
|
или возгонки: |
|||||||||||||||
|
среднюю энтальпию испаренияln − |
= − |
∆ф.п. |
|||||||||||||
|
ф.п. |
|||||||||||||||
|
l |
− |
∆ф.п. |
= −2,303 ∙ |
∙ |
|||||||||||
|
координатах |
, то |
||||||||||||||
|
Если график построен в |
∆ |
= − |
∙ |
||||||||||||
|
Кроме того, уравнение прямой может быть представлено в виде |
|||||||||||||||
|
ln |
= + , где А и В |
||||||||||||||
|
– некоторые числовые коэффициенты. Тогда |
∆ф.п. |
= − ∙ |
. |
||||||||||||
Расчет истинной теплоты испарения или возгонки
При расчете истинного теплового эффекта испарения или возгонки (т.е. энтальпии фазового перехода при заданной конкретной температуре) используют дифференциальную форму уравнения Клапейрона-Клаузиуса.
ln = ∆ф.п.
или
= ∆ф.п.
Выражаем:
ln
∆ф.п. =
2

И далее задача сводится к нахождению производной, которую можно найти
аналитически или графически. 1) Аналитический расчет
Аналитический расчет возможен, если имеется функциональная зависимость вида
|
= |
( ) |
||||||||||||
|
. |
|||||||||||||
|
Например: |
|||||||||||||
|
где A, B, C, D – постоянныеlnкоэффициенты= + |
+ уравненияln + . |
||||||||||||
|
Дифференцируем данное выражение по температуре: |
|||||||||||||
|
ln |
|||||||||||||
|
Далее, |
умножаем на |
и |
получаем= − |
зависимость+ + |
теплоты фазового превращения от |
||||||||
|
температуры: |
ln |
||||||||||||
|
ф.п. |
ф.п. . |
||||||||||||
|
Подставляя в полученное∆уравнение= |
заданную температуру= − + , рассчитываем+ |
значение |
|||||||||||
|
Если имеется функциональная зависимость вида |
, то расчет |
теплового эффекта |
|||||||||||
|
∆ |
|||||||||||||
|
проводят по такому же принципу, с той лишь разницей, что=его( |
выражают из уравнения |
||||||||||||
|
) |
= ∆ф.п.
∆ф.п. =
2)Графический расчет
Взависимости от координат, в которых представлена графическая зависимость, расчет
∆проводится по соответствующему уравнению:
|
а) график в координатах |
∆ |
. |
|||||
|
В этом случае определение |
основано на уравнении: |
||||||
|
= ( |
) |
∆ф.п. |
|||||
|
ln |
= |
= |
|||||
|
Тангенс угла наклона касательной к графику в этих координатах равен: |
|||||||
|
Значит, |
= ∆ф.п.
3

Отсюда расчетная формула, связывающая тепловой эффект с тангенсом угла наклона касательной
∆ф.п. =
|
Если график построен в координатах l |
− |
, то |
|
∆ф.п. = 2,3
б) график в координатах = ( ).
Определение ∆ф.п. основано на уравнении:
= ∆ф.п.
Тангенс угла наклона касательной к графику в этих координатах равен:
=
= ∆ф.п.
Отсюда расчетная формула, связывающая тепловой эффект с тангенсом угла наклона касательной:
∆ф.п. =
Подставляя в это выражение найденный тангенс угла наклона касательной и конкретные значения Р* и Т*, находим тепловой эффект.
4
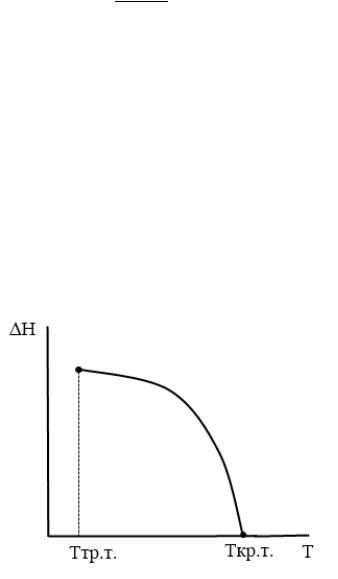
Зависимость теплоты испарения от температуры
Характер зависимости теплоты испарения от температуры определяется уравнением Кирхгофа:
∆исп. = ∆исп. . = ,пар − ,ж < 0
Следовательно, теплота испарения уменьшается с ростом температуры. В уравнении Кирхгофа записана производная функции одной переменной – температуры. В данной форме оно справедливо в той области температур и давлений, в которой пар можно считать идеальным газом и энтальпия испарения практически не зависит от давления. С приближением к критической точке для многих веществ пар становится неидеальным газом (например, у воды давление критической точки 218 атм и пар нельзя считать идеальным газом), но характер температурной зависимости энтальпии испарения сохраняется.
Графически эту зависимость в области температур существования жидкости (вдоль линии насыщенного пара) можно представить следующим образом:
График зависимости теплоты испарения от температуры начинается от температуры
тройной точки.
При низких и средних температурах теплота испарения убывает незначительно, от температуры практически не зависит.
По мере приближения к критической точке, эта зависимость становится все более ярко выраженной, наклон линии резко возрастает, и при критической температуре теплота испарения обращается в ноль:
|
∆исп. кр.т. = |
||||
|
Т.о. в области высоких температур зависимость |
||||
|
ln − будет отклоняться от прямолиней- |
||||
|
ной: |
||||
|
5 |

Правило Трутона
Теплоты испарения различных жидкостей закономерно связаны с их нормальными
температурами кипения.
Существует эмпирическое правило, которое носит название правила Трутона: Мольные
энтропии испарения неполярных неассоциированных жидкостей при нормальной
температуре кипения примерно одинаковы и в среднем составляют:
|
∆исп. = |
∆исп. |
≈ |
± |
Дж |
|
н.т.к. |
моль ∙ К |
В справочнике, на стр. 109 правило Трутона приведено в следующем виде:
|
∆исп. |
≈ , |
Дж |
|
н.т.к. |
моль ∙ К |
Это правило выполняется только для неполярных, неассоциированных в паровой фазе жидкостей и только при нормальной температуре кипения, которая у каждого вещества
единственная.
Интегрирование уравнения Клапейрона для процесса плавления
Т.к. мольные (удельные) объемы твердой и жидкой фаз очень близки друг другу по величине ( ж ≈ тв), уравнение Клапейрона для процесса плавления (а равно как и для процессов полиморфного превращения) преобразовать нельзя, и оно используется только в
таком виде:
= ∆пл.
∆
Или, что больше отвечает физическому смыслу процесса:
= ∆
∆пл.
Величина , определяющая наклон линии плавления к оси температур, хоть и является,
в свою очередь, функцией давления и температуры, но изменяется незначительно при
6

достаточно большом увеличении давления. Поэтому при изменении давления до 10 атм (иногда
|
и более) в хорошем приближении можно считать, что |
= |
, и линия плавления является |
||||||||
|
прямой линией. |
||||||||||
|
Соответственно, интегрирование уравнения Клапейрона-Клаузиуса для процесса |
||||||||||
|
плавления проводится следующим образом: |
∆пл. |
|||||||||
|
= |
||||||||||
|
приблизительно постоянная величина, рассчитанная, |
||||||||||
|
Cоотношение |
∆ |
берется как |
∆ |
|||||||
|
∆ |
||||||||||
|
например, при температуре , и выносится за знак интеграла: |
||||||||||
|
= |
∆пл. |
|||||||||
|
∆ |
∆
Другими словами, заменяем на ∆ .
|
∆ |
= |
∆пл. |
|
∆ |
||
|
− |
= |
∆пл. |
|
∆ |
||
|
= |
+ |
∆пл. |
|
∆ |
Так можно рассчитать, при каком давлении температура плавления станет равной ,
если известна при ,
или рассчитать температуру плавления при заданном давлении:
Расчет теплоты плавления
В основе – уравнение Клапейрона:
= ∆пл.
∆
1) Аналитический расчет Проводится по известной зависимости = ( ).
Пусть эта зависимость имеет вид:
=+ +
где А, В, С – постоянные коэффициенты уравнения.
Выразим теплоту плавления из уравнения Клапейрона:
7
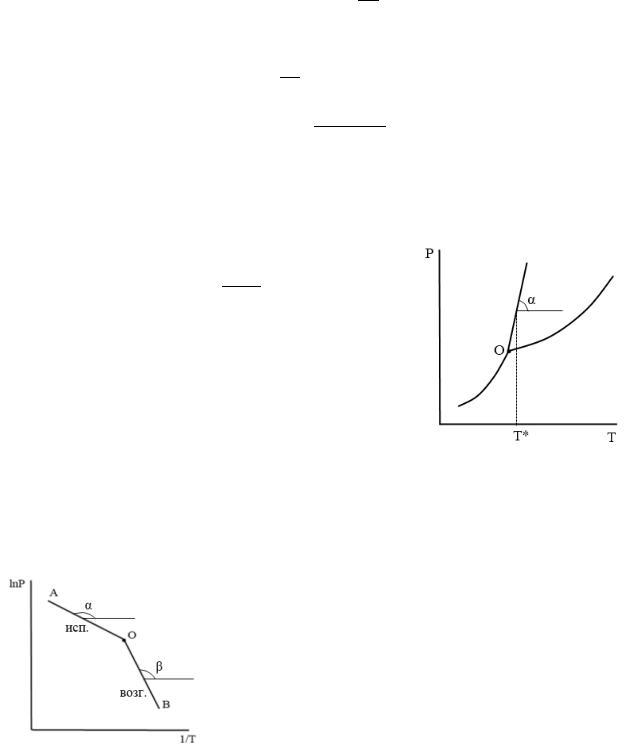
∆пл. = ∆
Продифференцируем зависимость = ( ) по давлению:
=+ 2
∆
∆ = ( + 2 )
Подставляя в полученное выражение необходимые значения p и Т, находим ∆Н.
2) Графический расчет По наклону линии плавления:
|
= |
= |
∆пл. |
||
|
∆ |
||||
|
Отсюда выражаем ∆ |
: |
∆пл. = ∆
Подставляя сюда значение Т* и тангенса угла наклона линии плавления, получаем значение теплоты плавления.
3) Расчет теплоты плавления в тройной точке по теплотам испарения и возгонки
Находим теплоты испарения и возгонки по тангенсу угла наклона соответствующих прямых:
∆исп. = − ∙
∆возг. = − ∙
Затем находим теплоту плавления по соотношению:
∆пл. = ∆возг. − ∆исп.
ОА – линия испарения, ОВ – линия возгонки, т. О – тройная точка.
8
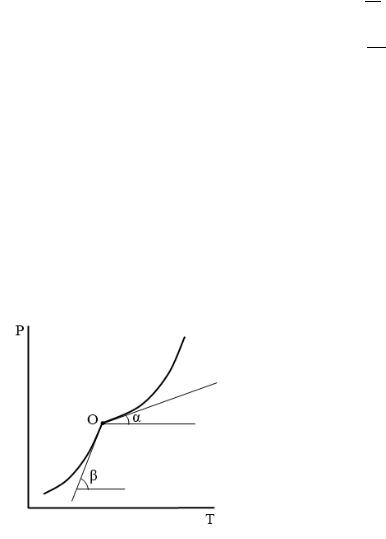
Если известны уравнения линий испарения и возгонки:
то можно найти теплоты испарения и возгонки через коэффициенты уравнений:
∆исп. = − ∙ и ∆возг. = − ∙ ′′
Теплоту плавления находим по разности теплот испарения и возгонки.
∆пл. = ( − )
Теплота плавления:
∆пл. = ∆возг. − ∆исп.
б) по графику − .
Проводим касательные к кривым испарения и возгонки в тройной точке:
|
∆исп. |
= |
|||||||||
|
∆возг. |
= |
|||||||||
|
В этих формулах Т и Р соответствуют температуре и |
||||||||||
|
давлению тройной точки. |
= ∆возг. − ∆исп. или: |
|||||||||
|
Теплота плавления: |
∆пл. |
|||||||||
|
∆пл. = |
− |
= |
( |
− |
) |
|||||
Расчет изменения внутренней энергии и энтропии при фазовых превращениях
|
Расчет изменения внутренней энергии |
и энтропии |
∆ |
для фазового перехода осуще- |
||
|
ствляется после того, как найдено значение |
теплового эффекта |
. |
|||
|
∆ |
∆ |
Изменение внутренней энергии
Рассчитывается по соотношению:
∆ф.п. = ∆ф.п. − ∆ф.п.
а) Плавление
∆пл. = 0
Следовательно
∆пл. = ∆пл.
9

б) Испарение, возгонка
∆исп.(возг.). = 1 ∆исп.(возг.) = ∆исп.(возг.) −
Для обратного перехода (конденсации):
∆конд = −1
∆конд. = −∆исп.(возг.)
Изменение энтропии
∆ф.п. = ∆ф.п.
Для конденсации:
∆конд. = −∆исп.(возг.)
10
Соседние файлы в предмете Физическая химия
- #
20.05.2020168.33 Кб3кр.png
- #
- #
20.05.2020933.47 Кб3лекции 1-5 фх
- #
- #
- #
- #
20.05.2020452.73 Кб2лекция 6
- #
20.05.2020596.4 Кб2лекция 7
- #
20.05.2020484.98 Кб1лекция 8
- #
- #
20.05.2020412.29 Кб1семинар 1
Фазовые переходы — это термодинамические процессы, приводящие к изменению агрегатного состояния вещества.
Плавление и отвердевание
ОпределениеПлавление — переход вещества из твердого состояния в жидкое.
Для расчета количества теплоты, необходимого для процесса плавления, следует применять формулу:
Q=λm
m — масса вещества, λ (Дж/кг) — удельная теплота плавления.
Плавление каждого вещества происходит при определенной температуре, которую называют температурой плавления. Все проводимое тепло идет на разрушение кристаллической решетки, при этом увеличивается потенциальная энергия молекул. Кинетическая энергия остается без изменения и температура в процессе плавления не изменяется.
Удельная теплота плавления показывает, какое количество теплоты необходимо сообщить 1 кг данного вещества, чтобы перевести его из твердого состояния в жидкое при условии, что оно уже нагрето до температуры плавления. В процессе отвердевания 1 кг данной жидкости, охлажденной до температуры отвердевания, выделится такое же количество теплоты.
Внимание! Удельная теплота плавления — табличная величина.
ОпределениеОтвердевание, или кристаллизация — переход состояния из жидкого состояния в твердое (это процесс, обратный плавлению).
Отвердевание происходит при той же температуре, что и плавление. В процессе отвердевания температура также не изменяется. Количество теплоты, выделяемое в процессе отвердевания:
Q=−λm
Парообразование и конденсация
ОпределениеПарообразование, или кипение — переход вещества из жидкого состояния в газообразное.
Количество теплоты, необходимое для процесса кипения, вычисляют по формуле:
Q=rm
m — масса вещества, r (Дж/кг) — удельная теплота парообразования.
Парообразование происходит при определенной температуре, которую называют температурой кипения. В отличие от испарения, процесс парообразования идет со всего объема жидкости. Несмотря на то, что к кипящему веществу подводят тепло, температура не изменяется. Все затраты энергии идут на увеличение промежутком между молекулами. Температура кипения зависит от рода вещества и внешнего атмосферного давления.
Удельная теплота парообразования показывает, какое количество теплоты необходимо затратить, чтобы перевести в пар 1 кг жидкости, нагретой до температуры кипения. Такое же количество теплоты выделится в процессе конденсации 1 кг пара, охлажденного до температуры конденсации.
Внимание! Удельная теплота парообразования — табличная величина.
ОпределениеКонденсация — процесс, обратный кипению. Это переход вещества из газообразного состояния в жидкое.
Конденсация происходит при температуре кипения, которая также не изменяется во время всего процесса. Количество теплоты, выделяемое в процессе конденсации:
Q=−rm
Тепловые процессы при нагревании и охлаждении
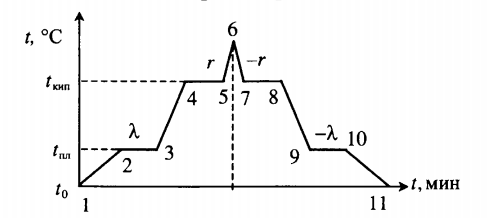
Все фазовые переходы, а также процессы нагревания и остывания вещества можно отобразить графически. Посмотрите на график фазовых переходов вещества:
Он показывает зависимость температуры вещества от времени в процессе его нагревания и остывания. Опишем процессы, отображаемые на графике, в таблице.
| Процесс | Что происходит | Количество выделенной теплоты |
| 1–2 | Нагревание твердого тела |
Q=cтm(tпл−t0) ст — удельная теплоемкость вещества в твердом состоянии. |
| 2–3 | Плавление при температуре плавления (tпл) |
Q=λm |
| 3–4 | Нагревание жидкости |
Q=cжm(tкип−tпл) сж — удельная теплоемкость вещества в жидком состоянии. |
| 4–5 | Кипение при температуре кипения (tкип) |
Q=rm |
| 5–6 | Нагревание пара |
Q=cпm(t−tкип) сп — удельная теплоемкость вещества в газообразном состоянии. |
| 6–7 | Охлаждение пара |
Q=cпm(tкип−t) |
| 7–8 | Кипение при температуре кипения (tкип) |
Q=−rm |
| 8–9 | Охлаждение жидкости |
Q=cжm(tпд−tкип) |
| 9–10 | Отвердевание при температуре плавления (tпл) |
Q=−λm |
| 10–11 | Охлаждение твердого тела |
Q=cтm(t0−tпл) |
Внимание! На участках 2–3 и 9–10 вещество частично находится в жидком и твердом состояниях, а на 4–5 и 7–8 — в жидком и газообразном.
Частные случаи тепловых процессов
| Что происходит | График | Формула количества теплоты |
| Полностью растопили лед, имеющий отрицательную температуру. | 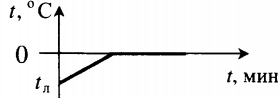 |
Q=cлm(tпл−tл)+λm cл — удельная теплоемкость льда, tл — начальная температура льда. |
| Лед, взятый при отрицательной температуре, превратили в воду при комнатной температуре. | 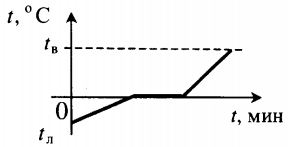 |
Q=cлm(tпл−tл)+λm+cвm(tв−tпл) cв — удельная теплоемкость воды. |
| Взяли лед при температуре 0 оС и полностью испарили. | 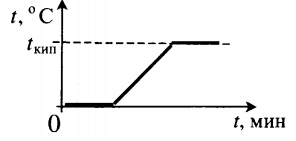 |
Q=λm+cвm(tкип−tпл)+rm |
| Взяли воду при комнатной температуре и половину превратили в пар. | 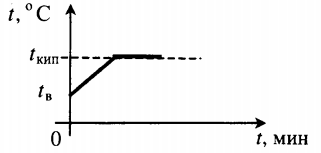 |
Q=cвm(tкип−tв)+rm2 |
Подсказки к задачам
| Единицы измерения | Температуру можно оставлять в градусах Цельсия, так как изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах. |
| Кипяток | Вода, которая при нормальном атмосферном давлении имеет температуру в 100 оС. |
| Объем воды 5 л | m = 5 кг, так как:
m=ρV=103· Внимание! Равенство V (л) = m (кг) справедливо только для воды. |
Пример №1. Какое количество теплоты нужно сообщить льду массой 2 кг, находящемуся при температуре –10 оС, чтобы превратить его в воду и нагреть ее до температуры +30 оС?
Можно выделить три тепловых процесса:
- Нагревание льда до температуры плавления.
- Плавление льда.
- Нагревание воды до указанной температуры.
Поэтому количество теплоты будет равно сумме количеств теплоты для каждого из этих процессов:
Q=Q1+Q2+Q3
Q=cлm(0−t1)+λm+cвm(t2−0)
Удельные теплоемкости и удельную теплоту плавления смотрим в таблицах:
- Удельная теплоемкость льда = 2050 Дж/(кг∙К).
- Удельная теплоемкость воды = 4200 Дж/(кг∙К).
- Удельная теплота плавления льда = 333,5∙103 Дж/кг.
Отсюда:
Q=2050·2(0−(−10))+333,5·103·2+4220·2·30=961200 (дж)=961,2 (кДж)
Уравнение теплового баланса
Суммарное количество теплоты, которое выделяется в теплоизолированной системе равно количеству теплоты (суммарному), которое в этой системе поглощается.
Математически уравнение теплового баланса с учетом знаков количества теплоты записывается так:
Qотд=−Qпол
Отданное количество теплоты меньше нуля (Qотд < 0), а полученное количество теплоты положительно (Qполуч > 0).
Подсказки к задачам на уравнение теплового баланса
| Теплообмен происходит в калориметре | Потерями энергии можно пренебречь. |
| Жидкость нагревают в некотором сосуде | Начальные и конечные температуры жидкости и сосуда совпадают. |
| В жидкость опускают термометр | Через некоторое время он покажет конечную температуру жидкости и термометра. |
| Мокрый снег | Содержит воду и лед при 0 оС. Учтите, что лед плавится, если он находится при температуре 0 оС и получает энергию от более нагретого тела. Вода кристаллизируется при температуре 0 оС, если она отдает энергию более холодному телу. Если лед и вода находятся при температуре 0 оС, то никаких агрегатных переходов между ними не происходит. |
Частные случаи теплообмена
| В воду комнатной температуры бросили ком снега, содержащий некоторое количество воды, после чего установилась некоторая положительная температура. | 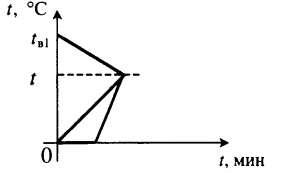
Уравнение теплового баланса: Q1+Q2+Q3=0 cвmв1(t−tв1)+cвmв2(t−0)+λmл+cвmл(t−0)=0 |
| Для получения некоторой положительной температуры воды используют горячую воду и лед, имеющий отрицательную температуру. | 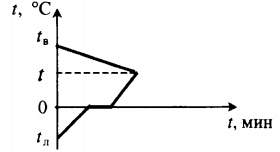
Уравнение теплового баланса: Q1+Q2=0 cвmв(t−tв)+cлmл(0−tл)+λmл+cвmл(t−0)=0 |
| В воду комнатной температуры бросают раскаленное твердое тело, в результате часть воды испаряется. | 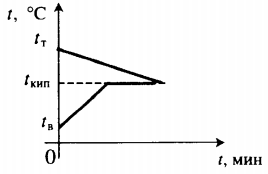
Уравнение теплового баланса: Q1+Q2=0 cтmт(100−tт)+cвmв(100−tв)+rmп=0 |
| Воду комнатной температуры нагревают до кипения, вводя пар при t = 100 оС. | 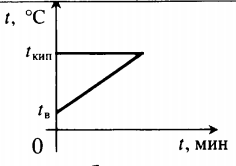
Уравнение теплового баланса: Q1+Q2=0 −rmп+cвmв(100−tв)=0 |
| Лед, имеющий температуру плавления, нагревают до положительной температуры, вводя пар при t = 100 оС. | 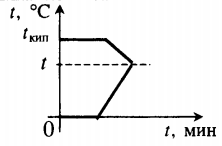
Уравнение теплового баланса: Q1+Q2=0 −rmп+cвmп(t−tкип)+λmл+cвmл(t−tпл)=0 |
Пример №2. В кастрюлю, где находится вода объемом 2 л при температуре 25 оС, долили 3 л кипятка. Какая температура воды установилась?
2 л = 2 кг
3 л = 3 кг
Количество теплоты, отданное кипятком, равно количеству теплоты, принятому более прохладной водой. Поэтому:
cm1(t−t0)=−cm2(t−tкип)
Или:
m1(t−t0)=−m2(t−tкип)
m1t+m2t=m1t0+m2tкип
(m1+m2)t=m1t0+m2tкип
t=m1t0+m2tкипm1+m2
t=2·25+3·1002+3=3505=70 (°C)
Взаимные превращения механической и внутренней энергии
Если в тексте задачи указан процент одного вида энергии, перешедший в другой, то он указывается в виде десятичной дроби перед этой энергией, которой тело обладало вначале.
Частные случаи закона сохранения энергии
| При неупругом ударе о стенку пуля нагрелась |
mv22=cmΔt |
| Тело падает с некоторой высоты и в момент падения нагревается |
mgh=cmΔt |
| В результате того, что пуля пробивает стену, ее скорость уменьшается, 50% выделившейся при этом энергии идет на нагревание пули |
0,5(mv202−mv22)=cmΔt |
| Летящая пуля при ударе о стенку расплавилась. Начальная температура пули меньше температуры плавления |
mv22=cmΔt+λm |
| Капля воды, падая с некоторой высоты, в момент удара испарилась. Температура капли у поверхности земли меньше температуры кипения. На нагрев пошло 60% выделившейся механической энергии |
0,6mgh=cmΔt+rm |
| Вследствие сгорания топлива ракета поднялась на некоторую высоту |
qmтоп=mрgh |
| Вследствие сгорания топлива снаряд приобрел некоторую скорость, и на это было затрачено 25% энергии |
0,25qmтопmсv22 |
Пример №3. Свинцовая дробинка, летящая со скоростью 100 м/с, попадает в доску и входит в нее. 52% кинетической энергии дробинки идет на ее нагревание. На сколько градусов нагрелась дробинка? Удельная теплоемкость свинца 130 Дж/(кг∙К).
Запишем закон сохранения энергии для этого случая:
0,52mv22=cmΔt
Δt=0,52v22c=0,52·10022·130=20 (К)
Примеры КПД
| Устройство | Полезная энергия (работа), затраченная энергия (полная работа) | КПД |
| Электронагреватель, электроплитка, электрочайник, кипятильник. |
Qполезн=cmΔT Иногда: Qполезн=cmΔT+rm Wзатр=Pt (произведение мощности на время) |
η=cmΔTPt100% |
| Газовая горелка, паровая турбина, спиртовка, плавильная печь. |
Qполезн=cmΔT Qзатр=qmтоп |
η=cmΔTqmтоп100% |
| Двигатель автомобиля, самолета. |
Aполезн=Nt=Nsv Qзатр=qmтоп |
η=cmΔTvqmтоп100 |
| Ружье с пороховым зарядом, пушка |
Eполезн=mv22 Qзатр=qmпор |
η=mv22qmпор100 |
Внимание! Если в задаче указано время, в течение которого происходит один тепловой процесс, а спрашивают о времени протекания другого, то считайте, что мощность нагревателя или холодильника постоянна:
Q1t1=Q2t2
Пример №4. Для нагревания на электроплитке некоторого количества воды от 20 до 100 оС потребовалась 21 минута. Сколько времени после этого необходимо для полного испарения воды? Удельная теплоемкость воды 4200 Дж (кг∙К), удельная теплота парообразования 2,24 МДж/кг.
Будем считать, что мощность электроплитки постоянна. Поэтому:
Q1t1=Q2t2
Количество теплоты, сообщенное воде при нагревании:
Q1=сm(t2−t1)
Количество теплоты, которое нужно сообщить, чтобы вода полностью испарилась:
Q1=rm
Отсюда:
сm(t2−t1)t1=rmt2
Задание EF17544
Кусок льда, имеющий температуру 0°С, помещён в калориметр с электронагревателем. Чтобы превратить этот лёд в воду с температурой 12°С, требуется количество теплоты 80 кДж. Какая температура установится внутри калориметра, если лёд получит от нагревателя количество теплоты 60 кДж? Теплоёмкостью калориметра и теплообменом с внешней средой пренебречь.
Ответ:
а) 0°С
б) 4°С
в) 6°С
г) 9°С
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать уравнение теплового баланса для первого случая.
Решение
Запишем исходные данные:
• Начальная температура льда: t0 = 0 oC.
• Конечная температура воды в первом случае: t1 = 12 oC.
• Количество теплоты, выделенное электронагревателем в первом случае: Q1 = 80 кДж.
• Количество теплоты, выделенное электронагревателем во втором случае: Q2 = 60 кДж.
Составим уравнение теплового баланса для первого случая:
Q1=λm+cmt1
Внимание! Вместо разности температур используется значение только конечной температуры, так как начальная температура равна 0.
Найдем массу льда из уравнения теплового баланса для первого случая. Учтем что:
• Удельная теплоемкость воды: c = 4200 Дж/(кг∙К).
• Удельная теплота плавления льда: λ = 333,5 кДж/(кг∙К).
Отсюда:
Чтобы расплавить кусок льда массой 0,5 кг, нужно затратить следующее количество теплоты:
Лед не расплавится весь, так как ему будет сообщено лишь 60 кДж теплоты. Поэтому в калориметре температура будет равна 0 оС.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18791
Внимательно прочитайте текст задания и выберите верный ответ из списка
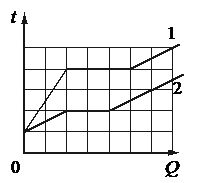
Используя данные графиков, выберите из предложенного перечня два верных утверждения и укажите их номера.
Ответ:
а) Температура плавления первого тела в 1,5 раза больше, чем второго.
б) Тела имеют одинаковую удельную теплоёмкость в твёрдом агрегатном состоянии.
в) Удельная теплоёмкость второго тела в твёрдом агрегатном состоянии
в 3 раза больше, чем первого.
г) Оба тела имеют одинаковую удельную теплоту плавления.
д) Тела имеют одинаковую удельную теплоёмкость в жидком агрегатном состоянии.
Алгоритм решения
- Проанализировать каждое из утверждений.
- Проверить истинность утверждений с помощью графика.
- Выбрать и записать верные утверждения.
Решение
Проверим первое утверждение, согласно которому, температура плавления первого тела в 1,5 раза больше, чем второго.
Если это было бы так, то количество клеток до горизонтального участка графика 1 относилось к количеству клеток до горизонтального участка графика 2 как 3 к 2. Но мы видим, что до 1 графика 4 клетки, до 1 — 2. Следовательно, температура плавления первого тела в 2 раза больше, чем второго.
Первое утверждение неверно.
Проверим второе утверждение, согласно которому тела имеют одинаковую удельную теплоёмкость в твёрдом агрегатном состоянии.
Если бы это было так, то соответствующие участки графиков совпадали бы. Только в таком случае температура тел увеличивалась на одну и ту же температуру при получении одного и того же количества теплоты. Но мы видим, что это не так.
Второе утверждение неверно.
Проверим третье утверждение, согласно которому удельная теплоёмкость второго тела в твёрдом агрегатном состоянии в 3 раза больше, чем первого.
Если это было бы так, то первое тело при сообщении телам одинакового количества теплоты нагревалось бы втрое быстрее второго. И это действительно так, потому что температура второго во время нагревания в твердом состоянии увеличилась только на 1 клетку, в то время как температура первого тела — на 2 клетки.
Третье утверждение верно.
Проверим четвертое утверждение, согласно которому оба тела имеют одинаковую удельную теплоту плавления.
Если это было бы так, то протяженность горизонтальных участков обоих графиков была бы одинаковой. Но это не так. Протяженность этого участка для тела 1 составляет 3 клетки, для тела 2 — 2 клетки.
Четвертое утверждение верно.
Проверим пятое утверждение, согласно которому тела имеют одинаковую удельную теплоёмкость в жидком агрегатном состоянии.
Если бы это было так, то соответствующие участки графиков были параллельными. Только при таком условии при повышении температуры на одно и то же количество градусов тела бы получли одинаковое количество теплоты. И это действительно так.
Пятое утверждение верно.
Вывод: верным утверждения «в» и «д».
Ответ: вд
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22685
В сосуде лежит кусок льда. Температура льда t1 = 0 °C. Если сообщить ему количество теплоты Q = 50 кДж, то 3/4 льда растает. Какое количество теплоты q надо после этого сообщить содержимому сосуда дополнительно, чтобы весь лёд растаял и образовавшаяся вода нагрелась до температуры t2 = 20 °C? Тепловыми потерями на нагрев сосуда пренебречь.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать уравнение теплового баланса.
3.Выполнить решение в общем виде.
4.Определить и вычислить искомую величину.
Решение
Запишем исходные данные:
• Начальная температура льда: t1 = 0 oC.
• Конечная температура воды: t2 = 20 oC.
• Количество теплоты, переданное льду изначально: Q = 50 кДж.
• Удельная теплоемкость воды: c = 4200 Дж/(кг∙К).
• Удельная теплота плавления льда: λ = 333,5 кДж/(кг∙К).
50 кДж = 50000 Дж
333,5 кДж = 333500 Дж
Составим уравнение теплового баланса:
Qобщ=Q+q
где q — количество теплоты, необходимое для того, чтобы окончательно растопить лед и нагреть воду:
q=Q2+Q3
Мы знаем, что изначально было растоплено 3/4 льда. Поэтому:
Q=3λm4
Отсюда масса льда равна:
m=4Q3λ
На растопку оставшегося льда уйдет следующее количество теплоты:
Q2=λm4
На нагревание воды уйдет следующее количество теплоты:
Q3=cmt2
Внимание! Вместо разности температур используется значение только конечной температуры, так как начальная температура равна 0.
Отсюда:
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 13.1k