Как найти теплоту подведенную к газу

Моль идеального одноатомного газа участвует в процессе, так как это показано на рисунке. Найдите суммарное подведенное к газу количество теплоты, если разность температур равна T₄ − T₁ = 300 К.

Задача получена от учителя спецкурса ТГУ, 10 класс, первая гимназия имени А. С. Пушкина, профиль информационно-технический, 2013 г.

Участки координатах V и T.

V₁ = V₂,   V₃ = V₄,   T₁ = T₃,   T₂ = T₄.

1-2: V = const, изохора;   T, P — увеличивается,   A = 0,   Q = ΔU = (3/2) VR (T₂ − T₁) = 450 VR;

2-3: P = const, изобара;   V, T — уменьшается;   Q = ΔU + A = ΔU + pΔV = (3/2) VR (T₃ − T₂) + p (V₃ − V₂);

3-4: абсолютно такой же, как первый участок Q = 450 VR.

Непонятен второй участок, как найти P, если оно const ?

Первый закон термодинамики

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.

Начнём с обсуждения работы газа.

Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где — давление газа, — площадь поршня. Если при этом поршень перемещается, то газ совершает работу.

При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).

к оглавлению ▴

Работа газа в изобарном процессе

Предположим, что газ расширяется при постоянном давлении . Тогда сила , с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние (рис. 1).

Рис. 1.

Работа газа равна:

Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:

(1)

Если и — начальный и конечный объём газа, то для работы газа имеем: . Изобразив данный процесс на -диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).

Рис. 2. Работа газа как площадь

Пусть теперь газ изобарно сжимается от объёма до объёма . С помощью аналогичных рассуждений приходим к формуле:

Но , и снова получается формула (1).

Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.

Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.

к оглавлению ▴

Работа газа в произвольном процессе

Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.

Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление будет оставаться приблизительно постоянным. Газ совершит малую работу . Тогда работа газа во всём процессе найдётся суммированием этих малых работ:

Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):

Рис. 3. Работа газа как площадь

к оглавлению ▴

Работа, совершаемая над газом

Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу , которую поршень совершает над газом.

Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой , равной силе по модулю и противоположной по направлению: (рис. 4).

Рис. 4. Внешняя сила , действующая на газ

Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:

Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна . Наоборот, при сжатии работа газа отрицательна , а работа, совершаемая поршнем над газом, положительна 0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.

Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .

Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.

Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа , то изменение внутренней энергии тела будет равно:

(2)

Нас больше всего интересует случай, когда тело является газом. Тогда (где , как всегда, есть работа самого газа). Формула (2) принимает вид: , или

(3)

Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.

Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.

к оглавлению ▴

Применение первого закона термодинамики к изопроцессам

Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.

1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:

Всё подведённое к газу тепло идёт на совершение газом работы.

2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:

Всё тепло, переданное газу, идёт на изменение его внутренней энергии.

3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:

к оглавлению ▴

Адиабатный процесс

Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.

Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.

Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.

При адиабатном процессе . Из первого закона термодинамики получаем: , или .

В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.

Наоборот, в процессе адиабатного сжатия будет , поэтому : газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.

Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).

Рис. 5. Сравнительный ход изотермы и адиабаты

В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?

При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.

А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.

Д) Теплота, подводимая (отводимая) к газу за процесс

Для
определения теплоты в процессе существуют
три формулы:

1)
dq
= TdS
– по этой формуле теплота не
рассчитывается, она существует лишь
для построения тепловой диаграммы

2)
dq
= C_ndT
– рассчитывается теплота, если известно
теплоемкость C_n

3)
dq=du+dl

q=
∆u
+l
(15)

Е) Теплоемкость газа за процесс

q=
∆u
+l
(а)

1. dq

с_n
= dT
=> dq
= с_ndT
;

q
= с_n(T₂
–
T₁)

1. ∆u
   =c_v(T₂-T₁)

1. R

l

= 1-n
(T₂
– T₁)

Подставляем
в (а) 1), 2), 3):

R

c
_n(T₂
– T₁)
= c_v(T₂
– T₁)
+ 1-n (T₂
– T₁)

R

c_n

= c_v

+ 1-n (16) (n≠1,
т.е. эта формула не подходит к изотермическому
процессу)

Так
как с_v,
R,
n
= const,
то для данного процесса значит с_n
=
const

Ж) Показатель политропы “n”

p₁v₁ⁿ
=p₂v₂ⁿ

p
_1
=
v₂
ⁿ

p₂
v₁

p₁
p₁

n
= log p₂
=
ln
p₂

v₂
v₁
(17)

log
v₁
ln
v₂

§3 Связь энтропии с основными параметрами газа

dq=Tds

Отсюда
видно, что т.к. T
– параметр состояния, а с_n

= сonst,
то и s
– тоже параметр состояния.

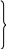
T₂

∆s_1-2
= c_n
ln T₁

∆s_1-2
= s₂
– s₁
(1)

∆s₂
=
s₁
+
∆s_1-2

Для
построения кривой процесса необходимо
знать параметры в промежуточных точках.
Для этого задаются значения температур
Т_х1,
Т_х2
,
Т_х3,
и по формуле (1) определяют энтропию s_x1,
s_x2,
s_x3
.

T_x1

∆s_1-x1=
c_n ln
T₁
(2) , где
∆s_1-x1 =
s_x1
– s₁
; s_x1 =
s₁ +
∆s_1-x1

Формулы
(1) и (2) справедливы лишь для политропных
процессов, где c_n

– const . Если неизвестно политропный – ли
процесс, необходимо использовать другие
связи энтропии с основными параметрами
газа.

dq
по
1 закону
du+pdv

d
s=
T
ds
= T

dT
p

dq
= du + dl ds = c_v
T + T dv

dl = pdv

p
R

d
u
= c_vdT
pv = RT T = v

dT
dv

ds
= c_v T
+ R v (a)

Найдены
связи энтропии с другими основными
параметрами

[s
= ƒ(T,υ)]
[ s
= ƒ(T,p)]

Воспользуемся
уравнением состояния в дифференциальной
форме.

pv=RT
→

pdv
+ vdp
= RdT
|:
υ,p

dv
dp dT

v
+ p = T (б)

Заменим
в уравнении (а) температуру, используя
уравнение (б)

dv
dp dv

ds
= c_v
v + c_v
p + R v

dV
dp

ds
= c_p
V + c_v
p (в)
[s = ƒ(p;v)]

Заменим
в (а) объемы, используя (б):

dT
dT dp

ds
= c_v
T + R T – R p

dT
dp

ds
= c_p
T – R p (г)

И
получаем:

Проинтегрировав
уравнение (а)

T

₂

v

₂

∆s_1-2
= C_vlnT₁
+
R
lnv₁
(3)

Проинтегрировав
уравнение (б)

v

₂

p

₂

∆s_1-2
= C_pln
v₁
+ C_v
ln p₁
(4)

Проинтегрировав
уравнение (в)

T

₂

p

₂

∆s_1-2
= C_pln
T₁
– R ln p₁
(5)

∆s_1-2
= s₂
– s₁

s₂
= s₁
+ ∆s_1-2

Для
определения s₁
используют понятие условный нуль.
Условно считают, что при нормальных
физических условиях энтропия s₀=0

p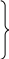
_0
= 1.0336•10⁵
Па

T₀
= 273 K
нормальные физические
условия.

s₀
= 0

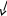
T₁
p₁

∆s_0-1
= s₁
– s₀
= s₁
= c_p
ln T₀
– R ln p₀

0

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В данной теме продолжаем решать задачи на тепловые двигатели и
коэффициент полезного действия теплового двигателя. В частности подробно
остановимся на решении задач, связанных с графиками тепловых процессов.

Задача 1. Одноатомный идеальный
газ совершает цикл, состоящий из двух адиабат и двух изохор. В процессе
адиабатного расширения 1—2 температура газа Т₂ = 0,75Т₁,
а в процессе адиабатного сжатия 3—4 температура газа Т₃ =
0,75Т₄. Определите КПД цикла.

ДАНО:	РЕШЕНИЕ Коэффициент полезного действия цикла Q1 – количество теплоты, подведенное к газу; Q2 – количество теплоты, отведенное от газа. Теплота к газу подводится в процессе 4–1 в количестве Теплота отводится от газа в процессе 2–3 в количестве Тогда КПД цикла

Ответ: КПД
цикла составляет 25%.

Задача 2. КПД теплового
двигателя, рабочим телом которого является v моль одноатомного
идеального газа, равен η. Газ совершает цикл, представленный на рисунке. Разность
максимальной и минимальной температур газа в цикле равна ΔТ. Определите работу газа в изотермическом процессе.

ДАНО:	РЕШЕНИЕ Коэффициент полезного действия цикла равен Процесс 1–2 является изотермическим и поэтому и Следовательно, из первого закона термодинамики Процесс 2–3 является изохорным, следовательно работа расширения равна нулю Тогда из первого закона термодинамики Тогда КПД Искомая работа газа равна

Задача 3. На рисунке изображен
цикл, проводимый с одноатомным газом. Определите КПД этого цикла.

РЕШЕНИЕ

Запишем формулу для расчета коэффициента полезного действия цикла

Из графика видно, что при расширении работа, совершаемая газом,
положительна и численно равна площади фигуры, ограниченной графиком , осью V и отрезками V₀–2 и 2V₀–3.

Работа, совершаемая при сжатии газа в ходе процесса 3–1,
отрицательна и численно равна площади фигуры, ограниченной графиком процесса 3–1,
осью V и отрезками V₀–1 и 2V₀–3.

Тогда, полезная работа газа за цикл, равна разности этих площадей

Из графика видим, что в процессе 1–2 происходит изохорное
нагревание газа, а в процессе 2–3 — его изобарное расширение. Следовательно, в
этих процессах газ получает теплоту

Из первого закона термодинамики следует

Так как работа газа зависит от вида процесса, то работа 1–2–3
равна сумме работ на участке 1–2 и участке 2–3

При изохорном процессе работа равна нулю

Изменение внутренней энергии

Тогда теплота, подведённая к газу

Тогда

Ответ: КПД
цикла равен 10,3%.

Задача 4. Тепловой двигатель,
рабочим телом которого является идеальный газ, совершает цикл, изображенный на
рисунке. Определите КПД двигателя.

РЕШЕНИЕ

Коэффициент полезного действия цикла

Полезная работа газа

Теплота подводится к газу в изохорном процессе 1–2 и в изобарном процессе
2–3. Согласно первому закону термодинамики эта теплота равна

Работа газа в процессе 1–2–3 равна сумме работ в процессах 1–2 и 2–3

Так как процесс 1–2 изохорный работа расширения газа равна нулю. Тогда
работа в процессе 1–2–3

Внутренняя энергия является функцией состояния термодинамической
системы и не зависит от того, каким образом система перешла в это состояние.
Поэтому изменение внутренней энергии не зависит от вида процессов и равно
разности ее значений в конечном и начальном состояниях

Т.к. из уравнения Менделеева-Клапейрона

Тогда количество теплоты, подведенное к газу

Тогда

Ответ: КПД
двигателя равен 19%.

Задача 5. КПД тепловой машины в
цикле 1—2—3—1 равен 50%, а в цикле 1—3—4—1 КПД равен 20%. Найдите КПД тепловой
машины, работающей по циклу 1—2—3—4.

ДАНО:

РЕШЕНИЕ Из графика видно, что процессы 1–2 и 3–4 представляют собой изотермы. График процесса 1–3 представляет собой адиабату, так как в этом случае давление газа уменьшается быстрее, чем при изотермическом процессе. Процессы один-четыре и два-три происходят при неизменном объеме газа. Следовательно, это изохорные процессы. Запишем формулу для определения коэффициента полезного действия для цикла 1–2–3–1 КПД для цикла 1–3–4–1 Т.к. процессы 2–3 и 4–1 изохорные, то подведенная теплота расходуется на изменение внутренней энергии. Температура газа в состояниях 1 и 2 одинакова, как и температура газа в состояниях 3 и 4. Следовательно, изменение внутренней энергии в процессах 2–3 и 4–1 одинаковое, а значит Q41 = Q23. Тогда для цикла 1–2–3–4–1

Ответ: КПД
тепловой машины, работающей по циклу 1—2—3—4 равен 40%.