2018-05-31 ![]()
Катушка и безындукционное сопротивление $R = 25 Ом$ подключены параллельно к сети переменного напряжения. Найти тепловую мощность, выделяемую в катушке, если из сети потребляется ток $I = 0,90 А$, а через катушку и сопротивление R текут токи соответственно $I_{1} = 0,50 А$ и $I_{2} = 0,60 А$.
Решение:

Иак как $I_{2} = frac{V}{R}, V =$ действительное напряжение
$I_{1} = frac{V}{ sqrt{R^{2} + X_{L}^{2}}}$
и $I = frac{V sqrt{(R + R_{1})^{2} + X_{L}^{2} } }{R sqrt{R_{1}^{2} + X_{L}^{2} } } = frac{V}{R_{эфф} }$
$R_{эфф}$ – импеданс катушки и сопротивления соединенных параллельно.
Тогда $frac{I^{2} – I_{2}^{2} }{I_{2}^{2} } = frac{R^{2} + 2RR_{1} }{R_{1}^{2} + X_{L}^{2} } = left ( frac{I_{1} }{I_{2} } right )^{2} + frac{2RR_{1} }{R^{2} + X_{L}^{2} }$
$frac{I^{2} – I_{2}^{2} – I_{1}^{2} }{I_{2}^{2} } = frac{2RR_{1} }{R^{2} + X_{L}^{2} }$
Средняя мощность, потребляемая в катушке
$= I_{1}^{2} R_{1} = frac{V^{2}R_{1} }{R_{2} + X_{L}^{2} } = I_{2}^{2}R frac{I^{2} – I_{1}^{2} – I_{2}^{2} }{2I_{2}^{2} } = 2,5 Вт$.
Тип 23 № 2058 

i
Однослойная катушка диаметром помещена в однородное магнитное поле, параллельное ее оси. Индукция поля равномерно изменяется со скоростью
Катушка содержит
витков медной проволоки (
) сечением
1. К концам катушки подключен конденсатор емкостью 10 мкФ. Определить заряд на нем.
2. Концы катушки замкнуты накоротко. Определить тепловую мощность, выделяющуюся в катушке.
Спрятать решение
Решение.
Видеорешение: https://youtu.be/xb5d4GlL-us?t=1548
Ответ: 1. 2.
Источник: Гольдфарб Н. И. Сборник вопросов и задач по физике, М.: «Высш. школа», 1982 (№ 23.27)
Катушка индуктивности в цепи переменного тока
Мы предполагаем, что катушка индуктивности
обладает пренебрежимо малым активным
сопротивлением R. Такой
элемент включать в цепь постоянного
тока нельзя, потому что произойдет
короткое замыкание.
В цепи переменного тока мгновенному
нарастанию силы тока препятствует ЭДС
самоиндукции. При этом для сверхпроводника
ei+u=0.
Используя закон Фарадея для самоиндукции
ei= -Li/ ,
можно показать, что, если сила тока в
цепи изменяется по гармоническому
закону
i= I0cos(ωt),
то колебания напряжения на катушке
описываются
у равнением
равнением
U = – I0
Lωsin
ωt = I0
Lω cos(ωt+π/2),
то есть колебания напряжения опережают
по фазе колебания силы тока на π/2.
Произведение U0
= I0 Lω
является амплитудой напряжения:
U = U0
cos(ωt+π/2)
Индуктивное
сопротивление
Величину
![]()
называют индуктивным сопротивлением.
Связь между амплитудными значениями
силы тока и напряжения формально
совпадает с законом Ома для участка
цепи
![]()
Такое же соотношение выполняется для
действующих значений силы тока и
напряжения.
Индуктивное сопротивление зависит от
частоты переменного напряжения. С
увеличением частоты колебаний напряжения
индуктивное сопротивление увеличивается,
поэтому амплитуда силы тока уменьшается
обратно пропорционально частоте I0
= U0 /ωL.
При уменьшении частоты амплитуда силы
тока возрастает и при ω=0 стремится к
бесконечности. Отметим, что нулевая
частота колебаний означает, что в цепи
протекает постоянный ток.
Мощность в цепи переменного тока
Рассчитаем тепловую мощность, выделяющуюся
на конденсаторе в цепи переменного
тока. По закону Джоуля-Ленца, мгновенное
значение мощности определяется как
произведение мгновенных значений
силы тока и напряжения:
P = UI =U0cos
ω t* I0sin
ω t =1/2 I0U0sin
2ωt
Среднее значение мощности за период
<P> = <1/2I0U0sin
2 ω t> = 1/2I0U0<sin
2 ω t>
<sin 2 ω t>=
0
<P> = 0
Аналогичный результат получается и для
мощности на катушке индуктивности.
Вывод В цепи переменного тока
тепловая мощность выделяется только
на участке цепи с резистором, где нет
сдвига фаз между током и напряжением.
По этой причине резистор в цепи
переменного тока называют активным
сопротивлением, а конденсатор и катушку
индуктивности – реактивным.
Вопрос: Директор
кинотеатра собирается установить
систему, которая обеспечивала бы
медленное затухание осветительных ламп
перед сеансом и медленное их включение
– после. Ему предлагают на выбор два
способа: 1) – воспользоваться реостатом,
чтобы постепенно изменять активное
сопротивление цепи и 2) использовать
соленоид с большой индуктивностью,
чтобы мгновенному изменению силы тока
в цепи препятствовала ЭДС индукции.
Какой из двух способов выгоднее?
Ответ: Использование реактивного
сопротивления не связано с дополнительным
выделением Джоулевого тепла, и поэтому
всегда экономичнее.
Лекция 7 Полная цепь переменного тока
Любая реальная цепь переменного тока
содержит одновременно активное
сопротивление (нагревательные приборы,
лампы накаливания, соединительные
провода и т.п.), емкостное сопротивление
(емкости проводников, конденсаторов
и т.п.) и индуктивное сопротивление
(обмотки электродвигателей, катушки
электромагнитных приборов и т.п.).
П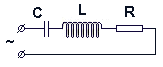 усть
усть
все эти элементы соединены последовательно,
как показано на рисунке.
В такой цепи колебания тока и напряжения
не совпадают по фазе. Фазовый сдвиг
между этими величинами зависит от
индуктивности катушки и емкости
конденсатора.
Во всех последовательно включенных
элементах цепи сила тока изменяется
практически одновременно, потому что
распространение электромагнитных
взаимодействий происходит со скоростью
света. Поэтому можно считать, что
колебания тока во всех элементах
последовательной цепи совпадают по
фазе и выражаются формулой:
I = I0·cos
ω ·t
Тогда
Напряжение на резисторе U
= U0
cos(ωt)
Напряжение на конденсаторе U
= U0
cos(ωt–π/2)
=+ U0 sin(ωt)
Напряжение на катушке U
= U0
cos(ωt+π/2)
= –
U0 sin(ωt)
Uc.
выходит из нуля, возрастает, первую
четветь>0
Разность фаз колебаний напряжения на
конденсаторе и катушке индуктивности
в любой момент времени равна π.
О таких колебаниях говорят, что они
присходят в противофазе.
Uc.
выходит из нуля, возрастает, первую
четветь>0
UL
выходит из нуля, убывает, первую четветь<0
,


Uc(t)
UL(t)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
7. Мощность в цепи с индуктивностью
Из формулы видно, что мощность на индуктивности колеблется с удвоенной частотой и принимает как положительные, так и отрицательные значения (см. временную диаграмму для мощности).
За период изменения тока в цепи поступление и возврат энергии в индуктивности равны друг другу. Энергия поступает от источника и временно запасается в магнитном поле индуктивности, а затем возвращается источнику при исчезновении магнитного поля. Т.о, происходит колебание энергии между источником и индуктивностью. В среднем катушка не потребляет энергии и следовательно, активная мощность равна нулю: Р = 0.
Такой режим работы электрической цепи является вредным, поскольку существуют встречные потоки энергии, бесполезно загружаются провода, и в результате снижается пропускная способность линии.
Для количественной характеристики интенсивности обмена энергией между источником и катушкой служит реактивная мощность
Реактивная мощность обозначается [Q]. Единицей реактивной мощности является вольт-ампер реактивный (Вар).
8. Электрическая цепь с емкостью
Конденсатор – элемент цепи, обладающий значительной емкостью.
Конструктивно конденсатор представляет собой две пластины с большой поверхностью; выполнены они из проводящего материала и разделены слоем диэлектрика.
Конденсатор характеризуется емкостью С. Емкость определяет величину заряда, который накапливается на пластинах при разности потенциалов 1 В:
Хотя пластины конденсатора и разделены слоем диэлектрика, при переменном напряжении ток в цепи с конденсатором существует. Это связано с тем, что синусоидальное напряжение непрерывно меняется по значению и направлению, =>но, и заряд на пластинах конденсатора непрерывно меняется.
Это изменение заряда и связанное с ним движение электронов и есть электрический ток в цепи.
Рассмотрим электрическую цепь, состоящую из источника питания и конденсатора емкостью С.
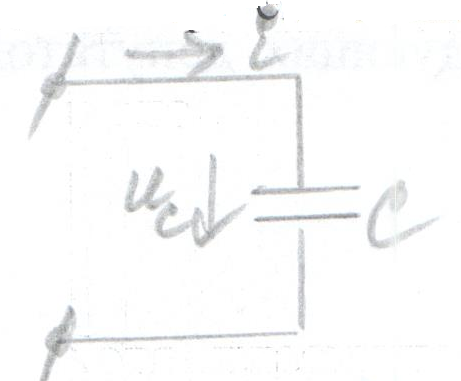
Пусть в цепи с емкостью протекает ток
Так как , а q=C∙uC, то , и следовательно,
В результате интегрирования получаем ,
где – амплитуда напряжения на емкости.
Таким образом, ток в цепи с емкостью опережает по фазе напряжение на (или, что то же самое, напряжение отстает по фазе от тока на ).

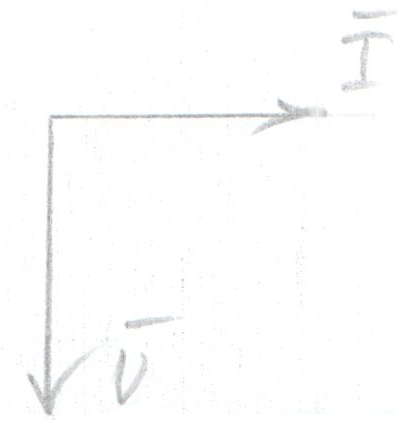
Векторная диаграмма тока и напряжения для цепи с емкостью
Это объясняется тем, что напряжение на обкладках конденсатора появляется только после возникновения тока.
Емкость запасает внутри себя энергию электрического поля.
ХС – емкостное сопротивление цепи.
Из формулы видно, что с увеличением частоты емкость уменьшается.
Закон Ома для цепи с емкостью
– закон Ома для амплитудных значений;
– закон Ома для действующих значений;
– закон Ома в комплексной форме.
Множитель (–j) перед емкостным сопротивлением ХС необходим для обеспечения сдвига фаз между током и напряжением.
9. Мощность в цепи с емкостью
(см. график на временной диаграмме)
Из графика и формулы для мгновенной мощности следует, что в цепи с емкостью, так же, как и в цепи с индуктивностью, происходит переход энергии от источника к нагрузке, и наоборот. В данном случае энергия источника преобразуется в энергию электрического поля конденсатора.
Мощность колеблется с удвоенной частотой. За период изменения тока, поступление и возврат энергии в емкостном элементе равны друг другу. Это значит, что, сколько энергии поступает в нагрузку, столько же возвращается обратно в генератор. Энергия здесь не тратится, а колеблется между нагрузкой и генератором. В результате этого снижается пропускная способность линии.
Средняя мощность в цепи с емкостью Р = 0.
Для количественной характеристики интенсивности обмена энергией между источником и конденсатором служит реактивная мощность:
Мощность переменного тока
Переменный ток несёт энергию. Поэтому крайне важным является вопрос о мощности в цепи переменного тока.
Пусть и — мгновенные значение напряжения и силы тока на данном участке цепи. Возьмём малый интервал времени — настолько малый, что напряжение и ток не успеют за это время сколько-нибудь измениться; иными словами, величины и можно считать постоянными в течение интервала .
Пусть за время через наш участок прошёл заряд (в соответствии с правилом выбора знака для силы тока заряд считается положительным, если он переносится в положительном направлении, и отрицательным в противном случае). Электрическое поле движущихся зарядов совершило при этом работу
Мощность тока — это отношение работы электрического поля ко времени, за которое эта работа совершена:
Точно такую же формулу мы получили в своё время для постоянного тока. Но в данном случае мощность зависит от времени, совершая колебания вместе током и напряжением; поэтому величина (1) называется ещё мгновенной мощностью.
Из-за наличия сдвига фаз сила тока и напряжение на участке не обязаны совпадать по знаку (например, может случиться так, что напряжение положительно, а сила тока отрицательна, или наоборот). Соответственно, мощность может быть как положительной, так и отрицательной. Рассмотрим чуть подробнее оба этих случая.
1. Мощность положительна: . Напряжение и сила тока имеют одинаковые знаки. Это означает, что направление тока совпадает с направлением электрического поля зарядов, образующих ток. В таком случае энергия участка возрастает: она поступает на данный участок из внешней цепи (например, конденсатор заряжается).
2. Мощность отрицательна: . Напряжение и сила тока имеют разные знаки. Стало быть, ток течёт против поля движущихся зарядов, образующих этот самый ток.
Как такое может случиться? Очень просто: электрическое поле, возникающее на участке, как бы «перевешивает» поле движущихся зарядов и «продавливает» ток против этого поля. В таком случае энергия участка убывает: участок отдаёт энергию во внешнюю цепь (например, конденсатор разряжается).
Если вы не вполне поняли, о чём только что шла речь, не переживайте — дальше будут конкретные примеры, на которых вы всё и увидите.
Мощность тока через резистор
Пусть переменный ток протекает через резистор сопротивлением . Напряжение на резисторе, как нам известно, колеблется в фазе с током:
Поэтому для мгновенной мощности получаем:
График зависимости мощности (2) от времени представлен на рис. 1 . Мы видим, что мощность всё время неотрицательна — резистор забирает энергию из цепи, но не возвращает её обратно в цепь.

Рис. 1. Мощность переменного тока через резистор
Максимальное значение нашей мощности связано с амплитудами тока и напряжения привычными формулами:
На практике, однако, интерес представляет не максимальная, а средняя мощность тока. Это и понятно. Возьмите, например, обычную лампочку, которая горит у вас дома. По ней течёт ток частотой Гц, т. е. за секунду совершается колебаний силы тока и напряжения. Ясно, что за достаточно продолжительное время на лампочке выделяется некоторая средняя мощность, значение которой находится где-то между и . Где же именно?
Посмотрите ещё раз внимательно на рис. 1 . Не возникает ли у вас интуитивное ощущение, что средняя мощность соответствует «середине» нашей синусоиды и принимает поэтому значение ?
Это ощущение совершенно верное! Так оно и есть. Разумеется, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу догадку прямым вычислением, но нам это не нужно. Достаточно интуитивного понимания простого и важного факта:
среднее значение квадрата синуса (или косинуса) за период равно .
Этот факт иллюстрируется рисунком 2 .

Рис. 2. Среднее значение квадрата синуса равно
Итак, для среднего значения мощности тока на резисторе имеем:
В связи с этими формулами вводятся так называемые действующие (или эффективные) значения напряжения и силы тока (на самом деле это есть не что иное, как средние квадратические значения напряжения и тока. Такое у нас уже встречалось: средняя квадратическая скорость молекул идеального газа (листок «Уравнение состояния идеального газа»):
Формулы (3) , записанные через действующие значения, полностью аналогичны соответствующим формулам для постоянного тока:
Поэтому если вы возьмёте лампочку, подключите её сначала к источнику постоянного напряжения , а затем к источнику переменного напряжения с таким же действующим значением , то в обоих случаях лампочка будет гореть одинаково ярко.
Действующие значения (4) чрезвычайно важны для практики. Оказывается, вольтметры и амперметры переменного тока показывают именно действующие значения (так уж они устроены). Знайте также, что пресловутые вольт из розетки — это действующее значение напряжения бытовой электросети.
Мощность тока через конденсатор
Пусть на конденсатор подано переменное напряжение . Как мы знаем, ток через конденсатор опережает по фазе напряжение на :
Для мгновенной мощности получаем:
График зависимости мгновенной мощности от времени представлен на рис. 3 .

Рис. 3. Мощность переменного тока через конденсатор
Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в данном случае равно нулю! Мы видим это сейчас как математический факт. Но интересно было бы с физической точки зрения понять, почему мощность тока через конденсатор оказывается нулевой.
Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе на протяжении одного периода колебаний (рис. 4 ).

Рис. 4. Напряжение на конденсаторе и сила тока через него
Рассмотрим последовательно все четыре четверти периода.
1. Первая четверть, . Напряжение положительно и возрастает. Ток положителен (течёт в положительном направлении), конденсатор заряжается. По мере увеличения заряда на конденсаторе сила тока убывает.
Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счёт работы внешнего электрического поля, продвигающего заряды на конденсатор.
2. Вторая четверть, . Напряжение продолжает оставаться положительным, но идёт на убыль. Ток меняет направление и становится отрицательным: конденсатор разряжается против направления внешнего электрического поля.В конце второй четверти конденсатор полностью разряжен.
Мгновенная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать).
3. Третья четверть, . Внешнее электрическое поле меняет направление: напряжение отрицательно и возрастает по модулю. Сила тока отрицательна: идёт зарядка конденсатора в отрицательном направлении.
Ситуация полностью аналогична первой четверти, только знаки напряжения и тока — противоположные. Мощность положительна: конденсатор вновь накапливает энергию.
4. Четвёртая четверть, . Напряжение отрицательно и убывает по модулю. Конденсатор разряжается против внешнего поля: сила тока положительна.
Мощность отрицательна: конденсатор возвращает энергию в цепь. Ситуация аналогична второй четверти — опять-таки с заменой заменой знаков тока и напряжения на противоположные.
Мы видим, что энергия, забранная конденсатором из внешней цепи в ходе первой четверти периода колебаний, полностью возвращается в цепь в ходе второй четверти. Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.
Мощность тока через катушку
Пусть на катушку подано переменное напряжение . Ток через катушку отстаёт по фазе от напряжения на :
Для мгновенной мощности получаем:
Снова средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики напряжения и силы тока через катушку за период (рис. 5 ).

Рис. 5. Напряжение на катушке и сила тока через неё
Мы видим, что в течение второй и четвёртой четвертей периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по модулю; для создания тока внешнее электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на увеличение энергии магнитного поля катушки.
В первой и третьей четвертях периода напряжение и сила тока имеют разные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против внешнего электрического поля и совершает тем самым положительную работу. А за счёт чего совершается эта работа? За счёт энергии, накопленной ранее в катушке.
Таким образом, энергия, запасаемая в катушке за одну четверть периода, полностью возвращается в цепь в ходе следующей четверти. Поэтому средняя мощность, потребляемая катушкой, оказывается равной нулю.
Мощность тока на произвольном участке
Теперь рассмотрим самый общий случай. Пусть имеется произвольный участок цепи — он может содержать резисторы, конденсаторы, катушки. На этот участок подано переменное напряжение .
Как мы знаем из предыдущего листка «Переменный ток. 2», между напряжением и силой тока на данном участке имеется некоторый сдвиг фаз . Мы записывали это так:
Тогда для мгновенной мощности имеем:
Теперь нам хотелось бы определить, чему равна средняя мощность. Для этого мы преобразуем выражение (5) , используя формулу:
В результате получим:
Но среднее значение величины равно нулю! Поэтому средняя мощность оказывается равной:
Данную формулу можно записать с помощью действующих значений (4) напряжения и силы тока:
Формула (7) охватывает все три рассмотренные выше ситуации. В случае резистора имеем , и мы приходим к формуле (3) . Для конденсатора и катушки , и средняя мощность равна нулю.
Кроме того, формула (7) даёт представление о весьма общей проблеме, связанной с передачей электроэнергии. Чрезвычайно важно, чтобы у потребителя был как можно ближе к единице. Иначе потребитель начнёт возвращать значительную часть энергии назад в сеть (что ему совсем невыгодно), и к тому же возвращаемая энергия будет безвозвратно расходоваться на нагревание проводов и других элементов цепи.
С этой проблемой приходится сталкиваться разработчикам электрических схем, содержащих электродвигатели. Обмотки электродвигателей обладают большими индуктивностями, и возникает ситуация, близкая к «чистой» катушке. Чтобы избежать бесполезного циркулирования энергии по сети, в цепь включают дополнительные элементы, сдвигающие фазу — например, так называемые компенсирующие конденсаторы.
Благодарим за то, что пользуйтесь нашими статьями. Информация на странице «Мощность переменного тока» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Мощность цепи.
Вырабатываемая мощность цепи переменного тока обладает свойством постоянно изменяться. Но при разделении периода такого тока и напряжения на маленькие временные промежутки величина тока и напряжения могут быть приняты как константы в данных временных промежутках. За каждый такой промежуток, который мы обозначим Δt, вырабатывается энергия, которая равна по величине средней величине тока, умноженной на среднюю величину напряжения, само собой, за данный промежуток времени:
Вообще говоря, ток и напряжение в цепи можно сместить по отношению друг к другу по фазе на произвольный угол, который мы назовем φ (рис. 1, а).

Рис. 1. Мощность переменного тока.
а — ток и напряжение смещены по фазе на угол φ;
б — ток и напряжение смещены по фазе на угол, равный 90°.
Будем считать началом временного отсчета момент, в который напряжение меняет свои значения с отрицательных на положительные. Тогда в момент, когда время равно нулю:
За маленький временной промежуток Δt в цепи выделится следующая энергия:
Тогда, если мы применим формулу из тригонометрии:
то у нас получится:
За один период переменного тока будет выработана энергия, которая складывается из энергий, которые были выработаны за все маленькие промежутки времени, которые составляют период:
Так как величины, которые перемножаются в первом члене разности, константы, а во втором члене косинус в течение одной половины периода положителен, а вторую часть – отрицателен при тех же численных значениях, что в итоге дает ноль:
За один период средняя активная мощность цепи переменного тока равна:
В случае, когда ток и напряжение одинаковы по фазе, как если бы ток проходил через активное сопротивление:
Отсюда видно, что активная мощность цепи переменного тока равна мощности, которую вырабатывает постоянный ток, но только если его величина и величина напряжения будут меньше в √2 раз, чем амплитуда переменного. Такие значения переменного тока I и напряжения U называются действующими, или эффективными:
Так как в данной ситуации Um = Im•r, формула средней мощности цепи может быть выражена следующим образом:
Если взять конкретные амплитуды тока и напряжения, то вырабатываемая мощность цепи будет обратно зависеть от угла между их сдвигом фаз. Когда он равен 90° (рис. 1, б), а это аналогично цепям с реактивными элементами — идеальными конденсаторами и катушками индуктивности, работающими без потерь, средняя мощность цепи за один период будет равна нулю, потому что 25% периода будет предназначено для накопления энергии, а еще 25% — ее трате.
Условно отдаваемую и получаемую источником переменной э. д. с. мощность цепи называют реактивной, Рр. Если при этом будет происходить обмен энергией с реактивной нагрузкой (амплитуды тока и напряжения, умноженные на нагрузку на синус угла φ между ними и деленные пополам):
Примем во внимание, что напряжение на идеальной реактивной нагрузке Um = Im•X. Тогда:
Довольно распространен случай, когда на каком-то участке цепи существует переменное напряжение u = Um cosωt. Если через участок течет постоянный ток и токи различных частот, кратных ω, тогда:
Но какой энергетический эффект будет, если данные токи будут взаимодействовать с напряжением круговой частоты ω?
Ясно, что за один период средняя мощность взаимодействия постоянного тока с переменным напряжением равняется нулю. Первую половину периода она принимает положительные значения, так как источник расходует энергию, а вторую половину – отрицательные, так как источник получает ту же энергию обратно. Труднее понять, как происходит взаимодействие напряжения круговой частоты ω с токами кратных частот n•ω.
Чтобы вычислить среднюю за один период мощность напряжения T, необходимо, как и в прежних случаях, разделить период на маленькие временные участки Δt, на протяжении которых ток и напряжения можно принять за константы. Тогда мощность, достигнутая за такой промежуток, равна
Для вычисления средней мощности цепи за промежуток времени T, надо посчитать произведение всех pi на временные промежутки Δt, сложить их, а потом разделить на период T. В нашем случае будут суммироваться произведения вида
Ясно, что все такие суммы равняются нулю. На рис. 2 показаны напряжение и ток в ситуации, когда ток по частоте в два раза больше, чем напряжение (n = 2), и приведен график произведений их мгновенных значений. Если посмотреть на график произведений мгновенных значений внимательно, станет ясно, что мгновенная мощность цепи тоже изменяется во времени с определенным периодом и за время T два раза переходит от положительных к таким же, но отрицательным значениям. Так что средняя мощность цепи за временной интервал T будет равняться нулю. Ясно, что при всяком сочетании кратных частот будет наблюдаться та же картина.

Рис. 2. Мощность взаимодействия тока и напряжения кратных частот.
Основываясь на информации, которая была изложена в данном параграфе, можно сделать следующий вывод: если в цепи источника переменного напряжения протекают постоянный ток и переменные токи кратных частот, то энергетическое взаимодействие происходит только с током, частота которого равна частоте источника напряжения; источник постоянного напряжения дает эффект энергетического взаимодействия только с постоянной составляющей проходящего через него тока.
Как определить мощность трансформатора по формуле

В быту и технике широко применяется низковольтная аппаратура. Этот факт требует использования устройств, понижающих стандартное напряжение до необходимого уровня. Нужно создать прибор, который соответствует предъявляемым нормам. Перед электриком встаёт задача, как определить мощность трансформатора. Знание элементарных физических законов помогает решить проблему.
Теория и история
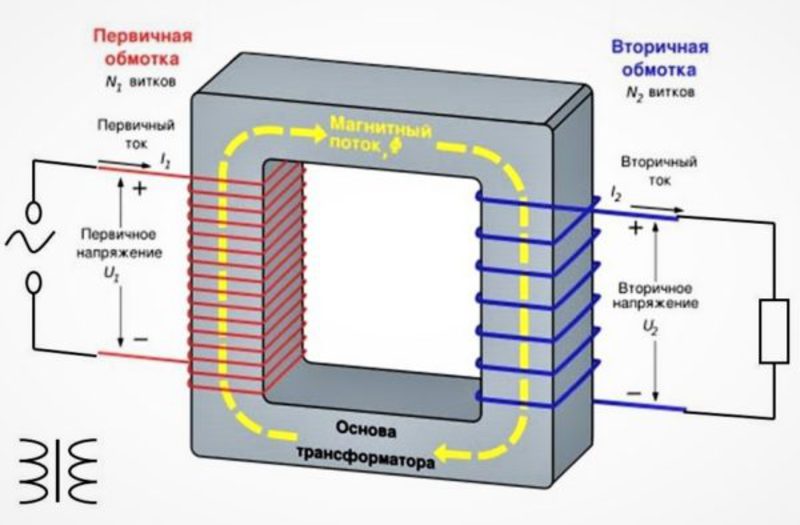
Латинское слово transformare переводится на русский язык как «превращение». Трансформатор предназначен для изменения уровня входного напряжения на определённую величину. Устройство состоит из одной или нескольких обмоток на замкнутом магнитопроводе. Катушки наматываются из алюминиевого или медного провода. Сердечник набирается из пластин с повышенными ферромагнитными свойствами.
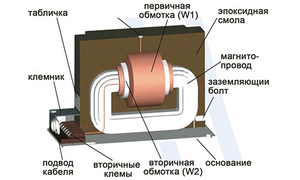
Первичная обмотка присоединяется к электрической сети переменного тока. Во вторичную обмотку включается устройство, которому требуется напряжение другой величины.
После подключения к трансформатору питания в магнитопроводе появляется замкнутый магнитный поток, который индуцирует в каждой катушке переменную электродвижущую силу. Закон Фарадея гласит, что ЭДС равна скорости изменения магнитного потока, который проходит через электромагнитный контур. Знак «минус» указывает на противоположность направлений магнитного поля и ЭДС.
Формула e = − n (∆Ф ∕ ∆ t) объединяет следующие понятия:
- Электродвижущая сила e, исчисляемая в вольтах.
- Количество витков n в индукторе.
- Магнитный поток Ф, единица измерения которого называется вебером.
- Время t, необходимое для одной фазы изменения магнитного поля.
Учитывая незначительность потерь в катушке индуктивности, ЭДС приравнивается к напряжению в обмотке. Отношение напряжений в первичной и вторичной обмотке равно отношению количества витков в двух катушках. Отсюда выводится формула трансформатора:
K ≈ U ₁ ∕ U ₂ ≈ n ₁ ∕ n ₂.
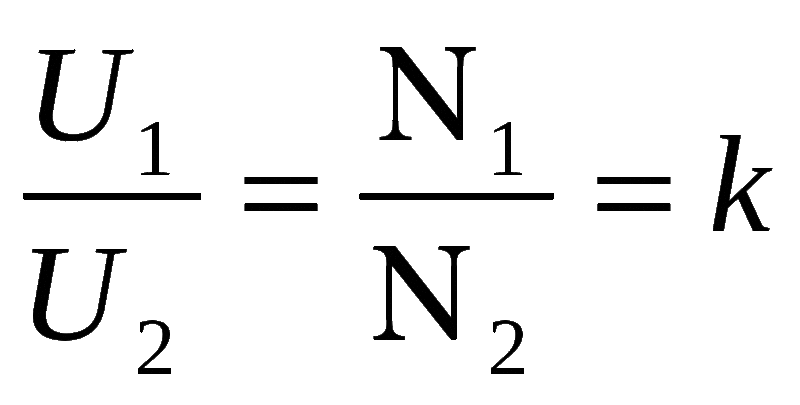
Коэффициент K всегда больше единицы. В трансформаторе изменяется только напряжение и сила тока. Умноженные друг на друга, они определяют мощность прибора, постоянную величину для конкретного устройства. Соотношение тока и напряжения в обмотках раскрывает формула:
K = n₁ ∕ n₂ = I ₂ ∕ I₁ = U₁ ∕ U₂.
Иначе говоря, во сколько раз уменьшено напряжение во вторичной обмотке в сравнении с напряжением в первичной катушке, во столько раз сила тока во вторичной катушке больше тока в первичной обмотке. Различное напряжение устанавливается количеством витков в каждом индукторе. Формула, описывающая коэффициент K, объясняет, как рассчитать трансформатор.
Трансформатор предназначен для работы в цепи переменного напряжения. Постоянный ток не индуцирует ЭДС в магнитопроводе, и электрическая энергия не передаётся в другую обмотку.
Ещё в 1822 году Фарадей озаботился мыслью, как превратить магнетизм в электрический ток. Многолетние исследования приводят к созданию цикла статей, в которых описывалось физическое явление электромагнитной индукции. Фундаментальный труд публиковался в научном журнале английского Королевского общества.

Суть опытов состояла в том, что исследователь намотал два куска медной проволоки на кольцо из железа. К одной из катушек подключался постоянный ток. Гальванометр, соединённый с контактами другой обмотки, фиксировал кратковременное появление напряжения. Чтобы восстановить индукцию, экспериментатор отключал источник питания, а затем вновь замыкал контакты на батарею.
Работу Майкла Фарадея высоко оценило научное сообщество Великобритании. В 1832 году физик удостоился престижной награды. За выдающиеся работы в области электромагнетизма учёный награждён медалью Копли.
Однако устройство, собранное Фарадеем, ещё трудно назвать трансформатором. Аппарат, который действительно преобразовывал напряжение и ток, запатентован в Париже 30 ноября 1876 года. В 80-х годах позапрошлого столетия автор изобретения и конструктор трансформатора П. Н. Яблочков жил во Франции. В это же время выдающийся русский электротехник представил миру и прообраз прожектора — «свечу Яблочкова».
Расчёт параметров прибора
Иногда в руки к электрику попадает прибор без описания технических характеристик. Тогда специалист определяет мощность трансформатора по сечению магнитопровода. Площадь сечения находится перемножением ширины и толщины сердечника. Полученное число возводится в квадрат. Результат укажет на примерную мощность устройства.
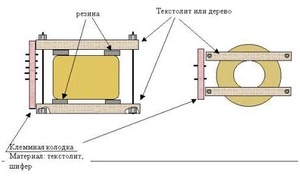
Желательно, чтобы площадь магнитопровода немного превышала расчётное значение. Иначе тело сердечника попадёт в область насыщения магнитного поля, что приведёт к падению индуктивности и сопротивления катушки. Этот процесс увеличит уровень проходящего тока, вызовет перегрев устройства и поломку.
Практический расчёт силового трансформатора не займёт много времени. Например, перед домашним мастером стоит задача осветить рабочий уголок в гараже. В помещении имеется бытовая розетка на 220 В, в которую необходимо подключить светильник с лампой мощностью 40 Вт на 36 В. Требуется рассчитать технические параметры понижающего трансформатора.
Определение мощности
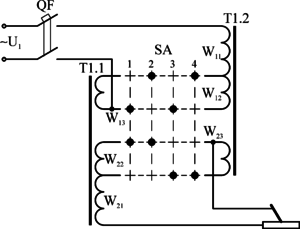
Во время работы устройства неизбежны тепловые потери. При нагрузке, не превышающей 100 Вт, коэффициент полезного действия равен 0,8. Истинная потребная мощность трансформатора P₁ определяется делением мощности лампы P₂ на КПД:
P₁ = P₂ ∕ μ = 40 ∕ 0‚8 = 50
Округление осуществляется в бо́льшую сторону. Результат 50 Вт.
Вычисление сечения сердечника
От мощности трансформатора зависят размеры магнитопровода. Площадь сечения определяется следующим образом.
S = 1‚2∙√P₁ = 1‚2∙ 7‚07 = 8‚49
Поперечное сечение сердечника должно иметь площадь не менее 8‚49 см².
Расчёт количества витков
Площадь магнитопровода помогает определить количество витков провода на 1 вольт напряжения:
n = 50 ∕ S = 50 ∕ 8‚49 = 5‚89.
Разности потенциалов в один вольт будут соответствовать 5‚89 оборотам провода вокруг сердечника. Поэтому первичная обмотка с напряжением 220 В состоит из 1296 витков, а для вторичной катушки потребуется 212 витков. Во вторичной обмотке происходят потери напряжения, вызванные активным сопротивлением провода. Вследствие этого специалисты рекомендуют увеличить количество витков в выходной катушке на 5−10%. Скорректированное число витков будет равно 233.
Токи в обмотках
Следующий этап — нахождение силы тока в каждой обмотке, которое вычисляется делением мощности на напряжение. После нехитрых подсчётов получается требуемый результат.
В первичной катушке I₁ = P₁ ∕ U₁ = 50 ∕ 220 = 0‚23 ампера, а во вторичной катушке I₂ = P₂ ∕ U₂ = 40 ∕ 36 = 1‚12 ампера.
Диаметр провода
Расчёт обмоток трансформатора завершается определением толщины провода, сечение которого вычисляется по формуле: d = 0‚8 √ I. Слой изоляции в расчёт не берётся. Проводник входной катушки должен иметь диаметр:
d₁ = 0‚8 √I₁ =0‚8 √0‚23 = 0‚8 ∙ 0‚48 = 0‚38.
Для намотки выходной обмотки потребуется провод с диаметром:
d₂ = 0‚8 √I₂ =0‚8 √1‚12 = 0‚8 ∙ 1‚06 = 0‚85.
Размеры определены в миллиметрах. После округления получается, что первичная катушка наматывается проволокой толщиной 0‚5 мм, а на вторичную обмотку подойдёт провод в 1 мм.
Виды и применение трансформаторов
Области использования трансформаторов разнообразны. Устройства, повышающие напряжение, эксплуатируются в промышленных целях для транспортировки электроэнергии на значительные расстояния. Понижающие трансформаторы используются в радиоэлектронике и для подсоединения бытовой техники.
Некоторые народные умельцы, недовольные пониженным напряжением в сети, рискуют включать бытовые приборы через повышающий трансформатор. Спонтанный скачок напряжения может привести к тому, что яркий комнатный свет заменит очень яркое пламя пожара.
По задачам, которые решает трансформатор, приборы делятся на основные виды:
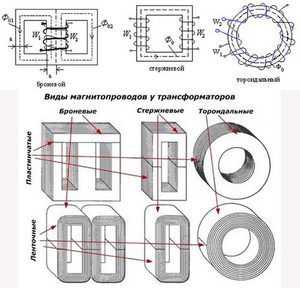
- Автотрансформатор имеет один магнитопровод, на котором собран индуктор. Часть витков выполняет функции первичной обмотки, а остальные витки действуют как вторичные катушки.
- Преобразователи напряжения работают в измерительных приборах и в цепях релейной защиты.
- Преобразователи тока предназначены для гальванической развязки в сетях сигнализации и управления.
- Импульсные трансформаторы применяются в вычислительной технике, автоматике, системах связи.
- Силовые устройства работают с напряжением до 750 киловольт.
Любое изменение параметров электричества в цепи связано с трансформатором. Специалисту, проектирующему электронные схемы, необходимо знание природы электромагнетизма. Технология расчёта обмоток трансформатора основана на базовых формулах физики.
Электротехнику, занятому рутинным делом намотки трансформатора, стоит помянуть добрым словом дядюшку Фарадея, который открыл замечательный закон электромагнитной индукции. Глядя на готовое устройство, следует также вспомнить великого соотечественника, русского изобретателя Павла Николаевича Яблочкова.
