На чтение 6 мин. Просмотров 2.9k. Опубликовано 27.07.2021
Практически все электроприборы содержат в своих схемах резисторы. Это объясняется тем, что для каждого прибора или проводника избирается своя сила тока для функционирования. Для того чтобы компенсировать значение между напряжением и движением заряженных частиц, в схемы вводят сопротивление. Основной параметр – это его мощность.
Что такое тепловая мощность резистора
Другое название – рассеивание. Этим понятием называют максимальные токи, которые без вреда могут протекать через него для осуществления работы и образования ЭДС в контактах и т.п.
Важно! Для каждой электрической схемы параметры рассеивания подбираются индивидуально.
Вычисляется по физической формуле с алгебраическими значениями: P = I * R.
В СИ:
- I – сила тока, Ампер.
- R – сопротивление, Ом.
- Р – мощность, Вт.
В физическом плане рассеивание – это способность проводника отдавать тепло в окружающую среду в том количестве, которое не вредит составным частям самого элемента. Это очень важный параметр, так как от него зависит исправность и долговечность электроприбора.
Важно! Все компоненты работают, подчиняясь закону Ома, но сам нагрев происходит из-за разности величин напряжения на входе и выходе. Это и является основным условием движения заряженных частиц через проводник.
Как определить и подобрать мощность
Данный параметр избирается от максимального значения силы заряженных частиц, которые будут протекать через проводник.
Для того чтобы подбирать тепловое рассеивание участков сопротивления для конкретных электроприборов, необходимо изучить параметры входного и выходного напряжения, а также силу электроцепи.
Важно! Необходимо понимать, что городские и промышленные цепи различаются по нагрузке и напряжению. Для бытовых используется 220V, для промышленных часто применяется значение в 380V.
Далее будет представлен стандартный ряд с графическим изображением мощностного отбора резистантов. Абсолютное большинство фабричных электроприборов оснащаются схемами, где указан конкретный диапазон элементов. Такие схемы незаменимы при ремонте и позволяют быстро подбирать необходимое.
Стандартный ряд мощностей и их обозначение на схемах
| Вт | Условное обозначение на электросхемах |
| 0,05 Вт |  |
| 0,125 Вт |  |
| 0,025 Вт |  |
| 0,5 Вт |  |
| 1 Вт |  |
| 2 Вт |  |
| 5 Вт |  |
В качестве графических обозначений используются римские цифры и черточки, раскрывающие диапазон от 0,05 до 25
Важно! Очень важно запомнить то, что слабые устройства обозначается косыми линиями.
Формула для расчета мощности тока в активном сопротивлении, как узнать сколько ватт
Как уже было упомянуто, классическая формула для расчета формируется так: квадрат силы движущихся заряженных частиц, помноженный на величину резистента.
Так показатели работоспособности напрямую зависят от напряжения. При работе и возникновении ЭДС частицы протекают через элемент, «осаживаясь» сопротивлением, и происходит нагрев элемента. Нагрев – это выделение тепла, который может быть измерен в Вт.
Важно! Что будет, если неправильно подобрать изделие? Если величина рассеивания слишком маленькая, то сопротивление перегорит, а если установить слишком «сильный» резистант, то движение заряженных частиц не начнется, и произойдет замыкание. Если из строя вышел элемент в 0,5 Вт, то он заменяется точным аналогом с соответствующими параметрами.
Действует еще одно правило подбора – оно касается не графических изображений на схеме, а самого типоразмера устройства. Чем больше элемент по габаритам, тем выше характеристика его параметров.
Как рассчитать рассеивание для сопротивления
Рассеиванием в физике и электромеханике называется процесс образования тепловой энергии, при чем это касается не только резисторов, но и прочих электрических элементов: кабелей, проводов, штекеров и катушек.
Главное не допускать перегрева, так как это кратно снижает долговечность электроприборов и их отдельных элементов. Следующий ряд является типовым в отборе характеристик зависимости производительности от напряжения:
- 0,125
- 0,25
- 0,5
- 1
- 2
- Более 2 Ватт.
Им соответствует значение для сопротивлений, Ом: 10, 20, 25, 50, 60, 100.
Приведем конкретный пример алгебраического вычисления.
Мы имеем изделие с параметром в 10 Ом и пропускаем через него поток заряда в 0,1 А. Используем значения для того, чтобы подставить их в известную формулу с переменными. Получаем P = 1
P(Ватт) – теплота, выделяемая на резисторе;
R(Ом) – сопротивление цепочки;
I(А) – движение заряженных частиц.
Как определить по внешнему виду
Если на схеме имеется конкретное обозначение, то тепловая мощность на резисторе определяется по символам, но как определить параметр по внешнему виду элементов на плате?
Известно, что чем больше площадь поверхности, тем больше она может поглощать или отдавать количества теплоты на резисторе.
Кроме того, существуют буквенные обозначения для российских и импортных устройств.
Для отечественных:
В – Маломощные от 0,125 до 0,25
Для импортных:
W — Маломощные от 0,125 до 0,25
V – Средний диапазон.
SW – Более 2
Важно! Существуют миниатюрные устройства, на корпусе которых невозможно нанести маркировку. Такие сопротивления окрашиваются в белый, желтый или красный цвет. Цвета в соответствии с диапазонами по возрастающей. В частности, это касается импортных изделий.
Как рассчитать мощность в схеме
Для схем также обязательны знания о силе тока и сопротивлении, без знания этих параметров расчет будет невозможен. Тепловые потери на резисторе формируются из квадрата силы тока, помноженного на сопротивление: P = I² * R (количество теплоты на резисторе формула). Актуальна только при расчетах готовой и известной схемы, во всех случаях предварительного расчета используется прямое значение силы тока, а не ее квадрат.
Величина указывается исключительно в Омах, если используются значения в кило- или мегаомах, то их необходимо округлять до классического значения в одну единицу сопротивления – Ом.
Схема с последовательным соединением элементов
Последовательное соединение означает тот факт, что через все элементы схемы проходит одно и то же значение силы тока. Это означает, что и рассеивание будет тождественным на всех резистантах. Для подсчета необходимо:
- Суммировать значения на всех участках, то есть: 200 Ом + 100 Ом + 51 Ом + 39 Ом = 390 Ом. Сила тока рассчитывается по закону: I = U/R. Алгебраически значение формируется в следующем виде: I = 100 В / 390 Ом = 0,256 А.
- Рассчитать параметр: P = 0,256² * 390 Ом = 25,549
Это ответ на вопрос о том, какая тепловая мощность будет выделяться на резисторе r1 в схеме.
Таким образом становится возможным подсчитать индивидуальное рассеивание на каждом участке, указанном в схеме.
Как подобрать резистор на замену
Для замены всегда подбирается точно такой же элемент. Допускается временное использование сопротивлений с параметром на 1 порядок выше, чем у перегоревшего или вышедшего из строя по другим причинам. Это основное условие замкнутого контура в цепи. Установить неисправный участок цепи – означает разомкнуть цепь.
Определить параметры можно приблизительно по маркировке и размерам.
Элементы для замены оснащены выводами с обоих концов – их паяют на плату. Рекомендуется не подрезать выводы, так как они тоже обладают дополнительным сопротивлением.
На резисторе внешней цепи аккумулятора выделяется тепловая мощность 10 Вт
Этот параметр и условие являются актуальными при последовательном подключении трех аккумуляторов. Если к концам подведена внешняя цепь с аккумулятором, то для каждого следующего аккумулятора значение будет увеличиваться в 2 раза. Но поскольку мощность зависит от напряжения через силу тока, то для третьего аккумулятора возрастание мощности составит значение в 25%. Тепловые потери составят 26,9Вт.
Используя сведения, которые были представлены в данной статье, можно самостоятельно и быстро подобрать необходимые элементы электроцепи в электроприборе для замены. Для этого в настоящее время существует множество магазинов электроники, которые удовлетворят запросы самых претенциозных клиентов.
Данную статью можно использовать в качестве конкретного руководства по выбору резисторов не только в бытовые электроприборы, но и в промышленные установки.
Мощность на резисторе в цепи переменного тока
По закону Джоуля-Ленца, мгновенное
значение тепловой мощности на участке
цепи определяется как произведение
силы тока на напряжение:
P = UI =U0cos
ω t* I0cos
ω t = I0U0cos
2ωt
Эта величина непрерывно изменяется. В
промышленной сети частота изменения
равна 50 Гц, то есть 50 раз в секунду
изменяется значение тепловой мощности.
Поэтому практического значения знание
мгновенной мощности не имеет.
Вычислим среднее значение мощности
за период колебаний:
<P> = <I0U0cos
2
ω t> = I0U0<cos
2
ω t>
<cos2ωt>
= ½
<P>
= 1/2I0U0
Введем определение:
Действующим значением силы тока (или
напряжения) называется сила такого
постоянного тока (или напряжения),
который, протекая по данной цепи, выделяет
в ней мощность, равную средней мощности
в цепи переменного тока за период
<P> = IДUД
Средняя мощность, выделяющаяся на
резисторе в цепи переменного тока за
период, равна произведению действующего
значения силы тока на действующее
значение напряжения.
Домашнее задание Повторить:
конденсатор, емкость конденсатора,
единицы измерения электроемкости,
энергия заряженного конденсатора,
последовательное и параллельное
соединение конденсаторов, энергия
электрического поля заряженного
конденсатора, закон Ома для участка
цепи.
Лекция 6 Конденсатор в цепи переменного тока
Включим конденсатор в цепь постоянного
тока. Некоторый заряд перетечет от
источника тока на обкладки конденсатора.
В цепи возникает кратковременный
импульс зарядного тока. Конденсатор
заряжается до напряжения источника,
после чего ток прекращается. Через
конденсатор постоянный ток течь не
может!
Р
процессы, происходящие при включении
конденсатора в цепь переменного тока
зарядный ток
.
Через диэлектрик, разделяющий обкладки
конденсатора, электрический ток
протекать, как и прежде, не может. Но в
результате периодически повторяющихся
процессов зарядки и разрядки конденсатора
в цепи появится переменный ток.
Если напряжение в цепи изменяется по
гармоническому закону,
U = U0cos ωt
т
заряд на обкладках конденсатора
изменяется
также по гармоническому закону
q=Cu = CU0cos ωt
и силу тока в цепи можно найти как
производную заряда
i = q/
i= -CU0
ω sin ωt
= CU0ω
cos(ωt+π/2),
i= I0ω
cos(ωt+π/2)
Амплитуда силы
тока I0
= CU0ω
Из полученной формулы видно, что в любой
момент времени
фаза тока больше фазы напряжения на
π/2.
В цепи переменного напряжение на
конденсаторе тока отстает по фазе от
тока на π/2, или
на четверть периода.
Емкостное сопротивление
Величину
называют емкостным сопротивлением.
Связь между амплитудными значениями
силы тока и напряжения формально
совпадает с законом Ома для участка
цепи
Такое же соотношение выполняется для
действующих значений силы тока и
напряжения.
Емкостное сопротивление конденсатора
зависит от частоты переменного
напряжения. С увеличением частоты
колебаний напряжения емкостное
сопротивление уменьшается, поэтому
амплитуда силы тока увеличивается прямо
пропорционально частоте I0
= CU0ω.
При уменьшении частоты амплитуда силы
тока уменьшается и при ω=0 обращается в
0. Отметим, что нулевая частота колебаний
означает, что в цепи протекает постоянный
ток.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Тепловая мощность, выделяемая на резисторе
Электрический ток, проходящий по проводнику, нагревает его. Это объясняется тем, что свободные электроны, перемещаясь под действием электрического поля, взаимодействуют с ионами или атомами вещества и передают им свою энергию. В результате работы электрического тока внутренняя энергия вещества увеличивается, повышается его температура. Нагретый проводник передает свою энергию окружающим телам. Если проводник не движется, то вся энергия электрического тока переходит во внутреннею энергию проводника. Работа тока определяется
(A = U*I*T)
Количество теплоты, выделяемое на резисторе, обозначим через Q Так как Q = A, то
(Q = U*I*R*t)
или используя закон Ома (U = I*R), получим
(Q = {I^2}Rt)
Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления и времени.
Эта формулировка называется законом Джоуля — Ленца
Содержание
- Как найти тепло на резисторе
- § 19. Закон Джоуля-Ленца. Энергетические превращения в электрической цепи
- Тепловая мощность на резисторе формула
- Как рассчитать мощность резистора?
- Как рассчитать мощность резистора?
- Тепловая мощность, выделяемая на резисторе
- Как определить тепловую мощность резистора
- Мощность резистора — что это такое, на что влияет
- Стандартный ряд мощностей резисторов и их обозначение на схемах
- Формула для расчета мощности тока в резисторе, как узнать сколько ватт
- Как рассчитать мощность рассеивания резистора
- Как определить по внешнему виду
- Определение мощности SMD-резистора по размерам
Как найти тепло на резисторе
§ 19. Закон Джоуля-Ленца. Энергетические превращения в электрической цепи
Для любого участка цепи, даже содержащего ЭДС, справедлив закон Джоуля – Ленца:
количество теплоты, выделяемое на участке цепи с сопротивлением $$ R$$ при прохождении постоянного тока $$ I$$ в течение времени $$ t$$, есть $$ W=^<2>Rt$$.
Отсюда мощность выделяемого тепла `P=W//t=I^2R`.
Пусть на участке `1-2` идёт постоянный ток $$ I$$, перенося за время $$ t$$ от т. `1` к т. `2` заряд $$ q=It$$.
Работой тока на участке `1-2` называется работа сил электростатического поля по перемещению $$ q$$ из т. `1` в т. `2:` $$ _<mathrm<Т>>=q(<varphi >_<1>—<varphi >_<2>)$$.
Работой источника с ЭДС $$ mathcal$$ при прохождении через него заряда $$ q$$ называется работа сторонних сил над зарядом `q:`
Если заряд переносится постоянным током $$ I$$, то $$ _<mathrm<ист>>=pm mathcalIt$$.
Когда заряд (ток) через источник идёт в направлении действия сторонних сил, то работа источника положительна (он отдаёт энергию). Аккумулятор в таком режиме разряжается. При обратном направлении тока работа источника отрицательна (он поглощает энергию). В этом режиме аккумулятор заряжается, запасая энергию. Мощность источника:
Источник
Тепловая мощность на резисторе формула
Как рассчитать мощность резистора?
У резистора есть довольно важный параметр, который целиком и полностью влияет на надёжность его работы. Этот параметр называется мощностью рассеивания. Он уже упоминался в статье о параметрах резистора.
Сама по себе мощность постоянного тока рассчитывается по простой формуле:
Как видим, мощность зависит от напряжения и тока. В реальной цепи через резистор протекает определённый ток. Поскольку резистор обладает сопротивлением, то под действием протекающего тока резистор нагревается. На нём выделяется какое-то количество тепла. Это и есть та мощность, которая рассеивается на резисторе.
Если в схему установить резистор меньшей мощности рассеивания, чем требуется, то резистор будет нагреваться и в результате сгорит. Поэтому, если в схеме нужно заменить резистор мощностью 0,5 Ватт, то ставим на 0,5 Ватт и более. Но никак не меньше !
Каждый резистор рассчитан на свою мощность. Стандартный ряд мощностей рассеивания резисторов состоит из значений:
Чем больше резистор по размерам, тем, как правило, на большую мощность рассеивания он рассчитан.
Допустим, у нас есть резистор с номинальным сопротивлением 100 Ом. Через него течёт ток 0,1 Ампер. На какую мощность должен быть рассчитан этот резистор?
Тут нам потребуется формула. Выглядит она так:
R(Ом) – сопротивление цепи (в данном случае резистора);
I(А) – ток, протекающий через резистор.
Все расчёты следует производить, строго соблюдая размерность. Так, если сопротивление резистора не 100 Ом, а 1 кОм, то в формулу нужно подставить значение в Омах, т.е. 1000 Ом (1 кОм = 1000 Ом). Тоже правило касается и других величин (тока, напряжения).
Рассчитаем мощность для нашего резистора:
Мы получили мощность 1 Ватт. Теперь небольшое отступление.
В реальную схему необходимо устанавливать резистор с мощностью в полтора – два раза выше рассчитанной.
Поэтому нам подойдёт резистор мощностью 2 Вт (см. стандартный ряд мощностей резисторов).
Также есть и другая формула для расчёта мощности. Она применяется в том случае, если неизвестен ток, который протекает через резистор.
Всё бы хорошо, но в жизни бывают случаи, когда применяется последовательное или параллельное соединение резисторов. Как рассчитать мощность рассеивания для каждого из резисторов в последовательной или параллельной цепи?
Допустим, нам требуется заменить резистор сопротивлением 100 Ом. Протекающий через него ток равен 0,1 Ампер. Следовательно, мощность этого резистора 1 Ватт.
Для его замены можно применить два соединённых последовательно резистора сопротивлением 20 Ом и 80 Ом. На какую мощность должны быть рассчитаны эти резисторы?
Для последовательной цепи действует одно правило. Через последовательно соединённые резисторы течёт один и тот же ток. Теперь применим формулу для расчёта мощности и получим, что мощность рассеивания резистора на 20 Ом должна быть равна 0,2 Вт, а резистора на 80 Ом — 0,8 Вт. Выбираем резисторы согласно стандартному ряду мощностей:
Как видим, если сопротивления резисторов будут разные, то и мощность на них будет выделяться разная.
Мощность, рассеивающаяся на резисторе, зависит в первую очередь от тока, который течёт через данный резистор. А ток зависит от сопротивления резистора. Поэтому, если вы соединяете последовательно резисторы разных номиналов, то и рассеивающаяся мощность распределиться между ними.
Это обстоятельство необходимо учитывать при самостоятельном конструировании электронных самоделок иначе при неправильном подборе резисторов может получиться так, что на одном резисторе выделиться больше мощности, чем на другом, и он будет работать в тяжёлом температурном режиме.
Чтобы не ломать голову и не рассчитывать мощность каждого в отдельности резистора, можно поступать так:
Мощность каждого резистора, входящего в составляемую нами цепь (параллельную или последовательную) должна быть равна мощности заменяемого резистора. Иными словами, если нам надо заменить резистор, мощностью 1 Вт, то каждый из резисторов для его замены должен иметь мощность не менее 1 Ватта. На практике это самое быстрое и эффективное решение.
Для параллельного соединения резисторов нужно учитывать, что через резистор с меньшим сопротивлением протекает больший ток. Следовательно, и мощности на нём будет рассеиваться больше.
Как рассчитать мощность резистора?
У резистора есть довольно важный параметр, который целиком и полностью влияет на надёжность его работы. Этот параметр называется мощностью рассеивания. Он уже упоминался в статье о параметрах резистора.
Сама по себе мощность постоянного тока рассчитывается по простой формуле:
Как видим, мощность зависит от напряжения и тока. В реальной цепи через резистор протекает определённый ток. Поскольку резистор обладает сопротивлением, то под действием протекающего тока резистор нагревается. На нём выделяется какое-то количество тепла. Это и есть та мощность, которая рассеивается на резисторе.
Если в схему установить резистор меньшей мощности рассеивания, чем требуется, то резистор будет нагреваться и в результате сгорит. Поэтому, если в схеме нужно заменить резистор мощностью 0,5 Ватт, то ставим на 0,5 Ватт и более. Но никак не меньше !
Каждый резистор рассчитан на свою мощность. Стандартный ряд мощностей рассеивания резисторов состоит из значений:
Чем больше резистор по размерам, тем, как правило, на большую мощность рассеивания он рассчитан.
Допустим, у нас есть резистор с номинальным сопротивлением 100 Ом. Через него течёт ток 0,1 Ампер. На какую мощность должен быть рассчитан этот резистор?
Тут нам потребуется формула. Выглядит она так:
R(Ом) – сопротивление цепи (в данном случае резистора);
I(А) – ток, протекающий через резистор.
Все расчёты следует производить, строго соблюдая размерность. Так, если сопротивление резистора не 100 Ом, а 1 кОм, то в формулу нужно подставить значение в Омах, т.е. 1000 Ом (1 кОм = 1000 Ом). Тоже правило касается и других величин (тока, напряжения).
Рассчитаем мощность для нашего резистора:
Мы получили мощность 1 Ватт. Теперь небольшое отступление.
В реальную схему необходимо устанавливать резистор с мощностью в полтора – два раза выше рассчитанной.
Поэтому нам подойдёт резистор мощностью 2 Вт (см. стандартный ряд мощностей резисторов).
Также есть и другая формула для расчёта мощности. Она применяется в том случае, если неизвестен ток, который протекает через резистор.
Всё бы хорошо, но в жизни бывают случаи, когда применяется последовательное или параллельное соединение резисторов. Как рассчитать мощность рассеивания для каждого из резисторов в последовательной или параллельной цепи?
Допустим, нам требуется заменить резистор сопротивлением 100 Ом. Протекающий через него ток равен 0,1 Ампер. Следовательно, мощность этого резистора 1 Ватт.
Для его замены можно применить два соединённых последовательно резистора сопротивлением 20 Ом и 80 Ом. На какую мощность должны быть рассчитаны эти резисторы?
Для последовательной цепи действует одно правило. Через последовательно соединённые резисторы течёт один и тот же ток. Теперь применим формулу для расчёта мощности и получим, что мощность рассеивания резистора на 20 Ом должна быть равна 0,2 Вт, а резистора на 80 Ом — 0,8 Вт. Выбираем резисторы согласно стандартному ряду мощностей:
Как видим, если сопротивления резисторов будут разные, то и мощность на них будет выделяться разная.
Мощность, рассеивающаяся на резисторе, зависит в первую очередь от тока, который течёт через данный резистор. А ток зависит от сопротивления резистора. Поэтому, если вы соединяете последовательно резисторы разных номиналов, то и рассеивающаяся мощность распределиться между ними.
Это обстоятельство необходимо учитывать при самостоятельном конструировании электронных самоделок иначе при неправильном подборе резисторов может получиться так, что на одном резисторе выделиться больше мощности, чем на другом, и он будет работать в тяжёлом температурном режиме.
Чтобы не ломать голову и не рассчитывать мощность каждого в отдельности резистора, можно поступать так:
Мощность каждого резистора, входящего в составляемую нами цепь (параллельную или последовательную) должна быть равна мощности заменяемого резистора. Иными словами, если нам надо заменить резистор, мощностью 1 Вт, то каждый из резисторов для его замены должен иметь мощность не менее 1 Ватта. На практике это самое быстрое и эффективное решение.
Для параллельного соединения резисторов нужно учитывать, что через резистор с меньшим сопротивлением протекает больший ток. Следовательно, и мощности на нём будет рассеиваться больше.
- Главная
- Обучение
- Предварительный просмотр
- Мероприятия / ВИШР
- Обучение
- Тренажер ЕГЭ
- Учебные пособия
- Игры
- 120 лет ТПУ. Викторина онлайн
- Университетские субботы
- Высшая инженерная школа России
Физика
3.2.9.1. Тепловая мощность, выделяемая на резисторе
Тепловая мощность, выделяемая на резисторе
Электрический ток, проходящий по проводнику, нагревает его. Это объясняется тем, что свободные электроны, перемещаясь под действием электрического поля, взаимодействуют с ионами или атомами вещества и передают им свою энергию. В результате работы электрического тока внутренняя энергия вещества увеличивается, повышается его температура. Нагретый проводник передает свою энергию окружающим телам. Если проводник не движется, то вся энергия электрического тока переходит во внутреннею энергию проводника. Работа тока определяется
Количество теплоты, выделяемое на резисторе, обозначим через Q Так как Q = A, то
или используя закон Ома (U = I*R) , получим
Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления и времени.
Эта формулировка называется законом Джоуля — Ленца
Источник
Как определить тепловую мощность резистора
Резисторы присутствуют в каждой электросхеме. Но в различных схемах течет разной величины ток. Не могут же одни и те же компоненты функционировать при 0,1 А и при 100 Ампер. Ведь при протекании тока сопротивление нагревается. Чем выше сила тока, тем интенсивнее нагрев. Значит, и резисторные компоненты должны быть на разную токовую величину. Отражает их возможность функционировать при различных токах такой параметр, как мощность.
Мощность резистора — что это такое, на что влияет
Рассеиваемая мощность резисторного элемента — это макс. ток, который может выдерживать сопротивление долгое время без ущерба для работоспособности.
То есть, этот параметр необходимо подбирать для каждой электросхемы отдельно. Мощность вычисляется с помощью следующей формулы: P = I * R.
Физически рассеиваемый параметр резисторного устройства — это то количество тепла, которое его корпус может «передать» и не сгореть. Мощность в первую очередь влияет на надёжность работы резисторного устройства.
Важно! Все резисторные компоненты, вне зависимости от установленных параметров, функционируют на основании закона Ома, это главный ключ благодаря которому определяется напряжение. Спад напряжения – это разница в показателях на входе и выходе. Внутри механизма протекающий ток меняется или ограничивается – электроны сталкиваются с неоднородной структурой материала проводниковой.
Стандартный ряд мощностей резисторов и их обозначение на схемах
Не забывайте, что резисторные компоненты одного номинала, могут иметь разную мощность. Все зависит от техники создания, материала корпуса. Ниже указан ряд мощностей и их официальное обозначение.
| Вт | Условное обозначение на электросхемах |
| мощность резисторного компонента 0,05 Вт | Как подписывается на схеме 0,05 В. |
| мощность элемента 0,125 Вт | мощность резистора 0,125 Ватт. |
| мощность 0,025 Вт | как на схеме выделяется элемент с мощностью 0,25 Вт |
| мощность 0,5 Вт | таким образом, на схеме выделяется резистор мощностью 0,5 Ватт. |
| мощность 1 Вт | мощность резистора 1 В. |
| мощность 2 Вт | мощность рассеивания резистора 2 Вт. |
| мощность резисторного элемента 5 Вт | так выделяется мощность 5 Вт |
Графическая кодировка мощностей резисторов на электросхеме — черточки и римские символы. Самое маленькое типовое значение 0,05 Ватт, максимальное — 25 Ватт, но есть и помощнее.
Как указывается мощность слабых деталей необходимо запомнить. Это косого типа линии на прямоугольниках, которыми выделяют сопротивления. При номиналах сопротивлений от 1 Ватта на схеме выставляются определенные римские символы: I, II, III, и так далее. Цифровые обозначения выделяют мощность резисторного компонента в ваттах. О том к ак определить сопротивление резистора по цвету читайте здесь.
Формула для расчета мощности тока в резисторе, как узнать сколько ватт
Мощность резистора формула:
Здесь, P(Вт) – показатели мощности;
Расчет выполнить несложно, как можно заметить, мощность зависит от напряжения и тока.
Если вы не любите формулы, можете попробовать воспользоваться мультиметром, он поможет определить, сколько потребляет резистор.
Как рассчитать мощность рассеивания резистора
Вот мы и узнали, что мощность тока в резисторе рассчитывается по формуле. В реальной цепочке(последовательной или параллельной) через резисторные элементы протекает ток. Поскольку резистор имеет сопротивление, то под влиянием проходящего тока резисторный компонент греется. На нём выделяется немного тепловой энергии. Это и есть та мощность, которая рассеивается на резисторном элементе.
Если в электросхему вмонтировать резистор с мощностью меньше, чем надо, то резисторный компонент в итоге сгорит из-за перегрева. Поэтому, если в схеме требуется заменить резисторное устройство мощностью 0,5 Вт, то устанавливает на 0,5 Ватт и больше.
Каждый резисторный компонент рассчитан на конкретные показатели мощности. Типовой ряд мощностей рассеивания резисторных компонент состоит из значений:
Чем крупнее резистор, тем, он мощнее.
К примеру, у нас есть резисторный элемент с сопротивлением 100 Ом. Через него течет ток 0,1 Ампер. Как вычислить его хар-ки мощности?
Тут потребуется сопротивление резистора формула:
R(Ом) – сопротивление цепочки (а точнее резистора);
Все расчёты необходимо выполнять, помня про размерность, даже связанные с площадью.
Определим показатели мощности для нашего резисторного компонента:
на выходе, получается мощность 1 Ватт.
Здесь подойдёт резисторный компонент мощностью 2 В.
Мощность резистора должна быть равна мощности заменяемого.
Как определить по внешнему виду
На принципиальной электросхеме выделена, необходимая мощность резисторного элемента — тут все ясно. Но как вычислить мощность по визуальному виду на плате для печати? В общем, чем огромнее корпус, тем больше он может рассеивать тепла.
На российских сопротивлениях рядом с цифрами ставят букву В и все. А в зарубежных указывают W. Но эти символы есть не всегда. В иностранных может выделяться V или SW перед цифрами. Еще в импортных может также красоваться буква B, а в российских МЛТ может быть пустота или буква W. Сложно что-то понять, конечно. Подробнее о буквенной маркировке резисторов, читайте тут.
Еще есть небольшие замкнутые резисторные устройства, на которых и номинал невозможно поместить. В зарубежных он нанесен цветовыми полосами. Как в таком случае вычислить мощность рассеивания, насколько важен цвет?
В старом ГОСТе была табличка соответствий габаритов и мощностей. Отечественные резисторные элементы по-прежнему изготавливают в соответствии с ней. Импортные, кстати, тоже, но они по габаритам уступают нашим. Однако и с ними можно разобраться.
Если не можете решить, к какой группе причислить определенный экземпляр, лучше считать что он слабый в плане мощности. Тогда компонент точно не сгорит.
Важно! Есть резисторные элементы крупные с малой рассеивающей способностью и наоборот. Но в подобных случаях, обозначают этот параметр в маркировке, как и информацию о соединении.
Определение мощности SMD-резистора по размерам
Так же, как и иные детали, SMD-резисторы рассчитаны на конкретную мощность рассеивания. Но, как её вычислить? Мощность стандартных чип-резисторов, которых сейчас много, можно определить исходя из их размерных характеристик.
Ниже, будет показана табличка №1, в которой выделено соответствие типоразмера СМД-резисторного компонента и его мощности. Также там выделен типовой размер резисторов в дюймовой системе маркировки, а реальные размерные хар-ки указаны в мм.
Так сделали, потому что самой популярной считается система маркировки типоразмера чип-резисторных компонентов в дюймах. Её все эксплуатируют: изготовители, люди занимающиеся поставками и магазины. А для того, чтобы вычислить типовой размер и мощность выделяемую на резисторе, вы должны определить длину и ширину с помощью линейки.
Таблица №1.
| Типовой размер (дюймы) | Параметры мощности (PR at 70°C) | Мощность, Ватт. | Длина (L) /Ширина (W), мм. |
| 0075 | 1/50W | 0,02 Ватт | 0,3/0,15 |
| 01005 | 1/32W | 0,03 Ватт | 0,4/0,2 |
| 0201 | 1/20W | 0,05 Ватт | 0,6/0,3 |
| 0402 | 1/16W, 1/8W | 0,063 Вт; 0,125 Ватт | 1,0/0,5 |
| 0603 | 1/10W, 1/5W | 0,1 Вт; 0,2 Ватт | 1,6/0,8 |
| 0805 | 1/8W, 1/4W | 0,125 Вт; 0,25 В | 2,0/1,25 |
| 1206 | 1/4W, 1/2W | 0,25 В; 0,5 В | 3,2/1,6 |
| 1210 | 1/2W | 0,5 Ватт | 3,2/2,5 |
| 1218 | 1W; 1,5W | 1 Вт; 1,5 Ватт | 3,2/4,8 |
| 1812 | 1/2W, 3/4W | 0,5 Вт; 0,75 Ватт | 4,5/3,2 |
| 2010 | 3/4W | 0,75 Ватт | 5,0/2,5 |
| 2512 | 1W; 1,5W; 2W | 1 Вт; 1,5 Вт; 2 Ватт | 6,4/3,2 |
Необходимо выделить тот факт, что в колонке (Мощность, PR 70°C) для некоторых типовых размеров указано много значений мощностей. Дело в том, что компании занимающиеся производством, создают разные модели СМД-резисторов. В одних модификациях мощность компонентов для типового размера 0,5 Ватт, а в иной 0,25 Ватт.
К примеру, чип-резисторные элементы серии CRM компании Bourns ® рассчитаны на макс. параметры мощности: CRM0805 (0,25W), CRM1206 (0,5W), CRM2010 (1W). Эксплуатируются такие в импульсных питательных источниках в виде токовых сенсоров, токоограничительных резисторов, и так далее.
Об этом необходимо помнить, если вы будете эксплуатировать электрический резистор, мощность которого была установлена исходя из типовых размеров. Еще придется остановиться на минимальном значении мощности, взятом из таблички №1. Увеличить нельзя.
Данные в табличке №1 можно отнести лишь к стандартным SMD-резисторам.
Чаще всего, это чип резисторные компоненты на базе толстенькой плёнки. Они недорогие и самые популярные.
Уже давно известно, что есть немало специальных SMD-резисторов, которые выделяются своими фишками. К таким можно причислить элементы, которые функционируют при высоких температурных нагрузках (до 230°C), в агрессивных условиях среды, миллиомные чип резисторы, СМД резисторы-перемычки.
Их хар-ки, в том числе и мощность рассеивания, может быть отличной от значений, которые указаны в табличке №1 и считаются типовыми для обычных СМД-резисторов, количество которых в электронном графическом документе бывает огромным.
Источник
При упорядоченном движении заряженных частиц в проводнике электрическое поле совершает работу. Ее принято называть работой тока.
Рассмотрим произвольный участок цепи. Это может быть однородный проводник, к примеру, обмотка электродвигателя или нить лампы накаливания. Пусть за время ∆t через поперечное сечение проводника проходит заряд ∆q. Тогда электрическое поле совершит работу:
A=ΔqU
Но сила тока равна:
I=ΔqΔt
Выразим заряд:
Δq=IΔt
Тогда работа тока равна:
A=IUΔt
Работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого совершалась работа.
Выражая через закон Ома силу тока и напряжение, получим следующие формулы для вычисления работы тока:
A=I2RΔt=U2RΔt
Работа тока измеряется в Джоулях (Дж).
Пример №1. Определите работу тока, совершенную за 10 секунд на участке цепи напряжением 200В и силой тока 16 А.
A=IUΔt=16·220·10=35200 (Дж)=35,2 (кДж)
Закон Джоуля-Ленца
В случае, когда на участке цепи не совершается механическая работа, и ток не производит химических действий, происходит только нагревание проводника. Нагретый проводник отдает теплоту окружающим телам.
Закон, определяющий количество теплоты, которое выделяет проводник с током в окружающую среду, был впервые установлен экспериментально английским ученым Д. Джоулем (1818—1889) и русским Э.Х. Ленцем (1804—1865). Закон Джоуля—Ленца сформулирован следующим образом:
Закон Джоуля—Ленца
Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику.
Q=I2RΔt
Количество теплоты измеряется в Джоулях (Дж).
Пример №2. Определить, какое количество теплоты было выделено за 2 минуты проводником при напряжении 12 В и сопротивлении 2 Ом.
Используем закон Ома и закон Джоуля—Ленца:
Q=I2RΔt=(UR)2Δt=U2RΔt=1222=72 (Дж)
Мощность тока
Любой электрический прибор (лампа, электродвигатель и пр.) рассчитан на потребление определенной энергии в единицу времени. Поэтому наряду с работой тока очень важное значение имеет понятие мощности тока.
Определение
Мощность тока — это работа, производимая за 1 секунду. Обозначается как P. Единица измерения — Ватт (Вт).
Численно мощность тока равна отношению работы тока за время ∆t к этому интервалу времени:
P=AΔt
Это выражение для мощности можно переписать в нескольких эквивалентных формах, если использовать закон Ома для участка цепи:
P=IU=I2R=U2R
Пример №3. При силе тока в электрической цепи 0,3 А сопротивление лампы равно 10 Ом. Определите мощность электрического тока, выделяющуюся на нити лампы.
P=I2R=0,32·10=0,9 (Вт)
Выразив силу тока через заряд, прошедший за единицу времени, получим:
P=qUt
Мощность тока равна мощности на внешней цепи. Ее также называют мощностью на нагрузке, полезной мощностью или тепловой мощностью. Ее можно выразить через ЭДС:
P=(εR+r)2R
Мощность тока на внешней цепи будет максимальная, если сопротивление внешней цепи равно внутреннему сопротивлению: R = r.
Pmax=(εr+r)2r=ε24r
Мощность тока внутренней цепи:
Pвнутр=I2r=(εR+r)2r
Полная мощность:
Pполн=I2(R+r)=ε2R+r
Пример №4. ЭДС постоянного тока ε = 2 В, а его внутреннее сопротивление r = 1 Ом. Мощность тока в резисторе, подключенном к источнику, P0 = 0,75 Вт. Чему равно минимальное значение силы тока в цепи?
Используем формулу для нахождения полезной мощности:
P=(εR+r)2R
Применим закон Ома для полной цепи:
I=εR+r
Выразим сопротивление внешней цепи:
R=εI−r
Отсюда:
P=(εεI−r+r)2(εI−r)=I2(εI−r)=Iε−rI2
Так как внутреннее сопротивление равно единице, получаем квадратное уравнение следующего вида:
rI2−Iε+P=0
I2−1I+0,75=0
Решив это уравнение, получим два корня: I = 0,5 и I = 1,5 А. Следовательно, наименьшая сила тока равна 0,5 А.
Подсказки к задачам
| Объем проводника цилиндрической формы |
V=Sl |
| Масса проводника цилиндрической формы |
m=ρV=ρSl |
| Количество теплоты и изменение температуры |
Q=cmΔT |
Конденсатор в цепи постоянного тока
Постоянный ток через конденсатор не идет, но заряд на нем накапливается, и напряжение между обкладками поддерживается. Напряжение на конденсаторе такое же, как на параллельном ему участке цепи.
Ток не проходит через те резисторы, что соединены с конденсатором последовательно. При расчете электрической цепи их сопротивления не учитывают.
Подсказки к задачам
| Электроемкость, заряд и напряжение |
C=qU |
| Напряженность и напряжение |
E=Ud |
| Энергия конденсатора |
W=q22C=CU22 |
| Количество теплоты |
Q=ΔW |
Пример №5. К источнику тока с ЭДС ε = 9 В и внутренним сопротивлением r = 1 Ом подключили параллельно соединенные резистор с сопротивлением R = 8 Ом и плоский конденсатор, расстояние между пластинами которого d = 0,002 м. Какова напряженность электрического поля между пластинами конденсатора?
Напряжение на конденсаторе равно напряжению на резисторе, так как он подключен к нему последовательно. Чтобы найти это напряжение, сначала выразим силу тока на этом резисторе:
I=εR+r
Применим закон Ома:
I=UR
Приравняем правые части выражений и получим:
εR+r=UR
Отсюда напряжение на конденсаторе равно:
U=εRR+r
Напряженность электрического поля равна:
E=Ud=εRd(R+r)=9·80,002(8+1)=720,018=4000 (Вм)
Задание EF17564
Ответ:
а) 5 Дж
б) 4 Дж
в) 3 Дж
г) 1 Дж
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу для нахождения количества теплоты, выделенной внутри источника тока.
3.Выполнить решение в общем виде.
4.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• ЭДС источника тока: ε = 3 В.
• Внутреннее сопротивление источника тока: r = 1 Ом.
• Сила тока в цепи: I = 2 А.
• Напряжение на внешней цепи: U = 5 В.
Количество теплоты, выделенной внутри источника тока, равно:
Q=I2rt=22·1·1=4 (Дж)
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17573
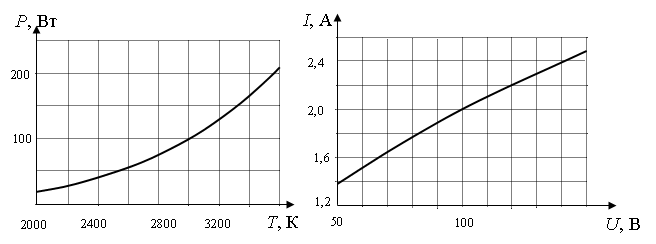
При нагревании спирали лампы накаливания протекающим по ней электрическим током основная часть подводимой энергии теряется в виде теплового излучения. На рисунке изображены графики зависимости мощности тепловых потерь лампы от температуры спирали P=P(T) и силы тока от приложенного напряжения I=I(U). При помощи этих графиков определите примерную температуру спирали лампы при силе тока I=2 A.
Ответ:
Алгоритм решения
1.Записать исходные данные.
2.С помощью графика зависимости силы тока от напряжения вычислить мощность.
3.С помощью графика зависимости мощности от температуры спирали определить ее температуру.
Решение
Нас интересует сила тока, равная 2 А. По графику зависимости силы тока от напряжения этому значение соответствует U = 100 В. Мощность определяется формулой:
P=IU=2·100=200 (Вт)
Этой мощности соответствует температура, равная около 3600 К.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17608
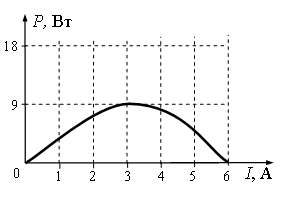
Какое из утверждений соответствует результатам опыта?
А. При коротком замыкании в цепи сила тока будет равна 6 А.
Б. При силе тока в цепи 3 А на реостате выделяется минимальная мощность.
Ответ:
а) только А
б) только Б
в) и А, и Б
г) ни А, ни Б
Алгоритм решения
- Проверить истинность каждого из утверждений.
- Выбрать верный ответ.
Решение
Согласно первому утверждению, при коротком замыкании в цепи сила тока будет равна 6 А. Это действительно так, потому что при этом значении силы тока мощность равна нулю. А это значит, что сопротивление на внешней цепи было нулевым.
Согласно второму утверждению, при силе тока в цепи 3 А на реостате выделяется минимальная мощность. Это не так. На графике этой силе тока соответствует максимальная мощность.
Верно только первое утверждение «А».
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 8.3k