17 авг. 2022 г.
читать 2 мин
Одновыборочный t-критерий используется для проверки того, равно ли среднее значение совокупности некоторому значению.
В этом руководстве объясняется, как провести один образец t-критерия в Excel.
Как провести одновыборочный t-тест в Excel
Предположим, ботаник хочет знать, равна ли средняя высота определенного вида растения 15 дюймам. Она собирает случайную выборку из 12 растений и записывает их высоту в дюймах.
На следующем изображении показана высота (в дюймах) каждого растения в образце:
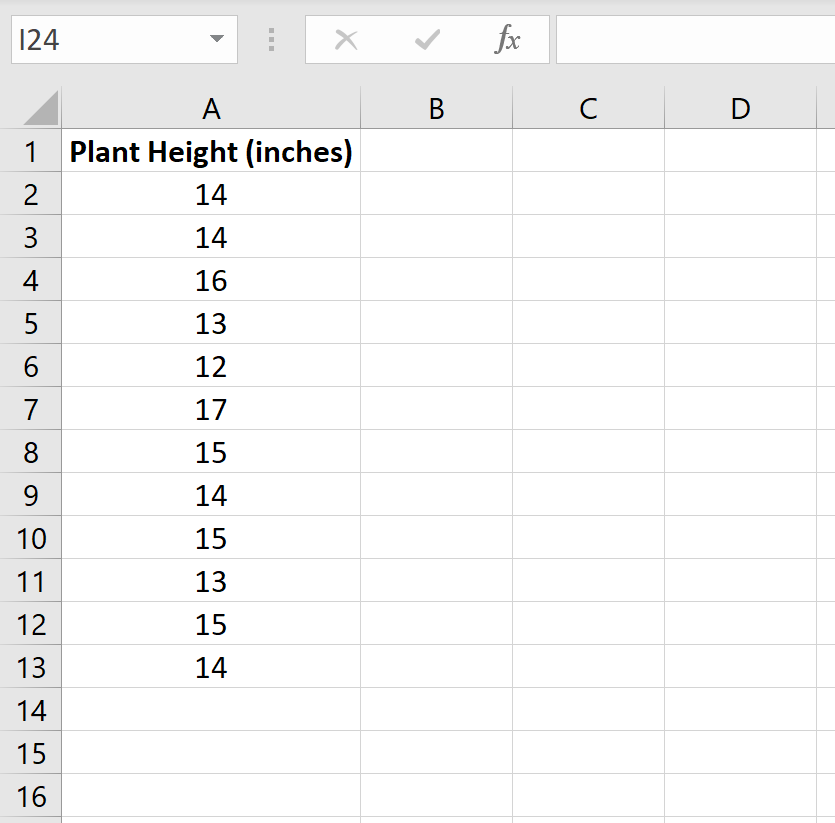
Мы можем использовать следующие шаги, чтобы провести t-тест для одной выборки, чтобы определить, действительно ли средняя высота для этого вида растений равна 15 дюймам.
Шаг 1: Найдите размер выборки, среднее значение выборки и стандартное отклонение выборки.
Во-первых, нам нужно найти размер выборки, среднее значение выборки и стандартное отклонение выборки, которые будут использоваться для проведения одновыборочного t-теста.
На следующем изображении показаны формулы, которые мы можем использовать для расчета этих значений:
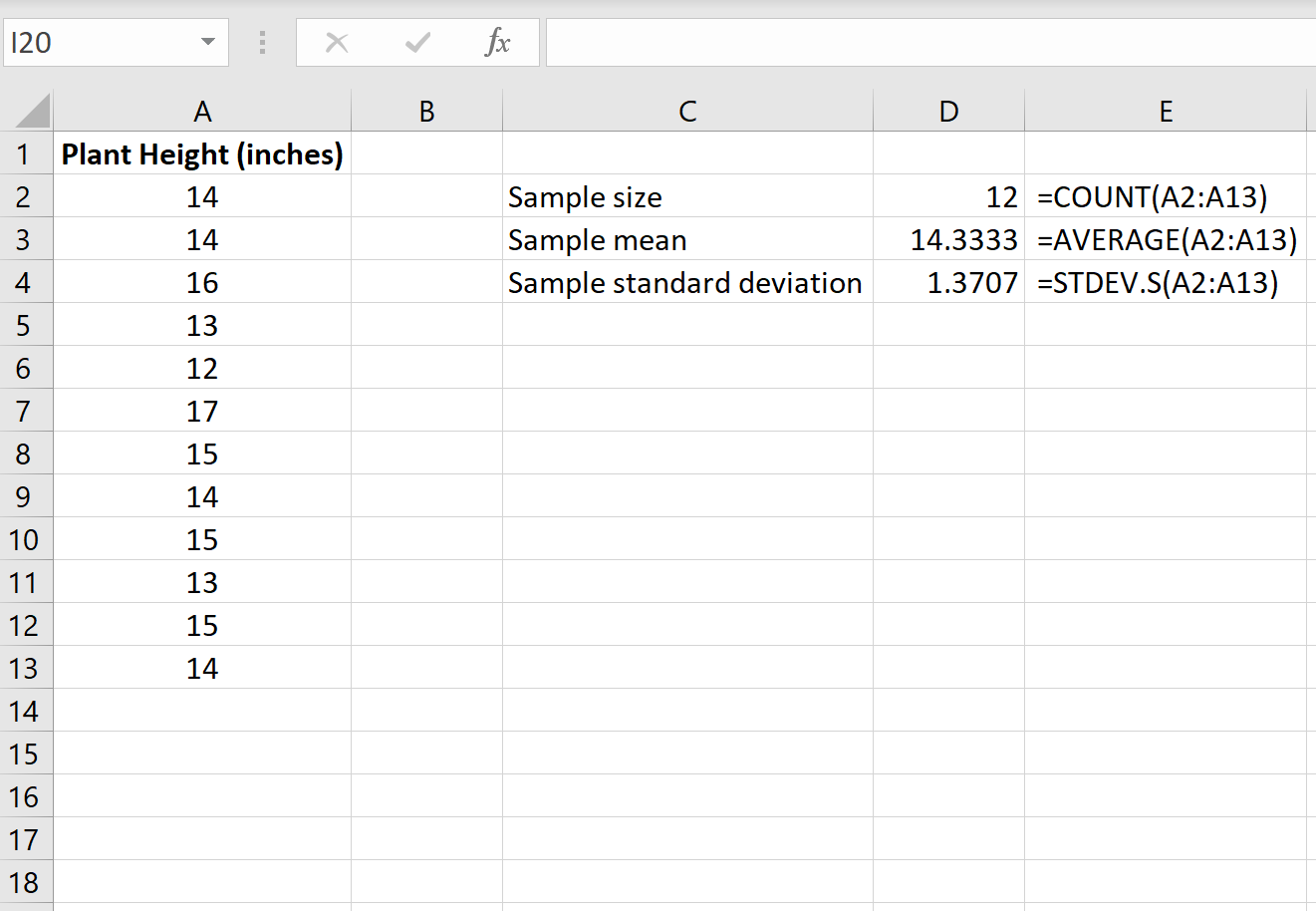
Шаг 2: Рассчитайте тестовую статистику t .
Далее мы рассчитаем тестовую статистику t по следующей формуле:
т = х – µ / (с / √ п )
куда:
x = выборочное среднее
µ = предполагаемое среднее значение населения
s = стандартное отклонение выборки
n = размер выборки
На следующем изображении показано, как рассчитать t в Excel:
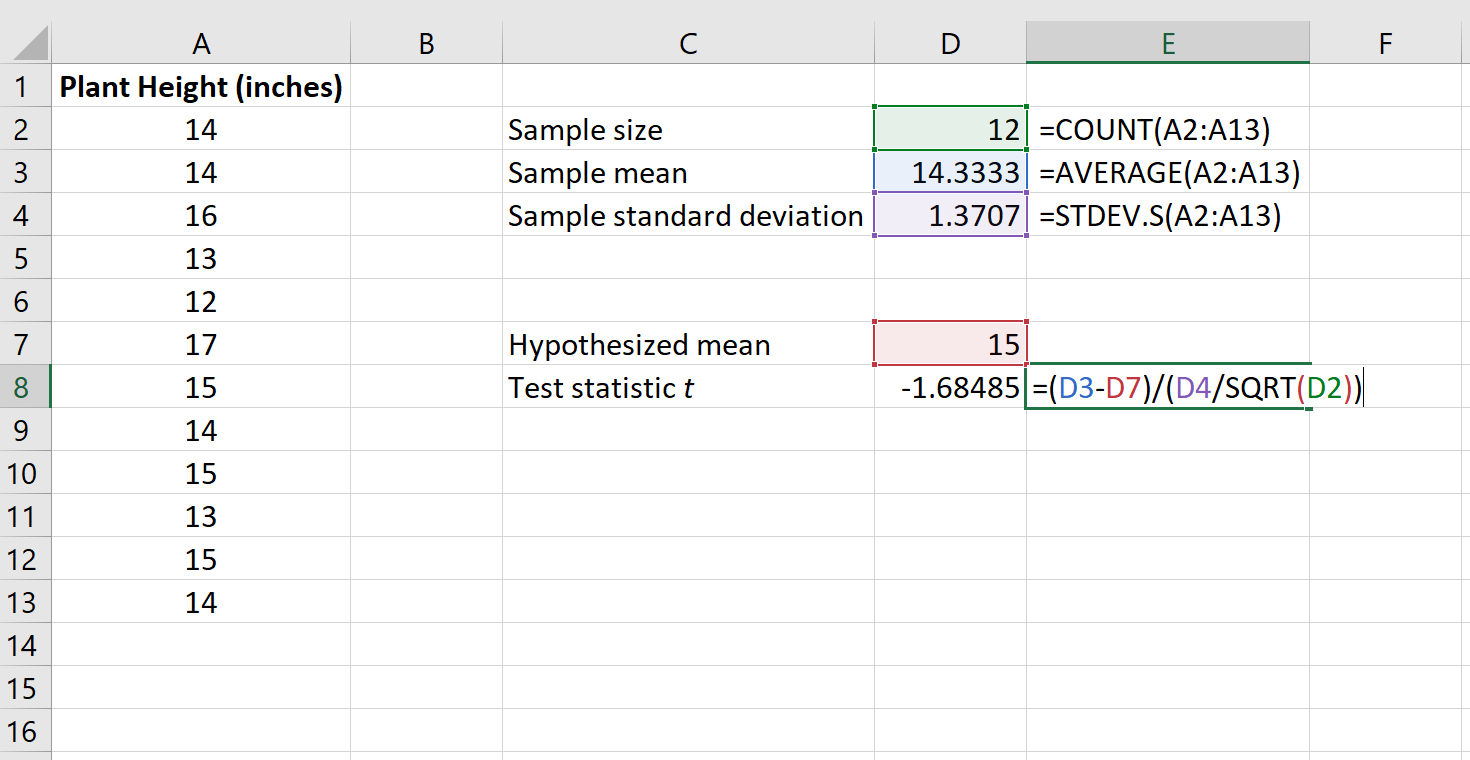
Тестовая статистика t оказывается равной -1,68485 .
Шаг 3: Рассчитайте p-значение тестовой статистики.
Затем нам нужно рассчитать значение p, связанное со статистикой теста, с помощью следующей функции в Excel:
=T.РАСП.2T(ABS(x), степень_свободы)
куда:
x = тестовая статистика t
deg_freedom = степени свободы для теста, которые рассчитываются как n-1
Технические примечания:
Функция T.DIST.2T() возвращает p-значение для двустороннего t-критерия. Если вместо этого вы проводите левосторонний t-критерий или правосторонний t-критерий, вы должны вместо этого использовать функции T.DIST() или T.DIST.RT() соответственно.
На следующем изображении показано, как рассчитать p-значение для нашей тестовой статистики:
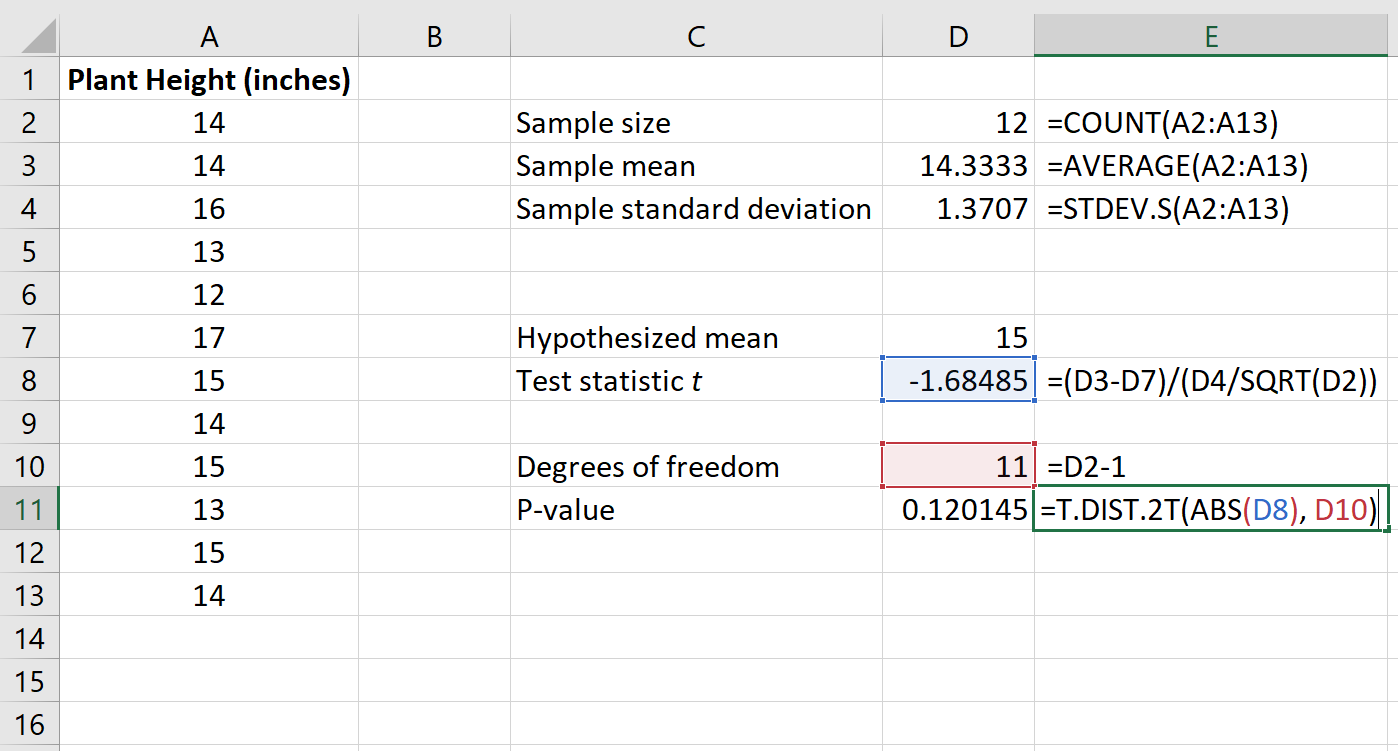
Значение p оказывается равным 0,120145 .
Шаг 4: Интерпретируйте результаты.
Две гипотезы для этого конкретного t-критерия с одной выборкой следующие:
H 0 : µ = 15 (средняя высота этого вида растений составляет 15 дюймов)
H A : µ ≠15 (средняя высота не 15 дюймов)
Поскольку p-значение нашего теста (0,120145) больше, чем альфа = 0,05, мы не можем отвергнуть нулевую гипотезу теста.
У нас нет достаточных доказательств, чтобы сказать, что средняя высота этого конкретного вида растений отличается от 15 дюймов.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные типы t-тестов в Excel.
Как провести двухвыборочный t-тест в Excel
Как провести t-тест для парных выборок в Excel
Предыдущий пост см. здесь.
Проверка статистических гипотез
Для статистиков и исследователей данных проверка статистической гипотезы представляет собой формальную процедуру. Стандартный подход к проверке статистической гипотезы подразумевает определение области исследования, принятие решения в отношении того, какие переменные необходимы для измерения предмета изучения, и затем выдвижение двух конкурирующих гипотез. Во избежание рассмотрения только тех данных, которые подтверждают наши субъективные оценки, исследователи четко констатируют свою гипотезу заранее. Затем, основываясь на данных, они применяют выборочные статистики с целью подтвердить либо отклонить эту гипотезу.
Проверка статистической гипотезы подразумевает использование тестовой статистики, т.е. выборочной величины, как функции от результатов наблюдений. Тестовая статистика (test statistic) – это вычисленная из выборочных данных величина, которая используется для оценивания прочности данных, подтверждающих нулевую статистическую гипотезу и служит для выявления меры расхождения между эмпирическими и гипотетическими значениями. Конкретные методы проверки называются тестами, например, z-тест, t-тест (соответственно z-тест Фишера, t-тест Студента) и т.д. в зависимости от применяемых в них тестовых статистик.
Примечание. В отечественной статистической науке используется «туманный» термин «статистика критерия». Туманный потому здесь мы снова наблюдаем мягкую подмену: вместо теста возникает критерий. Если уж на то пошло, то критерий – это принцип или правило. Например, выполняя z-тест, t-тест и т.д., мы соответственно используем z-статистику, t-статистику и т.д. в правиле отклонения гипотезы. Это хорошо резюмируется следующей ниже таблицей:
|
Тестирование гипотезы |
Тестовая статистика |
Правило отклонения гипотезы |
|
z-тесты |
z-статистика |
Если тестовая статистика ≥ z или ≤ -z, то отклонить нулевую гипотезу H0. |
|
t-тесты |
t-статистика |
Если тестовая статистика ≥ t или ≤ -t, то отклонить нулевую гипотезу H0. |
|
Анализ дисперсии (ANOVA) |
F-статистика |
Если тестовая статистика ≥ F, то отклонить нулевую гипотезу H0. |
|
Тесты хи-квадрат |
Статистика хи-квадрат |
Если тестовая статистика ≥ χ, то отклонить нулевую гипотезу H0. |
Для того, чтобы помочь сохранить поток посетителей веб-сайта, дизайнеры приступают к работе над вариантом веб-сайта с использованием всех новейших методов по поддержанию внимания аудитории. Мы хотели бы удостовериться, что наши усилия не напрасны, и поэтому стараемся увеличить время пребывания посетителей на обновленном веб-сайте.
Отсюда главный вопрос нашего исследования состоит в том, «приводит ли обновленный вид веб-сайта к увеличению времени пребывания на нем посетителей»? Мы принимаем решение проверить его относительно среднего значения времени пребывания. Теперь, мы должны изложить две наши гипотезы. По традиции считается, что изучаемые данные не содержат того, что исследователь ищет. Таким образом, консервативное мнение заключается в том, что данные не покажут ничего необычного. Все это называется нулевой гипотезой и обычно обозначается как H0.
При тестировании статистической гипотезы исходят из того, что нулевая гипотеза является истинной до тех пор, пока вес представленных данных, подтверждающих обратное, не сделает ее неправдоподобной. Этот подход к поиску доказательств «в обратную сторону» частично вытекает из простого психологического факта, что, когда люди пускаются на поиски чего-либо, они, как правило, это находят.
Затем исследователь формулирует альтернативную гипотезу, обозначаемую как H1. Она может попросту заключаться в том, что популяционное среднее отличается от базового уровня. Или же, что популяционное среднее больше или меньше базового уровня, либо больше или меньше на некоторую указанную величину. Мы хотели бы проверить, не увеличивает ли обновленный дизайн веб-сайта время пребывания, и поэтому нашей нулевой и альтернативной гипотезами будут следующие:
-
H0: Время пребывания для обновленного веб-сайта не отличается от времени пребывания для существующего веб-сайта
-
H1: Время пребывания для обновленного веб-сайта больше по сравнению с временем пребывания для существующего веб-сайта
Наше консервативное допущение состоит в том, что обновленный веб-сайт никак не влияет на время пребывания посетителей на веб-сайте. Нулевая гипотеза не обязательно должна быть «нулевой» (т.е. эффект отсутствует), но в данном случае, у нас нет никакого разумного оправдания, чтобы считать иначе. Если выборочные данные не поддержат нулевую гипотезу (т.е. если данные расходятся с ее допущением на слишком большую величину, чтобы носить случайный характер), то мы отклоним нулевую гипотезу и предложим альтернативную в качестве наилучшего альтернативного объяснения.
Указав нулевую и альтернативную гипотезы, мы должны установить уровень значимости, на котором мы ищем эффект.
Статистическая значимость
Проверка статистической значимости изначально разрабатывалась независимо от проверки статистических гипотез, однако сегодня оба подхода очень часто используются во взаимодействии друг с другом. Задача проверки статистической значимости состоит в том, чтобы установить порог, за пределами которого мы решаем, что наблюдаемые данные больше не поддерживают нулевую гипотезу.
Следовательно, существует два риска:
-
Мы можем принять расхождение как значимое, когда на самом деле оно возникло случайным образом
-
Мы можем приписать расхождение случайности, когда на самом деле оно показывает истинное расхождение с популяцией
Эти две возможности обозначаются соответственно, как ошибки 1-го и 2-го рода:
|
H0 ложная |
H0 истинная |
|
|
Отклонить H0 |
Истинноотрицательный исход |
Ошибка 1-го рода (ложноположительный исход) |
|
Принять H0 |
Ошибка 2-го рода (ложноотрицательный исход) |
Истинноположительный исход |
Чем больше мы уменьшаем риск совершения ошибок 1-го рода, тем больше мы увеличиваем риск совершения ошибок 2-го рода. Другими словами, с чем большей уверенностью мы хотим не заявлять о наличии расхождения, когда его нет, тем большее расхождение между выборками нам потребуется, чтобы заявить о статистической значимости. Эта ситуация увеличивает вероятность того, что мы проигнорируем подлинное расхождение, когда мы с ним столкнемся.
В статистической науке обычно используются два порога значимости. Это уровни в 5% и 1%. Расхождение в 5% обычно называют значимым, а расхождение в 1% — крайне значимым. В формулах этот порог часто обозначается греческой буквой α (альфа) и называется уровнем значимости. Поскольку, отсутствие эффекта по результатам эксперимента может рассматриваться как неуспех (эксперимента либо обновленного веб-сайта, как в нашем случае), то может возникнуть желание корректировать уровень значимости до тех пор, пока эффект не будет найден. По этой причине классический подход к проверке статистической значимости требует, чтобы мы устанавливали уровень значимости до того, как обратимся к нашим данным. Часто выбирается уровень в 5%, и поэтому мы на нем и остановимся.
Проверка обновленного дизайна веб-сайта
Веб-команда в AcmeContent была поглощена работой, конструируя обновленный веб-сайт, который будет стимулировать посетителей оставаться на нем в течение более длительного времени. Она употребила все новейшие методы и, в результате мы вполне уверены, что веб-сайт покажет заметное улучшение показателя времени пребывания.
Вместо того, чтобы запустить его для всех пользователей сразу, в AcmeContent хотели бы сначала проверить веб-сайт на небольшой выборке посетителей. Мы познакомили веб-команду с понятием искаженности выборки, и в результате там решили в течение одного дня перенаправлять случайные 5% трафика на обновленный веб-сайт. Результат с дневным трафиком был нам предоставлен одним текстовым файлом. Каждая строка показывает время пребывания посетителей. При этом, если посетитель пользовался исходным дизайном, ему присваивалось значение “0”, и если он пользовался обновленным (и надеемся, улучшенным) дизайном, то ему присваивалось значение “1”.
Выполнение z-теста
Ранее при тестировании с интервалами уверенности мы располагали лишь одним популяционным средним, с которым и выполнялось сравнение.
При тестировании нулевой гипотезы с помощью z-теста мы имеем возможность сравнивать две выборки. Посетители, которые видели обновленный веб-сайт, отбирались случайно, и данные для обеих групп были собраны в тот же день, чтобы исключить другие факторы с временной зависимостью.
Поскольку в нашем распоряжении имеется две выборки, то и стандартных ошибок у нас тоже две. Z-тест выполняется относительно объединенной стандартной ошибки, т.е. квадратного корня суммы дисперсий (вариансов), деленных на размеры выборок. Она будет такой же, что и результат, который мы получим, если взять стандартную ошибку обеих выборок вместе:
Здесь σ2a — это дисперсия выборки a, σ2b — дисперсия выборки b и соответственно na и nb — размеры выборок a и b. На Python объединенная стандартная ошибка вычисляется следующим образом:
def pooled_standard_error(a, b, unbias=False):
'''Объединенная стандартная ошибка'''
std1 = a.std(ddof=0) if unbias==False else a.std()
std2 = b.std(ddof=0) if unbias==False else b.std()
x = std1 ** 2 / a.count()
y = std2 ** 2 / b.count()
return sp.sqrt(x + y)С целью выявления того, является ли видимое нами расхождение неожиданно большим, можно взять наблюдавшиеся расхождения между средними значениями на объединенной стандартной ошибке. Эту статистическую величину принято обозначать переменной z:
Используя функции pooled_standard_error, которая вычисляет объединенную стандартную ошибку, z-статистику можно получить следующим образом:
def z_stat(a, b, unbias=False):
return (a.mean() - b.mean()) / pooled_standard_error(a, b, unbias)Соотношение z объясняет, насколько средние значения отличаются относительно величины, которую мы ожидаем при заданной стандартной ошибке. Следовательно, z-статистика сообщает нам о том, на какое количество стандартных ошибок расходятся средние значения. Поскольку стандартная ошибка имеет нормальное распределение вероятностей, мы можем связать это расхождение с вероятностью, отыскав z-статистику в нормальной ИФР:
def z_test(a, b):
return stats.norm.cdf([ z_stat(a, b) ])В следующем ниже примере z-тест используется для сравнения результативность двух веб-сайтов. Это делается путем группировки строк по номеру веб-сайта, в результате чего возвращается коллекция, в которой конкретному веб-сайту соответствует набор строк. Мы вызываем groupby('site')['dwell-time'] для конвертирования набора строк в набор значений времени пребывания. Затем вызываем функцию get_group с номером группы, соответствующей номеру веб-сайта:
def ex_2_14():
'''Сравнение результативности двух вариантов
дизайна веб-сайта на основе z-теста'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(1)
print('a n: ', a.count())
print('b n: ', b.count())
print('z-статистика:', z_stat(a, b))
print('p-значение: ', z_test(a, b))a n: 284
b n: 16
z-статистика: -1.6467438180091214
p-значение: [0.04980536]Установление уровня значимости в размере 5% во многом аналогично установлению интервала уверенности шириной 95%. В сущности, мы надеемся убедиться, что наблюдавшееся расхождение попадает за пределы 95%-го интервала уверенности. Если это так, то мы можем утверждать, что нашли результат с 5%-ым уровнем значимости.
P-значение — это вероятность совершения ошибки 1-го рода в результате неправильного отклонения нулевой гипотезы, которая в действительности является истинной. Чем меньше p-значение, тем больше определенность в том, что нулевая гипотеза является ложной, и что мы нашли подлинный эффект.
Этот пример возвращает значение 0.0498, или 4.98%. Поскольку оно немногим меньше нашего 5% порога значимости, мы можем утверждать, что нашли нечто значимое.
Приведем еще раз нулевую и альтернативную гипотезы:
-
H0: Время пребывания на обновленном веб-сайте не отличается от времени пребывания на существующем веб-сайте
-
H1: Время пребывания на обновленном веб-сайте превышает время пребывания на существующем веб-сайте.
Наша альтернативная гипотеза состоит в том, что время пребывания на обновленном веб-сайте больше.
Мы готовы заявить о статистической значимости, и что время пребывания на обновленном веб-сайте больше по сравнению с существующим веб-сайтом, но тут есть одна трудность — чем меньше размер выборки, тем больше неопределенность в том, что выборочное стандартное отклонение совпадет с популяционным. Как показано в результатах предыдущего примера, наша выборка из обновленного веб-сайта содержит всего 16 посетителей. Столь малые выборки делают невалидным допущение о том, что стандартная ошибка нормально распределена.
К счастью, существует тест и связанное с ним распределение, которое моделирует увеличенную неопределенность стандартных ошибок для выборок меньших размеров.
t-распределение Студента
Популяризатором t-распределения был химик, работавший на пивоварню Гиннес в Ирландии, Уилльям Госсетт, который включил его в свой анализ темного пива Стаут.
В 1908 Уильям Госсет опубликовал статью об этой проверке в журнале Биометрика, но при этом по распоряжению своего работодателя, который рассматривал использованную Госсеттом статистику как коммерческую тайну, был вынужден использовать псевдоним. Госсет выбрал псевдоним «Студент».
В то время как нормальное распределение полностью описывается двумя параметрами — средним значением и стандартным отклонением, t-распределение описывается лишь одним параметром, так называемыми степенями свободы. Чем больше степеней свободы, тем больше t-распределение похоже на нормальное распределение с нулевым средним и стандартным отклонением, равным 1. По мере уменьшения степеней свободы, это распределение становится более широким с более толстыми чем у нормального распределения, хвостами.
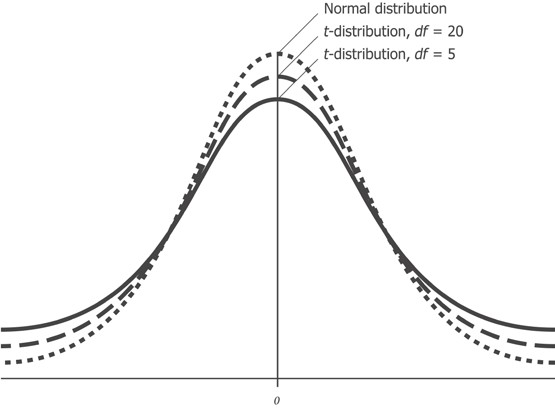
Приведенный выше рисунок показывает, как t-распределение изменяется относительно нормального распределения при наличии разных степеней свободы. Более толстые хвосты для выборок меньших размеров соответствуют увеличенной возможности наблюдать более крупные отклонения от среднего значения.
Степени свободы
Степени свободы, часто обозначаемые сокращенно df от англ. degrees of freedom, тесно связаны с размером выборки. Это полезная статистика и интуитивно понятное свойство числового ряда, которое можно легко продемонстрировать на примере.
Если бы вам сказали, что среднее, состоящее из двух значений, равно 10 и что одно из значений равно 8, то Вам бы не потребовалась никакая дополнительная информация для того, чтобы суметь заключить, что другое значение равно 12. Другими словами, для размера выборки, равного двум, и заданного среднего значения одно из значений ограничивается, если другое известно.
Если напротив вам говорят, что среднее, состоящее из трех значений, равно 10, и первое значение тоже равно 10, то Вы были бы не в состоянии вывести оставшиеся два значения. Поскольку число множеств из трех чисел, начинающихся с 10, и чье среднее равно 10, является бесконечным, то прежде чем вы сможете вывести значение третьего, второе тоже должно быть указано.
Для любого множества из трех чисел ограничение простое: вы можете свободно выбрать первые два числа, но заключительное число ограничено. Степени свободы могут таким образом быть обобщены следующим образом: количество степеней свободы любой отдельной выборки на единицу меньше размера выборки.
При сопоставлении двух выборок степени свободы на две единицы меньше суммы размеров этих выборок, что равно сумме их индивидуальных степеней свободы.
t-статистика
При использовании t-распределения мы обращаемся к t-статистике. Как и z-статистика, эта величина количественно выражает степень маловероятности отдельно взятого наблюдавшегося отклонения. Для двухвыборочного t-теста соответствующая t-статистика вычисляется следующим образом:
Здесь Sa̅b̅ — это объединенная стандартная ошибка. Объединенная стандартная ошибка вычисляется таким же образом, как и раньше:
Однако это уравнение допускает наличие информации о популяционных параметрах σa и σb, которые можно аппроксимировать только на основе крупных выборок. t-тест предназначен для малых выборок и не требует от нас принимать допущения о поплуляционной дисперсии (вариансе).
Как следствие, объединенная стандартная ошибка для t-теста записывается как квадратный корень суммы стандартных ошибок:
На практике оба приведенных выше уравнения для объединенной стандартной ошибки дают идентичные результаты при заданных одинаковых входных последовательностях. Разница в математической записи всего лишь служит для иллюстрации того, что в условиях t-теста мы на входе зависим только от выборочных статистик. Объединенная стандартная ошибка может быть вычислена следующим образом:
def pooled_standard_error_t(a, b):
'''Объединенная стандартная ошибка для t-теста'''
return sp.sqrt(standard_error(a) ** 2 +
standard_error(b) ** 2)Хотя в математическом плане t-статистика и z-статистика представлены по-разному, на практике процедура вычисления обоих идентичная:
t_stat = z_stat
def ex_2_15():
'''Вычисление t-статистики
двух вариантов дизайна веб-сайта'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(1)
return t_stat(a, b)-1.6467438180091214Различие между двумя выборочными показателями является не алгоритмическим, а концептуальным — z-статистика применима только тогда, когда выборки подчинены нормальному распределению.
t-тест
Разница в характере работы t-теста вытекает из распределения вероятностей, из которого вычисляется наше p-значение. Вычислив t-статистику, мы должны отыскать ее значение в t-распределении, параметризованном степенями свободы наших данных:
def t_test(a, b):
df = len(a) + len(b) - 2
return stats.t.sf([ abs(t_stat(a, b)) ], df)Значение степени свободы обеих выборок на две единицы меньше их размеров, и для наших выборок составляет 298.

Напомним, что мы выполняем проверку статистической гипотезы. Поэтому выдвинем нашу нулевую и альтернативную гипотезы:
-
H0: Эта выборка взята из популяции с предоставленным средним значением
-
H1: Эта выборка взята из популяции со средним значением большего размера
Выполним следующий ниже пример:
def ex_2_16():
'''Сравнение результативности двух вариантов
дизайна веб-сайта на основе t-теста'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(1)
return t_test(a, b)array([ 0.05033241])Этот пример вернет p-значение, составляющее более 0.05. Поскольку оно больше α, равного 5%, который мы установили для проверки нулевой гипотезы, то мы не можем ее отклонить. Наша проверка с использованием t-теста значимого расхождения между средними значениями не обнаружила. Следовательно, наш едва значимый результат z-теста отчасти объясняется наличием слишком малой выборки.
Двухсторонние тесты
В нашей альтернативной гипотезе было принято неявное допущение, что обновленный веб-сайт будет работать лучше существующего. В процедуре проверки нулевой статистической гипотезы предпринимаются особые усилия для обеспечения того, чтобы при поиске статистической значимости мы не делали никаких скрытых допущений.
Проверки, при выполнении которых мы ищем только значимое количественное увеличение или уменьшение, называются односторонними и обычно не приветствуются, кроме случая, когда изменение в противоположном направлении было бы невозможным. Название термина «односторонний» обусловлено тем, что односторонняя проверка размещает всю α в одном хвосте распределения. Не делая проверок в другом направлении, проверка имеет больше мощности отклонить нулевую гипотезу в отдельно взятом направлении и, в сущности, понижает порог, по которому мы судим о результате как значимом.
Статистическая мощность — это вероятность правильного принятия альтернативной гипотезы. Она может рассматриваться как способность проверки обнаруживать эффект там, где имеется искомый эффект.
Хотя более высокая статистическая мощность выглядит желательной, она получается за счет наличия большей вероятности совершить ошибку 1-го рода. Правильнее было бы допустить возможность того, что обновленный веб-сайт может в действительности оказаться хуже существующего. Этот подход распределяет нашу α одинаково по обоим хвостам распределения и обеспечивает значимый результат, не искаженный под воздействием априорного допущения об улучшении работы обновленного веб-сайта.

В действительности в модуле stats библиотеки scipy уже предусмотрены функции для выполнения двухвыборочных t-проверок. Это функция stats.ttest_ind. В качестве первого аргумента мы предоставляем выборку данных и в качестве второго – выборку для сопоставления. Если именованный аргумент equal_var равен True, то выполняется стандартная независимая проверка двух выборок, которая предполагает равные популяционные дисперсии, в противном случае выполняется проверка Уэлша (обратите внимание на служебную функцию t_test_verbose, (которую можно найти среди примеров исходного кода в репо):
def ex_2_17():
'''Двухсторонний t-тест'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(1)
return t_test_verbose(a, sample2=b, fn=stats.ttest_ind) #t-тест Уэлша{'p-значение': 0.12756432502462475,
'степени свободы ': 17.761382349686098,
'интервал уверенности': (76.00263198799597, 99.89877646270826),
'n1 ': 284,
'n2 ': 16,
'среднее x ': 87.95070422535211,
'среднее y ': 122.0,
'дисперсия x ': 10463.941024237296,
'дисперсия y ': 6669.866666666667,
't-статистика': -1.5985205593851322}По результатам t-теста служебная функция t_test_verbose возвращает много информации и в том числе p-значение. P-значение примерно в 2 раза больше того, которое мы вычислили для односторонней проверки. На деле, единственная причина, почему оно не совсем в два раза больше, состоит в том, что в модуле stats имплементирован легкий вариант t-теста, именуемый t-тестом Уэлша, который немного более робастен, когда две выборки имеют разные стандартные отклонения. Поскольку мы знаем, что для экспоненциальных распределений среднее значение и дисперсия тесно связаны, то этот тест немного более строг в применении и даже возвращает более низкую значимость.
Одновыборочный t-тест
Независимые выборки в рамках t-тестов являются наиболее распространенным видом статистического анализа, который обеспечивает очень гибкий и обобщенный способ установления, что две выборки представляют одинаковую либо разную популяцию. Однако в случаях, когда популяционное среднее уже известно, существует еще более простая проверка, представленная функцией библиотеки sciзy stats.ttest_1samp.
Мы передаем выборку и популяционное среднее относительно которого выполняется проверка. Так, если мы просто хотим узнать, не отличается ли обновленный веб-сайт значимо от существующего популяционного среднего времени пребывания, равного 90 сек., то подобную проверку можно выполнить следующим образом:
def ex_2_18():
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
b = groups.get_group(1)
return t_test_verbose(b, mean=90, fn=stats.ttest_1samp) {'p-значение ': 0.13789520958229415,
'степени свободы df ': 15.0,
'интервал уверенности': (78.4815276659039, 165.5184723340961),
'n1 ': 16,
'среднее x ': 122.0,
'дисперсия x ': 6669.866666666667,
't-статистика ': 1.5672973291495713}Служебная функция t_test_verbose не только возвращает p-значение для выполненной проверки, но и интервал уверенности для популяционного среднего. Интервал имеет широкий диапазон между 78.5 и 165.5 сек., и, разумеется, перекрывается 90 сек. нашего теста. Как раз он и объясняет, почему мы не смогли отклонить нулевую гипотезу.
Многократные выборки
В целях развития интуитивного понимания относительно того, каким образом t-тест способен подтвердить и вычислить эти статистики из столь малых данных, мы можем применить подход, который связан с многократными выборками, от англ. resampling. Извлечение многократных выборок основывается на допущении о том, что каждая выборка является лишь одной из бесконечного числа возможных выборок из популяции. Мы можем лучше понять природу того, какими могли бы быть эти другие выборки, и, следовательно, добиться лучшего понимания опорной популяции, путем извлечения большого числа новых выборок из нашей существующей выборки.
На самом деле существует несколько методов взятия многократных выборок, и мы обсудим один из самых простых — бутстрапирование. При бустрапировании мы генерируем новую выборку, неоднократно извлекая из исходной выборки случайное значение с возвратом до тех пор, пока не сгенерируем выборку, имеющую тот же размер, что и оригинал. Поскольку выбранные значения возвращаются назад после каждого случайного отбора, то в новой выборке то же самое исходное значение может появляться многократно. Это как если бы мы неоднократно вынимали случайную карту из колоды игральных карт и каждый раз возвращали вынутую карту назад в колоду. В результате время от времени мы будем иметь карту, которую мы уже вынимали.
Бутстраповская выборка, или бутстрап, — синтетический набор данных, полученный в результате генерирования повторных выборок (с возвратом) из исследуемой выборки, используемой в качестве «суррогатной популяции», в целях аппроксимации выборочного распределения статистики (такой как, среднее, медиана и др.).
В библиотеке pandas при помощи функции sample можно легко извлекать бутстраповские выборки и генерировать большое число многократных выборок. Эта функция принимает ряд опциональных аргументов, в т.ч. n (число элементов, которые нужно вернуть из числового ряда), axis (ось, из которой извлекать выборку) и replace (выборка с возвратом или без), по умолчанию равный False. После этой функции можно задать метод агрегирования, вычисляющий сводную статистику в отношении бутстраповских выборок:
def ex_2_19():
'''Построение графика синтетических времен пребывания
путем извлечения бутстраповских выборок'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
b = groups.get_group(1)
xs = [b.sample(len(b), replace=True).mean() for _ in range(1000)]
pd.Series(xs).hist(bins=20)
plt.xlabel('Бутстрапированные средние значения времени пребывания, сек.')
plt.ylabel('Частота')
plt.show()Приведенный выше пример наглядно показывает результаты на гистограмме:

Гистограмма демонстрирует то, как средние значения изменялись вместе с многократными выборками, взятыми из времени пребывания на обновленном веб-сайте. Хотя на входе имелась лишь одна выборка, состоящая из 16 посетителей, бутстрапированные выборки очень четко просимулировали стандартную ошибку изначальной выборки и позволили визуализировать интервал уверенности (между 78 и 165 сек.), вычисленный ранее в результате одновыборочного t-теста.
Благодаря бутстрапированию мы просимулировали взятие многократных выборок, при том, что у нас на входе имелась всего одна выборка. Этот метод обычно применяется для оценивания параметров, которые мы не способны или не знаем, как вычислить аналитически.
Проверка многочисленных вариантов дизайна
Было разочарованием обнаружить отсутствие статистической значимости на фоне увеличенного времени пребывания пользователей на обновленном веб-сайте. Хотя хорошо, что мы обнаружили это на малой выборке пользователей, прежде чем выкладывать его на всеобщее обозрение.
Не позволяя себя обескуражить, веб-команда AcmeContent берется за сверхурочную работу и создает комплект альтернативных вариантов дизайна веб-сайта. Беря лучшие элементы из других проектов, они разрабатывают 19 вариантов для проверки. Вместе с нашим изначальным веб-сайтом, который будет действовать в качестве контрольного, всего имеется 20 разных вариантов дизайна веб-сайта, куда посетители будут перенаправляться.
Вычисление выборочных средних
Веб-команда разворачивает 19 вариантов дизайна обновленного веб-сайта наряду с изначальным. Как отмечалось ранее, каждый вариант дизайна получает случайные 5% посетителей, и при этом наше испытание проводится в течение 24 часов.
На следующий день мы получаем файл, показывающий значения времени пребывания посетителей на каждом варианте веб-сайта. Все они были промаркированы числами, при этом число 0 соответствовало веб-сайту с исходным дизайном, а числа от 1 до 19 представляли другие варианты дизайна:
def ex_2_20():
df = load_data('multiple-sites.tsv')
return df.groupby('site').aggregate(sp.mean)Этот пример сгенерирует следующую ниже таблицу:
|
site |
dwell-time |
|
0 |
79.851064 |
|
1 |
106.000000 |
|
2 |
88.229167 |
|
3 |
97.479167 |
|
4 |
94.333333 |
|
5 |
102.333333 |
|
6 |
144.192982 |
|
7 |
123.367347 |
|
8 |
94.346939 |
|
9 |
89.820000 |
|
10 |
129.952381 |
|
11 |
96.982143 |
|
12 |
80.950820 |
|
13 |
90.737705 |
|
14 |
74.764706 |
|
15 |
119.347826 |
|
16 |
86.744186 |
|
17 |
77.891304 |
|
18 |
94.814815 |
|
19 |
89.280702 |
Мы хотели бы проверить каждый вариант дизайна веб-сайта, чтобы увидеть, не генерирует ли какой-либо из них статистически значимый результат. Для этого можно сравнить варианты дизайна веб-сайта друг с другом следующим образом, причем нам потребуется вспомогательный модуль Python itertools, который содержит набор функций, создающих итераторы для эффективной циклической обработки:
import itertools
def ex_2_21():
'''Проверка вариантов дизайна веб-сайта на основе t-теста
по принципу "каждый с каждым"'''
groups = load_data('multiple-sites.tsv').groupby('site')
alpha = 0.05
pairs = [list(x) # найти сочетания из n по k
for x in itertools.combinations(range(len(groups)), 2)]
for pair in pairs:
gr, gr2 = groups.get_group( pair[0] ), groups.get_group( pair[1] )
site_a, site_b = pair[0], pair[1]
a, b = gr['dwell-time'], gr2['dwell-time']
p_val = stats.ttest_ind(a, b, equal_var = False).pvalue
if p_val < alpha:
print('Варианты веб-сайта %i и %i значимо различаются: %f'
% (site_a, site_b, p_val))Однако это было бы неправильно. Мы скорее всего увидим статистическое расхождение между вариантами дизайна, показавшими себя в особенности хорошо по сравнению с вариантами, показавшими себя в особенности плохо, даже если эти расхождения носили случайный характер. Если вы выполните приведенный выше пример, то увидите, что многие варианты дизайна веб-сайта статистически друг от друга отличаются.
С другой стороны, мы можем сравнить каждый вариант дизайна веб-сайта с нашим текущим изначальным значением — средним значением времени пребывания, равным 90 сек., измеренным на данный момент для существующего веб-сайта:
def ex_2_22():
groups = load_data('multiple-sites.tsv').groupby('site')
alpha = 0.05
baseline = groups.get_group(0)['dwell-time']
for site_a in range(1, len(groups)):
a = groups.get_group( site_a )['dwell-time']
p_val = stats.ttest_ind(a, baseline, equal_var = False).pvalue
if p_val < alpha:
print('Вариант %i веб-сайта значимо отличается: %f'
% (site_a, p_val))В результате этой проверки будут идентифицированы два варианта дизайна веб-сайта, которые существенно отличаются:
Вариант 6 веб-сайта значимо отличается: 0.005534
Вариант 10 веб-сайта 10 значимо отличается: 0.006881Малые p-значения (меньше 1%) указывают на то, что существует статистически очень значимые расхождения. Этот результат представляется весьма многообещающим, однако тут есть одна проблема. Мы выполнили t-тест по 20 выборкам данных с уровнем значимости α, равным 0.05. Уровень значимости α определяется, как вероятность неправильного отказа от нулевой гипотезы. На самом деле после 20-кратного выполнения t-теста становится вероятным, что мы неправильно отклоним нулевую гипотезу по крайней мере для одного варианта веб-сайта из 20.
Сравнивая таким одновременным образом многочисленные страницы, мы делаем результаты t-теста невалидными. Существует целый ряд альтернативных технических приемов решения проблемы выполнения многократных сравнений в статистических тестах. Эти методы будут рассмотрены в следующем разделе.
Поправка Бонферрони
Для проведения многократных проверок используется подход, который объясняет увеличенную вероятность обнаружить значимый эффект в силу многократных испытаний. Поправка Бонферрони — это очень простая корректировка, которая обеспечивает, чтобы мы вряд ли совершили ошибки 1-го рода. Она выполняется путем настройки значения уровня значимости для тестов.
Настройка очень простая — поправка Бонферрони попросту делит требуемое значение α на число тестов. Например, если для теста имелось k вариантов дизайна веб-сайта, и α эксперимента равно 0.05, то поправка Бонферрони выражается следующим образом:
Она представляет собой безопасный способ смягчить увеличение вероятности совершения ошибки 1-го рода при многократной проверке. Следующий пример идентичен примеру ex-2-22, за исключением того, что значение α разделено на число групп:
def ex_2_23():
'''Проверка вариантов дизайна веб-сайта на основе t-теста
против исходного (0) с поправкой Бонферрони'''
groups = load_data('multiple-sites.tsv').groupby('site')
alpha = 0.05 / len(groups)
baseline = groups.get_group(0)['dwell-time']
for site_a in range(1, len(groups)):
a = groups.get_group(site_a)['dwell-time']
p_val = stats.ttest_ind(a, baseline, equal_var = False).pvalue
if p_val < alpha:
print('Вариант %i веб-сайта значимо отличается от исходного: %f'
% (site_a, p_val))Если вы выполните приведенный выше пример, то увидите, что при использовании поправки Бонферрони ни один из веб-сайтов больше не считается статистически значимым.
Метод проверки статистической значимости связан с поддержанием равновесия — чем меньше шансы совершения ошибки 1-го рода, тем больше риск совершения ошибки 2-го рода. Поправка Бонферрони очень консервативна, и весьма возможно, что из-за излишней осторожности мы пропускаем подлинное расхождение.
Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.
В заключительном посте, посте №4, этой серии постов мы проведем исследование альтернативного подхода к проверке статистической значимости, который позволяет устанавливать равновесие между совершением ошибок 1-го и 2-го рода, давая нам возможность проверить все 20 вариантов веб-сайта одновременно.
Маркетинг – та сфера, где больше всего любят работать с большими данными (англ. big data), однако излюбленный инструмент маркетологов – A/B-тестирование – предполагает использование малых данных (англ. small data). При этом какие бы цифры ни были получены по итогам теста, все сводится к анализу статистической выборки и определению статистической значимости результатов эксперимента. Неотъемлемой частью данного исследования является P-значение, о котором мы хотим рассказать в этой статье.
Что такое P-значение
P-value или p-значение – одна из ключевых величин, используемых в статистике при тестировании гипотез. Она показывает вероятность получения наблюдаемых результатов при условии, что нулевая гипотеза верна, или вероятность ошибки в случае отклонения нулевой гипотезы.
Этот термин первым упомянул в своих работах К. А. Браунли в 1960 году. Он описал p-уровень значимости как показатель, который находится в обратной зависимости от истинности результатов. Чем выше р-value, тем ниже степень доверия в выборке зависимости между переменными.
Другими словами, в статистике p-значение – это наименьшее значение уровня значимости, при котором полученная проверочная статистика ведет к отказу от основной (нулевой) гипотезы.
Значение p-уровня чаще всего соответствует статистической значимости, равной 0,05. Если значение р меньше 0,05, нулевую гипотезу отклоняют. При этом чем меньше это значение, тем лучше, т. к. растет предполагаемая значимость альтернативной гипотезы и «сила» отвержения нулевой.
Часто p-значение понимают неправильно. Например, если значение р = 0,05, можно сказать о том, что существует 5% вероятности, что результат получен случайно и не соответствует действительности.

Кратко о главном
- Р-значение показывает вероятность того, что наблюдаемая разница в результатах могла быть случайной.
- Значение p применяется как альтернатива выбранным уровням достоверности для тестирования идей или в дополнение к ним.
- Со снижением p-значения повышается статистическая значимость разницы, полученной в ходе исследования.
Статистическая значимость
Эксперимент начинается с формулирования нулевой гипотезы. Она показывает, что два исследуемых явления никаким образом не связаны друг с другом.
Эксперимент проводится с целью выявить или показать какое-либо влияние или тип взаимодействия рассматриваемых явлений. Если в итоге анализа подтверждается нулевая гипотеза, значит, тест провалился.

Чтобы правильно интерпретировать результаты, рассчитывают показатель статистической значимости.
Статистическая значимость – это критерий, с помощью которого можно определить, необходимо ли отвергнуть или принять ту или иную гипотезу.
Перед началом тестирования следует установить порог значимости (альфа). Если значение р меньше альфа, можно говорить о том, что наш результат является статистически значимым. Это говорит о том, что наблюдаемое явление действительно имело место, и нулевую гипотезу нужно отклонить.
Порог значимости альфа устанавливается обычно на уровне 0,05 или 0,01. Выбор значения определяется поставленной задачей.
Порог значимости равен 0,05, а p-значение – 0,02. Т. к. установленное значение альфа больше p-уровня, делаем вывод, что это статистически значимый результат.
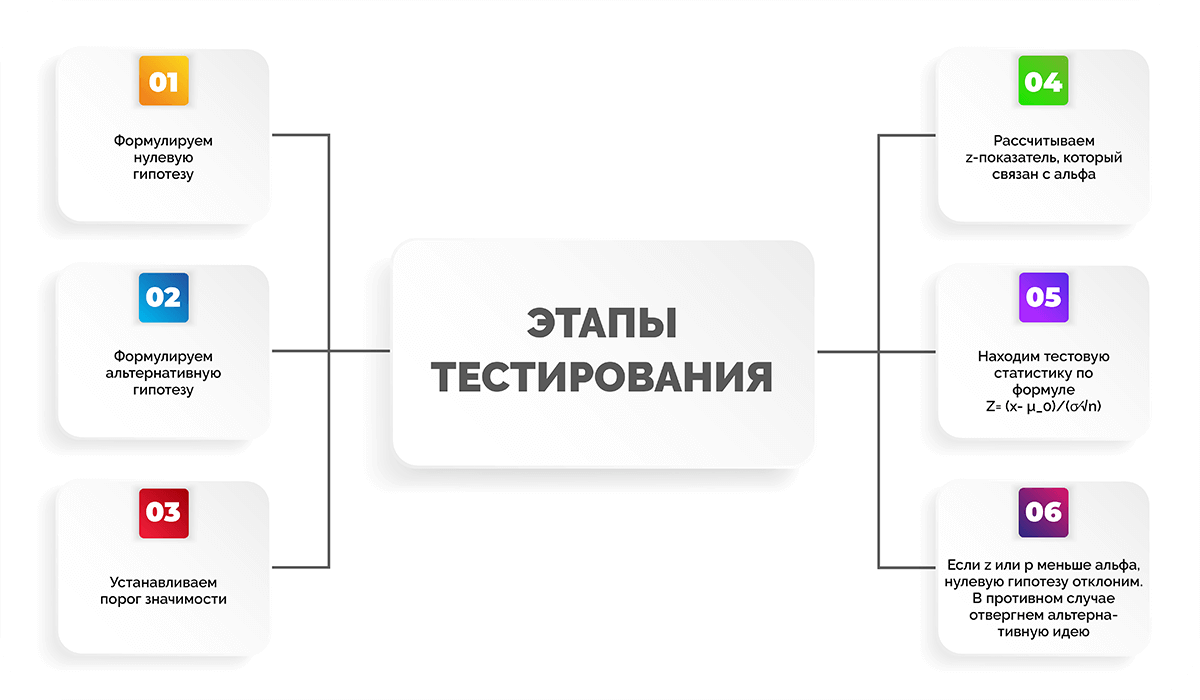
Все тестирование можно разделить на несколько этапов:
- Формулируем нулевую гипотезу.
- Формулируем альтернативную гипотезу.
- Устанавливаем порог значимости.
- Рассчитываем z-показатель, который связан с альфа.
- Находим тестовую статистику по формуле
 .
. - Если z-показатель или p-значение меньше уровня альфа, нулевую гипотезу отклоним. В противном случае отвергнем альтернативную идею.
Если идет речь о явлениях, которые управляются случайными процессами, обычно это приводит к нормальному распределению значений. В этом случае нулевую гипотезу представляют в виде кривой Гаусса, которая отражает распределение ожидаемых наблюдений. Это распределение актуально в случае, если одна переменная в эксперименте не зависит от другой.
Порог вероятности
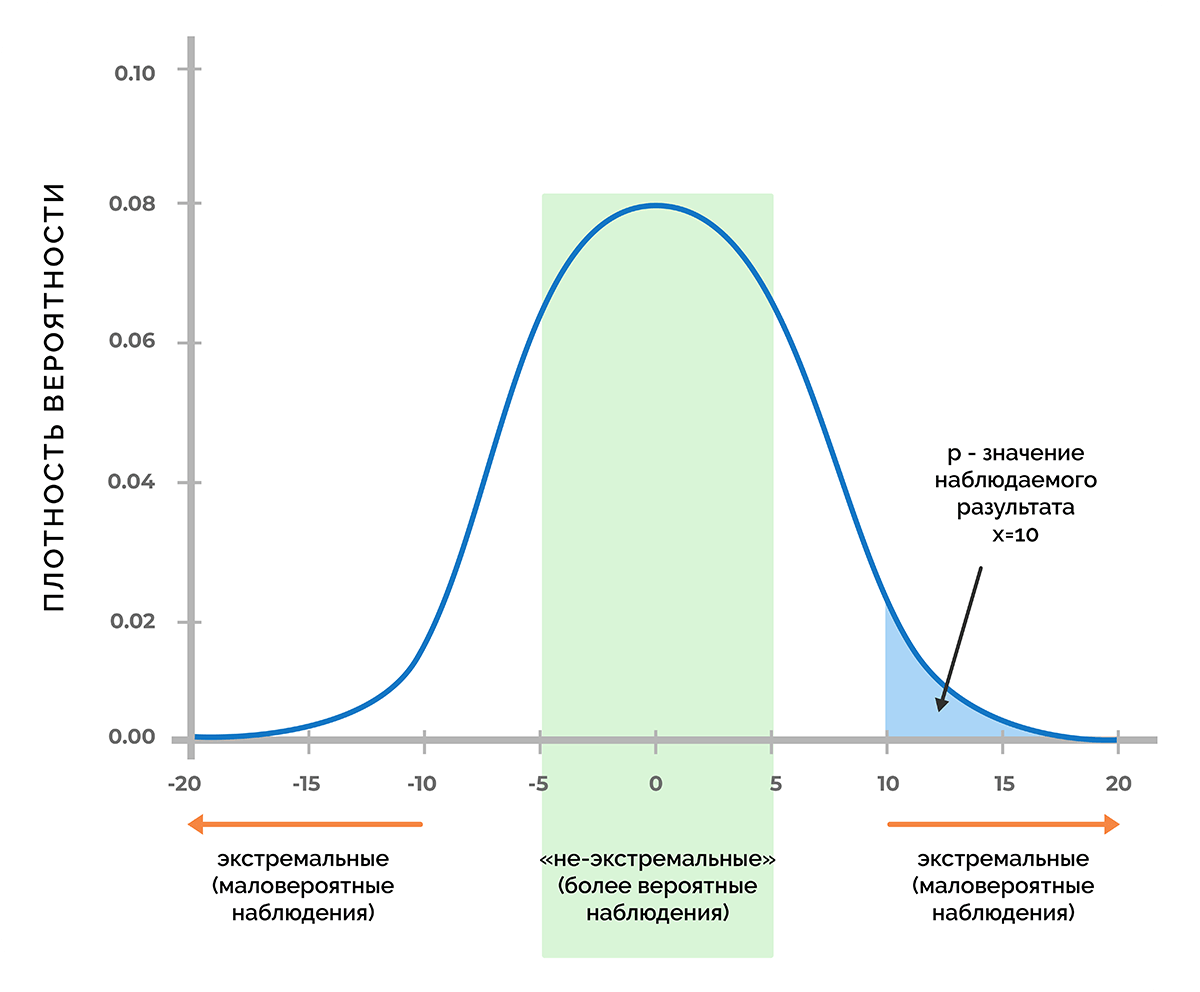
В основе статистической значимости лежит вероятность получения определенного результата при верности нулевой гипотезы. Чтобы разобрать смысл этого определения, предположим, что в процессе тестирования получили некое число х. Это может быть любая метрика, например, прибыль от продаж, величина конверсии, количество довольных покупателей и т. д.
Используя функцию плотности вероятности, которая связана с нулевой гипотезой, можно выяснить, удастся ли получить число х (или любое другое значение, которое маловероятнее, чем х) с вероятностью менее 5% (p < 0,05) или менее 1% (p < 0,01), или другого порога, при котором p меньше заданного уровня значимости.
Таким образом, p-критерий отражает вероятность получения результата, который равен или является более экстремальным, чем фактически наблюдаемый результат, в случае отсутствия взаимосвязи между исследуемыми переменными.
Доверительные уровни
Доверительный уровень значимости выбирается перед запуском статистического эксперимента. Чаще всего используются значения 90%, 95% или 99%.
Ниже в таблице приводим критические p-значения, а также z-оценки для разных доверительных уровней.
|
Доверительный уровень |
Стандартное отклонение (z-оценка) |
Вероятность (p-уровень) |
|
90% |
< -1,65 или > +1,65 |
< 0,10 |
|
95% |
< -1,96 или > +1,96 |
< 0,05 |
|
99% |
< -2,58 или > +2,58 |
< 0,01 |
Значения, которые находятся в пределах области нормального распределения z-оценки (стандартного отклонения), представляют ожидаемый результат.
Проверка статистических гипотез
Проверка гипотезы – это статистическое исследование, которое проводится, чтобы подтвердить или опровергнуть какую-либо гипотезу (простую или сложную).
Можно предположить, что посадочная страница с красной кнопкой CTA даст больше конверсий, чем текущая версия лендинга с синей. Проверить это можно путем тестирования, в котором будут участвовать нулевая и альтернативная гипотезы.

Нулевая гипотеза – первоначальное условие, при котором нет никакой разницы между текущей и новой версиями лендинга в плане конверсии
Альтернативная гипотеза – подразумевает, что изменение цвета кнопки на странице является причиной роста конверсии.
В статистике применяется рандомизация и нормализация нулевой гипотезы.
Рандомизация нулевой гипотезы – пространственная модель данных, которую мы наблюдаем, является одним из многих вариантов пространственных организаций данных. При этом все другие варианты не будут заметно отличаться от наблюдаемых.
Нормализация нулевой гипотезы подразумевает, что наблюдаемые значения являются одним из многих случайных вариантов выборок. При этом ни пространственное расположение данных, ни их значения не установлены.
Благодаря значению p можно увидеть, насколько нулевая гипотеза правдоподобна с учетом данных выборки. Таким образом, если нулевая гипотеза подтвердится, p-значение будет свидетельствовать об отсутствии увеличения конверсии вследствие изменения цвета кнопки.
Подход p-value к проверке гипотез
Значение р может использоваться для выявления доказательства для отклонения нулевой (первоначальной) гипотезы в ходе эксперимента.
Мы уже упоминали выше о том, что уровень значимости обозначается до начала исследования, чтобы определить, насколько малое значение p нужно получить для опровержения нулевой гипотезы. Однако в разных случаях разные люди могут использовать разные уровни значимости, поэтому при интерпретации итогов двух разных тестирований другими людьми могут возникать трудности. Решить эту проблему помогает p-value.
Рассмотрим пример, в котором в компании провели исследование, в ходе него сравнили доходность двух активов. Тест и анализ проводили два специалиста, которые брали за основу одни и те же самые исходные данные, но использовали разные уровни значимости. Есть вероятность, что эти люди сделают противоположные выводы о различии активов. Предположим, что один специалист для отклонения нулевой гипотезы взял уровень достоверности 90%, а другой – 95%. При этом среднее значение p наблюдаемой разницы между результатами равнялось 0,08, что отвечает уровню достоверности 92%. В таком случае первый специалист выявит значимое различие между двумя доходами, а второй статистически значимой разницы не обнаружит.
Чтобы избежать подобной ситуации, можно сообщить значение p-value эксперимента и дать возможность независимым наблюдателям самостоятельно оценивать статистическую значимость итоговых данных. Данный подход к проверке утверждений стали называть «подход p-value».
Как рассчитать P-value
Чаще всего p-значения определяют с помощью таблиц p-value или специализированного статистического ПО. Также помогает в этом калькулятор на тематических сайтах. Подобные расчеты основываются на известном или предполагаемом распределении вероятностей определенной статистики. Определение среднего значения р зависит от отклонения между выбранным эталонным и тестовым значением. При этом учитывается нормальное распределение вероятностей статистики.
Что касается ручного математического расчета значения р, существуют разные способы, которые рассмотрим далее в статье.
Как рассчитать p-значение, используя тестовую статистику
Распределение тестовой статистики происходит с предполагаемым условием, что верна нулевая гипотеза. Чтобы выразить вероятность того, что статистика эксперимента будет такой же экстремальной, как значение x для выборки, используется кумулятивная функция распределения.
Левосторонний эксперимент:
P-value = cdf (x)
Правосторонний эксперимент:
P-value = 1 – cdf (x)
Двусторонний эксперимент:
P-value = 2 × мин {{cdf (x), 1 – cdf (x)}}
Ручной расчет значения p затрудняют распространенные распределения вероятностей, которыми характеризуется проверка гипотез. Для расчета примерных показателей cdf удобнее использовать статистическую таблицу или ПК.
Пошаговый алгоритм расчета p-значения
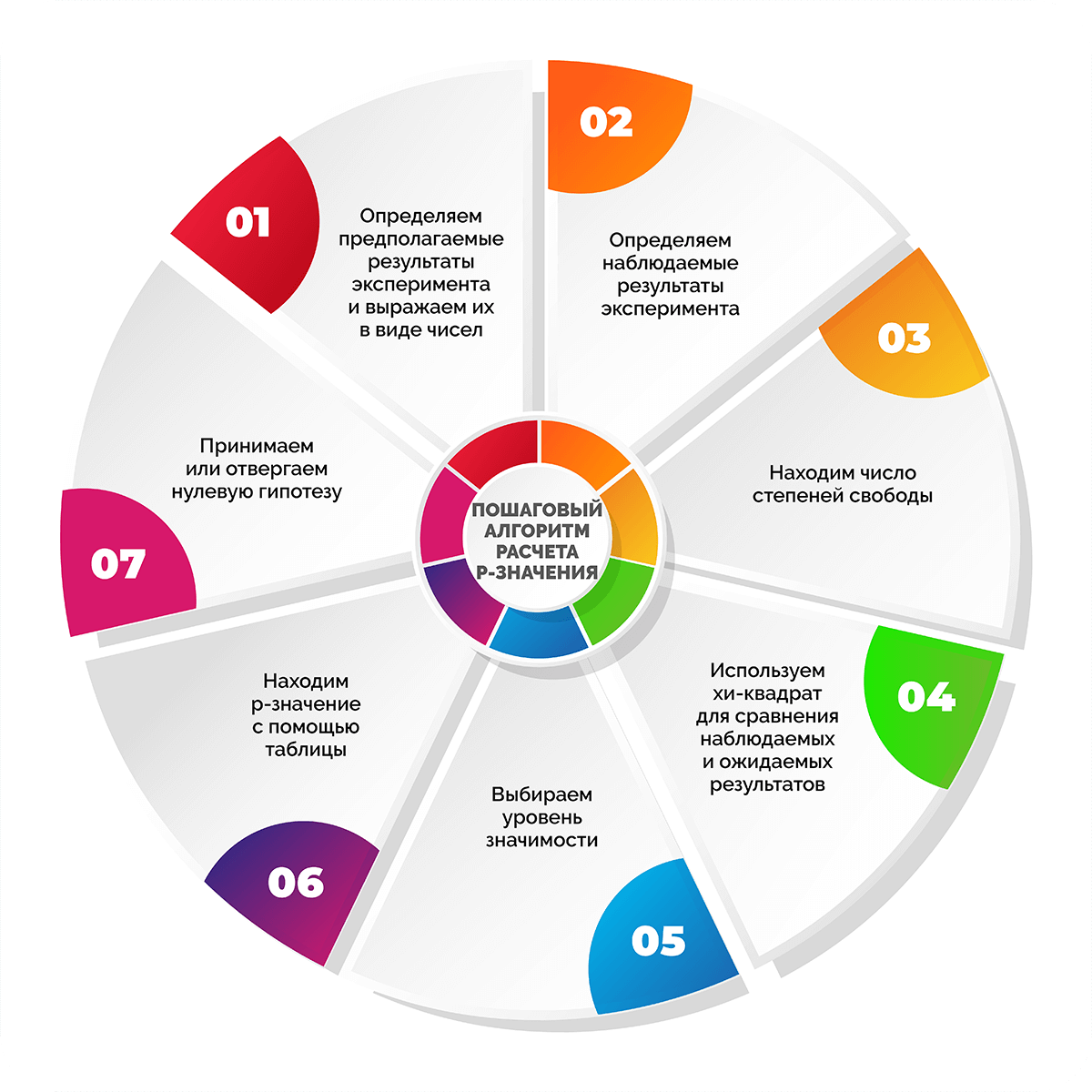
Шаг 1. Определяем предполагаемые результаты эксперимента и выражаем их в виде чисел
Как правило, на начало исследования уже есть видение того, какие числа можно считать приемлемыми. Выводы могут быть основаны на опыте проведения предыдущих экспериментов, наборах достоверных данных или общих сведеньях из научной литературы и других источников.
Опыт работы с лендингами показывает, что посадочные страницы с CTA-кнопкой на первом экране приводят примерно вдвое больше покупателей, чем версии без таких кнопок. Необходимо определить, действительно ли наличие кнопки влияет на посетителей сайта. Для этого будем анализировать конверсии в покупку. Если взять условные 300 конверсий, то предполагается, что 200 из них произойдут благодаря лендингам с CTA-кнопкой, а 100 – сайтам без кнопки при условии, что пользователи требовательны к наличию кнопок.
Шаг 2. Определяем наблюдаемые результаты эксперимента
Теперь нужно провести тест и получить реальные, т. е. наблюдаемые значения, которые таже будут выражаться в числовом формате. Если в экспериментальных условиях реальные цифры не совпадут с ожидаемыми, то будет два варианта – или это обусловлено действиями в ходе эксперимента, или получилось случайно. В данном случае цель определения p-value – понять, действительно ли наблюдаемые значения отличаются от ожидаемых настолько, что нулевая гипотеза не будет опровергнута.
Предположим, что мы выбрали 300 случайных конверсий с наших сайтов, на которых либо была кнопка на первом экране, либо ее не было. Определили, что 220 конверсий произошли благодаря лендингам с кнопкой и 80 – без нее. Результаты отличаются от ожидаемых, которые составляли 200 и 100 соответственно. Теперь предстоит узнать, действительно ли к изменению в значениях привел наш тест (добавление кнопки на первый экран) или это случайное отклонение. Определить это поможет p-значение.
Шаг 3. Находим число степеней свободы
Число степеней свободы показывает, насколько может измениться эксперимент. При этом степень изменяемости зависит от количества исследуемых категорий.
Число степеней свободы = n – 1, где n – количество анализируемых переменных или категорий.
В нашем эксперименте 2 условия и, соответственно, две категории результатов: для лендингов без кнопки на первом экране и для лендингов с ней.
Число степеней свободы = 2 – 1 = 1.
Если бы в эксперименте мы сравнивали посадочные станицы с CTA-кнопкой, без кнопки и с pop-up окном, то получили бы 2 степени свободы и т. д.
Шаг 4. Используем хи-квадрат для сравнения наблюдаемых и ожидаемых результатов
Хи-квадрат (х2) – числовое отражение разницы между наблюдаемыми (фактическими) и ожидаемыми значениями тестирования.

где:
о – наблюдаемое значение;
е – ожидаемое значение.
Подставляем наши цифры в уравнение и учитываем, что  нужно подсчитать дважды – для двух видов лендинга.
нужно подсчитать дважды – для двух видов лендинга.
х2 = ((220 – 200)2/200) + ((80 – 100)2/100) = ((20)2/200)) + ((-20)2/100) = (400/200) + (400/100) = 2 + 4 = 6.
Шаг 5. Выбираем уровень значимости
Уровень значимости отражает степень уверенности в полученных результатах. Если статистическая значимость низкая, это говорит о низкой вероятности случайного получения экспериментальных результатов.
Для большинства тестов достаточно статистической значимости, равной 0,05 или 5%. При этом будет вероятность 95%, что исследователь получил значимый результат вследствие проведенных мероприятий, а не случайно.
В нашем случае примем статистическую значимость, равную 0,05.
Шаг 6. Находим p-значение с помощью таблицы
Для облегчения расчетов статисты применяют специализированные таблицы. Они довольно простые и позволяют легко найти значение р, зная число степеней свободы и хи-значение. Слева по вертикали располагаются значения числа степеней свободы. Вверху по горизонтали находятся p-значения. По данным таблицы сначала находят нужное число степеней свободы, затем в соответствующем ему ряду выбирают первое значение, которое превышает расчетное значение хи-квадрата. Число в верхней горизонтальной строке будет соответствовать p-значению. При этом нужное значение р находится в диапазоне чисел между найденным и следующим за ним слева.
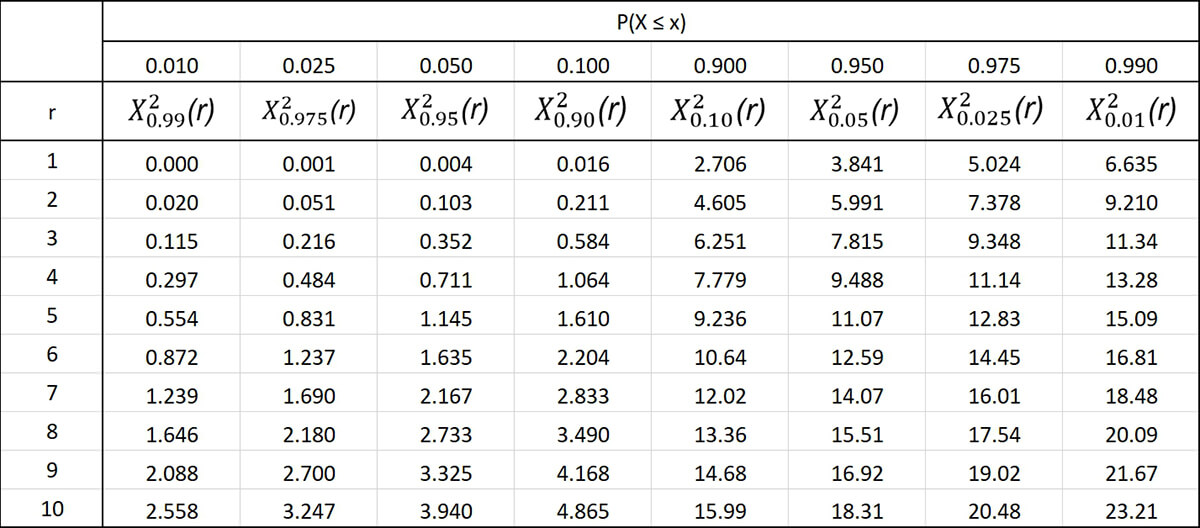
В нашем примере всего одна степень свободы, а хи-квадрат равен 6. Поэтому в таблице выбираем первую строку и движемся по ней слева направо до тех пор, пока не увидим первое значение больше 6 – это число 6,635. Оно соответствует p-значению 0,01, а значит, наше p-значение находится в диапазоне между 0,01 и 0,025.
Шаг 7. Принимаем или отвергаем нулевую гипотезу
Если найденное приблизительное значение p меньше уровня значимости, можно заключить, что вероятна связь между экспериментальными переменными и полученными результатами. В противном случае нельзя утверждать с уверенностью, связаны ли результаты с манипуляцией переменными или стали случайностью.
В нашем эксперименте диапазон значений р 0,01-0,025 определенно меньше установленной статистической значимости 0,05, что позволяет отклонить нулевую гипотезу. А значит, можно сделать вывод, что посадочные страницы с CTA-кнопкой на 1-м экране конвертируют лучше, чем аналогичные версии без такой кнопки. Вероятность того, что рост конверсий на лендингах с кнопкой является случайностью, составляет не больше 1-2,5%.
Как интерпретировать P-значение
P-уровень тесно связан с уровнем статистической значимости. Последний таже определяет исход эксперимента.
- Если p-значение меньше уровня значимости, то нулевую гипотезу можно смело отклонить и считать истинной альтернативную гипотезу.
- Если p-значение больше уровня значимости, это означает, что в ходе эксперимента выявили недостаточно оснований для отклонения нулевой гипотезы.
Отвержение нулевой гипотезы говорит о том, что в процессе исследования была обнаружена закономерная связь между тестируемыми переменными.
P-значение – это…
- вероятность того, что в ходе исследования наблюдения были случайными. То есть, если p = 0,05, есть 5% вероятности того, что наблюдаемое явление случайно и 95% вероятности того, что результат является следствием созданных условий;
- вероятность того, что будет сделан неверный вывод о взаимосвязи переменных. Если р = 0,05, то на каждые 100 экспериментов, где наблюдалась взаимосвязь, 95 их них действительно была, а 5 – нет.
Что нужно помнить о P-значениях
- «Неожиданность» определяет тот, кто проводит эксперимент. Подводит итоги теста по факту тот, кто его проводит. Чем выше значение р, тем чаще вы будете получать неожиданные результаты.
- Применение p-значения имеет довольно извилистую логику. Чтобы оценить аргументы в пользу отклонения нулевой гипотезы, необходимо изначально считать, что она верна. Именно это является причиной путаницы.
- По значению p невозможно оценить вероятность того, что один исследуемый вариант лучше другого. Также по этому показателю нельзя понять, какая вероятность того, что предпочтение одного варианта другому ошибочно. На самом деле, p-значение показывает лишь вероятность того, что при верности нулевой гипотезы удастся вычислить результат, отличный от нуля.
- Значимость p-значения при подведении итогов сплит-тестов – тема неутихающих споров в научном сообществе. Большинство маркетологов остаются приверженцами классической проверки на статистическую значимость и отстаивают ее как «золотой стандарт». При этом специалисты по статистике приводят аргументы в пользу других методов проверки, что провоцирует жаркие дебаты.
- Всегда можно получить существенное (высшее) значение p. Есть типичная ошибка, которая зависит с одной стороны от объема выборки, с другой – от изменений генеральной совокупности данных. Если во втором случае повлиять на изменения никак нельзя, то собирать и накапливать данные ничто не мешает. Но есть ли польза от такого количества сведений? Сам факт того, что у полученного параметра высокое p-значение, практического значения не имеет.
- Не стоит волноваться раньше времени. В первую очередь нужно собрать данные, которые помогут сформировать рабочую идею. Всегда трудно делать выбор между вариантами, которые почти не отличаются друг от друга. Если выделить предпочтительный вариант проблематично из-за похожих результатов, можно просто выбрать один из них и не беспокоиться о том, правильный ли это выбор.
- P-значение не повод прекращать тест. Для получения достоверных результатов, которые позволят интерпретировать p-значение, необходимо вычислить размер выборки, затем провести эксперимент. В процессе тестирования предстоит выбрать время, когда пора его закончить. При этом оно не должно быть связано с достижением статистической значимости или высокого показателя p-значения. Главное – получить реальные результаты в конце теста, например, обеспечить рост прибыли, оптимизировать конверсию и т. д.
Примеры интерпретации P-значений
На нескольких примерах рассмотрим, как правильно интерпретировать p-значения при проверке разных идей.
По мнению интернет-провайдера, 90% пользователей довольны качеством предоставляемых услуг. Чтобы это проверить, была собрана простая выборка, куда вошли 500 случайных абонентов. 85% дали утвердительный ответ на вопрос об удовлетворенности услугами провайдера. По данным выборки удалось вычислить p-значение, равное 0,018.
Если выдвинуть гипотезу о том, что 90% пользователей действительно довольны обслуживанием провайдера, получим реальную наблюдаемую разницу или более экстремальную разницу, которая составит 1,8% потребителей услуг вследствие ошибки случайной выборки.
Ресторан вводит услугу доставки еды и утверждает, что время доставки составляет около 30 минут или меньше. Однако есть мнение, что реальный срок доставки превышает заявленное время. Для проверки этих вариантов были отобраны случайные заказы еды с доставкой и проведены расчеты. По результатам выяснили, что среднее время доставки составляет 40 минут (больше на 10 минут, чем заявляет ресторан), а p-значение равно 0,03.
Результаты показывают, что в случае, когда нулевая гипотеза верна, т. е. доставка еды занимает 30 минут или меньше, есть вероятность 3%, что среднее время доставки будет как минимум на 10 минут больше из-за эффекта случайности.
Отдел маркетинга разрабатывает новый скрипт продаж для менеджеров. Предполагается, что с его помощью компания будет продавать минимум на 30% больше, чем со старым скриптом. Чтобы это проверить, собирается простая случайная выборка из 100 контактов с клиентами по новому скрипту и 100 – по старому. В результате эксперимента новый скрипт привел 60 покупателей, а старый – 45. Вычислили среднее значение p, равное 0,011.
Если взять за основу мнение, что новый скрипт приводит столько же клиентов, сколько и старый, или меньше, будет получена крайняя разница в 1,1% тестирований вследствие случайной ошибки выборки.
Часто задаваемые вопросы
P-значение – вероятность того, что исследуемая статистика удовлетворит конкретным условиям. Поскольку вероятности отрицательными не бывают, отрицательного значения p тоже быть не может.
Если p-значение высокое, это свидетельствует о том, что статистика эксперимента для другой выборки будет иметь столь же экстремальное значение, как и в тестируемой выборке. При высоком p-значении отвергнуть нулевую гипотезу нельзя.
Если получено низкое p-значение, это значит, что вероятность получить такое же критическое значение, как и наблюдаемое в текущей выборке, в тестовой статистике для другой выборки окажется очень низкой. При низком p-значении нулевую гипотезу отвергают и принимают альтернативную.
Некоторые считают, что p-значения показывают вероятность совершить ошибку при отклонении истинной нулевой гипотезы (ошибка первого типа) – это заблуждение. P-значения не свидетельствуют о частоте вероятных ошибок по двум причинам:
- При расчете p-значения в основе утверждение, что верна нулевая гипотеза, а разница в итоговых данных обусловлена случайностью. То есть величина p-значения не отражает вероятность того, что ноль будет ложным или истинным, т. к. с учетом изначального предположения он полностью верен.
- Несмотря на то, что при низком p-значении при условии истинности нулевого значения выборочные данные маловероятны, p-значение все еще не может четко показать, какой из вариантов имеет большую вероятность стать истиной: когда нуль действительно является ложным или когда нуль является верным, но выборка нечеткая.
Заключение
Несмотря на то, что при интерпретации результатов исследований часто допускают ошибки, неправильно используя статистическую значимость, она продолжает оставаться важным методом в экспериментах. P-значение или p-value является одной из обязательных составляющих при оценке результатов тестирования. Именно этот показатель дает возможность понять, с какой вероятностью полученные итоги удовлетворяют определенным значениям.

Олег Вершинин
Специалист по продукту
Все статьи автора
Нашли ошибку в тексте? Выделите нужный фрагмент и нажмите
ctrl
+
enter
Содержание
Спрятать
- Что такое T-статистика?
- Формула для расчета T-статистики:
- Пример расчета T-статистики
- Понимание T-статистики
- Что такое T-статистика по сравнению с P-значением?
- Что говорит вам T-статистика в регрессии?
- Как рассчитать T-статистику
- Как узнать, является ли T Stat значительным?
- Какие три типа t-тестов существуют в статистике?
- Что говорит вам большая T-статистика?
- Что такое хорошее статистическое значение T?
- В чем разница между статистикой Z и T?
- Z-тест
- Т-тест
- Предположения Т-теста
- Использование T-статистики
- №1. Проверка гипотез о населении означает:
- № 2. Доверительные интервалы
- №3. Проверка значимости коэффициентов регрессии:
- Другой статистический тест
- №1. F-значение
- № 2. Z-значение
- №3. P-значение
- Статьи по теме
- Рекомендации
Если вы пытаетесь узнать значительную разницу между двумя средними выборочными наборами данных по отношению к заданным переменным, вам следует проверить t-статистику. Будь то в сфере образования, науки или даже чего-то связанного с бизнесом, мы все пытаемся проверить наши гипотезы и догадки в тот или иной момент. Интересно, что t-статистика является одним из инструментов, используемых для проверки нашей оценки данных. Стьюдентная статистика, часто называемая по значению, описывает отношение набора выборок к набору населения. Он используется для сведения огромных объемов данных к одному значению. В этом руководстве рассматриваются формулы, типы, интерпретация их значений, а также использование t-статистики.
Стьюдентная статистика измеряет, насколько значительна разница между двумя выборочными средними по отношению к изменчивости данных. Это стандартный инструмент для оценки гипотез о значимости различий между выборками. Статистическая формула
Формула для расчета T-статистики:
t = (x̄1 – x̄2) / (s√((1/n1)+(1/n2)))
Где:
x̄1 и x̄2 – выборочные средние двух выборок
s – объединенное стандартное отклонение двух выборок.
n1 и n2 — размеры двух выборок.
t-статистика рассчитывается путем вычитания среднего значения одной выборки из среднего значения другой выборки. Затем вы должны разделить его на стандартную ошибку разницы между двумя средними значениями. Ошибка оценивается путем суммирования стандартных отклонений выборок.
Пример расчета T-статистики
Предположим, мы хотим проверить, одинаков ли средний вес яблок из двух садов. Мы берем по 10 яблок из каждого сада и записываем их вес. Данные следующие:
Фруктовый сад 1: 100 г, 110 г, 120 г, 130 г, 140 г, 150 г, 160 г, 170 г, 180 г, 190 г
Фруктовый сад 2: 90 г, 100 г, 110 г, 120 г, 130 г, 140 г, 150 г, 160 г, 170 г, 180 г
Мы можем рассчитать выборочные средние значения и стандартные отклонения следующим образом:
х̄1 = 150 г
х̄2 = 130 г
с1 = 36.06 г
с2 = 36.06 г
Теперь мы можем рассчитать статистику t по формуле:
t = (150 – 130) / (36.06 √ ((1/10) + (1/10))) = 2.79
Чтобы определить, является ли эта t-статистика значимой, мы сравним ее с критическим значением t-распределения с 18 степенями свободы (10 + 10 – 2). Нулевая гипотеза о том, что средние веса садов равны, может быть отвергнута. Но это при условии, что статистика t больше критического значения.
В целом, t-статистика является полезным инструментом для проверки гипотез. Это потому, что, как правило, это помогает нам определить, являются ли различия, которые мы наблюдаем в наших данных, статистически значимыми.
Понимание T-статистики
T-статистика — это отношение разницы между оценочными и прогнозируемыми значениями параметра, деленное на стандартную ошибку оценки. Это обычное дело при проверке студенческих гипотез в исследовательской работе и выводах. Как правило, они используются, чтобы выяснить, следует ли принимать нулевую гипотезу. Когда размер выборки мал или стандартное отклонение совокупности неизвестно, вместо z-показателя используется t-статистика. Если стандартное отклонение генеральной совокупности неизвестно, можно использовать t-статистику для оценки средних значений генеральной совокупности на основе выборочного распределения выборочных средних значений. Он также используется в сочетании с p-значением для определения статистической значимости результата проверки гипотезы.
Критическое значение t-статистики зависит от размера выборки, уровня значимости и степеней свободы. Большее значение t-статистики указывает на большую разницу между средними значениями двух сравниваемых групп, а меньшее значение p указывает на более высокий уровень значимости.
В общем, если рассчитанное значение t-статистики больше критического значения из t-распределения, нулевая гипотеза отклоняется в пользу альтернативной гипотезы. Точное отсечение для «хорошего» значения t-статистики зависит от уровня значимости и степеней свободы, но, как правило, t-статистика с абсолютным значением больше 2 считается статистически значимой при уровне значимости 5%.
Важно отметить, что интерпретация значения t-статистики также зависит от конкретного контекста исследования и величины эффекта. Большая t-статистика может быть значимой в одном контексте, но не в другом, в зависимости от величины изучаемого эффекта. Поэтому всегда важно учитывать контекст и размер эффекта при интерпретации значимости значения t-статистики.
Что такое T-статистика по сравнению с P-значением?
Значение t — это инструмент для количественной оценки разницы между средними значениями совокупности для каждого теста, а значение p оценивает вероятность нахождения значения t с абсолютным значением, по крайней мере, таким же большим, как наблюдаемое в выборке данных, если нулевая гипотеза верна.
Что говорит вам T-статистика в регрессии?
Статистику T-теста можно использовать для изучения взаимосвязи между результатом и переменными, используемыми для его прогнозирования. Чтобы определить, равен ли наклон или коэффициент в линейном регрессионном анализе нулю, выполняется одновыборочный t-критерий. При выполнении линейной регрессии одновыборочный t-критерий используется для отклонения нулевой гипотезы о том, что наклон или коэффициент равен 0.
Как рассчитать T-статистику
Определить свой t-тест относительно легко, если вы выполните следующие шаги;
- Найдите среднее значение выборки вашего набора данных
- Затем определите расчетным путем среднее значение генеральной совокупности.
- Используя правильную формулу, рассчитайте стандартное отклонение выборочных данных.
- Рассчитайте t-статистику, используя данные шагов 1-3 и размер выборки, используя приведенный выше расчет.
Как узнать, является ли T Stat значительным?
Статистическая значимость указывается, когда t-показатель значительно отличается от среднего. То есть оно должно сильно отличаться от среднего значения распределения, что вряд ли произойдет случайно, если они не связаны между собой.
Какие три типа t-тестов существуют в статистике?
Три типа статистики t-критерия — это t-критерий с одной выборкой, t-критерий с двумя выборками и парный t-критерий, и они используются для сравнения средних значений.
Что говорит вам большая T-статистика?
Если t имеет высокое значение (высокое отношение), то наблюдаемое расхождение между данными и гипотезой больше, чем можно было бы предсказать, если бы лечение не имело никакого эффекта. В статистическом анализе t-показатель (или t-значение) чаще всего используется, чтобы показать, насколько разные или похожие две группы.
Что такое хорошее статистическое значение T?
Чаще всего приемлемыми считаются значения Т от +2 до -2. Чем больше значение t, тем больше мы уверены, что коэффициент является хорошим предиктором. Если t-значение низкое, предсказательная сила коэффициента слабая.
В чем разница между статистикой Z и T?
Z-тест и T-тест являются статистическими процедурами для анализа данных; оба находят применение в науке, бизнесе и других областях; тем не менее, они отличаются друг от друга. Когда известны и среднее значение (или среднее), и дисперсия (или стандартное отклонение) генеральной совокупности (как это обычно и бывает), можно использовать Т-критерий для проверки нулевой гипотезы о том, что они существенно не отличаются друг от друга. Напротив, Z-тест представляет собой обычный односторонний анализ дисперсионного теста.
Z-тест
Когда размер выборки большой, дисперсии известны, и Z-тест используется для определения того, различаются ли два средних значения совокупности, тест считается надежным и действительным.
Предположения Z-теста
Как правило, Z-тесты основаны на следующих предположениях;
- Результаты каждого эксперимента можно считать отдельными.
- Что касается размеров, размер образцов должен быть до 30
- Предполагая, что среднее значение равно нулю, а дисперсия равна единице, распределение Z является нормальным.
Т-тест
Стьюдентный критерий используется в статистике и в основном используется, когда дисперсия недоступна. T-тест можно использовать, чтобы определить, имеют ли два набора данных разные средние значения.
T-критерии в сочетании с t-распределением используются, когда размеры выборки ограничены, а стандартное отклонение населения неизвестно. Т-распределение принимает форму, которая очень чувствительна к степени свободы. Термин «степень свободы» используется для обозначения количества отдельных точек данных, составляющих конкретный набор данных.
Термин «степень свободы» используется для обозначения количества отдельных точек данных, составляющих конкретный набор данных.
Предположения Т-теста
Т-тест основан на следующих предположениях:
- Небольшой размер выборки
- Точки данных следует считать независимыми.
- Необходимо точно задокументировать количество образцов.
Использование T-статистики
Два наиболее распространенных способа использования t-статистики — это t-критерии Стьюдента, которые представляют собой тип статистической проверки гипотез, и расчет доверительных интервалов.
Статистика t является важным числом, потому что, хотя она дается в терминах выборочного среднего, ее размер выборки не зависит от параметров генеральной совокупности.
Ниже приведены некоторые распространенные варианты использования t-статистики.
№1. Проверка гипотез о населении означает:
Стьюдентный критерий обычно используется для проверки того, существенно ли различаются средние значения двух популяций. Например, исследователь может использовать t-критерий для сравнения среднего веса двух групп людей, чтобы определить, есть ли значительная разница в весе между двумя группами.
Сравнение среднего значения выборки с известным средним значением генеральной совокупности. В некоторых случаях исследователь может захотеть проверить, значительно ли среднее значение выборки отличается от известного среднего значения генеральной совокупности. Для этой цели можно использовать t-тест, сравнивая среднее значение выборки со средним значением генеральной совокупности и вычисляя t-статистику.
№ 2. Доверительные интервалы
Стьюдентная статистика используется для расчета доверительных интервалов для средних значений генеральной совокупности. Доверительный интервал обеспечивает диапазон значений, в пределах которого мы можем быть достаточно уверены в том, что истинное значение генеральной совокупности ложно.
№3. Проверка значимости коэффициентов регрессии:
Стьюдентный тест используется для проверки того, значительно ли оценочные коэффициенты регрессии в модели линейной регрессии отличаются от нуля. Это важно для определения того, оказывают ли независимые переменные в модели значительное влияние на зависимую переменную.
В целом, t-статистика является широко используемым инструментом статистического вывода, особенно при проверке гипотез и оценке параметров популяции.
Другой статистический тест
Помимо t-статистики, существуют и другие подходы к измерению подлинности.
выводов гипотез, некоторые из них приведены ниже;
№1. F-значение
Первым в нашем списке стоит значение F. Лучше всего это работает при анализе дисперсии. Значение f демонстрирует статистическую значимость средних различий и, следовательно, показывает, существует ли корреляция между дисперсиями групп. Этот статистический анализ сравнивает средние значения двух или более образцов, которые можно рассматривать отдельно. Со значением f результаты могут быть приняты или отклонены по двум основаниям;
Во-первых, нулевая гипотеза принимается, если f-значение больше или равно межгрупповой дисперсии. Во-вторых, нулевая гипотеза отклоняется, если f-значение меньше, чем дисперсия в группах выборки.
№ 2. Z-значение
Помимо теста t-статистики, другим важным подходом, который каждый может использовать для измерения гипотез, является тест Z-значения. При сравнении двух популяций, где предполагается, что среднее значение одинаково, это отличный выбор. Профессионал может предпочесть это t-критерию, потому что он дает более точный результат.
Значение Z можно получить по приведенной ниже формуле;
z = (X – μ) / σ
№3. P-значение
Следующим по типам подходов к проверке гипотез является проверка P-значения. У этого самого есть одна цель, и это состоит в том, чтобы отвергнуть или принять нулевую гипотезу. Более низкое значение р больше свидетельствует об отклонении нулевой гипотезы, а большее значение р больше свидетельствует о подтверждении нулевой гипотезы.
Критерий p-значения — это мера статистической значимости, которая рассчитывается с использованием степени свободы теста и оценки, основанной на альфа-значении теста. Степень свободы можно рассчитать, взяв размер выборки n и вычтя 1 (n – 1). Значение p можно оценить, сравнив результат с заданным уровнем альфа.
Статьи по теме
- СТАТИСТИЧЕСКИЙ АНАЛИЗ: виды, методы и цель
- HR АНАЛИТИКА: актуальность, примеры, курсы, вакансии
- ЧТО ОЗНАЧАЕТ СКЕВ: значение, типы и примеры
- Коэффициент ликвидности: виды, формулы и расчеты
- Прогнозная аналитика: определение, примеры и преимущества
- Логотип Tesla: история и значение логотипа
- НОМИНАЛЬНЫЕ ЗНАЧЕНИЯ: определение, важность и отличие
Рекомендации
- https://en.wikipedia.org/
- www.indeed.com
From Wikipedia, the free encyclopedia
A test statistic is a statistic (a quantity derived from the sample) used in statistical hypothesis testing.[1] A hypothesis test is typically specified in terms of a test statistic, considered as a numerical summary of a data-set that reduces the data to one value that can be used to perform the hypothesis test. In general, a test statistic is selected or defined in such a way as to quantify, within observed data, behaviours that would distinguish the null from the alternative hypothesis, where such an alternative is prescribed, or that would characterize the null hypothesis if there is no explicitly stated alternative hypothesis.
An important property of a test statistic is that its sampling distribution under the null hypothesis must be calculable, either exactly or approximately, which allows p-values to be calculated. A test statistic shares some of the same qualities of a descriptive statistic, and many statistics can be used as both test statistics and descriptive statistics. However, a test statistic is specifically intended for use in statistical testing, whereas the main quality of a descriptive statistic is that it is easily interpretable. Some informative descriptive statistics, such as the sample range, do not make good test statistics since it is difficult to determine their sampling distribution.
Two widely used test statistics are the t-statistic and the F-test.
Example[edit]
Suppose the task is to test whether a coin is fair (i.e. has equal probabilities of producing a head or a tail). If the coin is flipped 100 times and the results are recorded, the raw data can be represented as a sequence of 100 heads and tails. If there is interest in the marginal probability of obtaining a tail, only the number T out of the 100 flips that produced a tail needs to be recorded. But T can also be used as a test statistic in one of two ways:
- the exact sampling distribution of T under the null hypothesis is the binomial distribution with parameters 0.5 and 100.
- the value of T can be compared with its expected value under the null hypothesis of 50, and since the sample size is large, a normal distribution can be used as an approximation to the sampling distribution either for T or for the revised test statistic T−50.
Using one of these sampling distributions, it is possible to compute either a one-tailed or two-tailed p-value for the null hypothesis that the coin is fair. Note that the test statistic in this case reduces a set of 100 numbers to a single numerical summary that can be used for testing.
Common test statistics[edit]
One-sample tests are appropriate when a sample is being compared to the population from a hypothesis. The population characteristics are known from theory or are calculated from the population.
Two-sample tests are appropriate for comparing two samples, typically experimental and control samples from a scientifically controlled experiment.
Paired tests are appropriate for comparing two samples where it is impossible to control important variables. Rather than comparing two sets, members are paired between samples so the difference between the members becomes the sample. Typically the mean of the differences is then compared to zero. The common example scenario for when a paired difference test is appropriate is when a single set of test subjects has something applied to them and the test is intended to check for an effect.
Z-tests are appropriate for comparing means under stringent conditions regarding normality and a known standard deviation.
A t-test is appropriate for comparing means under relaxed conditions (less is assumed).
Tests of proportions are analogous to tests of means (the 50% proportion).
Chi-squared tests use the same calculations and the same probability distribution for different applications:
- Chi-squared tests for variance are used to determine whether a normal population has a specified variance. The null hypothesis is that it does.
- Chi-squared tests of independence are used for deciding whether two variables are associated or are independent. The variables are categorical rather than numeric. It can be used to decide whether left-handedness is correlated with height (or not). The null hypothesis is that the variables are independent. The numbers used in the calculation are the observed and expected frequencies of occurrence (from contingency tables).
- Chi-squared goodness of fit tests are used to determine the adequacy of curves fit to data. The null hypothesis is that the curve fit is adequate. It is common to determine curve shapes to minimize the mean square error, so it is appropriate that the goodness-of-fit calculation sums the squared errors.
F-tests (analysis of variance, ANOVA) are commonly used when deciding whether groupings of data by category are meaningful. If the variance of test scores of the left-handed in a class is much smaller than the variance of the whole class, then it may be useful to study lefties as a group. The null hypothesis is that two variances are the same – so the proposed grouping is not meaningful.
In the table below, the symbols used are defined at the bottom of the table. Many other tests can be found in other articles. Proofs exist that the test statistics are appropriate.[2]
| Name | Formula | Assumptions or notes | |
|---|---|---|---|
| One-sample z-test | 
|
(Normal population or n large) and σ known.
(z is the distance from the mean in relation to the standard deviation of the mean). For non-normal distributions it is possible to calculate a minimum proportion of a population that falls within k standard deviations for any k (see: Chebyshev’s inequality). |
|
| Two-sample z-test | 
|
Normal population and independent observations and σ1 and σ2 are known where  is the value of is the value of  under the null hypothesis under the null hypothesis
|
|
| One-sample t-test | 
|
(Normal population or n large) and  unknown unknown
|
|
| Paired t-test | 
|
(Normal population of differences or n large) and  unknown unknown
|
|
| Two-sample pooled t-test, equal variances | 
|
(Normal populations or n1 + n2 > 40) and independent observations and σ1 = σ2 unknown | |
| Two-sample unpooled t-test, unequal variances (Welch’s t-test) | 
|
(Normal populations or n1 + n2 > 40) and independent observations and σ1 ≠ σ2 both unknown | |
| One-proportion z-test | 
|
n .p0 > 10 and n (1 − p0) > 10 and it is a SRS (Simple Random Sample), see notes. | |
Two-proportion z-test, pooled for 
|

|
n1 p1 > 5 and n1(1 − p1) > 5 and n2 p2 > 5 and n2(1 − p2) > 5 and independent observations, see notes. | |
Two-proportion z-test, unpooled for 
|

|
n1 p1 > 5 and n1(1 − p1) > 5 and n2 p2 > 5 and n2(1 − p2) > 5 and independent observations, see notes. | |
| Chi-squared test for variance | 
|
df = n-1
• Normal population |
|
| Chi-squared test for goodness of fit | 
|
df = k − 1 − # parameters estimated, and one of these must hold.
• All expected counts are at least 5.[4] • All expected counts are > 1 and no more than 20% of expected counts are less than 5[5] |
|
| Two-sample F test for equality of variances | 
|
Normal populations Arrange so  and reject H0 for and reject H0 for  [6] [6]
|
|
Regression t-test of 
|

|
Reject H0 for  [7] [7]*Subtract 1 for intercept; k terms contain independent variables. |
|
In general, the subscript 0 indicates a value taken from the null hypothesis, H0, which should be used as much as possible in constructing its test statistic. … Definitions of other symbols:
|
See also[edit]
- Null distribution
- Likelihood-ratio test
- Neyman–Pearson lemma
= coefficient of determination
- Sufficiency (statistics)
References[edit]
- ^ Berger, R. L.; Casella, G. (2001). Statistical Inference, Duxbury Press, Second Edition (p.374)
- ^ Loveland, Jennifer L. (2011). Mathematical Justification of Introductory Hypothesis Tests and Development of Reference Materials (M.Sc. (Mathematics)). Utah State University. Retrieved April 30, 2013. Abstract: “The focus was on the Neyman–Pearson approach to hypothesis testing. A brief historical development of the Neyman–Pearson approach is followed by mathematical proofs of each of the hypothesis tests covered in the reference material.” The proofs do not reference the concepts introduced by Neyman and Pearson, instead they show that traditional test statistics have the probability distributions ascribed to them, so that significance calculations assuming those distributions are correct. The thesis information is also posted at mathnstats.com as of April 2013.
- ^ a b NIST handbook: Two-Sample t-test for Equal Means
- ^ Steel, R. G. D., and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 350.
- ^ Weiss, Neil A. (1999). Introductory Statistics (5th ed.). pp. 802. ISBN 0-201-59877-9.
- ^ NIST handbook: F-Test for Equality of Two Standard Deviations (Testing standard deviations the same as testing variances)
- ^ Steel, R. G. D., and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.)


































