
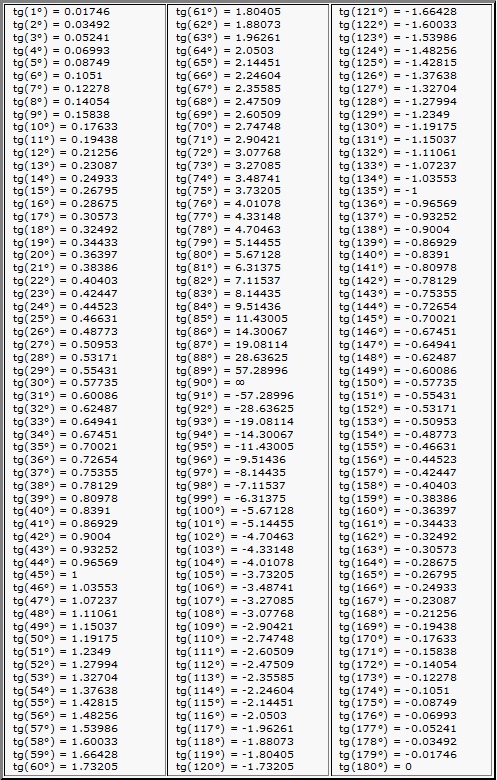
Измерение углов и определение их математических свойств является важной составляющей понимания основ геометрии. В математике существует шесть функций циклических углов, основными из которых являются синус, косинус и тангенс. В данной статье мы углу погрузимся в изучение значения тангенса угла и как его найти.
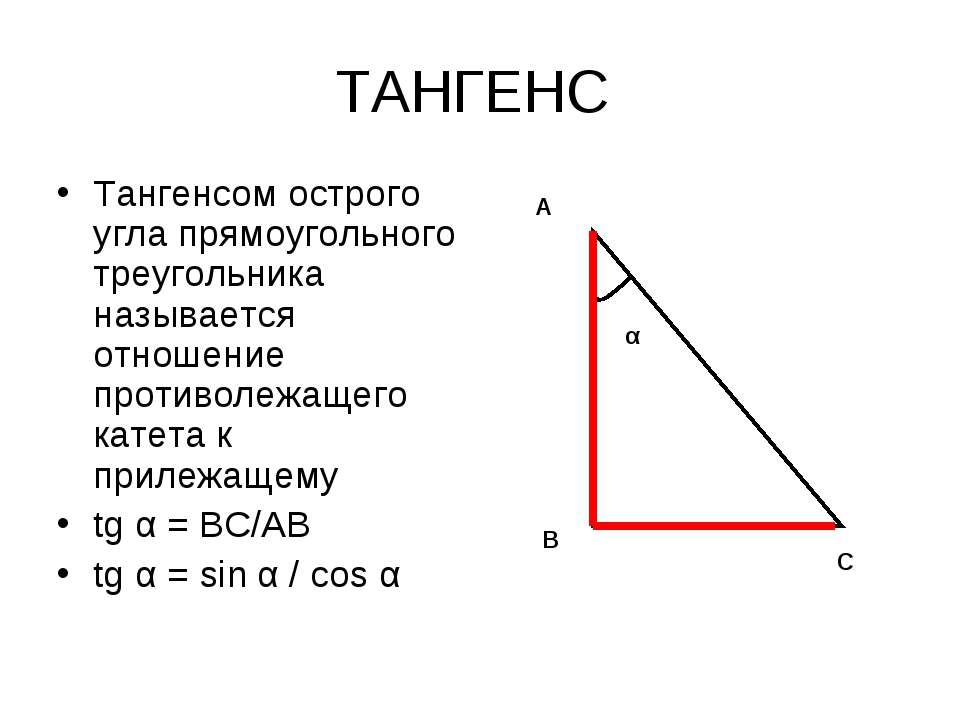
Тангенс – это математическая функция, которая позволяет найти соотношение между противоположными и прилегающими сторонами в прямоугольном треугольнике. Он определяется как соотношение противолежащей стороны к прилежащей стороне при измерении данного угла. Наряду с синусом и косинусом тангенс рассматривается как составная часть комплекса тригонометрических функций.
В предыдущих работах мы уже изучали основы, такие как: математическую интерпретацию угла, геометрические методы измерения углов и определения соотношений сторон прямоугольного треугольника. Сейчай статье будет более акцентировано внимания на понятии тенгенса, его свойств и способах вычисления. Пора провести исследование на поприще геометрии и углубленные знания, пусть наши знания и опыт помогут тебе больше узнать об основных треугольных функциях и их практической пользе.
Основы теории углов
Определение угла

Углом называется фигура, отграниченная двумя половинами прямой, возникающая при пересечении двух прямых линий. Углы можно классифицировать по величине, направлению и положению. Величина угла определяется по радиусу окружности, вписанной в угол – количеством градусов или радианов этого угла.
Система углов
Существует три основных системы, используемых для измерения углов: градусная, радианная и град-минутная. Градусная система основана на 360 градусов, которые делятся на минуты (60 в 1 градусе) и секунды (60 в 1 минуте) для более точной конструкции этих величин. Радианная система основана на радиане, который равен длине дуги окружности, которая соответствует единичному радиусу.
| Система измерения | Число углов | Размер единичного угла |
|---|---|---|
| Градусная | 360 | 1 градус |
| Радианная | 2π | 1 радиан |
| Град-минутная | 360 | 1 минута (1/60 градуса) |
Тригонометрия
Тригонометрия – это раздел математики, который изучает отношения между сторонами и углами треугольника. Кроме того, тригонометрические функции также используются для интерполяции функций и решении линейных дифференциальных уравнений. Три основополагающих тригонометрических функция – синус, косинус и тангенс – используются для анализа и вычисления углов.
Основы теории углов являются неотъемлемой частью изучения практически всех областей математики и требуют тщательного и глубокого изучения.
Наиболее важным в данном разделе служат три основные тригонометрические функции: синус (tg), косинус (cos) и тангенс (tg). Теперь мы пойдем немного глубже, чтобы рассмотреть более подробно каждую из этих функций.
Синус и косинус угла
Синус и косинус угла можно определить, используя размеры сторон прямоугольного треугольника (триугольника с одним прямым углом).
Синус угла равен отношению противолежащей стороны к гипотенузе, которые являются частью угла. Если у вас есть три пропорциональные стороны треугольника определены как a, b и c, где c = гипотенуза, а a и b являются прилежащими сторонами угла, тогда синус (tg) угла можно найти следующим образом:
tg = a / c.
В то же время, косинус определяется как отношение косвенной стороны к гипотенузе в том же треугольнике. Затем он вызывается:
cos = b / c.
Эти функции позволяют нам определить отношения между углами и сторонами треугольника, и это влияет на многое – от покрытия зданий до изучения приложений небесной механики.
Так как найти tg угла?
Тангенс угла может быть найден путём деления синуса угла на косинус угла следующим образом:
tg = sin / cos.
Важно помнить, что тангенс угла может быть имее как положительное, так и отрицательное значение, в зависимости от угла, который мы рассматриваем. К счастью, вы можете использовать компьютерные программы или калькуляторы для более точных вычислений содержащих гипотенузу, прямые и противолежащие стороны a, b и c.
Теперь, уже получив и представя фундаментальной информаци, ваш путь к пониманию тg угла намного проще и понятнее.
Связь физки с геометрией
Общие принципы
-
Геометрия служит основой для описания физических пространств и явлений. Геометрические концепции, такие как точки, линии, плоскости, размерности, являются фундаментальными для описания физических объектов и взаимодействий между ними.
-
Физические законы и законы геометрии взаимосвязаны. Например, законы сохранения энергии, импульса и моментора отвечают за неизменность геометрических свойств системы при её изменении во времени.
Связь физки с геометрией в анализе угла
Анализ угла и нахождение его тангенса являются непосредственным применением физических и геометрических принципов. В чистых геометрических рамках мы имеем дело с углами, равными 90 градусов. Однако, в равнобедренном треугольнике, где оба катета равны, даже если угол меньше 90 градусов, мы по прежнему можем найти тангенс угла, используя аналог формулы Герона.
Если есть равнобедренный треугольник c основанием a и боковыми сторонами a ± h, тангенс угла α между соседними сторонами можно вычислить по формуле:
tan(α) = h / a + h, если h > 0
tan(α) = h / a – h, если h < 0
В физическом контексте тангенс угла может быть связан с различными физическими величинами. Например, в оптиках используется эффект Аббе, который характеризует зависимость степени поляризации света от угла наклона света к кристаллу. Здесь тангенс угла является мерой нелинейности дифракции в кристалле и может быть связан с другими физическими величинами, такими как дисперсионная константа, коэффициент подвижности и т.д.
Физические законы и геометрические свойства

В физике многие законы выражаются через математические формулы и специализированные геометрии. Некоторые примеры:
-
Законы движения Ньютона основаны на геометрических свойствах пространства и времени, определяя претерпевающее перемещения тела и меняющееся направление.
-
Интерпретация Вейерштрасса гармонических функций представляет теорию электростатики и магнитных полей в физке и геометрии, используя математические функции для описания электромагнитного поля в пространстве и времени.
-
Теория относительности Эйнштейна использует геометрию для описания пространства-времени в гравитационных полях, превращая электромагнитное поля в геометрические изменения.
Заключение
Физика и геометрия внимательно взаимодействуют с момента начала развития науки. Проблемы, затрагивающие каждую область, становятся в конечном итоге доступными для решения и интуитивной интерпретации при помощи второй науки. Данная связь не ограничивается вопросами угла и его тангенса, но мы можем исходить из педагогической точки зрения, что отображение объектов и их свойств в геометрических формах значительно облегчает и улучшает понимание ключевых принципов физики для будущего поколения ученых и инженеров.
Термины и определения
Прежде чем погрузиться в процесс нахождения tg угла, необходимо быть знакомым с некоторыми ключевыми терминами и определениями, связанными с тригонометрическими функциями.
Косинус (cos)

Косинус угла – это отношение длины邻стороны гипотенузы в прямоугольном треугольнике. Выражение для косинуса выглядит так:
cos(угол) = adjacent/hypotenuse
Синус (sin)
Синус угла – это отношение длиныoppositeстороны к гипотенузе в прямоугольном треугольнике. Выражение для синуса выглядит так:
sin(угол) = opposite/hypotenuse
Тангенс (tg)
Тангенс угла – это относиение длиныoppositeстороны к длинеadjacentстороны в прямоугольном треугольнике. Выражение для тангенса выглядит так:
tg(угол) = opposite/adjacent
Катеты и стороны треугольника
В прямоугольном треугольнике катетами называются два угламиadjacent стороны иopposite сторона . Гипотенуза – это самая длинная сторона треугольника, находящаяся противоположного прямого угла.
Примеры
Рассмотрим следующие данные треугольника:
adjacent = 5, opposite = 12 и гипотенуза = 13
- cos = 5/13
- sin = 12/13
- Тангенс угла можно найти путем деления sin на cos, то есть,
(12/13) / (5/13)= 2,4.
Связь между функциями
Существует взаимосвязь между синусом, косинусом и тангенсом:
- tg(угол) = sin(угол) / cos(угол)
- cos(угол) = 1 / √[1 + (sin(угол))^2]
- sin(угол) =tg(угол) / cos(угол)
Это взаимосвязь позволяет вычислять соответствующие тригонометрические величины без прямого использования их определений через стороны треугольников.
Методы измерения углов
Методы на основе специальных инструментов
Перед рассмотрением методов измерения углов, стоит напомнить, что угол в сферической и эллиптической системе координат суммируется до 360 градусов. Углы плоскости суммируются со 180 градусов.
- Гномон – первый инструмент для измерения высот солнца и, соответственно, определения текущего времени суток. Он состоит из горизонтальной доски и вертикальной палочки (пикели, клинчало). Вертикальная рукавина отбрасывает тень на горизонтальную доску.
- Планшет солнца – прибор для измерения высоты Солнца. Работает на принципе увеличения изображения солнечных лучей через систему линз или призм. Менее чувствителен к атмосферным особенностям, чем гномон или квадрант.
- Диагель (диагель воздушный, самописец) – изобретен в XVII веке. Небольшой усовершенствованный квадрант с автоматическим письмом, использующий пружину для измерения высоты Солнца и луны к горизонту.
- Квадрант с ранцем (античная таблица для навигации, гнилой квадрант, квадрант Нострадамуса) – прибор для измерения высоты солнца или звезд к горизонту, чтобы определить широту.
- Секстант – усовершенствованный квадрант с микроскопом и баклетом, чтобы точно измерить дугу. Представляет собой важный для мореплавания инструмент навигации, поскольку позволяет использовать все данные отеля, наблюдая значения с этого инструмента. Угломер на самом деле позволяет определять угол отклонения точек небесной сферы от горизонта любыми трехмерными координатами нашей местности. В сферической системе координат, это мы называем горизонтальным углозоречением, т.е. высота солнца или звезд по точкам между собой.
Методы на основе традиционных инструментов
Также есть традиционные инструменты, на которых для измерения углов могут использоваться:
- Прямоугольник – это инструмент, состоящий из двух длинных палочек, которые закреплены под прямым углом. Используется в строительстве для измерения квадратов поверхностей, углов и др.
- Прямый угловник – предназначен для проверки угловой точности сразу трех плоскостей (также называется триметром). Есть специальный угломер и настенный маятник, созданный для высокой точности измерения.
- Пентаграмма – геометрический угломер, который позволяет измерять углы, встречающиеся в строительстве, достаточно точно.
- Астролябия – аналог квадранта, первоначально разработанного древнегреческим математиком и философом Платоном. Астролябий имеет рукоять красного цвета, равнобедренный треугольник и подставку, похожую на таблу для рисования.
Методы, основанные на основе опытов
Существуют опыты, основанные на методах измерения углов, которые можно проводить дома, такие как:
- Прямые углы в КПП (угол между тремя звездообразными широкими точками может быть любой величины).
- Проверка прямого угла углублением (проверка прямого угла методом составителя для определения его точности).
- Определение ориентировки север-юг (для ориентации своих сооружений или определения направления).
Использование данных методов позволяет находить точные и надёжные результаты измерений углов, в зависимости от потребностей и обстоятельств, в которых может оказаться респондент.
Применение теории углов
Применение в строительстве и архитектуре
Работая над проектом дома, инженера-строителя или архитектора могут использовать теорию углов для обеспечения прочности и устойчивости конструкций. Тенанд, площадь здания или высоту и создания интересной архитектуры, углы являются важнейшим элементом.
- Планирование архитектуры и дизайна помещений
- Структурное проектирование: вычисление гидравлических усовершенствований, статической устойчивости, и т.д.
- Прочностного расчета и проектирования железобетонных изделий
Применение в навигации и спутниковой технологии

Теория углов имеет важное значение в области навигации и экстренных сигналов радиолокационной связи. Когда нейроидные навигационные системы и ИНС используются для браузера реального времени местоположения, вычисления углов являются ключевым шагом в расчете траектории движения объектов.
- Сальтиллибратура: методика определения местоположения объектов на основе измерения углов, под которыми они видны из различных точек.
- Спутниковое навигационное оборудование, такое как GPS или ГЛОНАСС, использует теорию углов для точного определения местоположения на земной поверхности.
- Планирование маршрута и безопасности: морпехи и другие морские каппелери используют теорию углов для разработки эффективной науки управления движением и меньшего риска посесу.
На основе вышеуказанных примеров, становится очевидным, что теории углов не только сильно помогает нам понять микопору построения клина или треугольника тейблгейтоуров, тут и много исторических данных и числовой анализ теорий треугольников Тао, Сокра́тонеа и других ученых, которые посвятили свои жизни изучению этих явлений.
Практические примеры
Прежде чем приступить к рассмотрению практических примеров нахождения тангенса угла, необходимо определить, какими методами можно вычислять значение тангенса.
Методы вычисления тангенса угла
- Использование таблицы функции тангенса;
- Использование графического или карманного калькулятора;
- Использование формул и определения тангенса.
Примеры
-
Пример 1: найти тангенс угла, равного 30 градусам.
Используя таблицу функций, значение тангенса угла 30 градусов равно 0,5.
-
Пример 2: найти тангенс угла, равного 45 градусов.
Используя определение синуса и косинуса, тангенс угла 45 градусов будет равен синусу угла, деленному на косинус угла, или косинус угла, деленному на синус угла. Так как пропорции в равностороннем треугольнике равны, синус 45 и косинус 45 также равны, получим, что тангенс 45 градусов равен 1.
-
Пример 3: найти тангенс угла, равного 60 градусов.
Для нахождения тангенса угла 60 градусов можно воспользоваться теоремой Пифагора в равностороннем треугольнике. Получим равенство: тангенс 60 градусов = (товар/гипотенуза) = (общая сторона/половина основы) = (корень из 3)/1 = корень из 3.
В процессе решения практических примеров необходимо быть внимательным к точности вычисления тангенса в зависимости от выбранного метода. Использование таблиц или графических калькуляторов может обеспечить большую точность, чем ручные вычисления по формулам и определениям.
Вопрос-ответ:
Какие соотношения используются для нахождения тангенса угла?
Для нахождения тангенса угла мы используем соотношение сторон прилежащей и противолежащей. Тангенс (tg) угла равен отношению противолежащей стороны к прилежащей стороне треугольника: tg = противолежащая / прилежащая. Это соотношение основывается на теореме синусов и тангенсов и широко применяется в тригонометрии. Поэтому, чтобы найти тангенс угла, мы должны знать длины противолежащей и прилежащей сторон некоторого угла.
Могут ли существовать треугольники, для которых нельзя найти тангенс угла?
Да, существуют такие треугольники. Например, если данный треугольник прямоугольный и угол находится у гипотенузы, то для него определить тангенс угла невозможно, так как противолежащей стороны нет. Кроме того, для любых треугольников, у которых противолежащая и прилежащая стороны равны, тангенс угла будет равен единице, что также не даёт возможности однозначно рассчитать угол. Все эти случаи накладывают ограничения на способность определять тангенс угла.
Как определить тангенс угла, если треугольник не является прямоугольным?
Для определения тангенса угла в непрямоугольном треугольнике необходимо использовать методы и технику, связанную с тригонометрией и её применением в различных геометрических ситуациях. В этом случае соотношение сторон будет не столь очевидным, как в прямоугольном треугольнике. Для вычисления тангенса угла и подобных величин сюда необходимо привлечь другие тригонометрические функции – синус, косинус и так далее, а также применять более сложные теоремы и формулы. В общем случае определить тангенс угла в непрямоугольном треугольнике является более сложной задачей, чем в прямоугольном.
Могут ли противоречиться значения тангенса угла друг другу и в чем заключается проблема?
Да, значения тангенса угла могут противоречить друг другу на одном и том же углу в зависимости от контекста и ситуации. Например, в системе с отрицательными углами значения тангенсов могут варьироваться в более широких пределах (-∞, +∞) в зависимости от выбранного угла и соответствующих сторон треугольника. В результате такого отсутствия однозначности тщательное интерпретирование и анализ данных на уровне конкретной ситуации являются необходимостью для правильного решения проблемы.