7. Взаимосвязь функции и ее производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Значение производной в точке касания как тангенс угла наклона
Если к кривой (f(x)) проведена касательная в точке с абсциссой (x_0), то
[{large{color{royalblue}{f'(x_0)=mathrm{tg}, alpha, }}},]
где (alpha) – угол наклона касательной.
Значит, верна формула: (f'(x_0)=mathrm{tg}, alpha=k).
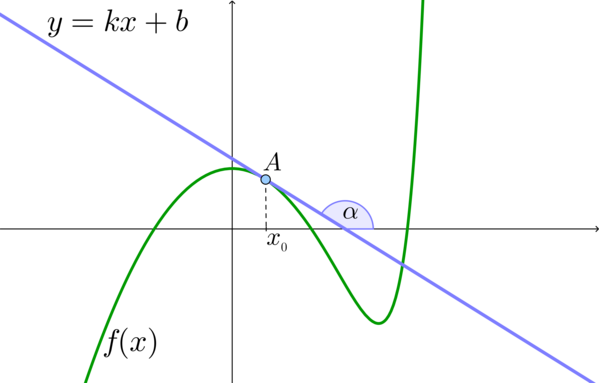
Заметим, что координаты точки (A) тогда можно записать как ( (x_0; f(x_0)) ) или ( (x_0; y_0) ),
где ( y_0=kx_0+b).
То есть ( y_0=f(x_0)).
Задание
1
#2090
Уровень задания: Равен ЕГЭ
На рисунке изображены график функции (y = f(x)) и касательная к нему в точке с абсциссой (x_0). Найдите значение производной функции (f(x)) в точке (x_0).
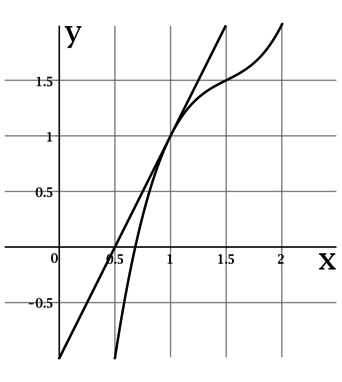
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))) (то есть угла между касательной к графику (f(x)) в точке ((x_0; f(x_0))) и положительным направлением оси (Ox)).
По рисунку видно, что касательная проходит через точки ((0,5; 0)) и ((1; 1)), тогда тангенс угла наклона касательной составляет (1 : 0,5
= 2), следовательно, (f'(x_0) = 2).
Ответ: 2
Задание
2
#2091
Уровень задания: Равен ЕГЭ
На рисунке изображены график функции (y = f(x)) и касательная к нему в точке с абсциссой (x_0). Найдите значение производной функции (f(x)) в точке (x_0).
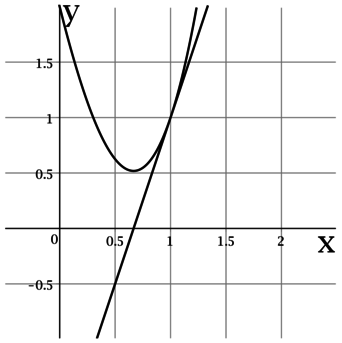
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))).
По рисунку видно, что касательная проходит через точки ((0,5; -0,5)) и ((1; 1)), тогда тангенс угла наклона касательной составляет (1,5 :
0,5 = 3), следовательно, (f'(x_0) = 3).
Ответ: 3
Задание
3
#2092
Уровень задания: Равен ЕГЭ
На рисунке изображены график функции (y = f(x)) и касательная к нему в точке с абсциссой (x_0). Найдите значение производной функции (f(x)) в точке (x_0).
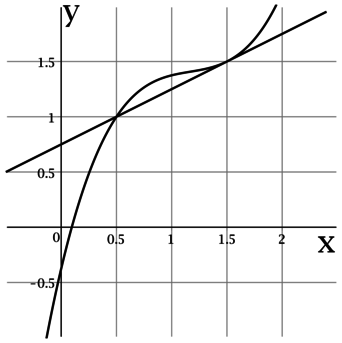
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))).
По рисунку видно, что касательная проходит через точки ((0,5; 1)) и ((1,5; 1,5)), тогда тангенс угла наклона касательной составляет (0,5
: 1 = 0,5), следовательно, (f'(x_0) = 0,5).
Ответ: 0,5
Задание
4
#2093
Уровень задания: Равен ЕГЭ
На рисунке изображены график функции (y = f(x)) и касательная к нему в точке с абсциссой (x_0). Найдите значение производной функции (f(x)) в точке (x_0).
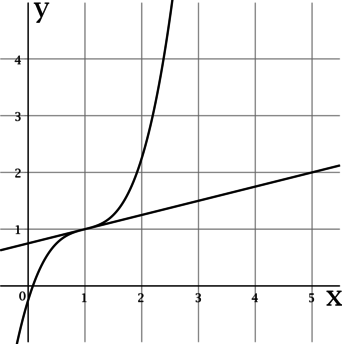
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))).
По рисунку видно, что касательная проходит через точки ((1; 1)) и ((5; 2)), тогда тангенс угла наклона касательной составляет ((2 – 1)
: (5 – 1) = 0,25), следовательно, (f'(x_0) = 0,25).
Ответ: 0,25
Задание
5
#3112
Уровень задания: Равен ЕГЭ
На рисунке изображен график функции (y=f(x)) и отмечены точки (-2;
0; 2; 8). В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
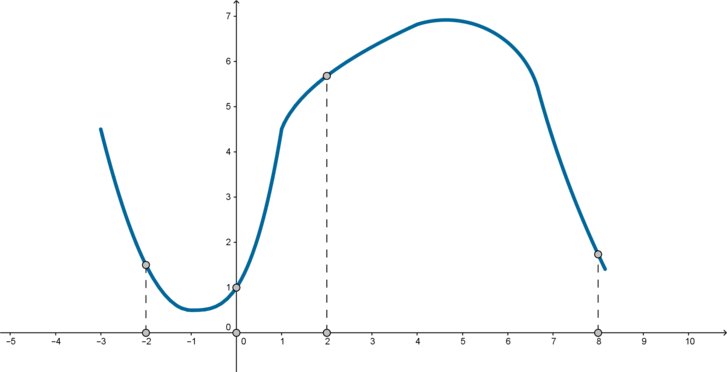
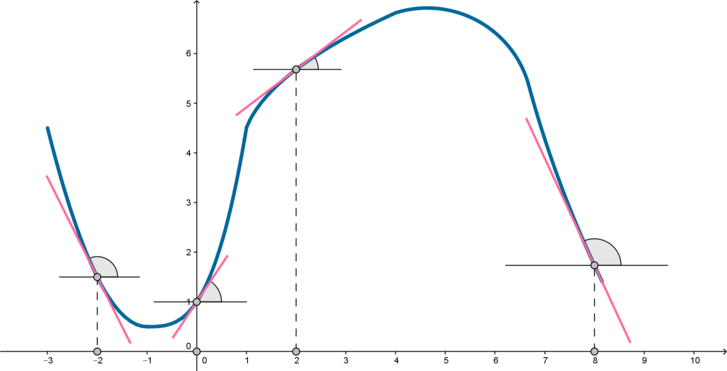
Проведем касательные к графику функции в этих точках. Так как тангенс угла (alpha) наклона касательной равен значению производной (f'(x)) в точке касания (x_0) ((f'(x_0)=mathrm{tg},alpha)), то нужно сравнить тангенсы углов, отмеченных на рисунке.
Вспомним, что если угол тупой, то его тангенс отрицательный, если острый – положительный. Следовательно, так как мы ищем наибольший тангенс, имеет смысл рассматривать только острые углы. Это углы, образованные касательными в точках (0) и (2). Заметим, что угол в точке (0) больше, следовательно, его тангенс также больше, чем тангенс угла в точке (2). Таким образом, ответ: (0).
Ответ: 0
Задание
6
#718
Уровень задания: Сложнее ЕГЭ
Производная (f'(x)) функции (f(x)) в точке (x_0) равна (10). Найдите котангенс угла наклона касательной к графику функции (f(x)) в точке ((x_0; f(x_0))).
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))).
При всех (alpha), при которых (mathrm{tg}, alpha) и (mathrm{ctg}, alpha) имеют смысл, выполнено (mathrm{tg}, alphacdotmathrm{ctg}, alpha = 1), откуда котангенс угла наклона касательной к графику функции (f(x)) в точке ((x_0; f(x_0))) равен (0,1).
Ответ: 0,1
Задание
7
#719
Уровень задания: Сложнее ЕГЭ
Производная (f'(x)) функции (f(x)) в точке (x_0) равна (5). Найдите сумму тангенса и котангенса угла наклона касательной к графику функции (f(x)) в точке ((x_0; f(x_0))).
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))).
При всех (alpha), при которых (mathrm{tg}, alpha) и (mathrm{ctg}, alpha) имеют смысл, выполнено (mathrm{tg}, alphacdotmathrm{ctg}, alpha = 1), откуда котангенс угла наклона касательной к графику функции (f(x)) в точке ((x_0; f(x_0))) равен (0,2), тогда сумма тангенса и котангенса угла наклона касательной к графику функции (f(x)) в точке ((x_0; f(x_0))) равна (5,2).
Ответ: 5,2

УСТАЛ? Просто отдохни
Как найти тангенс угла наклона касательной
Геометрический смысл производной первого порядка функции F(х) представляет собой касательную прямую к ее графику, проходящую через заданную точку кривой и совпадающую с ней в этой точке. Причем значение производной в данной точке х0 является угловым коэффициентом или иначе – тангенсом угла наклона касательной прямой k = tg a = F`(х0). Вычисление данного коэффициента – одна из наиболее распространенных задач теории функций.

Инструкция
Запишите заданную функцию F(x), например F(x) = (x³ + 15х +26). Если в задаче явно указана точка, через которую проводится касательная, например, ее координата х0 = -2, можно обойтись без построения графика функции и дополнительных прямых на декартовой системе ОХY. Найдите производную первого порядка от заданной функции F`(x). В рассматриваемом примере F`(x) = (3x² + 15). Подставьте заданное значение аргумента х0 в производную функции и вычислите ее значение: F`(-2) = (3(-2)² + 15) = 27. Таким образом, вы нашли tg a = 27.
При рассмотрении задачи, где требуется определить тангенс угла наклона касательной к графику функции в точке пересечения этого графика с осью абсцисс, вам понадобится сначала найти числовое значение координат точки пересечения функции с ОХ. Для наглядности лучше всего выполнить построение графика функции на двухмерной плоскости ОХY.
Задайте координатный ряд для абсцисс, например, от -5 до 5 с шагом 1. Подставляя в функцию значения х, вычислите соответствующие им ординаты у и отложите на координатной плоскости полученные точки (х, у). Соедините точки плавной линией. Вы увидите на выполненном графике место пересечения функцией оси абсцисс. Ордината функции в данной точке равна нулю. Найдите численное значение соответствующего ей аргумента. Для этого заданную функцию, например F(x) = (4x² – 16), приравняйте к нулю. Решите полученное уравнение с одной переменной и вычислите х: 4x² – 16 = 0, x² = 4, х = 2. Таким образом, согласно условию задачи, тангенс угла наклона касательной к графику функции необходимо найти в точке с координатой х0 = 2.
Аналогично описанному ранее способу определите производную функции: F`(x) = 8*x. Затем вычислите ее значение в точке с х0 = 2, что соответствует точке пересечения исходной функции с ОХ. Подставьте полученное значение в производную функции и вычислите тангенс угла наклона касательной: tg a = F`(2) = 16.
При нахождении углового коэффициента в точке пересечения графика функции с осью ординат (ОY) выполните аналогичные действия. Только координату искомой точки х0 сразу следует принять равной нулю.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Функция тангенса: формула, свойства, график
Содержание:
- Что такое тангенс
- Что такое функция тангенса: формула
- Свойства функции
- Как построить график
- Примеры решения задач
Что такое тангенс
Тангенсом какого-либо острого угла (alpha (tg alpha)) называют величину, выражающую отношение противоположного катета (а) к прилегающему катету (b) в треугольнике с углом 90°, то есть: (tg alpha = frac{a}{b})
Понятие тангенса угла можно проиллюстрировать таким образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Источник: microexcel.ru
Пример 1
Рассмотрим наглядный пример. Предположим, что катеты в треугольнике из определения тангенса имеют следующие значения: a = 3 b = 4 В таком случае справедливо записать выражение для расчета тангенса угла: (tg alpha = frac{a}{b} = frac{3}{4} = 0,75)
Что такое функция тангенса: формула
При решении задач можно нередко встретить примеры с тригонометрическими функциями, в том числе, функцией тангенса. Эта функция обладает специфическими свойствами, которые значительно упрощают вычисления. Запись имеет следующий вид:
(у = tg х)
Здесь х обозначает аргумент тригонометрической функции и играет роль независимой переменной, а у определяет непосредственно функцию, то есть зависимую переменную.
Свойства функции
С помощью знаний свойств функций в тригонометрии достаточно просто решать самые сложные и громоздкие примеры. Перечислим закономерности, характерные для функции тангенса:
- Функция тангенса определяется в области ((xnefracpi2+pi k)), то есть на множестве, в состав которого включены действительные числа, за исключением точек, характеризующихся нулевым значением для косинуса.
- Функция на графике не имеет ограничений в верхней и нижней части, поэтому ее область значений можно записать как (yinmathbb{R}).
- Функция тангенса является нечетной, что целесообразно записать в виде соотношения (tg(-x)=-tgx).
- Тригонометрическая функция тангенса является периодической, а ее период составляет pi. Таким образом:(tg(x+pi k)=tgx) .
- Стремление функции (к +infty) можно наблюдать при сближении с левой стороны с точками (x=fracpi2+pi k). Приближение к точке, обозначенной за a, слева формулируют таким образом: (xrightarrow) (a-0 lim_{xrightarrowfracpi2+pi k-0} tgx=+infty) .
- Стремление функции (к -infty) можно наблюдать при сближении с правой стороны с точками (x=fracpi2+pi k). Приближение к точке, обозначенной за а, справа следует зафиксировать как (xrightarrow) (a+0 lim_{xrightarrowfracpi2+pi k+0} tgx=-infty).
- Нули рассматриваемой функции (y_{0}=0) определены точками (x_0=pi k).
- Возрастание функции можно наблюдать на всей области, где она определена.
- Функция разрывается в точках (x=fracpi2+pi k), которые пересечены вертикальными асимптотами. На отрезках между ними функция не прерывается, то есть (left(-fracpi2+pi k; fracpi2+pi kright).)
- Функция не обладает максимальными и минимальными значениями.
Как построить график
Как и любую другую тригонометрическую функцию, тангенс достаточно просто изобразить в системе координат. Графическое изображение функции тангенса в обобщенном виде представлено на рисунке ниже:
Источник: microexcel.ru
Построить график функции тангенса несложно. Нужно лишь последовательно выполнять действия согласно стандартному алгоритму:
- определить контрольные точки для построения;
- начертить плавную кривую линию на плоскости координат;
- для выбранного промежутка построить значения, которые расположены симметрично по отношению к началу координат;
- так как для значений функции характерны повторы с некоторым периодом, то целесообразно скопировать график для каждого из промежутков области определения;
- в результате получен график под названием тангенсоида.
Примеры решения задач
Задача 1
Требуется путем применения свойств тригонометрической функции, изученных в теоретическом разделе, записать область определения для следующей функции: (y=text{tg}left( 2x+frac{pi }{3} right))
Решение
Зная, что функция тангенса не может быть определена в точках при нулевом значении косинуса, запишем справедливое соотношение и выполним необходимые преобразования:
(cos left( 2x+frac{pi }{3} right)=0)
(2x+frac{pi }{3}ne frac{pi }{2}+pi n,nin Z)
(xne frac{pi }{12}+frac{pi n}{2},nin Z)
В результате получена область, в которой определена функция из условия задания:
(D(y)=left( -frac{pi }{12}+frac{pi n}{2},frac{pi }{12}+frac{pi n}{2} right),nin Z)
Ответ: (D(y):xin left( -frac{pi }{12}+frac{pi n}{2},frac{pi }{12}+frac{pi n}{2} right),nin Z)
Задача 2
Дано уравнение, решение которого требуется найти: (sin 2x-sqrt{3}cos 2x=0)
Решение
Выполним преобразования исходного соотношения. В результате получим:
(sin 2x=sqrt{3}cos 2x)
После деления всех частей записи на выражение (cos 2x) соотношение изменится таким образом:
(text{tg}2x=sqrt{3})
При этом ОДЗ для полученного выражения примет следующий вид:
(left( -frac{pi }{4}+frac{pi n}{2},frac{pi }{4}+frac{pi n}{2} right),nin Z.)
Далее целесообразно приступить к решению уравнения:
(2=frac{pi }{3}+pi n,nin Z)
(x=frac{pi }{6}+frac{pi n}{2},nin Z)
Заметим, что корни, которые получились по итогам расчетов, соответствуют ОДЗ. Можно записать ответ.
Ответ: (x=frac{pi }{6}+frac{pi n}{2},nin Z)
Предмет: Алгебра,
автор: Nik00789
Ответы
Автор ответа: Vasily1975
0
Ответ: tg(α)=7.
Объяснение:
Пусть α – угол между касательной осью абсцисс. Угловой коэффициент касательной k=tg(α)=y'(x0). Производная y'(x)=1/x, отсюда y'(x0)=1/x0=1/(1/7)=7.
Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: История,
автор: jegvilsove
4. Борьба казахского народа против джунгарского нашествия, война с волжскими калмыкам – основная тема исторических рассказов
ВАРИАНТ ОТВЕТА
А. XIIIв.
В. XVIIIв.
С. XIXв.
D. IXв.
Е. XIIB.
– очень срочно!!!
3 года назад
Предмет: Українська мова,
автор: likiliqwid
Установи зв’язки між словами другого речення за допомогою Біля рідного будинку Олега чекала мальва
3 года назад
Предмет: Алгебра,
автор: kosare2015
Нужно срочно решить хотя-бы первые 3 кому не лень можно 4,5,6
3 года назад
Предмет: Математика,
автор: aliyaaaa3
узнайте площадь закрашеной части
6 лет назад
Предмет: Математика,
автор: ппачпоСофа111111
помогите очень срочно пж
6 лет назад
Влад Цапок
Профи
(560),
на голосовании
8 лет назад
Голосование за лучший ответ
marat aminov
Просветленный
(32951)
8 лет назад
tgA=y/x, отсюда угол А=arctg(y/x)
Влад ЦапокПрофи (560)
8 лет назад
Спасибо, z:=arctan(b/a);
z:=(z)*(180/Pi);
Юрий Моисеев
Оракул
(83754)
8 лет назад
Тангенс угла равен у/х
Похожие вопросы
