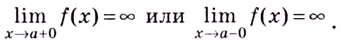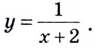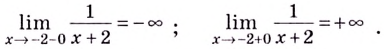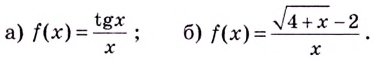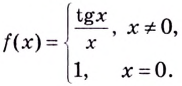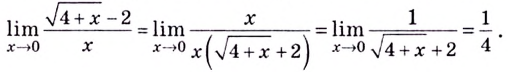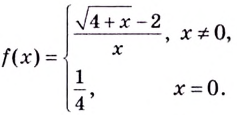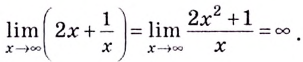Нахождение точек разрыва функции является одним из обязательных моментов исследования на непрерывность. Для кого-то это может прозвучать непонятно, а для остальных будет слишком банально.
Но и тем, и другим не стоит делать поспешные выводы: материал этой темы действительно предельно прост, но вместе с тем для успешного решения практических задач потребуется осмыслить и запомнить несколько технических приемов и нюансов.
Как минимум необходимо понимать, что за «зверь» кроется под понятием предела функции. И конечно же, нужно уметь их решать. Не менее полезным станет понимание геометрического смысла, дополненное графиком — большинство задач подобного характера требуют построения чертежа после решения.
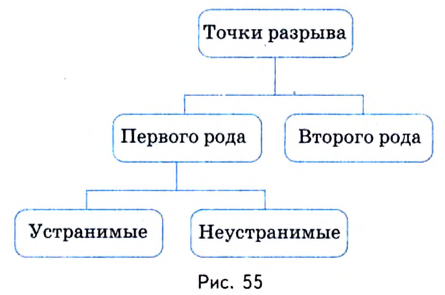
Определение точки разрыва
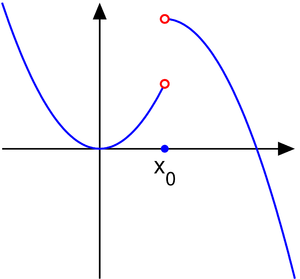
Как уже упоминалось, их поиск напрямую связан с темой непрерывности. Если говорить простым языком, то это не что иное, как координаты графика функции, в которых точки не соединяются между собой. Образуются «рваные области», которые и называют местом разрыва. Вообще, чтобы понять смысл, достаточно всего лишь взглянуть на рисунок:
Он более чем очевидно иллюстрирует определение понятия. Если функция прерывается в X0, то непрерывность в этом месте нарушена одним из двух возможных способов:
- первый род;
- второй род.
Задачи похожего типа, где необходимо находить точки разрыва, могут выступать не только, как один из этапов полного исследования на непрерывность, но и в качестве самостоятельных заданий. Чтобы определить их вид, потребуется отыскать предел для найденных значений. Поэтому, если вы еще не умеете их решать, самое время ненадолго отвлечься, чтобы изучить базовые основы.
К счастью, на практике это не так сложно — самый трудный этап заключается в приведении примера к одному из табличных. Остальные моменты легко запомнить. Не стоит забывать и о большом количестве сервисов, которые в несколько кликов выдадут значение предела любой сложности онлайн.
Классификация точек разрыва.
Точки разрыва первого и второго рода
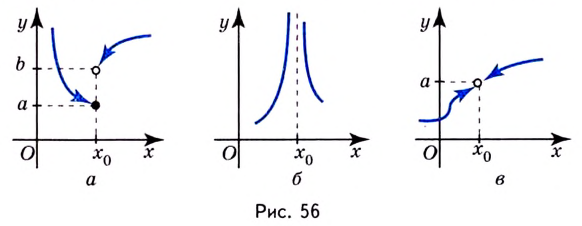
Если функция не определена, но односторонние пределы имеют конечное значение, то ее относят к случаю первого рода. Который, в свою очередь, может иметь характеристику устранимого или конечного:
- Точки устранимого разрыва функции. Значения вычислений обоих пределов для них равны. Но также имеется возможность «исправить ситуацию»: нахождения между двумя координатами такой, левый и правый пределы которой будут одинаковы, а сама она — соединит «порванный» участок, сделав график непрерывным.
-
Точки конечного разрыва первого рода — скачок функции. Пределы могут быть вычислены, но в то же время не равны друг другу, и поэтому доопределение уравнения невозможно. Разница первого и второго называется скачком.
- Точки разрыва второго рода отличаются тем, что вычисляемые пределы не просто различны по значению, но результат хотя бы одного из них обязательно должен быть равен бесконечности или несуществующему числу.
Как найти точки разрыва функции
Если в условиях задачи не были даны координаты проверяемого отрезка, то процесс решения делится на несколько этапов. Для начала нужно найти область определенных значений, с которой в дальнейшем пойдет работа. После это вычисляются односторонние пределы функции. Полученные результаты необходимо будет сравнить, чтобы однозначно определить род и характеристику разрыва.
Рассмотрим более подробно каждый из этих моментов на примере нахождения нужных нам точек у конкретного примера f (y)=(y² – 25)/(y – 5):
- Областью определения называют множество значений, в котором существует функция. Здесь не нужны никакие сложные вычисления, достаточно взять лишь знаменатель. Если y=5, то он будет (5−5)=0 и, как всем известно, делить на него нельзя. Таким образом, получаем область допустимых y ∈ (-∞; 5) ∪ (5; +∞) и предполагаем, что наша y = 5 является точкой разрыва.
- Вычисление односторонних пределов. Это самая сложная для учеников часть, т. к. пределы не всегда бывают удобными для вычисления, да не все на них «собаку съели». Но в этом случае функцию можно значительно упростить еще до начала вычисления: f (y) = (y ²-25)/(y — 5) = ((y-5)(y+5)) /(y — 5) = y+5. Никогда не пренебрегайте такой возможностью, если она есть. Заметим, что новая функция непрерывна при любом численном значении, т. ч. по всем математическим правилам пределы будут равны: lim (y + 5) = 5 + 5 = 10.
- Проверяя совпадение результатов, мы выяснили, что левый и правый предел функции в точке y=5 одинаковые. Но вместе с тем функция f(y) не может быть определена в этой координате, иначе ее знаменатель обращается в ноль, что невозможно по условиям. Следовательно, она действительно является разрывом, а именно: устранимым и первого рода.
Видео
Из этого видео вы узнаете, как исследовать непрерывность функции.
Содержание:
- Определение точки разрыва
- Точка разрыва первого рода
- Точка разрыва второго рода
- Точка устранимого разрыва
- Примеры решения задач
Определение точки разрыва
Определение
Точка $a$, в которой нарушено хотя бы одно
из трех условий непрерывности функции, а именно:
- функция $f(x)$ определена в точке и ее окрестности;
- существует конечный предел функции $f(x)$
в точке $a$; - это предел равен значению функции в точке $a$,
т.е. $lim _{x rightarrow a} f(x)=f(a)$
называется точкой разрыва функции.
Пример
Функция $y=sqrt{x}$ не определена в точке
$x=-1$, а значит, эта точка является точкой
разрыва указанной функции.
Точка разрыва первого рода
Определение
Если в точке $a$ существуют конечные
пределы $f(a-0)$ и
$f(a+0)$, такие, что
$f(a-0) neq f(a+0)$, то точка
$a$ называется точкой разрыва первого рода.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Функция $f(x)=left{begin{array}{l}{0, x>1} \ {1, x leq 1}end{array}right.$ в точке
$x=1$ имеет разрыв первого рода, так как
$f(1-0)=1$, а
$f(1+0)=0$
Точка разрыва второго рода
Определение
Если хотя б один из пределов $f(a-0)$ или
$f(a+0)$ не существует или равен бесконечности, то
точка $a$ называется точкой разрыва второго рода.
Пример
Для функции $y=frac{1}{x}$ точка
$x=0$ – точка разрыва второго рода, так как
$f(0-0)=-infty$ .
Точка устранимого разрыва
Определение
Если существуют
левый и правый пределы функции в точке и они равны друг другу, но не совпадают со значением
функции $f(x)$ в точке
$a$:
$f(a) neq f(a-0)=f(a+0)$ или функция
$f(x)$ не определена в точке
$a$, то точка
$a$ называется точкой устранимого разрыва.
Пример
Рассмотрим функцию $f(x)=left{begin{array}{l}{3 x+1, x lt 0} \ {1-4 x, x>0} \ {e^{2}, x=0}end{array}right.$ .
Найдем односторонние пределы и значение функции в точке $x=0$:
$f(0)=e^{2}$
$f(0-0)=lim _{x rightarrow 0-} f(x)=lim _{x rightarrow 0-}(3 x+1)=1$
$f(0+0)=lim _{x rightarrow 0+} f(x)=lim _{x rightarrow 0+}(1-4 x)=1$
Так как $f(0-0)=f(0+0)$ и не равны значению функции в
точке, то точка $x=0$ – точка устранимого разрыва.
Примеры решения задач
Пример
Задание. Исследовать функцию $f(x)=left{begin{array}{l}{x^{2}, x lt 1} \ {(x-1)^{2}, 1 leq x leq 2} \ {3-x, x>2}end{array}right.$ на непрерывность.
Решение. Рассматриваемая функция определена и
непрерывна на промежутках
$(-infty ; 1)$,
$(1 ; 2)$ и
$(2 ;+infty)$, на которых она задана непрерывными
элементарными функциями $y_{1}(x)=x^{2}$,
$y_{2}(x)=(x-1)^{2}$ и
$y_{3}(x)=3-x$ соответственно. А тогда, разрыв возможен
только на концах указанных промежутков, то есть в точках
$x=1$ и
$x=2$ .
Найдем односторонние пределы и значение функции в каждой из точек.
1) Рассмотрим точку $x=1$ . Для нее
$f(1)=left.(x-1)^{2}right|_{x=1}=0$
$f(1-0)=lim _{x rightarrow 1-} f(x)=lim _{x rightarrow 1-} y_{1}(x)=lim _{x rightarrow 1-} x^{2}=1$
$f(1+0)=lim _{x rightarrow 1+} f(x)=lim _{x rightarrow 1+} y_{2}(x)=lim _{x rightarrow 1+}(x-1)^{2}=0$
Так как $f(1-0) neq f(1+0)$ , то в точке
$x=1$ функция терпит разрыв первого рода.
2) Для точки $x=2$ имеем:
$f(2)=left.(x-1)^{2}right|_{x=2}=1$
$f(2-0)=lim _{x rightarrow 2-} f(x)=lim _{x rightarrow 2-} y_{2}(x)=lim _{x rightarrow 2-}(x-1)^{2}=1$
$f(2+0)=lim _{x rightarrow 2+} f(x)=lim _{x rightarrow 2+} y_{3}(x)=lim _{x rightarrow 2+}(3-x)=1$
Так как односторонние пределы и значение функции в этой точке равны, то это означает, что в точке
$x=2$ функция непрерывна.
Ответ. В точке $x=1$ функция
терпит разрыв первого рода, а в точке $x=2$ непрерывна.
Пример
Задание. Исследовать функцию $y=e^{frac{1}{x-1}}$
на непрерывность в точках $x_{1}=1$ и
$x_{2}=0$ .
Решение. 1) Исследуем функцию на
непрерывность в точке
$x_{1}=1$:
$f(1-0)=lim _{x rightarrow 1-} e^{frac{1}{x-1}}=e^{-infty}=0$
$f(1+0)=lim _{x rightarrow 1+} e^{frac{1}{x-1}}=e^{+infty}=infty$
Так как один из односторонних пределов бесконечен, то точка $x_{1}=1$
– точка разрыва второго рода.
2) Для точки $x_{2}=0$ получаем:
$f(0-0)=lim _{x rightarrow 0-} e^{frac{1}{x-1}}=e^{-1}=frac{1}{e}$
$f(0+0)=lim _{x rightarrow 0+} e^{frac{1}{x-1}}=e^{-1}=frac{1}{e}$
и значение функции в точке
$f(0)=e^{frac{1}{x-1}}=frac{1}{e}$
Таким образом, в точке $x_{2}=0$ заданная
функция является непрерывной.
Ответ. $x_{1}=1$
– точка разрыва второго рода, а в точке $x_{2}=0$
функция непрерывна.
Читать дальше: основные теоремы о непрерывности функций.
Процесс исследования функции на непрерывность неразрывно связан с навыком нахождения односторонних пределов функции. Поэтому, чтобы приступить к изучению материала данной статьи, желательно предварительно разобрать тему предела функции.
Непрерывность функции в точке
Функция f(x) является непрерывной в точке x0, если предел слева равен пределу справа и совпадает со значением функции в точке x0, т.е.: limx→x0-0f(x)=limx→x0+0f(x)=f(x0)
Данное определение позволяет вывести следствие: значение предела функции в точках непрерывности совпадает со значением функции в этих точках.
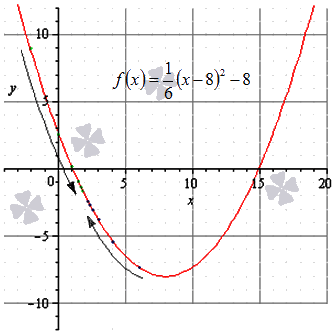
Дана функция f(x)=16(x-8)2-8. Необходимо доказать ее непрерывность в точке х0= 2.
Решение
В первую очередь, определим существование предела слева. Чтобы это сделать, используем последовательность аргументов хn, сводящуюся к х0 =2·(хn<2). Например, такой последовательностью может быть:
-2, 0, 1, 112, 134, 178, 11516,…, 110231024,…→2
Соответствующая последовательность значений функций выглядит так:
f(-2); f(0); f(1); f112; f134; f178; f11516;…; f110231024;…==8.667; 2.667; 0.167; -0.958; -1.489; -1.747; -1.874;…;-1.998;…→-2
на чертеже они обозначены зеленым цветом.
Достаточно очевидно, что такая последовательность сводится к -2, значит limx→2-016(x-8)2-8=-2.
Определим существование предела справа: используем последовательность аргументов хn, сводящуюся к х0= 2 (хn>2). Например, такой последовательностью может быть:
6, 4, 3, 212, 214, 218, 2116,…, 211024,…→2
Соответствующая последовательность функций:
f(6); f(4); f(3); f212; f214; f218; f2116;…; f211024;…==-7.333; -5.333; -3.833; -2.958; -2.489; -2.247; -2.247; -2.124;…; -2.001;…→-2
на рисунке обозначена синим цветом.
И эта последовательность сводится к -2, тогда limx→2+016(x-8)2-8=-2.
Действиями выше было показано, что пределы справа и слева являются равными, а значит существует предел функции f(x)=16x-82-8 в точке х0= 2, при этом limx→216(x-8)2-8=-2.
После вычисления значения функции в заданной точке очевидно выполнение равенства:
limx→2-0f(x)=limx→2+0f(x)=f(2)=16(2-8)2-8=-2 что свидетельствует о непрерывности заданной функции в заданной точке.
Покажем графически:
Ответ: Непрерывность функции f(x)=16(x-8)2-8 в заданной части доказано.
Устранимый разрыв первого рода
Функция имеет устранимый разрыв первого рода в точке х0, когда пределы справа и слева равны, но не равны значению функции в точке, т.е.:
limx→x0-0f(x)=limx→x0+0f(x)≠f(x0)
Задана функция f(x)=x2-25x-5. Необходимо определить точки ее разрыва и определить их тип.
Решение
Сначала обозначим область определения функции: D(f(x))⇔Dx2-25x-5⇔x-5≠0⇔x∈(-∞; 5)∪(5; +∞)
В заданной функции точкой разрыва может служить только граничная точка области определения, т.е. х0= 5. Исследуем функцию на непрерывность в этой точке.
Выражение x2-25x-5 упростим: x2-25x-5=(x-5)(x+5)x-5=x+5.
Определим пределы справа и слева. Поскольку функция g(x)=x+5 является непрерывной при любом действительном x, тогда:
limx→5-0(x+5)=5+5=10limx→5+0(x+5)=5+5=10
Ответ: пределы справа и слева являются равными, а заданная функция в точке х0= 5 не определена, т.е. в этой точке функция имеет устранимый разрыв первого рода.
Неустранимый разрыв первого рода
Неустранимый разрыв первого рода также определяется точкой скачка функции.
Функция имеет неустранимый разрыв первого рода в точке х0, когда пределы справа и слева не являются равными, т.е.: limx→x0-0f(x)≠limx→x0+0f(x). Точка х0 здесь – точка скачка функции.
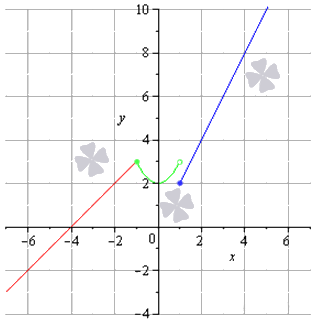
Задана кусочно-непрерывная функция f(x)=x+4, x<-1,x2+2, -1≤x<12x, x≥1. Необходимо изучить заданную функцию на предмет непрерывности, обозначить вид точек разрыва, составить чертеж.
Решение
Разрывы данной функции могут быть лишь в точке х0=-1 или в точке х0=1.
Определим пределы справа и слева от этих точек и значение заданной функции в этих точках:
- слева от точки х0=-1 заданная функция есть f(x)=x+4, тогда в силу непрерывности линейной функции: limx→-1-0f(x)=limx→-1-0(x+4)=-1+4=3;
- непосредственно в точке х0=-1 функция принимает вид: f(x)=x2+2, тогда: f(-1)=(-1)2+2=3;
- на промежутке (-1; 1) заданная функция есть: f(x)=x2+2. Опираясь на свойство непрерывности квадратичной функции, имеем: limx→-1+0f(x)=limx→-1+0(x2+2)=(-1)2+2=3limx→1-0f(x)=limx→1-0(x2+2)=(1)2+2=3
- в точке х0=-1 функция имеет вид: f(x)=2x и f(1)=2·1=2.
- справа от точки х0 заданная функция есть f(x)=2x. В силу непрерывности линейной функции: limx→1+0f(x)=limx→1+0(2x)=2·1=2
Ответ: в конечном счете мы получили:
- limx→-1-0f(x)=limx→-1+0f(x)=f(-1)=3 – это означает, что в точке х0=-1 заданная кусочная функция непрерывна;
- limx→-1-0f(x)=3, limx→1+0f(x)=2 – таким образом, в точке х0=1 определён неустранимый разрыв первого рода (скачок).
Нам остается только подготовить чертеж данного задания.
Разрыв второго рода (бесконечный разрыв)
Функция имеет разрыв второго рода в точке х0, когда какой-либо из пределов слева limx→x0-0f(x) или справа limx→x0+0f(x) не существует или бесконечен.
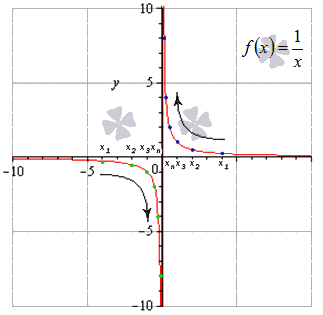
Задана функция f(x)=1x. Необходимо исследовать заданную функцию на непрерывность, определить вид точек разрыва, подготовить чертеж.
Решение
Запишем область определения функции: x∈(-∞; 0)∪(0; +∞).
Найдем пределы справа и слева от точки х0= 0.
Зададим произвольную последовательность значений аргумента, сходящуюся к х0 слева. К примеру:
-8; -4; -2; -1; -12; -14;…; -11024;…
Ей соответствует последовательность значений функции:
f(-8); f(-4); f(-2); f(-1); f-12; f-14;…; f-11024;…==-18;-14; -12; -1; -2; -4;…; -1024;…
Очевидно, что эта последовательность является бесконечно большой отрицательной, тогда limx→0-0f(x)=limx→0-01x=-∞.
Тепереь зададим произвольную последовательность значений аргумента, сходящуюся к х0 справа. К примеру: 8; 4; 2; 1; 12; 14;…; 11024;…, и ей соответствует последовательность значений функции:
f(8); f(4); f(2); f(1); f12; f14;…; f11024;…==18; 14; 12; 1; 2; 4;…; 1024;…
Эта последовательность – бесконечно большая положительная, а значит limx→0+0f(x)=limx→0+01x=+∞.
Ответ: точка х0= 0 – точка разрыва функции второго рода.
Проиллюстрируем:
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Рассмотрим
некоторую функцию f(x),
непрерывную в окрестности точки х0,
за исключением может быть самой этой
точки. Из определения точки разрыва
функции следует, что х = х0является
точкой разрыва, если функция не определена
в этой точке, или не является в ней
непрерывной.
Следует отметить также, что непрерывность
функции может быть односторонней.
Поясним это следующим образом.
Если
односторонний предел (см. выше)
,
то функция называется непрерывной
справа.
х0
Если
односторонний предел (см. выше)
,
то функция называется непрерывной
слева.
х0
Определение.Точка х0называетсяточкой разрыва функцииf(x), если
f(x) не определена в точке х0или не
является непрерывной в этой точке.
Определение.Точка х0называетсяточкой
разрыва 1- го рода, если в этой точке
функцияf(x)
имеет конечные, но не равные друг другу
левый и правый пределы.
Для выполнения условий этого определения
не требуется, чтобы функция была
определена в точке х = х0, достаточно
того, что она определена слева и справа
от нее.
Из определения можно сделать вывод, что
в точке разрыва 1 – го рода функция может
иметь только конечный скачок. В некоторых
частных случаях точку разрыва 1 – го
рода еще иногда называют устранимой
точкой разрыва, но подробнее об этом
поговорим ниже.
Определение.Точка х0называетсяточкой разрыва 2 – го рода,
если в этой точке функцияf(x)
не имеет хотя бы одного из односторонних
пределов или хотя бы один из них
бесконечен.
Пример.Функция Дирихле (Дирихле
Петер Густав(1805-1859) – немецкий математик,
член- корреспондент Петербургской АН
1837г)
не является
непрерывной в любой точке х0.
Пример.Функцияf(x)
=
имеет в точке х0= 0 точку разрыва
2 – го рода, т.к.
.
Пример.f(x) =
Функция не
определена в точке х = 0, но имеет в ней
конечный предел
,
т.е. в точке х = 0 функция имеет точку
разрыва 1 – го рода. Это – устранимая
точка разрыва, т.к. если доопределить
функцию:
График этой
функции:
Пример.f(x) =
=

1
0 x
-1
Эта функция
также обозначается sign(x)
– знак х. В точке х = 0 функция не определена.
Т.к. левый и правый пределы функции
различны, то точка разрыва – 1 – го рода.
Если доопределить функцию в точке х =
0, положивf(0) = 1, то функция
будет непрерывна справа, если положитьf(0) = -1, то функция будет
непрерывной слева, если положитьf(x)
равное какому- либо числу, отличному от
1 или –1, то функция не будет непрерывна
ни слева, ни справа, но во всех случаях
тем не менее будет иметь в точке х = 0
разрыв 1 – го рода. В этом примере точка
разрыва 1 – го рода не является устранимой.
Таким образом,
для того, чтобы точка разрыва 1 – го рода
была устранимой, необходимо, чтобы
односторонние пределы справа и слева
были конечны и равны, а функция была бы
в этой точке не определена.
§9. Непрерывность функции на интервале и на отрезке.
Определение.Функцияf(x)
называетсянепрерывной на интервале
(отрезке), если она непрерывна в любой
точке интервала (отрезка).
При этом не
требуется непрерывность функции на
концах отрезка или интервала, необходима
только односторонняя непрерывность на
концах отрезка или интервала.
Свойства
функций, непрерывных на отрезке.
Свойство
1:(Первая теорема Вейерштрасса
(Вейерштрасс Карл (1815-1897)- немецкий
математик)). Функция, непрерывная на
отрезке, ограничена на этом отрезке,
т.е. на отрезке [a,b]
выполняется условие –M£f(x)£M.
Доказательство этого свойства основано
на том, что функция, непрерывная в точке
х0, ограничена в некоторой ее
окрестности, а если разбивать отрезок
[a,b] на
бесконечное количество отрезков, которые
“стягиваются” к точке х0, то
образуется некоторая окрестность точки
х0.
Свойство 2:Функция, непрерывная
на отрезке [a,b],
принимает на нем наибольшее и наименьшее
значения.
Т.е. существуют такие значения х1и х2, чтоf(x1)
=m,f(x2)
=M, причем
m£f(x)£M
Отметим эти наибольшие и наименьшие
значения функция может принимать на
отрезке и несколько раз (например –
f(x) =sinx).
Разность между наибольшим и наименьшим
значением функции на отрезке называется
колебанием функции на отрезке.
Свойство 3:(Вторая теорема
Больцано – Коши). Функция, непрерывная
на отрезке [a,b],
принимает на этом отрезке все значения
между двумя произвольными величинами.
Свойство 4:Если функцияf(x)
непрерывна в точке х = х0, то
существует некоторая окрестность точки
х0, в которой функция сохраняет
знак.
Свойство 5:(Первая теорема
Больцано (1781-1848) – Коши). Если функцияf(x)- непрерывная
на отрезке [a,b]
и имеет на концах отрезка значения
противоположных знаков, то существует
такая точка внутри этого отрезка, гдеf(x) = 0.
Т.е. если
sign(f(a)) ¹
sign(f(b)), то $
х0:
f(x0)
= 0.
Определение.Функцияf(x)
называетсяравномерно непрерывнойна отрезке [a,b],
если для любогоe>0
существуетD>0 такое,
что для любых точек х1Î[a,b]
иx2Î[a,b]
таких, что
ïх2– х1ï<D
верно
неравенство ïf(x2)
–f(x1)ï<e
Отличие
равномерной непрерывности от “обычной”
в том, что для любого eсуществует своеD, не
зависящее от х, а при “обычной”
непрерывностиDзависит отeи х.
Свойство
6:Теорема Кантора (Кантор Георг
(1845-1918)- немецкий математик). Функция,
непрерывная на отрезке, равномерно
непрерывна на нем.
(Это свойство
справедливо только для отрезков, а не
для интервалов и полуинтервалов.)
Пример.
Функция
непрерывна на интервале (0, а), но не
является на нем равномерно непрерывной,
т.к. существует такое числоD>0
такое, что существуют значения х1и х2такие, чтоïf(x1)
–f(x2)ï>e,e- любое
число при условии, что х1и х2близки к нулю.
Свойство
7:Если функцияf(x)
определена, монотонна и непрерывна на
некотором промежутке, то и обратная ей
функция х =g(y)
тоже однозначна, монотонна и непрерывна.
Пример.Исследовать на непрерывность функцию
и определить тип точек разрыва, если
они есть.
в точке х = -1
функция непрерывна в точке х = 1
точка разрыва 1 – го рода

3
2
-4
-1 0 1 х
Пример.Исследовать на непрерывность
функцию и определить тип точек разрыва,
если они есть.
в точке х = 0
функция непрерывна в точке х = 1
точка разрыва 1 – го рода
у
2
1
-p-p/2 0 1x
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Точки разрыва и их классификация
Непрерывность или разрыв функции может зависеть от конкретных условий, в которых рассматривается задача. Рассмотрим, например, численность населения земного шара как функцию времени. Она увеличивается на 1 в момент рождения каждого человека и уменьшается на 1 в момент смерти. Но рождения и смерти следуют друг за другом через бесконечно малые интервалы времени и изменение численности населения планеты на 1 настолько мало его меняет, что практически функцию можно рассматривать непрерывной. По стоит перейти от численности населения земного шара к численности населения одной квартиры, как рождение или смерть отдельного ее жителя будут так заметно менять ее численность, что функцию нельзя будет рассматривать как непрерывную.
Если хотя бы одно из условий определения непрерывности функции в точке (см. п. 3.1) не выполнено, то в данной точке функция терпит разрыв. Различают три вида точек разрыва непрерывной функции.
1. Точка
Чтобы устранить разрыв в точке 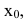
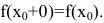
2. Точка 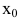
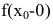
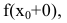
При этом величина 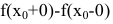
3. Если хотя бы один из односторонних пределов 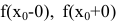
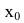
Пример №32
Исследовать функции на непрерывность. В случае устранимого разрыва доопределить функцию до непрерывной.
Решение:
1. Данная функция элементарная, т.к. получена с помощью конечного числа арифметических действий над основными элементарными функциями: экспоненциальной, постоянной и степенной. Следовательно, она непрерывна в области определения 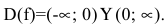
не определена и поэтому разрывна. Исследуем характер точки разрыва. Так как 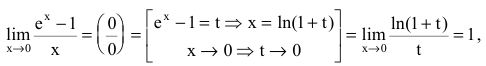
Если положить f(0)=0, то функция 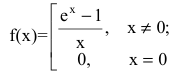
2. Функция 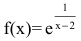
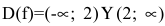
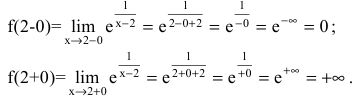
Пример №33
Исследовать функцию на непрерывность. Построить схематично график функции.
Решение:
Область определения этой функции – вся числовая прямая: 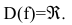
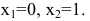
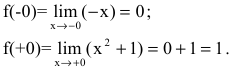
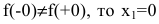
Исследуем точку
Поскольку 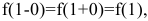
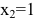
Построим график функции.
——
Точки разрыва и их классификация
Точка, в которой функция не является непрерывной, называется точкой разрыва функции, а сама функция называется разрывной в этой точке.
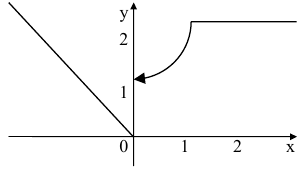
Точка 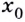
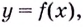
- функция в точке
не определена;
- не существует предела функции в точке
или он равен бесконечности;
- предел функции в точке
не совпадает со значением функции в этой точке.
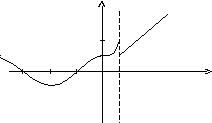
Различают два вида точек разрыва — первого рода и второго рода (рис.55).
Исследуя точки разрыва, используют односторонние пределы. Это означает, что рассматривают поведение функции для значений 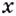
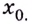
Обозначают:
Точку 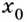
Точку 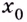
Если левосторонний и правосторонний пределы в точке 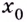
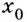
Пример №522
Найдите точки разрыва функции 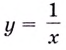
Решение:
Поскольку на ноль делить нельзя, то точкой разрыва данной функции является 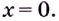
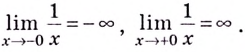
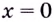
Пример №523
Исследуйте функцию 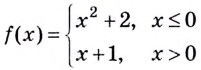
Решение:
На каждом из интервалов 
Если 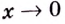
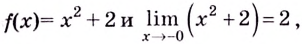
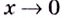
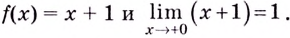
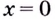
Односторонние пределы используют для нахождения вертикальных асимптот кривых.
Прямая 
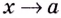
Например, ось 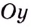
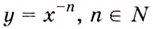
- Заказать решение задач по высшей математике
Пример №524
Найдите вертикальные асимптоты кривой
Решение:
Поскольку функция не определена в точке 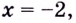
Следовательно, 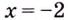
Замечание: Если 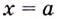
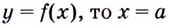
Пример №525
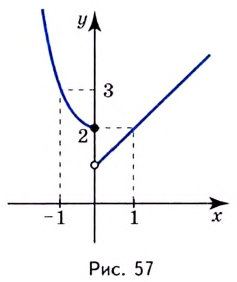
Исследуйте заданные функции на непрерывность и выясните характер их точек разрыва:
Решение:
Заданные в условии функции элементарные, а потому непрерывные в каждой точке области определения, а именно на множестве
а) Функция 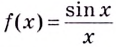
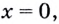
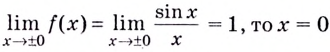
б) Функция 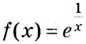

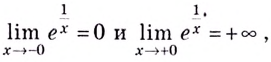
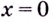
Пример №526
Заданные функции до определить в точке 
Решение:
а) Имеем 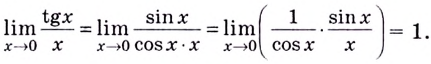
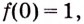
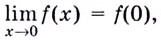

б) Вычислим предел заданной функции в точке 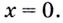
Если теперь за значение функции в точке 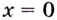
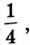
Итак,
Пример №527
Имеет ли уравнение 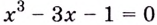
Рассмотрим функцию 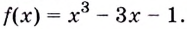
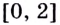
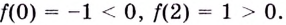
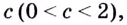
Пример №528
Имеет ли горизонтальные и вертикальные асимптоты кривая
Решение:
1) Найдём вертикальные асимптоты. Заданная функция не определена в точке 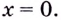
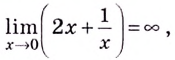

Горизонтальных асимптот нет.
- Дифференциальное исчисление
- Исследование функций с помощью производных
- Формула Тейлора и ее применение
- Интегрирование рациональных дробей
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
- Непрерывность функций и точки разрыва






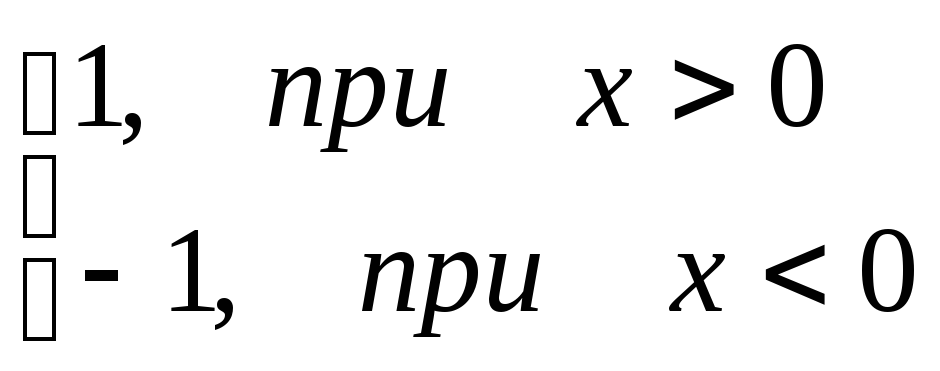




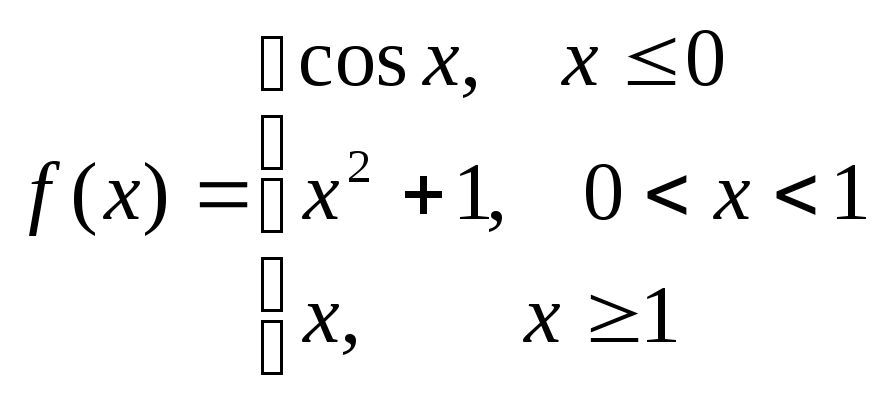


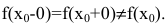
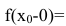
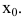
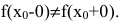
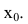
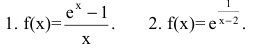
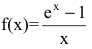
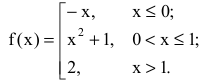
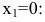
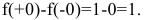
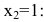
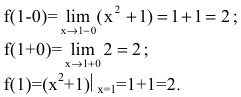
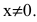
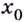 не определена;
не определена;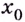 или он равен бесконечности;
или он равен бесконечности;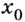 не совпадает со значением функции в этой точке.
не совпадает со значением функции в этой точке.