Определение вида треугольника по длинам его сторон
Пусть а, b и c – стороны треугольника, тогда
1) если а = b, то треугольник равнобедренный.
2) если а = b = c, то треугольник равносторонний.
3) если а ≠ b ≠ с, то треугольник разносторонний.
Пусть с – бóльшая сторона, тогда
4) если с2 > a2 + b2, то треугольник тупоугольный.
5) если с2 = a2 + b2, то треугольник прямоугольный.
6) если с2 < a2 + b2, то треугольник остроугольный.
Успешной сдачи экзаменов!
С уважением, Васильева Анна.
Онлайн калькулятор поможет узнать по сторонам, является ли треугольник прямоугольным, равнобедренным, равносторонним или разносторонним.
Как определить, что треугольник прямоугольный: по Теорема Пифагора — сумма квадратов длин катетов равна квадрату длины гипотенузы
c2 = a2 + b2
Как определить, что треугольник равнобедренный: один из признаков равнобедренного треугольника – две стороны равны.
Как определить, что треугольник равносторонний: все стороны равны.
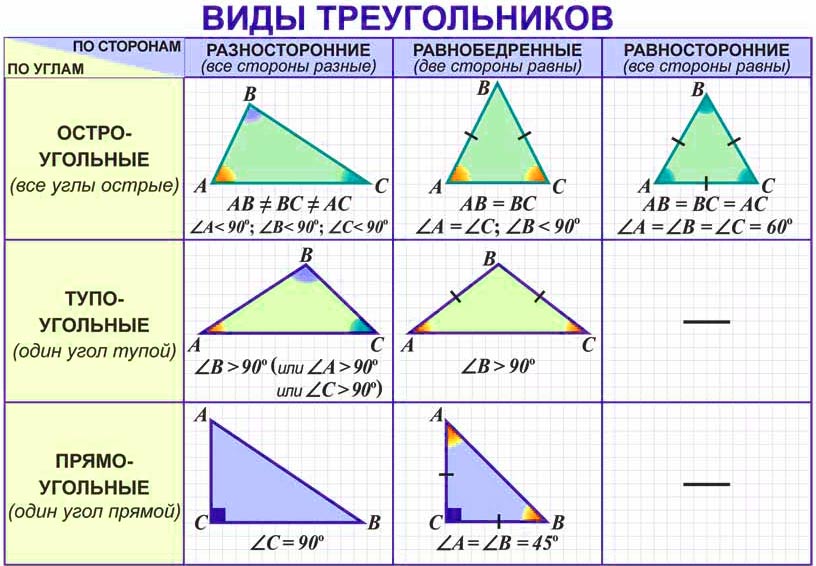
Принято выделять три типа треугольников:
тупоугольные – один из углов более 90 градусов,
прямоугольные – один из угол равен 90 градусов,
остроугольные – все углы менее 90 градусов.
Это классификация по типу углов.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также
Математика, 3 класс. Урок № 61
Виды треугольников (по соотношению сторон). Закрепление
Перечень вопросов, рассматриваемых в теме:
Какие виды треугольников различают по соотношению сторон?
Как определить вид треугольника?
Глоссарий по теме:
Виды треугольников по сторонам:
- равносторонние
- равнобедренные
- разносторонние



Отрезки равной длины на чертеже отмечают равным количеством черточек:
разносторонний треугольник
равносторонний треугольник
равнобедренный треугольник
Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства.
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки – сторонами треугольника.
Основная и дополнительная литература по теме урока:
1. Моро М. И. Учебник для 3 класса четырехлетней начальной школы. М. «Просвещение» — 2017. С. 73-80.
2. Волкова С. И. Карточки с математическими заданиями 3 кл. — М.: Просвещение, 2018.
3. Волкова С.И. математика. Тесты. 3 кл. — М.: Просвещение, 2018. С. 54-59.
4. Рудницкая В. Н. Математика. Дидактические материалы.ч.1 3 кл. – М. «Вентана- Граф», 2016, с. 47-53.
Теоретический материал для самостоятельного изучения
В огромном мире Математики есть очень интересная страна с красивым названием Геометрия. Эту страну населяют не числа, а различные линии и фигуры, плоские и объёмные. Сегодня, путешествуя по стране Геометрии, мы посетим город Треугольников.
Конечно, вы уже умеете отличать треугольники от других геометрических фигур. Но у жителей этого города есть, что рассказать о себе. И этих тайн так много, что вы будете их открывать все школьные годы.
Сегодня вы откроете некоторые секреты треугольников и подружитесь с жителями этого города.
Мы посетим город Треугольников.
Что вы уже знаете о жителях этого города?
Их легко отличить от других геометрических фигур по трём сторонам и трём углам.
У вас появились идеи по поводу названий этих треугольников?
Оказывается, по длине сторон все треугольники можно разделить на 3 вида:
те, у которых все стороны разные – разносторонние,
те, у которых имеются две равные стороны – равнобедренные,
а те, у которых все стороны равны – равносторонние.
Для того чтобы безошибочно определить вид треугольника по сторонам необходимо измерить все три стороны.
Теперь легко определить вид треугольника.
У первого треугольника все стороны разные, значит он разносторонний, у второго две стороны одинаковые, значит он равнобедренный, а у третьего все три стороны равны, значит он равносторонний.
Часто вид треугольника можно определить на глаз.
Попробуйте определить виды треугольников без измерений.
Проверим.
Разносторонний
– 1, 2, 4, 7
Равнобедренный
– 3 и 5
Равносторонний – 6
Сделаем вывод:
По сторонам различают 3 вида треугольников: разносторонние, равнобедренные и равносторонние.
Определить вид треугольника можно тремя способами: с помощью измерений, на глаз и по условным обозначениям.
Отрезки равной длины на чертеже отмечают равным количеством черточек:
разносторонний треугольник
равносторонний треугольник
равнобедренный треугольник
Теперь вы можете различать виды треугольников по сторонам. Эти знания необходимы в стране Геометрии.
Задания тренировочного модуля:
1. Выберите правильный ответ
Как называется треугольник, у которого все стороны равны?
a. одинаковосторонний треугольник
б. похожесторонний треугольник
в. равносторонний треугольник
г. равнодлинный треугольник
Правильные варианты ответов:
в. равносторонний треугольник
2. Закончите предложения:
Равносторонний треугольник— это треугольник, у которого ………………………….
Равнобедренный треугольник — это треугольник, у которого ………………………..
Разносторонний треугольник — треугольник, все стороны которого ………………………..
Правильные варианты ответов:
Равносторонний треугольник — это треугольник, у которого все три стороны равны.
Равнобедренный треугольник — это треугольник, у которого две стороны равны.
Разносторонний треугольник — треугольник, все стороны которого имеют разную длину.
3. Определите вид треугольника по сторонам и выпишите номера треугольников по порядку:
Правильный вариант:
- Равносторонние – 2,3
- Равнобедренные – 1, 6
- Разносторонние – 4, 5
4. Рассортируйте таблички по категориям.
|
Разносторонний треугольник |
Равнобедренный треугольник |
Равносторонний треугольник |
9 см, 9 см, 9 см
4 см, 6 см, 4 см
5 см, 7 см, 11см
9 см, 12 см, 9 см
8 см, 3 см, 6 см
6 см, 6 см, 6 см
Правильный вариант
|
Разносторонний треугольник |
Равнобедренный треугольник |
Равносторонний треугольник |
|
5 см, 7 см, 11 см |
4 см, 6 см, 4 см |
6 см, 6 см, 6 см |
|
8 см, 3 см, 6 см |
9 см, 12 см, 9 см |
9 см, 9 см, 9 см |
Как определить вид треугольника
Онлайн калькулятор поможет узнать по сторонам, является ли треугольник прямоугольным, равнобедренным, равносторонним или разносторонним.
Как определить, что треугольник прямоугольный: по Теорема Пифагора — сумма квадратов длин катетов равна квадрату длины гипотенузы c 2 = a 2 + b 2
Как определить, что треугольник равнобедренный: один из признаков равнобедренного треугольника – две стороны равны.
Как определить, что треугольник равносторонний: все стороны равны.
Принято выделять три типа треугольников:
тупоугольные – один из углов более 90 градусов,
прямоугольные – один из угол равен 90 градусов,
остроугольные – все углы менее 90 градусов.
Это классификация по типу углов.
Геометрия. Урок 3. Треугольники
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Определение треугольника
- Виды треугольников
- Отрезки в треугольнике
Определение треугольника
Треугольник – многоугольник с тремя сторонами и тремя углами.
Угол ∠ A – угол, образованный сторонами A B и A C и противолежащий стороне B C .
Угол ∠ B – угол, образованный сторонами B A и B C и противолежащий стороне A C .
Угол ∠ C – угол, образованный сторонами C B и C A и противолежащий стороне A B .
Виды треугольников
Треугольник остроугольный , если все три угла в треугольнике острые.
Треугольник прямоугольный , если у него один из углов прямой ( = 90 ° ) .
Треугольник тупоугольный , если у него один из углов тупой.

Основные свойства треугольника:
- Против большей стороны лежит больший угол.
- Против равных сторон лежат равные углы.
- Сумма углов в треугольнике равна 180 ° .
- Если продолжить одну из сторон треугольника, например, A C , и взять на продолжении стороны точку D , образуется внешний угол ∠ B C D к исходному углу ∠ A C B .
Отрезки в треугольнике
Биссектриса угла – луч, выходящий из вершины угла и делящий его пополам.
Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне.
Свойства биссектрис треугольника:
- Биссектриса угла – геометрическое место точек, равноудаленных от сторон угла.
- Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам:
Замечание: биссектриса угла – это луч, а биссектриса треугольника – отрезок.
Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Свойства медиан треугольника:
- Медиана разбивает треугольник на два равновеликих треугольника (два треугольника, имеющих одинаковую площадь).
- Медианы треугольника пересекаются в одной точке. Точка пересечения медиан делит их в отношении 2:1, считая от вершины.
Высота треугольника – это перпендикуляр, проведенный из вершины угла треугольника к прямой, содержащей противолежащую сторону этого треугольника.
Если треугольник остроугольный, то все три высоты будут лежать внутри треугольника. Если треугольник тупоугольный, то высоты, проведенные из вершин острых углов будут лежать вне треугольника, а высота, проведенная из вершины тупого угла будет лежать внутри треугольника.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Свойство средней линии треугольника: средняя линия параллельна одной из его сторон и равна половине этой стороны.
Всего в треугольнике можно провести три средние линии. Три средние линии разбивают исходный треугольник на четыре равных треугольника. Площадь каждого маленького треугольника будет равна четверти площади большого треугольника.
Площадь треугольника
Площадь произвольного треугольника можно найти следующими способами:
-
Полупроизведение стороны на высоту, проведенную к этой стороне.
Равнобедренный треугольник
Равнобедренным называется треугольник, у которого две стороны равны.
Равнобедренный треугольник может быть остроугольным, прямоугольным и тупоугольным.

Свойства равноберенного треугольника:
- В равнобедренном треугольнике углы при основании равны.
- В равнобедренном треугольнике медиана, высота и биссектриса, проведенные к основанию, совпадают.
Равносторонний треугольник
Равносторонним называется треугольник, у которого все стороны и все углы равны.
Площадь равностороннего треугольника находится по формуле S = a 2 3 4
Высота равностороннего треугольника находится по формуле h = a 3 2
Прямоугольный треугольник
Треугольник называется прямоугольным, если у него один из углов равен 90 ° .
Свойства прямоугольного треугольника:
- Сумма двух острых углов треугольника равна 90 ° .
- Катет, лежащий напротив угла в 30 ° , равен половине гипотенузы.
- Если катет равен половине гипотенузы, он лежит напротив угла в 30 ° .
Теорема Пифагора
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
У прямоугольного треугольника катеты перпендикулярны друг другу, следовательно, площадь можно найти по формуле:
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с треугольниками
Виды треугольников (по сторонам)
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На данном уроке учащимся предоставляется возможность обобщить знания о названиях и изученных свойствах геометрических фигур, познакомиться с основными свойствами треугольника, узнать виды треугольников по величине угла, по числу равных сторон, потренироваться в распознавании названных видов.
[spoiler title=”источники:”]
http://interneturok.ru/lesson/matematika/3-klass/undefined-0/vidy-treugolnikov-po-storonam
[/spoiler]
Виды треугольников
- Виды треугольников по углам
- Виды треугольников по сторонам
Треугольники различаются между собой по характеру углов и по характеру сторон.
Виды треугольников по углам
- Остроугольный треугольник – это треугольник, у которого все углы острые, то есть меньше 90°.
- Прямоугольный треугольник – это треугольник, у которого один из углов является прямым, то есть равен 90°.
Стороны, образующие прямой угол называются катетами, а сторона, лежащая напротив прямого угла, называется гипотенузой.
- Тупоугольный треугольник – это треугольник, у которого один из углов является тупым, то есть больше 90°.
Виды треугольников по сторонам
- Разносторонний треугольник – это треугольник, у которого все стороны имеют разную длину.
- Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой.
Равные стороны называются боковыми сторона треугольника, а третья сторона, не равная двум другим, называется его основанием.
- Равносторонний треугольник – это треугольник, у которого все три стороны равны, то есть имеют одинаковую длину.