Пусть
из генеральной совокупности в результате
n
испытаний над количественным признаком
X
извлечена выборка объемом n:
варианты x1,
… , xr
и
их частоты n1,
… , nr.
Точечной
называют
оценку, которая определяется одним
числом. Точечные оценки обычно используют
в тех случаях, когда число наблюдений
велико.
Выборочной
средней
xв
называют среднее арифметическое значение
вариант выборки. Если значения вариант
x1,
x2,
… , xr
имеют
соответственно частоты n1,
n2,
… , nr,
то
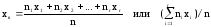 .
.
(5)
Выборочной
дисперсией Dв
называют среднее арифметическое
квадратов отклонений вариант xi
от их среднего значения xв,
т.е.
 .
.
(6)
Выборочным
средним квадратическим отклонением σв
называют
квадратный корень из выборочной дисперсии
Dв
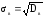 .
.
(7)
Исправленную
(несмещенную оценку) дисперсию
s2
выборки получают по формуле
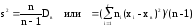 .
.
(8)
Аналогично
вводится исправленное
среднее квадратическое отклонение s
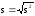 .
.
(9)
3. Интервальные оценки параметров распределения выборки
Интервальной
называют оценку, которая задается в
виде интервала. Интервальные оценки
удобно использовать в тех случаях, когда
число наблюдений n
относительно невелико.
Пусть
для неизвестного параметра θ количественного
признака X
генеральной совокупности статистическими
методами найдено значение θ*. Зададимся
точностью δ, т.е. | θ – θ* | < δ.
Надежностью
оценки
неизвестного параметра θ по вычисленному
статистическими методами значению θ*
называют вероятность γ, с которой
выполняется неравенство| θ – θ* | < δ,
при этом δ называется
точностью оценки.
В статистике обычно задаются надежностью
γ и определяют точность δ.
Доверительным
интервалом
для параметра θ называют интервал (θ* –
δ, θ* + δ), который покрывает неизвестный
параметр θ с вероятностью γ:
P[θ*
– δ <X
< θ* + δ] = γ.
Пусть
количественный признак X
генеральной совокупности распределен
нормально, причем среднее квадратическое
отклонение σ неизвестно. Требуется
оценить неизвестное математическое
ожидание a
по результатам выборки с заданной
надежностью γ.
Доверительный
интервал
с
уровнем надежности γ для математического
ожидания
a
признака
X,
распределенного нормально, при неизвестном
среднем квадратическом отклонении
определяется как
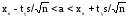 ,
,
(10)
где
xв
– выборочное среднее; s
– исправленное среднее квадратическое
отклонение выборки; n
– объем выборки. Точность оценки δ в
этом случае
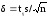 .
.
Значениеtγ
= t(γ,n)
можно найти из справочной таблицы
”Таблица значений tγ
= t(γ,n)”
для распределения Стьюдента.
Доверительный
интервал
с
уровнем надежности γ для
среднего
квадратического отклонения
σ признака X,
распределенного нормально, определяется
как
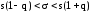 ,
,
(11)
где
s
– исправленное среднее квадратическое
отклонение выборки; n
– объем выборки. Значение q
= q(γ,n)
можно найти из справочной таблицы
”Таблица значений q
= q(γ,n)”
для распределения χ2.
В
случае, когда q
>1 доверительный интервал имеет вид
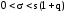 . (11′)
. (11′)
4. Статистическая проверка статистических
гипотез
Статистической
называют гипотезу (предположение) о
виде неизвестного распределения или о
параметрах известного распределения.
Основной
или нулевой гипотезой H0
называют выдвинутую гипотезу о неизвестном
распределении, вместе с основной H0
выдвигается
и конкурирующая
(альтернативная) гипотеза
H1,
противоречащая
основной.
Основной
принцип проверки статистических
гипотез состоит в следующем:
в
зависимости от вида гипотезы и характера
неизвестного распределения вводится
функция K,
называемая критерием,
по значениям ее будет приниматься
решение о принятии или отклонении
основной гипотезы H0.
Вводится также уровень
значимости
α как вероятность того, что будет
отвергнута верная нулевая гипотеза и
принята неверная гипотеза H1.
Областью
принятия гипотезы
H0
называют
те значения критерия K,
при которых основная гипотеза H0
принимается, критической
областью
– отвергается. Для каждой выборки и
конкретного вида критерия K
по специальным таблицам находятся
значения kкр,
называемые критическими
точками;
критические точки отделяют область
принятия гипотезы от критической
области. Правосторонней
называют критическую область, где K
> kкр,
левосторонней
K
< kкр
и
двусторонней
(и симметричной) | K|
> kкр.
Пусть
из генеральной совокупности в результате
n
испытаний над количественным признаком
X
извлечена выборка объемом n:
равноотстоящие с шагом h
варианты x1,
… , xr
и
их частоты n1,
… , nr.
Для нее подсчитаны по формулам (5-9)
выборочное среднее xв
и выборочное среднее квадратическое
отклонение σв.
Для
проверки гипотезы
о нормальном распределении
генеральной совокупности c
уровнем значимости α используется
критерий
χ2
Пирсона:
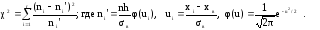 (12)
(12)
Критическое
значение χ2кр
= χ2
(α,k)
для этого критерия находится из справочной
таблицы “Критические точки распределения
χ2”.
Здесь k
= r
– 3. Если вычисленное по результатам
наблюдений по формуле (12) значение
критерия χ2набл
больше χ2кр,
основная гипотеза отвергается, если
меньше – нет оснований отвергнуть
основную гипотезу.
Если
варианты x1,
x2,
… , xr
не
являются равноотстоящими или число их
сравнительно велико, удобно сгруппировать
варианты в отдельные интервалы ( не
обязательно равноотстоящие ) [x1*;x2*),
[x2*;x3*),
…, [xm-1*;xm*).
Каждому интервалу назначается
представительное значение, равное
середине интервала xi.ср*
= (xi*
+ xi-1*)/2
и частота ni*,
равная сумме частот, попавших на интервал.
В соответствии с критерием Пирсона,
частоты ni*,
попавшие на интервалы [xi*
; xi-1*),
сравниваются с теоретическими частотами
ni‘,
вычисленными для соответствующих
интервалов нормальной случайной величины
Z
с нулевым математическим ожиданием и
единичным средним квадратическим
отклонением (Z
принадлежит N(0,1)).
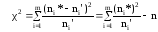 ,
,
(13)
ni‘
= nPi,
где n
– обьем выборки;
Pi
= Ф(zi+1)
– Ф(zi),
вероятности попадания X
на интервал (xi*,xi+1*)
или
Z
на (zi,zi+1);
zi
= (xi
ср*–xв*)
/ σ*; i
= 2,3,..,m-1;
крайние интервалы открываем z1
= –∞,
zm
= ∞, а Ф(zi)
– значение функции Лапласа.
Критическое
значение χ2кр
= χ2
(α,k)
для этого критерия находится из справочной
таблицы “Критические точки распределения
χ2”.
Здесь k
= m
– 3. Если вычисленное по результатам
наблюдений по формуле (13) значение
критерия χ2набл
меньше χ2кр,
нет оснований отвергнуть основную
гипотезу, если больше – основная гипотеза
не принимается.
Для
проверки гипотез
о дисперсии σ2
генеральной совокупности
с нормальным законом распределения при
заданном уровне значимости α используется
критерий
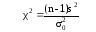 ,
,
(14)
где
s2
– исправленная дисперсия выборки; n
– объем выборки; σ02
– гипотетическое значение дисперсии.
А)
Пусть выдвинута нулевая гипотеза H0:
σ2
=
σ02
о
равенстве неизвестной генеральной
дисперсии σ2
предполагаемому значению σ02
при конкурирующей гипотезе H1:
σ2
≠
σ02.
Для проверки этой гипотезы по результатам
выборки вычисляется значение критерия
(14) χ2выб.
Затем по таблице «Критические точки
распределения χ2»,
по заданному уровню значимости α и числу
степеней свободы k
= n
– 1 находятся левое критическое значение
χ2лев.кр(1
– α/2;k)
и правое критическое значение
χ2прав.кр(α/2;k).
Если при этом χ2лев.кр
< χ2выб
< χ2прав.кр,
нет
оснований отвергнуть основную гипотезу,
конкурирующая – отвергается. В противном
случае принимается конкурирующая
гипотеза и отвергается основная.
Б)
Пусть теперь выдвинута нулевая гипотеза
H0:
σ2
=
σ02
о
равенстве неизвестной генеральной
дисперсии σ2
предполагаемому значению σ02
при конкурирующей гипотезе H1:
σ2
>
σ02.
Для проверки этой гипотезы по результатам
выборки вычисляется значение критерия
(14) χ2выб.
Затем по таблице «Критические точки
распределения χ2»,
по заданному уровню значимости α и числу
степеней свободы k
= n
– 1 находится критическое значение
χ2кр(
α;k).
Если при этом χ2выб
< χ2кр,
нет оснований отвергнуть основную
гипотезу, а конкурирующая – отвергается.
В)
Пусть теперь выдвинута нулевая гипотеза
H0:
σ2
=
σ02
о
равенстве неизвестной генеральной
дисперсии σ2
предполагаемому значению σ02
при конкурирующей гипотезе H1:
σ2
<
σ02.
Для проверки этой гипотезы по результатам
выборки вычисляется значение критерия
(14) χ2выб.
Затем по таблице «Критические точки
распределения χ2»,
по заданному уровню значимости α и числу
степеней свободы k
= n
– 1 находится критическое значение
χ2кр(
1- α;k).
Если при этом χ2выб
> χ2кр,
нет оснований отвергнуть основную
гипотезу, конкурирующая – отвергается.
Для
проверки гипотез
неизвестной средней a
генеральной совокупности
с
нормальным законом распределения
с неизвестной дисперсией при заданном
уровне значимости α используется
критерий Стьюдента
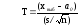 ,
,
(15)
где
xвыб
– выборочное среднее;
a0
гипотетическое значение средней; n
– объем выборки; s
– исправленное среднее квадратическое
отклонение.
А)
Пусть выдвинута нулевая гипотеза H0:
a
=
a0
о
равенстве неизвестной генеральной
средней a
предполагаемому значению a0
при конкурирующей гипотезе H1:
a
≠
a0
.
Для проверки этой гипотезы по результатам
выборки вычисляется значение критерия
(15) Tвыб.
Затем по таблице «Критические точки
распределения Стьюдента», по заданному
уровню значимости α и числу степеней
свободы k
= n
– 1 находится двустороннее критическое
значение Tдвустор.кр(α;k).
Если при этом | Tвыб
| <
Tдвустор.кр,
нет оснований отвергнуть основную
гипотезу, а конкурирующая – отвергается.
Б)
Пусть теперь выдвинута нулевая гипотеза
H0:
a
=
a0
о
равенстве неизвестной генеральной
средней a
предполагаемому значению a0
при конкурирующей гипотезе H1:
a
>
a0
.
Для проверки этой гипотезы по результатам
выборки вычисляется значение критерия
(15) Tвыб.
Затем по таблице «Критические точки
распределения Стьюдента», по заданному
уровню значимости α и числу степеней
свободы k
= n
– 1 находится критическое значение
Tправостор.кр(α;k).
Если при этом Tвыб
< Tправостор.кр,
нет оснований отвергнуть основную
гипотезу
,
а конкурирующая – отвергается.
В)
Пусть теперь выдвинута нулевая гипотеза
H0:
a
=
a0
о
равенстве неизвестной генеральной
средней a
предполагаемому значению a0
при конкурирующей гипотезе H1:
a
< a0
.
Для проверки этой гипотезы по результатам
выборки вычисляется значение критерия
(15) Tвыб.
Затем по таблице «Критические точки
распределения Стьюдента», по заданному
уровню значимости α и числу степеней
свободы k
= n
– 1 находится критическое значение
Tправостор.кр(α;k)
и полагают Tлевостор.кр
= –Tправостор.кр.
Если при этом Tвыб
> Tлевостор.кр,
нет оснований отвергнуть основную
гипотезу, а конкурирующая – отвергается.
Содержание:
- Точечные статистические оценки параметров генеральной совокупности
- Методы определения точечных статистических оценок
- Законы распределения вероятностей для
- Интервальные статистические оценки для параметров генеральной совокупности
- Построение доверчивого интервала для при известном значении с заданной надежностью
- Построение доверительного интервала для при неизвестном значении из заданной надежности
- Построение доверительных интервалов с заданной надежностью для
- Построение доверительного интервала для генеральной совокупности с заданной надежностью
- Построение доверительного интервала для с помощью неравенства Чебишова с заданной надежностью
Информация, которую получили на основе обработки выборки про признак генеральной совокупности, всегда содержит определенные погрешности, поскольку выборка содержит только незначительную часть от нее  то есть объем выборки значительно меньше объема генеральной совокупности.
то есть объем выборки значительно меньше объема генеральной совокупности.
Потому, следует организовать выборку так, чтобы эта информация была более полной (выборка может быть репрезентабельной) и обеспечивала с наибольшей степенью доверия о параметрах генеральной совокупности ил закон распределение ее признака.
Параметры генеральной совокупности  являются величинами постоянными, но их числовые значения неизвестные. Эти параметры оцениваются параметрами выборки:
являются величинами постоянными, но их числовые значения неизвестные. Эти параметры оцениваются параметрами выборки:  которые получаются при обработке выборки. Они являются величинами непредсказуемыми, то есть случайными. Схематично это можно показать так (рис. 115).
которые получаются при обработке выборки. Они являются величинами непредсказуемыми, то есть случайными. Схематично это можно показать так (рис. 115).

Тут через  обозначен оценочный параметр генеральной совокупности, а через
обозначен оценочный параметр генеральной совокупности, а через  – его статистическую оценку, Которую называют еще статистикой. При этом
– его статистическую оценку, Которую называют еще статистикой. При этом  а
а  – случайная величина, что имеет полный закон распределения вероятностей. заметим, что для реализации выборки каждую ее варианту рассматривают как случайную величину, что имеет закон распределения вероятностей признака генеральной совокупности с соответственными числовыми характеристиками:
– случайная величина, что имеет полный закон распределения вероятностей. заметим, что для реализации выборки каждую ее варианту рассматривают как случайную величину, что имеет закон распределения вероятностей признака генеральной совокупности с соответственными числовыми характеристиками:

Точечные статистические оценки параметров генеральной совокупности
Статистическая оценка  , которая обозначается одном числом, называется точечной. Возьмем во внимание, что
, которая обозначается одном числом, называется точечной. Возьмем во внимание, что  является случайной величиной, точечная статистическая оценка может быть смещенной или несмещенной: когда математическое надежда этой оценки точно равны оценочному параметру
является случайной величиной, точечная статистическая оценка может быть смещенной или несмещенной: когда математическое надежда этой оценки точно равны оценочному параметру  а именно:
а именно:

то  называется несмещенной; в противоположном случае, то есть когда
называется несмещенной; в противоположном случае, то есть когда

точечная статистическая оценка  называется смещенной относительно параметра генеральной совокупности
называется смещенной относительно параметра генеральной совокупности 
Разница

называется смещением статистической оценки 
Оценочный параметр может иметь несколько точечных несмещенных статистических оценок, что можно изобразить так (рис. 116):

Например, пусть  которая имеет две несмещенные точечные статистические оценки –
которая имеет две несмещенные точечные статистические оценки –  и
и  Тогда плотность вероятностей для
Тогда плотность вероятностей для 
 имеют такой вид (рис. 117):
имеют такой вид (рис. 117):

Из графиков плотности видим, что оценка  сравнено с оценкой
сравнено с оценкой  имеет то преимущество, что около параметра
имеет то преимущество, что около параметра 
 Отсюда получается, что оценка
Отсюда получается, что оценка  чаще получает значение в этой области, чем оценка
чаще получает значение в этой области, чем оценка 
Но на “хвостах” распределений имеет другую картину: большие отклонения от  будут наблюдаться для статистической оценки
будут наблюдаться для статистической оценки  , чаще, чем для
, чаще, чем для  Потому, сравнивая дисперсии статистических
Потому, сравнивая дисперсии статистических  как меру рассеивания, видим, что
как меру рассеивания, видим, что  имеет меньшую дисперсию, чем оценка
имеет меньшую дисперсию, чем оценка  .
.
Точечная статистическая оценка называется эффективной, когда при заданном объеме выборки она имеет минимальную дисперсию. Следует, оценка  будет несмещенной и эффективной.
будет несмещенной и эффективной.
Точечная статистическая оценка называется основой, если в случае неограниченного увеличения объема выборки  приближается к оценке параметра
приближается к оценке параметра  , а именно:
, а именно:

Методы определения точечных статистических оценок
Существует три метода определения точечных статистических оценок для параметров генеральной совокупности.
Метод аналогий. Этот метод основывается на том, что для параметров генеральной совокупности выбирают такие же параметры выборки, то есть для оценки  выбирают аналогичные статистики –
выбирают аналогичные статистики – 
Метод наименьших квадратов. Согласно с этим методом статистические оценки обозначаются с условием минимизации суммы квадратов отклонений вариант выборки от статистической оценки  .
.
Итак, используя метод наименьших квадратов, можно, например, обозначить статистическую оценку для  Для этого воспользуемся функцией
Для этого воспользуемся функцией  Используя условие экстремума, получим:
Используя условие экстремума, получим:

Отсюда, для  точечной статистической оценкой будет
точечной статистической оценкой будет  – выборочная средняя.
– выборочная средняя.
Метод максимальной правдоподобности. Этот метод занимает центральное место в теории статистической оценки параметров  На него в свое время обратил внимание К. Гаусс, а разработал его Р. Фишер. Этот метод рассмотрим подробнее.
На него в свое время обратил внимание К. Гаусс, а разработал его Р. Фишер. Этот метод рассмотрим подробнее.
Пусть признак генеральной совокупности  обозначается только одном параметром
обозначается только одном параметром  и имеет плотность вероятности
и имеет плотность вероятности  В случае реализации выборки с вариантами
В случае реализации выборки с вариантами  плотность вероятности выборки будет такой:
плотность вероятности выборки будет такой:

В этом варианте рассматриваются как независимые случайные величины, которые имеют один и тот же закон распределения, что ее признак генеральной совокупности  .
.
Суть этого метода состоит в том, что фиксируя значение вариант  , обозначают такие значение параметра
, обозначают такие значение параметра  , при котором функция
, при котором функция  максимизуется. Она называется функцией максимальной правдоподобности и обозначается так:
максимизуется. Она называется функцией максимальной правдоподобности и обозначается так: 
Например, когда признак генеральной совокупности  имеет нормальный закон распределения, то функция максимальной правдоподобности приобретет такой вид:
имеет нормальный закон распределения, то функция максимальной правдоподобности приобретет такой вид:

При этом статистические оценки  выбирают и ее значения, по которых заданная выборка будет верной, то есть функция
выбирают и ее значения, по которых заданная выборка будет верной, то есть функция  достигает максимума.
достигает максимума.
На практике удобно от функции  перейти к ее логарифму, а именно:
перейти к ее логарифму, а именно:

согласно с необходимым условием экстремума для этой функции получим:

Из первого уравнения системы  получим:
получим:

из уравнение системы  получим:
получим:

Следует, для  точечной функции статистической оценкой будет
точечной функции статистической оценкой будет  для
для 
Свойства  Исправленная дисперсия, исправленное среднее квадратичное отклонение. Точечной несмещенной статистической оценкой для
Исправленная дисперсия, исправленное среднее квадратичное отклонение. Точечной несмещенной статистической оценкой для  будет
будет 
И на самом деле,
 учитывая то. что
учитывая то. что 

Следует, 
Проверим на несмещенность статистической оценки 



Таким образом, получим 
Следует,  будет точечной смещенной статистической оценкой для
будет точечной смещенной статистической оценкой для  , где
, где  – коэффициент смещения, который уменьшается с увеличением объема выборки
– коэффициент смещения, который уменьшается с увеличением объема выборки 
Когда  умножить на
умножить на  то получим
то получим 
Тогда

Следует,  будут точеной несмещенной статистической оценкой для
будут точеной несмещенной статистической оценкой для  Ее называли исправленной дисперсией и обозначили через
Ее называли исправленной дисперсией и обозначили через 
Отсюда точечной несмещенной статистической оценкой для  будет исправленная дисперсия
будет исправленная дисперсия  или
или

Величину

называют исправленным средним квадратичным отклонением.
Исправленное среднее квадратичное отклонение, следует подчеркнуть, будет смещенной точечной статистической оценкой для  поскольку
поскольку

где  является ступенью свободы;
является ступенью свободы;
 – коэффициенты смещения.
– коэффициенты смещения.
Пример. 200 однотипных деталей были отданы на шлифование. Результаты измерения приведены как дискретное статистическое распределение, подан в табличной форме:

Найти точечные смещенные статистические оценки для 

Решение. Поскольку точечной несмещенной оценки для  будет
будет  то вычислим
то вычислим

Для обозначение точечной несмещенной статистической оценки для  вычислим
вычислим 


тогда точечная несмещенная статистическая оценка для  равно:
равно:

Пример. Граничная нагрузка на стальной болт  что измерялась в лабораторных условий, задано как интервальное статистическое распределение:
что измерялась в лабораторных условий, задано как интервальное статистическое распределение:

Обозначить точечные несмещенные статистические оценки для 
Решение. Для обозначения точечных несмещенных статистических распределений к дискретному, который приобретает такой вид:

Вычислим 

Следует, точечная несмещенная статистическая оценка для 

Для обозначения  вычислим
вычислим 

Отсюда точечная несмещенная статистическая оценка для  будет
будет 
Законы распределения вероятностей для 
Как уже обозначалось, числовые характеристики выборки являются случайными величинами, что имеют определенные законы распределения вероятностей. Так,  (выборочная средняя) на основании центральной граничной теоремы теории вероятностей (теоремы Ляпунова) имеем нормальный закон распределения с числовыми характеристиками
(выборочная средняя) на основании центральной граничной теоремы теории вероятностей (теоремы Ляпунова) имеем нормальный закон распределения с числовыми характеристиками

следует, случайная величина  имеет закон распределения
имеет закон распределения 
Чтобы обозначить закон распределения для  необходимо выявить связь между
необходимо выявить связь между  и распределением
и распределением  .
.
Пусть признак генеральной совокупности  имеет нормальный закон распределения
имеет нормальный закон распределения  . При реализации выборки каждую из вариант
. При реализации выборки каждую из вариант  рассматривают как случайную величину. то также имеет закон распределения
рассматривают как случайную величину. то также имеет закон распределения  . При этом вариант выборки является независимым, то есть
. При этом вариант выборки является независимым, то есть  а случайная величина
а случайная величина  соответственно имеет закон распределения
соответственно имеет закон распределения 
Рассмотрим случай, когда варианты выборки имеют частоты  тогда
тогда

Перейдем от случайных величин  к случайным величинам
к случайным величинам  которые линейно выражаются через
которые линейно выражаются через  а именно:
а именно:

Поскольку случайные величины  будут линейными комбинациями случайных величин
будут линейными комбинациями случайных величин  то
то  тоже имеют нормальный закон распределения с числовыми характеристиками:
тоже имеют нормальный закон распределения с числовыми характеристиками:


Следует, случайные величины  имеют закон распределения
имеют закон распределения 
Построим матрицу  элементы которой будут коэффициенты при
элементы которой будут коэффициенты при  в линейных зависимостях для
в линейных зависимостях для 

Транспортируем матрицу  получим:
получим:

Если перемножить матрицы  и
и  то получим:
то получим:

где  будет единичная матрица.
будет единичная матрица.
Следует, случайные величины  обозначены ортогональными преобразованиями случайных величин
обозначены ортогональными преобразованиями случайных величин  В векторной – матричной форме это можно записать так:
В векторной – матричной форме это можно записать так:
Из курса алгебры известно, что во время ортогональных преобразований вектора сохраняется его длина, то есть

Тогда из формулы для  получим:
получим:

Поскольку  далее вычислим:
далее вычислим:

Следует, получим 
Когда поделим левую и правую часть  на
на  то получим,
то получим,

Поскольку  имеет закон распределения
имеет закон распределения  то
то  получим закон распределения
получим закон распределения  то есть нормированный нормальный закон.
то есть нормированный нормальный закон.
То случайная величина

получим распределение  из
из  ступенями свободы.
ступенями свободы.
Отсюда получается, что случайная величина  получим распределение
получим распределение  из
из  ступенями свободы.
ступенями свободы.
Таким образом, приведена: случайная величина  тут символ
тут символ  нужно читать “распределена как”;
нужно читать “распределена как”;
случайная величина 
случайная величина 
Интервальные статистические оценки для параметров генеральной совокупности
Точечные статистические оценки  являются случайными величинами, а потому приближенная замена
являются случайными величинами, а потому приближенная замена  на
на  часто приводит к существенным погрешностям, особенно когда объем выборки не большой. В этом случае используют интервальные статистические оценки.
часто приводит к существенным погрешностям, особенно когда объем выборки не большой. В этом случае используют интервальные статистические оценки.
Статистическая оценка, что обозначается двумя числами, концами интервалов, называется интервальной.
Разница между статистической оценкой  и ее оценкой параметром
и ее оценкой параметром  взята с абсолютным значением, называется точностью оценки, а именно:
взята с абсолютным значением, называется точностью оценки, а именно:

где  является точностью оценки.
является точностью оценки.
Поскольку  является случайной величиной, то и
является случайной величиной, то и  будет случайной, потому неравенство
будет случайной, потому неравенство  справедливо с определенной вероятностью.
справедливо с определенной вероятностью.
Вероятность, с которой берется неравенство  , то есть
, то есть

называется надежностью
Равенство  можно записать так:
можно записать так:

Интервал  что покрывает оценочный параметр
что покрывает оценочный параметр  генеральной совокупности с заданной надежностью
генеральной совокупности с заданной надежностью  называют доверчивым.
называют доверчивым.
Построение доверчивого интервала для  при известном значении
при известном значении  с заданной надежностью
с заданной надежностью 
Пусть признак  генеральной совокупностью имеет нормальный закон распределению. Построим доверительный интервал для
генеральной совокупностью имеет нормальный закон распределению. Построим доверительный интервал для  зная числовое значение среднего квадратичному отклонению генеральной совокупности
зная числовое значение среднего квадратичному отклонению генеральной совокупности  с заданной надежностью
с заданной надежностью  Поскольку
Поскольку  как точечная несмещенная статистическая оценка для
как точечная несмещенная статистическая оценка для  имеет нормальный закон распределения с числовыми характеристиками
имеет нормальный закон распределения с числовыми характеристиками 
 то воспользовавшись
то воспользовавшись  получим
получим

Случайная величина  имеет нормальный закон распределения с числовыми характеристиками
имеет нормальный закон распределения с числовыми характеристиками

Потому  будет нормированный нормальный закон распределения
будет нормированный нормальный закон распределения 
Отсюда равенство  можно записать, обозначив
можно записать, обозначив  так;
так;

или

Согласно с формулой нормированного нормального закона

для  она получает такой вид:
она получает такой вид:

Из равенства  находим аргументы
находим аргументы  а именно:
а именно:

Аргумент  находим значение функции Лапласа, которая равна
находим значение функции Лапласа, которая равна  по таблице (дополнение 2).
по таблице (дополнение 2).
Следует, доверительный интервал равен:

что можно изобразить условно на рисунке 118.

Величина  называется точностью оценки, или погрешностью выборки.
называется точностью оценки, или погрешностью выборки.
Пример. Измеряя 40 случайно отобранных после изготовления деталей, нашли выборку средней, что равна 15 см. Из надежности  построить доверительный интервал для средней величины всей партии деталей, если генеральная дисперсия равна
построить доверительный интервал для средней величины всей партии деталей, если генеральная дисперсия равна 
Решение. Для построенного доверчивого интервала необходимо найти: 
Из условия задачи имеем: 
 Величина
Величина  вычисляется из уравнения
вычисляется из уравнения

 {с таблицей значения функции Лапласа}.
{с таблицей значения функции Лапласа}.
Найдем числовые значения концов доверчивого интервала:

Таким образом, получим: 
Следует, с надежностью  (99% гарантии) оценочный параметр
(99% гарантии) оценочный параметр  пребывает в середина интервала
пребывает в середина интервала 
Пример. Имеем такие данные про размеры основных фондов (в млн руб.) на 30-ти случайно выбранных предприятий:

построить интервальное статистическое распределение с длиной шага  млн рублей.
млн рублей.
С надежностью  найти доверительный интеграл для
найти доверительный интеграл для  если
если  млн рублей.
млн рублей.
Решение. Интервальное статистическое распределение будет таким:

Для обозначение  необходимо построить дискретное статистическое распределение, что имеет такой вид:
необходимо построить дискретное статистическое распределение, что имеет такой вид:

Тогда

 млн рублей.
млн рублей.
Для построения доверительного интервала с заданной надежностью  необходимо найти
необходимо найти 

Вычислим концы интервала:
 млн руб.
млн руб.
 млн руб.
млн руб.
Следует, доверительный интервал для  будет
будет 
Пример. Какое значение может получит надежность оценки  чтобы за объем выборки
чтобы за объем выборки  погрешность ее не превышала
погрешность ее не превышала  при
при 
Решение. Обозначим погрешность выборки

Далее получим:

как видим, надежность мала.
Пример. Обозначить объем выборки  по которому погрешность
по которому погрешность  гарантируется с вероятностью
гарантируется с вероятностью  если
если 
Решение. По условию задачи  Поскольку
Поскольку  то получим:
то получим:  Величину
Величину  находим из равенства
находим из равенства  Тогда
Тогда 
Построение доверительного интервала для  при неизвестном значении
при неизвестном значении  из заданной надежности
из заданной надежности 
Для малых выборок, с какими сталкиваемся, исследуя разные признаки в техники или сельском хозяйстве, для оценки  при неизвестном значении
при неизвестном значении  невозможно воспользоваться нормальным законом распределения. Потому для построения доверительного интервала используется случайная величина.
невозможно воспользоваться нормальным законом распределения. Потому для построения доверительного интервала используется случайная величина.

что имеет распределение Стьюдента с  ступенями свободы.
ступенями свободы.
Тогда  получает вид:
получает вид:

поскольку  для распределения Стьюдента является функцией четной.
для распределения Стьюдента является функцией четной.
Вычислив по данному статистическому распределению 
 и обозначив по таблице распределения Стьюдента значения
и обозначив по таблице распределения Стьюдента значения  построим доверительный интервал
построим доверительный интервал

Тут  вычислим по заданной надежностью
вычислим по заданной надежностью  и числом степеней свободы
и числом степеней свободы  по таблице (дополнение 3).
по таблице (дополнение 3).
Пример. Случайно выбранная партия из двадцати примеров была испытана относительно срока безотказной работы каждого из них  Результаты испытаний приведено в виде дискретного статистического распределения:
Результаты испытаний приведено в виде дискретного статистического распределения:

С надежностью  построить доверительный интервал для
построить доверительный интервал для  (среднего времени безотказной работы прибора.)
(среднего времени безотказной работы прибора.)
Решение. Для построения доверительного интеграла необходимо найти среднее выборочное и исправленное среднее квадратичное отклонение.
Вычислим 

следует, получили  часов.
часов.
Обозначим 

следует, 
Исправленное среднее квадратичное отклонение равно:
 часов.
часов.
По таблице значений  (дополнение 3) распределение Стьюдента по заданной надежностью
(дополнение 3) распределение Стьюдента по заданной надежностью  и числом ступеней свободы
и числом ступеней свободы  находим значение
находим значение 
Вычислим концы доверительного интервала:
 час.
час.
 час.
час.
Следует, с надежностью  можно утверждать, что
можно утверждать, что  будет содержится в интервале
будет содержится в интервале

При больших объемах выборки, а именно:  на основании центральной граничной теоремы теории вероятностей (теоремы Ляпунова) распределение Стьюдента приближается к нормальному закону. В этом случае
на основании центральной граничной теоремы теории вероятностей (теоремы Ляпунова) распределение Стьюдента приближается к нормальному закону. В этом случае  находиться по таблице значений функции Лапласа.
находиться по таблице значений функции Лапласа.
Пример. В таблице приведены отклонения диаметров валиков, изготовленных на станке, от номинального размера:

с надежностью  построить доверительный интервал для
построить доверительный интервал для 
Решение. Для постройки доверительного интервала необходимо найти 
Для этого от интегрального статистического распределения, приведенного в условии задачи, необходимо перейти к дискретному, а именно:

Вычислим 
 поскольку
поскольку 

Следует, 
Обозначим 

Вычислим исправленное среднее квадратичное отклонение 

Учитывая на большой  объем выборки можно считать, что распределение Стьюдента близкий к нормальному закону. Тогда по таблице значения функции Лапласа
объем выборки можно считать, что распределение Стьюдента близкий к нормальному закону. Тогда по таблице значения функции Лапласа

Вычислим концы интервалов:


Итак, доверчивый интервал для среднего значения отклонений будет таким: 
Отсюда с надежностью  можно утверждать, что
можно утверждать, что
Построение доверительных интервалов с заданной надежностью  для
для 
В случае, если признак  имеем нормальный закон распределения, для построения доверительного интервала с заданной надежностью
имеем нормальный закон распределения, для построения доверительного интервала с заданной надежностью  для
для  используем случайную величину
используем случайную величину

что имеет распределение  из
из  ступенями свободы.
ступенями свободы.
Поскольку случайные действия
 и
и 
являются равновероятными, то есть их вероятности равны  получим:
получим:

Подставляя в 
 получим
получим

Следует, доверительный интервал для  получит вид:
получит вид:

Тогда доверительный интервал для  получается из
получается из  и будет таким:
и будет таким:

Значения  находятся по таблице (дополнение 4) согласно с равенствами:
находятся по таблице (дополнение 4) согласно с равенствами:

где 
Пример. Проверена партия однотипных телевизоров  на чувствительность к видео-программ
на чувствительность к видео-программ  данные проверки приведены как дискретное статистическое распределение:
данные проверки приведены как дискретное статистическое распределение:

С надежностью  построить доверительные интервалы для
построить доверительные интервалы для 
Решение. Для построении доверительных интервалов необходимо найти значения 
Вычислим значения 
 так как
так как 

Вычислим 


Следует 
Исправленная дисперсия и исправленное среднее квадратичное отклонение равны:

Поскольку  то согласно с
то согласно с  находим значения
находим значения  а именно:
а именно:

По таблице (дополнение 4) находим:

вычислим концы доверительного интервала для 


Следует, доверительный интеграл для  будет таким:
будет таким:

Доверительный интервал для  станет
станет

Доверительный интервал для  можно построить с заданной надежностью
можно построить с заданной надежностью  взяв распределение
взяв распределение 
Поскольку

то равенство  можно записать так:
можно записать так:

или

Обозначив  получим
получим

чтобы найти  возьмем случайную величину
возьмем случайную величину

что имеет распределение 
Учитывая то, что события
 и
и 
при  является равновероятными, получим:
является равновероятными, получим:

Если умножить все члены двойного неравенства 
 на
на  то получим:
то получим:

Отсюда получим:

Из уравнения  по заданной надежностью
по заданной надежностью  и объемом выборки
и объемом выборки  находим по таблице (дополнение 5) значение величины
находим по таблице (дополнение 5) значение величины 
Доверительный интервал будет таким:

Пример. С надежностью  построить доверительный интервал вычислим значения
построить доверительный интервал вычислим значения  по таблице (дополнение 5).
по таблице (дополнение 5). 
Обозначим концы интервала:

Следует, доверительный интервал для  с надежностью
с надежностью  будет такой
будет такой

Построение доверительного интервала для  генеральной совокупности с заданной надежностью
генеральной совокупности с заданной надежностью 
Как величина, полученная по результатам выборки,  является случайной и представляет собой точечную несмещенную статистическую оценку для
является случайной и представляет собой точечную несмещенную статистическую оценку для 
Исправленное среднее квадратичное отклонение для 

Для построения доверительного интервала для  используется случайная величина
используется случайная величина

что имеет нормированный нормальный закон распределения 
Воспользовавшись  получим
получим

Следует. доверительный интервал для  будет таким:
будет таким:

где  находим из равенства
находим из равенства

по таблице значений функции Лапласа.
Пример. Случайно выбранных студентов из потока университета были подвергнуты тестированию по математике и химии. Результаты этих тестирования преподнесено статистическим распределением, где  – оценки по математике,
– оценки по математике,  – по химии. Ответы оценивались по десятибалльной системе:
– по химии. Ответы оценивались по десятибалльной системе:

Необходимо:
1) с надежностью  построить доверительный интервал для
построить доверительный интервал для  если
если 
2) с надежностью  построить доверительный интервал для
построить доверительный интервал для 
Решение. Вычислим основные числовые характеристики признак  и
и  а также
а также  Поскольку
Поскольку  получим:
получим:


1. Построим доверительный интервал с надежностью  для
для  если
если 

нам известные значения  Значения
Значения  вычисляем из уравнения
вычисляем из уравнения

где  находим по таблице значений функции Лапласа.
находим по таблице значений функции Лапласа.
Обозначим концы интервала:

Следует, доверительный интервал для  будет таким:
будет таким:

2. Построим доверительный интервал с надежностью  для
для 
Поскольку  нам не известно, то доверительный интервал в этом случае обозначается так:
нам не известно, то доверительный интервал в этом случае обозначается так:

На известное значение  находим по таблице распределения Стьюдента (дополнение 3),
находим по таблице распределения Стьюдента (дополнение 3),

Вычислим концы доверительного интервала:

Таким образом, доверительный интервал для  будет в таких границах:
будет в таких границах:

Доверительный интеграл с надежностью  для
для  будет таким:
будет таким:

Нам известно значение  Учитывая, что
Учитывая, что  найдем по таблице (дополнение 5) значения
найдем по таблице (дополнение 5) значения 
Обозначим концы доверительного интервала:

Следует, доверительный интервал для  подается таким неравенством:
подается таким неравенством:

Доверительный интервал для  с заданной надежностью
с заданной надежностью  будет таким:
будет таким:

Нам известны значения  обозначаем по таблице значений функции Лапласа
обозначаем по таблице значений функции Лапласа  где
где 
Обозначим концы доверительного интервала:

таким образом, доверительный интервал для  будет в таких границах:
будет в таких границах:

Построение доверительного интервала для  с помощью неравенства Чебишова с заданной надежностью
с помощью неравенства Чебишова с заданной надежностью
В случае, если отсутствует информация про закон распределения признака генеральной совокупности  оценка вероятностей события
оценка вероятностей события  где
где  и построение доверительного интервала для
и построение доверительного интервала для  с заданной надежностью
с заданной надежностью  выполняется с использованием неравенства Чебишова по условию, что известно значение
выполняется с использованием неравенства Чебишова по условию, что известно значение  а именно:
а именно:

Из  обозначаем величину
обозначаем величину 

Доверительный интервал дается таким неравенством:

Когда  неизвестно, используем исправленную дисперсию
неизвестно, используем исправленную дисперсию  и доверительный интервал приобретает такой вид:
и доверительный интервал приобретает такой вид:

Пример. Полученные данные с 100 наугад выбранных предприятий относительно возрастания выработки на одного работника  которые имеют такой интервальное статистическое распределение:
которые имеют такой интервальное статистическое распределение:

Воспользовавшись неравенством Чебишова, построить доверительный интервал для  если известно значение
если известно значение  с надежностью
с надежностью 
Решение. Для построения доверительного интервала с помощью неравенства Чебишова необходимо вычислить  Чтобы обозначить
Чтобы обозначить  перейдем от интервального к дискретному статистическому распределению, а именно:
перейдем от интервального к дискретному статистическому распределению, а именно:

Тогда получим:

Воспользовавшись  вычислим
вычислим 

таким образом, доверительный интервал для  преподноситься такими неравенствами:
преподноситься такими неравенствами:

или

Пример. Заданы размеры основных фондов  на 30- ти предприятий дискретным статистическим распределением:
на 30- ти предприятий дискретным статистическим распределением:

Воспользовавшись неравенством Чебишова с надежностью  построить доверительный интервал для
построить доверительный интервал для 
Решение. Для постройки доверительного интервала для  с помощью неравенства Чебишова необходимо вычислить
с помощью неравенства Чебишова необходимо вычислить 

 млн руб.
млн руб.
Следует,  млн рублей.
млн рублей.

 млн рублей.
млн рублей.
Обозначить концы доверительного интервала:
 млн рублей
млн рублей
 н рублей
н рублей
Итак, доверительный интервал для  подается неравенствами
подается неравенствами

Лекции:
- Статистические гипотезы
- Корреляционный и регрессионный анализ
- Комбинаторика основные понятия и формулы с примерами
- Число перестановок
- Количество сочетаний
- Действия над событиями. Теоремы сложения и умножения вероятностей примеры с решением
- Примеры решения задач на тему: Случайные величины
- Примеры решения задач на тему: основные законы распределения
- Примеры решения задач на тему: совместный закон распределения двух случайных величин
- Статистические распределения выборок и их числовые характеристики
Статистические оценки параметров генеральной совокупности
Определение статистической оценки. Точечные статистические оценки: смещенные и несмещенные, эффективные и состоятельные. Интервальные статистические оценки. Точность и надежность оценки; определение доверительного интервала; построение доверительных интервалов для средней при известном и неизвестном среднеквадратическом отклонении.
Определение статистической оценки
Пусть требуется изучить количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак. Возникает задача оценки параметров, которыми определяется это распределение. Например, если известно, что изучаемый признак распределен в генеральной совокупности по нормальному закону, то необходимо оценить математическое ожидание и среднеквадратическое отклонение, так как эти два параметра полностью определяют нормальное распределение. Если имеются основания считать, что признак имеет распределение Пуассона, то необходимо оценить параметр , которым это распределение определяется. Обычно имеются лишь данные выборки, полученные в результате
наблюдений:
. Через эти данные и выражают оцениваемый параметр. Рассматривая
как значения независимых случайных величин
можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения означает найти функцию от наблюдаемых случайных величин, которая и дает приближенное значение оцениваемого параметра.
Точечные статистические оценки
Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин. Статистическая оценка неизвестного параметра генеральной совокупности одним числом называется точечной. Рассмотрим следующие точечные оценки: смещенные и несмещенные, эффективные и состоятельные.
Для того чтобы статистические оценки давали хорошие приближения оцениваемых параметров, они должны удовлетворять определенным требованиям. Укажем эти требования. Пусть есть статистическая оценка неизвестного параметра
теоретического распределения. Допустим, что по выборке объема
найдена оценка
. Повторим опыт, т. е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным найдем оценку
и т. д. Получим числа
, которые будут различаться. Таким образом, оценку
можно рассматривать как случайную величину, а числа
— как возможные ее значения.
Если оценка дает приближенное значение
с избытком, то найденное по данным выборок число
будет больше истинного значения
. Следовательно, и математическое ожидание (среднее значение) случайной величины
будет превышать
, то есть
. Если
дает приближенное значение
с недостатком, то
.
Использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, приводит к систематическим ошибкам. Поэтому нужно потребовать, чтобы математическое ожидание оценки было равно оцениваемому параметру. Соблюдение требования
устраняет систематические ошибки.
Несмещенной называют статистическую оценку , математическое ожидание которой равно оцениваемому параметру
, то есть
.
Смещенной называют статистическую оценку , математическое ожидание которой не равно оцениваемому параметру.
Однако ошибочно считать, что несмещенная оценка всегда дает хорошее приближение оцениваемого параметра. Действительно, возможные значения могут быть сильно рассеяны вокруг своего среднего значения, т. е. дисперсия величины
может быть значительной. В этом случае найденная по данным одной выборки оценка, например
, может оказаться удаленной от своего среднего значения
, а значит, и от самого оцениваемого параметра
. Приняв
в качестве приближенного значения
, мы допустили бы ошибку. Если потребовать, чтобы дисперсия величины
была малой, то возможность допустить ошибку будет исключена. Поэтому к статистической оценке предъявляются требования эффективности.
Эффективной называют статистическую оценку, которая (при заданном объеме выборки ) имеет наименьшую возможную дисперсию. При рассмотрении выборок большого объема к статистическим оценкам предъявляется требование состоятельности.
Состоятельной называют статистическую оценку, которая при стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при
стремится к нулю, то такая оценка оказывается также состоятельной.
Рассмотрим вопрос о том, какие выборочные характеристики лучше всего в смысле несмещённости, эффективности и состоятельности оценивают генеральную среднюю и дисперсию.
Пусть изучается дискретная генеральная совокупность относительно количественного признака. Генеральной средней называется среднее арифметическое значений признака генеральной совокупности. Она вычисляется по формуле
или
где — значения признака генеральной совокупности объема
;
— соответствующие частоты, причем
Пусть из генеральной совокупности в результате независимых наблюдений над количественным признаком извлечена выборка объема со значениями признака
. Выборочной средней называется среднее арифметическое значений признака выборочной совокупности и вычисляется по формуле
или
где — значения, признака в выборочной совокупности объема
;
— соответствующие частоты, причем
Если генеральная средняя неизвестна и требуется оценить ее по данным выборки, то в качестве оценки генеральной средней принимают выборочную среднюю, которая является несмещенной и состоятельной оценкой. Отсюда следует, что если по нескольким выборкам достаточно большого объема из одной и той же генеральной совокупности будут найдены выборочные средние, то они будут приближенно равны между собой. В этом состоит свойство устойчивости выборочных средних.
Если дисперсии двух совокупностей одинаковы, то близость выборочных средних к генеральным не зависит от отношения объема выборки к объему генеральной совокупности. Она зависит- от объема выборки: чем больше объем выборки, тем меньше выборочная средняя отличается от генеральной.
Для того чтобы охарактеризовать рассеяние значений количественного признака генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику — генеральную дисперсию. Генеральной дисперсией
называется среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения
, которое вычисляется по формуле
или
Для того чтобы охарактеризовать рассеяние наблюденных значений количественного признака выборки вокруг своего среднего значения хв, вводят сводную характеристику — выборочную дисперсию. Выборочной дисперсией называется среднее арифметическое квадратов отклонений наблюденных значений признака от их среднего значения
, которое вычисляется по формуле
или
Кроме дисперсии для характеристики рассеяния значений признака генеральной (выборочной) совокупности вокруг своего среднего значения используют сводную характеристику — среднее квадратическое отклонение. Генеральным средним квадратическим отклонением называют квадратный корень из генеральной дисперсии: . Выборочным средним квадратическим отклонением называют квадратный корень из выборочной дисперсии:
.
Пусть из генеральной совокупности в результате независимых наблюдений над количественным признаком
извлечена выборка объема
. Требуется по данным выборки оценить неизвестную генеральную дисперсию
. Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то эта оценка приведет к систематическим ошибкам, давая заниженное значение генеральной дисперсии. Объясняется это тем, что выборочная дисперсия является смещенной оценкой
. Другими словами, математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно
.
Легко исправить выборочную дисперсию так, чтобы ее математическое ожидание было равно генеральной дисперсии. Для этого нужно умножить на дробь
. В результате получим исправленную дисперсию
, которая будет несмещенной оценкой генеральной дисперсии:
Интервальные оценки
Наряду с точечным оцениванием, статистическая теория оценивания параметров занимается вопросами интервального оценивания. Задачу интервального оценивания можно сформулировать так: по данным выборки построить числовой интервал, относительно которого с заранее выбранной вероятностью можно сказать, что внутри него находится оцениваемый параметр. Интервальное оценивание особенно необходимо при малом количестве наблюдений, когда точечная оценка малонадежна.
Доверительным интервалом для параметра
называется такой интервал, относительно которого с заранее выбранной вероятностью
, близкой к единице, можно утверждать, что он содержит неизвестное значение параметра
, то есть
. Чем меньше для выбранной вероятности число
, тем точнее оценка неизвестного параметра
. И, наоборот, если это число велико, то оценка, проведенная с помощью данного интервала, малопригодна для практики. Так как концы доверительного интервала зависят от элементов выборки, то значения
и
могут изменяться от выборки к выборке. Вероятность
принято называть доверительной (надежностью). Обычно надежность оценки задается наперед, причем в качестве
берут число, близкое к единице. Выбор доверительной вероятности не является математической задачей, а определяется конкретной решаемой проблемой. Наиболее часто задают надежность, равную 0,95; 0,99; 0,999.
Доверительный интервал для генеральной средней при известном значении среднего квадратического отклонения и при условии, что случайная величина (количественный признак ) распределена нормально, задается выражением
где — наперед заданное число, близкое к единице, а значения функции
приведены в таблице прил. 2.
Смысл этого соотношения заключается в следующем: с надежностью можно утверждать, что доверительный интервал
покрывает неизвестный параметр
, точность оценки
. Число
определяется из равенства
, или
. По прил. 2 находят аргумент
, которому соответствует значение функции Лапласа, равное
.
Пример 1. Случайная величина имеет нормальное распределение с известным средним квадратическим отклонением
. Найти доверительные интервалы для оценки неизвестной генеральной средней по выборочным средним, если объем выборок
и надежность оценки
.
Решение. Найдем . Из соотношения
получим, что
. По прил. 2 находим
. Найдем точность оценки
. Доверительные интервалы будут таковы:
. Например, если
, то доверительный интервал имеет следующие доверительные границы:
. Таким образом, значения неизвестного параметра
, согласующиеся с данными выборки, удовлетворяют неравенству
.
Доверительный интервал для генеральной средней нормального распределения признака при неизвестном значении среднего квадратического отклонения задается выражением
Отсюда следует, что с надежностью можно утверждать, что доверительный интервал
покрывает неизвестный параметр
.
Существуют таблицы (прил. 4), пользуясь которыми, по заданным и
находят вероятность
и, наоборот, по заданным
и
находят
.
Пример 2. Количественный признак генеральной совокупности распределен нормально. По выборке объема
найдены выборочная средняя
и исправленное среднеквадратическое отклонение
. Оценить неизвестную генеральную среднюю с помощью доверительного интервала с надежностью
.
Решение. Найдем . Пользуясь прил. 4 по
и
находим
. Найдем доверительные границы:
Итак, с надежностью неизвестный параметр
заключен в доверительном интервале
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
4. Статистические оценки параметров генеральной совокупности
Вспомним основной метод математической статистики. Он состоит в том, что для изучения генеральной совокупности объёма ![]() из неё производится выборка объёма
из неё производится выборка объёма ![]() , которая хорошо характеризует всю совокупность (свойство представительности). И на основании исследования этой выборочной совокупности мы с некоторой достоверностью можем оценить генеральные характеристики. Само собой, чем выше достоверность – тем лучше, тем качественнее исследование. Этому вопросу и посвящена данная глава.
, которая хорошо характеризует всю совокупность (свойство представительности). И на основании исследования этой выборочной совокупности мы с некоторой достоверностью можем оценить генеральные характеристики. Само собой, чем выше достоверность – тем лучше, тем качественнее исследование. Этому вопросу и посвящена данная глава.
Чаще всего требуется выявить закон распределения генеральной совокупности (о чём пойдёт речь позже) и оценить его важнейшие числовые параметры, такие как генеральная средняя ![]() , генеральная дисперсия
, генеральная дисперсия ![]() и стандартное отклонение
и стандартное отклонение ![]() .
.
4.1. Точечные оценки
Очевидно, что для оценки этих параметров нужно вычислить соответствующие выборочные значения. Так, выборочная средняя ![]() позволяет нам оценить генеральную среднюю
позволяет нам оценить генеральную среднюю ![]() , причём, оценить её точечно. Почему точечно? Потому что
, причём, оценить её точечно. Почему точечно? Потому что ![]() – это отдельно взятое, конкретное значение. Если из той же генеральной совокупности мы будем проводить многократные выборки, то в общем случае у нас будут получаться различные выборочные средние, и каждая из них представляет собой точечную оценку генерального значения
– это отдельно взятое, конкретное значение. Если из той же генеральной совокупности мы будем проводить многократные выборки, то в общем случае у нас будут получаться различные выборочные средние, и каждая из них представляет собой точечную оценку генерального значения ![]() .
.
Аналогично, точечной оценкой генеральной дисперсии ![]() является исправленная выборочная дисперсия
является исправленная выборочная дисперсия ![]() , и соответственно, стандартного отклонения
, и соответственно, стандартного отклонения ![]() – исправленное стандартное отклонение
– исправленное стандартное отклонение ![]() .
.
4.2. Интервальная оценка и доверительный интервал
Недостаток точечных оценок состоит в том, что при небольшом объёме выборки (как оно часто бывает), мы можем получать выборочные значения, которые далеки от истины. И в этих случаях логично потребовать, чтобы выборочная характеристика ![]() (средняя, дисперсия или какая-то другая) отличалась от своего генерального значения
(средняя, дисперсия или какая-то другая) отличалась от своего генерального значения ![]() не более чем на некоторое положительное значение
не более чем на некоторое положительное значение ![]() .
.
Справка: ![]() – греческая буква «тета»,
– греческая буква «тета», ![]() – греческая буква «дельта», вместо «дельты» также используют
– греческая буква «дельта», вместо «дельты» также используют ![]() («эпсилон»).
(«эпсилон»).
Значение ![]() называется точностью оценки, и озвученное выше требование можно записать с помощью модуля:
называется точностью оценки, и озвученное выше требование можно записать с помощью модуля: ![]()
Но статистические методы не позволяют 100%-но утверждать, что рассчитанное значение ![]() будет удовлетворять этому неравенству – ведь в статистике всегда есть место случайности, когда мы можем «выиграть в лотерею» в плохом смысле этого слова. Таким образом, можно говорить лишь о вероятности
будет удовлетворять этому неравенству – ведь в статистике всегда есть место случайности, когда мы можем «выиграть в лотерею» в плохом смысле этого слова. Таким образом, можно говорить лишь о вероятности ![]() («гамма»), с которой это неравенство осуществится:
(«гамма»), с которой это неравенство осуществится: ![]() .
.
А теперь я раскрою модуль:
![]()
и сформулирую суть:
Интервал ![]() называется доверительным интервалом и представляет собой интервальную оценку генерального значения
называется доверительным интервалом и представляет собой интервальную оценку генерального значения ![]() по найденному выборочному значению
по найденному выборочному значению ![]() . Данный интервал с вероятностью
. Данный интервал с вероятностью ![]() «накрывает» истинное значение
«накрывает» истинное значение ![]() . Эта вероятность называется доверительной вероятностью или надёжностью интервальной оценки. Надёжность «гамма» часто задаётся наперёд, популярные варианты:
. Эта вероятность называется доверительной вероятностью или надёжностью интервальной оценки. Надёжность «гамма» часто задаётся наперёд, популярные варианты:
![]() .
.
Переходим к конкретике:
 4.3. Оценка генеральной средней нормально распределенной совокупности
4.3. Оценка генеральной средней нормально распределенной совокупности
 3.3. Статистические показатели (итоги по главе)
3.3. Статистические показатели (итоги по главе)
| Оглавление |
Задача 55. Из генеральной совокупности извлечена выборка объема N, заданная вариантами ХI и соответствующими им частотами. Найти несмещенную оценку генеральной средней.
|
Варианта ХI |
2 |
5 |
7 |
10 |
|
Частота Ni |
16 |
12 |
8 |
14 |
Решение. Множество всех объектов, подлежащих изучению, называется Генеральной совокупностью. Множество случайно отобранных объектов называется выборочной совокупностью или Выборкой.
Для оценки неизвестных параметров теоретического распределения служат статистические оценки. Статистическая оценка, определяемая одним числом, называется Точечной оценкой.
Точечная статистическая оценка, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки, называется Несмещенной оценкой. Статистическая оценка, математическое ожидание которой не равно оцениваемому параметру является Смещенной.
Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя
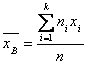 (1),
(1),
Где ХI – варианта выборки (элемент выборки); Ni – частота варианты ХI (число наблюдений варианты ХI); ![]() – объем выборки (число элементов совокупности).
– объем выборки (число элементов совокупности).
Объем данной выборки равен ![]() .
.
Далее по формуле (1) вычисляем несмещенную оценку генеральной средней:
![]()
Задача 56. По выборке объема N=41 найдена смещенная оценка генеральной дисперсии ![]() . Найти несмещенную оценку дисперсии генеральной совокупности.
. Найти несмещенную оценку дисперсии генеральной совокупности.
Решение. Смещенной оценкой генеральной дисперсии служит выборочная дисперсия
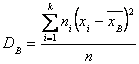
Несмещенной оценкой генеральной дисперсии является «исправленная дисперсия»
![]() или
или 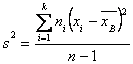
Таким образом, мы получаем искомую несмещенную оценку дисперсии генеральной совокупности:
![]()
Задача 57. Найти доверительный интервал для оценки с надежностью P=0,95 неизвестного математического ожидания A нормально распределенного признака Х генеральной совокупности, если даны генеральное среднее квадратическое отклонение S=5, выборочная средняя ![]() , а объем выборки N=25.
, а объем выборки N=25.
Решение. Интервальной оценкой называется интервал, покрывающий оцениваемый параметр. Доверительным интервалом является интервал, который с данной надежностью покрывает оцениваемый параметр.
Для оценки математического ожидания A нормально распределенного количественного признака Х по выборочной средней ![]() при известном среднем квадратическом отклонении s генеральной совокупности служит доверительный интервал
при известном среднем квадратическом отклонении s генеральной совокупности служит доверительный интервал
![]() ,
,
Где ![]() – точность оценки, T – значение аргумента функции Лапласа
– точность оценки, T – значение аргумента функции Лапласа ![]() (приложение, таблица 2).
(приложение, таблица 2).
В данной задаче T находим из условия ![]() . По таблице 2 определяем
. По таблице 2 определяем ![]() . Таким образом, T=1,96.
. Таким образом, T=1,96.
Далее получаем
![]()
Или ![]()
Задача 58. По данным N=9 независимых равноточных измерений некоторой физической величины найдены среднее арифметическое результатов измерений ![]() и исправленное среднее квадратическое отклонение S=6. Оценить истинное значение измеряемой величины при помощи доверительного интервала с надежностью
и исправленное среднее квадратическое отклонение S=6. Оценить истинное значение измеряемой величины при помощи доверительного интервала с надежностью ![]() =0,99.
=0,99.
Решение. Оценкой математического ожидания A нормально распределенного количественного признака Х в случае неизвестного среднего квадратического отклонения является доверительный интервал
![]() .
.
По таблице 3 приложения, по заданным N и ![]() находим
находим ![]() =3,36.
=3,36.
Таким образом
![]()
Окончательно получаем
![]()
Задача 59. Из генеральной совокупности извлечена выборка объема N. Оценить с надежностью ![]() =0,95 математическое ожидание A нормально распределенного признака Х генеральной совокупности по выборочной средней с помощью доверительного интервала.
=0,95 математическое ожидание A нормально распределенного признака Х генеральной совокупности по выборочной средней с помощью доверительного интервала.
|
Значение признака ХI |
-2 |
1 |
1 |
3 |
4 |
5 |
|
Частота Ni |
2 |
1 |
2 |
2 |
2 |
1 |
Решение. Объем данной выборки равен ![]()
![]()
По данным задачи находим выборочную среднюю:
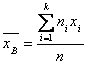
![]()
Далее находим исправленное среднее квадратическое отклонение S:
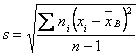
![]()
Для оценки математического ожидания A нормально распределенного количественного признака Х в случае неизвестного среднего квадратического отклонения служит доверительный интервал
![]() .
.
По таблице 3 приложения по заданным N и ![]() находим
находим ![]() =2,26.
=2,26.
Таким образом
![]()
Окончательно получаем
![]()
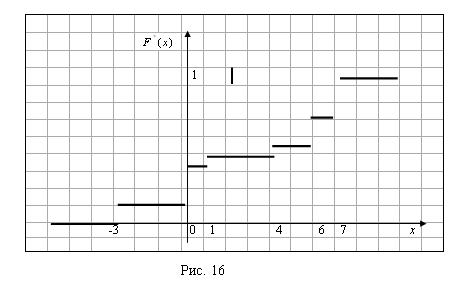
Задача 60. Построить полигон частот и эмпирическую функцию по данному распределению выборки:
|
Варианты ХI |
-3 |
0 |
1 |
4 |
6 |
7 |
|
Частоты Ni |
3 |
6 |
1 |
2 |
5 |
1 |
Решение. Полигоном частот называют ломаную, отрезки которой соединяют точки ![]() ;
; ![]() ;…;
;…;![]() , где ХI – варианты выборки, Ni – соответствующие им частоты.
, где ХI – варианты выборки, Ni – соответствующие им частоты.
Полигон частот для данного распределения изображен на рисунке 15.

Рис. 15
Эмпирической функцией распределения (функцией распределения выборки) называют функцию ![]() , определяющую для каждого значения X относительную частоту события
, определяющую для каждого значения X относительную частоту события ![]() :
:
![]() ,
,
Где ![]() – число вариант, меньших Х; N – объем выборки.
– число вариант, меньших Х; N – объем выборки.
Из определения следует, что ![]() .
.
Найдем эмпирическую функцию распределения.
Объем данной выборки равен ![]() =18.
=18.
Если ![]() , то
, то ![]() =0 (так как -3 – наименьшая варианта). Если
=0 (так как -3 – наименьшая варианта). Если ![]() , то значение
, то значение ![]() , а именно
, а именно ![]() наблюдалось 3 раза, следовательно,
наблюдалось 3 раза, следовательно, ![]() . При
. При ![]() значения
значения ![]() , а именно
, а именно ![]() и
и ![]() наблюдались 3+6=9 раз, следовательно,
наблюдались 3+6=9 раз, следовательно, ![]() .
.
Аналогично получаем, что при ![]() функция распределения
функция распределения ![]() ; при
; при ![]() функция распределения
функция распределения ![]() ; при
; при ![]() функция распределения
функция распределения ![]() . Далее, если
. Далее, если ![]() , то
, то ![]() (так как 7 – наибольшая варианта).
(так как 7 – наибольшая варианта).
Таким образом, эмпирическая функция распределения равна:

График полученной эмпирической функции распределения изображен на рисунке 16.
Задача 61. Найти методом сумм асимметрию и эксцесс по заданному распределению выборки объема N=100:
|
Варианта ХI |
48 |
52 |
56 |
60 |
64 |
68 |
72 |
76 |
80 |
84 |
|
Частота Ni |
2 |
4 |
6 |
8 |
12 |
30 |
18 |
8 |
7 |
5 |
Решение. Асимметрия ![]() эмпирического распределения определяется равенством:
эмпирического распределения определяется равенством:
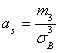 ,
,
Где ![]() – центральный эмпирический момент третьего порядка, вычисляемый по формуле:
– центральный эмпирический момент третьего порядка, вычисляемый по формуле: 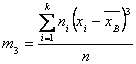
Эксцесс ![]() эмпирического распределения определяется равенством:
эмпирического распределения определяется равенством:
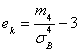 ,
,
Где ![]() – центральный эмпирический момент четвертого порядка, вычисляемый по формуле:
– центральный эмпирический момент четвертого порядка, вычисляемый по формуле: 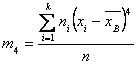
Асимметрия и эксцесс служат для оценки отклонения эмпирического распределения от нормального. Для нормального распределения эти характеристики равны нулю. Поэтому, если для изучаемого распределения асимметрия и эксцесс имеют небольшие значения, то можно предположить близость этого распределения к нормальному. Наоборот, большие значения асимметрии и эксцесса указывают на значительное отклонение от нормального. Кроме того, если эксцесс положительный, то распределение будет островершинным; если отрицательный, то распределение будет плосковершинным по сравнению с нормальным распределением.
Для практического расчета асимметрии и эксцесса непосредственно пользоваться вышеуказанными формулами довольно затруднительно, поэтому воспользуемся методом сумм. Составим расчетную таблицу 1, для этого:
1) Запишем варианты в первый столбец.
2) Запишем частоты во второй столбец; сумму частот (100) поместим в нижнюю клетку столбца.
3) В качестве ложного нуля С выберем варианту (68), которая имеет наибольшую частоту (в качестве С можно взять любую варианту, расположенную примерно в середине столбца); в клетках строки, содержащей ложный нуль, запишем нули; в четвертом столбце над и под уже помещенным нулем запишем еще по одному нулю.
4) В оставшихся незаполненными над нулем клетках третьего столбца (исключая самую верхнюю) запишем последовательно накопленные частоты:
2; 2+4=6; 6+6=12; 12+8=20; 20+12=32.
Сложив все накопленные частоты, получим число B1=72, которое поместим в верхнюю клетку третьего столбца. В оставшихся незаполненными под нулем клетках третьего столбца (исключая самую нижнюю) запишем последовательно накопленные частоты:
5; 5+7=12; 12+8=20; 20+18=38.
Сложив все накопленные частоты, получим число A1=75, которое поместим в нижнюю клетку третьего столбца.
5) Аналогично заполняется четвертый столбец, причем суммируют частоты третьего столбца. Сложив все накопленные частоты, расположенные над нулем, получим число B2=70, которое поместим в верхнюю клетку четвертого столбца. Сумма накопленных частот, расположенных под нулем, равна числу A2=59, которое поместим в нижнюю клетку четвертого столбца.
6) Для заполнения столбца 5 запишем нуль в клетке строки, содержащей ложный нуль (68); над этим нулем и под ним поставим еще по два нуля. В клетках над нулями запишем накопленные частоты, для чего просуммируем частоты столбца 4 сверху вниз; в итоге будем иметь следующие накопленные частоты:
2; 2+8=10; 10+20=30.
Сложив накопленные частоты, получим число B3=42, которое поместим в верхнюю клетку пятого столбца. В клетках под нулями запишем накопленные частоты, для чего просуммируем частоты столбца 4 снизу вниз; в итоге будем иметь следующие накопленные частоты:
5; 5+17=22.
Сложив накопленные частоты, получим число A3=27, которое поместим в нижнюю клетку пятого столбца.
7) Аналогично заполняется столбец 6, причем суммируют частоты столбца 5.
В итоге получим расчетную таблицу 1:
Расчетная таблица 1
|
1 |
2 |
3 |
4 |
5 |
6 |
|
ХI |
Ni |
B1=72 |
B2=70 |
B3=42 |
B4=14 |
|
48 |
2 |
2 |
2 |
2 |
2 |
|
52 |
4 |
6 |
8 |
10 |
12 |
|
56 |
6 |
12 |
20 |
30 |
0 |
|
60 |
8 |
20 |
40 |
0 |
0 |
|
64 |
12 |
32 |
0 |
0 |
0 |
|
68 |
30 |
0 |
0 |
0 |
0 |
|
72 |
18 |
38 |
0 |
0 |
0 |
|
76 |
8 |
20 |
37 |
0 |
0 |
|
80 |
7 |
12 |
17 |
22 |
0 |
|
84 |
5 |
5 |
5 |
5 |
5 |
|
N=100 |
A1=75 |
A2=59 |
A3=27 |
A4=5 |
Теперь найдем Di (I=1, 2, 3) и si (I=1, 2, 3, 4):
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Найдем условные моменты первого, второго, третьего и четвертого порядков:
![]() ;
; ![]() ;
;
![]() ;
;
![]() .
.
Найдем далее центральные эмпирические моменты третьего и четвертого порядков, учитывая, что шаг ![]() (разность между двумя соседними вариантами):
(разность между двумя соседними вариантами):
![]() ;
;

Так как дисперсия ![]() , то выборочное среднее квадратическое отклонение
, то выборочное среднее квадратическое отклонение ![]() .
.
Учитывая определения асимметрии и эксцесса, окончательно получаем:
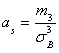
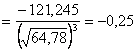 ;
; 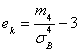
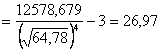 .
.
| < Предыдущая | Следующая > |
|---|
