Содержание:
Точечные оценки:
Пусть случайная величина имеет неизвестную характеристику а. Такой характеристикой может быть, например, закон распределения, математическое ожидание, дисперсия, параметр закона распределения, вероятность определенного значения случайной величины и т.д. Пронаблюдаем случайную величину n раз и получим выборку из ее возможных значений 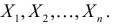
Существует два подхода к решению этой задачи. Можно по результатам наблюдений вычислить приближенное значение характеристики, а можно указать целый интервал ее значений, согласующихся с опытными данными. В первом случае говорят о точечной оценке, во втором – об интервальной.
Определение. Функция результатов наблюдений 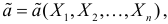
Для одной и той же характеристики можно предложить разные точечные оценки. Необходимо иметь критерии сравнения оценок, для суждения об их качестве. Оценка 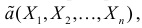 как функция случайных результатов наблюдений
как функция случайных результатов наблюдений 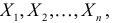 сама является случайной величиной. Значения
сама является случайной величиной. Значения 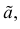 найденные по разным сериям наблюдений, могут отличаться от истинного значения характеристики
найденные по разным сериям наблюдений, могут отличаться от истинного значения характеристики 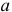 в ту или другую сторону. Естественно потребовать, чтобы оценка систематически не завышала и не занижала оцениваемое значение, а с ростом числа наблюдений становилась более точной. Формализация названных требований приводит к следующим понятиям.
в ту или другую сторону. Естественно потребовать, чтобы оценка систематически не завышала и не занижала оцениваемое значение, а с ростом числа наблюдений становилась более точной. Формализация названных требований приводит к следующим понятиям.
Определение. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемой величине: 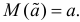 В противном случае оценку называют смещенной.
В противном случае оценку называют смещенной.
Определение. Оценка называется состоятельной, если при увеличении числа наблюдений она сходится по вероятности к оцениваемой величине, т.е. для любого сколь угодно малого 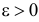
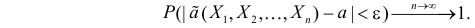
Если известно, что оценка 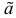 несмещенная, то для ее состоятельности достаточно, чтобы
несмещенная, то для ее состоятельности достаточно, чтобы
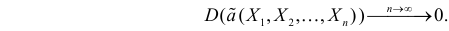
Последнее условие удобно для проверки. В качестве меры разброса значений оценки 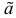 относительно
относительно 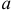 можно рассматривать величину
можно рассматривать величину 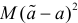 Из двух оценок предпочтительней та, для которой эта величина меньше. Если оценка имеет наименьшую меру разброса среди всех оценок характеристики, построенных по
Из двух оценок предпочтительней та, для которой эта величина меньше. Если оценка имеет наименьшую меру разброса среди всех оценок характеристики, построенных по 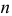 наблюдениям, то оценку называют эффективной.
наблюдениям, то оценку называют эффективной.
Следует отметить, что несмещенность и состоятельность являются желательными свойствами оценок, но не всегда разумно требовать наличия этих свойств у оценки. Например, может оказаться предпочтительней оценка хотя и обладающая небольшим смещением, но имеющая значительно меньший разброс значений, нежели несмещенная оценка. Более того, есть характеристики, для которых нет одновременно несмещенных и состоятельных оценок.
Оценки для математического ожидания и дисперсии
Пусть случайная величина имеет неизвестные математическое ожидание и дисперсию, причем 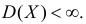 Если
Если 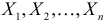 – результаты
– результаты 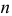 независимых наблюдений случайной величины, то в качестве оценки для математического ожидания можно предложить среднее арифметическое наблюдаемых значений
независимых наблюдений случайной величины, то в качестве оценки для математического ожидания можно предложить среднее арифметическое наблюдаемых значений 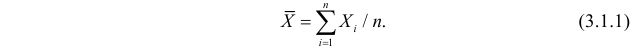
Несмещенность такой оценки следует из равенств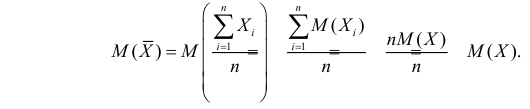
В силу независимости наблюдений 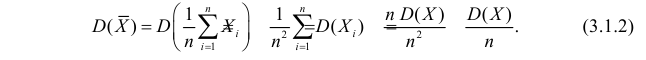
При условии 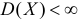 имеем
имеем 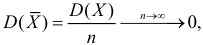 что означает состоятельность оценки
что означает состоятельность оценки 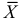 .
.
Доказано, что для математического ожидания нормально распределенной случайной величины оценка 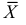 еще и эффективна.
еще и эффективна.
Оценка математического ожидания посредством среднего арифметического наблюдаемых значений наводит на мысль предложить в качестве оценки для дисперсии величину

Преобразуем величину 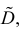 обозначая для краткости
обозначая для краткости 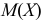 через
через 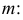
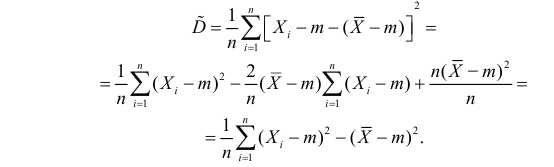
В силу (3.1.2) имеем 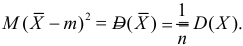 Поэтому
Поэтому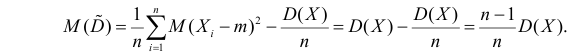
Последняя запись означает, что оценка 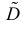 имеет смещение. Она систематически занижает истинное значение дисперсии. Для получения несмещенной оценки введем поправку в виде множителя
имеет смещение. Она систематически занижает истинное значение дисперсии. Для получения несмещенной оценки введем поправку в виде множителя 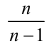 и полученную оценку обозначим через
и полученную оценку обозначим через 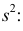
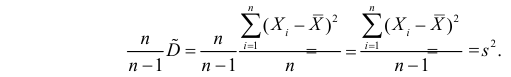
Величина
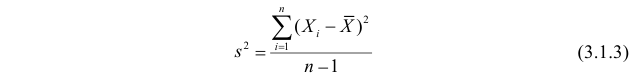
является несмещенной и состоятельной оценкой дисперсии.
Пример:
Оценить математическое ожидание и дисперсию случайной величины Х по результатам ее независимых наблюдений: 7, 3, 4, 8, 4, 6, 3.
Решение. По формулам (3.1.1) и (3.1.3) имеем 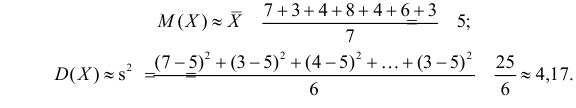
Ответ. 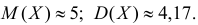
Пример:
Данные 25 независимых наблюдений случайной величины представлены в сгруппированном виде: 
Требуется оценить математическое ожидание и дисперсию этой случайной величины.
Решение. Представителем каждого интервала можно считать его середину. С учетом этого формулы (3.1.1) и (3.1.3) дают следующие оценки: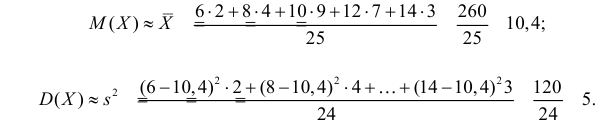
Ответ. 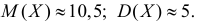
Метод наибольшего правдоподобия для оценки параметров распределений
В теории вероятностей и ее приложениях часто приходится иметь дело с законами распределения, которые определяются некоторыми параметрами. В качестве примера можно назвать нормальный закон распределения 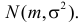 Его параметры
Его параметры 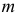 и
и 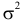 имеют смысл математического ожидания и дисперсии соответственно. Их можно оценить с помощью
имеют смысл математического ожидания и дисперсии соответственно. Их можно оценить с помощью 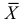 и
и 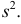 В общем случае параметры законов распределения не всегда напрямую связаны со значениями числовых 179 характеристик. Поэтому практический интерес представляет следующая задача.
В общем случае параметры законов распределения не всегда напрямую связаны со значениями числовых 179 характеристик. Поэтому практический интерес представляет следующая задача.
Пусть случайная величина Х имеет функцию распределения 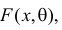 причем тип функции распределения F известен, но неизвестно значение параметра
причем тип функции распределения F известен, но неизвестно значение параметра 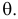 По данным результатов наблюдений нужно оценить значение параметра. Параметр может быть и многомерным.
По данным результатов наблюдений нужно оценить значение параметра. Параметр может быть и многомерным.
Продемонстрируем идею метода наибольшего правдоподобия на упрощенном примере. Пусть по результатам наблюдений, отмеченных на рис. 3.1.1 звездочками, нужно отдать предпочтение одной из двух функций плотности вероятности 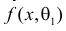 или
или 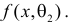
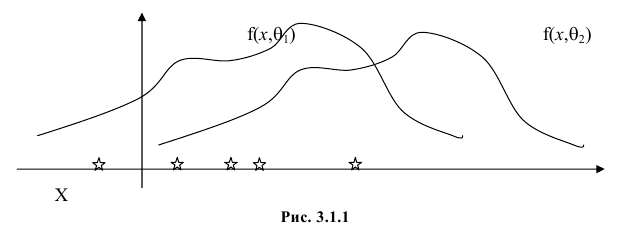
Из рисунка видно, что при значении параметра 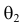 такие результаты наблюдений маловероятны и вряд ли бы реализовались. При значении же
такие результаты наблюдений маловероятны и вряд ли бы реализовались. При значении же 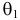 эти результаты наблюдений вполне возможны. Поэтому значение параметра
эти результаты наблюдений вполне возможны. Поэтому значение параметра 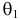 более правдоподобно, чем значение
более правдоподобно, чем значение 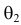 . Такая аргументация позволяет сформулировать принцип наибольшего правдоподобия: в качестве оценки параметра выбирается то его значение, при котором данные результаты наблюдений наиболее вероятны.
. Такая аргументация позволяет сформулировать принцип наибольшего правдоподобия: в качестве оценки параметра выбирается то его значение, при котором данные результаты наблюдений наиболее вероятны.
Этот принцип приводит к следующему способу действий. Пусть закон распределения случайной величины Х зависит от неизвестного значения параметра 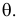 Обозначим через
Обозначим через 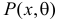 для непрерывной случайной величины плотность вероятности в точке
для непрерывной случайной величины плотность вероятности в точке 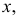 а для дискретной случайной величины – вероятность того, что
а для дискретной случайной величины – вероятность того, что 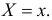 Если в
Если в 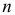 независимых наблюдениях реализовались значения случайной величины
независимых наблюдениях реализовались значения случайной величины 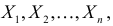 то выражение
то выражение 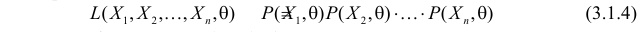
называют функцией правдоподобия. Величина 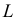 зависит только от параметра
зависит только от параметра 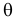 при фиксированных результатах наблюдений
при фиксированных результатах наблюдений 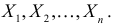 При каждом значении параметра
При каждом значении параметра 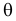 функция
функция  равна вероятности именно тех значений дискретной случайной величины, которые получены в процессе наблюдений. Для непрерывной случайной величины
равна вероятности именно тех значений дискретной случайной величины, которые получены в процессе наблюдений. Для непрерывной случайной величины  равна плотности вероятности в точке выборочного пространства
равна плотности вероятности в точке выборочного пространства 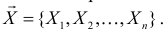
Сформулированный принцип предлагает в качестве оценки значения параметра выбрать такое 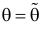 при котором
при котором  принимает наибольшее значение. Величина
принимает наибольшее значение. Величина 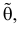 будучи функцией от результатов наблюдений
будучи функцией от результатов наблюдений 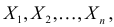 называется оценкой наибольшего правдоподобия.
называется оценкой наибольшего правдоподобия.
Во многих случаях, когда  дифференцируема, оценка наибольшего правдоподобия находится как решение уравнения
дифференцируема, оценка наибольшего правдоподобия находится как решение уравнения 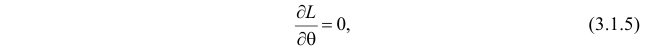
которое следует из необходимого условия экстремума. Поскольку  достигает максимума при том же значении
достигает максимума при том же значении 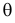 , что и
, что и  , то можно решать относительно
, то можно решать относительно 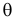 эквивалентное уравнение
эквивалентное уравнение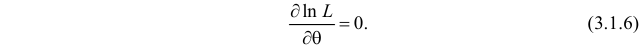
Это уравнение называют уравнением правдоподобия. Им пользоваться удобнее, чем уравнением (3.1.5), так как функция  равна произведению, а
равна произведению, а  – сумме, а дифференцировать
– сумме, а дифференцировать  проще.
проще.
Если параметров несколько (многомерный параметр), то следует взять частные производные от функции правдоподобия по всем параметрам, приравнять частные производные нулю и решить полученную систему уравнений.
Оценку, получаемую в результате поиска максимума функции правдоподобия, называют еще оценкой максимального правдоподобия.
Известно, что оценки максимального правдоподобия состоятельны. Кроме того, если для q существует эффективная оценка, то уравнение правдоподобия имеет единственное решение, совпадающее с этой оценкой. Оценка максимального правдоподобия может оказаться смещенной.
Метод моментов
Начальным моментом 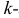 го порядка случайной величины Х называется математическое ожидание
го порядка случайной величины Х называется математическое ожидание 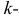 й степени этой величины, т.е.
й степени этой величины, т.е. 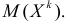 Само математическое ожидание считается начальным моментом первого порядка.
Само математическое ожидание считается начальным моментом первого порядка.
Центральным моментом 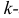 го порядка называется
го порядка называется 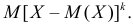 Очевидно, что дисперсия – это центральный момент второго порядка. Если закон распределения случайной величины зависит от некоторых параметров, то от этих параметров зависят и моменты случайной величины.
Очевидно, что дисперсия – это центральный момент второго порядка. Если закон распределения случайной величины зависит от некоторых параметров, то от этих параметров зависят и моменты случайной величины.
Для оценки параметров распределения по методу моментов находят на основе опытных данных оценки моментов в количестве, равном числу оцениваемых параметров. Эти оценки приравнивают к соответствующим теоретическим моментам, величины которых выражены через параметры. Из полученной системы уравнений можно определить искомые оценки.
Например, если Х имеет плотность распределения 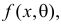 то
то 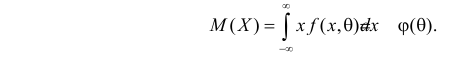
Если воспользоваться величиной 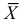 как оценкой для
как оценкой для 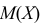 на основе опытных данных, то оценкой
на основе опытных данных, то оценкой 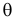 по методу моментов будет решение уравнения
по методу моментов будет решение уравнения 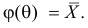
Пример:
Найти оценку параметра показательного закона распределения по методу моментов.
Решение. Плотность вероятности показательного закона распределения имеет вид 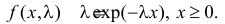 Поэтому
Поэтому 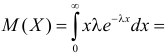
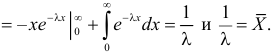 Откуда
Откуда 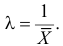
Ответ. 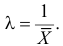
Пример:
Пусть имеется простейший поток событий неизвестной интенсивности 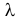 . Для оценки параметра
. Для оценки параметра 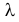 проведено наблюдение потока и зарегистрированы
проведено наблюдение потока и зарегистрированы 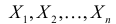 – длительности
– длительности  последовательных интервалов времени между моментами наступления событий. Найти оценку для
последовательных интервалов времени между моментами наступления событий. Найти оценку для 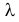 .
.
Решение. В простейшем потоке интервалы времени между последовательными моментами наступления событий потока имеют показательный закон распределения 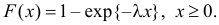 Так как плотность вероятности показательного закона распределения равна
Так как плотность вероятности показательного закона распределения равна 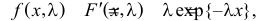 то функция правдоподобия (3.1.4) имеет вид
то функция правдоподобия (3.1.4) имеет вид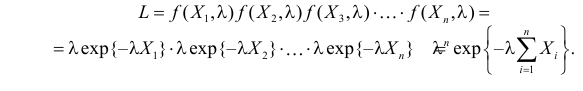
Тогда 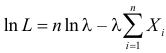 и уравнение правдоподобия
и уравнение правдоподобия 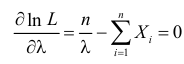 имеет решение
имеет решение 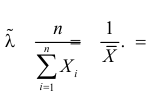
При таком значении 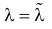 функция правдоподобия действительно достигает наибольшего значения, так как
функция правдоподобия действительно достигает наибольшего значения, так как 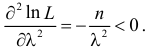
Ответ. 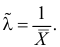
Определение. Пусть 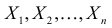 – результаты n независимых наблюдений случайной величины X. Если расставить эти результаты в порядке возрастания, то получится последовательность значений, которую называют вариационным рядом и обозначают:
– результаты n независимых наблюдений случайной величины X. Если расставить эти результаты в порядке возрастания, то получится последовательность значений, которую называют вариационным рядом и обозначают:

В этой записи 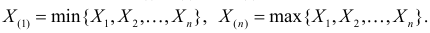
Величины 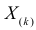 называют порядковыми статистиками.
называют порядковыми статистиками.
Пример:
Случайная величина Х имеет равномерное распределение на отрезке 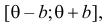 где
где  и
и  неизвестны. Пусть
неизвестны. Пусть 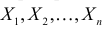 – результаты
– результаты  независимых наблюдений. Найти оценку параметра
независимых наблюдений. Найти оценку параметра  .
.
Решение. Функция плотности вероятности величины Х имеет вид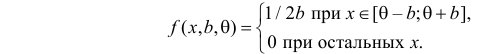
В этом случае функция правдоподобия 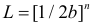 от
от  явно не зависит. Дифференцировать по
явно не зависит. Дифференцировать по  такую функцию нельзя и нет возможности записать уравнение правдоподобия. Однако легко видеть, что
такую функцию нельзя и нет возможности записать уравнение правдоподобия. Однако легко видеть, что  возрастает при уменьшении
возрастает при уменьшении  . Все результаты наблюдений лежат в
. Все результаты наблюдений лежат в 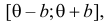 поэтому можно записать:
поэтому можно записать:
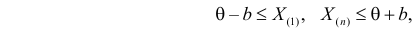
где 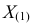 – наименьший, а
– наименьший, а 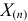 – наибольший из результатов наблюдений. При минимально возможном
– наибольший из результатов наблюдений. При минимально возможном 
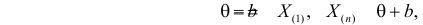
откуда 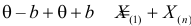 или
или 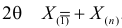
Оценкой наибольшего правдоподобия для параметра  будет величина
будет величина
Ответ. 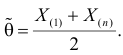
Пример:
Случайная величина X имеет функцию распределения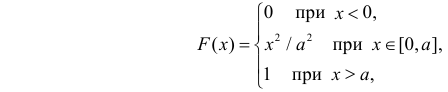
где 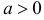 неизвестный параметр.
неизвестный параметр.
Пусть 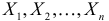 – результаты
– результаты  независимых наблюдений случайной величины X. Требуется найти оценку наибольшего правдоподобия для параметра
независимых наблюдений случайной величины X. Требуется найти оценку наибольшего правдоподобия для параметра 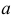 и найти оценку для M(X).
и найти оценку для M(X).
Решение. Для построения функции правдоподобия найдем сначала функцию плотности вероятности
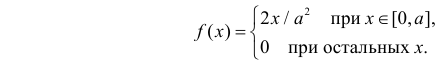
Тогда функция правдоподобия: 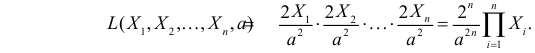
Логарифмическая функция правдоподобия: 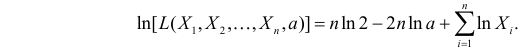
Уравнение правдоподобия

не имеет решений. Критических точек нет. Наибольшее и наименьшее значения  находятся на границе допустимых значений
находятся на границе допустимых значений  .
.
По виду функции  можно заключить, что значение
можно заключить, что значение  тем больше, чем меньше величина
тем больше, чем меньше величина  . Но
. Но  не может быть меньше
не может быть меньше 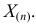 Поэтому наиболее правдоподобное значение
Поэтому наиболее правдоподобное значение 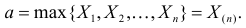
Так как 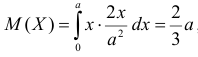 , то оценкой наибольшего правдоподобия для
, то оценкой наибольшего правдоподобия для 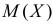 будет величина
будет величина 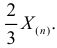
Ответ. 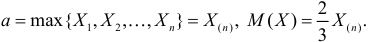
Пример:
Случайная величина Х имеет нормальный закон распределения 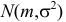 c неизвестными параметрами
c неизвестными параметрами 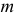 и
и 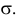 По результатам независимых наблюдений
По результатам независимых наблюдений 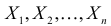 найти наиболее правдоподобные значения этих параметров.
найти наиболее правдоподобные значения этих параметров.
Решение. В соответствии с (3.1.4) функция правдоподобия имеет вид 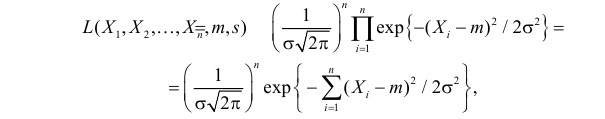
а логарифмическая функция правдоподобия: 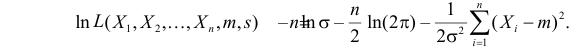
Необходимые условия экстремума дают систему двух уравнений: 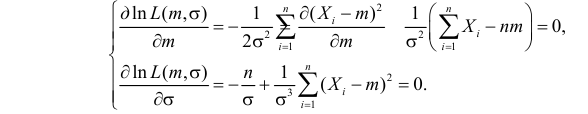
Решения этой системы имеют вид: 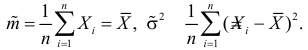
Отметим, что обе оценки являются состоятельными, причем оценка для 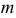 несмещенная, а для
несмещенная, а для 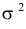 смещенная (сравните с формулой (3.1.3)).
смещенная (сравните с формулой (3.1.3)).
Ответ. 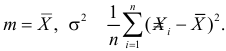
Пример:
По данным эксперимента построен статистический ряд:

Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения случайной величины X.
Решение. 1) Число экспериментальных данных вычисляется по формуле:
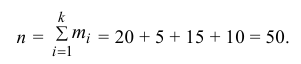
Значит, объем выборки n = 50.
2) Вычислим среднее арифметическое значение эксперимента:
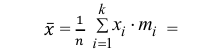
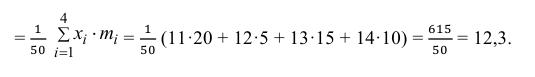
Значит, найдена оценка математического ожидания 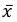 = 12,3.
= 12,3.
3) Вычислим исправленную выборочную дисперсию:
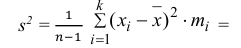
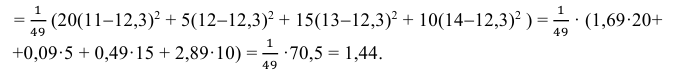
Значит, найдена оценка дисперсии: 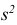 = 1,44.
= 1,44.
5) Вычислим оценку среднего квадратического отклонения:
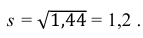
Ответ: 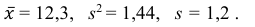
Пример:
По данным эксперимента построен статистический ряд:

Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения случайной величины X.
Решение. По формуле
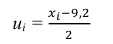
перейдем к условным вариантам:

Для них произведем расчет точечных оценок параметров:
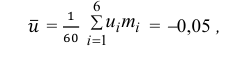
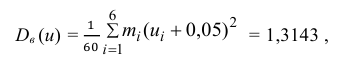
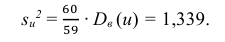
Следовательно, вычисляем искомые точечные оценки:
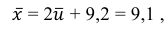
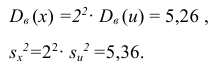
Ответ: 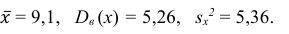
Пример:
По данным эксперимента построен интервальный статистический ряд:

Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения.
Решение. 1) От интервального ряда перейдем к статистическому ряду, заменив интервалы их серединами 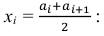

2) Объем выборки вычислим по формуле:
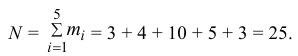
3) Вычислим среднее арифметическое значений эксперимента:
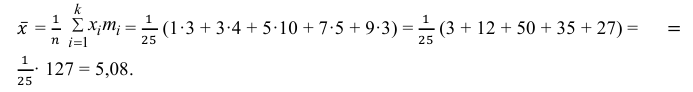
3) Вычислим исправленную выборочную дисперсию:
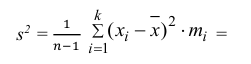
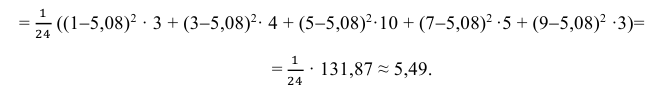
Можно было воспользоваться следующей формулой:
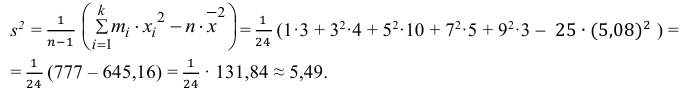
5) Вычислим оценку среднего квадратического отклонения:
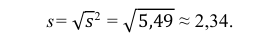
Ответ: 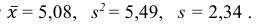
Пример:
Найти доверительный интервал с надежностью 0,95 для оценки математического ожидания M(X) нормально распределенной случайной величины X, если известно среднее квадратическое отклонение σ = 2, оценка математического ожидания 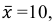 объем выборки n = 25.
объем выборки n = 25.
Решение. Доверительный интервал для истинного математического ожидания с доверительной вероятностью 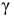 = 0,95 при известной дисперсии σ находится по формуле:
= 0,95 при известной дисперсии σ находится по формуле:
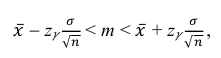
где m = M(X) – истинное математическое ожидание; 𝑥̅ − оценка M(X) по выборке; n – объем выборки; 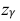 – находится по доверительной вероятности
– находится по доверительной вероятности 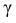 = 0,95 из равенства:
= 0,95 из равенства:
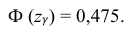
Из табл. П 2.2 приложения 2 находим: 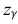 = 1,96. Следовательно, найден доверительный интервал для M(X):
= 1,96. Следовательно, найден доверительный интервал для M(X):
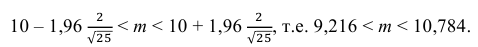
Ответ: (9,216 ; 10,784).
Пример:
По данным эксперимента построен статистический ряд:

Найти доверительный интервал для математического ожидания M (X) с надежностью 0,95.
Решение. Воспользуемся формулой для доверительного интервала математического ожидания при неизвестной дисперсии:
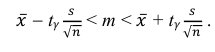
где n – объем выборки; 𝑥̅ оценка M(X); s – оценка среднего квадратического отклонения; 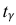 − находится по доверительной вероятности
− находится по доверительной вероятности 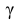 = 0,95.
= 0,95.
По числам 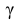 = 0,95 и n = 20 находим:
= 0,95 и n = 20 находим: 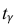 = 2,093.
= 2,093.
Теперь вычисляем оценки для M(X) и D(X):
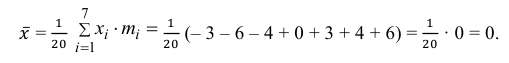
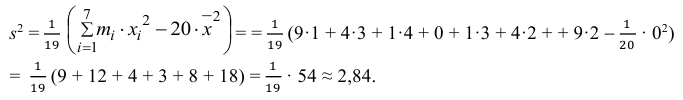
Следовательно, s ≈ 1,685. Поэтому искомый доверительный интервал математического ожидания задается формулой:
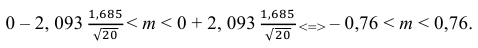
Ответ: (– 0,76; 0,76).
Пример:
По данным десяти независимых измерений найдена оценка квадратического отклонения 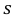 = 0,5. Найти доверительный интервал точности измерительного прибора с надежностью 99 %.
= 0,5. Найти доверительный интервал точности измерительного прибора с надежностью 99 %.
Решение. Задача сводится к нахождению доверительного интервала для истинного квадратического отклонения, так как точность прибора характеризуется средним квадратическим отклонением случайных ошибок измерений.
Доверительный интервал для среднего квадратического отклонения находим по формуле:
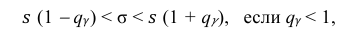
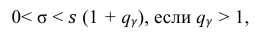
где 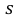 = 0,5 − оценка среднего квадратического отклонения;
= 0,5 − оценка среднего квадратического отклонения; 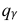 – число, определяемое из табл. П 2.4 приложения 2 по заданной доверительной вероятности
– число, определяемое из табл. П 2.4 приложения 2 по заданной доверительной вероятности 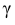 = 0,99 и заданному объему выборки n = 10.
= 0,99 и заданному объему выборки n = 10.
Находим: 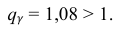
Тогда можно записать:
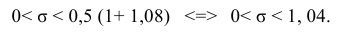
Ответ: (0; 1,04).
- Доверительный интервал для вероятности события
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Системы случайных величин
- Вероятность и риск
- Определения вероятности событий
- Предельные теоремы теории вероятностей
Пусть
из генеральной совокупности в результате
n
испытаний над количественным признаком
X
извлечена выборка объемом n:
варианты x1,
… , xr
и
их частоты n1,
… , nr.
Точечной
называют
оценку, которая определяется одним
числом. Точечные оценки обычно используют
в тех случаях, когда число наблюдений
велико.
Выборочной
средней
xв
называют среднее арифметическое значение
вариант выборки. Если значения вариант
x1,
x2,
… , xr
имеют
соответственно частоты n1,
n2,
… , nr,
то
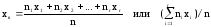 .
.
(5)
Выборочной
дисперсией Dв
называют среднее арифметическое
квадратов отклонений вариант xi
от их среднего значения xв,
т.е.
 .
.
(6)
Выборочным
средним квадратическим отклонением σв
называют
квадратный корень из выборочной дисперсии
Dв
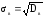 .
.
(7)
Исправленную
(несмещенную оценку) дисперсию
s2
выборки получают по формуле
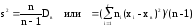 .
.
(8)
Аналогично
вводится исправленное
среднее квадратическое отклонение s
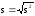 .
.
(9)
3. Интервальные оценки параметров распределения выборки
Интервальной
называют оценку, которая задается в
виде интервала. Интервальные оценки
удобно использовать в тех случаях, когда
число наблюдений n
относительно невелико.
Пусть
для неизвестного параметра θ количественного
признака X
генеральной совокупности статистическими
методами найдено значение θ*. Зададимся
точностью δ, т.е. | θ – θ* | < δ.
Надежностью
оценки
неизвестного параметра θ по вычисленному
статистическими методами значению θ*
называют вероятность γ, с которой
выполняется неравенство| θ – θ* | < δ,
при этом δ называется
точностью оценки.
В статистике обычно задаются надежностью
γ и определяют точность δ.
Доверительным
интервалом
для параметра θ называют интервал (θ* –
δ, θ* + δ), который покрывает неизвестный
параметр θ с вероятностью γ:
P[θ*
– δ <X
< θ* + δ] = γ.
Пусть
количественный признак X
генеральной совокупности распределен
нормально, причем среднее квадратическое
отклонение σ неизвестно. Требуется
оценить неизвестное математическое
ожидание a
по результатам выборки с заданной
надежностью γ.
Доверительный
интервал
с
уровнем надежности γ для математического
ожидания
a
признака
X,
распределенного нормально, при неизвестном
среднем квадратическом отклонении
определяется как
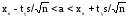 ,
,
(10)
где
xв
– выборочное среднее; s
– исправленное среднее квадратическое
отклонение выборки; n
– объем выборки. Точность оценки δ в
этом случае
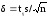 .
.
Значениеtγ
= t(γ,n)
можно найти из справочной таблицы
”Таблица значений tγ
= t(γ,n)”
для распределения Стьюдента.
Доверительный
интервал
с
уровнем надежности γ для
среднего
квадратического отклонения
σ признака X,
распределенного нормально, определяется
как
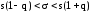 ,
,
(11)
где
s
– исправленное среднее квадратическое
отклонение выборки; n
– объем выборки. Значение q
= q(γ,n)
можно найти из справочной таблицы
”Таблица значений q
= q(γ,n)”
для распределения χ2.
В
случае, когда q
>1 доверительный интервал имеет вид
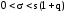 . (11′)
. (11′)
4. Статистическая проверка статистических
гипотез
Статистической
называют гипотезу (предположение) о
виде неизвестного распределения или о
параметрах известного распределения.
Основной
или нулевой гипотезой H0
называют выдвинутую гипотезу о неизвестном
распределении, вместе с основной H0
выдвигается
и конкурирующая
(альтернативная) гипотеза
H1,
противоречащая
основной.
Основной
принцип проверки статистических
гипотез состоит в следующем:
в
зависимости от вида гипотезы и характера
неизвестного распределения вводится
функция K,
называемая критерием,
по значениям ее будет приниматься
решение о принятии или отклонении
основной гипотезы H0.
Вводится также уровень
значимости
α как вероятность того, что будет
отвергнута верная нулевая гипотеза и
принята неверная гипотеза H1.
Областью
принятия гипотезы
H0
называют
те значения критерия K,
при которых основная гипотеза H0
принимается, критической
областью
– отвергается. Для каждой выборки и
конкретного вида критерия K
по специальным таблицам находятся
значения kкр,
называемые критическими
точками;
критические точки отделяют область
принятия гипотезы от критической
области. Правосторонней
называют критическую область, где K
> kкр,
левосторонней
K
< kкр
и
двусторонней
(и симметричной) | K|
> kкр.
Пусть
из генеральной совокупности в результате
n
испытаний над количественным признаком
X
извлечена выборка объемом n:
равноотстоящие с шагом h
варианты x1,
… , xr
и
их частоты n1,
… , nr.
Для нее подсчитаны по формулам (5-9)
выборочное среднее xв
и выборочное среднее квадратическое
отклонение σв.
Для
проверки гипотезы
о нормальном распределении
генеральной совокупности c
уровнем значимости α используется
критерий
χ2
Пирсона:
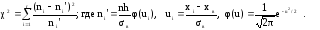 (12)
(12)
Критическое
значение χ2кр
= χ2
(α,k)
для этого критерия находится из справочной
таблицы “Критические точки распределения
χ2”.
Здесь k
= r
– 3. Если вычисленное по результатам
наблюдений по формуле (12) значение
критерия χ2набл
больше χ2кр,
основная гипотеза отвергается, если
меньше – нет оснований отвергнуть
основную гипотезу.
Если
варианты x1,
x2,
… , xr
не
являются равноотстоящими или число их
сравнительно велико, удобно сгруппировать
варианты в отдельные интервалы ( не
обязательно равноотстоящие ) [x1*;x2*),
[x2*;x3*),
…, [xm-1*;xm*).
Каждому интервалу назначается
представительное значение, равное
середине интервала xi.ср*
= (xi*
+ xi-1*)/2
и частота ni*,
равная сумме частот, попавших на интервал.
В соответствии с критерием Пирсона,
частоты ni*,
попавшие на интервалы [xi*
; xi-1*),
сравниваются с теоретическими частотами
ni‘,
вычисленными для соответствующих
интервалов нормальной случайной величины
Z
с нулевым математическим ожиданием и
единичным средним квадратическим
отклонением (Z
принадлежит N(0,1)).
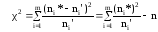 ,
,
(13)
ni‘
= nPi,
где n
– обьем выборки;
Pi
= Ф(zi+1)
– Ф(zi),
вероятности попадания X
на интервал (xi*,xi+1*)
или
Z
на (zi,zi+1);
zi
= (xi
ср*–xв*)
/ σ*; i
= 2,3,..,m-1;
крайние интервалы открываем z1
= –∞,
zm
= ∞, а Ф(zi)
– значение функции Лапласа.
Критическое
значение χ2кр
= χ2
(α,k)
для этого критерия находится из справочной
таблицы “Критические точки распределения
χ2”.
Здесь k
= m
– 3. Если вычисленное по результатам
наблюдений по формуле (13) значение
критерия χ2набл
меньше χ2кр,
нет оснований отвергнуть основную
гипотезу, если больше – основная гипотеза
не принимается.
Для
проверки гипотез
о дисперсии σ2
генеральной совокупности
с нормальным законом распределения при
заданном уровне значимости α используется
критерий
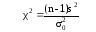 ,
,
(14)
где
s2
– исправленная дисперсия выборки; n
– объем выборки; σ02
– гипотетическое значение дисперсии.
А)
Пусть выдвинута нулевая гипотеза H0:
σ2
=
σ02
о
равенстве неизвестной генеральной
дисперсии σ2
предполагаемому значению σ02
при конкурирующей гипотезе H1:
σ2
≠
σ02.
Для проверки этой гипотезы по результатам
выборки вычисляется значение критерия
(14) χ2выб.
Затем по таблице «Критические точки
распределения χ2»,
по заданному уровню значимости α и числу
степеней свободы k
= n
– 1 находятся левое критическое значение
χ2лев.кр(1
– α/2;k)
и правое критическое значение
χ2прав.кр(α/2;k).
Если при этом χ2лев.кр
< χ2выб
< χ2прав.кр,
нет
оснований отвергнуть основную гипотезу,
конкурирующая – отвергается. В противном
случае принимается конкурирующая
гипотеза и отвергается основная.
Б)
Пусть теперь выдвинута нулевая гипотеза
H0:
σ2
=
σ02
о
равенстве неизвестной генеральной
дисперсии σ2
предполагаемому значению σ02
при конкурирующей гипотезе H1:
σ2
>
σ02.
Для проверки этой гипотезы по результатам
выборки вычисляется значение критерия
(14) χ2выб.
Затем по таблице «Критические точки
распределения χ2»,
по заданному уровню значимости α и числу
степеней свободы k
= n
– 1 находится критическое значение
χ2кр(
α;k).
Если при этом χ2выб
< χ2кр,
нет оснований отвергнуть основную
гипотезу, а конкурирующая – отвергается.
В)
Пусть теперь выдвинута нулевая гипотеза
H0:
σ2
=
σ02
о
равенстве неизвестной генеральной
дисперсии σ2
предполагаемому значению σ02
при конкурирующей гипотезе H1:
σ2
<
σ02.
Для проверки этой гипотезы по результатам
выборки вычисляется значение критерия
(14) χ2выб.
Затем по таблице «Критические точки
распределения χ2»,
по заданному уровню значимости α и числу
степеней свободы k
= n
– 1 находится критическое значение
χ2кр(
1- α;k).
Если при этом χ2выб
> χ2кр,
нет оснований отвергнуть основную
гипотезу, конкурирующая – отвергается.
Для
проверки гипотез
неизвестной средней a
генеральной совокупности
с
нормальным законом распределения
с неизвестной дисперсией при заданном
уровне значимости α используется
критерий Стьюдента
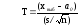 ,
,
(15)
где
xвыб
– выборочное среднее;
a0
гипотетическое значение средней; n
– объем выборки; s
– исправленное среднее квадратическое
отклонение.
А)
Пусть выдвинута нулевая гипотеза H0:
a
=
a0
о
равенстве неизвестной генеральной
средней a
предполагаемому значению a0
при конкурирующей гипотезе H1:
a
≠
a0
.
Для проверки этой гипотезы по результатам
выборки вычисляется значение критерия
(15) Tвыб.
Затем по таблице «Критические точки
распределения Стьюдента», по заданному
уровню значимости α и числу степеней
свободы k
= n
– 1 находится двустороннее критическое
значение Tдвустор.кр(α;k).
Если при этом | Tвыб
| <
Tдвустор.кр,
нет оснований отвергнуть основную
гипотезу, а конкурирующая – отвергается.
Б)
Пусть теперь выдвинута нулевая гипотеза
H0:
a
=
a0
о
равенстве неизвестной генеральной
средней a
предполагаемому значению a0
при конкурирующей гипотезе H1:
a
>
a0
.
Для проверки этой гипотезы по результатам
выборки вычисляется значение критерия
(15) Tвыб.
Затем по таблице «Критические точки
распределения Стьюдента», по заданному
уровню значимости α и числу степеней
свободы k
= n
– 1 находится критическое значение
Tправостор.кр(α;k).
Если при этом Tвыб
< Tправостор.кр,
нет оснований отвергнуть основную
гипотезу
,
а конкурирующая – отвергается.
В)
Пусть теперь выдвинута нулевая гипотеза
H0:
a
=
a0
о
равенстве неизвестной генеральной
средней a
предполагаемому значению a0
при конкурирующей гипотезе H1:
a
< a0
.
Для проверки этой гипотезы по результатам
выборки вычисляется значение критерия
(15) Tвыб.
Затем по таблице «Критические точки
распределения Стьюдента», по заданному
уровню значимости α и числу степеней
свободы k
= n
– 1 находится критическое значение
Tправостор.кр(α;k)
и полагают Tлевостор.кр
= –Tправостор.кр.
Если при этом Tвыб
> Tлевостор.кр,
нет оснований отвергнуть основную
гипотезу, а конкурирующая – отвергается.
17 авг. 2022 г.
читать 2 мин
Точечная оценка представляет собой число, которое мы вычисляем на основе выборочных данных для оценки некоторого параметра совокупности. Это служит нашей наилучшей возможной оценкой того, каким может быть истинный параметр населения.
В следующей таблице показана точечная оценка, которую мы используем для оценки параметров совокупности:
| Измерение | Параметр населения | Балльная оценка | | — | — | — | | Иметь в виду | μ (среднее значение населения) | х (выборочное среднее) | | Доля | π (доля населения) | p (пропорция выборки) |
Хотя точечная оценка представляет собой наше лучшее предположение о параметре совокупности, не гарантируется, что она точно соответствует истинному параметру совокупности.
По этой причине мы также часто рассчитываем доверительные интервалы — интервалы, которые могут содержать параметр генеральной совокупности с определенным уровнем достоверности.
В следующих примерах показано, как рассчитать точечные оценки и доверительные интервалы в Excel.
Пример 1. Точечная оценка среднего значения генеральной совокупности
Предположим, нас интересует вычисление среднего веса популяции черепах. Для этого мы собираем случайную выборку из 20 черепах:

Наша точечная оценка среднего значения населения — это просто среднее значение выборки, которое оказывается равным 300,3 фунта:

Затем мы можем использовать следующую формулу для расчета 95% доверительного интервала для среднего значения генеральной совокупности:
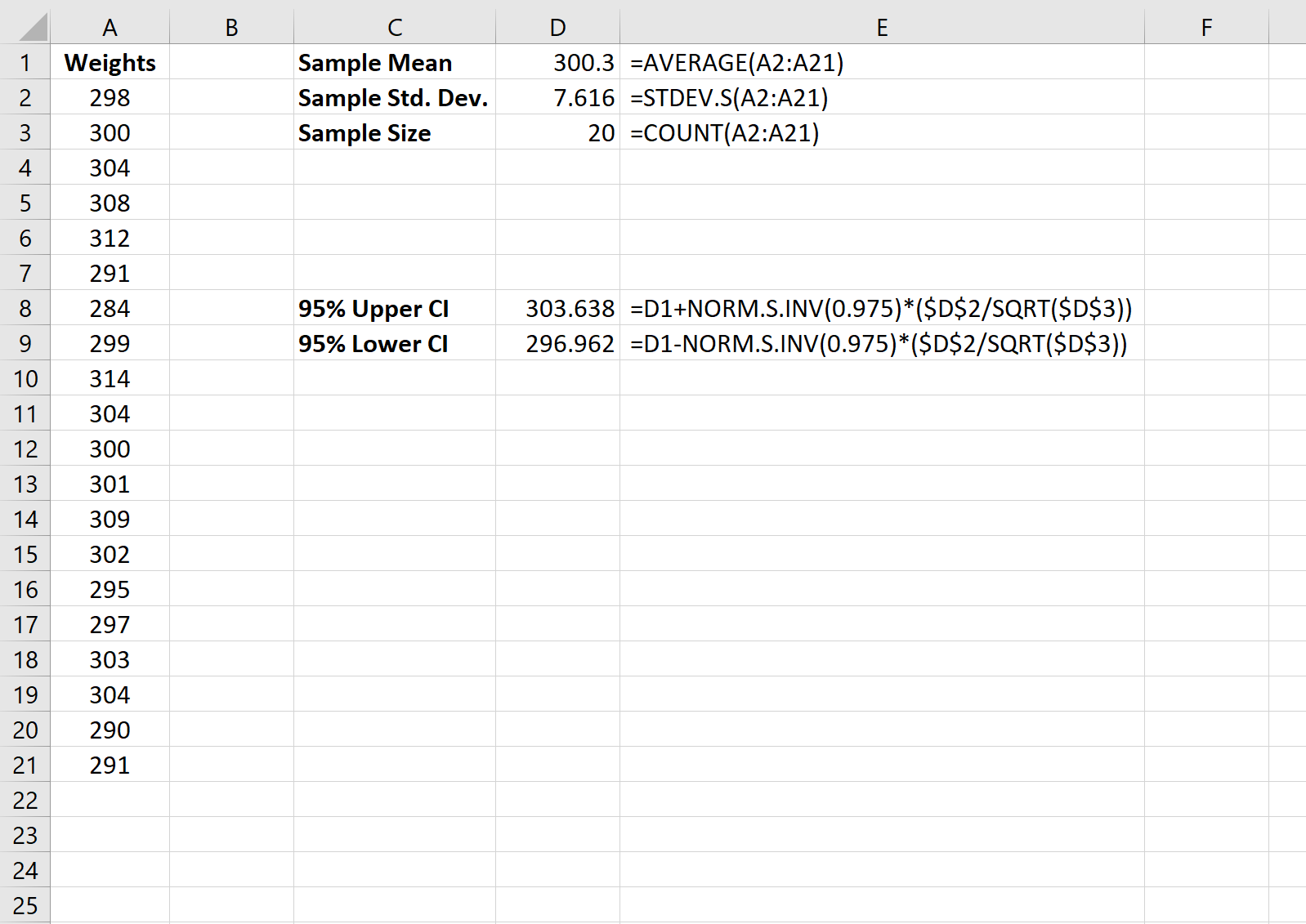
Мы на 95% уверены, что истинный средний вес черепах в этой популяции находится в диапазоне [296,96, 303,64] .
Мы можем подтвердить эти результаты, используя калькулятор доверительного интервала .
Пример 2: Точечная оценка доли населения
Предположим, нам нужно рассчитать долю черепах в популяции, имеющих пятна на панцире. Для этого мы собираем случайную выборку из 20 черепах и обнаруживаем, что у 13 из них есть пятна.
Наша точечная оценка доли черепах с пятнами составляет 0,65 :

Затем мы можем использовать следующую формулу для расчета 95% доверительного интервала для доли населения:

Мы на 95% уверены, что истинная доля черепах в этой популяции с пятнами находится в диапазоне [0,44, 0,86] .
Мы можем подтвердить эти результаты, используя калькулятор доверительного интервала для пропорции .
Дополнительные ресурсы
Как рассчитать доверительные интервалы в Excel
Как рассчитать интервал прогнозирования в Excel
Как рассчитать погрешность в Excel

