Пусть
из генеральной совокупности в результате
n
испытаний над количественным признаком
X
извлечена выборка объемом n:
варианты x1,
… , xr
и
их частоты n1,
… , nr.
Точечной
называют
оценку, которая определяется одним
числом. Точечные оценки обычно используют
в тех случаях, когда число наблюдений
велико.
Выборочной
средней
xв
называют среднее арифметическое значение
вариант выборки. Если значения вариант
x1,
x2,
… , xr
имеют
соответственно частоты n1,
n2,
… , nr,
то
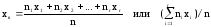 .
.
(5)
Выборочной
дисперсией Dв
называют среднее арифметическое
квадратов отклонений вариант xi
от их среднего значения xв,
т.е.
 .
.
(6)
Выборочным
средним квадратическим отклонением σв
называют
квадратный корень из выборочной дисперсии
Dв
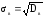 .
.
(7)
Исправленную
(несмещенную оценку) дисперсию
s2
выборки получают по формуле
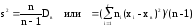 .
.
(8)
Аналогично
вводится исправленное
среднее квадратическое отклонение s
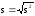 .
.
(9)
3. Интервальные оценки параметров распределения выборки
Интервальной
называют оценку, которая задается в
виде интервала. Интервальные оценки
удобно использовать в тех случаях, когда
число наблюдений n
относительно невелико.
Пусть
для неизвестного параметра θ количественного
признака X
генеральной совокупности статистическими
методами найдено значение θ*. Зададимся
точностью δ, т.е. | θ – θ* | < δ.
Надежностью
оценки
неизвестного параметра θ по вычисленному
статистическими методами значению θ*
называют вероятность γ, с которой
выполняется неравенство| θ – θ* | < δ,
при этом δ называется
точностью оценки.
В статистике обычно задаются надежностью
γ и определяют точность δ.
Доверительным
интервалом
для параметра θ называют интервал (θ* –
δ, θ* + δ), который покрывает неизвестный
параметр θ с вероятностью γ:
P[θ*
– δ <X
< θ* + δ] = γ.
Пусть
количественный признак X
генеральной совокупности распределен
нормально, причем среднее квадратическое
отклонение σ неизвестно. Требуется
оценить неизвестное математическое
ожидание a
по результатам выборки с заданной
надежностью γ.
Доверительный
интервал
с
уровнем надежности γ для математического
ожидания
a
признака
X,
распределенного нормально, при неизвестном
среднем квадратическом отклонении
определяется как
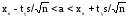 ,
,
(10)
где
xв
– выборочное среднее; s
– исправленное среднее квадратическое
отклонение выборки; n
– объем выборки. Точность оценки δ в
этом случае
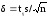 .
.
Значениеtγ
= t(γ,n)
можно найти из справочной таблицы
”Таблица значений tγ
= t(γ,n)”
для распределения Стьюдента.
Доверительный
интервал
с
уровнем надежности γ для
среднего
квадратического отклонения
σ признака X,
распределенного нормально, определяется
как
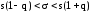 ,
,
(11)
где
s
– исправленное среднее квадратическое
отклонение выборки; n
– объем выборки. Значение q
= q(γ,n)
можно найти из справочной таблицы
”Таблица значений q
= q(γ,n)”
для распределения χ2.
В
случае, когда q
>1 доверительный интервал имеет вид
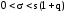 . (11′)
. (11′)
4. Статистическая проверка статистических
гипотез
Статистической
называют гипотезу (предположение) о
виде неизвестного распределения или о
параметрах известного распределения.
Основной
или нулевой гипотезой H0
называют выдвинутую гипотезу о неизвестном
распределении, вместе с основной H0
выдвигается
и конкурирующая
(альтернативная) гипотеза
H1,
противоречащая
основной.
Основной
принцип проверки статистических
гипотез состоит в следующем:
в
зависимости от вида гипотезы и характера
неизвестного распределения вводится
функция K,
называемая критерием,
по значениям ее будет приниматься
решение о принятии или отклонении
основной гипотезы H0.
Вводится также уровень
значимости
α как вероятность того, что будет
отвергнута верная нулевая гипотеза и
принята неверная гипотеза H1.
Областью
принятия гипотезы
H0
называют
те значения критерия K,
при которых основная гипотеза H0
принимается, критической
областью
– отвергается. Для каждой выборки и
конкретного вида критерия K
по специальным таблицам находятся
значения kкр,
называемые критическими
точками;
критические точки отделяют область
принятия гипотезы от критической
области. Правосторонней
называют критическую область, где K
> kкр,
левосторонней
K
< kкр
и
двусторонней
(и симметричной) | K|
> kкр.
Пусть
из генеральной совокупности в результате
n
испытаний над количественным признаком
X
извлечена выборка объемом n:
равноотстоящие с шагом h
варианты x1,
… , xr
и
их частоты n1,
… , nr.
Для нее подсчитаны по формулам (5-9)
выборочное среднее xв
и выборочное среднее квадратическое
отклонение σв.
Для
проверки гипотезы
о нормальном распределении
генеральной совокупности c
уровнем значимости α используется
критерий
χ2
Пирсона:
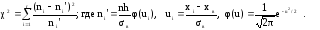 (12)
(12)
Критическое
значение χ2кр
= χ2
(α,k)
для этого критерия находится из справочной
таблицы “Критические точки распределения
χ2”.
Здесь k
= r
– 3. Если вычисленное по результатам
наблюдений по формуле (12) значение
критерия χ2набл
больше χ2кр,
основная гипотеза отвергается, если
меньше – нет оснований отвергнуть
основную гипотезу.
Если
варианты x1,
x2,
… , xr
не
являются равноотстоящими или число их
сравнительно велико, удобно сгруппировать
варианты в отдельные интервалы ( не
обязательно равноотстоящие ) [x1*;x2*),
[x2*;x3*),
…, [xm-1*;xm*).
Каждому интервалу назначается
представительное значение, равное
середине интервала xi.ср*
= (xi*
+ xi-1*)/2
и частота ni*,
равная сумме частот, попавших на интервал.
В соответствии с критерием Пирсона,
частоты ni*,
попавшие на интервалы [xi*
; xi-1*),
сравниваются с теоретическими частотами
ni‘,
вычисленными для соответствующих
интервалов нормальной случайной величины
Z
с нулевым математическим ожиданием и
единичным средним квадратическим
отклонением (Z
принадлежит N(0,1)).
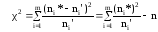 ,
,
(13)
ni‘
= nPi,
где n
– обьем выборки;
Pi
= Ф(zi+1)
– Ф(zi),
вероятности попадания X
на интервал (xi*,xi+1*)
или
Z
на (zi,zi+1);
zi
= (xi
ср*–xв*)
/ σ*; i
= 2,3,..,m-1;
крайние интервалы открываем z1
= –∞,
zm
= ∞, а Ф(zi)
– значение функции Лапласа.
Критическое
значение χ2кр
= χ2
(α,k)
для этого критерия находится из справочной
таблицы “Критические точки распределения
χ2”.
Здесь k
= m
– 3. Если вычисленное по результатам
наблюдений по формуле (13) значение
критерия χ2набл
меньше χ2кр,
нет оснований отвергнуть основную
гипотезу, если больше – основная гипотеза
не принимается.
Для
проверки гипотез
о дисперсии σ2
генеральной совокупности
с нормальным законом распределения при
заданном уровне значимости α используется
критерий
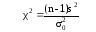 ,
,
(14)
где
s2
– исправленная дисперсия выборки; n
– объем выборки; σ02
– гипотетическое значение дисперсии.
А)
Пусть выдвинута нулевая гипотеза H0:
σ2
=
σ02
о
равенстве неизвестной генеральной
дисперсии σ2
предполагаемому значению σ02
при конкурирующей гипотезе H1:
σ2
≠
σ02.
Для проверки этой гипотезы по результатам
выборки вычисляется значение критерия
(14) χ2выб.
Затем по таблице «Критические точки
распределения χ2»,
по заданному уровню значимости α и числу
степеней свободы k
= n
– 1 находятся левое критическое значение
χ2лев.кр(1
– α/2;k)
и правое критическое значение
χ2прав.кр(α/2;k).
Если при этом χ2лев.кр
< χ2выб
< χ2прав.кр,
нет
оснований отвергнуть основную гипотезу,
конкурирующая – отвергается. В противном
случае принимается конкурирующая
гипотеза и отвергается основная.
Б)
Пусть теперь выдвинута нулевая гипотеза
H0:
σ2
=
σ02
о
равенстве неизвестной генеральной
дисперсии σ2
предполагаемому значению σ02
при конкурирующей гипотезе H1:
σ2
>
σ02.
Для проверки этой гипотезы по результатам
выборки вычисляется значение критерия
(14) χ2выб.
Затем по таблице «Критические точки
распределения χ2»,
по заданному уровню значимости α и числу
степеней свободы k
= n
– 1 находится критическое значение
χ2кр(
α;k).
Если при этом χ2выб
< χ2кр,
нет оснований отвергнуть основную
гипотезу, а конкурирующая – отвергается.
В)
Пусть теперь выдвинута нулевая гипотеза
H0:
σ2
=
σ02
о
равенстве неизвестной генеральной
дисперсии σ2
предполагаемому значению σ02
при конкурирующей гипотезе H1:
σ2
<
σ02.
Для проверки этой гипотезы по результатам
выборки вычисляется значение критерия
(14) χ2выб.
Затем по таблице «Критические точки
распределения χ2»,
по заданному уровню значимости α и числу
степеней свободы k
= n
– 1 находится критическое значение
χ2кр(
1- α;k).
Если при этом χ2выб
> χ2кр,
нет оснований отвергнуть основную
гипотезу, конкурирующая – отвергается.
Для
проверки гипотез
неизвестной средней a
генеральной совокупности
с
нормальным законом распределения
с неизвестной дисперсией при заданном
уровне значимости α используется
критерий Стьюдента
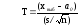 ,
,
(15)
где
xвыб
– выборочное среднее;
a0
гипотетическое значение средней; n
– объем выборки; s
– исправленное среднее квадратическое
отклонение.
А)
Пусть выдвинута нулевая гипотеза H0:
a
=
a0
о
равенстве неизвестной генеральной
средней a
предполагаемому значению a0
при конкурирующей гипотезе H1:
a
≠
a0
.
Для проверки этой гипотезы по результатам
выборки вычисляется значение критерия
(15) Tвыб.
Затем по таблице «Критические точки
распределения Стьюдента», по заданному
уровню значимости α и числу степеней
свободы k
= n
– 1 находится двустороннее критическое
значение Tдвустор.кр(α;k).
Если при этом | Tвыб
| <
Tдвустор.кр,
нет оснований отвергнуть основную
гипотезу, а конкурирующая – отвергается.
Б)
Пусть теперь выдвинута нулевая гипотеза
H0:
a
=
a0
о
равенстве неизвестной генеральной
средней a
предполагаемому значению a0
при конкурирующей гипотезе H1:
a
>
a0
.
Для проверки этой гипотезы по результатам
выборки вычисляется значение критерия
(15) Tвыб.
Затем по таблице «Критические точки
распределения Стьюдента», по заданному
уровню значимости α и числу степеней
свободы k
= n
– 1 находится критическое значение
Tправостор.кр(α;k).
Если при этом Tвыб
< Tправостор.кр,
нет оснований отвергнуть основную
гипотезу
,
а конкурирующая – отвергается.
В)
Пусть теперь выдвинута нулевая гипотеза
H0:
a
=
a0
о
равенстве неизвестной генеральной
средней a
предполагаемому значению a0
при конкурирующей гипотезе H1:
a
< a0
.
Для проверки этой гипотезы по результатам
выборки вычисляется значение критерия
(15) Tвыб.
Затем по таблице «Критические точки
распределения Стьюдента», по заданному
уровню значимости α и числу степеней
свободы k
= n
– 1 находится критическое значение
Tправостор.кр(α;k)
и полагают Tлевостор.кр
= –Tправостор.кр.
Если при этом Tвыб
> Tлевостор.кр,
нет оснований отвергнуть основную
гипотезу, а конкурирующая – отвергается.
Содержание:
Точечные оценки:
Пусть случайная величина имеет неизвестную характеристику а. Такой характеристикой может быть, например, закон распределения, математическое ожидание, дисперсия, параметр закона распределения, вероятность определенного значения случайной величины и т.д. Пронаблюдаем случайную величину n раз и получим выборку из ее возможных значений 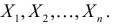
Существует два подхода к решению этой задачи. Можно по результатам наблюдений вычислить приближенное значение характеристики, а можно указать целый интервал ее значений, согласующихся с опытными данными. В первом случае говорят о точечной оценке, во втором – об интервальной.
Определение. Функция результатов наблюдений 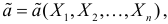
Для одной и той же характеристики можно предложить разные точечные оценки. Необходимо иметь критерии сравнения оценок, для суждения об их качестве. Оценка 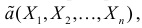 как функция случайных результатов наблюдений
как функция случайных результатов наблюдений 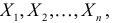 сама является случайной величиной. Значения
сама является случайной величиной. Значения 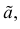 найденные по разным сериям наблюдений, могут отличаться от истинного значения характеристики
найденные по разным сериям наблюдений, могут отличаться от истинного значения характеристики 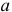 в ту или другую сторону. Естественно потребовать, чтобы оценка систематически не завышала и не занижала оцениваемое значение, а с ростом числа наблюдений становилась более точной. Формализация названных требований приводит к следующим понятиям.
в ту или другую сторону. Естественно потребовать, чтобы оценка систематически не завышала и не занижала оцениваемое значение, а с ростом числа наблюдений становилась более точной. Формализация названных требований приводит к следующим понятиям.
Определение. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемой величине: 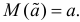 В противном случае оценку называют смещенной.
В противном случае оценку называют смещенной.
Определение. Оценка называется состоятельной, если при увеличении числа наблюдений она сходится по вероятности к оцениваемой величине, т.е. для любого сколь угодно малого 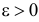
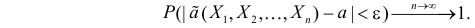
Если известно, что оценка 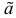 несмещенная, то для ее состоятельности достаточно, чтобы
несмещенная, то для ее состоятельности достаточно, чтобы
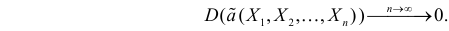
Последнее условие удобно для проверки. В качестве меры разброса значений оценки 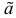 относительно
относительно 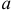 можно рассматривать величину
можно рассматривать величину 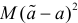 Из двух оценок предпочтительней та, для которой эта величина меньше. Если оценка имеет наименьшую меру разброса среди всех оценок характеристики, построенных по
Из двух оценок предпочтительней та, для которой эта величина меньше. Если оценка имеет наименьшую меру разброса среди всех оценок характеристики, построенных по 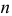 наблюдениям, то оценку называют эффективной.
наблюдениям, то оценку называют эффективной.
Следует отметить, что несмещенность и состоятельность являются желательными свойствами оценок, но не всегда разумно требовать наличия этих свойств у оценки. Например, может оказаться предпочтительней оценка хотя и обладающая небольшим смещением, но имеющая значительно меньший разброс значений, нежели несмещенная оценка. Более того, есть характеристики, для которых нет одновременно несмещенных и состоятельных оценок.
Оценки для математического ожидания и дисперсии
Пусть случайная величина имеет неизвестные математическое ожидание и дисперсию, причем 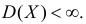 Если
Если 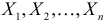 – результаты
– результаты 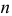 независимых наблюдений случайной величины, то в качестве оценки для математического ожидания можно предложить среднее арифметическое наблюдаемых значений
независимых наблюдений случайной величины, то в качестве оценки для математического ожидания можно предложить среднее арифметическое наблюдаемых значений 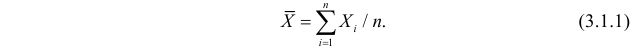
Несмещенность такой оценки следует из равенств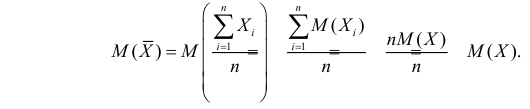
В силу независимости наблюдений 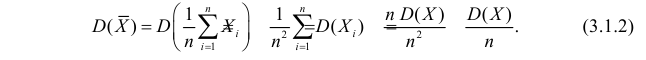
При условии 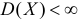 имеем
имеем 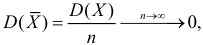 что означает состоятельность оценки
что означает состоятельность оценки 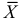 .
.
Доказано, что для математического ожидания нормально распределенной случайной величины оценка 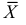 еще и эффективна.
еще и эффективна.
Оценка математического ожидания посредством среднего арифметического наблюдаемых значений наводит на мысль предложить в качестве оценки для дисперсии величину

Преобразуем величину 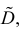 обозначая для краткости
обозначая для краткости 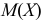 через
через 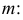
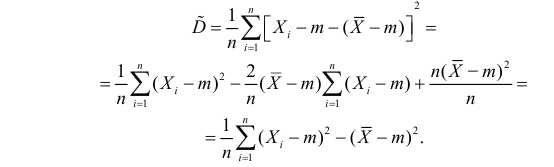
В силу (3.1.2) имеем 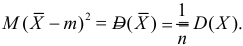 Поэтому
Поэтому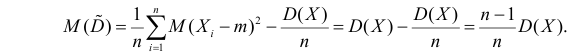
Последняя запись означает, что оценка 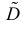 имеет смещение. Она систематически занижает истинное значение дисперсии. Для получения несмещенной оценки введем поправку в виде множителя
имеет смещение. Она систематически занижает истинное значение дисперсии. Для получения несмещенной оценки введем поправку в виде множителя 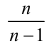 и полученную оценку обозначим через
и полученную оценку обозначим через 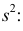
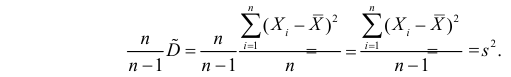
Величина
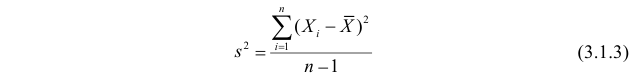
является несмещенной и состоятельной оценкой дисперсии.
Пример:
Оценить математическое ожидание и дисперсию случайной величины Х по результатам ее независимых наблюдений: 7, 3, 4, 8, 4, 6, 3.
Решение. По формулам (3.1.1) и (3.1.3) имеем 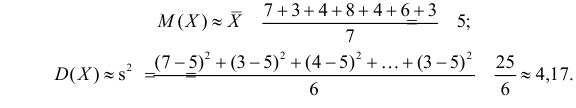
Ответ. 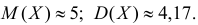
Пример:
Данные 25 независимых наблюдений случайной величины представлены в сгруппированном виде: 
Требуется оценить математическое ожидание и дисперсию этой случайной величины.
Решение. Представителем каждого интервала можно считать его середину. С учетом этого формулы (3.1.1) и (3.1.3) дают следующие оценки: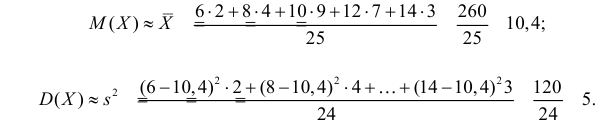
Ответ. 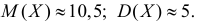
Метод наибольшего правдоподобия для оценки параметров распределений
В теории вероятностей и ее приложениях часто приходится иметь дело с законами распределения, которые определяются некоторыми параметрами. В качестве примера можно назвать нормальный закон распределения 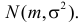 Его параметры
Его параметры 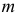 и
и 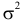 имеют смысл математического ожидания и дисперсии соответственно. Их можно оценить с помощью
имеют смысл математического ожидания и дисперсии соответственно. Их можно оценить с помощью 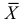 и
и 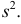 В общем случае параметры законов распределения не всегда напрямую связаны со значениями числовых 179 характеристик. Поэтому практический интерес представляет следующая задача.
В общем случае параметры законов распределения не всегда напрямую связаны со значениями числовых 179 характеристик. Поэтому практический интерес представляет следующая задача.
Пусть случайная величина Х имеет функцию распределения 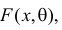 причем тип функции распределения F известен, но неизвестно значение параметра
причем тип функции распределения F известен, но неизвестно значение параметра 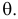 По данным результатов наблюдений нужно оценить значение параметра. Параметр может быть и многомерным.
По данным результатов наблюдений нужно оценить значение параметра. Параметр может быть и многомерным.
Продемонстрируем идею метода наибольшего правдоподобия на упрощенном примере. Пусть по результатам наблюдений, отмеченных на рис. 3.1.1 звездочками, нужно отдать предпочтение одной из двух функций плотности вероятности 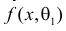 или
или 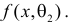
Из рисунка видно, что при значении параметра  такие результаты наблюдений маловероятны и вряд ли бы реализовались. При значении же
такие результаты наблюдений маловероятны и вряд ли бы реализовались. При значении же  эти результаты наблюдений вполне возможны. Поэтому значение параметра
эти результаты наблюдений вполне возможны. Поэтому значение параметра 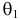 более правдоподобно, чем значение
более правдоподобно, чем значение 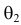 . Такая аргументация позволяет сформулировать принцип наибольшего правдоподобия: в качестве оценки параметра выбирается то его значение, при котором данные результаты наблюдений наиболее вероятны.
. Такая аргументация позволяет сформулировать принцип наибольшего правдоподобия: в качестве оценки параметра выбирается то его значение, при котором данные результаты наблюдений наиболее вероятны.
Этот принцип приводит к следующему способу действий. Пусть закон распределения случайной величины Х зависит от неизвестного значения параметра 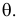 Обозначим через
Обозначим через 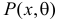 для непрерывной случайной величины плотность вероятности в точке
для непрерывной случайной величины плотность вероятности в точке 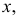 а для дискретной случайной величины – вероятность того, что
а для дискретной случайной величины – вероятность того, что 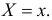 Если в
Если в 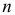 независимых наблюдениях реализовались значения случайной величины
независимых наблюдениях реализовались значения случайной величины 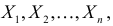 то выражение
то выражение 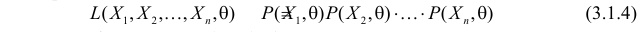
называют функцией правдоподобия. Величина 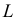 зависит только от параметра
зависит только от параметра 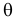 при фиксированных результатах наблюдений
при фиксированных результатах наблюдений 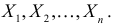 При каждом значении параметра
При каждом значении параметра 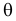 функция
функция  равна вероятности именно тех значений дискретной случайной величины, которые получены в процессе наблюдений. Для непрерывной случайной величины
равна вероятности именно тех значений дискретной случайной величины, которые получены в процессе наблюдений. Для непрерывной случайной величины  равна плотности вероятности в точке выборочного пространства
равна плотности вероятности в точке выборочного пространства 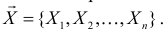
Сформулированный принцип предлагает в качестве оценки значения параметра выбрать такое 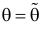 при котором
при котором  принимает наибольшее значение. Величина
принимает наибольшее значение. Величина 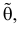 будучи функцией от результатов наблюдений
будучи функцией от результатов наблюдений 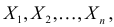 называется оценкой наибольшего правдоподобия.
называется оценкой наибольшего правдоподобия.
Во многих случаях, когда  дифференцируема, оценка наибольшего правдоподобия находится как решение уравнения
дифференцируема, оценка наибольшего правдоподобия находится как решение уравнения 
которое следует из необходимого условия экстремума. Поскольку  достигает максимума при том же значении
достигает максимума при том же значении  , что и
, что и  , то можно решать относительно
, то можно решать относительно 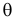 эквивалентное уравнение
эквивалентное уравнение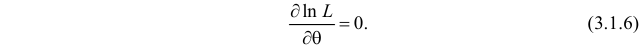
Это уравнение называют уравнением правдоподобия. Им пользоваться удобнее, чем уравнением (3.1.5), так как функция  равна произведению, а
равна произведению, а  – сумме, а дифференцировать
– сумме, а дифференцировать  проще.
проще.
Если параметров несколько (многомерный параметр), то следует взять частные производные от функции правдоподобия по всем параметрам, приравнять частные производные нулю и решить полученную систему уравнений.
Оценку, получаемую в результате поиска максимума функции правдоподобия, называют еще оценкой максимального правдоподобия.
Известно, что оценки максимального правдоподобия состоятельны. Кроме того, если для q существует эффективная оценка, то уравнение правдоподобия имеет единственное решение, совпадающее с этой оценкой. Оценка максимального правдоподобия может оказаться смещенной.
Метод моментов
Начальным моментом 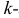 го порядка случайной величины Х называется математическое ожидание
го порядка случайной величины Х называется математическое ожидание 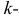 й степени этой величины, т.е.
й степени этой величины, т.е. 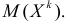 Само математическое ожидание считается начальным моментом первого порядка.
Само математическое ожидание считается начальным моментом первого порядка.
Центральным моментом 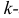 го порядка называется
го порядка называется 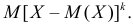 Очевидно, что дисперсия – это центральный момент второго порядка. Если закон распределения случайной величины зависит от некоторых параметров, то от этих параметров зависят и моменты случайной величины.
Очевидно, что дисперсия – это центральный момент второго порядка. Если закон распределения случайной величины зависит от некоторых параметров, то от этих параметров зависят и моменты случайной величины.
Для оценки параметров распределения по методу моментов находят на основе опытных данных оценки моментов в количестве, равном числу оцениваемых параметров. Эти оценки приравнивают к соответствующим теоретическим моментам, величины которых выражены через параметры. Из полученной системы уравнений можно определить искомые оценки.
Например, если Х имеет плотность распределения 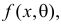 то
то 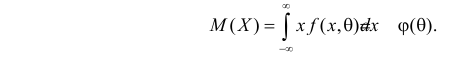
Если воспользоваться величиной 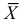 как оценкой для
как оценкой для 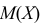 на основе опытных данных, то оценкой
на основе опытных данных, то оценкой 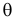 по методу моментов будет решение уравнения
по методу моментов будет решение уравнения 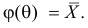
Пример:
Найти оценку параметра показательного закона распределения по методу моментов.
Решение. Плотность вероятности показательного закона распределения имеет вид 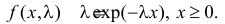 Поэтому
Поэтому 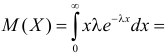
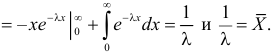 Откуда
Откуда 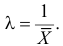
Ответ. 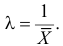
Пример:
Пусть имеется простейший поток событий неизвестной интенсивности 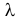 . Для оценки параметра
. Для оценки параметра 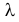 проведено наблюдение потока и зарегистрированы
проведено наблюдение потока и зарегистрированы 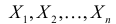 – длительности
– длительности  последовательных интервалов времени между моментами наступления событий. Найти оценку для
последовательных интервалов времени между моментами наступления событий. Найти оценку для 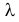 .
.
Решение. В простейшем потоке интервалы времени между последовательными моментами наступления событий потока имеют показательный закон распределения 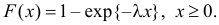 Так как плотность вероятности показательного закона распределения равна
Так как плотность вероятности показательного закона распределения равна 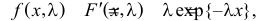 то функция правдоподобия (3.1.4) имеет вид
то функция правдоподобия (3.1.4) имеет вид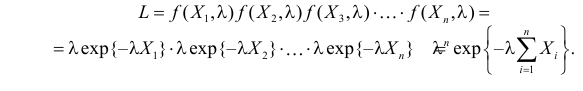
Тогда 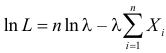 и уравнение правдоподобия
и уравнение правдоподобия 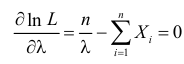 имеет решение
имеет решение 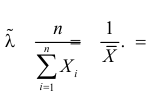
При таком значении  функция правдоподобия действительно достигает наибольшего значения, так как
функция правдоподобия действительно достигает наибольшего значения, так как 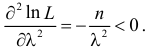
Ответ. 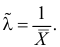
Определение. Пусть 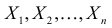 – результаты n независимых наблюдений случайной величины X. Если расставить эти результаты в порядке возрастания, то получится последовательность значений, которую называют вариационным рядом и обозначают:
– результаты n независимых наблюдений случайной величины X. Если расставить эти результаты в порядке возрастания, то получится последовательность значений, которую называют вариационным рядом и обозначают:

В этой записи 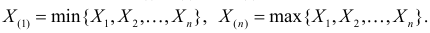
Величины 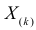 называют порядковыми статистиками.
называют порядковыми статистиками.
Пример:
Случайная величина Х имеет равномерное распределение на отрезке 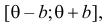 где
где  и
и  неизвестны. Пусть
неизвестны. Пусть 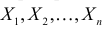 – результаты
– результаты  независимых наблюдений. Найти оценку параметра
независимых наблюдений. Найти оценку параметра  .
.
Решение. Функция плотности вероятности величины Х имеет вид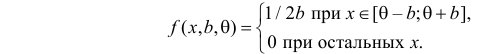
В этом случае функция правдоподобия 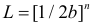 от
от  явно не зависит. Дифференцировать по
явно не зависит. Дифференцировать по  такую функцию нельзя и нет возможности записать уравнение правдоподобия. Однако легко видеть, что
такую функцию нельзя и нет возможности записать уравнение правдоподобия. Однако легко видеть, что  возрастает при уменьшении
возрастает при уменьшении  . Все результаты наблюдений лежат в
. Все результаты наблюдений лежат в 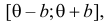 поэтому можно записать:
поэтому можно записать:
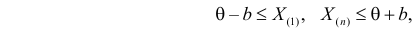
где 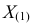 – наименьший, а
– наименьший, а 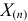 – наибольший из результатов наблюдений. При минимально возможном
– наибольший из результатов наблюдений. При минимально возможном 
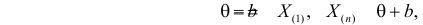
откуда 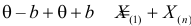 или
или 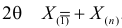
Оценкой наибольшего правдоподобия для параметра  будет величина
будет величина
Ответ. 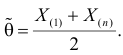
Пример:
Случайная величина X имеет функцию распределения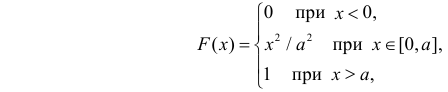
где 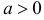 неизвестный параметр.
неизвестный параметр.
Пусть 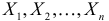 – результаты
– результаты  независимых наблюдений случайной величины X. Требуется найти оценку наибольшего правдоподобия для параметра
независимых наблюдений случайной величины X. Требуется найти оценку наибольшего правдоподобия для параметра 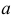 и найти оценку для M(X).
и найти оценку для M(X).
Решение. Для построения функции правдоподобия найдем сначала функцию плотности вероятности
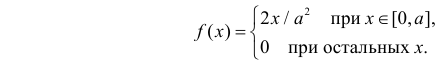
Тогда функция правдоподобия: 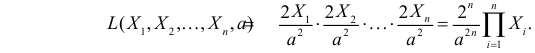
Логарифмическая функция правдоподобия: 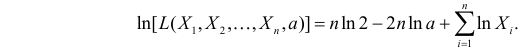
Уравнение правдоподобия

не имеет решений. Критических точек нет. Наибольшее и наименьшее значения  находятся на границе допустимых значений
находятся на границе допустимых значений  .
.
По виду функции  можно заключить, что значение
можно заключить, что значение  тем больше, чем меньше величина
тем больше, чем меньше величина  . Но
. Но  не может быть меньше
не может быть меньше 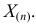 Поэтому наиболее правдоподобное значение
Поэтому наиболее правдоподобное значение 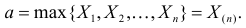
Так как 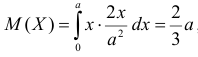 , то оценкой наибольшего правдоподобия для
, то оценкой наибольшего правдоподобия для 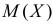 будет величина
будет величина 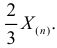
Ответ. 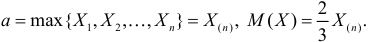
Пример:
Случайная величина Х имеет нормальный закон распределения 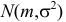 c неизвестными параметрами
c неизвестными параметрами 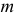 и
и 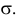 По результатам независимых наблюдений
По результатам независимых наблюдений 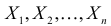 найти наиболее правдоподобные значения этих параметров.
найти наиболее правдоподобные значения этих параметров.
Решение. В соответствии с (3.1.4) функция правдоподобия имеет вид 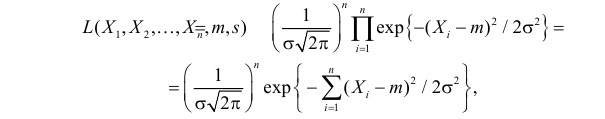
а логарифмическая функция правдоподобия: 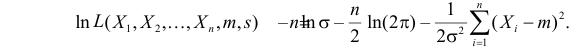
Необходимые условия экстремума дают систему двух уравнений: 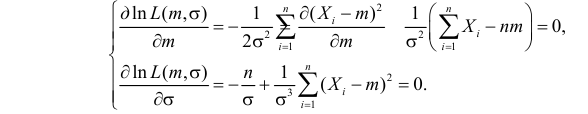
Решения этой системы имеют вид: 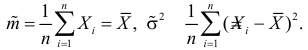
Отметим, что обе оценки являются состоятельными, причем оценка для 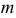 несмещенная, а для
несмещенная, а для 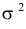 смещенная (сравните с формулой (3.1.3)).
смещенная (сравните с формулой (3.1.3)).
Ответ. 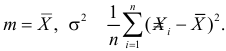
Пример:
По данным эксперимента построен статистический ряд:

Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения случайной величины X.
Решение. 1) Число экспериментальных данных вычисляется по формуле:
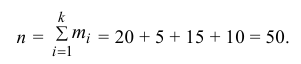
Значит, объем выборки n = 50.
2) Вычислим среднее арифметическое значение эксперимента:
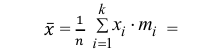
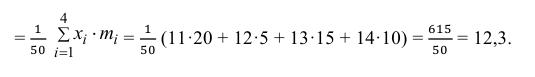
Значит, найдена оценка математического ожидания 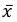 = 12,3.
= 12,3.
3) Вычислим исправленную выборочную дисперсию:
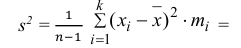
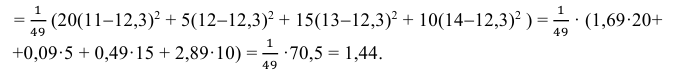
Значит, найдена оценка дисперсии: 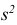 = 1,44.
= 1,44.
5) Вычислим оценку среднего квадратического отклонения:
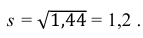
Ответ: 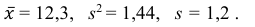
Пример:
По данным эксперимента построен статистический ряд:

Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения случайной величины X.
Решение. По формуле
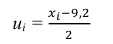
перейдем к условным вариантам:

Для них произведем расчет точечных оценок параметров:
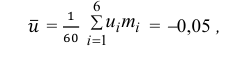
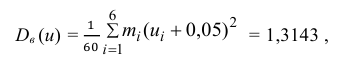
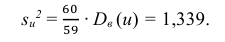
Следовательно, вычисляем искомые точечные оценки:
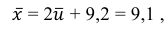
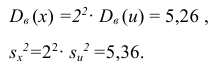
Ответ: 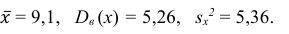
Пример:
По данным эксперимента построен интервальный статистический ряд:

Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения.
Решение. 1) От интервального ряда перейдем к статистическому ряду, заменив интервалы их серединами 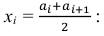

2) Объем выборки вычислим по формуле:
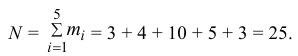
3) Вычислим среднее арифметическое значений эксперимента:
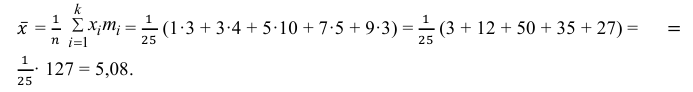
3) Вычислим исправленную выборочную дисперсию:
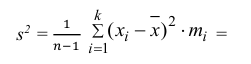
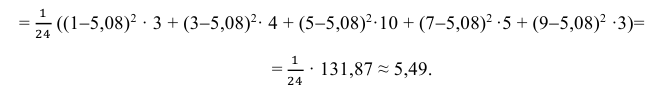
Можно было воспользоваться следующей формулой:
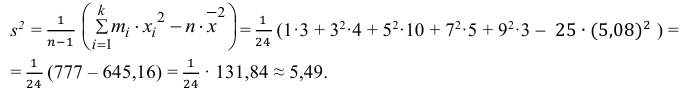
5) Вычислим оценку среднего квадратического отклонения:
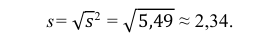
Ответ: 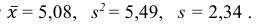
Пример:
Найти доверительный интервал с надежностью 0,95 для оценки математического ожидания M(X) нормально распределенной случайной величины X, если известно среднее квадратическое отклонение σ = 2, оценка математического ожидания 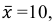 объем выборки n = 25.
объем выборки n = 25.
Решение. Доверительный интервал для истинного математического ожидания с доверительной вероятностью 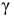 = 0,95 при известной дисперсии σ находится по формуле:
= 0,95 при известной дисперсии σ находится по формуле:
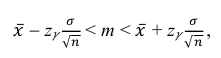
где m = M(X) – истинное математическое ожидание; 𝑥̅ − оценка M(X) по выборке; n – объем выборки; 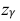 – находится по доверительной вероятности
– находится по доверительной вероятности 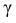 = 0,95 из равенства:
= 0,95 из равенства:
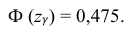
Из табл. П 2.2 приложения 2 находим: 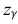 = 1,96. Следовательно, найден доверительный интервал для M(X):
= 1,96. Следовательно, найден доверительный интервал для M(X):
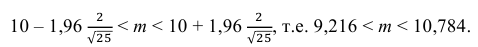
Ответ: (9,216 ; 10,784).
Пример:
По данным эксперимента построен статистический ряд:

Найти доверительный интервал для математического ожидания M (X) с надежностью 0,95.
Решение. Воспользуемся формулой для доверительного интервала математического ожидания при неизвестной дисперсии:
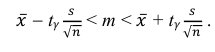
где n – объем выборки; 𝑥̅ оценка M(X); s – оценка среднего квадратического отклонения; 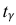 − находится по доверительной вероятности
− находится по доверительной вероятности 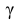 = 0,95.
= 0,95.
По числам 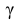 = 0,95 и n = 20 находим:
= 0,95 и n = 20 находим: 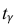 = 2,093.
= 2,093.
Теперь вычисляем оценки для M(X) и D(X):
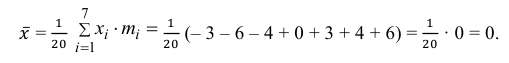
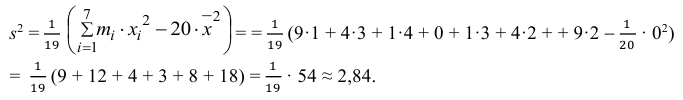
Следовательно, s ≈ 1,685. Поэтому искомый доверительный интервал математического ожидания задается формулой:
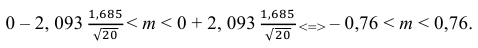
Ответ: (– 0,76; 0,76).
Пример:
По данным десяти независимых измерений найдена оценка квадратического отклонения 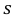 = 0,5. Найти доверительный интервал точности измерительного прибора с надежностью 99 %.
= 0,5. Найти доверительный интервал точности измерительного прибора с надежностью 99 %.
Решение. Задача сводится к нахождению доверительного интервала для истинного квадратического отклонения, так как точность прибора характеризуется средним квадратическим отклонением случайных ошибок измерений.
Доверительный интервал для среднего квадратического отклонения находим по формуле:
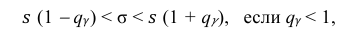
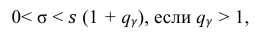
где 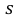 = 0,5 − оценка среднего квадратического отклонения;
= 0,5 − оценка среднего квадратического отклонения; 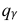 – число, определяемое из табл. П 2.4 приложения 2 по заданной доверительной вероятности
– число, определяемое из табл. П 2.4 приложения 2 по заданной доверительной вероятности 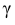 = 0,99 и заданному объему выборки n = 10.
= 0,99 и заданному объему выборки n = 10.
Находим: 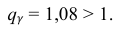
Тогда можно записать:
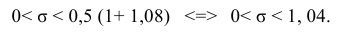
Ответ: (0; 1,04).
- Доверительный интервал для вероятности события
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Системы случайных величин
- Вероятность и риск
- Определения вероятности событий
- Предельные теоремы теории вероятностей
Содержание:
- Точечные статистические оценки параметров генеральной совокупности
- Методы определения точечных статистических оценок
- Законы распределения вероятностей для
- Интервальные статистические оценки для параметров генеральной совокупности
- Построение доверчивого интервала для при известном значении с заданной надежностью
- Построение доверительного интервала для при неизвестном значении из заданной надежности
- Построение доверительных интервалов с заданной надежностью для
- Построение доверительного интервала для генеральной совокупности с заданной надежностью
- Построение доверительного интервала для с помощью неравенства Чебишова с заданной надежностью
Информация, которую получили на основе обработки выборки про признак генеральной совокупности, всегда содержит определенные погрешности, поскольку выборка содержит только незначительную часть от нее  то есть объем выборки значительно меньше объема генеральной совокупности.
то есть объем выборки значительно меньше объема генеральной совокупности.
Потому, следует организовать выборку так, чтобы эта информация была более полной (выборка может быть репрезентабельной) и обеспечивала с наибольшей степенью доверия о параметрах генеральной совокупности ил закон распределение ее признака.
Параметры генеральной совокупности  являются величинами постоянными, но их числовые значения неизвестные. Эти параметры оцениваются параметрами выборки:
являются величинами постоянными, но их числовые значения неизвестные. Эти параметры оцениваются параметрами выборки:  которые получаются при обработке выборки. Они являются величинами непредсказуемыми, то есть случайными. Схематично это можно показать так (рис. 115).
которые получаются при обработке выборки. Они являются величинами непредсказуемыми, то есть случайными. Схематично это можно показать так (рис. 115).

Тут через  обозначен оценочный параметр генеральной совокупности, а через
обозначен оценочный параметр генеральной совокупности, а через  – его статистическую оценку, Которую называют еще статистикой. При этом
– его статистическую оценку, Которую называют еще статистикой. При этом  а
а  – случайная величина, что имеет полный закон распределения вероятностей. заметим, что для реализации выборки каждую ее варианту рассматривают как случайную величину, что имеет закон распределения вероятностей признака генеральной совокупности с соответственными числовыми характеристиками:
– случайная величина, что имеет полный закон распределения вероятностей. заметим, что для реализации выборки каждую ее варианту рассматривают как случайную величину, что имеет закон распределения вероятностей признака генеральной совокупности с соответственными числовыми характеристиками:

Точечные статистические оценки параметров генеральной совокупности
Статистическая оценка  , которая обозначается одном числом, называется точечной. Возьмем во внимание, что
, которая обозначается одном числом, называется точечной. Возьмем во внимание, что  является случайной величиной, точечная статистическая оценка может быть смещенной или несмещенной: когда математическое надежда этой оценки точно равны оценочному параметру
является случайной величиной, точечная статистическая оценка может быть смещенной или несмещенной: когда математическое надежда этой оценки точно равны оценочному параметру  а именно:
а именно:

то  называется несмещенной; в противоположном случае, то есть когда
называется несмещенной; в противоположном случае, то есть когда

точечная статистическая оценка  называется смещенной относительно параметра генеральной совокупности
называется смещенной относительно параметра генеральной совокупности 
Разница

называется смещением статистической оценки 
Оценочный параметр может иметь несколько точечных несмещенных статистических оценок, что можно изобразить так (рис. 116):

Например, пусть  которая имеет две несмещенные точечные статистические оценки –
которая имеет две несмещенные точечные статистические оценки –  и
и  Тогда плотность вероятностей для
Тогда плотность вероятностей для 
 имеют такой вид (рис. 117):
имеют такой вид (рис. 117):

Из графиков плотности видим, что оценка  сравнено с оценкой
сравнено с оценкой  имеет то преимущество, что около параметра
имеет то преимущество, что около параметра 
 Отсюда получается, что оценка
Отсюда получается, что оценка  чаще получает значение в этой области, чем оценка
чаще получает значение в этой области, чем оценка 
Но на “хвостах” распределений имеет другую картину: большие отклонения от  будут наблюдаться для статистической оценки
будут наблюдаться для статистической оценки  , чаще, чем для
, чаще, чем для  Потому, сравнивая дисперсии статистических
Потому, сравнивая дисперсии статистических  как меру рассеивания, видим, что
как меру рассеивания, видим, что  имеет меньшую дисперсию, чем оценка
имеет меньшую дисперсию, чем оценка  .
.
Точечная статистическая оценка называется эффективной, когда при заданном объеме выборки она имеет минимальную дисперсию. Следует, оценка  будет несмещенной и эффективной.
будет несмещенной и эффективной.
Точечная статистическая оценка называется основой, если в случае неограниченного увеличения объема выборки  приближается к оценке параметра
приближается к оценке параметра  , а именно:
, а именно:

Методы определения точечных статистических оценок
Существует три метода определения точечных статистических оценок для параметров генеральной совокупности.
Метод аналогий. Этот метод основывается на том, что для параметров генеральной совокупности выбирают такие же параметры выборки, то есть для оценки  выбирают аналогичные статистики –
выбирают аналогичные статистики – 
Метод наименьших квадратов. Согласно с этим методом статистические оценки обозначаются с условием минимизации суммы квадратов отклонений вариант выборки от статистической оценки  .
.
Итак, используя метод наименьших квадратов, можно, например, обозначить статистическую оценку для  Для этого воспользуемся функцией
Для этого воспользуемся функцией  Используя условие экстремума, получим:
Используя условие экстремума, получим:

Отсюда, для  точечной статистической оценкой будет
точечной статистической оценкой будет  – выборочная средняя.
– выборочная средняя.
Метод максимальной правдоподобности. Этот метод занимает центральное место в теории статистической оценки параметров  На него в свое время обратил внимание К. Гаусс, а разработал его Р. Фишер. Этот метод рассмотрим подробнее.
На него в свое время обратил внимание К. Гаусс, а разработал его Р. Фишер. Этот метод рассмотрим подробнее.
Пусть признак генеральной совокупности  обозначается только одном параметром
обозначается только одном параметром  и имеет плотность вероятности
и имеет плотность вероятности  В случае реализации выборки с вариантами
В случае реализации выборки с вариантами  плотность вероятности выборки будет такой:
плотность вероятности выборки будет такой:

В этом варианте рассматриваются как независимые случайные величины, которые имеют один и тот же закон распределения, что ее признак генеральной совокупности  .
.
Суть этого метода состоит в том, что фиксируя значение вариант  , обозначают такие значение параметра
, обозначают такие значение параметра  , при котором функция
, при котором функция  максимизуется. Она называется функцией максимальной правдоподобности и обозначается так:
максимизуется. Она называется функцией максимальной правдоподобности и обозначается так: 
Например, когда признак генеральной совокупности  имеет нормальный закон распределения, то функция максимальной правдоподобности приобретет такой вид:
имеет нормальный закон распределения, то функция максимальной правдоподобности приобретет такой вид:

При этом статистические оценки  выбирают и ее значения, по которых заданная выборка будет верной, то есть функция
выбирают и ее значения, по которых заданная выборка будет верной, то есть функция  достигает максимума.
достигает максимума.
На практике удобно от функции  перейти к ее логарифму, а именно:
перейти к ее логарифму, а именно:

согласно с необходимым условием экстремума для этой функции получим:

Из первого уравнения системы  получим:
получим:

из уравнение системы  получим:
получим:

Следует, для  точечной функции статистической оценкой будет
точечной функции статистической оценкой будет  для
для 
Свойства  Исправленная дисперсия, исправленное среднее квадратичное отклонение. Точечной несмещенной статистической оценкой для
Исправленная дисперсия, исправленное среднее квадратичное отклонение. Точечной несмещенной статистической оценкой для  будет
будет 
И на самом деле,
 учитывая то. что
учитывая то. что 

Следует, 
Проверим на несмещенность статистической оценки 



Таким образом, получим 
Следует,  будет точечной смещенной статистической оценкой для
будет точечной смещенной статистической оценкой для  , где
, где  – коэффициент смещения, который уменьшается с увеличением объема выборки
– коэффициент смещения, который уменьшается с увеличением объема выборки 
Когда  умножить на
умножить на  то получим
то получим 
Тогда

Следует,  будут точеной несмещенной статистической оценкой для
будут точеной несмещенной статистической оценкой для  Ее называли исправленной дисперсией и обозначили через
Ее называли исправленной дисперсией и обозначили через 
Отсюда точечной несмещенной статистической оценкой для  будет исправленная дисперсия
будет исправленная дисперсия  или
или

Величину

называют исправленным средним квадратичным отклонением.
Исправленное среднее квадратичное отклонение, следует подчеркнуть, будет смещенной точечной статистической оценкой для  поскольку
поскольку

где  является ступенью свободы;
является ступенью свободы;
 – коэффициенты смещения.
– коэффициенты смещения.
Пример. 200 однотипных деталей были отданы на шлифование. Результаты измерения приведены как дискретное статистическое распределение, подан в табличной форме:

Найти точечные смещенные статистические оценки для 

Решение. Поскольку точечной несмещенной оценки для  будет
будет  то вычислим
то вычислим

Для обозначение точечной несмещенной статистической оценки для  вычислим
вычислим 


тогда точечная несмещенная статистическая оценка для  равно:
равно:

Пример. Граничная нагрузка на стальной болт  что измерялась в лабораторных условий, задано как интервальное статистическое распределение:
что измерялась в лабораторных условий, задано как интервальное статистическое распределение:

Обозначить точечные несмещенные статистические оценки для 
Решение. Для обозначения точечных несмещенных статистических распределений к дискретному, который приобретает такой вид:

Вычислим 

Следует, точечная несмещенная статистическая оценка для 

Для обозначения  вычислим
вычислим 

Отсюда точечная несмещенная статистическая оценка для  будет
будет 
Законы распределения вероятностей для 
Как уже обозначалось, числовые характеристики выборки являются случайными величинами, что имеют определенные законы распределения вероятностей. Так,  (выборочная средняя) на основании центральной граничной теоремы теории вероятностей (теоремы Ляпунова) имеем нормальный закон распределения с числовыми характеристиками
(выборочная средняя) на основании центральной граничной теоремы теории вероятностей (теоремы Ляпунова) имеем нормальный закон распределения с числовыми характеристиками

следует, случайная величина  имеет закон распределения
имеет закон распределения 
Чтобы обозначить закон распределения для  необходимо выявить связь между
необходимо выявить связь между  и распределением
и распределением  .
.
Пусть признак генеральной совокупности  имеет нормальный закон распределения
имеет нормальный закон распределения  . При реализации выборки каждую из вариант
. При реализации выборки каждую из вариант  рассматривают как случайную величину. то также имеет закон распределения
рассматривают как случайную величину. то также имеет закон распределения  . При этом вариант выборки является независимым, то есть
. При этом вариант выборки является независимым, то есть  а случайная величина
а случайная величина  соответственно имеет закон распределения
соответственно имеет закон распределения 
Рассмотрим случай, когда варианты выборки имеют частоты  тогда
тогда

Перейдем от случайных величин  к случайным величинам
к случайным величинам  которые линейно выражаются через
которые линейно выражаются через  а именно:
а именно:

Поскольку случайные величины  будут линейными комбинациями случайных величин
будут линейными комбинациями случайных величин  то
то  тоже имеют нормальный закон распределения с числовыми характеристиками:
тоже имеют нормальный закон распределения с числовыми характеристиками:


Следует, случайные величины  имеют закон распределения
имеют закон распределения 
Построим матрицу  элементы которой будут коэффициенты при
элементы которой будут коэффициенты при  в линейных зависимостях для
в линейных зависимостях для 

Транспортируем матрицу  получим:
получим:

Если перемножить матрицы  и
и  то получим:
то получим:

где  будет единичная матрица.
будет единичная матрица.
Следует, случайные величины  обозначены ортогональными преобразованиями случайных величин
обозначены ортогональными преобразованиями случайных величин  В векторной – матричной форме это можно записать так:
В векторной – матричной форме это можно записать так:
Из курса алгебры известно, что во время ортогональных преобразований вектора сохраняется его длина, то есть

Тогда из формулы для  получим:
получим:

Поскольку  далее вычислим:
далее вычислим:

Следует, получим 
Когда поделим левую и правую часть  на
на  то получим,
то получим,

Поскольку  имеет закон распределения
имеет закон распределения  то
то  получим закон распределения
получим закон распределения  то есть нормированный нормальный закон.
то есть нормированный нормальный закон.
То случайная величина

получим распределение  из
из  ступенями свободы.
ступенями свободы.
Отсюда получается, что случайная величина  получим распределение
получим распределение  из
из  ступенями свободы.
ступенями свободы.
Таким образом, приведена: случайная величина  тут символ
тут символ  нужно читать “распределена как”;
нужно читать “распределена как”;
случайная величина 
случайная величина 
Интервальные статистические оценки для параметров генеральной совокупности
Точечные статистические оценки  являются случайными величинами, а потому приближенная замена
являются случайными величинами, а потому приближенная замена  на
на  часто приводит к существенным погрешностям, особенно когда объем выборки не большой. В этом случае используют интервальные статистические оценки.
часто приводит к существенным погрешностям, особенно когда объем выборки не большой. В этом случае используют интервальные статистические оценки.
Статистическая оценка, что обозначается двумя числами, концами интервалов, называется интервальной.
Разница между статистической оценкой  и ее оценкой параметром
и ее оценкой параметром  взята с абсолютным значением, называется точностью оценки, а именно:
взята с абсолютным значением, называется точностью оценки, а именно:

где  является точностью оценки.
является точностью оценки.
Поскольку  является случайной величиной, то и
является случайной величиной, то и  будет случайной, потому неравенство
будет случайной, потому неравенство  справедливо с определенной вероятностью.
справедливо с определенной вероятностью.
Вероятность, с которой берется неравенство  , то есть
, то есть

называется надежностью
Равенство  можно записать так:
можно записать так:

Интервал  что покрывает оценочный параметр
что покрывает оценочный параметр  генеральной совокупности с заданной надежностью
генеральной совокупности с заданной надежностью  называют доверчивым.
называют доверчивым.
Построение доверчивого интервала для  при известном значении
при известном значении  с заданной надежностью
с заданной надежностью 
Пусть признак  генеральной совокупностью имеет нормальный закон распределению. Построим доверительный интервал для
генеральной совокупностью имеет нормальный закон распределению. Построим доверительный интервал для  зная числовое значение среднего квадратичному отклонению генеральной совокупности
зная числовое значение среднего квадратичному отклонению генеральной совокупности  с заданной надежностью
с заданной надежностью  Поскольку
Поскольку  как точечная несмещенная статистическая оценка для
как точечная несмещенная статистическая оценка для  имеет нормальный закон распределения с числовыми характеристиками
имеет нормальный закон распределения с числовыми характеристиками 
 то воспользовавшись
то воспользовавшись  получим
получим

Случайная величина  имеет нормальный закон распределения с числовыми характеристиками
имеет нормальный закон распределения с числовыми характеристиками

Потому  будет нормированный нормальный закон распределения
будет нормированный нормальный закон распределения 
Отсюда равенство  можно записать, обозначив
можно записать, обозначив  так;
так;

или

Согласно с формулой нормированного нормального закона

для  она получает такой вид:
она получает такой вид:

Из равенства  находим аргументы
находим аргументы  а именно:
а именно:

Аргумент  находим значение функции Лапласа, которая равна
находим значение функции Лапласа, которая равна  по таблице (дополнение 2).
по таблице (дополнение 2).
Следует, доверительный интервал равен:

что можно изобразить условно на рисунке 118.

Величина  называется точностью оценки, или погрешностью выборки.
называется точностью оценки, или погрешностью выборки.
Пример. Измеряя 40 случайно отобранных после изготовления деталей, нашли выборку средней, что равна 15 см. Из надежности  построить доверительный интервал для средней величины всей партии деталей, если генеральная дисперсия равна
построить доверительный интервал для средней величины всей партии деталей, если генеральная дисперсия равна 
Решение. Для построенного доверчивого интервала необходимо найти: 
Из условия задачи имеем: 
 Величина
Величина  вычисляется из уравнения
вычисляется из уравнения

 {с таблицей значения функции Лапласа}.
{с таблицей значения функции Лапласа}.
Найдем числовые значения концов доверчивого интервала:

Таким образом, получим: 
Следует, с надежностью  (99% гарантии) оценочный параметр
(99% гарантии) оценочный параметр  пребывает в середина интервала
пребывает в середина интервала 
Пример. Имеем такие данные про размеры основных фондов (в млн руб.) на 30-ти случайно выбранных предприятий:

построить интервальное статистическое распределение с длиной шага  млн рублей.
млн рублей.
С надежностью  найти доверительный интеграл для
найти доверительный интеграл для  если
если  млн рублей.
млн рублей.
Решение. Интервальное статистическое распределение будет таким:

Для обозначение  необходимо построить дискретное статистическое распределение, что имеет такой вид:
необходимо построить дискретное статистическое распределение, что имеет такой вид:

Тогда

 млн рублей.
млн рублей.
Для построения доверительного интервала с заданной надежностью  необходимо найти
необходимо найти 

Вычислим концы интервала:
 млн руб.
млн руб.
 млн руб.
млн руб.
Следует, доверительный интервал для  будет
будет 
Пример. Какое значение может получит надежность оценки  чтобы за объем выборки
чтобы за объем выборки  погрешность ее не превышала
погрешность ее не превышала  при
при 
Решение. Обозначим погрешность выборки

Далее получим:

как видим, надежность мала.
Пример. Обозначить объем выборки  по которому погрешность
по которому погрешность  гарантируется с вероятностью
гарантируется с вероятностью  если
если 
Решение. По условию задачи  Поскольку
Поскольку  то получим:
то получим:  Величину
Величину  находим из равенства
находим из равенства  Тогда
Тогда 
Построение доверительного интервала для  при неизвестном значении
при неизвестном значении  из заданной надежности
из заданной надежности 
Для малых выборок, с какими сталкиваемся, исследуя разные признаки в техники или сельском хозяйстве, для оценки  при неизвестном значении
при неизвестном значении  невозможно воспользоваться нормальным законом распределения. Потому для построения доверительного интервала используется случайная величина.
невозможно воспользоваться нормальным законом распределения. Потому для построения доверительного интервала используется случайная величина.

что имеет распределение Стьюдента с  ступенями свободы.
ступенями свободы.
Тогда  получает вид:
получает вид:

поскольку  для распределения Стьюдента является функцией четной.
для распределения Стьюдента является функцией четной.
Вычислив по данному статистическому распределению 
 и обозначив по таблице распределения Стьюдента значения
и обозначив по таблице распределения Стьюдента значения  построим доверительный интервал
построим доверительный интервал

Тут  вычислим по заданной надежностью
вычислим по заданной надежностью  и числом степеней свободы
и числом степеней свободы  по таблице (дополнение 3).
по таблице (дополнение 3).
Пример. Случайно выбранная партия из двадцати примеров была испытана относительно срока безотказной работы каждого из них  Результаты испытаний приведено в виде дискретного статистического распределения:
Результаты испытаний приведено в виде дискретного статистического распределения:

С надежностью  построить доверительный интервал для
построить доверительный интервал для  (среднего времени безотказной работы прибора.)
(среднего времени безотказной работы прибора.)
Решение. Для построения доверительного интеграла необходимо найти среднее выборочное и исправленное среднее квадратичное отклонение.
Вычислим 

следует, получили  часов.
часов.
Обозначим 

следует, 
Исправленное среднее квадратичное отклонение равно:
 часов.
часов.
По таблице значений  (дополнение 3) распределение Стьюдента по заданной надежностью
(дополнение 3) распределение Стьюдента по заданной надежностью  и числом ступеней свободы
и числом ступеней свободы  находим значение
находим значение 
Вычислим концы доверительного интервала:
 час.
час.
 час.
час.
Следует, с надежностью  можно утверждать, что
можно утверждать, что  будет содержится в интервале
будет содержится в интервале

При больших объемах выборки, а именно:  на основании центральной граничной теоремы теории вероятностей (теоремы Ляпунова) распределение Стьюдента приближается к нормальному закону. В этом случае
на основании центральной граничной теоремы теории вероятностей (теоремы Ляпунова) распределение Стьюдента приближается к нормальному закону. В этом случае  находиться по таблице значений функции Лапласа.
находиться по таблице значений функции Лапласа.
Пример. В таблице приведены отклонения диаметров валиков, изготовленных на станке, от номинального размера:

с надежностью  построить доверительный интервал для
построить доверительный интервал для 
Решение. Для постройки доверительного интервала необходимо найти 
Для этого от интегрального статистического распределения, приведенного в условии задачи, необходимо перейти к дискретному, а именно:

Вычислим 
 поскольку
поскольку 

Следует, 
Обозначим 

Вычислим исправленное среднее квадратичное отклонение 

Учитывая на большой  объем выборки можно считать, что распределение Стьюдента близкий к нормальному закону. Тогда по таблице значения функции Лапласа
объем выборки можно считать, что распределение Стьюдента близкий к нормальному закону. Тогда по таблице значения функции Лапласа

Вычислим концы интервалов:


Итак, доверчивый интервал для среднего значения отклонений будет таким: 
Отсюда с надежностью  можно утверждать, что
можно утверждать, что
Построение доверительных интервалов с заданной надежностью  для
для 
В случае, если признак  имеем нормальный закон распределения, для построения доверительного интервала с заданной надежностью
имеем нормальный закон распределения, для построения доверительного интервала с заданной надежностью  для
для  используем случайную величину
используем случайную величину

что имеет распределение  из
из  ступенями свободы.
ступенями свободы.
Поскольку случайные действия
 и
и 
являются равновероятными, то есть их вероятности равны  получим:
получим:

Подставляя в 
 получим
получим

Следует, доверительный интервал для  получит вид:
получит вид:

Тогда доверительный интервал для  получается из
получается из  и будет таким:
и будет таким:

Значения  находятся по таблице (дополнение 4) согласно с равенствами:
находятся по таблице (дополнение 4) согласно с равенствами:

где 
Пример. Проверена партия однотипных телевизоров  на чувствительность к видео-программ
на чувствительность к видео-программ  данные проверки приведены как дискретное статистическое распределение:
данные проверки приведены как дискретное статистическое распределение:

С надежностью  построить доверительные интервалы для
построить доверительные интервалы для 
Решение. Для построении доверительных интервалов необходимо найти значения 
Вычислим значения 
 так как
так как 

Вычислим 


Следует 
Исправленная дисперсия и исправленное среднее квадратичное отклонение равны:

Поскольку  то согласно с
то согласно с  находим значения
находим значения  а именно:
а именно:

По таблице (дополнение 4) находим:

вычислим концы доверительного интервала для 


Следует, доверительный интеграл для  будет таким:
будет таким:

Доверительный интервал для  станет
станет

Доверительный интервал для  можно построить с заданной надежностью
можно построить с заданной надежностью  взяв распределение
взяв распределение 
Поскольку

то равенство  можно записать так:
можно записать так:

или

Обозначив  получим
получим

чтобы найти  возьмем случайную величину
возьмем случайную величину

что имеет распределение 
Учитывая то, что события
 и
и 
при  является равновероятными, получим:
является равновероятными, получим:

Если умножить все члены двойного неравенства 
 на
на  то получим:
то получим:

Отсюда получим:

Из уравнения  по заданной надежностью
по заданной надежностью  и объемом выборки
и объемом выборки  находим по таблице (дополнение 5) значение величины
находим по таблице (дополнение 5) значение величины 
Доверительный интервал будет таким:

Пример. С надежностью  построить доверительный интервал вычислим значения
построить доверительный интервал вычислим значения  по таблице (дополнение 5).
по таблице (дополнение 5). 
Обозначим концы интервала:

Следует, доверительный интервал для  с надежностью
с надежностью  будет такой
будет такой

Построение доверительного интервала для  генеральной совокупности с заданной надежностью
генеральной совокупности с заданной надежностью 
Как величина, полученная по результатам выборки,  является случайной и представляет собой точечную несмещенную статистическую оценку для
является случайной и представляет собой точечную несмещенную статистическую оценку для 
Исправленное среднее квадратичное отклонение для 

Для построения доверительного интервала для  используется случайная величина
используется случайная величина

что имеет нормированный нормальный закон распределения 
Воспользовавшись  получим
получим

Следует. доверительный интервал для  будет таким:
будет таким:

где  находим из равенства
находим из равенства

по таблице значений функции Лапласа.
Пример. Случайно выбранных студентов из потока университета были подвергнуты тестированию по математике и химии. Результаты этих тестирования преподнесено статистическим распределением, где  – оценки по математике,
– оценки по математике,  – по химии. Ответы оценивались по десятибалльной системе:
– по химии. Ответы оценивались по десятибалльной системе:

Необходимо:
1) с надежностью  построить доверительный интервал для
построить доверительный интервал для  если
если 
2) с надежностью  построить доверительный интервал для
построить доверительный интервал для 
Решение. Вычислим основные числовые характеристики признак  и
и  а также
а также  Поскольку
Поскольку  получим:
получим:


1. Построим доверительный интервал с надежностью  для
для  если
если 

нам известные значения  Значения
Значения  вычисляем из уравнения
вычисляем из уравнения

где  находим по таблице значений функции Лапласа.
находим по таблице значений функции Лапласа.
Обозначим концы интервала:

Следует, доверительный интервал для  будет таким:
будет таким:

2. Построим доверительный интервал с надежностью  для
для 
Поскольку  нам не известно, то доверительный интервал в этом случае обозначается так:
нам не известно, то доверительный интервал в этом случае обозначается так:

На известное значение  находим по таблице распределения Стьюдента (дополнение 3),
находим по таблице распределения Стьюдента (дополнение 3),

Вычислим концы доверительного интервала:

Таким образом, доверительный интервал для  будет в таких границах:
будет в таких границах:

Доверительный интеграл с надежностью  для
для  будет таким:
будет таким:

Нам известно значение  Учитывая, что
Учитывая, что  найдем по таблице (дополнение 5) значения
найдем по таблице (дополнение 5) значения 
Обозначим концы доверительного интервала:

Следует, доверительный интервал для  подается таким неравенством:
подается таким неравенством:

Доверительный интервал для  с заданной надежностью
с заданной надежностью  будет таким:
будет таким:

Нам известны значения  обозначаем по таблице значений функции Лапласа
обозначаем по таблице значений функции Лапласа  где
где 
Обозначим концы доверительного интервала:

таким образом, доверительный интервал для  будет в таких границах:
будет в таких границах:

Построение доверительного интервала для  с помощью неравенства Чебишова с заданной надежностью
с помощью неравенства Чебишова с заданной надежностью
В случае, если отсутствует информация про закон распределения признака генеральной совокупности  оценка вероятностей события
оценка вероятностей события  где
где  и построение доверительного интервала для
и построение доверительного интервала для  с заданной надежностью
с заданной надежностью  выполняется с использованием неравенства Чебишова по условию, что известно значение
выполняется с использованием неравенства Чебишова по условию, что известно значение  а именно:
а именно:

Из  обозначаем величину
обозначаем величину 

Доверительный интервал дается таким неравенством:

Когда  неизвестно, используем исправленную дисперсию
неизвестно, используем исправленную дисперсию  и доверительный интервал приобретает такой вид:
и доверительный интервал приобретает такой вид:

Пример. Полученные данные с 100 наугад выбранных предприятий относительно возрастания выработки на одного работника  которые имеют такой интервальное статистическое распределение:
которые имеют такой интервальное статистическое распределение:

Воспользовавшись неравенством Чебишова, построить доверительный интервал для  если известно значение
если известно значение  с надежностью
с надежностью 
Решение. Для построения доверительного интервала с помощью неравенства Чебишова необходимо вычислить  Чтобы обозначить
Чтобы обозначить  перейдем от интервального к дискретному статистическому распределению, а именно:
перейдем от интервального к дискретному статистическому распределению, а именно:

Тогда получим:

Воспользовавшись  вычислим
вычислим 

таким образом, доверительный интервал для  преподноситься такими неравенствами:
преподноситься такими неравенствами:

или

Пример. Заданы размеры основных фондов  на 30- ти предприятий дискретным статистическим распределением:
на 30- ти предприятий дискретным статистическим распределением:

Воспользовавшись неравенством Чебишова с надежностью  построить доверительный интервал для
построить доверительный интервал для 
Решение. Для постройки доверительного интервала для  с помощью неравенства Чебишова необходимо вычислить
с помощью неравенства Чебишова необходимо вычислить 

 млн руб.
млн руб.
Следует,  млн рублей.
млн рублей.

 млн рублей.
млн рублей.
Обозначить концы доверительного интервала:
 млн рублей
млн рублей
 н рублей
н рублей
Итак, доверительный интервал для  подается неравенствами
подается неравенствами

Лекции:
- Статистические гипотезы
- Корреляционный и регрессионный анализ
- Комбинаторика основные понятия и формулы с примерами
- Число перестановок
- Количество сочетаний
- Действия над событиями. Теоремы сложения и умножения вероятностей примеры с решением
- Примеры решения задач на тему: Случайные величины
- Примеры решения задач на тему: основные законы распределения
- Примеры решения задач на тему: совместный закон распределения двух случайных величин
- Статистические распределения выборок и их числовые характеристики
Реферат
на тему «Точечные оценки»
по учебной дисциплине
«ОСНОВЫ МАТЕМАТИЧЕСКОЙ ОБРАБОТКИ ИНФОРМАЦИИ»
Выполнил(а):
Савкина Юлия Камильевна
2022 г
Оглавление
Введение
Статистика есть наука о том, как,
не умея мыслить и понимать,
заставить делать это цифры.
В. О. Ключевский
Математическая статистика – это наука, изучающая методы сбора и обработки статистической информации для получения научных и практических выводов.
Одной из центральных задач математической статистики является задача оценивания теоретического распределения случайной величины на основе выборочных данных. При этом часто предполагается, что вид закона распределения генеральной совокупности известен, но неизвестны параметры этого распределения, такие как математическое ожидание, дисперсия и др. Требуется найти приближенные значения этих параметров, то есть получить статистические оценки указанных параметров.
Основным методом математической статистики является выборочный метод, его суть состоит в исследовании представительной выборочной совокупности – для достоверной характеристики совокупности генеральной. Данный метод экономит временные, трудовые и материальные затраты, поскольку исследование всей совокупности зачастую затруднено или невозможно.
Для нахождения вида функции оценивания того или иного параметра используют один из следующих методов: 1) метод максимального правдоподобия; 2) метод моментов; 3) оценивание с помощью метода наименьших квадратов
Числовые характеристики, полученные по выборкам, называют статистическими оценками параметров. Различают два вида оценок параметров точечные и интервальные.
В данной работе речь пойдет именно о точечных оценках.
Глава 1. Основная часть
Основные понятия математической статистики
Введем основные понятия, связанные с выборками. Генеральной совокупностью называется совокупность объектов, из которых производится выборка. Выборочной совокупностью (выборкой) называется совокупность случайно отобранных объектов из генеральной совокупности. Число объектов в совокупности называется ее объемом.
Числовые характеристики всей генеральной совокупности называются параметрами. Так как всю генеральную совокупность изучить достаточно часто не представляется возможным, о параметрах судят по выборочным характеристикам. На основании выборочных данных можно получить лишь приближенное значение параметра, которое является его оценкой.
Выборочная характеристика, используемая в качестве приближенного значения неизвестного параметра генеральной совокупности, называется точечной оценкой, т.к представляет собой число или точку на числовой оси.
Числовые характеристики выборки
По результатам выборочных наблюдений вычисляются такие статистические выборочные характеристики, как выборочные средняя, дисперсия, среднее квадратичное отклонение, коэффициент корреляции и т.д. Эти характеристики определяют соответствующие параметры генеральной совокупности.
Пусть x1, x2, …, xn – выборка из генеральной совокупности объёма n.
Выборочной средней (или средним значение выборки) называется среднее арифметическое значение признака выборочной совокупности.
Генеральная средняя для изучаемого количественного признака Х по генеральной совокупности
 и выборочная средняя
и выборочная средняя

Если все значения x1, x2, …, xn признака выборки объема n различны, то среднее значение выборки оценивается по формуле:
 .
.
Для обозначения среднего значения выборки чаще всего используются обозначения  и
и 
Если значения признака Х1, X2, …, Хk в выборке имеют соответственно частоты n1, n2, …, nk, то последнюю формулу можно переписать в виде

Математическое ожидание характеризует среднее значение случайной величины и определяется по формулам:
|
|
(1.1) |
где mx обозначает число, полученное после вычислений по формуле (1.1); M[X] – оператор математического ожидания, ДСВ – дискретная случайная величина, НСВ – непрерывная случайная величина. Как видно из (1.1), в качестве математического ожидания используется «среднее взвешенное значение», причем каждое из значений случайной величины учитывается с «весом», пропорциональным вероятности этого значения.
Начальный момент k-го порядка случайной величины X есть математическое ожидание k-й степени этой случайной величины:
|
|
(1.2) |
При k=0 значение α0(x) = M[X0] = M [1] = 1; при k=1 — α1(x) = M[X1] = M [Х] = mx – математическое ожидание; при k=2 — α2(x) = M[X2].
Центрированной случайной величиной Х° называется случайная величина, математическое ожидание которой находится в начале координат (в центре числовой оси), т.е. M[X°] = 0. Операция центрирования (переход от нецентрированной величины Х к центрированной X°) имеет вид X° =X − mX .
Центральный момент порядка k случайной величины X есть математическое ожидание k-й степени центрированной случайной величины X:
|
|
(1.3) |
При k=0 значение 0(x)=M [X°0]=M [1]=1; при k=1 — 1(x)=M [X°1]=M [Х°] = 0; при k=2 — 2 (x)=M[X°2]= M [(X – mx)2]=M[X 2] – 2mx M [X ]+ mx2= α2 – mx2=Dx – дисперсия.
Дисперсия случайной величины характеризует степень рассеивания (разброса) значений случайной величины относительно ее математического ожидания и определяется по формулам:
|
|
(1.4) |
Дисперсия выборки или выборочная дисперсия оценивается по (слегка измененной) формуле:
 , где m*– среднее значение выборки.
, где m*– среднее значение выборки.
Дисперсия случайной величины имеет размерность квадрата случайной величины, поэтому для анализа диапазона значений величины Х дисперсия не совсем удобна. Этого недостатка лишено среднее квадратическое отклонение (СКО), размерность которого совпадает с размерностью случайной величины. Выборочным средним квадратичным отклонением (стандартом) называют квадратный корень из выборочной дисперсии:
|
|
(1.5) |
Мода случайной величины равна ее наиболее вероятному значению, т.е. то значение, для которого вероятность pi (для дискретной случайной величины) или f(x) (для непрерывных случайной величины) достигает максимума: f (Mo) = max, p(X = Mo) = max.
Медиана случайной величины X равна такому ее значению, для которого выполняется условие p { X < Me } = p { X Me }. Медиана, как правило, существует только для непрерывных случайных величин. Значение Me может быть определено как решение одного из следующих уравнений:
|
|
(1.6) |
В точке Me площадь, ограниченная кривой распределения делится пополам.Медиана вычисляется следующим образом. Изучаемая выборка упорядочивается в порядке возрастания (N – объем выборки). Получаемая последовательность ak, где k=1,…, N называется вариационным рядом или порядковыми статистиками.
Если число наблюдений N нечетно, то медиана оценивается как m = aN+1/2
Если число наблюдений N четно, то медиана оценивается как m = ( aN/2 + aN/2+1 ) / 2
Квантиль хp случайной величины X – это такое ее значение, для которого выполняется условие
|
p { X < xp } = F(xp)= p. (1.7) |
(1.7) |
Очевидно, что медиана – это квантиль x0,5.
Свойства точечных оценок
Статистической оценкой Qˆ неизвестного параметра Q теоретического распределения называется приближенное значение параметра, вычисленное по результатам эксперимента (по выборке). Статистические оценки делятся на точечные и интервальные. Точечной называется оценка, определяемая одним числом. Точечная оценка Qˆ параметра Q случайной величины X в общем случае равна
|
Qˆ= (x1, x2, …, xn), где xi – значения выборки. |
(1.8) |
Очевидно, что оценка Qˆ – это случайная величина, так как она является функцией от n-мерной случайной величины (Х1, …, Хn), где Хi, – значение величины Х в i-м опыте, и значения будут изменяться от выборки к выборке случайным образом. Чтобы точечная оценка была наилучшей с точки зрения точности, необходимо, чтобы она была состоятельной, несмещенной и эффективной.
Оценка Qˆ называется состоятельной, если при увеличении объема выборки n она сходится по вероятности к значению параметра Q:
|
|
(1.9) |
Состоятельность – это минимальное требование к оценкам.
Оценка Qˆ называется несмещенной, если ее математическое ожидание точно равно параметру Q для любого объема выборки:
Несмещенная оценка Qˆ является эффективной, если ее дисперсия минимальна по отношению к дисперсии любой другой оценки этого параметра:
|
|
(1.11) |
Первые два требования к оценке являются обязательными, выполнение последнего требования – желательно.
Точечная оценка математического ожидания. На основании теоремы Чебышева в качестве состоятельной оценки математического ожидания может быть использовано среднее арифметическое значений выборки  , называемое выборочным средним:
, называемое выборочным средним:
Определим числовые характеристики оценки  .
.
 т.е. оценка несмещенная.
т.е. оценка несмещенная.
Оценка (1.12) является эффективной, т.е. ее дисперсия минимальна, если величина X распределена по нормальному закону.
Состоятельная оценка начального момента k-го порядка определяется по формуле
Точечная оценка дисперсии. В качестве состоятельной оценки дисперсии может быть использовано среднее арифметическое квадратов отклонений значений выборки от выборочного среднего:
Определим математическое ожидание оценки S2. Так как дисперсия не зависит от того, где выбрать начало координат, выберем его в точке mX, т.е. перейдем к центрированным величинам:

Ковариация Kij =0, так как опыты, а, следовательно, и Хi − значение величины Х в i‑м опыте − независимы. Таким образом, величина является смещенной оценкой дисперсии, а несмещенная состоятельная оценка дисперсии равна:
Дисперсия величины S02 равна:
Для нормального закона распределения величины X формула (1.17) примет вид
Для равномерного закона распределения –
Состоятельная несмещенная оценка среднеквадратического отклонения определяется по формуле: (1.20)
Состоятельная оценка центрального момента k-го порядка равна:
Точечная оценка вероятности. На основании теоремы Бернулли несмещенная состоятельная и эффективная оценка вероятности случайного события A в схеме независимых опытов равна частоте этого события:
где m – число опытов, в которых произошло событие A; n – число проведенных опытов. Числовые характеристики оценки вероятности p*(A) = p* равны:
Среднее арифметическое х, выборочная дисперсия Дх, частость р – это точечные статистические оценки соответственно математического ожидания (генерального среднего) МХ, дисперсии (генеральной дисперсии) ДХ, истиной (генеральной) вероятности р. Чтобы не заблудиться в этом многообразии, удобно пользоваться таблицей 1, представленной ниже [3].
Методы построения точечных оценок
Выше мы рассматривали точечные оценки основных генеральных характеристик: математического ожидания, дисперсии, вероятности и др. Однако осталось неясным, каким образом получены эти оценки. В математической статистике разработано большое число методов оценивания неизвестных параметров по данным случайной выборки, из которых наиболее часто используются:
метод моментов1;
метод максимального правдоподобия2;
метод наименьших квадратов;
графический метод (или метод номограмм).
Рассмотрим первые два из них.
Метод моментов. Пусть имеется выборка {x1, …, xn} независимых значений случайной величины с известным законом распределения f(x, Q1 , …, Qm) и m неизвестными параметрами Q1, …, Qm. Необходимо вычислить оценки Qˆ1, …, Qˆm параметров Q1, …, Qm. Последовательность вычислений следующая:
Вычислить значения m начальных и/или центральных теоретических моментов
Определить m соответствующих выборочных начальных αkˆ(x) и/или центральных µkˆ(x) моментов по формулам (1.14, 1.21).
Составить и решить относительно неизвестных параметров Q1, …, Qm систему из m уравнений, в которых теоретические моменты приравниваются к выборочным моментам. Каждое уравнение имеет вид αk(x) =αkˆ(x) или µ k(x) = µ kˆ(x). Найденные корни являются оценками Q1ˆ, …, Qmˆ неизвестных параметров.
Замечание. Часть уравнений может содержать начальные моменты, а оставшаяся часть – центральные.
Метод максимального правдоподобия. Согласно данному методу оценки Qˆ1, …, Qˆm получаются из условия максимума по параметрам Q1, …, Qm положительной функции правдоподобия L ( x1, …, xn, Q1, …, Qm). Если случайная величина X непрерывна, а значения xi независимы, то функция правдоподобия равна

Если случайная величина X дискретна и принимает независимые значения xi с вероятностями p (X=xi) = pi ( xi, Q1, …, Qm), то функция правдоподобия равна

Система уравнений согласно этому методу может записываться в двух видах:
или
Найденные корни выбранной системы уравнений являются оценками Q1ˆ, …, Qmˆ неизвестных параметров Q1, …, Qm.
Как правило оценка максимального правдоподобия эффективнее оценки, полученной методом моментов, и более того, если существует несмещенная эффективная оценка параметра, то она будет получена методом максимального правдоподобия.
Глава 2. Практическая часть
Примеры вычисления точечных оценок
Пример 1. Найдем оценку для вероятности P наступления события A по данному числу m появления этого события в n испытаниях.
Решение. Воспользуемся методом максимального правдоподобия: в этом случае функция правдоподобия L равна L = Cnm P m (1–P) n–m.
Тогда ln (L) = ln Cnm + m ln (P) + (n–m) ln (1 – P).
Уравнение для определения оценки:

Значит, оценкой методом максимального правдоподобия вероятности наступления события будет его относительная частота w.

Пример 2. Случайная величина X (число появлений события А в t независимых испытаниях) подчинена биномиальному закону распределения с неизвестным параметром р. Ниже приведено эмпирическое распределение числа появлений события в 10 опытах по 5 испытаний в каждом (в первой строке указано число xi появлений события А в одном опыте; во второй строке указана частота ni — количество опытов, в которых наблюдалось столько появлений события А).
Найти методом моментов точечную оценку параметра р биномиального распределения. Оценить вероятность p0=P(X=0).
Решение. Математическое ожидание биномиального распределения известно: MX = m p. Приравняв математическое ожидание к выборочному среднему, получим уравнение:  , откуда
, откуда  . Для рассматриваемого примера имеем:
. Для рассматриваемого примера имеем:
|
|
(05+12+21+31+41) / 10=1,1; |
||
|
|
= 1,1/5=0,22; |
|
Если распределение определяется двумя параметрами, то для построения их оценок два теоретических момента приравнивают двум соответствующим эмпирическим моментам тех же порядков (обычно первым двум).
Пример 3. Для изучения генеральной совокупности относительно некоторого количественного признака была извлечена выборка:
Найти несмещенные оценки генеральной средней и генеральной дисперсии.
Решение. Несмещенной оценкой генеральной средней является выборочная средняя: .
.
Несмещенной оценкой генеральной дисперсии является исправленная выборочная дисперсия:
 Ответ: 50; 2,57.
Ответ: 50; 2,57.
Пример 4. По выборке объема N=41 найдена смещенная оценка генеральной дисперсии DB=3. Найти несмещенную оценку дисперсии генеральной совокупности.
Решение. Смещенной оценкой генеральной дисперсии служит выборочная дисперсия

Несмещенной оценкой генеральной дисперсии является «исправленная дисперсия»
 или
или 
Таким образом, мы получаем искомую несмещенную оценку дисперсии генеральной совокупности:

Пример 5. Для анализа лингвистических терминологических систем взято 7 фрагментов по 250 терминоупотреблений из русских лингвистических текстов. После подсчёта в каждом фрагменте числа употреблений слова «лицо» получен следующий вариационный ряд: 1,1,3,4,9,10,12.
1) Определите по выборке несмещённую и состоятельную оценку математического ожидания М(Х) и дисперсии D(X) случайной величины Х – «число употреблений слова «лицо» в русских лингвистических текстах.
2) Найдите несмещённую, состоятельную и эффективную оценку вероятности события А= «слово лицо использовано более 5 раз».
Решение
1) Несмещённая и состоятельная оценка М(Х) есть среднее выборочное.

Несмещённая и состоятельная оценка D(X) есть исправленная выборочная дисперсия: 

2) Несмещённой, состоятельной и эффективной оценкой вероятности события А= «слово лицо использовано более 5 раз» является частота этого события Р(А): 
Пример 6. Выборка задана таблицей распределения

Найти выборочные характеристики: среднюю, дисперсию и среднее квадратическое отклонение.
Решение. Cначала находим  в:
в:

Затем по формулам находим две другие искомые величины:

Пример 7. Из 1500 деталей отобрано 250, распределение которых по размеру Х задано в таблице:
|
xi |
7,8-8,0 |
8,0-8,2 |
8,2-8,4 |
8,4-8,6 |
8,6-8,8 |
8,8-9,0 |
|
ni |
5 |
20 |
80 |
95 |
40 |
10 |
Найти точечные оценки для среднего и дисперсии, а также дисперсию оценки среднего при повторном и бесповторном отборах.
Решение. Вычислим по формулам (используем середины интервалов сi, число интервалов r=6, объем выборки n=250):
|
сi |
7,9 |
8,1 |
8,3 |
8,5 |
8,7 |
8,9 |
|
|
ni |
5 |
20 |
80 |
95 |
40 |
10 |
n=250 |





Вычислим дисперсию оценки среднего:
для повторной выборки:

для бесповторной выборки

Пример 8. Выборочно обследовали партию кирпича. Из 100 проб в 12 случаях кирпич оказался бракованным. Найти оценку доли бракованного кирпича и дисперсию этой оценки.
Решение. По условию задачи, число бракованных изделий m=12, объем выборки n=100, тогда оценкой доли бракованных является выборочная доля

Дисперсия этой оценки для повторной выборки равна

А среднее квадратическое отклонение этой оценки равно 
Задачи подобраны таким образом, чтобы показать их разнообразную тематику и способы решений. Это и доказательство свойств точечной оценки, представление выборок разными способами и вычисление точечных оценок. Чтобы облегчить свою работу, можно воспользоваться таблицей 1 (см Приложение 1).
Заключение
Точечная оценка параметра – это оценка, которая характеризуется одним конкретным числом (например, математическим ожиданием, дисперсией, средним квадратичным отклонением и т.д.). Точечные оценки параметров генеральной совокупности могут быть приняты в качестве ориентировочных, первоначальных результатов обработки выборочных данных. Их основной недостаток заключается в том, что неизвестно, с какой точностью оценивается параметр. Если для выборок большого объема точность обычно бывает достаточной (при условии несмещенности, эффективности и состоятельности оценок), то для выборок небольшого объема вопрос точности становится очень важным. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.
Решение задач математической статистики обусловливает существенный объем вычислений. Во избежание ошибок, можно воспользоваться инженерным калькулятором или выполнить вычисления с помощью офисного пакета MS Excel, в котором есть различные статистические функции и надстройки, в том числе и возможность решить задачи по теме «Анализ данных»
Список литературы
- Гмурман, В. Е. Теория вероятностей и математическая статистика: учебник для прикладного бакалавриата / В. Е. Гмурман. — 12-е изд. — Москва: Издательство Юрайт, 2019. — 479 с. — (Бакалавр. Прикладной курс). — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://biblio-online.ru/bcode/431095.
- Гмурман, В. Е. Руководство к решению задач по теории вероятностей и математической статистике: учебное пособие для бакалавриата и специалитета / В. Е. Гмурман. — 11-е изд., перераб. и доп. — Москва: Издательство Юрайт, 2019. — 406 с. — (Бакалавр и специалист). — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://biblio-online.ru/bcode/431094.
- Малугин, В. А. Теория вероятностей и математическая статистика: учебник и практикум для вузов / В. А. Малугин. — Москва: Издательство Юрайт, 2022. — 470 с. — (Высшее образование). — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/viewer/teoriya-veroyatnostey-i-matematicheskaya-statistika-493318
- Малугин, В. А. Математическая статистика: учебное пособие для бакалавриата и магистратуры / В. А. Малугин. — Москва: Издательство Юрайт, 2019. — 218 с. — (Бакалавр и магистр. Академический курс). — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://biblio-online.ru/bcode/441413.
- Энатская, Н. Ю. Математическая статистика и случайные процессы: учебное пособие для вузов / Н. Ю. Энатская. — Москва: Издательство Юрайт, 2022. — 201 с. — (Высшее образование). — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/viewer/matematicheskaya-statistika-i-sluchaynye-processy-490096
Приложение 1
Таблица 1. Точечные оценки случайных величин

окончание таблицы 1
Таблица1. Точечные оценки случайных величин

1 Метод моментов был впервые предложен английским ученым, основателем математической статистики К. Пирсоном (1857-1936) в 1894 году.
2 Метод максимального правдоподобия разработал английский статистик Р. Фишер, который в 1921 г доказал, что ММ-оценки чаще всего не эффективны.









