Точка пересечения прямой и плоскости онлайн
С помощю этого онлайн калькулятора можно найти точку пересечения прямой и плоскости. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямой и плоскости задайте вид уравнения прямой (“канонический” или “параметрический” ), введите данные в уравнения прямой и плоскости и нажимайте на кнопку “Решить”. Теоретическую часть и численные примеры смотрите ниже.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Точка пересечения прямой и плоскости − теория, примеры и решения
- Содержание
- 1. Точка пересечения плоскости и прямой, заданной в каноническом виде.
- 2. Точка пересечения плоскости и прямой, заданной в параметрическом виде.
- 3. Примеры нахождения точки пересечения прямой и плоскости.
1. Точка пересечения плоскости и прямой, заданной в каноническом виде
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямая L1:
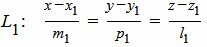 , , |
(1) |
и плоскость α:
где M1(x1, y1, z1) − точка, лежащая на прямой L1, q1={m1, p1, l1} − направляющий вектор прямой L1, а n={A,B,C} − нормальный вектор плоскости α.
Найти точку пересечения прямой L1 и плоскости α (Рис.1).
Запишем уравнение (1) в виде системы двух линейных уравнений:
Сделаем перекрестное умножение в уравнениях (3) и (4):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Решим систему линейных уравнений (2), (5), (6) с тремя неизвестными x, y, z. Для этого в уравнении (2) переведем свободный член в правую часть уравнения и запишем эту систему в матричном виде:
Как решить систему линейных уравнений (11)(или (2), (5), (6)) посмотрите на странице Метод Гаусса онлайн или на примерах ниже. Если система линейных уравнениий (7) несовместна, то прямая L1 и плоскость α не пересекаются. Если система (7) имеет множество решений, то прямая L1 лежит на плоскости α. Единственное решение системы линейных уравнений (7) указывает на то, что это решение определяет координаты точки пересечения прямой L1 и плоскости α.
Замечание. Если прямая задана параметрическим уравнением, то уранение прямой нужно приводить к каноническому виду и применить метод, описанный выше, или же
2. Точка пересечения плоскости и прямой, заданной в параметрическом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L1 в параметрическом виде:
и плоскость α:
где M1(x1, y1, z1) − точка, лежащая на прямой L1, q1={m1, p1, l1} − направляющий вектор прямой L1, а n={A,B,C} − нормальный вектор плоскости α.
Задачу нахождения нахождения точки пересечения прямых L1 и плоскости α можно решить разными методами.
Метод 1. Приведем уравнения прямой L1 к каноническому виду.
Для приведения уравнения (8) к каноническому виду, выразим параметр t через остальные переменные:
Так как левые части уравнений (10) равны, то можем записать:
Далее, для нахождения точки пересечения прямой и плоскости нужно воспользоваться параграфом 1.
Метод 2. Для нахождения точки пересечения прямой L1 и плоскости α решим совместно уравнения (8) и (9). Из уравнений (8) подставим x, y, z в (9):
Откроем скобки и найдем t:
Если числитель и знаменатель в уравнении (14) одновременно равны нулю, то это значит, что прямая L1 лежит на полскости α. Если в уравнении (14) числитель отличен от нуля, а знаменатель равен нулю, то прямая и плоскость параллельны.
Если же числитель и знаменатель в уравнении (14) отличны от нуля, то прямая и плоскость пересекаются в одной точке. Для нахождения координат точки пересечения прямой L1 и плоскости α подставим полученное значение t из (14) в (8).
3. Примеры нахождения точки пересечения прямой и плоскости.
Пример 1. Найти точку пересечения прямой L1:
и плоскости α:
Представим уравнение (15) в виде двух уравнений:
Сделаем перекрестное умножение в уравнениях (17) и (18):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Упростим:
Для нахождения точки пересечения прямой L1 и плосклсти α нужно решить совместно уравнения (2), (19) и (20). Для этого переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (19) и (20):
Решим систему линейных уравнений (21) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −7/3:
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 3 со строкой 2, умноженной на 4/3:
Второй этап. Обратный ход Гаусса.
Исключим элементы 3-го столбца матрицы выше элемента a33. Для этого сложим строку 2 со строкой 3, умноженной на −3/2:
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на 1/2:
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
Запишем решение:
Ответ. Точка пересечения прямой L1 и плоскости α имеет следующие координаты:
Пример 2. Найти точку пересечения прямой L1:
и плоскости α:
Представим уравнение (22) в виде двух уравнений:
Сделаем перекрестное умножение в уравнениях (24) и (25):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Упростим:
Для нахождения точки пересечения прямой L1 и плосклсти α нужно решить совместно уравнения (2), (26) и (27). Переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (26) и (27):
Решим систему линейных уравнений (21) отностительно x, y, z. Для этого построим расширенную матрицу:
Обозначим через aij элементы i-ой строки и j-ого столбца.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строку 3 со строкой 1, умноженной на 6/5:
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 3 со строкой 2, умноженной на −1/5:
Из расширенной матрицы восстановим систему линейных уравнений:
Легко можно заметить, что последнее уравнение в (29) несовместна, так как несуществуют такие x, y, z чтобы выполнялось это равенство. Следовательно система линейных уравнений (2), (26) и (27) несовместна. Тогда прямая L1 и плоскость α не пересекаются, т.е. они параллельны.
Ответ. Прямая L1 и плоскость α параллельны, т.е. не имеют общую точку.
Пример 3. Найти точку пересечения прямой в параметрическом виде L1:
и плоскости α:
Решение. Для нахождения точки пересечения прямой L1 и плоскости α нужно найти такое значение t, при котором точка M(x, y, z) удовлетворяет уравнению (31). Поэтому подставим значения x, y, z из (30) в (31):
Откроем скобки:
Упростив уравнение, получим:
Как видим, любое значение t удовлетворяет уравнению (33), т.е. любая точка на прямой L1 удовлетворяет уравнению плоскости α. Следовательно прямая L1 лежит на плоскости α.
Ответ. Прямая L1 лежит на плоскости α.
Построение точки пересечения прямой и плоскости
Известно, что прямая пересекает плоскость, если она не принадлежит этой плоскости и не параллельна ей. Следуя приведенному ниже алгоритму, найдем точку пересечения прямой a с плоскостью общего положения α, заданной следами h0α, f0α.
Алгоритм
- Через прямую a проводим вспомогательную фронтально-проецирующую плоскость γ. На рисунке обозначены её следы h0γ, f0γ.
- Строим проекции прямой AB, по которой пересекаются плоскости α и γ. В данной задаче точка B’ = h0α ∩ h0γ, A” = f0α ∩ f0γ. Точки A’ и B” лежат на оси x, их положение определяется по линиям связи.
- Прямые a и AB пересекаются в искомой точке K. Её горизонтальная проекция K’ = a’ ∩ A’B’. Фронтальная проекция K” лежит на прямой a”.

Алгоритм решения останется тем же, если пл. α будет задана параллельными, скрещивающимися прямыми, отсеком фигуры или другими возможными способами.
Видимость прямой a относительно плоскости α. Метод конкурирующих точек

- Отметим на чертеже фронтально-конкурирующие точки A и С (рис. ниже). Будем считать, что точка A принадлежит пл. α, а С лежит на прямой a. Фронтальные проекции A” и С” совпадают, но при этом т. A и С удалены от плоскости проекций П2 на разное расстояние.
- Найдем горизонтальные проекции A’ и C’. Как видно на рисунке, точка C’ удалена от плоскости П2 на большее расстояние, чем т. A’, принадлежащая пл. α. Следовательно, участок прямой а”, расположенный левее точки K”, будет видимым. Участок a” правее K” является невидимым. Отмечаем его штриховой линией.
- Отметим на чертеже горизонтально-конкурирующие точки D и E. Будем считать, что точка D принадлежит пл. α, а E лежит на прямой a. Горизонтальные проекции D’ и E’ совпадают, но при этом т. D и E удалены от плоскости П1 на разное расстояние.
- Определим положение фронтальных проекций D” и E”. Как видно на рисунке, точка D”, находящаяся в пл. α, удалена от плоскости П1 на большее расстояние, чем т. E”, принадлежащая прямой a. Следовательно, участок а’, расположенный правее точки K’, будет невидимым. Отмечаем его штриховой линией. Участок a’ левее K’ является видимым.
Дополнительные материалы:
- Построение линии пересечения двух плоскостей
- Способы задания плоскости на чертеже
На
прошлой лекции мы рассмотрели случай
параллельности прямой и плоскости. Еоли
прямая не параллельна плоскости, она
будет с ней пересекаться. Возникает
одна из основных позиционных задач –
отыскание точки пересечения прямой с
плоскостью.
Как
же решть эту задачу?
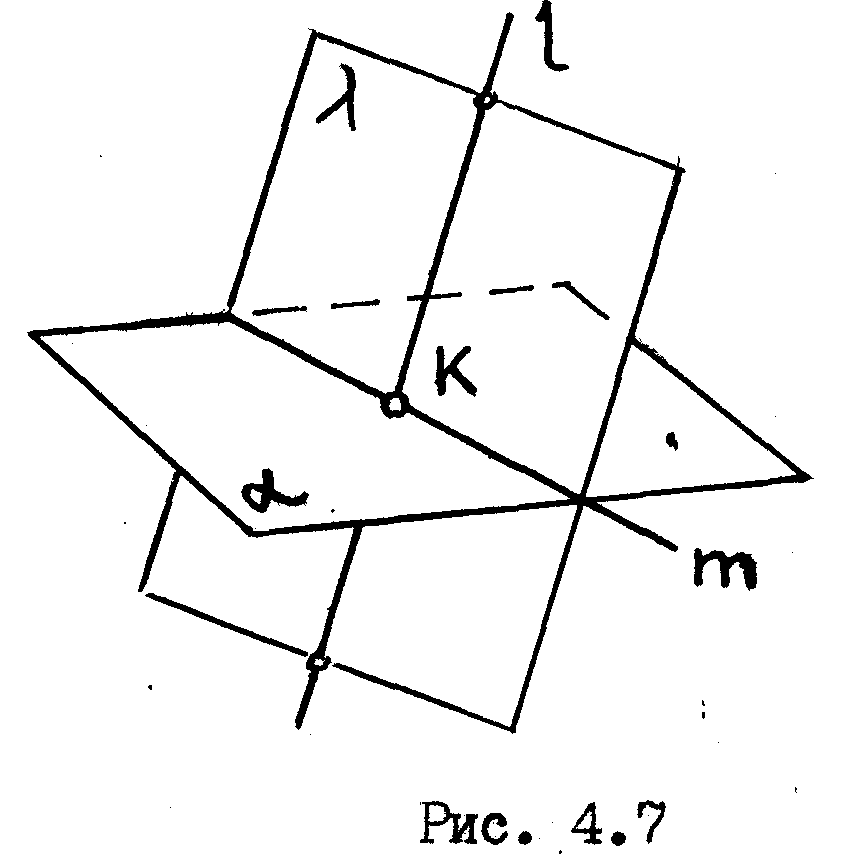
Для
того, чтобы отыскать точку пересечения
прямой L
с плоскостью
![]() .
.
необходимо
применить следующий порядок /алгоритм/
решения /
рис.4.7/.
1.
Заключить прямую 1
во вспомогательную секущую плоскость
![]() .
.
В качестве такой плоскости берется одна
из проецирующих плоскостей.
![]()
2.
Найти линию пересечения m
данной плоскости
![]()
и вспомогательной
![]() .
.
![]()
3.
Найти точку пересечения К
прямой
1
с данной плоскостью
![]() ,
,
как точку пересечения прямой l
с найденой линией пересечения двух
плоскостей m
.
![]()
4.
Выделить видимые и невидимые участки
прямой
1.
4.6
Рассмотрим
применение этого алгоритма к решению
конкретных задач.
4.2.1 Определение точки пересечения прямой с плоскостью /прямая и
плоскость
– общего положения/.
Задача
Построить
точку пересечения прямой l
с
плоскостью
![]() .Задачу
.Задачу
решим в двух вариантах./рис.4.8/.
а/
Плоскость
![]()
задана треугольником АВС.
б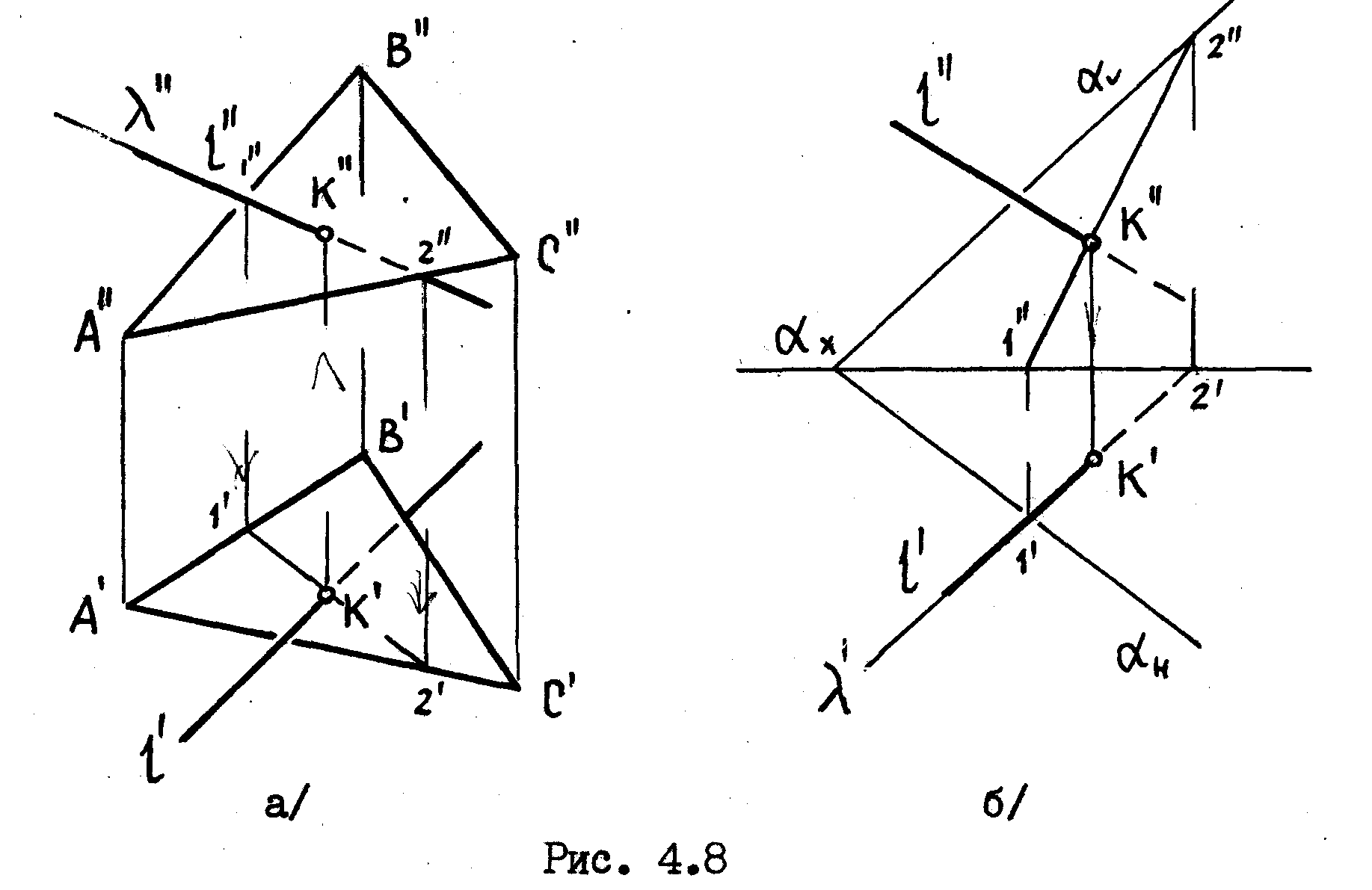
/
Плоскость
![]()
задана следами
![]() H
H
и
![]() v.
v.
Пояснить
на данном примере графическое выражение
алгоритма решения задачи.
Отметить,
что если в варианте, а/ в качестве
вспомогательной секущей плоскости
![]()
мы выбираем фронтально-проецирущую
плоскость,
то в варианте б/ – горизонтально-проецирующую.
Указать
на равнозначность этих плоскостей.
Далее
рассмотрим частные случаи этой задачи.
Частными будем считать те задачи, в
которых либо плоскость, либо прямая,
являются фигурами частного, или точнее
– проецирующего положения. Частное
расположение одной из фигур вносит
значительные упрощения в решение
поставленной задачи, которые необходимо
всегда учитывать.
4.7
4.2.2
Определение точки пересечеиия прямой
с плоскостью
/плоскость
– проецирующая, прямая – общего положения/.
В
задаче 4.9а заданная плоскость
![]()
– фронтально-проецирующая, в задаче 4.9
б плоскость, заданная треугольником
АВС,
является горизонтаиьно-проецирующей
плоскостью.
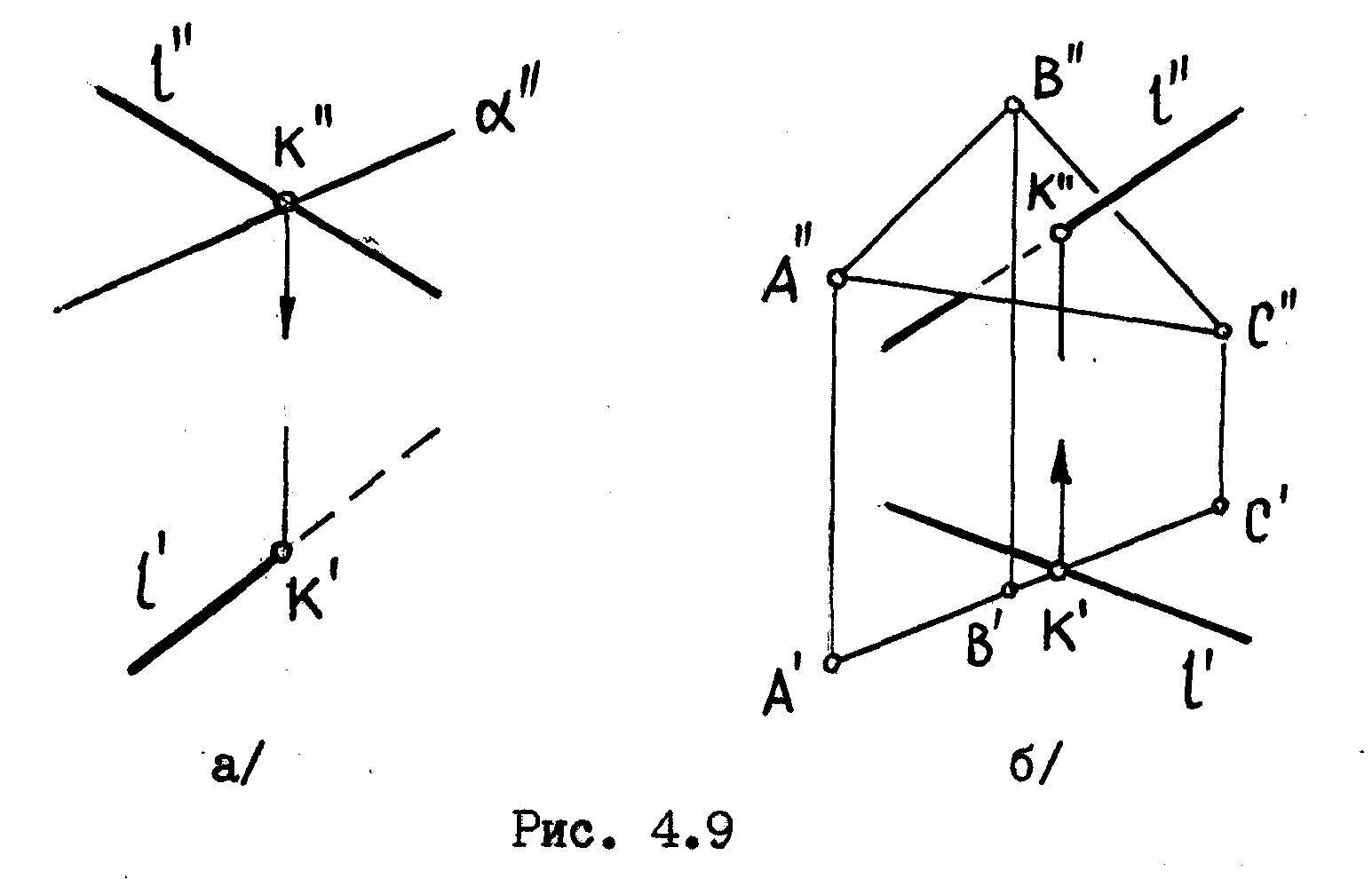
Упрощение
решения в данном случае состоит в том,
что одну проекцию точки пересечения
прямой с плоскостью мы
видим
на чертеже сразу, из условия ее
принадлежности проецирующей фигуре –
плоскости / это К”
на
рис.4.9а и К’
на рис.4.9б/.
Вторая
проекция точки определяется из условия
ее принадлежности фигуре общего положения
– прямой.
Далее,
считая плоскость непрозрачной, определяем
видимые и невидимые участки прямой.
4.2.3
Определение
точки пересечения прямой с плоскостью
/плоскость – общего положения, прямая –
проецирующая/.
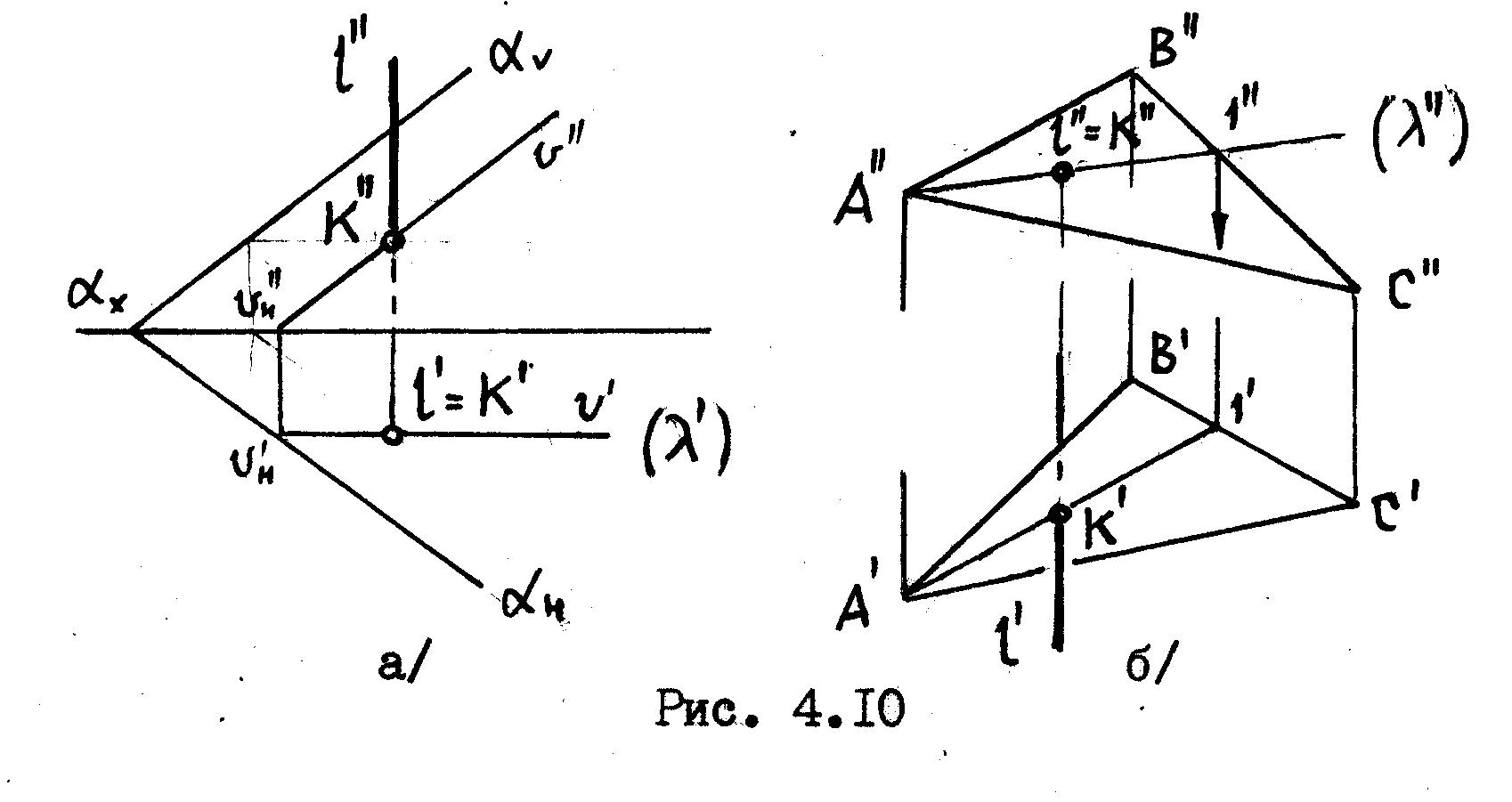
4.8
В
первом примере /рис.4.10а/ прямая l
является
горизонтально-проецирущей прямой, во
втором /рис.4.10б/ – фронтально-проецирующей
прямой.
Как
и в предыдущей задаче одну проекцию
точки пересечения прямой с плоскостью
видим сразу / К’
в зад.4.10а/ и К”
в зад. 4.10б//, т.е. из условия ее принадлежности
проецирующей фигуре – прямой.
Вторую
проекию точки находим из условия ее
принадлежности фигуре общего положения
– плоскости.
Если
угодно, то можно говорить о построении
второй проекции точки с помощью
вспомогательной секущей плоскости
![]() .
.
Но,
как видно из чертежа, оба решения будут
графически совпадать.
Окончанием
решения задачи, как и во всех предыдущих
случаях, будет выделение видимых и
невидимых участков прямой.
Содержание
лекции Р 4 изложено в учебнике С.А.Фролова
на стр. 118-
124
.
5.1
Р
А 3 Д Е Л № 2
Преобразование
комплексного чертежа
/ Лекции №
5,6 /
ЛЕКЦИЯ
№5
Тема
лекции.
Способы
преобразования комплексного чертежа.
Содержание
лекции.
Общие
понятия. Способ
перемены плоскостей проекций.
Способ плоскопараллельного перемещения.
5.1
Общие понятия.
Из
изложенного на предыдущих лекциях
материала легко установить, что проекции
прямой, плоскости или фигуры, находящейся
в случайном положении относительно
плоскостей проекций, не всегда удобны
для решения той или иной конкретной
задачи. Например, проекции отрезка,
расположенного наклонно ко всем
плоскостям проекций, не дают
непосредственного представления о
натуральной его длине. Можно сказать
поэтому, что в данном случае проекции
отрезка «неудобны» для решения
поставленного вопроса. Между тем, если
бы тот же отрезок был параллелен одной
из плоскостей проекций, он проецировался
бы на эту плоскость без искажения, и мы
могли бы судить о его действительной
длине без всяких дополнительных
построений. При таком положении отрезка
можно считать его поекции «удобными»
для решения
интересующего
нас вопроса.
Можно
привести много примеров подобного рода.
Студент,
изучивший предыдущие лекции, сумеет и
сам найти ряд других примеров,
подтверждащих, что при одном расположении
на эпюре заданных элементов задача
решается сложнее, а при другом – проще.
Способы
преобразования чертежа, которые нам
предстоит изучит,как раз и создают
возможность так изменить проекционный
чертеж, чтобы геометрическая фигура
/фигуры/ после преобразования заняла
такое частное положение, которое давало
бы решение поставленной задачи или
значительно его упрощало.
При
любом способе преобразования чертежа,
мы должны различать и уметь выполнять
следующие четыре основные задачи.
5.1
1.
Преобразование прямой общего положения
в прямую уровня.
2.
Преобразование прямой общего положения
в проецирующую прямую.
3.
Преобразование плоскости общего
положения в проецирующую плоскость.
4.
Преобразование плоскости общего
положения в пло-
скость
уровня.
Эти
четыре основные задачи на преобразование
чертежа будут в дальнейшем, при решении
метрических и позиционных задач, играть
исключительно важную роль.
Переход
от общего положения геометрической
фигуры к частному
можно осуществить за счет изменения
взаимного положения проецируемой фигуры
и плоскости проекций. При сохранении
ортогонального проецирования этого
можно достичь двумя принципиально
различными путями.
Во-первых,
введением
новых плоскостей проекций,
по отношению к которым проецируемая
фигура, не изменяющая при этом своего
положения в пространстве, окажется в
частном положении.
Во-вторых,
перемещением
в пространстве проецируемой фигуры
так, чтобы она заняла частное положение
относительно плоскостей проекций,
остающихся неподвижными и не меняющими
своего положения в пространстве.
Первый
путь лежит в основе способа перемены
плоскостей проекций, второй составляет
теоретическую базу способа
плоскопараллельного перемещения.
Рассмотрим эти способы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
1. Найти точку пересечения плоскости (x-2y+3z-8=0) с прямой, заданной общими уравнениями:
.
Решение сводится к решению системы трех уравнений с тремя неизвестными:

2. Найти точку пересечения плоскости (x+y+3z-1=0) с прямой, заданной каноническими уравнениями:
Можно было бы перейти от канонических уравнений к общему виду и свести задачу к рассмотренной в предыдущем примере. Но можно рассуждать и по-другому. Точка пересечения должна принадлежать и прямой, и плоскости, то есть можно подставить выражения для x,y и z из канонического уравнения в уравнение плоскости и определить их.
1) Перейдем к параметрическим уравнениям прямой:
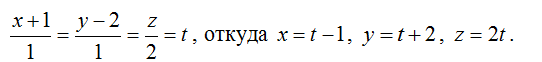
2) Подставим найденные выражения в уравнение плоскости:
((t-1)+(t+2)+3*2t-1=0), откуда t=0
3) Подставляем в выражения для x,y,z, находим ответ: x=-1, y=2, z=0.
Ответ: искомая точка M(-1;2;0).
Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
3.7. Пересечение прямой и плоскости
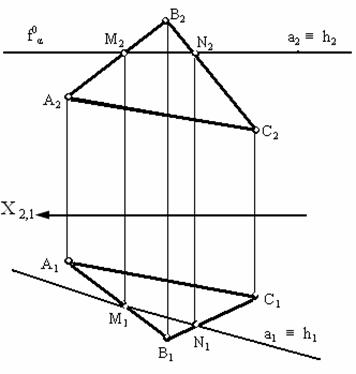
Линия пересечения двух плоскостей – прямая линия. Рассмотрим сначала частный случай (рис. 3.9), когда одна из пересекающихся плоскостей параллельна горизонтальной плоскости проекций (α ![]() π1, f0α
π1, f0α![]() Х). В этом случае линия пересечения а, принадлежащая плоскости α, будет также параллельна плоскости π1, (рис. 3.9. а), т. е. будет совпадать с горизонталью пересекающихся плоскостей (а ≡ h).
Х). В этом случае линия пересечения а, принадлежащая плоскости α, будет также параллельна плоскости π1, (рис. 3.9. а), т. е. будет совпадать с горизонталью пересекающихся плоскостей (а ≡ h).
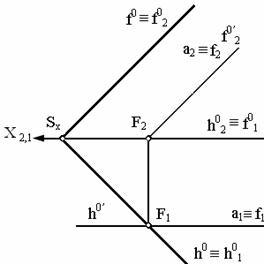
Если одна из плоскостей параллельна фронтальной плоскости проекций (рис. 3.9. б), то линия пересечения а, принадлежащая этой плоскости, будет параллельна плоскости π2 и будет совпадать с фронталью пересекающихся плоскостей (а ≡ f).
 .
.
а
 .
.
б
Рис. 3.9. Частный случай пересечения плоскости общего положения с плоскостями: а – горизонтального уровня; б – фронтального уровня
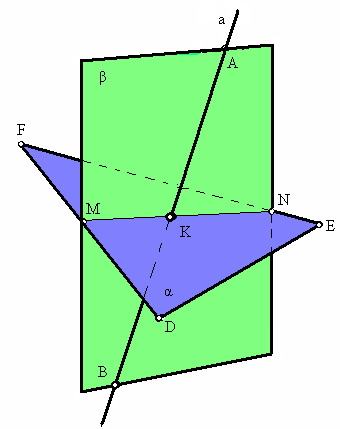
Пример построения точки пересечения (К) прямой а (АВ) с плоскостью α (DEF) показан на рис. 3.10. Для этого прямая а заключена в произвольную плоскость β и определена линия пересечения плоскостей α и β.
В рассматриваемом примере прямые АВ и MN принадлежат одной плоскости β и пересекаются в точке К, а так как прямая MN принадлежит заданной плоскости α (DEF), то точка К является и точкой пересечения прямой а (АВ) с плоскостью α. (рис. 3.11).
 .
.
Рис. 3.10. Построение точки пересечения прямой с плоскостью
Для решения подобной задачи на комплексном чертеже необходимо уметь находить точку пересечения прямой общего положения с плоскостью общего положения.
Рассмотрим пример нахождения точки пересечения прямой АВ c плоскостью треугольника DEF представленный на рис. 3.11.
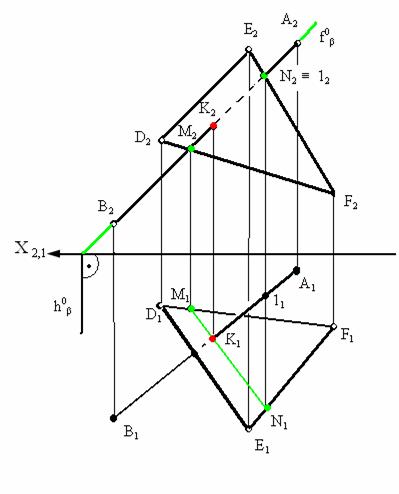
Для нахождения точки пересечения через фронтальную проекцию прямой А2В2 проведена фронтально-проецирующая плоскость β которая пересекла треугольник в точках M и N. На фронтальной плоскости проекций (π2) эти точки представлены проекциями M2, N2. Из условия принадлежности прямой плоскости на горизонтальной плоскости проекций (π1) находятся горизонтальные проекции полученных точек M1 N1. В пересечении горизонтальных проекций прямых А1В1 и M1N1 образуется горизонтальная проекция точки их пересечения (К1). По линии связи и условиям принадлежности на фронтальной плоскости проекций находится фронтальная проекция точки пересечения (К2).
 .
.
Рис. 3.11. Пример определения точки пересечения прямой и плоскости
Видимость отрезка АВ относительно треугольника DEF определена методом конкурирующих точек.
На плоскости π2 рассмотрены две точки N![]() EF и 1
EF и 1![]() АВ. По горизонтальным проекциям этих точек можно установить, что точка N расположена ближе к наблюдателю (YN>Y1 ), чем точка 1 (направление луча зрения параллельно S). Следовательно, прямая АВ, т. е. часть прямой АВ (К1) закрыта плоскостью DEF на плоскости π2 (ее проекция К212 показана штриховой линии). Аналогично установлена видимость на плоскости π1.
АВ. По горизонтальным проекциям этих точек можно установить, что точка N расположена ближе к наблюдателю (YN>Y1 ), чем точка 1 (направление луча зрения параллельно S). Следовательно, прямая АВ, т. е. часть прямой АВ (К1) закрыта плоскостью DEF на плоскости π2 (ее проекция К212 показана штриховой линии). Аналогично установлена видимость на плоскости π1.
Вопросы для самоконтроля
1) В чем заключается сущность метода конкурирующих точек?
2) Какие свойства прямой вы знаете?
3) Каков алгоритм определения точки пересечения прямой и плоскости?
4) Какие задачи называются позиционными?
5) Сформулируйте условия принадлежности прямой плоскости.
