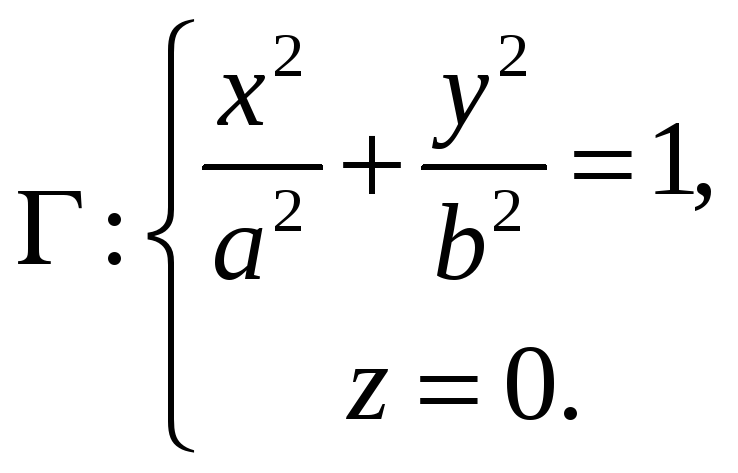Астро́ида (от греч. αστρον — звезда и ειδος — вид, то есть звездообразная)[1] — плоская кривая, описываемая точкой окружности радиуса 


История[править | править код]
Название кривой в форме «Astrois» предложил австрийский астроном Йозеф Иоганн фон Литров в 1838 г.[2][3][1]
Уравнения[править | править код]
Уравнение в декартовых прямоугольных координатах:
Параметрическое уравнение:[4]
Астроида также является алгебраической кривой 1 рода (и шестого порядка). Уравнение в алгебраическом виде:
Свойства[править | править код]
Вытянутая астроида как эволюта эллипса
- Имеются четыре каспа.
- Длина дуги от точки с 0 до
- Длина всей кривой
.
- Радиус кривизны:
- Площадь, ограниченная кривой:
- Объём тела вращения относительно любой координатной оси:
- Астроида является огибающей семейства отрезков постоянной длины, концы которых расположены на двух взаимно перпендикулярных прямых[1].
- Эволюта астроиды подобна ей, но вдвое больше неё и повёрнута относительно неё на 45°.
- Астроида (вытянутая вдоль оси) является эволютой эллипса[1]. В этом случае параметрическое выражение имеет вид:
-
- Неопределённый интеграл правой части последнего уравнения является интегралом от дифференциального бинома и равен
-
- Это выражение полезно при вычислении площадей элементов фигуры.
Примечания[править | править код]
- ↑ 1 2 3 4 Александрова, 2008, с. 17.
- ↑ J. J. v. Littrow. §99. Die Astrois // Kurze Anleitung zur gesammten Mathematik. — Wien, 1838. — P. 299.
- ↑ Loria, Gino. Spezielle algebraische und transscendente ebene kurven. Theorie und Geschichte. — Leipzig, 1902. — P. 224.
- ↑ Уравнение в прямоугольных координатах следует из параметрического уравнения и основного тригонометрического тождества. Вывод параметрического уравнения такой. Возьмём уравнение гипоциклоиды, подставим k=4. Синус/косинус тройного угла разложим по формуле синуса/косинуса суммы, то же для синуса/косинуса двойного угла. Учтём R=4r и получим наши уравнения.
Литература[править | править код]
- Савёлов А. А. Плоские кривые: Систематика, свойства, применения. М.: Физматгиз, 1960. 293 с. Переиздана в 2002 году, ISBN 5-93972-125-7.
- Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник. — 3-е изд., испр. — М.: ЛКИ, 2008. — 248 с. — ISBN 978-5-382-00839-4.
Линией (кривой) четвертого порядка
называют линию, определяемую алгебраическим уравнением четвертой степени относительно декартовых прямоугольных координат. Аналогично определяются линии (кривые) пятого, шестого и других порядков.
Множество линий (кривых) четвертого порядка содержат уже не десятки, а тысячи линий частного вида. Еще более разнообразными являются множества линий пятого и шестого порядка. Здесь рассматриваются отдельные виды линий четвертого и высших порядков, имеющие интересные свойства и практические применения.
Лемниската Бернулли
Обратимся к кривой, описываемой точкой М на плоскости так, что остается неизменным произведение р расстояний этой точки до двух определенных точек F 1 и F 2 той же плоскости. Такая кривая называется лемнискатой (лемниската по-гречески значит «ленточная»). Если длина отрезка F 1 F 2 есть с, то расстояния от середины О отрезка F 1 F 2 до F1 и F2 равны с/2 и произведение этих расстояний равно – с 2 /4. Потребуем сначала, чтобы величина р неизменного произведения равнялась как раз с 2 /4; тогда
линия порядок трансцендентный спираль
Рис. 8
точка О будет лежать на лемнискате, а сама лемниската будет иметь вид «лежащей восьмерки» (рис. 8). Если продолжить отрезок F 1 F 2 в обе стороны до пересечения с лемнискатой, то получим две точки А 1 и А 2 . Выразим расстояние между А 1 А 2 = х через известное расстояние с:
Фокусы лемнискаты – F1 (? c; 0) и F2 (c; 0). Возьмём произвольную точку M (x; y). Произведение расстояний от фокусов до точки M есть
И по определению оно равно c2:
Возводим в квадрат обе части равенства:
Раскрываем скобки в левой части:
Раскрываем скобки и свёртываем новый квадрат суммы:
Выносим общий множитель и переносим:
В данном случае a – радиус окружности, описывающей лемнискату. Проведя несложные преобразования, можно получить явное уравнение:
Возводим в квадрат и раскрываем скобки:
Приводим к виду
Это квадратное уравнение относительно y”. Решив его, получим
Взяв корень и отбросив вариант с отрицательным вторым слагаемым, получим:
где положительный вариант определяет верхнюю половину лемнискаты, отрицательный – нижнюю.
Если величину неизменного произведения р взять не равной с 2 /4, то лемниската изменит свой вид. И при р меньше с 2 /4, лемниската состоит из двух овалов, каждый из которых содержит точки F 1 и F 2 , соответственно (рис. 9).
Рис. 9
Т.о. задавая различные условия для р и с 2 /4 будем получать лемнискаты различного вида (рис. 10).
Рис. 10
Возьмем теперь на плоскости любое количеств точек. F 1 , F 2 ,…, F n и заставим точку М двигаться так, чтобы для нее оставалось неизменным произведение расстояний до каждой из взятых точек. Получим Кривую, форма которой будет зависеть от того, как расположены точки F 1 , F 2 ,…, F n друг относительно друга и какова величина неизменного произведения. Кривая эта называется лемнискатой с n фокусами.
Выше мы рассматривали лемнискаты с двумя фокусами. Беря разное число фокусов, располагая их по-разному и назначая ту или иную величину для произведения расстояний, можно получать лемнискаты самых причудливых очертаний. Будем вести острие карандаша из некоторой точки А, не отрывая от бумаги, так, чтобы оно в конце вернулось в исходную точку А. Тогда оно опишет некоторую кривую; мы потребуем только, чтобы эта кривая нигде не пересекала
Рис. 11
самое себя. Очевидно, что таким путем могут получиться кривые, имеющие, например, очертания человеческой головы или птицы (рис. 11). Оказывается, что, имея такую произвольную кривую, можно так подобрать число п и расположение фокусов
F 1 , F 2 ,…, F n
и назначить такую величину для неизменного произведения расстояний
МF 1 МF 2 … МF n = p
что соответствующая лемниската на глаз не будет отличаться от этой кривой. Иными словами, возможные отклонения точки М, описывающей лемнискату, от нарисованной кривой – не будут превосходить ширину карандашного штриха (карандаш можно заранее отточить как угодно хорошо так, что штрих будет очень узким). Этот замечательный факт, говорящий о необычайном разнообразии н богатстве форм лемнискат с многими фокусами, доказывается совершенно строго, нo очень сложно, при помощи высшей математики.
Улитка Паскаля
Геометрическое место точек М и M”, расположенных на прямых пучка (центр которого О лежит на окружности радиуса R) на расстоянии а по обе стороны от точки Р пересечения прямых с окружностью; т. о., PM = PM” = а. уравнение в прямоугольных координатах: (x2 + y2 – 2Rx)2 – а2(х2 + y2) = 0, в полярных координатах: r = 2R cos j + а. При а = 2R петля стягивается в точку, в этом случае улитка Паскаля превращается в кардиоиду. Название по имени французского учёного Б. Паскаля (1588-1651), впервые изучавшего её.
Циклоидальные кривые
Представим, что некоторая кривая катится без скольжения по другой кривой; какая либо точка, неизменно связанная с первой кривой, будет описывать при этом новую кривую. Так можно представить себе эллипс, катящийся по другому эллипсу, и исследовать линию, по которой будет перемещаться его центр, или определить траекторию фокуса параболы, катящейся по прямой, и т.д.
Среди кривых, образуемых указанным способом, выделяются кривые, являющиеся траекториями точки, неизменно связанной скругом, который катится без скольжения по другому кругу. Получаемые при этом линии называются циклоидальными.
При образовании циклоидальных кривых вычерчивающая точка отстоит от центра производящего (подвижного) круга на определенном расстоянии. В частном случае она находится на окружности производящего круга. При этом условии получаемые кривые подразделяются на эпициклоиды и гипоциклоиды в зависимости от того, располагается ли производящий круг с наружной или с внутренней стороны неподвижного круга.
К алгебраическим кривым относятся такие известные кривые, как кардиоида, астроида, рассмотрим эти кривые.
Кардиоида
1.
Уравнение
. Кардиоиду можно определить как траекторию точки, лежащей на окружности круга радиуса r, который катится по окружности неподвижного круга с таким же радиусом. Она будет представлять собой, таким образом, эпициклоиду с модулем m, равным 1.
Это обстоятельство позволяет сразу же записать параметрические уравнения кардиоиды, заменяя в ранее приведенных параметрических уравнениях эпициклоид модуль m единицей. Будем иметь:
Чтобы получить полярное уравнение кардиоиды, удобно принять за полюс точку А (рис. 13), а полярную ось направить по оси абсцисс. Так как четырехугольник AOO 1 M будет равнобедренной трапецией, то полярный угол точки М окажется равным углу поворота производящего круга, т.е. параметру t. Учитывая это обстоятельство, заменим во втором уравнении системы (1) у через sin t. Сокращая полученное таким образом равенство на sin t, получим полярное уравнение кардиоиды
Рис. 13
По виду этого уравнения
можно заключить, что кардиоида является одной из улиток Паскаля. Она может быть определена, следовательно, как конхоида круга.
Переводя уравнение (2) в прямоугольную систему координат, получим:
Из этого уравнения следует, что кардиоида является алгебраической кривой 4-го порядка.
2. Свойства. Прежде всего, поскольку кардиоида является эпициклоидой с m=1, на нее можно перенести все свойства рассмотренных нами в предыдущем параграфе эпициклоид.
Вот эти свойства и характеристики.
1. Касательная в произвольной точке кардиоиды проходит через точку окружности производящего круга, диаметрально противоположную точке касания кругов, а нормаль – через точку их касания.
2. Угол, составляемый касательной к кардиоиде с радиусом-вектором точки касания, равен половине угла, образуемого этим радиусом-вектором с полярной осью. Действительно
Из этого соотношения непосредственно вытекает, что угол, составляемый касательной к кардиоиде с осью абсцисс, равняется (как внешний угол треугольника AMN Рис. 14). Располагая формулой можно доказать, что касательные к кардиоиде, проведенные в концах хорды, проходящей через полюс, взаимно перпендикулярны.
Действительно, так как
Рис. 14
Заметим еще, что геометрическое место точек пересечения этих касательных есть окружность Действительно, уравнение первой касательной на основании уравнений (1) кардиоиды, будет иметь вид
а второй касательной Исключая из этих уравнений параметр, получим уравнение указанной окружности.
3. Радиус кривизны в произвольной точке кардиоиды определится по формуле
Можно показать также, что радиус кривизны равняется 2/3 полярной нормали N в заданной точке.
Действительно, откуда на основании (4) получаем Соотношение это может быть использовано для построения центра кривизны кардиоиды.
4. Эволюта кардиоиды, согласно общему свойству эволют эпициклоид, будет также кардиоидой, подобной данной, с коэффициентом подобия, равным 1/3, и повернутой относительно данной на угол 180°.
5. Длина дуги кардиоиды от точки А до произвольной точки М определится по формуле
Если длину дуги отсчитывать от точки А 1 , диаметрально противоположной точке А, то формула для определения длины дуги может быть записана в виде
6. Натуральное уравнение кардиоиды получится, если из равенств (4) и (6) исключить параметр. Оно будет иметь вид
7. Площадь, ограниченная кардиоидой, определится по формуле
и, как видно, равна ушестеренной площади производящего круга.
Длина всей кардиоиды определится по формуле
и, как видно, равна восьми диаметрам производящего круга. Объем тела, полученного от вращения кардиоиды вокруг ее оси, равен
Поверхность тела, полученного от вращения кардиоиды вокруг ее оси, равняется
Мы видели, что кардиоида органически связана с окружностью. Она является конхоидой круга и эпициклоидой. Она имеет с окружностью и иной характер родства – кардиоида является подэрой окружности относительно точки, принадлежащей этой окружности.
Рис. 15
Действительно, пусть ОМ есть перпендикуляр, опущенный на касательную к окружности с радиусом, равным 2r, проведенную в точке N.
Так как ОМ = OB + ВМ, или == 2r cos + 2r, то геометрическим местом точек М будет кардиоида с уравнением = 2r (1 + cos)
Заметим в заключение, что кардиоида относится также к семейству синусоидальных спиралей, и отдельные свойства ее повторяют общие свойства этих кривых. Из этих свойств следует, в частности, что инверсия кардиоиды, относительно точки возврата дает параболу.
Астроида
1. Свойства.
Астроида является частным случаем гипоциклоид, а именно, гипоциклоидой с модулем m, равным 1/4. Она представляет собой, следовательно, траекторию точки, лежащей на окружности круга радиуса r, который катится по внутренней стороне другого, неподвижного круга, радиус R которого в четыре раза больше.
Параметрические уравнения астроиды можно получить, полагая в уравнениях гипоциклоиды, m=1/4. Вот эти уравнения:
Рис. 16
где t, как и ранее, угол поворота производящего круга (рис. 16)
Исключая из уравнений (1) параметр t, получим:
Из уравнения (2) следует, что астроида является алгебраической кривой 6-го порядка.
Параметрические уравнения (1) астроиды можно привести к виду
Исключая из этих уравнений параметр t, получим часто употребляемый вид уравнения астроиды
Полагая в ранее выведенных общих соотношениях для циклоидальных кривых модуль
m = -1/4, получим соответствующие соотношения для астроиды:
1) радиус кривизны в произвольной точке астроиды определяется по формуле
2) длина дуги астроиды от точки А до произвольной точки M(t) определится по формуле
длина одной ветви равна а длина всей кривой 6R;
3) для получения натурального уравнения астроиды заметим предварительно, что если началом отсчета длины дуги полагать не точку А, для которой t = 0, а точку, для которой t = , то длина дуги определится формулой
исключая параметр t из уравнений (5) и (6), получим натуральное уравнение астроиды
4) эволюта астроиды есть также астроида, подобная данной, с коэффициентом подобия, равным 2, повернутая относительно данной на угол /4 (рис. 16)
5) площадь, ограниченная всей астроидой, равна объем тела, полученного от вращения астроиды, равняется 32/105 R 3
поверхность тела, образованного вращением астроиды, равна
Обратимся теперь к рассмотрению некоторых частных свойств астроиды.
Астроида является огибающей отрезка постоянной длины, концы. которого скользят по двум взаимно перпендикулярным прямым.
Принимаем эти прямые за оси координат и, обозначая угол наклона скользящего отрезка ND=R через (рис. 4), будем иметь уравнение прямой ND в виде
Дифференцируя это уравнение по параметру, получим:
Исключая из последнего уравнения и уравнения (7) параметр, будем иметь уравнение огибающей в виде т.е. астроиду.
Практически перемещение отрезка ND можно осуществить с помощью так называемых кардановых кругов. Один из этих кругов с радиусом R неподвижен, а другой, с радиусом r, в два раза меньшим, катится по внутренней стороне неподвижного круга. Любые две диаметрально противоположные точки N и D катящегося круга будут перемещаться по двум взаимно перпендикулярным диаметрам Ох и Оу неподвижного круга. Ясно, что огибающей диаметра катящегося круга и будет астроида.

Рис. 17 |

Рис. 18 |
Рассмотренный способ образования астроиды можно истолковать также следующим образом. Прямоугольник ODCN, две стороны которого лежат на двух взаимно перпендикулярных прямых, деформируется так, что диагональ его сохраняет длину, равную R, огибающая диагонали и будет астроидой. Так как при этом перпендикуляр, опущенный из вершины С на диагональ DN, служит нормалью к огибающей, то астроида представляет собой геометрическое место оснований перпендикуляров, опущенных из вершины С прямоугольника на его диагональ.
При эти уравнения выражают рассмотренную ранее прямую астроиду.
КУРСОВАЯ РАБОТА
на тему:
«Практическое
применение свойств замечательных кривых»
Введение
Актуальность темы
заключается в
демонстрации применения математических знаний в практической деятельности
человека. В курсе изучения аналитической геометрии не предусмотрено
рассматривание свойств замечательных кривых, которые широко используются в
жизни.
Гипотеза
:
Использование данного материала расширяет
кругозор учащихся по кривым и их свойствам, и показывает их практическое
применение в жизни человека.
Цель данной работы
:
Собрать материал для
применения его во время самостоятельного изучения замечательных кривых.
Задачи
:
В помощь учащемуся. Используя минимум времени,
принести максимум пользы.
Практическая значимость работы:
Я считаю, что моя работа
пригодится студентам доступно и наглядно разобраться в материале. Покажет
практическое применение свойств замечательных кривых, научить строить кривые.
Выбор темы
При современном уровне развития технической мысли имеется
необходимость в знаниях о замечательных кривых. Они не так уж редки в природе,
имеют практическое приложение в жизни человека. Знание их замечательных свойств
используется в различных механизмах, используемых человеком в жизни.
Я выбрала эту тему, так как считаю её, интересной и
содержательной, развивающей познавательный интерес к аналитической геометрии,
открывающей практическое приложение геометрии в жизни. Использование данного
материала на лекциях геометрии расширяет кругозор учащихся по кривым, изучаемым
по программе. В разных разделах математики и на разных этапах изучения мы
встречаемся с кривыми, как третьего, так и второго порядка. Но, нигде не
говорится о замечательных свойствах данных кривых, а тем более об их
практическом применении. Я считаю, что очень важно учащимся знать замечательные
свойства данных кривых, которые широко применяются в жизни. Изучая и даже
просто знакомясь с этими свойствами, учащиеся видят действительно практическое
применение геометрии.
Для этого я познакомилась с материалом о замечательных кривых
и их свойствах в различных пособиях и энциклопедиях по математике.
1. Из истории развития учения о линиях
Понятие линии возникло в сознании человека в доисторические
времена. Траектория брошенного камня, очертания цветов и листьев растений,
извилистая линия берега реки и другие явления природы с давних пор привлекали
внимания людей. Наблюдаемые многократно, они послужили основой для постепенного
установления понятия о линии. Но потребовался значительный промежуток времени
для того, чтобы наши предки стали сравнивать между собой формы кривых линий.
Первые рисунки на стенах пещер, примитивные орнаменты на домашней утвари
показывают, что люди умели не только отличать прямую от кривой, но и различать
отдельные кривые. Памятники глубокой древности свидетельствуют о том, что у
всех народов на некоторой степени их развития имелись понятия прямой и их
окружности. Для построения этих линий использовались простейшие инструменты.
Однако лишь с возникновением математических теорий стало
развиваться учение о линиях. Греческие ученые создали теорию линий второго
порядка. Эти линии рассматривались как сечение конуса плоскостью, вследствие
чего в древности их называли коническими сечениями. Конические сечения впервые
рассматривал Менехм, который жил в IV веке до н.э..Первое систематическое изложение
теории этих линий дал Аполлоний Пергский (III-II вв до н.э.) у своем
сочинении «Конические сечения», которое почти целиком дошло до нас. В поисках
решения различных задач греческие ученые рассматривали и некоторые
трансцендентные линии.
В средневековую эпоху важное достижение греческих ученых были
забыты. Математическая наука снова обратилась к изучению кривых только в VII веке. Для исследования
линий первостепенное значение имело открытее Декартом и Ферма метода координат
способствовавшего возникновению исчисления бесконечно малых. Метод координат в
соединении с анализом бесконечно малых позволил перейти к исследованию линий
общим способом. Разнообразные проблемы механики, астрономии, геодэзии, оптики,
возникши в VII-VIII века, привели к открытию многих новых линий и изучению их
геометрических механических свойств. Этими вопросами с большим энтузиазмом
занимались крупнейшие математики эпохи – Декарт, Гюйгенс, Лейбниц, братья
Бернулли.
Следующий важный шаг в изучении линий был сделан Ньютоном,
который начал разработку теории кривых третьего порядка. Впоследствии были
поставлены задачи: исследовать кривые четвертого и высших порядков, создать
общую теорию алгебраических кривых на плоскости, приступить к систематическому
изучению алгебраических поверхностей, начиная с поверхности второго порядка. В
решении последней задачи большой вклад внес знаменитый математик VIII Леонард Эйлер, академик
Петербургской академии наук. Он описал первое пособие по аналитической
геометрии, в котором излагалось теория линий и поверхностей второго порядка.
. Замечательные линии третьего порядка
Все прямые и кривые второго порядка (окружности, эллипсы,
параболы, гиперболы) являются частными случаями кривых третьего порядка.
В общем случае уравнение кривой линии третьего порядка можно
записать так: х 3 +а 1 у 3 +3а 2 х 2 у+3а 3 ху 2 +3а 4 х 2 +3а 5 у 2 +3а 6 ху+3а 7 х+3а 8 у+а 9 =0.
Предполагается, что коэффициенты одновременно в нуль не
обращаются (в противном случае получилось бы уравнение второй степени) Если все
не распадающиеся линии второго порядка исчерпываются окружностью, эллипсом,
гиперболой, параболой, то множество линий третьего порядка является более
богатым – оно содержит. Свыше 70 видов этих линий. Здесь рассматриваются только
некоторые из них, замечательные по своим свойствам и применениям.
Декартов лист
. Особенности формы.
Декартовым листом
называется кривая 3-го порядка, уравнение которой в прямоугольной системе имеет
вид
Иногда удобно пользоваться параметрическими уравнениями
декартова листа, которые можно получить, полагая y
=
tx
,
присоединяя к этому
равенству равенство (1) и решая полученную систему относительно х
и у,
в результате будем иметь:
|
|
откуда следует, что декартов лист является рациональной
кривой.
Заметим еще, что полярное уравнение декартова листа имеет вид
(3)
Координаты х
и у
входят в уравнение декартова
листа симметрично, откуда следует, что кривая симметрична относительно
биссектрисы у=х.
Обычное исследование на особые точки приводит к
заключению, что начало координат является узловой точкой декартова листа.
Уравнения касательных к алгебраической кривой в ее особой точке, совпадающей с
началом координат, можно получить, как известно, приравнивая нулю группу членов
низшей степени из уравнения этой кривой. В нашем случае имеем З аху = 0,
откуда
получим х = 0 и у = 0 – искомые уравнения касательных в узловой точке. Эти
касательные совпадают с координатными осями и, следовательно, в начале координат
кривая пересекает сама себя под прямым углом. Легко видеть, что в первом
координатном угле кривая делает петлю, которая пересекается с прямой у = х
в точке
Точки этой петли, в которых касательные параллельны координатным
осям, имеют координаты
И (cм. рис. 1)
Для окончательного заключения о форме кривой следует еще
найти асимптоту Заменяя в уравнении кривой у на приравняем нулю в
полученном уравнении коэффициенты двух членов с высшими степенями х.
Получим
и b = – а.
Таким образом, декартов лист имеет асимптоту
у = – х – а;
следовательно, во 2-м и 4-м координатных
углах ветви декартова листа уходят в бесконечность.
Рис. 1
Часто рассматривают повёрнутую на 135 градусов кривую. Её
уравнения выглядят так. В прямоугольной системе: , где
Параметрическое:
Вывод уравнений повёрнутой кривой:
Систему координат XOY преобразуют в систему координат UOV,
которая получается поворотом осей OX и OY по часовой стрелке на угол и переориентацией оси OX
в противоположном направлении:
Выражение старых координат XY через новые UV выглядит так:
После подстановки выражений старых координат через новые
уравнение декартова листа преобразуется к следующему виду: 
Вводим параметр , последнее уравнение
перепишется так:
Или 
Заменяем переменные u и v на привычные x и y и получаем
уравнение декартового листа в новой системе координат:
Подставив в уравнение предыдущее получаем уравнение
декартова листа в полярной системе координат:
Решая данное выражение относительно ρ, получаем:

2. Свойства.
Согласно теореме Маклорена, если в трех
точках алгебраической кривой 3-го порядка, лежащих на одной прямой, провести
касательные к этой кривой, то точки их пересечения с кривой будут лежать также
на прямой линии. Применительно к декартову листу эта теорема доказывается просто.
Выведем с этой целью предварительно условие пребывания трех точек декартова
листа, соответствующих значениям t
1
, t
2
и t
3
параметра, на одной
прямой. Если уравнение прямой имеет вид y
=
kx
+
b
,
то значения параметра,
соответствующие точкам пересечения этой прямой с кривой, должны удовлетворять
системе
Система эта приводит к уравнению
корни которого и будут искомыми значениями t
1
, t
2
и t
3
параметра, откуда
следует, что
Это равенство и является условием пребывания трех точек M
1
(t
1)
, M
2
(t
2
),
М 3 (t 3) декартова листа на
одной прямой.
Располагая этим условием, покажем справедливость теоремы
Маклорена для декартово листа. Действительно, касательную в точке M
1
(t
1
)
можно рассматривать как
прямую, которая пересекает декартов лист в двух совпадающих между собой точках,
для которых t
2
=
t
1
,
и в третьей точке, для
которой соответствующее значение параметра обозначим через T 1 . Условие (4) примет вид t
1
2
T
1
= –
1. Для касательных в
точках М 2
и M
3
получим аналогичные соотношения t 2 2 T 2 = -1 и t 3
2
T
3
= -1
. Перемножая эти три равенства,
будем иметь
(t
1
t
2
t
3
) 2
T
1
T
2
T
3
= -1
. откуда на основании (4)
заключаем, что и T
1
T
2
T
3
= -1,
т.е. точки N
1
(T
1
),
N 2 (T 2) и N 3 (T 3) лежат на одной прямой.
Определяя площадь, ограниченную петлей декартова листа,
получим:
. Способ построения.
Заметим предварительно,
что если ось симметрии декартова листа принять за ось абсцисс, то уравнение его
примет вид

Пусть теперь имеется окружность с радиусом r и центром в точке
и прямая х= –
h
.
Возьмем произвольную
точку Q этой окружности и проведем прямую QA
и прямую QN
,
перпендикулярную к оси
абсцисс (рис. 2). Из точки пересечения R
прямой QA
с прямой х= – h
проводим прямую RO
до пересечения ее в точке Q
1
с прямой QN.
Таким образом, точке Q
на окружности будет поставлена в соответствие
точка Q 1 .
Геометрическое место точек Q 1 представляет собой
декартов лист.
Для доказательства заметим, что координаты точки Q
можно записать в виде
угол, составляемый радиусом круга, проведенным в точку Q,
с положительным направлением оси абсцисс. В соответствии с этим уравнение
прямой QA
может быть записано в виде
Полагая в этом уравнении х= –
h
,
находим ординату
точки R
.
Отсюда следует, что уравнение прямой RQ
1
запишется в виде
(6)
В то же время уравнение прямой Q
1
N
имеет вид
(7)
Исключая из уравнений (6) и (7) параметр w
,
находим уравнение
геометрического места точек Q 1 в виде
Сопоставляя его с уравнением (5), заключаем, что найденное
геометрическое место точек является декартовым листом.
Преобразование точек окружности в точки декартова листа,
осуществляемое при таком его построении, называется преобразованием
Маклорена
.
4. Историческая справка.
Впервые в истории
математики кривая, названная впоследствии декартовым листом, определяется в
письме Декарта к Ферма в 1638 г. как кривая, для которой сумма объемов кубов,
построенных на абсциссе и ординате каждой точки, равняется объему
параллелепипеда, построенного на абсциссе, ординате и некоторой константе.
Форма кривой устанавливается впервые Робервалем, который находит узловую точку
кривой, однако в его представлении кривая состоит лишь из петли. Повторяя эту
петлю в четырех квадрантах, он получает фигуру, напоминающую ему цветок с
четырьмя лепестками. Поэтическое название кривой «лепесток жасмина», однако, не
привилось. Полная форма кривой с наличием асимптоты была определена позднее
(1692) Гюйгенсом и И. Бернулли. Название «декартов лист» прочно установилось
только с начала 18 века.
Циссоида
Диоклеса
1. Особенности формы.
Среди многих способов
образования циссоиды
–
кривой, открытой древними в поисках
решения знаменитой задачи об удвоении куба, мы остановимся сначала на
простейшем. Возьмем окружность (называемую производящей)
с диаметром
ОА=2а и касательную АВ
к ней. Через точку О проведем луч ОВ и на нем
отложим отрезок ОМ=ВС.
Построенная таким образом точка М принадлежит
циссоиде. Повернув луч 0В
на некоторый угол и проделав указанное
построение, мы найдем вторую точку циссоиды, и т.д. (Рис. 3).
Если точку О принять за полюс, то но откуда получаем полярное
уравнение циссоиды
Пользуясь формулами перехода от полярных координат к
декартовым, найдем уравнение циссоиды в прямоугольной системе:
(2)
Параметрические уравнения циссоиды можно получить, полагая
x=ty, тогда, на основании уравнения (2), придем к системе
Рис. 3
Уравнение (2) показывает, что циссоида является
алгебраической кривой 3-го порядка, а из уравнений (3) следует, что она
является рациональной кривой.
Циссоида симметрична относительно оси абсцисс, имеет
бесконечные ветви; касательная к производящей окружности, т.е. прямая х =
2а, служит для нее асимптотой; начало координат является точкой возврата 1-го
рода.
2. Свойства.
Кинематически циссоида может быть
получена как траектория середины М
катета ВС
треугольника АВС,
передвигающегося в плоскости чертежа так, что его вершина В
скользит по
оси ординат, а другой катет АС
всегда проходит через неподвижную точку Е
на оси абсцисс. (Рис. 4)
Действительно, обозначив середину отрезка ОЕ
через D
,
замечаем, что поскольку ВС=ЕО,
ê
ВСЕ=
ê
ВЕО,
откуда /_ ВЕО = /_
СВЕ,
и, следовательно, ê
NBE
–
равнобедренный, а так
как Е
D
=ЕО/2=ВС/2=ВМ,
то отрезок DM
параллелен отрезку BE
.
Пусть, далее, точка К
есть точка пересечения с продолжением отрезка DM
прямой, проходящей через
точку В
параллельно оси абсцисс. Опишем окружность с центром в начале
координат и радиусом, равным OD,
и проведем к ней касательную во второй точке
пересечения с прямой ЕО.
Она пройдет, очевидно, через точку К.
Обозначив точку пересечения прямой DMK
с окружностью через F
,
заметим, что
треугольники DOF
и МВК
равны между собой. Из равенства их следует, что DF
=
MK
,
а значит, и DM
=
FK
.
Последнее равенство и
показывает, что геометрическое место точек М
будет циссоидой.
Другие способы образования циссоиды основаны на ее
соотношениях с параболой. Покажем в первую очередь, что циссоида является
подэрой параболы относительно ее вершины.
Уравнение данной параболы. Уравнение
касательной в произвольной точке М
(x, h)
этой параболы можно
записать в виде уравнение перпендикуляра, опущенного из начала
координат на эту касательную, будет координаты точки N
пересечения его с касательной определятся по формулам

Исключая из этих равенств параметр h, мы получим уравнение
Выражающее циссоиду.
Заметим далее, что координаты точки, симметричной началу
координат относительно касательной к параболе у 2
= 2 рх,
получатся, если правые части формул (4) удвоить, и, следовательно, определятся
формулами
Исключая из этих равенств параметр h, мы снова получим
циссоиду с уравнением Отсюда следует, что циссоида является
геометрическим местом точек, симметричных вершине параболы относительно ее
касательных.
Следует заметить, что геометрическое место точек,
симметричных началу координат относительно касательной к параболе, можно
рассматривать как траекторию вершины другой параболы, одинаковой с данной,
которая катится по данной параболе. Таким образом, возникает новый способ
кинематического образования циссоиды как траектории вершины параболы,
которая без скольжения катится по другой такой же параболе.
Строфоида
Строфоида
(от греч. stróphos – кручёная лента и éidos
– вид)
Пусть имеется неподвижная прямая АВ и точка С вне её на
расстоянии CO = а
; вокруг С вращается прямая, пересекающая АВ в
переменной точке N. Если от точки N отложить по обе стороны прямой АВ отрезки
NM = NM” = NO, то геометрическое место точек М и М” для всех положений
вращающегося луча CN и есть строфоида. Уравнение в прямоугольных координатах: ; в полярных координатах:
r = – a cos 2j/cosj. Впервые строфоиду исследовал Э. Торричелли (1645),
название было введено в середине 19 в. Рис. 6
Верзьера (верзиера) Аньези (
иногда ло́кон Анье́зи) – плоская кривая,
геометрическое место точек M, для которых выполняется соотношение , где OA – диаметр
окружности, BC – полухорда этой окружности, перпендикулярная OA. Своё название
верзьера Аньези получила в честь итальянского математика Марии Гаэтаны Аньези,
исследовавшей эту кривую.
Уравнения
O = (0,0), A = (0, a)
В прямоугольной системе координат:
Координаты точки M, лежащей на верзьере – это x = BM, y = OB.
OA = a и по определению строим пропорцию
Отсюда
С другой стороны BC может быть найден из уравнения
окружности:
Нам известен y = OB, значит выражаем :
Приравниваем оба выражения для BC:
Возводим в квадрат, переносим и выносим за скобки:
Выражаем y (y=0 не подходит по определению):

Свойства:
1. Верзьера – кривая третьего порядка.
Диаметр OA единственная ось симметрии кривой.
Кривая имеет один максимум – A (0; a) и две точки перегиба –
В окрестности вершины A верзьера приближается к окружности
диаметра OA. В точке A происходит касание, и кривая совпадает с окружностью.
Это показывает величина радиуса кривизны в точке A: .
Площадь под графиком S = πa2. Она вычисляется интегрированием уравнения
по всему .
Объём тела вращения верзьеры вокруг своей асимптоты (оси OX) .
Ань
é
зи Мария Гаэтана
(Agnesi Maria Gaetana),
род. 16.05.1718, Милан – ум. 09.01.1799, там же. Итальянский математик,
профессор университета в Болонье (с 1750). Сочинение Аньези «Основания анализа
для употребления итальянского юношества» («Instituzioni
analitiche ad uso della gioventú italiana», v. 1-2, Mil., 1748) содержит изложение
аналитической геометрии, в частности там рассмотрена кривая третьего порядка,
названная «локоном Аньези» (или верзиера), уравнение которой y=a 3 /
(x 2 +a 2).
Для того чтобы построить эту линию, надо нарисовать
окружность радиусом a с центром в точке (0, a). Затем из начала координат
проводят прямые и отмечают две точки. Точка А (x1, y1) – точка пересечения
прямой и окружности, точка B (x2,2a) точка пересечения прямой и верхней
горизонтальной касательной к окружности. Затем строится точка кривой (x2, y1).
Английский математик Джон Колсон взял на себя труд переводить
«Начала анализа» с итальянского. Однако для него, европейца XVIII века, было
нелегко воспринять, что автор книги – женщина, и что для нее, для автора,
кривая может ассоциироваться с прической. В результате в англоязычной
литературе кривая получила название – witch of Agnesi. – что-то из области
полетов на лысую гору…
3. Замечательные линии четвертого и высших
порядков
Линией (кривой) четвертого порядка
называют линию,
определяемую алгебраическим уравнением четвертой степени относительно
декартовых прямоугольных координат. Аналогично определяются линии (кривые)
пятого, шестого и других порядков.
Множество линий (кривых) четвертого порядка содержат уже не
десятки, а тысячи линий частного вида. Еще более разнообразными являются
множества линий пятого и шестого порядка. Здесь рассматриваются отдельные виды
линий четвертого и высших порядков, имеющие интересные свойства и практические
применения.
Лемниската
Бернулли
Обратимся к кривой, описываемой точкой М на плоскости так,
что остается неизменным произведение р расстояний этой точки до двух
определенных точек F 1 и F 2 той же плоскости. Такая кривая называется лемнискатой (лемниската
по-гречески значит «ленточная»). Если длина отрезка F 1 F 2 есть с, то расстояния от
середины О отрезка F 1 F 2 до F1 и F2 равны с/2 и произведение этих расстояний равно – с 2 /4.
Потребуем сначала, чтобы величина р неизменного произведения равнялась как раз
с 2 /4; тогда
точка О будет лежать на лемнискате, а сама лемниската будет
иметь вид «лежащей восьмерки» (рис. 8). Если продолжить отрезок F 1 F 2 в обе стороны до
пересечения с лемнискатой, то получим две точки А 1 и А 2 .
Выразим расстояние между А 1 А 2 = х через известное
расстояние с:
Фокусы лемнискаты – F1 (− c; 0) и F2 (c; 0). Возьмём
произвольную точку M (x; y). Произведение расстояний от фокусов до точки M есть
И по определению оно равно c2:
Возводим в квадрат обе части равенства:
Раскрываем скобки в левой части:
Раскрываем скобки и свёртываем новый квадрат суммы:
Выносим общий множитель и переносим:
В данном случае a – радиус окружности, описывающей
лемнискату. Проведя несложные преобразования, можно получить явное уравнение:
Возводим в квадрат и раскрываем скобки:
Приводим к виду
Это квадратное уравнение относительно y”. Решив его, получим
Взяв корень и отбросив вариант с отрицательным вторым
слагаемым, получим:
где положительный вариант определяет верхнюю половину
лемнискаты, отрицательный – нижнюю.
Если величину неизменного произведения р взять не равной с 2 /4,
то лемниската изменит свой вид. И при р меньше с 2 /4, лемниската
состоит из двух овалов, каждый из которых содержит точки F 1 и F 2 , соответственно (рис.
9).
Т.о. задавая различные условия для р и с 2 /4 будем
получать лемнискаты различного вида (рис. 10).
Рис. 10
Возьмем теперь на плоскости любое количеств точек. F 1 , F 2 ,…, F n и заставим точку М
двигаться так, чтобы для нее оставалось неизменным произведение расстояний до
каждой из взятых точек. Получим Кривую, форма которой будет зависеть от того,
как расположены точки F 1 , F 2 ,…, F n друг относительно друга
и какова величина неизменного произведения. Кривая эта называется лемнискатой с
n фокусами.
Выше мы рассматривали лемнискаты с двумя фокусами. Беря
разное число фокусов, располагая их по-разному и назначая ту или иную величину
для произведения расстояний, можно получать лемнискаты самых причудливых
очертаний. Будем вести острие карандаша из некоторой точки А, не отрывая от
бумаги, так, чтобы оно в конце вернулось в исходную точку А. Тогда оно опишет
некоторую кривую; мы потребуем только, чтобы эта кривая нигде не пересекала
самое себя. Очевидно, что таким путем могут получиться
кривые, имеющие, например, очертания человеческой головы или птицы (рис. 11).
Оказывается, что, имея такую произвольную кривую, можно так подобрать число п и
расположение фокусов
F 1 , F 2 ,…, F n
и назначить такую величину для неизменного произведения
расстояний
МF 1 МF 2 … МF n = p
что соответствующая лемниската на глаз не будет отличаться от
этой кривой. Иными словами, возможные отклонения точки М, описывающей
лемнискату, от нарисованной кривой – не будут превосходить ширину карандашного
штриха (карандаш можно заранее отточить как угодно хорошо так, что штрих будет
очень узким). Этот замечательный факт, говорящий о необычайном разнообразии н
богатстве форм лемнискат с многими фокусами, доказывается совершенно строго, нo очень сложно, при помощи
высшей математики.
Улитка Паскаля
Геометрическое место точек М и M”, расположенных на прямых
пучка (центр которого О лежит на окружности радиуса R) на расстоянии а по обе
стороны от точки Р пересечения прямых с окружностью; т. о., PM = PM” = а
.
уравнение в прямоугольных координатах: (x 2 + y 2 – 2Rx
) 2
– а 2
(х 2 + y 2
) = 0, в полярных
координатах: r = 2R
cos j + а
. При а =
2R
петля
стягивается в точку, в этом случае улитка Паскаля превращается в кардиоиду.
Название по имени французского учёного Б. Паскаля (1588-1651), впервые
изучавшего её.
Циклоидальные кривые
Представим, что некоторая кривая катится без скольжения по
другой кривой; какая либо точка, неизменно связанная с первой кривой, будет
описывать при этом новую кривую. Так можно представить себе эллипс, катящийся
по другому эллипсу, и исследовать линию, по которой будет перемещаться его
центр, или определить траекторию фокуса параболы, катящейся по прямой, и т.д.
Среди кривых, образуемых указанным способом, выделяются
кривые, являющиеся траекториями точки, неизменно связанной скругом, который
катится без скольжения по другому кругу. Получаемые при этом линии называются циклоидальными.
При образовании циклоидальных кривых вычерчивающая точка
отстоит от центра производящего (подвижного) круга на определенном расстоянии.
В частном случае она находится на окружности производящего круга. При этом
условии получаемые кривые подразделяются на эпициклоиды и гипоциклоиды в
зависимости от того, располагается ли производящий круг с наружной или с
внутренней стороны неподвижного круга.
К алгебраическим кривым относятся такие известные кривые, как
кардиоида, астроида, рассмотрим эти кривые.
Кардиоида
1.
Уравнение
. Кардиоиду можно определить как
траекторию точки, лежащей на окружности круга радиуса r, который катится по
окружности неподвижного круга с таким же радиусом. Она будет представлять
собой, таким образом, эпициклоиду с модулем m, равным 1.
Это обстоятельство позволяет сразу же записать
параметрические уравнения кардиоиды, заменяя в ранее приведенных
параметрических уравнениях эпициклоид модуль m единицей. Будем иметь:
(1)
Чтобы получить полярное уравнение кардиоиды, удобно принять
за полюс точку А (рис. 13), а полярную ось направить по оси абсцисс. Так как
четырехугольник AOO 1 M будет равнобедренной трапецией, то полярный
угол j
точки М окажется равным углу поворота производящего круга, т.е. параметру t.
Учитывая это обстоятельство, заменим во втором уравнении системы (1) у через r sin t. Сокращая
полученное таким образом равенство на sin t, получим полярное уравнение
кардиоиды
По виду этого уравнения
можно заключить, что кардиоида является одной из улиток
Паскаля. Она может быть определена, следовательно, как конхоида круга.
Из этого уравнения следует, что кардиоида является
алгебраической кривой 4-го порядка.
2. Свойства
. Прежде всего, поскольку кардиоида
является эпициклоидой с m=1, на нее можно перенести все свойства рассмотренных нами в
предыдущем параграфе эпициклоид.
Вот эти свойства и характеристики.
Касательная в произвольной точке кардиоиды проходит через
точку окружности производящего круга, диаметрально противоположную точке
касания кругов, а нормаль – через точку их касания.
Угол m, составляемый касательной к кардиоиде с
радиусом-вектором точки касания, равен половине угла, образуемого этим
радиусом-вектором с полярной осью. Действительно
Из этого соотношения непосредственно вытекает, что угол,
составляемый касательной к кардиоиде с осью абсцисс, равняется (как внешний угол
треугольника AMN Рис. 14). Располагая формулой можно доказать, что
касательные к кардиоиде, проведенные в концах хорды, проходящей через полюс,
взаимно перпендикулярны.
Действительно, так как
Рис. 14
Заметим еще, что геометрическое место точек пересечения этих
касательных есть окружность Действительно, уравнение первой касательной на
основании уравнений (1) кардиоиды, будет иметь вид
А второй касательной Исключая из этих
уравнений параметр, получим уравнение указанной окружности.
Радиус кривизны в произвольной точке кардиоиды определится
по формуле
Можно показать также, что радиус кривизны равняется 2/3 полярной
нормали N в заданной точке.
Действительно, откуда на основании (4)
получаем Соотношение это может
быть использовано для построения центра кривизны кардиоиды.
Эволюта кардиоиды, согласно общему свойству эволют
эпициклоид, будет также кардиоидой, подобной данной, с коэффициентом подобия,
равным 1/3, и повернутой относительно данной на угол 180°.
Длина дуги кардиоиды от точки А до произвольной точки М
определится по формуле
Если длину дуги отсчитывать от точки А 1 ,
диаметрально противоположной точке А, то формула для определения длины дуги
может быть записана в виде
(6)
Натуральное уравнение кардиоиды получится, если из равенств
(4) и (6) исключить параметр. Оно будет иметь вид
(7)
Площадь, ограниченная кардиоидой, определится по формуле
и, как видно, равна ушестеренной площади производящего круга.
Длина всей кардиоиды определится по формуле
и, как видно, равна восьми диаметрам производящего круга.
Объем тела, полученного от вращения кардиоиды вокруг ее оси, равен
Поверхность тела, полученного от вращения кардиоиды вокруг ее
оси, равняется
Мы видели, что кардиоида органически связана с окружностью.
Она является конхоидой круга и эпициклоидой. Она имеет с окружностью и иной
характер родства – кардиоида является подэрой окружности относительно точки,
принадлежащей этой окружности.
Действительно, пусть ОМ есть перпендикуляр, опущенный на
касательную к окружности с радиусом, равным 2r, проведенную в точке N.
Так как ОМ = OB + ВМ, или r == 2r cos j + 2r, то геометрическим
местом точек М будет кардиоида с уравнением r = 2r (1 + cos j)
Заметим в заключение, что кардиоида относится также к
семейству синусоидальных спиралей, и отдельные свойства ее повторяют общие
свойства этих кривых. Из этих свойств следует, в частности, что инверсия
кардиоиды, относительно точки возврата дает параболу.
Астроида
1. Свойства.
Астроида является частным случаем
гипоциклоид, а именно, гипоциклоидой с модулем m, равным 1/4. Она
представляет собой, следовательно, траекторию точки, лежащей на окружности
круга радиуса r,
который катится по внутренней стороне другого, неподвижного круга, радиус R
которого в четыре раза больше.
Параметрические уравнения астроиды можно получить, полагая в
уравнениях гипоциклоиды, m=1/4. Вот эти уравнения:
где t, как и ранее, угол поворота производящего круга (рис.
16)
Исключая из уравнений (1) параметр t, получим:
Из уравнения (2) следует, что астроида является алгебраической
кривой 6-го порядка.
Параметрические уравнения (1) астроиды можно привести к виду

Исключая из этих уравнений параметр t, получим часто
употребляемый вид уравнения астроиды
(4)
Полагая в ранее выведенных общих соотношениях для
циклоидальных кривых модуль
m = -1/4, получим соответствующие соотношения для астроиды:
) радиус кривизны в произвольной точке астроиды определяется
по формуле
(5)
) длина дуги астроиды от точки А до произвольной точки M(t)
определится по формуле
длина одной ветви равна а длина всей кривой 6R;
) для получения натурального уравнения астроиды заметим
предварительно, что если началом отсчета длины дуги полагать не точку А, для
которой t = 0, а точку, для которой t = p, то длина дуги определится
формулой
исключая параметр t из уравнений (5) и (6), получим
натуральное уравнение астроиды
) эволюта астроиды есть также астроида, подобная данной, с
коэффициентом подобия, равным 2, повернутая относительно данной на угол p/4 (рис. 16)
) площадь, ограниченная всей астроидой, равна объем тела, полученного
от вращения астроиды, равняется 32/105p R 3
поверхность тела, образованного вращением астроиды, равна
Обратимся теперь к рассмотрению некоторых частных свойств
астроиды.
Астроида является огибающей отрезка постоянной длины, концы.
которого скользят по двум взаимно перпендикулярным прямым.
Принимаем эти прямые за оси координат и, обозначая угол
наклона скользящего отрезка ND=R через a (рис. 4), будем иметь
уравнение прямой ND в виде
Дифференцируя это уравнение по параметру a, получим:
Практически перемещение отрезка ND можно осуществить с
помощью так называемых кардановых кругов. Один из этих кругов с радиусом R
неподвижен, а другой, с радиусом r, в два раза меньшим, катится по внутренней стороне
неподвижного круга. Любые две диаметрально противоположные точки N и D
катящегося круга будут перемещаться по двум взаимно перпендикулярным диаметрам
Ох и Оу неподвижного круга. Ясно, что огибающей диаметра катящегося круга и
будет астроида.
|
|
|
Рассмотренный способ образования астроиды можно истолковать
также следующим образом. Прямоугольник ODCN, две стороны которого лежат на двух
взаимно перпендикулярных прямых, деформируется так, что диагональ его сохраняет
длину, равную R, огибающая диагонали и будет астроидой. Так как при этом
перпендикуляр, опущенный из вершины С на диагональ DN, служит нормалью к
огибающей, то астроида представляет собой геометрическое место оснований
перпендикуляров, опущенных из вершины С прямоугольника на его диагональ.
При эти уравнения выражают рассмотренную ранее
прямую астроиду.
. Некоторые трансцендентные линии
Трансцендентными
называют линии, уравнения которых в прямоугольных декартовых
координатах не являются алгебраическими. Простейшими примерами трансцендентных
линий могут служить графика функций, y=, y= и других тригонометрических функций. Рассмотрим некоторые другие
трансцендентные линии.
Спираль
Архимеда
Вообразим бесконечно длинную секундную стрелку, по которой,
начиная от центра циферблата, неутомимо бежит маленький жучок с постоянной скоростью
v см/с. Через минуту жучок
будет на расстоянии 60v см от центра, через две – 120v и т.д. Вообще, через t секунд после начала
пробега расстояние жучка от центра будет равно vt см. За это время стрелка
повернется на угол, содержащий 6 t° (ведь за одну секунду она успевает повернуться на угол
360°:60 = 6°). Поэтому положение жучка на плоскости циферблата через любое
число t секунд после начала движения находится так. Нужно отложить от
начального положения стрелки в направлении ее вращения угол а, содержащий 6t°, и отмерить от центра
вдоль нового положения стрелки расстояние r = vt см. Тут мы и
настигнем жучка (рис. 21).
Рис. 21.
Очевидно, что соотношение между углом поворота a стрелки (в градусах) и
пройденным расстоянием r (в сантиметрах) будет такое:
Иными словами, r прямо пропорционально a, причем коэффициент
пропорциональности k = v/6.
Приладим к нашему бегуну маленькую, но неистощимую баночку с
черной краской и допустим, что краска, вытекая через крошечное отверстие,
оставляет на бумаге след от уносимого вместе со стрелкой жучка. Тогда на бумаге
будет постепенно вырисовываться кривая, впервые изученная Архимедом (287 – 212
до н.э.). В его честь она называется спиралью Архимеда. Нужно только сказать, что
у Архимеда не было речи ни о секундной стрелке (тогда и часов с пружиной не
было: их изобрели только в XVII в.), ни о жучке. Мы ввели их здесь для
наглядности.
Рис. 22 Рис.
23.
Спираль Архимеда состоит из бесконечно многих витков. Она
начинается в центре циферблата, и все более и более удаляется от него по мере
того, как растет число оборотов. На рис. 22 изображены первый виток и часть
второго.
Вы, наверное, слышали, что с помощью циркуля и линейки
невозможно разделить на три равные части наудачу взятый угол (в частных
случаях, когда угол содержит, например, 180°, 135° или 90°, эта задача легко
решается). А вот если пользоваться аккуратно начерченной архимедовой спиралью,
то любой угол можно разделить на какое угодно число равных частей.
Разделим, например, угол АОВ на три равные части (рис. 23.).
Если считать, что стрелка повернулась как раз на этот угол, то жучок, будет
находиться в точке N на стороне угла. Но когда угол поворота был втрое меньше, то и
жучок был втрое ближе к центру О. Чтобы найти это его положение, разделим
сначала отрезок ON на три равные части. Это можно сделать с помощью циркуля и
линейки. Получим отрезок ON 1 , длина которого втрое меньше, чем ON. Чтобы вернуть жучка на
спираль, нужно сделать засечку этой кривой радиусом ON 1 (снова
циркуль!). Получим точку М. Угол АОМ и будет втрое меньше угла AON.
Циклоида
Приложим к нижнему краю классной доски линейку и будем катить
по ней обруч или круг (картонный или деревянный), прижимая его к линейке и к
доске. Если прикрепить к обручу или кругу кусок мела (в точке соприкосновения
его с линейкой), то мел будет вычерчивать кривую (рис. 24), называемую
циклоидой (что по-гречески значит «кругообразная»). Одному обороту обруча
соответствует одна «арка» циклоиды MM”M””N”, если обруч будет катиться дальше, то будут получаться еще и еще
арки той же циклоиды.
Рис. 24.
Чтобы построить на бумаге приближенно одну арку циклоиды,
описанную при качении обруча диаметром, равным, например, трем сантиметрам,
отложим на прямой отрезок, равный 3х3,14 = 9,42 см.
Получим отрезок, длина которого равна длине обода обруча,
т.е. длине окружности диаметром в три сантиметра. Разделим далее этот отрезок
на некоторое число равных частей, например на 6, и для каждой точки деления
изобразим наш обруч в том его положении, когда он опирается именно на данную
точку (рис. 24), занумеровав эти положения цифрами:
О, 1, 2, 3, 4, 5, 6.
Чтобы перейти из одного положения в соседнее, обруч должен
повернуться на одну шестую полного оборота ^так как расстояние между соседними
точками деления равно шестой части окружности). Поэтому если в положении 0 мел
будет находиться в точке М 0 , то в положении 1 он будет лежать в
точке M 1 – на одной шестой окружности от точки касания, в положении
2 – в точке М 2 – на две шестых от точки касания и т.д. Чтобы
получить точки M 1 , M 2 , М 3 и т.д., нужно лишь производить засечки
соответствующей окружности, начиная от точки касания, радиусом, равным
Рис. 25.
5 см, причем в положении 1 нужна одна засечка, в положении 2
– две засечки, выполненные одна за другой, в положении 3 – три засечки и т.д.
Теперь для вычерчивания циклоиды остается соединить точки
М 0 , M 1 , М 2 , М 3 , M 4 , M 5 , M 6
плавной кривой (на глаз).
Кривая
кратчайшего спуска
Среди многих замечательных свойств циклоиды отметим одно,
из-за которого она заслужила громко звучащее мудреное название:
«брахистохрона». Это название составлено из двух греческих слов, означающих
«кратчайший» и «время».
Рассмотрим такой вопрос: какую форму следует придать хорошо
отшлифованному металлическому желобу, соединяющему две заданные точки А и В
(рис. 26.), чтобы полированный металлический шарик скатывался по этому желобу
из точки А в точку В в кратчайшее время? На первый взгляд кажется, что нужно
остановиться на прямолинейном желобе, так как только вдоль него шарик пройдет
кратчайший путь от А до В. Однако речь идет не о кратчайшем пути, а о
кратчайшем времени; время же зависит не только от длины пути, но и от скорости,
с которой бежит шарик. Если желоб прогнуть вниз, то его часть, начиная от точки
А, будет круче опускаться вниз, чем в случае прямолинейного желоба, и шарик,
падая по нему, приобретет скорость большую, чем на участке такой же длины
прямолинейного желоба. Но если сделать начальную часть очень крутой и
сравнительно длинной, то тогда часть, примыкающая к точке В, будет очень
пологой и также сравнительно длинной; первую часть шарик пройдет быстро, вторую
очень медленно и шарик может запоздать с приходом в точку В. Итак, желобу,
по-видимому, нужно придавать вогнутую форму, но делать выгиб не слишком
значительным
Рис. 26.
Рис. 27.
Итальянский физик и астроном Галилей (1564-1642) думал, что
желоб кратчайшего времени нужно выгибать по дуге окружности. Но швейцарские
математики братья Бернулли около трехсот лет тому назад доказали точным
расчетом, что это не так и что желоб нужно выгибать по дуге циклоиды
(опрокинутой вниз, рис. 27.). С тех пор циклоида и заслужила прозвище
брахистохроны, а доказательства Бернулли послужили, началом новой отрасли
математики – вариационного исчисления. Последнее занимается отысканием вида
кривых, для которых та или иная интересующая нас величина достигает своего
наименьшего (а в некоторых вопросах – наибольшего) значения.
Логарифмическая
спираль
Кривую эту можно было бы назвать по имени Декарта, так как
впервые о ней говорится в одном из его писем (1638 г.). Однако подробное
изучение ее свойств было проведено только полвека спустя Якобом Бернулли. На
современных ему математиков эти свойства произвели сильное впечатление. На
каменной плите, водруженной на могиле этого знаменитого математика, изображены
витки логарифмической спирали.
Архимедову спираль описывает точка, движущаяся вдоль луча
(«бесконечной стрелки») так, что расстояние от начала луча возрастает
пропорционально углу его поворота: r = ka. Логарифмическая спираль получится, если
потребовать, чтобы не само расстояние, а его логарифм возрастал прямо пропорционально
углу поворота. Обычно уравнение логарифмической спирали записывают, пользуясь в
качестве основания системы логарифмов неперовым числом е (п. 25). Такой
логарифм числа r называют натуральным логарифмом и обозначают In r. Итак, уравнение
логарифмической спирали записывается в виде ln r = ka
Конечно, угол поворота а можно измерять по-прежнему в
градусах. Но математики предпочитают измерять его в радианах, т.е. принимать за
меру угла отношение длины дуги окружности между сторонами центрального угла к радиусу
этой окружности. Тогда ловорот стрелки на прямой угол будет измеряться числом л
1,57, поворот на величину развернутого угла – числом л 3,14, а полный поворот,
измеряемый в градусах числом 360, в радианах будет измеряться числом 2 л 6,28.
Рис. 28.
Из многих свойств логарифмической спирали, отметим одно:
любой луч, выходящий из начала, пересекает любой виток спирали под одним и тем
же углом. Величина этого угла зависит только от числа k в уравнении спирали. При
этом под углом между лучом и спиралью понимается угол между этим лучом и
касательной к спирали, проведенной в точке пересечения (Рис. 28).
Заключение
В ходе рассматревания кривых третьего и четвертого
порядков
мы познакомились с некоторыми поистине замечательными
кривыми, населяющими удивительный мир аналитической геометрии, которые
встречаются в нашей жизни гораздо чаще, чем кажется. Рассмотрели практическое
применение их в жизни человека, значение их замечательных свойств в различных
механизмах, используемых человеком в жизни. В данной работе собрали материал с
уклоном на практическое построение кривых.
Итак, было достигнуто поставленной цели и решены
обозначенные, соответственно, к цели задания.
Литература
линия порядок трансцендентный спираль
1.
Маркушевич А.И. Замечательные кривые. – М.:.Краснопролетарская, 1951. -23 с.;
1978., – 48 стр. с илл.
История математики с древнейших времен до начала XIX столетия/ Под ред. А.П.
Юшкевича. – М.: Наука, 1970, т. 1. – 352 с.; 1970, т. 2. – 300 с.; 1972, т. 3 –
496 с.
Никифоровский В.А., Фрейман Л.С. Рождение новой математики. – М.: Наука, 1976.
– 198 с.
Савелов А.А. Плоские кривые. – М.: Физматгиз, 1960 – 294 с.
Ильин В.А., Позняк Э.Г. Аналитическая геометрия. – М.: Наука, 1971. – 232 с.
Тышкевич Р.И., Феденко А.С. Линейная алгебра и аналитическая геометрия. – 2-е
изд. – Минск: Выш. Шк., 1976.544 с.
Почему наш мир прекрасен? Потому что формы и цвета живой природы во многом следуют общим закономерностям гармонии, выявляющимся путем строгого математического анализа. При изучении природы мы находим в ней все больше эстетических признаков, которые выявляются, как правило, не сразу, но после детального математического анализа.
Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии.
Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.
При использовании законов геометрии природы в новой ситуации, для изучения курсов предметов, связанных с геометрическими построениями, мы заново переосмысливаем изученные геометрические законы, развиваем геометрическую интуицию.
В процессе выполнения творческих заданий различного содержания, мы познакомились с возможными сферами применения геометрических знаний (художниками, архитекторами, дизайнерами и т. д.).
Графические средства отображения информации используются во всех сферах жизни общества. Они имеют законченный образ, характеризуются символичностью, компактностью, относительной легкостью прочтения. Именно эти качества графических изображений обуславливают их расширенное использование. В недалеком будущем более половины представляемой информации будет иметь графическую форму предъявления. Развитие теоретических основ начертательной геометрии, инженерной графики и других смежных наук расширило способы получения графических изображений. Наряду с ручными способами формирования графических изображений, составления проектной документации все более широкое применение находят компьютерные способы. Использование новых информационных технологий обеспечивает создание, редактирование, хранение, тиражирование графических изображений с помощью различных программных средств.
I. Начальные сведения об алгебраических кривых
1. Астроида
Астроида (от греч. >-звезда) – это кривая, описываемая точкой подвижной окружности, которая касается изнутри неподвижной окружности вчетверо большего радиуса и катится по ней без скольжения. Площадь, ограниченная астроидой, составляет /8 площади неподвижного круга, а полная длина астроиды равна ушестеренному радиусу этого круга.
Уравнение астроиды в декартовых прямоугольных координатах:
x + y = R.
Построение графика астроиды выполнили в > следующим образом:
:: Построили график функции при у > 0 (радиус R = 5);
:: Построили график функции.
2. Кардиоида
Кардиоида (от греч. >-сердце и eidos-вид)- плоская кривая, описываемая фиксированной точкой окружности, которая извне касается неподвижной окружности того же радиуса и катится по ней без скольжения. Кривая получила своё название из-за сходства с сердцем.
Построение графиков кардиоид также выполнили в >.
3. Нефроида
Нефроида (от греч. hephros-почка, eidos-вид) – кривая которую описывает фиксированная точка окружности, катящейся снаружи по большей в два раза окружности. Впервые свойства нефроиды изучил в 17 веке саксонский дворянин Э. В. Чирнгауз. Нефроида состоит из двух кардиоид.
4. Улитка Паскаля.
Улитка Паскаля – плоская алгебраическая кривая. Названа по имени Этьена Паскаля (отца Блеза Паскаля), впервые рассмотревшего её. Уравнение в полярных координатах. При l = 2a получается кардиоида.
II. Применение математического моделирования.
1. История создания нитяной графики
Нитяная графика (или изонить) – это графическое изображение, особым способом выполненное нитками на картоне или другом твердом основании. Нитяную графику также иногда называют изографика или вышивка по картону.
Термин > (нитяная графика или изонить) используется в России, в англоязычных странах используется словосочетание – вышивка на бумаге, в немецкоязычных странах – термин.
Нитяная графика, как вид декоративно-прикладного искусства, впервые появилась в Англии в XVII веке. Английские ткачи придумали особый способ переплетения ниток. Они забивали в дощечки гвозди и в определенной последовательности натягивали на них нити. В результате получались ажурные кружевные изделия, которые использовались для украшения жилища. (Возникла версия, что эти работы были своего рода эскизами для узоров на ткани). Современные расходные материалы позволяют получать очень эффектные изделия.
Наряду с оригинальной техникой исполнения нитяной графики, существует другое направление ниточного дизайна – вышивка на картоне (изонить) теми же приемами (прием заполнения угла и окружности).
Интерес к нитяной графике то появлялся, то исчезал. Один из пиков популярности был в конце ХIХ века. Издавались книги по рукоделию, в которых описывался необычный способ вышивки на бумаге, простой и легкий, доступный детям. В работе использовались перфорированные карты (готовые шаблоны) и прием заполнения угла, стежки >, > (для вышивания кривых). Используя минимум средств, любой человек (а главное дети) смог бы изготовить причудливые сувениры к праздникам.
Сейчас этим искусством занимаются во многих странах мира.
В нашей стране информации по изонити имеется в небольшом количестве, в основном ознакомительного характера: отдельные публикации в журналах >, В 1995 году вышла книга минского профессора Г. А. Браницкого > и книга Нагибиной М. И. > с небольшой главой об изонити.
Проанализировав доступную информацию, удалось узнать, что по этому виду рукоделия издаётся множество книг в виде пошаговых инструкций и альбомов идей, в которых везде используется только репродуктивный метод работы.
Достоинство изонити в том, что выполняется она быстро и придумать можно много интересных узоров. Этот вид творчества развивает воображение, глазомер, мелкую моторику пальцев, художественные способности и эстетический вкус. В технике нитяной графики можно изготовить не только декоративное панно, но и поздравительные открытки, сувенирные обложки, закладки для книг.
А направлений у изонити (нитяной графики или ниточного дизайна) может быть несколько:
1) репродуктивный способ: работа по шаблону, пошаговая инструкция, раздача готовых схем и наборов вышивания
2) частично-поисковый (проектный): обучение расчету на картоне (т. е. создание собственных шедевров), поиск своих приемов и комбинаций, “игра” с фоном, нитками – с материалом исполнения
3) комбинированный – когда начинается всё с “азбуки”, работаем с готовыми схемами, но изменяем вид материала (цвет) и доходим до “шедевра”.
2. Основные приемы нитяной графики
Нитяная графика известна и под другими названиями: изонить (т. е. изображение нитью), графическая вышивка. Для освоения техники достаточно знать, как заполняются угол, окружность и дуга.
Прием 1. Заполнение угла.
На изнанке картона начертим угол, разделим каждую сторону на равное количество частей. Проколем точки булавкой или тонким шилом, вдеваем нить в иглу и заполним по схеме.
Прием 2. Заполнение окружности.
Начертим циркулем окружность. Поделим ее на 12 равных частей и заполним по схеме.
Прием 3. Заполнение дуги.
Начертим дугу, разделим ее на равные части и сделаем проколы в точках деления. Вдеваем нитку в иглу и заполним по схеме
III. Исследовательская работа.
Построения в программе >.
Задача 1. Деление отрезка на n равных частей.
Решение 1. Деление на 2, 4, 8, 16 и т. д. частей выполняли в > путем построения середин отрезка.
Решение 2. Деление отрезка на произвольное количество частей мы выполнили также в > с применением теоремы Фалеса.
Задача 2. Деление окружности на 6, 12, 24 части.
Решение 1. Мы искали различные способы деления окружности на части. В программе > мы чертили окружность, в произвольном порядке расставляли точки, измеряли полученные углы, а затем > двигали точки по окружности до получения нужной величины. Это была монотонная и неинтересная работа. Погрешность первого деления на 12 частей составила + 0,15 см в длине хорд. Мы стали анализировать ситуацию и искать оптимальные способы решения поставленных задач. В итоге мы нашли несколько решений деления окружности на 6, 12, 24 частей.
Решение 2. На окружности отметили 6 точек, измерили все углы, выровняли точки так, чтобы каждый угол был равен 60 [о]. Затем с помощью программы провели биссектрисы каждого угла. Получилось деление на 12 частей. А для деления на 24 части провели еще раз биссектрисы полученных углов. Погрешность такого построения оказалась равной + 0,01 градуса.
Решение 3. С помощью программы построили 3 окружности одинакового радиуса (применение копирования), совместили их, как показано на рисунке. Отметили точки пересечения окружностей. Измерили получившиеся углы, они оказались равными по 60 [о]. Далее построили биссектрисы углов для деления на 12 и 24 части. Погрешность такого решения равна нулю.
Задача 3. Деление окружности на 9, 18, 36 частей.
Найдя оптимальный способ решения предыдущей задачи, мы аналогично стали искать способы деления окружности на 9, 18 и 36 частей. Деление на 18 и 36 частей можно выполнить только после построения 9 точек, применив построение биссектрис.
Решение. 360 [о] : 9 = 40 [о]. Мы на > разделили полуокружность на 4 дуги примерно по 40 [о] и дугу в 20 [о]. С помощью программы выполнили все необходимые измерения углов, двигая точки. Далее выделили построенные точки и с помощью команды > отразили точки на 180 градусов относительно центра окружности на вторую полуокружность. Погрешность такого построения составила + 0,04 градуса..
Задача 4. Построение алгебраических кривых
Астроида
Решение 1. Астроида строится на координатной плоскости по следующему алгоритму:
:: Нужно соединить точки оси ординат с точками оси абсцисс так, чтобы в сумме цифры делений давали 10 (например:1 и 9, 2 и 8, 3 и 7 и т. Д.).
:: Соединяем точки в такой же последовательности в остальных четвертях координатной плоскости.
Решение 2. Начертили окружность, построили перпендикулярные диаметры, разделили каждый радиус на четное количество частей. Соединили точки отрезками по предыдущему алгоритму.
Решение 3. Освоив оптимальный прием деления окружности на 6 частей, мы выполнили построение 6-звездочной астроиды.
Решение 4. Построение 8-зведочной астроиды выполнили с построением биссектрис прямых углов.
Кардиоида
Решение. Для построения кардиоиды основанием будет являться окружность. Кардиоиду построили по следующему плану:
:: начертили окружность и поделили её на 36 частей (по 10 градусов);
:: пронумеровали внешние точки от 1 до 36 против часовой стрелки;
:: внутренние точки пронумеровали в соответствие со схемой 1;
:: соединили точки с одинаковыми внутренними и внешними номерами;
:: огибающей и будет кардиоида.
Схема 1 Схема 2
IV. Наше творчество.
Освоив основные приемы конструирования и моделирования в >, мы попробовали себя реализовать в роли дизайнеров и художников. Нами разработаны и воплощены в практику следующие работы:
Заключение, выводы
>, – заметил 2500 лет назад Аристотель. Наш современник Сухомлинский считал, что >. А математика замечательный предмет для удивления.
Углубленно изучив доступный материал, мы познакомилась с новым методом конструирования кривых – математическим вышиванием, используя знакомые приемы построения геометрических фигур (построение угла, деление отрезка на равные части, соединение точек в определенной последовательности, деление окружности на равные части в программе >). Мы нашли удивительное сходство математического вышивания с давно известным видом декоративно-прикладного искусства – изонитью.
В Интернете, специальной литературе много фотографий с вышивкой изонитью, но к ним не прилагаются схемы. Мы пришли к выводу, что математическое вышивание – это творческий процесс. Зная основы математического моделирования, которые изложены в нашей работе, применяя творческое мышление, логику, терпение, можно изготавливать индивидуальные > прикладного искусства.
Математическое вышивание заинтересовало не только нас, но и многих учеников школы (как девочек, так и мальчиков). Мы считаем, что современные информационные технологии позволят соединить воедино математику и искусство.
– (от греч. astron звезда и eidos вид) плоская кривая, описываемая точкой окружности, которая касается изнутри неподвижной окружности вчетверо большего радиуса и катится по ней без скольжения. Принадлежит к гипоциклоидам. Астроида алгебраическая… … Большой Энциклопедический словарь
Сущ., кол во синонимов: 1 кривая (56) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
– (от греч. ástron звезда и éidos вид), плоская кривая, описываемая точкой окружности, которая касается изнутри неподвижной окружности вчетверо большего радиуса и катится по ней без скольжения. Принадлежит к гипоциклоидам. Астроида … … Энциклопедический словарь
– (астро… гр. eidos вид) мат. плоская кривая, описываемая точкой окружности, катящейся без скольжения по внутренней стороне другой, неподвижной окружности с радиусом, вчетверо большим, чем у первой; имеет вид четырехконечной звезды. Новый словарь … Словарь иностранных слов русского языка
Плоская алгебраич. кривая ti ro порядка, к рая описывается точкой Мокружности радиуса r, катящейся по внутренней стороне окружности радиуса R=4r; гипоциклоида с модулем r=4. Уравнение в декартовых прямоугольных координатах: параметрич. уравнения … Математическая энциклопедия
Кривая или линия – геометрическое понятие, определяемое в разных разделах различно.
КРИВАЯ (линия), след, оставленный движущейся точкой или телом. Обычно кривую представляют лишь как плавно изгибающуюся линию, вроде параболы или окружности. Но математическое понятие кривой охватывает и прямую, и фигуры, составленные из отрезков прямых, например, треугольник или квадрат.
Кривые можно разделить на плоские и пространственные. Плоская кривая, например, парабола или прямая, образуется при пересечении двух плоскостей или плоскости и тела и поэтому целиком лежит в одной плоскости. Пространственную кривую, например, винтовую линию, имеющую форму спиральной пружины, нельзя получить как пересечение какой-нибудь поверхности или тела с плоскостью, и она не лежит в одной плоскости. Кривые можно также подразделить на замкнутые и открытые. Замкнутая кривая, например квадрат или окружность, не имеет концов, т.е. движущаяся точка, порождающая такую кривую, периодически повторяет свой путь.
Кривая есть геометрическое место, или множество, точек, удовлетворяющих некоторому математическому условию или уравнению.
Например, окружность – это геометрическое место точек плоскости, равноудаленных от данной точки. Кривые, определяемые алгебраическими уравнениями, называются алгебраическими кривыми.
Например, уравнение прямой y = mx + b, где m – угловой коэффициент, а b – отрезок, отсекаемый на оси y, – алгебраическое.
Кривые, уравнения которых содержат трансцендентные функции, например, логарифмы или тригонометрические функции, называются трансцендентными кривыми.
Например, y = log x и y = tg x – уравнения трансцендентных кривых.
Форму алгебраической кривой можно определить по степени ее уравнения, которая совпадает с наивысшей степенью членов уравнения.
Если уравнение первой степени, например Ax + By + C = 0, то кривая имеет форму прямой.
Если уравнение второй степени, например,
Ax 2 + By + C = 0 или Ax 2 + By 2 + C = 0, то кривая квадратична, т.е. представляет собой одно из конических сечений; к числу таких кривых относятся параболы, гиперболы, эллипсы и окружности.
Перечислим общие формы уравнений конических сечений:
x 2 + y 2 = r 2 – окружность,
x
2 /a 2 + y 2 /b 2 = 1 – эллипс,
y = ax 2 – парабола,
x
2 /a 2 – y 2 /b 2 = 1 – гипербола.
Кривые, соответствующие уравнениям третьей, четвертой, пятой, шестой и т.д. степеней, называются кривыми третьего, четвертого, пятого, шестого и т.д. порядка. Как правило, чем выше степень уравнения, тем больше изгибов будет у открытой кривой.
Многие сложные кривые получили специальные наименования.
Циклоидой называется плоская кривая, описываемая фиксированной точкой окружности, катящейся по прямой, называемой образующей циклоиды; циклоида состоит из серии повторяющихся дуг.
Эпициклоида – это плоская кривая, описываемая фиксированной точкой окружности, катящейся по другой неподвижной окружности вне ее.
Гипоциклоидой называется плоская кривая, описываемая фиксированной точкой окружности, катящейся изнутри по неподвижной окружности.
Спиралью называется плоская кривая, которая виток за витком раскручивается от неподвижной точки (или накручивается на нее).
Математики занимались изучением свойств кривых с глубокой древности, и названия многих необычных кривых связаны с именами тех, кто впервые их исследовал. Таковы, например, спираль Архимеда, локон Аньези, циссоида Диоклеса, кохоида Никомеда и лемниската Бернулли.
В рамках элементарной геометрии понятие кривой не получает отчётливой формулировки и иногда определяется как «длина без ширины» или как «граница фигуры». По существу в элементарной геометрии изучение кривых сводится к рассмотрению примеров (,
,
,
и др.). Не располагая общими методами, элементарная геометрия довольно глубоко проникла в изучение свойств конкретных кривых (, некоторые
и также
), применяя в каждом случае специальные приёмы.
Чаще всего кривая определяется как непрерывное отображение из отрезка в :
При этом, кривые могут быть различными, даже если их
совпадают. Такие кривые называют
параметризованными кривыми
или, если
[
a
,
b
] =
,
путями
.
Иногда кривая определяется с точностью до , то есть с точностью до минимального отношения эквивалентности такого что параметрические кривые
эквивалентны, если существует непрерывная (иногда неубывающая) h
из отрезка [a
1 ,b
1 ] на отрезок [a
2 ,b
2 ], такая что
Определяемые этим отношением называются или просто кривыми.
Аналитические определения
В курсах аналитической геометрии доказывается, что среди линий, записываемых в декартовых прямоугольных (или даже в общих аффинных) координатах общим уравнением второй степени
Ax 2 + 2Bxy + Cy 2 + 2Dx + 2Ey + F = 0
(где хотя бы один из коэффициентов A, B, C отличен от нуля) встречаются лишь следующие восемь типов линий:
а) эллипс;
б) гипербола;
в) парабола (невырожденные кривые второго порядка);
г) пара пересекающихся прямых;
д) пара параллельных прямых;
е) пара совпавших прямых (одна прямая);
ж) одна точка (вырожденные линии второго порядка);
з) “линия”, совсем не содержащая точек.
Обратно, любая линия каждого из указанных восьми типов записывается в декартовых прямоугольных координатах некоторым уравнением второго порядка. (В курсах аналитической геометрии обычно говорят о девяти (а не о восьми) типах конических сечений, поскольку там различают “мнимый эллипс” и “пару мнимых параллельных прямых”, – геометрически эти “линии” одинаковы, поскольку обе не содержат ни одной точки, но аналитически они записываются разными уравнениями.) Поэтому (вырожденные и невырожденные) конические сечения можно определить также как линии второго порядка.
В
кривая на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению
F
(
x
,
y
) = 0
. При этом на функцию
F
накладываются ограничения, которые гарантируют, что это уравнение имеет бесконечное множество несовпадающих решений и
это множество решений не заполняет «куска плоскости».
Алгебраические кривые
Важный класс кривых составляют те, для которых функция
F
(
x
,
y
)
есть
от двух переменных. В этом случае кривая, определяемая уравнением
F
(
x
,
y
) = 0
, называется
.
Алгебраические кривые, задаваемые уравнением 1-й степени, суть .
Уравнение 2-й степени, имеющее бесконечное множество решений, определяет , то есть вырожденные и невырожденные .
Примеры кривых, задаваемых уравнениями 3-ей степени: , .
Примеры кривых 4-ой степени: и .
Пример кривой 6-ой степени: .
Пример кривой, определяемой уравнением чётной степени: (многофокусная)
.
Алгебраические кривые, определяемые уравнениями высших степеней, рассматриваются в . При этом большую стройность приобретает их теория, если рассмотрение ведется на . В этом случае алгебраическая кривая определяется уравнением вида
F
(
z
1
,
z
2
,
z
3
) = 0
,
где F
– многочлен трех переменных, являющихся точек.
Типы кривых
Плоская кривая – кривая, все точки которой лежат в одной плоскости.
(простая линия или жорданова дуга, также контур) – множество точек плоскости или пространства, находящихся во взаимно однозначном и взаимно непрерывном соответствии с отрезками прямой.
Путь – отрезка в .
аналитические кривые, не являющиеся алгебраическими. Более точно – кривые, которые можно задать через линию уровня аналитической функции (или, в многомерном случае, системы функций).
Синусоида,
Циклоида,
Спираль Архимеда,
Трактриса,
Цепная линия,
Гиперболическая спираль и др.
-
Способы задания кривых:
аналитический – кривая задана математическим уравнением;
графический – кривая задана визуально на носителе графической информации;
табличный – кривая задана координатами последовательного ряда точек.
параметрический (наиболее общий способ задать уравнение кривой) :
где
– гладкие функции параметра
t
, причем
(x
“) 2 + (y
“) 2 + (z
“) 2 > 0 (условие регулярности).
Часто удобно использовать инвариантную и компактную запись уравнения кривой с помощью :
где в левой части стоит точек кривой, а правая определяет его зависимость от некоторого параметра t
. Раскрыв эту запись в координатах, мы получаем формулу (1).
-
Циклоида.
История исследования циклоиды связана с именами таких великих учёных, философов, математиков и физиков, как Аристотель, Птолемей, Галилей, Гюйгенс, Торричелли и др.
Циклоида
(от
κυκλοειδής
– круглый) – , которую можно определить как траекторию точки, лежащей на границе круга, катящегося без скольжения по прямой. Эту окружность называют порождающей.
Одним из древнейших способов образования кривых является кинематический способ, при котором кривая получается как траектория движения точки. Кривая, которая получается как траектория движения точки, закрепленной на окружности, катящейся без скольжения по прямой, по окружности или другой кривой, называется циклоидальной, что в переводе с греческого языка означает кругообразная, напоминающая о круге.
Рассмотрим сначала случай, когда окружность катится по прямой. Кривая, которую описывает точка, закрепленная на окружности, катящейся без скольжения по прямой линии, называется циклоидой.
Пусть окружность радиуса R катится по прямой а. С – точка, закрепленная на окружности, в начальный момент времени находящаяся в положении А (рис. 1). Отложим на прямой а отрезок АВ, равный длине окружности, т.е. АВ = 2 π R. Разделим этот отрезок на 8 равных частей точками А1, А2, …, А8 = В.
Ясно, что когда окружность, катясь по прямой а, сделает один оборот, т.е. повернется на 360, то она займет положение (8), а точка С переместится из положения А в положение В.
Если окружность сделает половину полного оборота, т.е. повернется на 180, то она займет положение (4), а точка С переместится в самое верхнее положение С4.
Если окружность повернется на угол 45, то окружность переместится в положение (1), а точка С переместится в положение С1.
На рисунке 1 показаны также другие точки циклоиды, соответствующие оставшимся углам поворота окружности, кратным 45.
Соединяя плавной кривой построенные точки, получим участок циклоиды, соответствующий одному полному обороту окружности. При следующих оборотах будут получаться такие же участки, т.е. циклоида будет состоять из периодически повторяющегося участка, называемого аркой циклоиды.
Обратим внимание на положение касательной к циклоиде (рис. 2). Если велосипедист едет по мокрой дороге, то оторвавшиеся от колеса капли будут лететь по касательной к циклоиде и при отсутствии щитков могут забрызгать спину велосипедиста.
Первым, кто стал изучать циклоиду, был Галилео Галилей (1564 – 1642). Он же придумал и ее название.
Свойства циклоиды:
Циклоида обладает целым рядом замечательных свойств. Упомянем о некоторых из них.
Свойство 1.
(Ледяная гора.) В 1696 году И.Бернулли поставил задачу о нахождении кривой наискорейшего спуска, или, иначе говоря, задачу о том, какова должна быть форма ледяной горки, чтобы, скатываясь по ней, совершить путь из начальной точки А в конечную точку В за кратчайшее время (рис. 3, а). Искомую кривую назвали “брахистохроной”, т.е. кривой кратчайшего времени.
Ясно, что кратчайшим путем из точки A в точку B является отрезок AB. Однако при таком прямолинейном движении скорость набирается медленно и затраченное на спуск время оказывается большим (рис. 3, б).
Скорость набирается тем быстрее, чем круче спуск. Однако при крутом спуске удлиняется путь по кривой и тем самым увеличивается время его прохождения.
Среди математиков, решавших эту задачу, были: Г.Лейбниц, И.Ньютон, Г.Лопиталь и Я.Бернулли. Они доказали, что искомой кривой является перевернутая циклоида (рис. 3, а). Методы, развитые этими учеными при решении задачи о брахистохроне, положили начало новому направлению математики – вариационному исчислению.
Свойство 2.
(Часы с маятником.) Часы с обычным маятником не могут идти точно, поскольку период колебаний маятника зависит от его амплитуды: чем больше амплитуда, тем больше период. Голландский ученый Христиан Гюйгенс (1629 – 1695) задался вопросом, по какой кривой должен двигаться шарик на нитке маятника, чтобы период его колебаний не зависел от амплитуды. Заметим, что в обычном маятнике кривой, по которой движется шарик, является окружность (рис. 4).
Искомой кривой оказалась перевернутая циклоида. Если, например, в форме перевернутой циклоиды изготовить желоб и пустить по нему шарик, то период движения шарика под действием силы тяжести не будет зависеть от начального его положения и от амплитуды (рис. 5). За это свойство циклоиду называют также “таутохрона” – кривая равных времен.
Гюйгенс изготовил две деревянные дощечки с краями в форме циклоиды, ограничивающие движение нити слева и справа (рис. 6). При этом сам шарик будет двигаться по перевернутой циклоиде и, таким образом, период его колебаний не будет зависеть от амплитуды.
Из этого свойства циклоиды, в частности следует, что независимо от того, с какого места ледяной горки в форме перевернутой циклоиды мы начнем спуск, на весь путь до конечной точки мы затратим одно и то же время.
Уравнение циклоиды
1.Уравнение циклоиды удобно записывать через α – угол поворота окружности, выраженный в радианах, заметим, что α также равняется пути, пройденному производящей окружностью по прямой.
x=rα
– r
sin α
y=r – r
cos α
2.Примем горизонтальную ось координат в качестве прямой, по которой катится производящая окружность радиуса r
.
Циклоида описывается параметрическими уравнениями
x
= rt
– r
sin t
,
y
= r
– r
cos t
.
Уравнение в :
Циклоида может быть получена как решение дифференциального уравнения:
Из истории о циклоиде
Первым из учёных обратил внимание на циклоиду
в
, но серьёзное исследование этой кривой началось только в
.
Первым, кто стал изучать циклоиду, был Галилео Галилей (1564-1642) – знаменитый итальянский астроном, физик и просветитель. Он же придумал название «циклоида», что значит: «напоминающая о круге». Сам Галилей о циклоиде ничего не писал, но о его работах в этом направлении упоминают ученики и последователи Галилея: Вивиани, Торичелли и другие. Торичелли – известный физик, изобретатель барометра – уделял немало времени и математике. В эпоху Возрождения не было узких ученых-специалистов. Талантливый человек занимался и философией, и физикой, и математикой и всюду получал интересные результаты и делал крупные открытия. Немного позже итальянцев за циклоиду принялись французы, назвавшие её «рулеттой» или «трохоидой». В 1634 году Роберваль – изобретатель известной системы весов системы весов – вычислил площадь, ограниченную аркой циклоиды и её основанием. Содержательное исследование циклоиды провёл современник Галилея . Среди , то есть кривых, уравнение которых не может быть записано в виде от x
,
y
, циклоида – первая из исследуемых.
Писал о циклоиде:
Рулетта является линией столь обычной, что после прямой и окружности нет более часто встречающейся линии; она так часто вычерчивается перед глазами каждого, что надо удивляться тому, как не рассмотрели её древние… ибо это не что иное, как путь, описываемый в воздухе гвоздём колеса.
Новая кривая быстро завоевала популярность и подверглась глубокому анализу, в котором участвовали
,
, Ньютон,
, братья Бернулли и другие корифеи науки XVII-XVIII веков. На циклоиде активно оттачивались методы появившегося в те годы
. Тот факт, что аналитическое исследование циклоиды оказалось столь же успешным, как и анализ алгебраических кривых, произвёл большое впечатление и стал важным аргументом в пользу «уравнения в правах» алгебраических и трансцендентных кривых.
Эпициклоида
Некоторые виды циклоид
Эпициклоида
– траектория точки А, лежащей на окружности диаметра D, которая катится без скольжения по направляющей окружности радиуса R (касание внешнее).
Построение эпициклоиды выполняется в следующей последовательности:
Из центра 0 проводят вспомогательную дугу радиусом равным 000=R+r;
Из точек 01, 02, …012, как из центров, проводят окружности радиуса r до пересечения с вспомогательными дугами в точках А1, А2, … А12, которые принадлежат эпициклоиде.

Гипоциклоида – траектория точки А, лежащей на окружности диаметра D, которая катится без скольжения по направляющей окружности радиуса R (касание внутреннее).
Построение гипоциклоиды выполняется в следующей последовательности:
Производящую окружность радиуса r и направляющую окружность радиуса R проводят так, чтобы они касались в точке А;
Производящую окружность делят на 12 равных частей, получают точки 1, 2, … 12;
Из центра 0 проводят вспомогательную дугу радиусом равным 000=R-r;
Центральный угол a определяют по формуле a =360r/R.
Делят дугу направляющей окружности, ограниченную углом a, на 12 равных частей, получают точки 11, 21, …121;
Из центра 0 через точки 11, 21, …121 проводят прямые до пересечения с вспомогательной дугой в точках 01, 02, …012;
Из центра 0 проводят вспомогательные дуги через точки деления 1, 2, … 12 производящей окружности;
Из точек 01, 02, …012, как из центров, проводят окружности радиуса r до пересечения с вспомогательными дугами в точках А1, А2, … А12, которые принадлежат гипоциклоиде.
-
Кардиоида.
Кардиоида
(
καρδία
– сердце, Кардиоида является частным случаем Термин «кардиоида» введен Кастиллоном в 1741 году.
Если взять окружность и в качестве полюса точку на ней, то кардиоиду получим только в том случае, если откладывать отрезки, равные диаметру окружности. При других величинах откладываемых отрезков конхоидами будут удлиненные или укороченные кардиоиды. Эти удлиненные и укороченные кардиоиды называются иначе улитками Паскаля.
Кардиоида имеет различные применения в технике. В форме кардиоиды делают эксцентрики, кулачки у машин. Ею пользуются иногда при вычерчивании зубчатых колес. Кроме того, она применяется в оптической технике.
Свойства кардиоиды
Кардиоида –
В
М
на подвижной окружности будет описывать замкнутую траекторию. Эта плоская кривая называется кардиоидой.
2)Кардиоиду можно получить и другим способом. Отметим на окружности точку О
и проведем из нее луч. Если от точки А
пересечения этого луча с окружностью отложить отрезок АМ,
по длине равный диаметру окружности, и луч вращать вокруг точки О
, то точка М
будет двигаться по кардиоиде.
3)Кардиоида может быть также представлена как кривая, касающаяся всех окружностей, имеющих центры на данной окружности и проходящих через ее фиксированную точку. Когда построены несколько окружностей, кардиоида оказывается построенной как бы сама собой.
4)Есть еще столь же изящный, сколь, неожиданный способ увидеть кардиоиду. На рисунке можно увидеть точечный источник света на окружности. После того как лучи света отразятся в первый раз от окружности, они идут по касательной к кардиоиде. Представьте себе теперь, что окружность – это края чашки, в одной точке ее отражается яркая лампочка. В чашку налит черный кофе, позволяющий увидеть яркие отраженные лучи. Кардиоида в результате оказывается выделенной лучами света.
-
Астроида.
Астроида
(от греч. astron – звезда и eidos – вид), плоская кривая, описываемая точкой окружности, которая касается изнутри неподвижной окружности вчетверо большего радиуса и катится по ней без скольжения. Принадлежит к гипоциклоидам. Астроида – алгебраическая кривая 6-го порядка.

Длина всей астроиды равна шести радиусам неподвижного круга, а площадь, ею ограниченная,- трем восьмым неподвижного круга.
Отрезок касательной к астроиде, заключенный между двумя взаимно перпендикулярными радиусами неподвижного круга, проведенными в острия астроиды, равен радиусу неподвижного круга, независимо от того, как была выбрана точка.
Свойства астроиды
Имеются четыре
каспа
.
Длина дуги от точки с 0 до
огибающей
семейства отрезков постоянной длины, концы которых расположены на двух взаимно перпендикулярных прямых.
Астроида является 6-го порядка.
Уравнения астроиды
Уравнение в декартовых прямоугольных координатах:
| x | 2 / 3 + | y | 2 / 3 = R 2 / 3
параметрическое уравнение:
x = Rcos 3 t y = Rsin 3 t
Способ построения астроиды
Чертим две взаимно перпендикулярные прямые и проводим ряд отрезков длиною
R
, концы которых лежат на этих прямых. На рисунке изображено 12 таких отрезков (включая отрезки самих взаимно перпендикулярных прямых). Чем больше проведем отрезков, тем точнее получим кривую. Построим теперь огибающую всех этих отрезков. Этой огибающей будет астроида.
-
Заключение
В работе приведены примеры задач с различными видами кривых, определяемых различными уравнениями или удовлетворяющих некоторому математическому условию. В частности циклоидальные кривые, способы их задания, различные способы построения, свойства этих кривых.
Свойства циклоидальных кривых очень часто используется в механике в зубчатых передачах, что существенно повышает прочность деталей в механизмах.
Графики функций, заданных параметрически:
Астроида (звездообразная кривая)
Астроид – это старое название астероидов, небесных тел, вращающихся вокруг Солнца, по размеру много меньше размеров планет.
При наблюдении в телескоп они выглядят как звезды.
Кривая астроид по форме напоминает звезду на ночном небе, поэтому и получила такое название.
Впервые данную кривую “астроидом” назвал астроном Карл Людвиг Литров в своей книге,
опубликованной в 1836 году в Вене. До этого времени кривая называлась кубоциклоид.
Исследованием данной кривой также занимались известные ученые: Рёмер, Бернулли, Лейбниц, д’Аламбер.

Астроидой называется кривая на плоскости, описываемая параметрическими уравнениями
при t от 0 до 2пи
То есть каждая точка (x,y) астроиды получается по вышеприведённым формулам при подстановке некоторого t.
Наша астроида имеет r=1.
Перебирая точки для различных значений t найдите расстояние от точки (0.75, 0) до ближайшей точки астроиды. Дайте ответ с точностью 10-4 (полученное вами расстояние должно отличаться от правильного ответа не больше, чем на 10-4).
Отправьте на проверку код, вычисляющий это число. Выведите число с указанной точностью.
| Python | ||
|
выводит 0,25, но при проверке не засчитывается, как верное
Астроида
Астроидой
называется кривая, которую описывает
точка окружности радиуса R/4,
когда окружность катится без скольжения
внутри окружности радиуса R.
Параметрические
уравнения астроиды

где
В декартовых
координатах уравнение астроиды
x2/3+y2/3=R2/3.
Длина
астроиды L=6R,
а площадь, ограниченная астроидой
S=3R2/8.
IV. ПоверхносТи второго порядка
Алгебраической
поверхностью второго порядка
называется
поверхность, уравнение которой в
декартовой системе координат имеет
вид:
Ax2+By2+Cz2+2Dxy+2Exz+2Fyz+gx+Hy+Iz+K=0,
где
не все коэффициенты при членах второго
порядка равны одновременно нулю (в
противном случае получаем алгебраическую
поверхность первого порядка, т.е.
плоскость).
В
зависимости от значений коэффициентов
возможны случаи, когда уравнение
определяет вырожденную
поверхность
(пустое множество, точку, плоскость,
пару плоскостей).
Например,
уравнение
не имеет решений и задает
пустое множество,
уравнение
задает точку
с координатами (0,0,0), уравнение
задает плоскость
х = 1, уравнение
задает пару
плоскостей
х
= у
и х
= у.
Исследование формы поверхностей второго порядка по их каноническим уравнениям
Основным
методом исследования формы поверхности
по ее уравнению является метод
сечений,
когда о форме
поверхности судят по форме кривых,
которые получаются при пересечении
данной поверхности плоскостями
Эллипсоид
Эллипсоидом
называется
поверхность второго порядка с каноническим
уравнением
.
Рассмотрим
сечение эллипсоида плоскостью
.
Линия пересечения эллипсоида и плоскости
задается системой уравнений
Г
– эллипс с полуосями а
и b
в плоскости
.
Рассмотрим
сечение эллипсоида плоскостью
.
Линия пересечения задается системой
уравнений
где
Таким образом, если
,
то Г – эллипс с полуосями
в плоскости
Если
,
Г – точка с координатами
Если
,
система решений не имеет, т.е. исследуемая
поверхность не имеет общих точек с
рассматриваемой плоскостью.
Далее,
так как переменная z
содержится
в уравнении во второй степени, плоскость
является плоскостью
симметрии
эллипсоида. Отсюда следует, что достаточно
исследовать форму поверхности и построить
ее часть в области
,
достроив затем остальную часть путем
зеркального отражения найденного
фрагмента поверхности относительно
координатной плоскости ОXY.
Аналогично
рассматриваются сечения поверхности
плоскостями
Эллипсоид
– замкнутая овальная поверхность, имеющая
три плоскости симметрии:
Если
,
каноническое уравнение эллипсоида
принимает вид
.
При этом линиями пересечения эллипсоида
с плоскостями
,
где –с < h
< c, являются
окружности, центры которых лежат на оси
OZ и,
следовательно, в этом случае эллипсоид
является фигурой вращения с осью OZ.
Если
,
каноническое уравнение принимает вид
и
задает сферу
с центром в начале координат и радиусом
R.
Гиперболоиды Однополостный гиперболоид
Однополостным
гиперболоидом
называется
поверхность второго порядка с каноническим
уравнением
.
Линия
пересечения гиперболоида и плоскости
задается системой уравнений
и
определяет эллипс с полуосями а
и b.
В
сечении плоскостью
получаем эллипс:
с
большими, чем в предыдущем случае
полуосями
Сечение
поверхности плоскостью
дает уравнение линии пересечения в
виде:
и
представляет гиперболу, пересекающую
ось OY.
Сечение
плоскостью
задает гиперболу, пересекающую ось OX.
Однополостный
гиперболоид
– поверхность,
имеющая вид расширяющейся трубки с
тремя плоскостями симметрии
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #





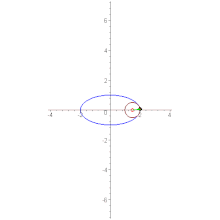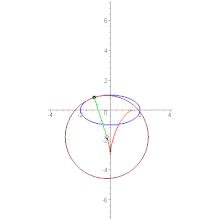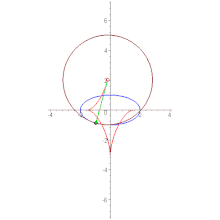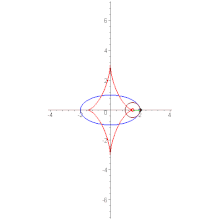
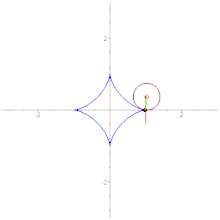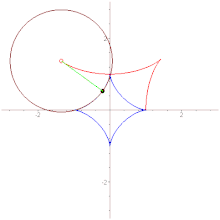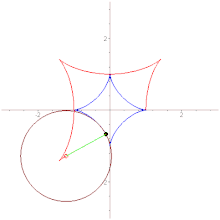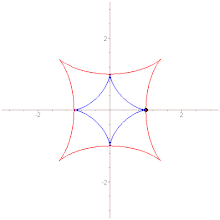







![{displaystyle int b{bigg [}1-{bigg (}{frac {x}{a}}{bigg )}^{frac {2}{3}}{bigg ]}^{frac {3}{2}}dx={frac {1}{16}}bleft({sqrt {1-left({frac {x}{a}}right)^{frac {2}{3}}}}left(-3a{sqrt[{3}]{frac {x}{a}}}+xleft(14-8left({frac {x}{a}}right)^{frac {2}{3}}right)right)+3aarcsin left({sqrt[{3}]{frac {x}{a}}}right)right)+C}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ae3a4b1c9373b0756313260473ab9282a142f73)



































 Рис. 17
Рис. 17 Рис. 18
Рис. 18