Кривые Безье — это способ определения кривой по опорным точкам.
Для наглядности можно рассматривать их как график передвижения точки от начала до конца маршрута в зависимости от времени движения.
Время изменяется от 0 до 1 (до 100%). То есть мы изначально знаем время, за которое нужно переместиться из начальной точки (P0) в конечную (Pn) (конкретная величина не имеет значения). На основании этого времени можно вычислить точную траекторию — по формулам.
Берем все время за 100% (или за единицу). В момент 0 (0%) точка находится в точке P0, в момент 1 (100%) – в точке Pn. Положение точки в любой момент между этими моментами можно вычислить по формуле.
Порядок кривой всегда на 1 меньше количества контрольных точек. Рассмотрим построение пошагово, начиная с самой простой кривой.
Кривая Безье первого порядка
Простейшая кривая Безье — это обычная линия. Порядок первый – значит, контрольных точек две. Ее академическое уравнение выглядит так:
B(t) = (1-t)*P0 + t*P1
А график — вот так:
Разберем на простейшем примере. Пусть:
- первая контрольная точка — P0 имеет координаты (0; 0),
- вторая (и последняя) – P1 – (5; 0).
Сразу же проверим формулу.
При t = 0 (в начальный момент времени) должна получиться точка P0, а при t = 1 должна получиться точка P1.
- B(0) = (1-0)*P0 + 0*P1 = P0 — (0; 0)
- B(1) = (1-1)*P0 + 1*P1 = P1 — (5; 0)
А теперь найдем несколько точек между началом и концом. Тут используется сложение и умножение векторов, но в данном случае все интуитивно понятно:
B(0.1) = (1-0.1)*P0 + 0.1*P1 = 0.9*P0 + 0.1*P1 = 0.9*(0;0) + 0.1*(5;0) = (0.5; 0)B(0.2) = (1-0.2)*P0 + 0.2*P1 = 0.8*P0 + 0.2*P1 = 0.8*(0;0) + 0.2*(5;0) = (1; 0)B(0.3) = (1-0.3)*P0 + 0.3*P1 = 0.7*P0 + 0.3*P1 = 0.7*(0;0) + 0.3*(5;0) = (1.5; 0)B(0.4) = (1-0.4)*P0 + 0.4*P1 = 0.6*P0 + 0.4*P1 = 0.6*(0;0) + 0.4*(5;0) = (2; 0)B(0.5) = (1-0.5)*P0 + 0.5*P1 = 0.5*P0 + 0.5*P1 = 0.5*(0;0) + 0.5*(5;0) = (2.5; 0)B(0.6) = (1-0.6)*P0 + 0.6*P1 = 0.4*P0 + 0.6*P1 = 0.4*(0;0) + 0.6*(5;0) = (3; 0)B(0.7) = (1-0.7)*P0 + 0.7*P1 = 0.3*P0 + 0.7*P1 = 0.3*(0;0) + 0.7*(5;0) = (3.5; 0)B(0.8) = (1-0.8)*P0 + 0.8*P1 = 0.2*P0 + 0.8*P1 = 0.2*(0;0) + 0.8*(5;0) = (4; 0)B(0.9) = (1-0.9)*P0 + 0.9*P1 = 0.1*P0 + 0.9*P1 = 0.1*(0;0) + 0.9*(5;0) = (4.5; 0)
Все полученные точки лежат на одной прямой – это и есть кривая Безье первого порядка.
Время идет, точка движется от старта к финишу. И в любой момент времени мы точно знаем, где она находится.
Кривые Безье второго порядка и больше
В определении кривых Безье выше первого порядка кроме начала и конца появляются дополнительные опорные точки, смысл которых сложно понять с первого захода.
Непосредственно через них кривая не проходит, так зачем же они нужны?
На самом деле эти точки определяют направление движения (направление изгиба кривой) и крутизну этого изгиба.
Квадратичная кривая
Кривая Безье второго порядка, или квадратичная, задается тремя контрольными точками:
- P0 – начало;
- P2 – конец;
- P1 – вспомогательная точка, определяющая изгиб кривой.
Маленький спойлер: кривая Безье второго порядка имеет форму параболы (не обязательно симметричной).
Формула у нее вот такая:
B(t) = (1 - t)2*P0 + 2t*(1 - t)*P1 + t2*P2
Проверим, что в начале и конце движения мы окажемся в точках P0 и P2 соответственно:
- B(0) = (1 — 0)2 *P0 + 2*0*(1 — 0) * P1 + 02*P2 = P0
- B(1) = (1 — 1)2 *P0 + 2*1*(1 — 1) * P1 + 12*P2 = P2
На примере:
- P0 (-1; 0)
- P2 (1; 0)
- опорная точка P1 (0; 2):
Найдем, где будет точка через половину времени t (0.5):
B(0.5) = 0.25*P0 + 0.5*P1 + 0.25*P2 = (-0.25; 0) + (0; 1) + (0.25; 0) = (0; 1)
То есть на половине временного интервала мы окажемся в точке (0; 1).
Если найти еще несколько точек, вырисуется ровная парабола. Так, в общем, и было задумано для простоты вычислений и визуальной ясности.
Рекурсивность кривых Безье
Волшебство кривых Безье заключается в том, что они рекурсивны. То есть умея строить кривую первого порядка, мы можем построить и квадратичную кривую, даже не зная ее формулы.
Вернемся к предыдущему примеру:
- P0 (-1; 0)
- P2 (1; 0)
- опорная точка P1 (0; 2):
Предположим, что мы не знаем, как построить кривую второго порядка между P0 и P2. Но мы можем построить простейшую кривую первого порядка между P0 и P1, а также между P1 и P2, пользуясь формулой:
B(t) = (1-t)*P0 + t*P1
Для каждого момента времени мы можем найти положение точки на каждой из этих кривых.
Например, в момент времени 0.25 соответствующие точки Q0 и Q1 будут в таких позициях:
Между этими точками тоже можно построить кривую первого порядка.
Магия заключается в том, что точка на этой кривой в момент времени t = 0.25 соответствует точке на искомой кривой второго порядка в этот же момент времени.
Распишем чуть подробнее.
Мы хотим найти точку на кривой второго порядка P0-P11-P2 в момент времени t.
- Этому моменту на кривой P0-P1 соответствует точка Q0;
- А на кривой P1-P2 – точка Q1.
Искомая точка – это точка на кривой Q0-Q1, соответствующая моменту времени t.
Этот рекурсивный алгоритм построения кривой Безье носит имя Поля де Кастельжо.
Кубическая кривая
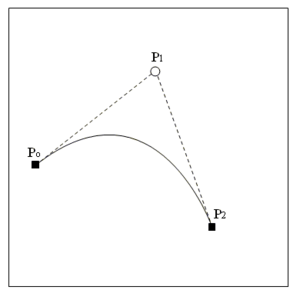
Кривая Безье третьего порядка, или кубическая кривая, определяется уже четырьмя опорными точками – началом, концом и двумя вспомогательными, через которые она не будет непосредственно проходить.
Две вспомогательные точки снова определяют направление и крутизну изгибов кривой.
Формула кубической кривой еще сложнее:
B(t) = (1 - t)3*P0 + 3t*(1-t)2*P1 + 3t2*(1 - t)*P2 + t3*P3
Вы можете попробовать эту кривую рассчитать самостоятельно.
Обратите внимание, ее тоже можно получить рекурсивно!
Найти точку кривой третьего порядка в момент времени t можно по следующему алгоритму:
- Строим кривые первого порядка P0-P1, P1-P2, P2-P3
- Находим на них соответствующие t точки Q0, Q1, Q2
- Строим кривые первого порядка Q0-Q1 и Q1-Q2
- Находим на них соответствующие t точки R0 и R1
- Строим кривую первого порядка R0-R1
- Находим на ней точку, соответствующую
t.
Зачем все это нужно?
Круто, теперь мы умеем строить кривые Безье любого порядка, но зачем нам это нужно? Каково практическое применение этих построений?
Кривые Безье используются в описаниях шрифтов TrueType, в SVG, GIMP и других графических форматах, в 3D-графике. Они используются даже в CSS для описания плавности анимации.
В общем, штука очень полезная.
Вслед
за построением кривой Безье, следующей
важной задачей будет нахождение точки
p(u)
на кривой по заданному u.
Простой вариант – развернуть описание
кривой в полную форму f(u)
= ( f(u),
g(u),
h(u)
) (см. Пример) и подставлять отдельные
значения u
в это уравнение, чтобы получать f(u).
Хот способ найден, но он не является
численно стойким (т.е. в процессе
вычисления многочленов могут возникать
числовые ошибки).
Далее
мы запишем номера [number]
контрольных точек. То есть, контрольные
точки – это 00
для p0,
01
для p1,
…, 0i
для pi,
…, 0n
для pn.
Нули (0)
в этих номерах обозначают начальную
или 0-ю
итерацию. Позже вместо нуля будет 1,
2,
3,
и так далее.
Принцип
алгоритма de
Casteljau’s
в таком выборе точки C
на отрезке AB,
чтобы отношение расстояния между A
и C
к расстоянию между A
и B
было равно, скажем, u.
Найдем способ определить точку C.
Вектор
от A
до B
равен B
– A.
Так как u
– это коэффициент в пределах от 0 до 1,
точка C
находится в u(B
– A).
Вводя в рассмотрение положение точки
A,
получаем C
равно A
+ u(B
– A)
= (1 – u)A
+ uB.
Таким образом, для данного u,
(1 – u)A
+ uB
– это точка C
между A
и B,
причем отношение расстояний между C
и A
и между A
и B
равно u.
Смысл
алгоритма de
Casteljau’s
таков. Допустим, надо найти p(u),
где u
в пределах [0,1]. Начиная с первой ломаной,
00-01-02-03…-0n,
на каждом сегменте 0i
… 0(i+1)
по вышеуказанной формуле находим точки
1i,
такие, чтобы отношение расстояний между
0i
и 1i
и между 0i
и 0(i+1)
было равно u.
В итоге получим n
точек 10,
11,
12,
…., 1(n-1).
Они
образуют новую ломаную из n
– 1 сегментов.

Я
тут написал прогу на Delphi,
строит кривые Безье по этому алгоритму.
Очень просто. Могу дать исходники 8-).
(прим. перев.)
На
рисунке выше, u
равно 0.4. 10
лежит на отрезке между 00
и 01,
11
– между 01
и 02,
…, а 14
– между 04
и 05.
Эти новые точки обозначены синим цветом.
Теперь
новые точки обозначены 1i.
Проделывая эту операцию с новой кривой,
затем с полученной и так далее, получим
в итоге одну точку. De
Casteljau
докаазал, что это – точка p(u)
на кривой, соответствующая u.
На
рисунке выше показано нахождение точки
на кривой, для u=0.4
– это точка 50.
Это
– геометрическое представление алгоритма
de
Casteljau,
одно из самых красивых в разработке
кривых.
Вычисления
На
рисунке показана схема нахождения точки
на кривой Безье по алгоритму de
Casteljau.

Вход
(Input):
массив p[0:n]
из n+1
точек и действительное число u
Выход
(Output):
точка на кривой, p(u)
Используется:
массив точек q[0:n]
for
i
:= 0 to
n
do
q[i]
:= p[i];
// сохраняем введенное
for
k
:= 1 to
n
do
for
i
:= 0 to
n
– k
do
q[i]
:= (1 – u)q[i]
+ uq[i
+ 1];
return
q[0];
Рекурсивное Представление
Вышеизложенные
вычисления можно провести и по-другому,
с помощью рекурсии. Пусть P0,j
будет Pj
для j
= 0, 1, …, n.
То есть, P0,j
– это j-й
элемент в 0 столбце. Элемент
j
в столбце i
находим так:
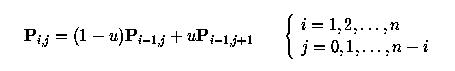
Говоря
точнее, элемент Pi,j
– это сумма (1-u)Pi-1,j
(сверху слева) и uPi-1,j+1
(снизу слева). Конечный результат (т.e.
точка на кривой) – это Pn,0.
Исходя из этого, можно сразу составить
такую рекурсивную процедуру:
function
deCasteljau(i,j)
begin
if
i
= 0 then
return
P0,j
else
return
(1-u)*
deCasteljau(i-1,j)
+ u*
deCasteljau(i-1,j+1)
end
Выглядит
она простой и короткой; тем не менее,
она очень неэффективна. И вот почему.
Блин,
не хочу я вам[SSN],
объяснять, почему она неэффективна. –
(прим. перев.)
We
start with a call to deCasteljau(n,0)
for computing Pn,0.
The else
part splits this call into two more calls, deCasteljau(n-1,0)
for computing Pn-1,0
and deCasteljau(n-1,1)
for computing Pn-1,1.
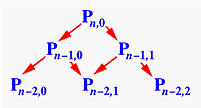
Consider
the call to deCasteljau(n-1,0).
It splits into two more calls, deCasteljau(n-2,0)
for computing Pn-2,0
and deCasteljau(n-2,1)
for computing Pn-2,1.
The call to deCasteljau(n-1,1)
splits into two calls, deCasteljau(n-2,1)
for computing Pn-2,1
and deCasteljau(n-2,2)
for computing Pn-2,2.
Thus, deCasteljau(n-2,1)
is called twice. If we keep expanding these function calls, we should
discover that almost all function calls for computing Pi,j
are repeated, not once but many many times. How bad is this? In fact,
the above computation scheme is very similar to the following way of
computing the n-th
Fibonacci number:
Тут
процедура сравнивается с процедурой
вычисления чисел Фибоначи – прим. перев.:
function
Fibonacci(n)
begin
if
n
= 0 or
n
= 1 then
return
1
else
return
Fibonacci
(n-1)
+ Fibonacci
(n-2)
end
Чтобы
найти касательный и нормальный вектора
в точке на кривой Безье, нам нужно знать
ее производную в этой точке. К счастью,
это просто, как два бита переслать.
Кривая
Безье, построенная по n
+ 1 контрольным точкам p0,
p1,
…, pn
имеет следующее уравнение:
где
коэффициент Безье Bn,i(u)
рассчитывается по формуле:
Так
как контрольные точки постоянны и не
зависят от переменной u,
вычисление p‘(u)
сводится к вычислению производных
коэффициентов Безье. После алгебраических
преобразований имеем такой результат
для B‘n,i(u):

Затем,
вычисляя производную кривой p(u),
получим:

Пусть
q0
= n(p1
– p0),
q1
= n(p2
– p1),
q2
= n(p3
– p2),
…, qn-1
= n(pn
– pn-1).
Вышеизложенное уравнение уменьшается
до
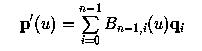
Таким
образом, производная p(u)
– это кривая Безье n
– 1 пстепени, построенная по n
контрольным точкам n(p1
– p0),
n(p2
– p1),
n(p3
– p2),
…, n(pn
– pn-1).
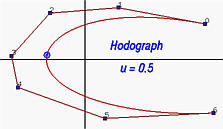
Эта производная кривая обычно называется
годографом
исходной кривой Безье. Заметьте, что
pi+1
– pi
– это вектор от pi
до pi+1
и n(pi+1
– pi)
в n
раз длиннее этого вектора. Имея в наличии
контрольные точки кривой, можно легко
получить контрольные точки ее производной.
Рисунок слева показывает кривую Безье
7 степени, а справа – ее производную, т.е.
кривую Безье
6 степени.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Кривые Безье. Немного о пересечениях и как можно проще
Время на прочтение
4 мин
Количество просмотров 6.6K
Вы сталкивались когда-нибудь с построением (непрерывного) пути обхода кривой на плоскости, заданной отрезками и кривыми Безье?
Вроде бы не сильно сложная задача: состыковать отрезки кривых в один путь и обойти его “не отрывая пера”. Замкнутая кривая обходится в одном направлении, ответвления — в прямом и обратном, начало и конец в одном узле.
Всё было хорошо, пока из-под рук дизайнеров не стали вылезать монструозные пути, где отдельные кривые могли пересекаться или не точно состыковываться. Объяснение было предельно простым — визуально они все лежат как надо, а для станка, который этот путь будет обходить, такие отклонения незаметны.
Вооружившись знанием о величине максимально допустимого отклонения, я приступил к исследованию, результатами которого хочу поделиться.
Первое что я сделал — это разобрался как на сегодняшний день (октябрь 2020) обстоят дела с поиском точек пересечения кривых. То ли я не там искал, то ли не то спрашивал, но найти простого решения не получилось. Хотя, идея с результантом пары полиномов довольно занимательна. Много разных алгоритмов связанных с кривыми Безье собрано здесь.
Что не понравилось в известных способах и что точно не хочется делать, так это численно искать корни полиномов, или даже решать квадратичные уравнения. Очень не хочется исследовать кривые на экстремумы. Да и вообще, хотелось бы избежать деления, возведения в степень и всего того, что может привести к неопределённому поведению.
Пример
Если пытаться продолжить кривую, то не факт что она вообще пересечётся с другой кривой, хотя они находятся достаточно близко
Итак, с чем придётся работать.
-
Точки задаются типом
Point, например так:using Point = std::array<double, 2>;Для
Pointопределены операторы сложения, вычитания, умножения на скаляр, скалярного умножения. -
Задана величина
Rдопустимого отклонения точек. -
Кривые заданы массивами опорных (контрольных) точек
std::vector<Point>. -
Почти совпадающие кривые следует отмечать и, по возможности, удалять, например, если это забытый дубликат (копипаста — это зло).
Первое, что точно понадобиться, это простой способ вычисления значения параметрической кривой. (Простой в смысле реализации и читабельности):
Point point(const std::vector<Point> &curve, double t, int n, int i)
{
return n == 0 ? curve[i] : (point(curve, t, n - 1, i - 1) * (1 - t) + point(curve, t, n - 1, i) * t);
}Оставлять функцию в таком виде для постоянного использования не стоит — лучше спрятать её подальше, а пользоваться такой:
Point point(const std::vector<Point> &curve, double t)
{
return point(curve, t, curve.size() - 1, curve.size() - 1);
}Здесь, curve — контейнер для опорных точек: для отрезка их две, для кривой Безье три или четыре или более.
Второе — точки надо как-то сравнивать, с учётом R:
template <>
struct std::less<Point>
{
bool operator()(const Point &a, const Point &b, const double edge = R) const
{
for (auto i = a.size(); i-- > 0;) {
if (a[i] + edge < b[i])
return true;
if (a[i] > b[i] + edge)
return false;
}
return false;
}
};Для поиска точек пересечения пары кривых я воспользовался идеей деления каждой кривой на две до тех пор пока есть пересечение области значений этих кривых. А чтобы не заморачиваться с экстремумами и интервалами монотонности, использовал тот факт, что кривая Безье ограничена выпуклым многоугольником, вершинами которого являются опорные точки кривой. Или даже ещё проще — достаточно ограничивающего эти точки прямоугольника:
struct Rect
{
Point topLeft, bottomRight;
Rect(const Point &point);
Rect(const std::vector<Point> &curve);
bool isCross(const Rect &rect, const double edge) const
{
for (auto i = topLeft.size(); i-- > 0;) {
if (topLeft[i] > rect.bottomRight[i] + edge
|| bottomRight[i] + edge < rect.topLeft[i])
return false;
}
return true;
}
};Алгоритм поиска рекурсивный и достаточно простой
void find(const std::vector<Point> &curveA, const std::vector<Point> &curveB,
double tA, double tB, double dt)
{1. Проверить, что эти кривые ещё не отмечены как подобные.
if (m_isSimilarCurve)
return;2. Проверить, что ограничивающие прямоугольники кривых пересекаются
Rect aRect(curveA);
Rect bRect(curveB);
if (!aRect.isCross(bRect, R))
return;3. Если отрезки кривых меньше R/2, то можно считать, что пересечение найдено
if (isNear(aRect.tl, aRect.br, R / 2) && isNear(bRect.tl, bRect.br, R / 2)) {
// 3.1 Для найденного пересечения сохранить наиболее близкие концы кривых
addBest(curveA.front(), curveA.back(), curveB.front(), curveB.back(), tA, tB, dt);
m_isSimilarCurve = (m_result.size() > curveA.size() * curveB.size());
return;
}4. Разделить кривые
const auto curveALeft = subCurve(curveA, 0, 0.5);
const auto curveARight = subCurve(curveA, 0.5, 1.0);
const auto curveBLeft = subCurve(curveB, 0, 0.5);
const auto curveBRight = subCurve(curveB, 0.5, 1.0);5. Продолжить поиск для каждого отрезка кривой
const auto dtHalf = dt / 2;
find(curveALeft, curveBLeft, tA, tB, dtHalf);
find(curveALeft, curveBRight, tA, tB + dtHalf, dtHalf);
find(curveARight, curveBLeft, tA + dtHalf, tB, dtHalf);
find(curveARight, curveBRight, tA + dtHalf, tB + dtHalf, dtHalf);}Вот тут-то и выполз самый главный вопрос: как найти опорные точки кривой, которая является частью исходной кривой в интервале t от t1 до t2?
После исследования к чему приводит подстановка t = (t2 - t1) t' + t1 я обнаружил простую закономерность. Первая опорная точка вычисляется по исходной кривой при t = t1, последняя при t = t2. Это логично, так как по свойствам кривых Безье (полиномов Бернштейна) крайние точки лежат на кривой. Для остальных точек нашлось простое правило: если в процессе вычисления на шаге k вместо t2 подставить t1, то в результате получим опорную точку под номером k:
Point point(const std::vector<Point> &curve, double t1, int n, int i, double t2, int k)
{
return n > k ? (point(curve, t1, n - 1, i - 1, t2, k) * (1 - t2) +
point(curve, t1, n - 1, i, t2, k) * t2)
: point(curve, t1, n, i);
}Эту функцию тоже лучше спрятать куда подальше, а для получения всех опорных точек воспользоваться этой:
std::vector<Point> subCurve(const std::vector<Point> &curve, double t1, double t2)
{
std::vector<Point> result(curve.size());
for (auto k = result.size(); k-- > 0;) {
result[k] = point(curve, t1, curve.size() - 1, curve.size() - 1, t2, curve.size() - 1 - k);
}
return result;
}Вот, собственно, и всё.
Примечания.
t1иt2могут быть любыми:subCurve(curve, 1, 0)даст кривую, которая “движется” от конечной точкиcurveк начальной,subCurve(curve, 1, 2)экстраполируетcurveза пределами последней опорной точки.
- Реализации некоторых методов опущены намеренно, так как не содержат ничего особенно интересного.
- Функция
point(curve, t)не подходит для вычисления множества точек на кривой (например для растрезации), для этого лучше подойдёт вычисление с помощью треугольной матрицы.
Кривы́е Безье́ — типы кривых, предложенные в 60-х годах XX века независимо друг от друга Пьером Безье из автомобилестроительной компании «Рено» и Полем де Кастельжо из компании «Ситроен», где применялись для проектирования кузовов автомобилей.
Несмотря на то, что открытие де Кастельжо было сделано несколько ранее Безье (1959), его исследования не публиковались и скрывались компанией как производственная тайна до конца 1960-х.
Кривая Безье является частным случаем многочленов Бернштейна, описанных русским математиком Сергеем Натановичем Бернштейном в 1912 году.
Впервые кривые были представлены широкой публике в 1962 году французским инженером Пьером Безье, который, разработав их независимо от де Кастельжо, использовал их для компьютерного проектирования автомобильных кузовов. Кривые были названы именем Безье, а именем де Кастельжо назван разработанный им рекурсивный способ определения кривых (алгоритм де Кастельжо).
Впоследствии это открытие стало одним из важнейших инструментов систем автоматизированного проектирования и программ компьютерной графики.
Определение[править | править код]
Пусть в пространстве
размерности
над
задана последовательность контрольных точек 
где 
а
для 
Тогда множество
точек
с координатами 
для
где
а
для
,
называется кривой Безье.
Многочлен
степени
по параметру
называется базисной функцией (соответствующей контрольной точке 
Здесь 
из
по 
Замечания[править | править код]
- Кривая Безье, соответствующая как
так и
, есть точка
.
- Кривая Безье, соответствующая паре
, то есть, при
, есть (линейно) параметризованный отрезок, соединяющий точку
(при
) с точкой
(при
).
- При любом порядке
кривая Безье содержит как точку
(это — образ параметра
), так и точку
(это — образ параметра
).
- Кривая Безье (в общем случае, то есть, если не выродилась в точку
) ориентируема, поскольку является образом ориентированного отрезка
. Последовательностям контрольных точек
и
соответствуют кривые Безье, которые совпадают как множества точек, но имеют (в общем случае) противоположные ориентации.
- Кривые Безье, соответствующие последовательностям контрольных точек
и
, при
не совпадают.
- Если изменить
, то изменяется только
.
Виды кривых Безье[править | править код]
Линейные кривые[править | править код]
При n = 1 кривая представляет собой отрезок прямой линии, опорные точки P0 и P1 определяют его начало и конец. Кривая задаётся уравнением:
.
Квадратичные кривые[править | править код]
Квадратичная кривая Безье
Квадратичная кривая Безье (n = 2) задаётся тремя опорными точками: P0, P1 и P2.
.
Квадратичные кривые Безье в составе сплайнов используются для описания формы символов в шрифтах TrueType и в SWF-файлах.
Кубические кривые[править | править код]
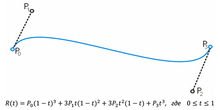
В параметрической форме кубическая кривая Безье (n = 3) описывается следующим уравнением:
.
Четыре опорные точки P0, P1, P2 и P3, заданные в 2- или 3-мерном пространстве, определяют форму кривой.
Линия берёт начало из точки P0, направляясь к P1 и заканчивается в точке P3, подходя к ней со стороны P2. То есть, кривая не проходит через точки P1 и P2, они используются для указания её направления. Длина отрезка между P0 и P1 определяет, как скоро кривая повернёт к P3.
В матричной форме кубическая кривая Безье записывается следующим образом:
,
где 
В современных графических системах и форматах, таких как PostScript (а также основанные на нём форматы Adobe Illustrator и Portable Document Format (PDF)), Scalable Vector Graphics (SVG)[1], Metafont, CorelDraw и GIMP для представления криволинейных форм используются сплайны Безье, составленные из кубических кривых.
Построение кривых Безье[править | править код]
Линейные кривые[править | править код]
Параметр t в функции, описывающей линейный случай кривой Безье, определяет, где именно на расстоянии от P0 до P1 находится B(t). Например, при t = 0,25 значение функции B(t) соответствует четверти расстояния между точками P0 и P1. Параметр t изменяется от 0 до 1, а B(t) описывает отрезок прямой между точками P0 и P1.
Квадратичные кривые[править | править код]
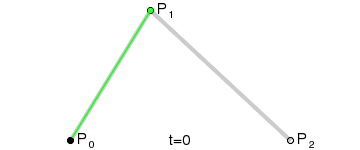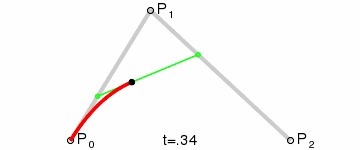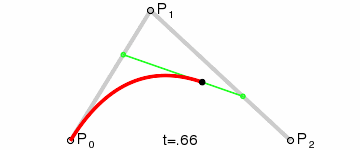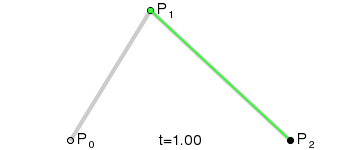
Для построения квадратичных кривых Безье требуется выделение двух промежуточных точек Q0 и Q1 из условия, чтобы параметр t изменялся от 0 до 1:
- Точка Q0 изменяется от P0 до P1 и описывает линейную кривую Безье.
- Точка Q1 изменяется от P1 до P2 и также описывает линейную кривую Безье.
- Точка B изменяется от Q0 до Q1 и описывает квадратичную кривую Безье.
|
Построение квадратичной кривой Безье |
Анимация t: [0;1] |
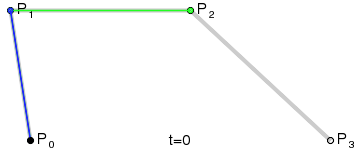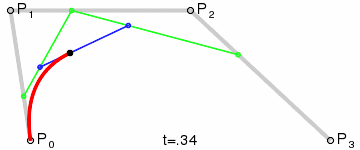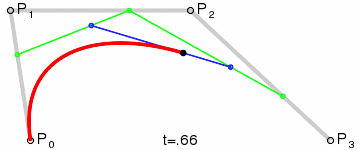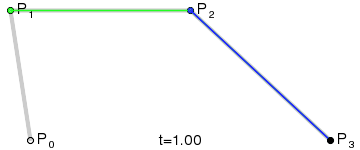
Кривые высших степеней[править | править код]
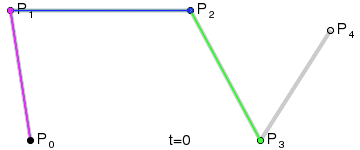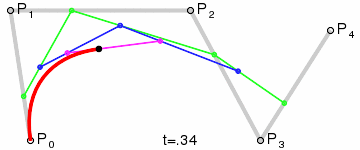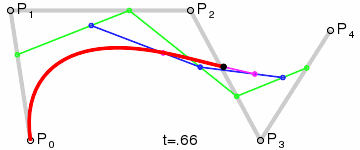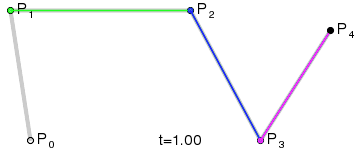
Для построения кривых высших порядков соответственно требуется больше промежуточных точек. Для кубической кривой это промежуточные точки Q0, Q1 и Q2, описывающие линейные кривые, а также точки R0 и R1, которые описывают квадратичные кривые: более простое уравнение 
|
Построение кубической кривой Безье |
Анимация t: [0;1] |
Для кривых четвёртой степени это будут точки Q0, Q1, Q2 и Q3, описывающие линейные кривые, R0, R1 и R2, которые описывают квадратичные кривые, а также точки S0 и S1, описывающие кубические кривые Безье:
|
Построение кривой Безье 4-й степени |
Анимация t: [0;1] |
Свойства кривой Безье[править | править код]
- непрерывность заполнения сегмента между начальной и конечной точками;
- кривая всегда располагается внутри фигуры, образованной линиями, соединяющими контрольные точки;
- при наличии только двух контрольных точек сегмент представляет собой прямую линию;
- прямая линия образуется при коллинеарном (на одной прямой) размещении управляющих точек;
- кривая Безье симметрична, то есть обмен местами между начальной и конечной точками (изменение направления траектории) не влияет на форму кривой;
- масштабирование и изменение пропорций кривой Безье не нарушает её стабильности, поскольку с математической точки зрения она «аффинно инвариантна»;
- изменение координат хотя бы одной из точек ведет к изменению формы всей кривой Безье;
- любой частичный отрезок кривой Безье также является кривой Безье;
- степень (порядок) кривой всегда на одну ступень меньше числа контрольных точек. Например, при трёх контрольных точках форма кривой — парабола, так как парабола — кривая 2-го порядка;
- окружность не может быть описана параметрическим уравнением кривой Безье;
- невозможно создать параллельные кривые Безье, за исключением тривиальных случаев (прямые линии и совпадающие кривые), хотя существуют алгоритмы, строящие приближённую параллельную кривую Безье с приемлемой для практики точностью.
Применение в компьютерной графике[править | править код]
Благодаря простоте задания и манипуляции кривые Безье нашли широкое применение в компьютерной графике для моделирования гладких линий. Кривая целиком лежит в выпуклой оболочке своих опорных точек. Это свойство кривых Безье с одной стороны значительно облегчает задачу нахождения точек пересечения кривых (если не пересекаются выпуклые оболочки опорных точек, то не пересекаются и сами кривые), а с другой стороны позволяет осуществлять интуитивно понятное управление параметрами кривой в графическом интерфейсе с помощью её опорных точек. Кроме того, аффинные преобразования кривой (перенос, масштабирование, вращение и др.) также могут быть осуществлены путём применения соответствующих трансформаций к опорным точкам.
Наибольшее значение имеют кривые Безье второй и третьей степеней (квадратичные и кубические). Кривые высших степеней при обработке требуют большего объёма вычислений и для практических целей используются реже. Для построения сложных по форме линий отдельные кривые Безье могут быть последовательно соединены друг с другом в сплайн Безье. Для того, чтобы обеспечить гладкость линии в месте соединения двух кривых, три смежные опорные точки обеих кривых должны лежать на одной прямой. В программах векторной графики, например Adobe Illustrator или Inkscape, подобные фрагменты известны под названием «путей» (path), а в 3DS Max и подобных программах 3D-моделирования кривые Безье имеют название «сплайны».
Преобразование квадратичных кривых Безье в кубические[править | править код]
Квадратичная кривая Безье с координатами 

Уровень дискретизации Кривых Безье[2][править | править код]
Уровень дискретизации определяется следующим образом:

, то есть каждая следующая точка должна отличаться от предыдущей на 1 (допустим пиксель). Причём, если задать 

Через него можно вычислить 
Решим это уравнение для кривых Безье первого порядка (линейных):


Запишем разницу точек для одной оси:

Вынесем общие множители за скобки:

Найдём 

так можно вычислить уровень дискретизации для обхода конкретной оси кривой Безье определённого порядка. То есть Вам нужно получить 16 таких уравнений для кривых Безье с 1го по 16 порядок, она всегда задаётся точками, их координаты достаточно будет подставить в полученное уравнение, чтобы обойти кривую с минимальным однозначным уровнем дискретизации.
См. также[править | править код]
- Поверхность Безье
- NURBS
- B-сплайн
- Кривые
Примечания[править | править код]
- ↑ World Wide Web Consortium (W3C). Scalable Vector Graphics (SVG) 1.1 (Second Edition). Chapter 8: Paths (англ.) (16 августа 2011). — W3C Recommendation. Дата обращения: 21 мая 2012. Архивировано 24 июня 2012 года.
- ↑ Алгоритмы: Кривые Безье. designermanuals.blogspot.com. Дата обращения: 9 января 2021. Архивировано 12 января 2021 года.
Литература[править | править код]
- Роджерс Д., Адамс Дж. Математические основы машинной графики. — М.: Мир, 2001.
Ссылки[править | править код]
- Wolfram Math World Bézier Curve (англ.)
- American Mathematical Society From Bézier to Bernstein (англ.)
- Кривые Безье в компьютерных играх [1] (рус.)
- Часы на кривых Безье (рус.)
- A Primer on Bézier Curves
Пока я тут мимо пробегаю оставлю ссылку на сообщение #416434. Возможно там есть что-то полезное.
Мне пока не понятна эта тема. Как я понимаю: сплайн может состоять из множества кривых Безье, т.е. по исходным точкам я смогу найти сплайны, и для каждого сплайна вычислить опорные точки криой безье, т.е. получается что я буду иметь отдельные опорные точки для каждого участка [


Или я что-то недопонимаю.
да, кривая без изломов
Переформулирую: есть 10 точек на плоскости, на всем промежутке функция либо возрастающая либо убывающая (не имеет экстремумов, т.е 

Имея ур-е кривой Безье:
Возьмем точку 





Наверное мне нужно построить 1 кубический сплайн, где взять 































![[0;1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc3bf59a5da5d8181083b228c8933efbda133483)








![{mathbf {B}}(t)=(1-t){mathbf {P}}_{0}+t{mathbf {P}}_{1}quad tin [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/184d535909668636476113a80ef52c158fb23e31)
![{mathbf {B}}(t)=(1-t)^{{2}}{mathbf {P}}_{0}+2t(1-t){mathbf {P}}_{1}+t^{{2}}{mathbf {P}}_{2},quad tin [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c39003f739f43fd3080ea11c28f4dba23944e9ac)




![{mathbf {B}}(t)=(1-t)^{3}{mathbf {P}}_{0}+3t(1-t)^{2}{mathbf {P}}_{1}+3t^{2}(1-t){mathbf {P}}_{2}+t^{3}{mathbf {P}}_{3},quad tin [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/26ff769812d3f7ad991b184a4ff63bfd08fd2919)






![$[x,y] = (1-t)^3 * P_0 +3*t*(1-t)^2*P_1 + 3*t^2 * (1-t)*P_2 + t^3*P_3; t in {[0,1]} $ $[x,y] = (1-t)^3 * P_0 +3*t*(1-t)^2*P_1 + 3*t^2 * (1-t)*P_2 + t^3*P_3; t in {[0,1]} $](https://dxdy-04.korotkov.co.uk/f/7/6/8/768c77a17618bab8a74c65f1f04c61a682.png)
