Дифференцируемость
функции
Операция
нахождения производной
называется дифференцированием функции.
Функция называетсядифференцируемой
в некоторой точке,
если она имеет в этой точке конечную
производную, идифференцируемой
на некотором множестве,
если она дифференцируема в каждой точке
этого множества.
В
силу геометрического смысла производной
следующие два свойства равносильны
друг другу: 1) функция ![]()
дифференцируема
при ![]()
;
2) график этой точки имеет касательную
в точке ![]()
,
не параллельную оси ординат (т.е. с
конечным угловым коэффициентом).
Теорема. Если
функция дифференцируема в некоторой
точке, она непрерывна в этой точке.
Доказательство.
Пусть в некоторой точке области
определения функции
существует
конечный предел
![]()
Запишем
приращение функции в виде
![]()
и
найдём
![]()
Следовательно,
если ![]()
,
то и ![]()
,
а это означает, что функция
непрерывна
в рассматриваемой точке.
Таким
образом, из дифференцируемости функции
вытекает её непрерывность. Обратная
теорема неверна, так как существуют
непрерывные функции, которые в некоторых
точках являются недифференцируемыми.
Пример
3. Функция
![]()
непрерывна
в точке ![]()
,
но не дифференцируема в этой точке,
так как в ней график не имеет касательной.
(рис. 79).
Из
сказанного выше следует, что непрерывность
в точке x является необходимым, но не
достаточным условием дифференцируемости
функции в этой точке, так как из
непрерывности функции в точке ![]()
не
всегда следует дифференцируемость в
этой точке.
51. Дифференциал функции. Связь с производной, геометрический смысл.
Пусть
функция
определена
на промежутке ![]()
и
дифференцируема в окрестности
точки ![]()
,тогда ![]()
или
по теореме о связи бесконечно малых с
пределами функций имеем ![]()
,
где ![]()
–
бесконечно малая величина при ![]()
.
Отсюда:
![]()
. (
7.1)
Таким
образом, приращение функции ![]()
состоит
из двух слагаемых:
1) ![]()
–
линейного относительно
,
т.к. ![]()
;
2) ![]()
–
нелинейного относительно
,
т.к. ![]()
.
Определение. Дифференциалом
функции называется главная, линейная
относительно
часть
приращения функции, равная произведению
производной на приращение независимой
переменной:
![]()
. (
7.2)
Пример. Найти
приращение функции ![]()
при ![]()
и ![]()
:
Решение. ![]()
![]()
, ![]()
Пример. Найти
дифференциал функции ![]()
.
Решение.
По формуле (7.2.) имеем ![]()
.
Определение. Дифференциал
независимой переменной ![]()
равен
приращению этой переменной:
![]()
(
7.3)
Тогда
формулу (7.2) для дифференциала функции
можно записать в виде:
![]()
(
7.4)
Откуда ![]()
,
поэтому ![]()
можно
рассматривать не только как символическое
обозначение производной, но и как обычную
дробь с числителем ![]()
и
знаменателем ![]()
.
|
|
Геометрический |
Следовательно,
с геометрической точки зрения дифференциал
функции есть приращение ординаты
касательной, проведенной к графику
функции
в
данной точке, когда
получает
приращение
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Рассмотрим функцию 
Известно, что если a ∈ X и является предельной точкой множества X , то функция  , определенная на X , непрерывна в точке a тогда и только тогда, когда функция
, определенная на X , непрерывна в точке a тогда и только тогда, когда функция  имеет представление
имеет представление
 (x) =
(x) =  (a) + o(1), x → a,
(a) + o(1), x → a,
то есть
∆ a(∆x) = o(∆x0), ∆x → 0.
a(∆x) = o(∆x0), ∆x → 0.
Выделим класс функций, для которых можно уточнить характеристику приращений ∆fa(∆x) функции f, соответствующих приращению ∆x аргумента.
Определение
Определение 4.1. Пусть функция  определена на множестве X, a ∈ X и a — предельная точка множества X . Функция
определена на множестве X, a ∈ X и a — предельная точка множества X . Функция  называется дифференцируемой в точке а по множеству X, если существует такое число A, что
называется дифференцируемой в точке а по множеству X, если существует такое число A, что
∆ a(∆x) = A∆x + o(∆x), a + ∆x ∈ X, ∆x → 0. (4.1)
a(∆x) = A∆x + o(∆x), a + ∆x ∈ X, ∆x → 0. (4.1)
Иными словами, функция  дифференцируема в точке a, если существует линейная относительно ∆x функция A∆x, которая отличается от приращения ∆
дифференцируема в точке a, если существует линейная относительно ∆x функция A∆x, которая отличается от приращения ∆ a(∆x) функции в точке a, соответствующего приращению аргумента ∆x, на бесконечно малую более высокого порядка малости по сравнению с ∆x, когда ∆x → 0, при этом ∆x может принимать только такие значения, чтобы a+∆x ∈ X.
a(∆x) функции в точке a, соответствующего приращению аргумента ∆x, на бесконечно малую более высокого порядка малости по сравнению с ∆x, когда ∆x → 0, при этом ∆x может принимать только такие значения, чтобы a+∆x ∈ X.
Учитывая представление функции вида o(∆x) при ∆x → 0, заметим, что дифференцируемая в точке a по множеству X функция имеет вид
 (a + ∆x) = f(a) + A∆x + α(∆x) ∆x, (4.2)
(a + ∆x) = f(a) + A∆x + α(∆x) ∆x, (4.2)
где a + ∆x ∈ X и α(∆x) → o при ∆x → o, или
 (x) =
(x) =  (a) + A(x – a) + α(x – a) (x – a),
(a) + A(x – a) + α(x – a) (x – a),
где x ∈ X и α(x – a) → o при x → a.
Определение 4.2. Пусть функция  дифференцируема в точке a по множеству X. Линейная функция A ∆x, ∆x ∈ R, из представления (4.2) называется дифференциалом функции
дифференцируема в точке a по множеству X. Линейная функция A ∆x, ∆x ∈ R, из представления (4.2) называется дифференциалом функции  в точке a и обозначается d
в точке a и обозначается d a(∆x).
a(∆x).
Из определения 4.1 следует
Лемма 4.1. Для того чтобы функция  была дифференцируемой в точке a по множеству X, необходимо и достаточно, чтобы существовал конечный предел
была дифференцируемой в точке a по множеству X, необходимо и достаточно, чтобы существовал конечный предел
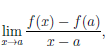 (4.3)
(4.3)
равный числу A из (4.1).
Следствие. Если функция  дифференцируема в точке a по множеству X, то представление (4.2) единственно и дифференциал функции
дифференцируема в точке a по множеству X, то представление (4.2) единственно и дифференциал функции  в точке a определяется однозначно. (Утверждение верно в силу единственности предела функции в точке).
в точке a определяется однозначно. (Утверждение верно в силу единственности предела функции в точке).
Определение 4.3. Пусть функция  определена на множестве X, a ∈ X и a — предельная точка множества X. Если существует в
определена на множестве X, a ∈ X и a — предельная точка множества X. Если существует в 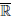 предел (4.3), то его называют производной функции
предел (4.3), то его называют производной функции  в точке a по множеству X и обозначают
в точке a по множеству X и обозначают  /(a) (по Лагранжу) или
/(a) (по Лагранжу) или 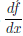 (a) (по Лейбницу).
(a) (по Лейбницу).
С учетом определения 4.3 лемма 4.1 принимает вид:
Лемма 4.2. Для того чтобы функция  была дифференцируемой в точке a по множеству X, необходимо и достаточно, чтобы она имела конечную производную в точке a по множеству X .
была дифференцируемой в точке a по множеству X, необходимо и достаточно, чтобы она имела конечную производную в точке a по множеству X .
Таким образом, если функция  дифференцируема в точке a по множеству X, то при a + ∆x ∈ X и ∆x → 0
дифференцируема в точке a по множеству X, то при a + ∆x ∈ X и ∆x → 0
∆ a(∆x) =
a(∆x) = /(a)∆x + o(∆x), d
/(a)∆x + o(∆x), d a(∆x) =
a(∆x) = /(a)∆x.
/(a)∆x.
Пример:
Пусть  :
:  →
→ 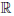 ,
,  (x) = c0 , ∀x ∈
(x) = c0 , ∀x ∈ 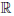 . Доказать, что функция
. Доказать, что функция  дифференцируема в каждой точке a ∈
дифференцируема в каждой точке a ∈ 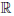 по множеству
по множеству 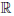 и
и  /(x) = 0, ∀ x ∈
/(x) = 0, ∀ x ∈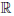 .
.
Пусть a — произвольная точка из 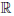 . Тогда
. Тогда
∆ a(∆x) = 0, ∀ ∆x ∈
a(∆x) = 0, ∀ ∆x ∈ 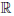 .
.
Поэтому 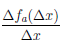 = 0,
= 0, 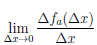 =0, а значит
=0, а значит  /(a) =0 и функция
/(a) =0 и функция  дифференцируема в точке a по множеству
дифференцируема в точке a по множеству 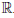 . Поскольку a — произвольная точка из
. Поскольку a — произвольная точка из 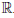 , то получили нужное.
, то получили нужное.
Пример:
Пусть h : 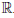 →
→ 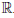 , h(x) = x, ∀x ∈
, h(x) = x, ∀x ∈ 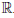 . Если a — некоторая точка из
. Если a — некоторая точка из 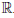 , то
, то
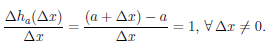
Отсюда следует, что производная функции h в точке a по множеству 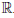 существует и равна 1. Таким образом, функция h дифференцируема в любой точке a ∈
существует и равна 1. Таким образом, функция h дифференцируема в любой точке a ∈ 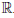 по множеству
по множеству 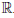 , при этом dha(∆x) = 1 ∙ ∆x.
, при этом dha(∆x) = 1 ∙ ∆x.
Как видим, для функции h(x) = x приращение функции в точке равно приращению переменной ∆x, а поэтому и дифференциал этой функции в точке так же равен ∆x, то есть, сокращая обозначение, можно написать, что dx = ∆x. Поэтому для произвольной дифференцируемой в точке a функции f равенство dfa(∆x) =  /(a)∆x можно переписать в виде
/(a)∆x можно переписать в виде
d a(dx) =
a(dx) =  /(a) dx или
/(a) dx или  /(a) =
/(a) = 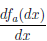
что напоминает символику Лейбница производной функции  в точке a.
в точке a.
Чтобы объяснить, как на дифференцируемость и значение производной влияет множество X , рассмотрим такой пример.
Пример:
Пусть 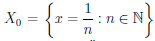 ,
, 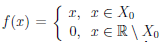 . Тогда, как легко следует из определений и двух предыдущих примеров, функция
. Тогда, как легко следует из определений и двух предыдущих примеров, функция 
В дальнейшем мы не будем явно указывать, по какому множеству X выполняется дифференцирование, поскольку это будет ясно из контекста определения функции, но забывать о множестве X и его роли в определении дифференцируемости функции не следует.
Теорема 4.1 (необходимое условие дифференцируемости). Если функция  дифференцируема в точке a, то она непрерывна в ней.
дифференцируема в точке a, то она непрерывна в ней.
Доказательство очевидно, поскольку представление (4.2) влечет существование 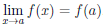 .
.
Замечание. Непрерывность функции в точке является необходимым, но не является достаточным условием дифференцируемости функции в точке. Для примера рассмотрим функцию  (x) = |x| в точке a = 0. Она непрерывна в точке
(x) = |x| в точке a = 0. Она непрерывна в точке
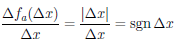 ,
,
поэтому не существует предел отношения 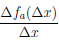 при ∆x → 0, то есть функция
при ∆x → 0, то есть функция  не дифференцируема в точке a = 0.
не дифференцируема в точке a = 0.
В полной аналогии с понятием левого и правого предела функции в данной точке вводятся понятия левой и правой производной функции  в точке.
в точке.
Определение 4.4. Пусть  определена на множестве X, a ∈ X, a — правосторонняя (левосторонняя) предельная точка X. Если в
определена на множестве X, a ∈ X, a — правосторонняя (левосторонняя) предельная точка X. Если в 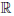 существует
существует
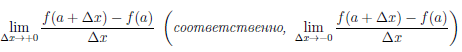
то его называют правой (левой) производной функции  в точке a и обозначают
в точке a и обозначают  /+0 (a) (соответственно,
/+0 (a) (соответственно,  /–0 (a)).
/–0 (a)).
Правая и левая производные функции  в точке a называются односторонними производными. Из сопоставления определений 4.3 и 4.4 и из теоремы о связи односторонних пределов функции с пределом вытекают следующие утверждения:
в точке a называются односторонними производными. Из сопоставления определений 4.3 и 4.4 и из теоремы о связи односторонних пределов функции с пределом вытекают следующие утверждения:
Теорема 4.2. Пусть функция  определена на множестве X и a ∈ X . Если a — односторонняя предельная точка множества X , то понятие производной функции
определена на множестве X и a ∈ X . Если a — односторонняя предельная точка множества X , то понятие производной функции  в точке a совпадает с односторонней производной функции
в точке a совпадает с односторонней производной функции  . Если же a — двусторонняя предельная точка X, то функция
. Если же a — двусторонняя предельная точка X, то функция  имеет в точке a производную тогда и только тогда, когда существуют обе односторонние производные функции
имеет в точке a производную тогда и только тогда, когда существуют обе односторонние производные функции  в этой точке, равные между собой. В случае выполнения последних условий
в этой точке, равные между собой. В случае выполнения последних условий  /(a) =
/(a) =  /+0 (a) =
/+0 (a) =  /–0 (a).
/–0 (a).
Возвращаясь к  (x) = ∣x∣, заметим, что
(x) = ∣x∣, заметим, что  /+0 (0) = 1,
/+0 (0) = 1,  /–0 (0) = -1.
/–0 (0) = -1.
Геометрический смысл производной и дифференциала
Пусть функция  определена и непрерывна на промежутке X , a — некоторая точка этого промежутка, ∆x — приращение аргумента, причем ∆x
определена и непрерывна на промежутке X , a — некоторая точка этого промежутка, ∆x — приращение аргумента, причем ∆x  0 и a + ∆x ∈ X. Поэтому точки M0(a,
0 и a + ∆x ∈ X. Поэтому точки M0(a,  (a)), M(a + ∆x,
(a)), M(a + ∆x,  (a + ∆x)) принадлежат графику Γ
(a + ∆x)) принадлежат графику Γ функции
функции  . Прямую, проходящую через точки M0 и M , называют секущей.
. Прямую, проходящую через точки M0 и M , называют секущей.
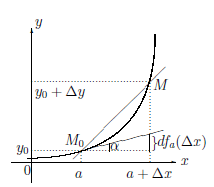
Поскольку точка M0 фиксирована, то угловой коэффициент k секущей MM0 является функцией от ∆x (величина ∆x приращения аргумента вполне определяет точку M графика функции), то есть k = k(∆x). Ясно, что k(∆x) = 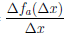 и секущая M0M имеет уравнение
и секущая M0M имеет уравнение
y = k(∆x)(x – a) +y0, где y0 =  (a).
(a).
Определение 4.5. Если существует конечный предел
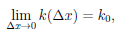
то прямая, соответствующая уравнению y = k0 (x – a) + y0, называется наклонной (невертикальной) касательной к графику Γфункции  в точке M0 (a0, y0). Если же существует бесконечный предел
в точке M0 (a0, y0). Если же существует бесконечный предел
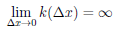
(функция k(∆x) является бесконечно большой в точке 0), то прямая x = a называется вертикальной касательной к Γ точке M0 .
точке M0 .
Поскольку угловой коэффициент касательной, в случае ее существования, получен из углового коэффициента секущей с помощью предельного перехода при ∆x → 0, то касательную часто называют предельным положением секущей M0M при M → M0 по Γ (при ∆x → 0
(при ∆x → 0  (a + ∆x) →
(a + ∆x) →  (a), так как функция
(a), так как функция  непрерывна в точке a).
непрерывна в точке a).
Теорема 4.3. Пусть функция  непрерывна на промежутке X и a ∈ X. Чтобы график Γ
непрерывна на промежутке X и a ∈ X. Чтобы график Γ функции
функции  имел в точке M0(a,
имел в точке M0(a,  (a)) невертикальную касательную, необходимо и достаточно, чтобы функция
(a)) невертикальную касательную, необходимо и достаточно, чтобы функция  была дифференцируемой в точке a. При этом уравнение касательной имеет вид
была дифференцируемой в точке a. При этом уравнение касательной имеет вид
y =  /(a)(x-a) +
/(a)(x-a) + (a). (4.4)
(a). (4.4)
Для того, чтобы график Γ функции
функции  имел в точке M0 вертикальную касательную, необходимо и достаточно, чтобы функция
имел в точке M0 вертикальную касательную, необходимо и достаточно, чтобы функция  имела в точке a бесконечную производную.
имела в точке a бесконечную производную.
Так как k(∆x) =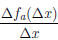 , то предел этой функции в
, то предел этой функции в 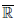 при ∆x → 0 существует тогда и только тогда, когда функция
при ∆x → 0 существует тогда и только тогда, когда функция  имеет в точке a производную
имеет в точке a производную  /(a), причем k0 =
/(a), причем k0 = 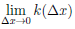 =
=  /(a). Учитывая определение 4.5, получаем ∆x→0 нужное.
/(a). Учитывая определение 4.5, получаем ∆x→0 нужное.
Из определений 4.1 и 4.5 и теоремы 4.3 получаем следующее определение невертикальной касательной к графику функции в точке M0 , которое равносильно определению 4.5.
в точке M0 , которое равносильно определению 4.5.
Определение 4.6. Пусть функция  непрерывна на промежутке X и a ∈ X. Прямая y = k x+b называется невертикальной касательной к графику функции
непрерывна на промежутке X и a ∈ X. Прямая y = k x+b называется невертикальной касательной к графику функции  в точке M0(a,
в точке M0(a,  (a)), если
(a)), если
 (x) – (kx + b) = o(x – a), x → a.
(x) – (kx + b) = o(x – a), x → a.
Выясним геометрический смысл дифференциала dfa(∆x). Будем считать, что функция  дифференцируема в точке a. Поэтому график функции
дифференцируема в точке a. Поэтому график функции  в точке M0(a,
в точке M0(a,  (a)) имеет невертикальную касательную, уравнением которой является (4.4). Так как d
(a)) имеет невертикальную касательную, уравнением которой является (4.4). Так как d a(∆x) =
a(∆x) =  /(a)∆x, где ∆x = x – a, то ykac(x) = d
/(a)∆x, где ∆x = x – a, то ykac(x) = d a(∆x) +
a(∆x) +  (a). Следовательно, дифференциал d
(a). Следовательно, дифференциал d a(∆x) функции
a(∆x) функции  в точке a есть приращение ординаты касательной, проведенной в точке M0 к Γ
в точке a есть приращение ординаты касательной, проведенной в точке M0 к Γ , то есть d
, то есть d a(∆x) = ykac(a+ ∆x) –
a(∆x) = ykac(a+ ∆x) –  (a).
(a).
Производная и дифференциал функции на множестве
Определение 4.7. Если каждая точка множества X является его предельной точкой и функция  дифференцируема в каждой точке множества X, то говорят, что функция
дифференцируема в каждой точке множества X, то говорят, что функция  дифференцируема на множестве X . Функцию, определенную правилом x(∈ X) →
дифференцируема на множестве X . Функцию, определенную правилом x(∈ X) →  /(x), называют производной функции
/(x), называют производной функции  на множестве X и обозначают
на множестве X и обозначают  / или
/ или 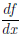 . Если ∆x — некоторое dx фиксированное число, причем ∆x
. Если ∆x — некоторое dx фиксированное число, причем ∆x  0, то функцию, определенную правилом x ∈ X → d
0, то функцию, определенную правилом x ∈ X → d x(∆x) ∈
x(∆x) ∈  , называют дифференциалом функции
, называют дифференциалом функции  на множестве X, соответствующим приращению ∆x аргумента, и обозначают d
на множестве X, соответствующим приращению ∆x аргумента, и обозначают d (∆x).
(∆x).
Напомним, что d a(∆x) является линейной функцией от ∆x ∈
a(∆x) является линейной функцией от ∆x ∈  . Учитывая, что d
. Учитывая, что d a(∆x) =
a(∆x) =  /(a)∆x, получаем, d
/(a)∆x, получаем, d (∆x) =
(∆x) = / ∆x.
/ ∆x.
Рассмотрим несколько примеров.
Пример:
Пусть  (x) = xα, α ∈
(x) = xα, α ∈  , Xα — область определения функции.
, Xα — область определения функции.
Заметим, что если α ≥ 0, то 0 ∈ Xα , если α  0, то 0 ∈/ Xα .
0, то 0 ∈/ Xα .
а) Пусть α = 0. Тогда  (x) = 1, ∀x ∈ X =
(x) = 1, ∀x ∈ X =  . В силу примера 1 функция
. В силу примера 1 функция  дифференцируема на
дифференцируема на  и
и  /(x) = 0, ∀x ∈
/(x) = 0, ∀x ∈  .
.
б) Пусть α ∈  {0}, и a ∈ Xα {0}. Тогда
{0}, и a ∈ Xα {0}. Тогда
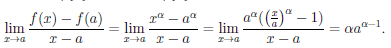
Следовательно, при α ∈  {0} функция
{0} функция дифференцируема на Xα {0} и
дифференцируема на Xα {0} и  /(x) = αxα-1.
/(x) = αxα-1.
в) Пусть α > 0 и a = 0. Тогда
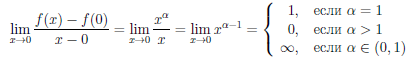
Последнее означает, что функция  (x) = xα дифференцируема в точке x = 0, если α ≥ 1;
(x) = xα дифференцируема в точке x = 0, если α ≥ 1;  /(0) = 0 при α > 1,
/(0) = 0 при α > 1,  / (0) = 1 при α = 1. Функция
/ (0) = 1 при α = 1. Функция  (x) = xα теряет свойство дифференцируемости в точке x = 0, если α ∈ (0, 1), при этом ее график имеет в точке x = 0 вертикальную касательную.
(x) = xα теряет свойство дифференцируемости в точке x = 0, если α ∈ (0, 1), при этом ее график имеет в точке x = 0 вертикальную касательную.
Пример:
Пусть  (x) = ax, где a > 0 и a
(x) = ax, где a > 0 и a  1. Фиксируем точку x0 ∈
1. Фиксируем точку x0 ∈  . Так как
. Так как
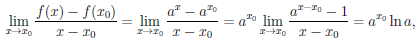
то функция  дифференцируема в точке x0 и
дифференцируема в точке x0 и  /(x0) = ax0 ln a. Следовательно, функция
/(x0) = ax0 ln a. Следовательно, функция  дифференцируема на
дифференцируема на  и (ax)/ = axln a. В частности, (ex)/ = ex, ∀x ∈
и (ax)/ = axln a. В частности, (ex)/ = ex, ∀x ∈  .
.
Пример:
Пусть  (x) = sin x, ∀x ∈
(x) = sin x, ∀x ∈  , a — некоторая точка из
, a — некоторая точка из  . Так как
. Так как
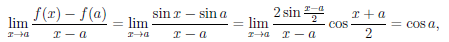
то функция  дифференцируема в точке a и
дифференцируема в точке a и  /(a) = cos a. Следовательно, функция
/(a) = cos a. Следовательно, функция  (x) = sinx дифференцируема на
(x) = sinx дифференцируема на  и (sin x)0 = cos x, ∀x ∈
и (sin x)0 = cos x, ∀x ∈  .
.
Аналогично доказывается, что функция  (x) = cos x дифференцируема на
(x) = cos x дифференцируема на  и (cos x)0 = — sin x, ∀x ∈
и (cos x)0 = — sin x, ∀x ∈  .
.
Основные правила вычисления производной
Теорема 4.4. Если функции  и ψ определены на множестве X и дифференцируемы в точке a ∈ X, то функции
и ψ определены на множестве X и дифференцируемы в точке a ∈ X, то функции  + ψ,
+ ψ,  ∙ ψ и, если ψ(a) = 0, — ψ дифференцируемы в точке a, при этом
∙ ψ и, если ψ(a) = 0, — ψ дифференцируемы в точке a, при этом
1) ( +ψ)0(a)=
+ψ)0(a)= /(a)+ψ/(a),
/(a)+ψ/(a),
d( +ψ)a(∆x) = d
+ψ)a(∆x) = d a(∆x) + dψa(∆x);
a(∆x) + dψa(∆x);
2) ( ∙ ψ)0(a) =
∙ ψ)0(a) =  /(a) ∙ ψ(a)+
/(a) ∙ ψ(a)+  (a) ∙ ψ/(a),
(a) ∙ ψ/(a),
d ( ∙ ψ)a(Ax) = d
∙ ψ)a(Ax) = d a(∆x) ∙ ψ(a) +
a(∆x) ∙ ψ(a) +  (a) ∙ dψa(∆x);
(a) ∙ dψa(∆x);
3) 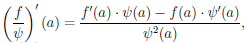
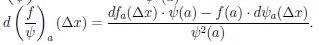
Докажем только третью часть утверждения. По условию теоремы функция ψ дифференцируема в точке a и ψ(a)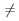 0. В силу локальных свойств непрерывной в точке функции найдется такая окрестность Ua точки a, что на множестве X ∩ Ua функция ψ отлична от нуля. Поэтому на множестве X ∩ Ua определена функция
0. В силу локальных свойств непрерывной в точке функции найдется такая окрестность Ua точки a, что на множестве X ∩ Ua функция ψ отлична от нуля. Поэтому на множестве X ∩ Ua определена функция  ∕ψ. Для любого x ∈ X ∩ Ua имеем
∕ψ. Для любого x ∈ X ∩ Ua имеем
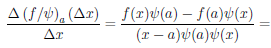
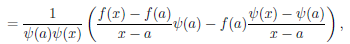
где ∆x = x – a. Учитывая дифференцируемость и непрерывность функций  и ψ в точке a, получим, что существует предел последнего выражения при x → a, который равен
и ψ в точке a, получим, что существует предел последнего выражения при x → a, который равен
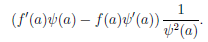 (4.5)
(4.5)
Поэтому существует предел левой части, равный числу (4.5). Значит, функция  ∕ψ дифференцируема в точке a, ее производная и дифференциал в точке a определяются формулами 3).
∕ψ дифференцируема в точке a, ее производная и дифференциал в точке a определяются формулами 3).
Замечание. Доказательство теоремы 4.4, опирающееся на определение дифференцируемой в точке функции, см. в [4, с.200-202].
Пример №1
Пусть  (x) = tg x, x
(x) = tg x, x 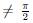 + kπ, k ∈ Z. Поскольку tg x = sin x/ cos x, то, согласно теореме 4.4, функция
+ kπ, k ∈ Z. Поскольку tg x = sin x/ cos x, то, согласно теореме 4.4, функция  дифференцируема в области определения и
дифференцируема в области определения и
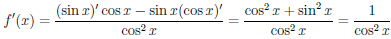 .
.
Аналогично доказывается, что функция  (x) = ctgx дифференцируема в своей области определения и
(x) = ctgx дифференцируема в своей области определения и
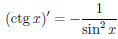 .
.
Теорема 4.5 (о дифференцируемости суперпозиции функций). Если X и Y — подмножества в  , функция
, функция  : X → Y дифференцируема в точке x0, а функция ψ : Y →
: X → Y дифференцируема в точке x0, а функция ψ : Y →  дифференцируема в точке y0 =
дифференцируема в точке y0 =  (x0), то суперпозиция функций ψ ◦
(x0), то суперпозиция функций ψ ◦  дифференцируема в точке x0 и (ψ ◦
дифференцируема в точке x0 и (ψ ◦  )/(x0) = ψ/(
)/(x0) = ψ/( (x0)) ∙
(x0)) ∙  /(χ0) или (ψ ◦
/(χ0) или (ψ ◦  )/(x0) = (ψ/ ◦
)/(x0) = (ψ/ ◦  ) (x0) ∙
) (x0) ∙  /(χo).
/(χo).
По условию теоремы функция ψ дифференцируема в точке y0 , поэтому ∀y ∈ Y {y0}
ψ(y) -ψ(y0) = ψ/(y0)(y-y0) +α(y – y0)(y – y0), (4.6)
где α(y – y0) → 0 при y → y0. Без ограничения общности можно считать, что α(0) = 0. Тогда представление (4.6) функции ψ имеет место на множестве Y . Поскольку  : X → Y , то ∀x ∈ X
: X → Y , то ∀x ∈ X
ψ( (x)) -ψ(y0) = ψ/(y0)(f(x) -y0) + α(
(x)) -ψ(y0) = ψ/(y0)(f(x) -y0) + α( (x) -y0)(
(x) -y0)( (x) – y0).
(x) – y0).
Учитывая, что y0 =  (x0), получим для x ∈ X{x0}
(x0), получим для x ∈ X{x0}
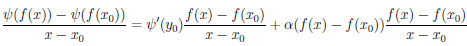 .
.
Так как при x → x0  f/(xo) ∈
f/(xo) ∈  , α(
, α( (x) —
(x) —  (x0)) → 0, то существует конечный предел правой части предыдущего равенства, равный числу Ψ/(y0) ∙
(x0)) → 0, то существует конечный предел правой части предыдущего равенства, равный числу Ψ/(y0) ∙  /(x0). Значит, существует предел его левой части при x → x0 и он равен Ψ/(y0)
/(x0). Значит, существует предел его левой части при x → x0 и он равен Ψ/(y0)  /(x0), то есть существует предел
/(x0), то есть существует предел
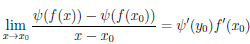 .
.
Следовательно, функция ψ ◦  дифференцируема в точке x0 и ее производная в точке x0 равна (ψ ◦
дифференцируема в точке x0 и ее производная в точке x0 равна (ψ ◦  )/(x0) = ψ/(
)/(x0) = ψ/( (x0))
(x0))  /(x0).
/(x0).
Следствие. Пусть функция  : X → Y дифференцируема на множестве X , а функция ψ : Y →
: X → Y дифференцируема на множестве X , а функция ψ : Y →  дифференцируема на множестве Y . Тогда суперпозиция функций ψ ◦
дифференцируема на множестве Y . Тогда суперпозиция функций ψ ◦  дифференцируема на множестве X и
дифференцируема на множестве X и
(ψ ◦  )/ = (ψ0 ◦
)/ = (ψ0 ◦  ) ∙
) ∙  /.
/.
Теорема 4.6 (о производной обратной функции). Пусть функция  определена, непрерывна и возрастает или убывает на промежутке X . Если функция
определена, непрерывна и возрастает или убывает на промежутке X . Если функция  дифференцируема в точке x0 промежутка X и
дифференцируема в точке x0 промежутка X и  /(x0)
/(x0) 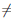 0, то обратная функция
0, то обратная функция  —1, определённая на промежутке Y =
—1, определённая на промежутке Y =  (X) дифференцируема в точке y0 =
(X) дифференцируема в точке y0 =  (x0 ) ∈ Y и
(x0 ) ∈ Y и
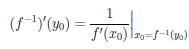 .
.
Пусть  — возрастающая функция на X . Тогда по теореме о непрерывности функции обратной к монотонной, обратная к
— возрастающая функция на X . Тогда по теореме о непрерывности функции обратной к монотонной, обратная к  функция
функция  —1 определена возрастает и непрерывна на промежутке Y, причем промежуток Y имеет тот же вид, что и промежуток X .
—1 определена возрастает и непрерывна на промежутке Y, причем промежуток Y имеет тот же вид, что и промежуток X .
Пусть ∆y 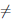 0 и y = y0 + ∆y ∈ Y . Тогда x0 + ∆x =
0 и y = y0 + ∆y ∈ Y . Тогда x0 + ∆x =  -1 (y0 + ∆y) ∈ X и ∆x
-1 (y0 + ∆y) ∈ X и ∆x 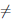 0. Покажем существование конечного предела
0. Покажем существование конечного предела
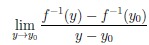 ,
,
воспользовавшись теоремой Гейне существования предела функции (см. теорему 2.31), и найдем его. Для этого фиксируем произвольную последовательность {yn}: yn ∈ Y , yn 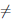 y0, yn → y0. Положим xn =
y0, yn → y0. Положим xn =  -1(yn), n ∈ N. Тогда yn =
-1(yn), n ∈ N. Тогда yn =  (xn), y0 =
(xn), y0 =  (x0 ) и по определению обратной функции имеем
(x0 ) и по определению обратной функции имеем
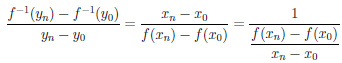 , (4 7)
, (4 7)
(воспользовались тем, что xn 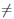 x0 в силу биективности функции
x0 в силу биективности функции  -1).
-1).
По непрерывности функции  -1 в точке y0, xn =
-1 в точке y0, xn =  -1 (yn) → x0. Кроме того,
-1 (yn) → x0. Кроме того,  дифференцируема в точке x0 и
дифференцируема в точке x0 и  / (x0 )
/ (x0 ) 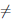 0. Поэтому существует предел
0. Поэтому существует предел
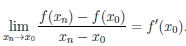 .
.
И из (4.7) получаем существование предела
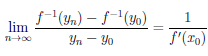 .
.
Поскольку {yn} — произвольная последовательность точек множества Y, отличных от y0 , стремящаяся к y0 , то по теореме Гейне
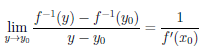 .
.
Поэтому функция -1 дифференцируема в точке y0 и (
-1 дифференцируема в точке y0 и ( -1 )/(y0) = (
-1 )/(y0) = ( /(x0))-1 .
/(x0))-1 .
Следствие. Пусть функция  возрастает (убывает) на промежутке X, дифференцируема на нем и
возрастает (убывает) на промежутке X, дифференцируема на нем и  /(x)
/(x) 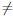
 0, ∀x ∈ X. Тогда обратная функция
0, ∀x ∈ X. Тогда обратная функция  -1 дифференцируема на промежутке
-1 дифференцируема на промежутке  (X) и
(X) и
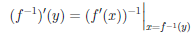 .
.
Замечание 1. Если выполняются условия теоремы и функция  -1 дифференцируема в точке yo, то из тождества (
-1 дифференцируема в точке yo, то из тождества ( -1 ◦
-1 ◦  )(x) = x по теореме о дифференцируемости суперпозиции функций следует, что
)(x) = x по теореме о дифференцируемости суперпозиции функций следует, что
( -1)/(yo)
-1)/(yo)  /(xo) = 1 и (
/(xo) = 1 и ( -1)/(yo) = (
-1)/(yo) = ( /(xo))-1.
/(xo))-1.
Замечание 2. Если функция  удовлетворяет условиям теоремы, но при этом
удовлетворяет условиям теоремы, но при этом  /(x0) = 0, то функция
/(x0) = 0, то функция  -1 имеет в точке y0 бесконечную производную.
-1 имеет в точке y0 бесконечную производную.
Замечание 3. Если функция  удовлетворяет условиям теоремы, но при этом
удовлетворяет условиям теоремы, но при этом  /(x0) = ∞, то функция
/(x0) = ∞, то функция  -1 имеет в точке y0 производную равную 0.
-1 имеет в точке y0 производную равную 0.
Пример №2
Покажем, что функция ψ(x) = loga x, a > 0, a 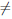 1 дифференцируема на промежутке (0, +∞) и ψ/(x) =
1 дифференцируема на промежутке (0, +∞) и ψ/(x) =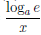 .
.
Пусть для определенности a > 1. Функция ψ является обратной к функции 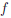 :
: 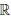 → (0, +∞),
→ (0, +∞), 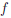 (x) = ax. Так как функция
(x) = ax. Так как функция  /(x) = ax ln a
/(x) = ax ln a 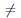 0, ∀x ∈
0, ∀x ∈ 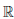 , то по теореме 4.6 функция
, то по теореме 4.6 функция 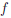 -1 дифференцируема на (0, +∞), причем
-1 дифференцируема на (0, +∞), причем
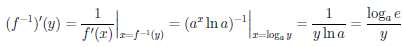 .
.
Значит функция ψ(x) = loga x дифференцируема на (0, +∞) и (loga x)/ =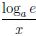 . В частности, (ln x) /=
. В частности, (ln x) /=  ,∀x ∈ (0, +∞).
,∀x ∈ (0, +∞).
Пример №3
Покажем дифференцируемость на интервале (—1, 1) функции ψ(x) = arcsin x и наличие у нее производной на отрезке [—1, 1].
Известно, что функция ψ : [—1,1] → [—π∕2,π∕2] является непрерывной обратной к функции 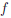 : [—π∕2,π∕2] → [—1,1], f(x) = sinx. Поскольку функция
: [—π∕2,π∕2] → [—1,1], f(x) = sinx. Поскольку функция 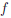 дифференцируема на отрезке [—π∕2,π∕2], и
дифференцируема на отрезке [—π∕2,π∕2], и
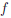 /(x) = cos x, ∀x ∈ [—π∕2,π∕2],
/(x) = cos x, ∀x ∈ [—π∕2,π∕2], 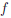 /(±π∕2) = 0,
/(±π∕2) = 0, 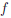 (±π∕2) = ±1,
(±π∕2) = ±1,
то согласно теореме 4.6 и замечания 2 к ней, функция ψ дифференцируема на (—1, 1),
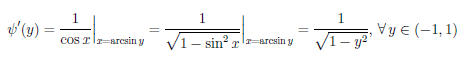
и ψ/(±1) = ∞.
Пример №4
Пусть функции y = U(x) и y = V (x) дифференцируемы на множестве X ⊂  и U (x) > 0, ∀ x ∈ X. Докажем, что функция g(x) = (U (x))V (x) дифференцируема на X.
и U (x) > 0, ∀ x ∈ X. Докажем, что функция g(x) = (U (x))V (x) дифференцируема на X.
Действительно, так как g(x) = exp(V (x) ln U (x)), то в силу теорем 4.4 — 4.6 и примера 8 функция g дифференцируема на X и
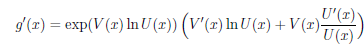 .
.
Инвариантность формы первого дифференциала
В начале главы показано, что если функция  : X ⊂
: X ⊂  →
→  дифференцируема в точке x0 и x — независимая переменная ее, то
дифференцируема в точке x0 и x — независимая переменная ее, то
dfx0 (∆x) = f/(x0)dx, где dx = ∆x. (4.8)
Пусть функция x = ψ(t), ψ : T → X, дифференцируема в точке t0 и ψ(t0) = x0 . В силу теоремы о дифференцируемости суперпозиции функций функция  ◦ ψ дифференцируема в точке t0 и
◦ ψ дифференцируема в точке t0 и
( ◦ ψ)/(t0) =
◦ ψ)/(t0) =  /(ψ(t0))ψ/(t0) =
/(ψ(t0))ψ/(t0) =  /(x0)ψ/(t0).
/(x0)ψ/(t0).
Поскольку t — независимая переменная функции y =  ◦ ψ(t), то
◦ ψ(t), то
d( ◦ ψ)t0 (∆t) = (
◦ ψ)t0 (∆t) = ( ◦ ψ)/(t0)dt =
◦ ψ)/(t0)dt =  /(x0)ψ/(t0)dt, где dt = ∆t.
/(x0)ψ/(t0)dt, где dt = ∆t.
Кроме того, ψ/(t0)dt = dψt0(∆t). Если обозначить dx = dψt0(∆t), то получим
d( ◦ ψ)t0(∆t) =
◦ ψ)t0(∆t) =  /(x0)dx. (4.9)
/(x0)dx. (4.9)
Сопоставляя полученную формулу с (4.8), замечаем, что форма дифференциала функции y =  (x) не зависит от того, является ли x независимой переменной или дифференцируемой функцией другой переменной. Это свойство называют свойством инвариантности формы дифференциала. Следует заметить, что в формуле (4.8) dx = ∆x, а в (4.9) dx = dψt0 (∆t).
(x) не зависит от того, является ли x независимой переменной или дифференцируемой функцией другой переменной. Это свойство называют свойством инвариантности формы дифференциала. Следует заметить, что в формуле (4.8) dx = ∆x, а в (4.9) dx = dψt0 (∆t).
Производные высших порядков
Пусть функция  : X ⊂
: X ⊂ 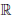 →
→ 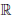 дифференцируема на множестве X1 ⊂ X . Тогда на множестве X1 определена функция
дифференцируема на множестве X1 ⊂ X . Тогда на множестве X1 определена функция  /. Если функция
/. Если функция  / дифференцируема в точке a ∈ X1 , то говорят, что функция
/ дифференцируема в точке a ∈ X1 , то говорят, что функция  дважды дифференцируема в точке a, а производную (
дважды дифференцируема в точке a, а производную ( /)/(a) называют второй производной функции
/)/(a) называют второй производной функции  в точке a и обозначают одним из следующих символов
в точке a и обозначают одним из следующих символов
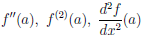 .
.
Если функция  дважды дифференцируема в каждой точке множества X2 ⊂ X1 , то говорят, что функция
дважды дифференцируема в каждой точке множества X2 ⊂ X1 , то говорят, что функция  дважды дифференцируема на множестве X2 . Функцию, определяемую правилом x(∈ X2) → f//(x), называют второй производной функции
дважды дифференцируема на множестве X2 . Функцию, определяемую правилом x(∈ X2) → f//(x), называют второй производной функции  на множестве X2 . Индуктивно можно ввести понятие n раз (n > 1) дифференцируемой в точке и на множестве функции и n-ой производной функции
на множестве X2 . Индуктивно можно ввести понятие n раз (n > 1) дифференцируемой в точке и на множестве функции и n-ой производной функции  в точке и на множестве Xn ⊂ Xn-1. Например, если n > 1, то
в точке и на множестве Xn ⊂ Xn-1. Например, если n > 1, то  (n) (x0) = (
(n) (x0) = ( (n-1))/(x0), если последняя производная существует. Заметим, что при n > 1 для любого k = 1, . . . , n – 1
(n-1))/(x0), если последняя производная существует. Заметим, что при n > 1 для любого k = 1, . . . , n – 1
 (n)(x0)=(
(n)(x0)=( (k))(n-k)(x0).
(k))(n-k)(x0).
Пример №5
Пусть  : (0, +∞) →
: (0, +∞) → 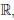 ,
,  (x) = xα, где α ∈
(x) = xα, где α ∈ 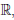 , α
, α 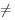 0. Покажем, что функция
0. Покажем, что функция  дифференцируема любое число раз на (0, +∞).
дифференцируема любое число раз на (0, +∞).
В силу примера 4 функция  дифференцируема на (0, +∞) и
дифференцируема на (0, +∞) и
f/(x) = αxα-1, ∀x ∈ (0, +∞).
Поскольку  / является произведением постоянной и степенной функций, то по теореме 4.4 она дифференцируема на интервале (0, +∞). Следовательно, функция
/ является произведением постоянной и степенной функций, то по теореме 4.4 она дифференцируема на интервале (0, +∞). Следовательно, функция  дважды дифференцируема на нем и
дважды дифференцируема на нем и
 //(x) = α(α – 1)xα-2.
//(x) = α(α – 1)xα-2.
Заметим, что если α = 1, то  /(x) = 1 и
/(x) = 1 и  // (x) = 0, ∀x ∈ (0, +∞).
// (x) = 0, ∀x ∈ (0, +∞).
Предположим, что n ∈ 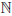 , n > 2, функция
, n > 2, функция  (n – 1) раз дифференцируема на (0, +∞) и
(n – 1) раз дифференцируема на (0, +∞) и  (n-1) (x) = α(α – 1)…(α – n + 2)xα-n+1.
(n-1) (x) = α(α – 1)…(α – n + 2)xα-n+1.
Функция  (n-1) является произведением числа α(α – 1)…(α – n + 2) и степенной функции xα-n+1 . Поэтому она дифференцируема на (0, +∞) и
(n-1) является произведением числа α(α – 1)…(α – n + 2) и степенной функции xα-n+1 . Поэтому она дифференцируема на (0, +∞) и  (n) (x) = α(α – 1)…(α – n + 2)(α – n + 1)xα-n. Следовательно, функция
(n) (x) = α(α – 1)…(α – n + 2)(α – n + 1)xα-n. Следовательно, функция  дифференцируема в области определения любое число раз и
дифференцируема в области определения любое число раз и
 (n) (x) = α(α – 1)…(α -n+ 1)xα-n, ∀n ∈ N.
(n) (x) = α(α – 1)…(α -n+ 1)xα-n, ∀n ∈ N.
В частности, если α = k0 ∈ 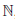 , то
, то
 (n) (x) = 0, ∀n > k0, ∀x ∈ (0, +∞);
(n) (x) = 0, ∀n > k0, ∀x ∈ (0, +∞);  (k0) (x) = k0!, ∀ x ∈ (0, +∞).
(k0) (x) = k0!, ∀ x ∈ (0, +∞).
Если α = -1, то  (n)(x) = (-1)nn!x-n-1, ∀x ∈ (0, +∞).
(n)(x) = (-1)nn!x-n-1, ∀x ∈ (0, +∞).
Из теоремы 4.5 получаем, что функция  (x) = (ax + b)α, где α ∈
(x) = (ax + b)α, где α ∈ 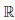 , дифференцируема любое число раз при x >
, дифференцируема любое число раз при x > 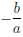 и
и
((ax + b)α)(n) = α(α – 1)…(α – n + 1)(ax + b)α-nan.
Наконец, согласно теореме 4.4, многочлен
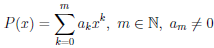 ,
,
дифференцируем на 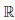 любое число раз и
любое число раз и
P (n) (x) = 0, ∀n > m, P (m) (x) = m! am, ∀ x ∈ 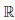 .
.
Пример №6
Докажем, что функция  (x) = ln x дифференцируема любое число раз на (0, +∞).
(x) = ln x дифференцируема любое число раз на (0, +∞).
В примере 8 показано, что рассматриваемая функция  дифференцируема в области определения и
дифференцируема в области определения и  /(x) = x-1. Учитывая предыдущий пример и определение производной n-го порядка, заключаем, что функция
/(x) = x-1. Учитывая предыдущий пример и определение производной n-го порядка, заключаем, что функция  дифференцируема любое число раз на интервале (0, +∞) и
дифференцируема любое число раз на интервале (0, +∞) и
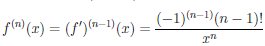
Замечание. Функция y = ln(ax + b) дифференцируема любое число раз в области её определения и
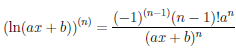
Можно доказать, что функции abx+c, sin(ax+b), cos(ax+b) дифференцируемы любое число раз на  и ∀n ∈
и ∀n ∈ 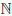
(abx+c)(n) = bnabx+c lnn a, (ebx+c)(n) = ebx+c bn,
(sin(ax + b))(n) = an sin (ax + b + n 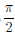 ),
),
(cos(ax + b))(n) = an cos (ax + b + n 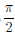 ) .
) .
Теорема 4.7. Пусть функции  и φ n раз дифференцируемы на множестве X (n ≥ 2). Тогда функции
и φ n раз дифференцируемы на множестве X (n ≥ 2). Тогда функции  + φ,
+ φ,  ∙ φ, n раз дифференцируемы на множестве X и
∙ φ, n раз дифференцируемы на множестве X и
( + φ) (n) =
+ φ) (n) =  (n) + φ(n) ,
(n) + φ(n) ,
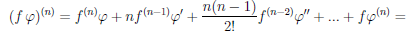
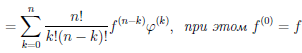 .
.
Последняя формула носит имя Лейбница и очень напоминает бином Ньютона. Только её и докажем, используя метод математической индукции. При n = 1 по утверждению 2) теоремы 4.4 имеем:  ∙ φ дифференцируема на множестве X и (
∙ φ дифференцируема на множестве X и ( φ)/ =
φ)/ =  /φ + φ/
/φ + φ/  , поэтому доказываемое утверждение верно при n = 1. Предположим, что для некоторого номера m
, поэтому доказываемое утверждение верно при n = 1. Предположим, что для некоторого номера m 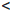 n функция
n функция  ∙ φ дифференцируема m раз на X и
∙ φ дифференцируема m раз на X и
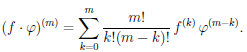 (4.10)
(4.10)
Так как функции  и φ дифференцируемы n раз на X и m
и φ дифференцируемы n раз на X и m 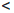 n, то функции
n, то функции  ,φ,
,φ, / ,φ/,… ,
/ ,φ/,… ,  (m), φ(m) дифференцируемы на множестве X. Поэтому правая часть равенства (4.10) является дифференцируемой на X функцией, а значит функция
(m), φ(m) дифференцируемы на множестве X. Поэтому правая часть равенства (4.10) является дифференцируемой на X функцией, а значит функция  ∙ φ (m + 1) раз дифференцируема на X и
∙ φ (m + 1) раз дифференцируема на X и
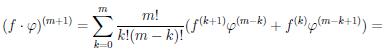
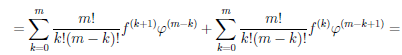
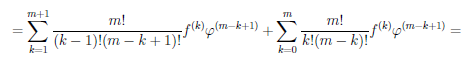
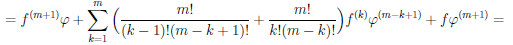
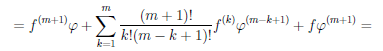
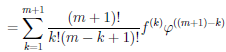
Пример №7
Используя формулу Лейбница, найдем n—ую производную функции f(x) = 2×2 sin2 x.
Так как  (x) = x2(1 — cos 2x) = x2 — x2 cos 2x и производные порядка выше, чем степень многочлена, тождественно равны нулю, то при n > 2
(x) = x2(1 — cos 2x) = x2 — x2 cos 2x и производные порядка выше, чем степень многочлена, тождественно равны нулю, то при n > 2
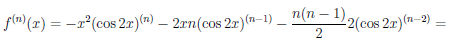
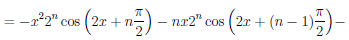
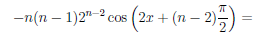
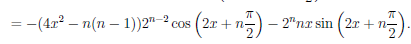
Дифференциалы высших порядков
Пусть функция  , определенная на множестве X ⊂
, определенная на множестве X ⊂  , дифференцируема n раз (n ≥ 2) на X.
, дифференцируема n раз (n ≥ 2) на X.
Зафиксируем число ∆x  0 и рассмотрим функцию d
0 и рассмотрим функцию d (∆x), определенную на множестве X . Так как
(∆x), определенную на множестве X . Так как
d (∆x) =
(∆x) =  / ∆x, (4.11) то функция d
/ ∆x, (4.11) то функция d (∆x) дифференцируема на множестве X. Если x0 ∈ X, то величину d(d
(∆x) дифференцируема на множестве X. Если x0 ∈ X, то величину d(d (∆x))x0 (∆x) называют вторым дифференциалом функции
(∆x))x0 (∆x) называют вторым дифференциалом функции  в точке x0, соответствующим приращению ∆x независимой переменной, и обозначают d2
в точке x0, соответствующим приращению ∆x независимой переменной, и обозначают d2 x0 (∆x). Из формулы (4.11) получаем, что
x0 (∆x). Из формулы (4.11) получаем, что
d2 x0(∆x) = d(
x0(∆x) = d( / ∆x)x0 (∆x) = (
/ ∆x)x0 (∆x) = ( / ∆x)/(x0) ∆x =
/ ∆x)/(x0) ∆x =  //(x0)(∆x)2.
//(x0)(∆x)2.
Для сокращения записи, используются обозначения
(∆x)2 = ∆x2, (dx)2 = dx2.
Следовательно, второй дифференциал функции f в точке x0 вычисляется по формуле
d2 x0(∆x) =
x0(∆x) =  //(x0) ∆x2, d2
//(x0) ∆x2, d2 x0 (dx) =
x0 (dx) =  //(x0) dx2.
//(x0) dx2.
По условию функция  дважды дифференцируема на множестве X , поэтому на X определена функция x → d2
дважды дифференцируема на множестве X , поэтому на X определена функция x → d2 x(∆x) (∆x — фиксированное число), которую называют вторым дифференциалом функции
x(∆x) (∆x — фиксированное число), которую называют вторым дифференциалом функции  на множестве X , соответствующим приращению ∆x независимой переменной. Ее обозначают d2
на множестве X , соответствующим приращению ∆x независимой переменной. Ее обозначают d2 (∆x). В силу предыдущего
(∆x). В силу предыдущего
d2 (∆x) =
(∆x) =  // ∙ ∆x2. (4.12)
// ∙ ∆x2. (4.12)
Индуктивно вводится понятие n-го дифференциала функции  в точке x0 из X и на множестве X . По индукции легко доказывается, что
в точке x0 из X и на множестве X . По индукции легко доказывается, что
dk x0 (∆x) =
x0 (∆x) =  (k)(x0) ∆xk, dk
(k)(x0) ∆xk, dk (∆x) =
(∆x) = (k) ∙ ∆xk, 1 ≤ k ≤ n.
(k) ∙ ∆xk, 1 ≤ k ≤ n.
В этой формуле ∆xk= (∆x)k. Аналогично предыдущему, в ней вместо ∆x можно использовать dx, сокращая в записи (dx)k до dxk.
Лемма 4.3. Дифференциалы второго и высших порядков, вообще говоря, не обладают свойством инвариантности формы.
Доказательство проведем для дифференциалов второго порядка. Пусть функция  дважды дифференцируема на множестве X ⊂
дважды дифференцируема на множестве X ⊂  , а функция φ : T → X дважды дифференцируема на множестве T. В силу теоремы 4.5 функция
, а функция φ : T → X дважды дифференцируема на множестве T. В силу теоремы 4.5 функция  ◦ φ дифференцируема на T и (
◦ φ дифференцируема на T и ( ◦ φ) = (
◦ φ) = ( / ◦ φ) ∙ φ/. Но
/ ◦ φ) ∙ φ/. Но и φ дважды дифференцируемы на T, поэтому
и φ дважды дифференцируемы на T, поэтому  / ◦ φ и φ/ дифференцируемые на T функции и функция
/ ◦ φ и φ/ дифференцируемые на T функции и функция  ◦ φ дважды дифференцируема на множестве T. Учитывая свойство инвариантности формы дифференциала первого порядка, получим, что
◦ φ дважды дифференцируема на множестве T. Учитывая свойство инвариантности формы дифференциала первого порядка, получим, что
d2(f ◦ φ)(∆t) = d (d( ◦ φ) ∆t)) ∆t) = d((
◦ φ) ∆t)) ∆t) = d(( / ◦ φ) dφ(∆t))(∆t) =
/ ◦ φ) dφ(∆t))(∆t) =
= d( / ◦ φ)(∆t) dφ(∆t) + (
/ ◦ φ)(∆t) dφ(∆t) + ( / ◦ φ) d2φ(∆t) =
/ ◦ φ) d2φ(∆t) =
= ( // ◦ φ) (dφ(∆t))2 + (
// ◦ φ) (dφ(∆t))2 + ( / ◦ φ) d2φ(∆t).
/ ◦ φ) d2φ(∆t).
Итак, функция  ◦ φ дважды дифференцируема и
◦ φ дважды дифференцируема и
d2(f ◦ φ)(∆t) = (f// ◦ φ) (dφ(∆t))2 + ( / ◦ φ) d2φ(∆t).
/ ◦ φ) d2φ(∆t).
Сравнивая представление второго дифференциала функции  (φ(t)) с формулой (4.12) для второго дифференциала функции
(φ(t)) с формулой (4.12) для второго дифференциала функции  (x), в котором x — независимая переменная, убеждаемся в том, что второй дифференциал не обладает свойством инвариантности формы. Тем более не обладают свойством инвариантности формы последующие дифференциалы.
(x), в котором x — независимая переменная, убеждаемся в том, что второй дифференциал не обладает свойством инвариантности формы. Тем более не обладают свойством инвариантности формы последующие дифференциалы.
Замечание. Если φ(t) = at + b, то формы дифференциалов высших порядков функции  и
и  ◦ φ совпадают
◦ φ совпадают
dn x(dx) =
x(dx) =  (n)(x)dxn,
(n)(x)dxn,
dn( ◦ φ)t(dt) =
◦ φ)t(dt) =  (n)(φ(t)) (dφt(dt))n, где dφt(dt) = a dt.
(n)(φ(t)) (dφt(dt))n, где dφt(dt) = a dt.
В заключение приведем определение, которым воспользуемся в дальнейшем.
Определение 4.8. Функция  называется n раз непрерывно дифференцируемой на множестве Х, если она n раз дифференцируема на нем и функция
называется n раз непрерывно дифференцируемой на множестве Х, если она n раз дифференцируема на нем и функция  (n) непрерывна на X . Класс функций непрерывно дифференцируемых n раз на множестве X будем обозначать Cn(X).
(n) непрерывна на X . Класс функций непрерывно дифференцируемых n раз на множестве X будем обозначать Cn(X).
Свойства функций, дифференцируемых на промежутках
Теорема 4.8 (Ферма). Пусть функция  определена на промежутке X, и в некоторой его внутренней точке c принимает наибольшее или наименьшее значение. Если функция
определена на промежутке X, и в некоторой его внутренней точке c принимает наибольшее или наименьшее значение. Если функция  дифференцируема в точке c, то
дифференцируема в точке c, то  /(c)
/(c) 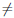 0.
0.
Для определенности будем считать, что функция  имеет в точке x = c наибольшее значение, то есть
имеет в точке x = c наибольшее значение, то есть  (x) –
(x) – (c) ≤ 0, ∀ x ∈ X. Предположим, что
(c) ≤ 0, ∀ x ∈ X. Предположим, что  /(c) 6= 0. По условию функция
/(c) 6= 0. По условию функция  дифференцируема в точке c, поэтому
дифференцируема в точке c, поэтому
 (x) –
(x) –  (c) = (
(c) = ( /(c) + α(x))(x -c), ∀x ∈ (a, b) {c} (4.13)
/(c) + α(x))(x -c), ∀x ∈ (a, b) {c} (4.13)
где α(x) → 0 при x → c. По локальному свойству функции, имеющей в точке ◦
конечный, отличный от нуля, предел, найдется окрестность Uc ⊂ X , в которой функция  /(c) + α(x) сохраняет знак числа
/(c) + α(x) сохраняет знак числа  /(c). Функция (x – c) имеет в этой окрестности по разные стороны от точки c значения разных знаков. Поэтому правая часть равенства (4.13) имеет в окрестности Uc по разные стороны от точки c значения разных знаков. Но по предположению на интервале X , а, значит, и в окрестности Uc,
/(c). Функция (x – c) имеет в этой окрестности по разные стороны от точки c значения разных знаков. Поэтому правая часть равенства (4.13) имеет в окрестности Uc по разные стороны от точки c значения разных знаков. Но по предположению на интервале X , а, значит, и в окрестности Uc,  (x) –
(x) –  (c) ≤ 0. Полученное противоречие доказывает, что
(c) ≤ 0. Полученное противоречие доказывает, что  /(c) = 0.
/(c) = 0.
Замечание 1. Если функция  определена на промежутке [a, b), принимает наибольшее или наименьшее значение в точке x = a и дифференцируема в ней, то может случиться, что
определена на промежутке [a, b), принимает наибольшее или наименьшее значение в точке x = a и дифференцируема в ней, то может случиться, что  /(a)
/(a) 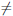 0. Как подтверждение можно рассмотреть функцию
0. Как подтверждение можно рассмотреть функцию  (x) = x на [0, 1).
(x) = x на [0, 1).
Замечание 2. Если функция  определена на (a, b), дифференцируема в точке c ∈ (a, b) и
определена на (a, b), дифференцируема в точке c ∈ (a, b) и  /(c) = 0, то не обязательно
/(c) = 0, то не обязательно  (c) есть наибольшее или наименьшее значение функции на интервале (a, b). Например, функция
(c) есть наибольшее или наименьшее значение функции на интервале (a, b). Например, функция  (x) = x3 дифференцируема на интервале (-1, 1), возрастает на нем и
(x) = x3 дифференцируема на интервале (-1, 1), возрастает на нем и  /(0) = 0.
/(0) = 0.
Замечание 3. Геометрически теорема Ферма означает, что в точке (c,  (c)) график функции y =
(c)) график функции y =  (x) имеет горизонтальную касательную.
(x) имеет горизонтальную касательную.
Теорема 4.9 (Дарбу). Если функция  дифференцируема на отрезке [a, b] и
дифференцируема на отрезке [a, b] и  /(a)
/(a)  / (b)
/ (b) 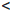 0 ( то есть
0 ( то есть  / принимает на концах отрезка значения разных знаков), то существует такая точка c ∈ (a, b), что
/ принимает на концах отрезка значения разных знаков), то существует такая точка c ∈ (a, b), что  /(c) = 0.
/(c) = 0.
Для определенности будем считать, что  /(a) > 0 и
/(a) > 0 и  /(b)
/(b) 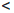 0. Поскольку функция
0. Поскольку функция  непрерывна на отрезке [a, b], то в силу теоремы Вейерштрасса она принимает на нем наибольшее значение, то есть
непрерывна на отрезке [a, b], то в силу теоремы Вейерштрасса она принимает на нем наибольшее значение, то есть
∃p ∈ [a, b] :  (p) = sup{
(p) = sup{ (x)|x ∈ [a, b]}.
(x)|x ∈ [a, b]}.
Покажем, что p 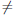 a. Так как
a. Так как  /(a) > 0, то найдется такое δ > 0, что
/(a) > 0, то найдется такое δ > 0, что
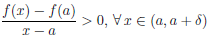 .
.
Но x-a > 0,∀x ∈(a, a+δ), поэтому  (x) >
(x) >  (a), ∀x ∈(a, a+δ). А это означает, что
(a), ∀x ∈(a, a+δ). А это означает, что  (a)
(a) 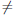 sup{
sup{ (x) : x ∈ [a, b]}.
(x) : x ∈ [a, b]}.
Аналогично доказывается, что p 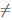 b. Значит, p ∈(a, b) и по теореме Ферма 4.8
b. Значит, p ∈(a, b) и по теореме Ферма 4.8  /(p) = 0.
/(p) = 0.
Следствие 1. Пусть функция  дифференцируема на отрезке [a, b], функция
дифференцируема на отрезке [a, b], функция  / принимает на концах его различные значения. Тогда для любого числа c, находящегося между
/ принимает на концах его различные значения. Тогда для любого числа c, находящегося между  /(a) и
/(a) и  /(b), найдется такая точка γ ∈ (a, b) что
/(b), найдется такая точка γ ∈ (a, b) что  /(γ) = c.
/(γ) = c.
Будем считать, что  /(a)
/(a) 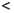
 /(b). Фиксируем число c ∈ (
/(b). Фиксируем число c ∈ ( / (a),
/ (a),  /(b)). Рассмотрим вспомогательную функцию φ(χy) =
/(b)). Рассмотрим вспомогательную функцию φ(χy) = (x) — cx. Она дифференцируема на отрезке [a, b] и
(x) — cx. Она дифференцируема на отрезке [a, b] и
φ/(a) =  /(a) – c
/(a) – c 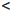 0, φ/(b) =
0, φ/(b) =  /(b) – c > 0.
/(b) – c > 0.
По теореме Дарбу есть такая точка γ ∈ (a, b), что φ,(γ) = 0, то есть /(γ) = с.
/(γ) = с.
Следствие 2. Если функция  дифференцируема на отрезке [a, b] и
дифференцируема на отрезке [a, b] и  /(x) = 0, ∀x ∈ [a, b], то функция
/(x) = 0, ∀x ∈ [a, b], то функция  / сохраняет знак на отрезке [a, b].
/ сохраняет знак на отрезке [a, b].
Замечание 1. Теорема Дарбу имеет сходство с теоремой Больцано-Коши о промежуточном значении непрерывной функции, но не является ее следствием, поскольку функция f/ не обязательно непрерывна на отрезке [a, b].
Замечание 2. Не всякая функция, определенная на отрезке [a, b] может быть производной какой-либо функции. Например, функция sgn x является производной функции y = |x| на промежутках [—1, 0) и (0, 1], но нет функции, для которой она является производной на отрезке [—1, 1].
Теорема 4.10 (Ролля). Пусть функция  непрерывна на отрезке [a, b], дифференцируема на интервале (a, b) и принимает на концах равные значения, то есть
непрерывна на отрезке [a, b], дифференцируема на интервале (a, b) и принимает на концах равные значения, то есть  (a) =
(a) =  (b). Тогда найдется точка c ∈ (a, b), в которой
(b). Тогда найдется точка c ∈ (a, b), в которой / (c) = 0.
/ (c) = 0.
По условию функция  непрерывна на отрезке [a, b]. Поэтому существуют точки p и q из [a, b] такие, что
непрерывна на отрезке [a, b]. Поэтому существуют точки p и q из [a, b] такие, что
 (p) = sup{
(p) = sup{ (x) : x ∈ [a, b]},
(x) : x ∈ [a, b]},  (q) = inf{
(q) = inf{ (x) : x ∈ [a, b]}.
(x) : x ∈ [a, b]}.
Если  (p) =
(p) =  (q), то функция
(q), то функция  постоянна на отрезке [a, b] и
постоянна на отрезке [a, b] и  /(x) = 0, ∀x ∈ [a, b].
/(x) = 0, ∀x ∈ [a, b].
Если  (p)
(p) 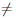
 (q), то одна из точек p, q лежит в интервале (a, b). Её мы обозначим через c. По теореме Ферма 4.8
(q), то одна из точек p, q лежит в интервале (a, b). Её мы обозначим через c. По теореме Ферма 4.8  /(c) = 0.
/(c) = 0.
Следствие 1. Пусть функция  непрерывна на отрезке [a,b], дифференцируема на интервале (a, b). Тогда между точками, в которых функция
непрерывна на отрезке [a,b], дифференцируема на интервале (a, b). Тогда между точками, в которых функция  равна нулю, найдется по крайней мере одна точка, в которой функция
равна нулю, найдется по крайней мере одна точка, в которой функция  / равна нулю. n
/ равна нулю. n
Следствие 2. Если Pn (x) = 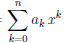 многочлен n-ой степени (то есть, an
многочлен n-ой степени (то есть, an 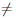 0), то уравнение Pn(x) = 0 имеет не более чем n различных корней.
0), то уравнение Pn(x) = 0 имеет не более чем n различных корней.
Пусть уравнение Pn(x) = 0 имеет не менее (n+ 1) различных корней 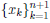 причем xj
причем xj 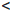 xj+1 , j = 1, . . . , n.
xj+1 , j = 1, . . . , n.
Тогда P/n(x) = 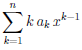 — многочлен (n- 1)-ой степени. По теореме Ролля
— многочлен (n- 1)-ой степени. По теореме Ролля
∃ bj ∈ (xj , xj+1), j = 1, . . . , n : P/n (bj) = 0,
то есть уравнение P/n (x) = 0 имеет не менее n различных корней. Продолжая дифференцирование уравнения, и применяя на каждом шаге теорему Ролля, получим, что для каждого m 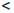 n
n
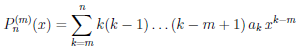 ,
,
и уравнение Pn(m) (x) = 0 имеет не менее (n – m + 1) различных корней. В частности, при m = n уравнение Pn(n) (x) = 0 имеет не менее 1-го корня. Но, с другой стороны, Pn(n) (x) = n! an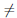 0, а, значит, уравнение Pn(n) (x) = 0 и не имеет корней. Полученное противоречие и доказывает следствие.
0, а, значит, уравнение Pn(n) (x) = 0 и не имеет корней. Полученное противоречие и доказывает следствие.
Из результата применения теоремы Ролля в начале доказательства этого
следствия сразу же следует ещё один результат.
Следствие 3. Если Pn(x)= 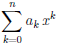 многочлен n-ой степени и уравнение Pn(x) = 0 имеет m (m ≤ n) различных корней, то уравнение P/n (x) = 0 имеет (m – 1) различных корней.
многочлен n-ой степени и уравнение Pn(x) = 0 имеет m (m ≤ n) различных корней, то уравнение P/n (x) = 0 имеет (m – 1) различных корней.
Замечание 1. Если для функции  не выполнено хотя бы одно условие теоремы 4.10, то для нее, вообще говоря, не имеет место утверждение теоремы.
не выполнено хотя бы одно условие теоремы 4.10, то для нее, вообще говоря, не имеет место утверждение теоремы.
Замечание 2. Геометрически теорема Ролля означает следующее: если график непрерывной на отрезке [a, b] функции имеет в точках (x,  (x)), x ∈ (a, b) невертикальные касательные и ординаты крайних точек равны, то есть
(x)), x ∈ (a, b) невертикальные касательные и ординаты крайних точек равны, то есть  (a) =
(a) =  (b), то на графике есть точка (c,
(b), то на графике есть точка (c,  (c)), c ∈ (a, b), в которой касательная параллельна оси OX .
(c)), c ∈ (a, b), в которой касательная параллельна оси OX .
Теорема 4.11 (Лагранжа). Пусть функция  непрерывна на отрезке [a, b] и дифференцируема на интервале (a, b). Тогда найдется точка c ∈ (a, b) такая, что
непрерывна на отрезке [a, b] и дифференцируема на интервале (a, b). Тогда найдется точка c ∈ (a, b) такая, что  (b) –
(b) –  (a) =
(a) =  /(c)(b – a). Последнюю формулу часто называют формулой Лагранжа.
/(c)(b – a). Последнюю формулу часто называют формулой Лагранжа.
Для доказательства теоремы рассмотрим вспомогательную функцию
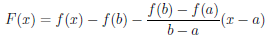 .
.
Функция F непрерывна на отрезке [a, b], дифференцируема на интервале (a, b) и F(a) = F (b). Применив к ней теорему Ролля 4.10, найдем точку c ∈ (a, b) такую, что F/ (c) = 0. Поскольку ∀x ∈ (a, b)
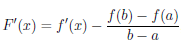 ,
,
то 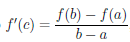 ,то есть имеет место формула Лагранжа.
,то есть имеет место формула Лагранжа.
Следствие. Пусть функция  непрерывна на [x0,x0 + δ), δ > 0, и дифференцируема на (x0 , x0 + δ). Тогда для любого x ∈ (x0 , x0 + δ) найдется такое
непрерывна на [x0,x0 + δ), δ > 0, и дифференцируема на (x0 , x0 + δ). Тогда для любого x ∈ (x0 , x0 + δ) найдется такое 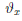 ∈ (0,1), что
∈ (0,1), что
 (x) –
(x) –  (xo) =
(xo) =  /(xo +
/(xo + 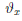 (x – xo)) (x – xo).
(x – xo)) (x – xo).
Последнюю формулу обычно называют формулой Лагранжа конечных приращений. Она имеет место, так как на отрезке [x0,x] ⊂ [x0,x0 + δ) выполнены все условия теоремы Лагранжа и соответствующая точка cx имеет представление сχ = xo + 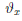 (x – xo), где
(x – xo), где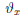 ∈ (0,1).
∈ (0,1).
Аналогичные результаты имеют место и на промежутке (x0 – δ, x0].
Замечание 1. Формулу конечных приращений Лагранжа следует отличать от приближенного равенства
 (x0 + ∆x) –
(x0 + ∆x) –  (x0) ≈
(x0) ≈  /(x0) ∆x,
/(x0) ∆x,
которое имеет место при условии дифференцируемости функции  в точке x0 . Последнюю формулу обычно называют формулой бесконечно малых приращений, поскольку
в точке x0 . Последнюю формулу обычно называют формулой бесконечно малых приращений, поскольку
 (x0 + ∆x) –
(x0 + ∆x) –  (x0) =
(x0) =  /(x0) ∆x + o(∆x), ∆x → 0.
/(x0) ∆x + o(∆x), ∆x → 0.
Замечание 2. Пусть график непрерывной на отрезке [a, b] функции в каждой точке (x,  (x)), x ∈ (a, b), имеет невертикальные касательные. Тогда на нем найдется точка (c,
(x)), x ∈ (a, b), имеет невертикальные касательные. Тогда на нем найдется точка (c,  (c)), в которой касательная параллельна хорде, соединяющей концы (a,
(c)), в которой касательная параллельна хорде, соединяющей концы (a,  (a)) и (b,
(a)) и (b,  (b)) графика.
(b)) графика.
Замечание верно, так как 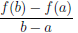 угловой коэффициент рассматриваемой хорды, а
угловой коэффициент рассматриваемой хорды, а  /(c) — угловой коэффициент касательной, проведенной к графику функции
/(c) — угловой коэффициент касательной, проведенной к графику функции  в точке (c,
в точке (c,  (c)).
(c)).
Теорема 4.12 (критерий монотонности функции). Пусть функция  непрерывна на промежутке X и дифференцируема в его внутренних точках. Для того чтобы функция
непрерывна на промежутке X и дифференцируема в его внутренних точках. Для того чтобы функция  не убывала на промежутке X , необходимо и достаточно, чтобы
не убывала на промежутке X , необходимо и достаточно, чтобы  /(x) ≥ 0 в каждой внутренней точке множества X .
/(x) ≥ 0 в каждой внутренней точке множества X .
Пусть функция  является неубывающей непрерывной на промежутке X функцией, которая дифференцируема в каждой внутренней точке, и x — некоторая точка из соответствующего интервала. Тогда для любого ∆x > 0
является неубывающей непрерывной на промежутке X функцией, которая дифференцируема в каждой внутренней точке, и x — некоторая точка из соответствующего интервала. Тогда для любого ∆x > 0
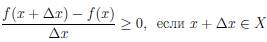 .
.
Поэтому  /(x) ≥ 0.
/(x) ≥ 0.
Пусть  / (x) ≥ 0 в каждой внутренней точке промежутка X и x1 , x2 — произвольные точки множества X, причем x1
/ (x) ≥ 0 в каждой внутренней точке промежутка X и x1 , x2 — произвольные точки множества X, причем x1 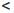 x2. Применяя к отрезку [x1 , x2] теорему Лагранжа 4.11, получим равенство
x2. Применяя к отрезку [x1 , x2] теорему Лагранжа 4.11, получим равенство
 (x2) –
(x2) –  (x1) =
(x1) =  / (c)(x2 – x1),
/ (c)(x2 – x1),
в котором c ∈ (x1, x2). Следовательно,  (x2) ≥
(x2) ≥  (x1), а поэтому функция
(x1), а поэтому функция  не убывает на промежутке X .
не убывает на промежутке X .
Замечание. Аналогично можно доказать, что при выполнении условий теоремы 4.12 функция  не возрастает на промежутке X тогда и только тогда, когда
не возрастает на промежутке X тогда и только тогда, когда  / (x) ≤ 0 в каждой точке промежутка X.
/ (x) ≤ 0 в каждой точке промежутка X.
Теорема 4.13 (критерий постоянства функции). Пусть функция  непрерывна на промежутке X и дифференцируема в его внутренних точках. Чтобы функция
непрерывна на промежутке X и дифференцируема в его внутренних точках. Чтобы функция  была постоянной на X, необходимо и достаточно, чтобы в каждой внутренней точке промежутка X
была постоянной на X, необходимо и достаточно, чтобы в каждой внутренней точке промежутка X  / (x) = 0.
/ (x) = 0.
Если функция  постоянна на промежутке X, то
постоянна на промежутке X, то  /(x) = 0 в каждой его точке. Первая часть утверждения доказана.
/(x) = 0 в каждой его точке. Первая часть утверждения доказана.
Пусть теперь  / (x) = 0 во внутренних точках промежутка X и x0 ∈ X. Тогда для любого x ∈ X, применяя к отрезку [x0, x] теорему Лагранжа 4.11, получим
/ (x) = 0 во внутренних точках промежутка X и x0 ∈ X. Тогда для любого x ∈ X, применяя к отрезку [x0, x] теорему Лагранжа 4.11, получим
 (x) –
(x) –  (x0) =
(x0) =  /(cx)(x- x0), cx ∈ (x0,x).
/(cx)(x- x0), cx ∈ (x0,x).
Следовательно,  (x) =
(x) =  (x0), ∀x ∈ X, что доказывает вторую часть утверждения.
(x0), ∀x ∈ X, что доказывает вторую часть утверждения.
Следствие 1. Пусть функция  непрерывна на промежутке X и дифференцируема в его внутренних точках. Для того чтобы функция
непрерывна на промежутке X и дифференцируема в его внутренних точках. Для того чтобы функция  была возрастающей (убывающей), необходимо и достаточно, чтобы
была возрастающей (убывающей), необходимо и достаточно, чтобы  /(x) ≥ 0 (
/(x) ≥ 0 ( / (x) ≤ 0) во внутренних точках промежутка X и не существовало интервала (α, β) ⊂ X, на котором
/ (x) ≤ 0) во внутренних точках промежутка X и не существовало интервала (α, β) ⊂ X, на котором  /(x) = 0.
/(x) = 0.
Следствие 2. Если на промежутке X функция  имеет положительную (отрицательную) производную, то функция
имеет положительную (отрицательную) производную, то функция  имеет обратную функцию
имеет обратную функцию  -1 :
-1 :  (X) → X, которая дифференцируема на промежутке
(X) → X, которая дифференцируема на промежутке  (X).
(X).
Теорема 4.14 (Коши). Пусть функции  и g непрерывны на отрезке [a, b] и дифференцируемы на интервале (a, b), при этом g/(x)
и g непрерывны на отрезке [a, b] и дифференцируемы на интервале (a, b), при этом g/(x) 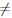 0, ∀x ∈ (a, b). Тогда найдется точка c ∈ (a, b) такая, что
0, ∀x ∈ (a, b). Тогда найдется точка c ∈ (a, b) такая, что
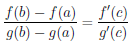 .
.
Последнюю формулу называют обобщенной формулой конечных приращений или формулой Коши.
Прежде всего заметим, что g (b) 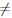 g(a), поскольку в противном случае в интервале (a, b) нашлась бы точка c такая, что g/ (c) = 0.
g(a), поскольку в противном случае в интервале (a, b) нашлась бы точка c такая, что g/ (c) = 0.
Рассмотрим вспомогательную функцию
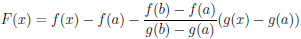 .
.
Функция F непрерывна на отрезке [a, b], дифференцируема на интервале (a, b) и F(a) = F (b). Применяя к F теорему Ролля 4.10 и имея в виду, что
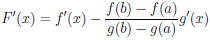
делаем вывод, что существует точка c ∈ (a, b) такая, что F/ (c) = 0, то есть
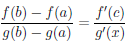 .
.
Замечание 1. Теорема Лагранжа 4.11 является частным случаем теоремы
Коши при g(x) = x.
Замечание 2. В формуле Коши конечных приращений не обязательно считать, что a 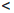 b. Эта формула верна и при b
b. Эта формула верна и при b 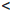 a.
a.
Дифференцирование параметрически заданных функций
Пусть заданы две функции φ : T → X, ψ : T → Y. Будем считать, что функция x = φ(t) биективна. Поэтому определена обратная функция t =φ– 1(x), φ-1 : X → T ,а значит и суперпозиция  (x) = ψ(φ-1(x)). Функцию
(x) = ψ(φ-1(x)). Функцию  = ψ ◦ φ-1 называют заданной параметрически и записывают одним из следующих способов:
= ψ ◦ φ-1 называют заданной параметрически и записывают одним из следующих способов:
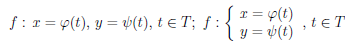 .
.
Переменную t называют параметром функции  : X → Y . Вопрос о дифференцировании параметрически заданной функции решает следующее утверждение.
: X → Y . Вопрос о дифференцировании параметрически заданной функции решает следующее утверждение.
Теорема 4.15. Пусть T — промежуток и параметрически заданная функция  : X → Y,
: X → Y,  : x = φ(t), y = ψ(t),t ∈ T, удовлетворяет условиям:
: x = φ(t), y = ψ(t),t ∈ T, удовлетворяет условиям:
1) функции φ и ψ дифференцируемы на T;
2) φ'(t) 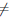 0, ∀t ∈ T;
0, ∀t ∈ T;
Тогда функция  дифференцируема на промежутке X, её производная
дифференцируема на промежутке X, её производная  /x является параметрически заданной функцией
/x является параметрически заданной функцией
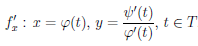 . (4.14)
. (4.14)
Так как функция φ удовлетворяет условиям 1) — 2), то по следствию 2 теоремы Дарбу (4.9) функция φ’ сохраняет знак на промежутке T. Поэтому, согласно следствию 1 теоремы 4.13, функция φ либо возрастает (если φ'(t) > 0 на T), либо убывает (если φ'(t) > 0 на T). Тогда по теореме 4.6 обратная функция φ-1 : X → T дифференцируема на промежутке X = φ(T) и
(φ- 1)'(x) = 1∕φ'(φ-1 (x)), ∀x ∈ X.
Поскольку функция ψ дифференцируема на X , то по теореме о дифференцируемости суперпозиции функция  = ψ ◦ φ-1 дифференцируема на X и
= ψ ◦ φ-1 дифференцируема на X и
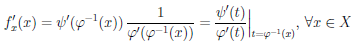 .
.
Последнее означает, что функция f/x является параметрически заданной
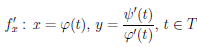 .
.
Правила Лопиталя раскрытия неопределенностей
Теорема 4.16. Пусть функции  и φ дифференцируемы на интервале (a,b), φ'(x)
и φ дифференцируемы на интервале (a,b), φ'(x) 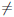 0, ∀x ∈ (a,b), и
0, ∀x ∈ (a,b), и 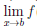 (x) =
(x) = 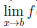 φ(x’) = 0. Если существует конечный или бесконечный предел
φ(x’) = 0. Если существует конечный или бесконечный предел
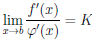 ,
,
то существует предел
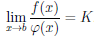 .
.
Рассмотрим два случая: b ∈ 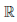 и b = +∞.
и b = +∞.
1) Пусть b ∈ 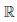 и для определенности b > a. Доопределим функции
и для определенности b > a. Доопределим функции  и φ в точке b, положив
и φ в точке b, положив  (b) = p(b) = 0. Теперь функции
(b) = p(b) = 0. Теперь функции  и φ непрерывны на промежутке (a, b] и удовлетворяют условиям теоремы Коши 4.14 на любом отрезке [x, b], где x ∈ (a, b). Поэтому для каждого x ∈ (a, b) найдется точка cx ∈ (x, b) такая, что
и φ непрерывны на промежутке (a, b] и удовлетворяют условиям теоремы Коши 4.14 на любом отрезке [x, b], где x ∈ (a, b). Поэтому для каждого x ∈ (a, b) найдется точка cx ∈ (x, b) такая, что
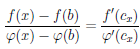 ,
,
то есть
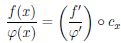 . (4.15)
. (4.15)
Поскольку 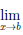 cx = b, cx
cx = b, cx  b, ∀x ∈ (a, b), и
b, ∀x ∈ (a, b), и
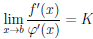 ,
,
то по теореме 2.37 о пределе суперпозиции функций, условия которой выполнены, правая часть равенства (4.15) имеет предел при x → b и он равен K. Следовательно, существует предел левой части равенства (4.15) при x → b и он равен K .
2) Пусть теперь b = +∞. Без ограничения общности будем считать, что a > 0. По условиям теоремы функции  и φ дифференцируемы на интервале (a, +∞), φ/ (x)
и φ дифференцируемы на интервале (a, +∞), φ/ (x) 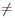 0, ∀x ∈ (a, +∞), и
0, ∀x ∈ (a, +∞), и 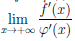 = K. Тогда вспомогательные функции F(t) =
= K. Тогда вспомогательные функции F(t) =  (1/t) и Φ(t) = p(1/t) дифференцируемы на интервале
(1/t) и Φ(t) = p(1/t) дифференцируемы на интервале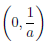
и
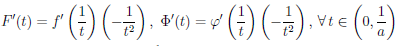 .
.
Кроме того, 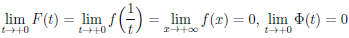 и
и
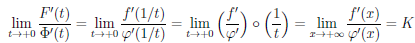
(снова воспользовались теоремой 2.37 о пределе суперпозиции функций).
В силу доказанной первой части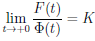 . Поэтому
. Поэтому
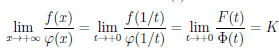 .
.
Теорема 4.17. Пусть функции  и φ дифференцируемы на интервале (α,b), φ'(x)
и φ дифференцируемы на интервале (α,b), φ'(x) 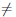 0, ∀x ∈ (α,b) и
0, ∀x ∈ (α,b) и 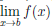 = ∞,
= ∞, 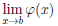 = ∞. Если существует конечный или бесконечный предел
= ∞. Если существует конечный или бесконечный предел
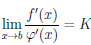 ,
,
то существует предел
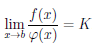 .
.
Мы опускаем доказательство этого утверждения, отсылая читателя к книгам [4, с. 318-320], [6, т.1, с. 280-284],[1, т.1, с. 256-260].
Совершенно аналогично формулируются и доказываются теоремы, аналогичные теоремам 4.16 и 4.17, когда 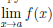 =
= 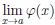 = 0 или ∞, a ∈
= 0 или ∞, a ∈ 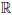 , или a = -∞.
, или a = -∞.
Замечание 1. Предел отношения функций  и φ может существовать в случае, когда не существует предел отношения производных этих функций. Например, если
и φ может существовать в случае, когда не существует предел отношения производных этих функций. Например, если  (x) = x2 sin
(x) = x2 sin  , φ(x} = x, то
, φ(x} = x, то
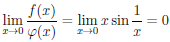 ,
,
но не существует предела при x → 0 поскольку отношения производных этих функций, поскольку
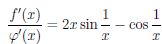 .
.
Замечание 2. Если выполнены условия теоремы 4.16 и функции  / и φ/ непрерывны в точке b, причем φ/(b)
/ и φ/ непрерывны в точке b, причем φ/(b) 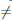 0, то
0, то
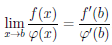 .
.
Замечание 3. Пусть функции  и φ дважды дифференцируемы на интервале (a, b), для всех x ∈ (a, b) φ/(x)
и φ дважды дифференцируемы на интервале (a, b), для всех x ∈ (a, b) φ/(x) 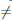 0, φ//(x)
0, φ//(x) 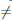 0, и
0, и
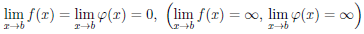 ,
,
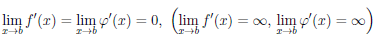 .
.
Если существует предел 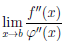 =K, то существуют пределы
=K, то существуют пределы
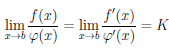 ,
,
то есть правило Лопиталя можно применить повторно.
Формула Тейлора
Теорема 4.18 (формула Тейлора для многочлена). Пусть a — некоторое число, P — многочлен степени n (n ≥ 1). Тогда
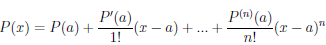 ,
,
то есть многочлен P степени n однозначно определяется значениями многочлена и его производных P (a), P /(a),…,P (n)(a) в точке a.
Прежде всего заметим, что многочлен 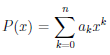 всегда можно представить в виде
всегда можно представить в виде
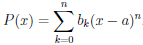 . (4.16)
. (4.16)
Для этого в многочлене P(x) = 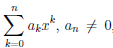 , заменим xk на ((x – a) + a)k , раскроем внешние скобки, приведем подобные и получим представление (4.16). Поэтому можно считать, что многочлен P(x) задан формулой (4.16). Выразим коэффициенты bk, k = 0, 1, . . . , n, многочлена P(x) через значения
, заменим xk на ((x – a) + a)k , раскроем внешние скобки, приведем подобные и получим представление (4.16). Поэтому можно считать, что многочлен P(x) задан формулой (4.16). Выразим коэффициенты bk, k = 0, 1, . . . , n, многочлена P(x) через значения
его производных в точке a.
Из равенства (4.16) следует, что P(a) = b0. Последовательно продифференцируем равенство (4.16) k раз (k = 1, . . . , n) и получим, что P(k) (x) =
k!bk + (k + 1)k … 2 bk+1(x — a) + ∙ ∙ ∙ + n(n — 1) … (n — k + 1)bn(x — a)n-k,
поэтому P(k) (a) = k!bk, то есть bk =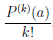 , k = 1,… ,n, и потому многочлен P имеет представление
, k = 1,… ,n, и потому многочлен P имеет представление
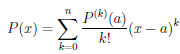
Пусть теперь функция 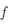 отлична от многочлена и дифференцируема n раз в точке a.
отлична от многочлена и дифференцируема n раз в точке a.
Многочлен 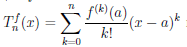 называют многочленом Тейлора порядка n функции
называют многочленом Тейлора порядка n функции 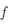 по степеням (x — a). Согласно предыдущей теореме
по степеням (x — a). Согласно предыдущей теореме 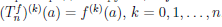 . Положим
. Положим
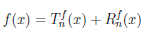 (4.17)
(4.17)
Если функция 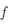 (x) не является многочленом степени n, то
(x) не является многочленом степени n, то 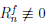 . Равенство (4.17) называют формулой Тейлора функции
. Равенство (4.17) называют формулой Тейлора функции 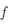 по степеням (x — a), а функцию
по степеням (x — a), а функцию 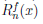 ее n-ным остаточным членом.
ее n-ным остаточным членом.
Теорема 4.19 (формула Тейлора с остаточным членом в форме Пеано). Пусть функция  дифференцируема (n – 1) раз в промежутке [a, a + δ) и n раз в точке a (n ∈ N). Тогда
дифференцируема (n – 1) раз в промежутке [a, a + δ) и n раз в точке a (n ∈ N). Тогда
 (x) =
(x) = 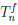 (x) + o((x – a)n) при x → a.
(x) + o((x – a)n) при x → a.
Из равенства (4.17) 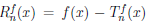 . Поэтому функция
. Поэтому функция 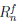 дифференцируема (n – 1) раз в промежутке [a, a + δ) и n раз в точке a. Кроме того, (
дифференцируема (n – 1) раз в промежутке [a, a + δ) и n раз в точке a. Кроме того, (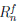 )(k)(a) = 0, k = 0, 1, . . . , n. Покажем, что
)(k)(a) = 0, k = 0, 1, . . . , n. Покажем, что 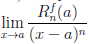 = 0. Рассматриваемое отношение удовлетворяет условиям первого правила Лопиталя и при (n — 1)-
= 0. Рассматриваемое отношение удовлетворяет условиям первого правила Лопиталя и при (n — 1)-
кратном его применении получим, что
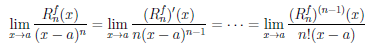 ,
,
если последний предел существует. Поскольку функция (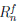 )(n—1) дифференцируема в точке a и (
)(n—1) дифференцируема в точке a и (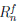 )(n—1)(a)= 0, то
)(n—1)(a)= 0, то
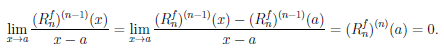
Следовательно, (n — 1)-кратное применение правила Лопиталя законно и при x → a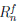 (x) = o((x — a)n), то есть при x → a
(x) = o((x — a)n), то есть при x → a
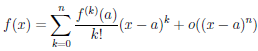 .
.
Полученное представление функции  называют формулой Тейлора с остаточным членом в форме Пеано. Если же a = 0 — формулой Маклорена с остаточным членом в форме Пеано.
называют формулой Тейлора с остаточным членом в форме Пеано. Если же a = 0 — формулой Маклорена с остаточным членом в форме Пеано.
Замечание. Формула Тейлора с остаточным членом в форме Пеано является обобщением представлений для непрерывной и дифференцируемой в точке a функции.
Следствие. Пусть функции  и g n раз дифференцируемы в точке a и
и g n раз дифференцируемы в точке a и  (k)(a) = g(k)(a), k = 0, 1, . . . , n. Тогда при x → a имеет место представление
(k)(a) = g(k)(a), k = 0, 1, . . . , n. Тогда при x → a имеет место представление  (x)—g(x) =o((x— a)n).
(x)—g(x) =o((x— a)n).
Так, например, для функций 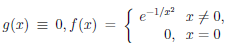 , условия следствия выполняются для любого n ∈
, условия следствия выполняются для любого n ∈  , поэтому при x → a
, поэтому при x → a  (x) = o((x—a)n) для любого n ∈
(x) = o((x—a)n) для любого n ∈  .
.
Теорема 4.20. Если выполнены условия теоремы 4.19 и существует многочлен Pn(x) такой, что  (x) = Pn(x) + o((x — a)n ) при x → a, то он единственен.
(x) = Pn(x) + o((x — a)n ) при x → a, то он единственен.
Пусть 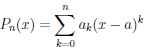 . Согласно теореме 4.19, при x→a
. Согласно теореме 4.19, при x→a
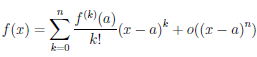
Следовательно,
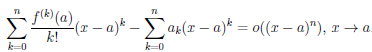 .
.
Переходя в этом равенстве к пределу при x → a, получим равенство
 (a) – a0 = 0, то есть a0 =
(a) – a0 = 0, то есть a0 =  (a)∙
(a)∙
Последнее означает, что
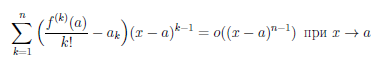
Отсюда при x → a получим равенство 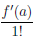 – a1 = 0, то есть a1=
– a1 = 0, то есть a1=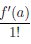
Продолжая этот процесс, по индукции получим, что
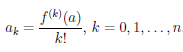 .
.
Поэтому многочлен Pn(x) является многочленом Тейлора 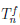 (x) функции
(x) функции  по степеням (x – a).
по степеням (x – a).
Замечание. Доказанная теорема означает, что никакой многочлен Pn(x) степени n, отличный от многочлена Тейлора 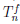 (x) порядка n не может приближать функцию
(x) порядка n не может приближать функцию  с точностью o((x – a)n) при x → a.
с точностью o((x – a)n) при x → a.
Применяя теорему 4.19 к элементарным функциям при a = 0, получим:
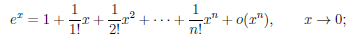
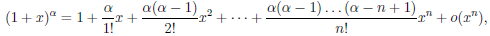
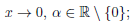
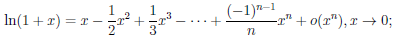
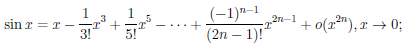
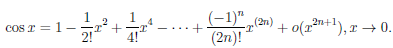
Вывод этих формул читатель может найти в [6, т.1, с. 192-195].
Пример №8
Пусть функция  дифференцируема (n+ 1) раз в точке a = 0 и известно, что
дифференцируема (n+ 1) раз в точке a = 0 и известно, что
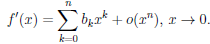 (4.18)
(4.18)
Найти локальную формулу Маклорена функции  .
.
По теореме 4.20 из (4.18) следует, что ( /)(k) (0) = k!bk, k = 0, 1, . . . , n. Поэтому
/)(k) (0) = k!bk, k = 0, 1, . . . , n. Поэтому  (k+1)(0) = k!bk или
(k+1)(0) = k!bk или  (k) (0) = (k — 1)!bk—1, k = 1,2, . . . ,n+ 1 и
(k) (0) = (k — 1)!bk—1, k = 1,2, . . . ,n+ 1 и
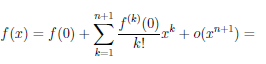
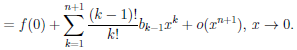
После преобразования получим
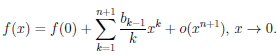
В частности, если (x) = arctg x, то
(x) = arctg x, то  /(x) = (1 + x2)—1 и
/(x) = (1 + x2)—1 и
 /(x) = 1 — x2 + x4 + (—1)nx2n + o(x2n), x → 0.
/(x) = 1 — x2 + x4 + (—1)nx2n + o(x2n), x → 0.
Отсюда, учитывая, что arctg 0 = 0, получаем представление
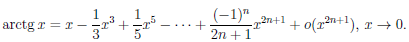
Теорема 4.21. Пусть функция  ∈ Cn([a, a + δ)), δ > 0, и дифференцируема (n+1) раз на интервале (a, a+δ). Тогда для любой точки x ∈ (a, a+δ), для любой функции φ, непрерывной на промежутке [a, a + δ), дифференцируемой на интервале (a, a + δ) и такой, что φ/(t)
∈ Cn([a, a + δ)), δ > 0, и дифференцируема (n+1) раз на интервале (a, a+δ). Тогда для любой точки x ∈ (a, a+δ), для любой функции φ, непрерывной на промежутке [a, a + δ), дифференцируемой на интервале (a, a + δ) и такой, что φ/(t)  0, ∀t ∈ (a,x), найдется такая точка cx ∈ (a, x), что
0, ∀t ∈ (a,x), найдется такая точка cx ∈ (a, x), что
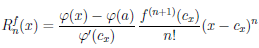 (4.19)
(4.19)
Фиксируем точку x ∈ (a, a + δ). Рассмотрим вспомогательную функцию
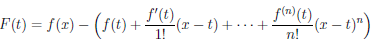 .
.
В силу условий теоремы, F ∈ C ([a, a + δ)), дифференцируема на интервале (a, a + δ) и ∀t ∈ (a, a + δ)
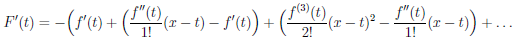
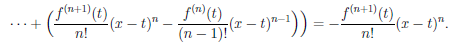
Применим к функциям F и φ на отрезке [a, х] теорему Коши 4.14 о конечных приращениях, получим, что существует точка cx ∈ (a, x) такая, что
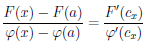 . (4.20)
. (4.20)
Поскольку F(x) = 0, а
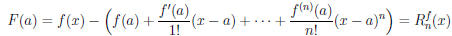 ,
,
то соотношение (4.20) принимает вид
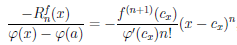 ,
,
из которого и следует представление (4.19) остаточного члена формулы Тейлора, которое называется формой Шлемильха и Роша.
формулы Тейлора, которое называется формой Шлемильха и Роша.
Следствие 1. Если функция  удовлетворяет условиям теоремы 4.21, то для любого х ∈ (a, a + δ) найдется такая точка cx ∈ (a, х), что
удовлетворяет условиям теоремы 4.21, то для любого х ∈ (a, a + δ) найдется такая точка cx ∈ (a, х), что
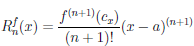
Замечание. Формулу (4.21) называют формулой Тейлора с остаточным членом в форме Лагранжа. Чтобы её получить, достаточно положить в представлении (4.19) φ(t) = (х – t)n+1. Формула Тейлора с остаточным членом в форме Лагранжа является обобщением теоремы Лагранжа 4.11, которая получается из формулы Тейлора с остаточным членом в форме Лагранжа при n = 0.
Следствие 2. Если функция  удовлетворяет условиям теоремы 4.21, то для любого х ∈ (a, a + δ) найдется такое θx ∈ (0, 1), что
удовлетворяет условиям теоремы 4.21, то для любого х ∈ (a, a + δ) найдется такое θx ∈ (0, 1), что
R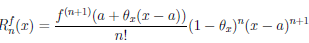 .
.
Замечание. Эта форма остаточного члена формулы Тейлора называется формой Коши. Чтобы её получить, достаточно положить в представлении (4.19) φ(t) = (x — t).
Завершая раздел, заметим, что все его результаты остаются в силе, если рассматривать функцию  на промежутках (a — δ, a] и (a — δ, a + δ)
на промежутках (a — δ, a] и (a — δ, a + δ)
Исследование поведения функции на множестве
Экстремум функции
Определение 4.9. Пусть  : X ⊂
: X ⊂  →
→  . Точка a ∈ X называется точкой локального максимума (минимума) функции
. Точка a ∈ X называется точкой локального максимума (минимума) функции  , если существует окрестность Ua , такая что
, если существует окрестность Ua , такая что
Ua ⊂ X и (x) ≤
(x) ≤  (a), ∀x ∈ Ua (
(a), ∀x ∈ Ua ( (x) ≥
(x) ≥  (a), ∀x ∈ Ua).
(a), ∀x ∈ Ua).
Если функция  имеет в точке a локальный максимум или минимум, то говорят, что
имеет в точке a локальный максимум или минимум, то говорят, что  имеет в точке a локальный экстремум, или что точка a является точкой локального экстремума функции
имеет в точке a локальный экстремум, или что точка a является точкой локального экстремума функции  .
.
Теорема 4.22 (необходимое условие локального экстремума). Если функция  имеет в точке a локальный экстремум и
имеет в точке a локальный экстремум и  дифференцируема в точке a, то
дифференцируема в точке a, то  /(a) = 0.
/(a) = 0.
Утверждение следует непосредственно из теоремы Ферма (теоремы 4.8), примененной к окрестности Ua , указанной в определении экстремума.
Определение 4.10. Стационарными точками функции  на множестве X называются те внутренние точки X, в которых
на множестве X называются те внутренние точки X, в которых  /(x) = 0.
/(x) = 0.
Заметим, что функция  (x) = x2/3 имеет в точке x = 0 локальный минимум, но
(x) = x2/3 имеет в точке x = 0 локальный минимум, но  /(0) = ∞. Поэтому справедлива
/(0) = ∞. Поэтому справедлива
Теорема 4.23. Если функция  имеет в точке a локальный экстремум, то либо
имеет в точке a локальный экстремум, то либо  дифференцируема в точке a и
дифференцируема в точке a и  /(a) = 0, либо функция
/(a) = 0, либо функция  не дифференцируема в точке a.
не дифференцируема в точке a.
Определение 4.11. Внутренняя точка множества X, в которой функция непрерывна, а ее производная либо равна нулю, либо бесконечности, либо не существует, называется критической точкой функции  .
.
Например, точка x = 0 является критической точкой функций  (x) = x2,
(x) = x2,  (x) = x3,
(x) = x3,  (x) = |x|,
(x) = |x|,  (x) = x1/3,
(x) = x1/3,  (x) = x2/3. Из графиков этих функций следует, что она является точкой локального минимума функций
(x) = x2/3. Из графиков этих функций следует, что она является точкой локального минимума функций  (x) = x2 ,
(x) = x2 ,  (x) = |x|,
(x) = |x|,  (x) = x2/3, а для функций
(x) = x2/3, а для функций  (x) = x3,
(x) = x3,  (x) = x1/3 она не является точкой локального экстремума. Таким образом, не всякая критическая точка функции является ее точкой экстремума.
(x) = x1/3 она не является точкой локального экстремума. Таким образом, не всякая критическая точка функции является ее точкой экстремума.
Теорема 4.24 (достаточное условие экстремума в критической точке). Пусть функция  определена на промежутке X , a — критическая точка функции и функция f дифференцируема в некоторой окрестности Ua(δ) точки a, кроме, быть может, самой точки a. Если функция
определена на промежутке X , a — критическая точка функции и функция f дифференцируема в некоторой окрестности Ua(δ) точки a, кроме, быть может, самой точки a. Если функция  /(x) меняет знак при переходе через точку a, то есть на интервалах (a – δ, a) и (a, a + δ) f/(x) имеет противоположные знаки, то a — точка экстремума функции
/(x) меняет знак при переходе через точку a, то есть на интервалах (a – δ, a) и (a, a + δ) f/(x) имеет противоположные знаки, то a — точка экстремума функции  . При этом, если
. При этом, если
 /(x) > 0, ∀ x ∈ (a – δ, a) и
/(x) > 0, ∀ x ∈ (a – δ, a) и  /(x)
/(x)  0, ∀x ∈ (a, a + δ),
0, ∀x ∈ (a, a + δ),
то a является точкой максимума функции, а если
 /(x)
/(x)  0, ∀ x ∈ (a – δ, a) и
0, ∀ x ∈ (a – δ, a) и /(x) > 0, ∀x ∈ (a, a + δ),
/(x) > 0, ∀x ∈ (a, a + δ),
то a — точка минимума функции. Если же функция  /(x) не меняет знак при переходе через a, то a не является точкой экстремума функции
/(x) не меняет знак при переходе через a, то a не является точкой экстремума функции  .
.
Пусть  /(x) > 0 на (a – δ, a) и
/(x) > 0 на (a – δ, a) и  / (x)
/ (x)  0 на интервале (a, a + δ). Так как a — критическая точка функции, то
0 на интервале (a, a + δ). Так как a — критическая точка функции, то  непрерывна в точке a. Поэтому функция
непрерывна в точке a. Поэтому функция  непрерывна на промежутке (a – δ, a] и
непрерывна на промежутке (a – δ, a] и  /(x) > 0, ∀x ∈ (a – δ, a), непрерывна на промежутке [a, a + δ) и
/(x) > 0, ∀x ∈ (a – δ, a), непрерывна на промежутке [a, a + δ) и  /(x)
/(x)  0, ∀x ∈ (a, a + δ). В силу критерия монотонности функции на промежутке (см. следствие 1 теорем 4.12 и 4.13) функция
0, ∀x ∈ (a, a + δ). В силу критерия монотонности функции на промежутке (см. следствие 1 теорем 4.12 и 4.13) функция  возрастает на (a – δ, a] и убывает на [a, a + δ), поэтому
возрастает на (a – δ, a] и убывает на [a, a + δ), поэтому  (x) ≤
(x) ≤  (a), ∀ x ∈ Ua, то есть функция
(a), ∀ x ∈ Ua, то есть функция  имеет в точке a локальный максимум.
имеет в точке a локальный максимум.
Аналогично рассматриваются и два других случая.
Замечание. Условие изменения знака производной при переходе через точку a является достаточным условием локального экстремума, но не является необходимым. Для примера можно рассмотреть в окрестности точки x = 0
функцию  (x) =
(x) =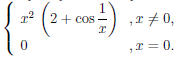
Теорема 4.25 (достаточное условие экстремума в стационарной точке). Пусть a — стационарная точка функции  : X →
: X →  ,
,  дифференцируема в некоторой окрестности точки a и дважды дифференцируема в точке a. Если
дифференцируема в некоторой окрестности точки a и дважды дифференцируема в точке a. Если  //(a) > 0 (
//(a) > 0 ( //(a)
//(a)  0), то точка a является точкой локального минимума (соответственно, максимума) функции
0), то точка a является точкой локального минимума (соответственно, максимума) функции  .
.
Так как a — стационарная точка функции  , то
, то  / (a) = 0. B силу формулы Тейлора с остаточным членом в форме Пеано (теорема 4.19) для всех x ∈ (a -δ, a + δ) {a}
/ (a) = 0. B силу формулы Тейлора с остаточным членом в форме Пеано (теорема 4.19) для всех x ∈ (a -δ, a + δ) {a}
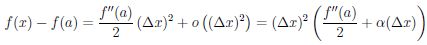 ,
,
где α(∆x) — бесконечно малая функция при ∆x → 0. Пусть  (a) > 0. Так как
(a) > 0. Так как 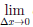 α(∆x) = 0, то существует такое δ0 ∈ (0, δ), что
α(∆x) = 0, то существует такое δ0 ∈ (0, δ), что
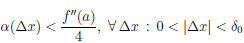 .
.
Но тогда для таких ∆x
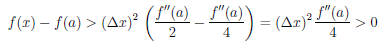 ,
,
то есть функция  имеет в точке a локальный минимум.
имеет в точке a локальный минимум.
Аналогично доказывается, что функция  имеет в точке a локальный максимум, если
имеет в точке a локальный максимум, если  // (a)
// (a)  0.
0.
Замечание. Если  //(a) = 0, то функция может иметь в точке a локальный экстремум (как функция
//(a) = 0, то функция может иметь в точке a локальный экстремум (как функция  (x) = x4 в точке a = 0), а может и не иметь (как функция
(x) = x4 в точке a = 0), а может и не иметь (как функция  (x) = x3 в точке a = 0). Для ответа на вопрос, является ли в этом случае точка a точкой экстремума можно привлечь информацию о производных более высокого порядка.
(x) = x3 в точке a = 0). Для ответа на вопрос, является ли в этом случае точка a точкой экстремума можно привлечь информацию о производных более высокого порядка.
Теорема 4.26. Пусть функция  : (a – δ, a + δ) →
: (a – δ, a + δ) →  (n – 1) раз дифференцируема в (a – δ, a + δ), n раз дифференцируема в точке a и
(n – 1) раз дифференцируема в (a – δ, a + δ), n раз дифференцируема в точке a и
 /(a) =
/(a) = //(a) = … =
//(a) = … = (n-1)(a) =0,
(n-1)(a) =0, (n) (a)
(n) (a) 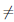 0. (4.22)
0. (4.22)
Тогда
a) если n — четное число, то a — точка локального экстремума  : максимума, если
: максимума, если  (n) (a)
(n) (a) 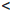 0, и минимума, если
0, и минимума, если  (n) (a) > 0.
(n) (a) > 0.
b) если n — нечетное число, то a не является точкой экстремума функции  .
.
Используя формулу Тейлора с остаточным членом в форме Пеано и условие (4.22), получим, что
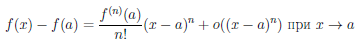
или
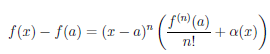 ,
,
где α(x) → 0 при x → a. Учитывая, что  (n) (a)
(n) (a)  0, а α(x) → 0 при x → a, найдем такое δ0 > 0, что ∣α(x)∣
0, а α(x) → 0 при x → a, найдем такое δ0 > 0, что ∣α(x)∣ 
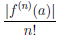 для всех x ∈ (a – δ0 , a + δ0) {a}.
для всех x ∈ (a – δ0 , a + δ0) {a}.
Поэтому в проколотой δ0-окрестности точки a
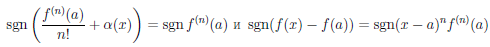 .
.
Если n — четное число, то для всех x ∈ (a – δ0, a + δ0) {a}
(x – a)n > 0 и sgn( (x) –
(x) –  (a)) = sgn
(a)) = sgn (n)(a).
(n)(a).
Если  (n) (a) > 0, то
(n) (a) > 0, то  (x) >
(x) >  (a), ∀x ∈ (a – δ0, a + δ0) {a}, и
(a), ∀x ∈ (a – δ0, a + δ0) {a}, и  имеет в точке a локальный минимум. Если
имеет в точке a локальный минимум. Если  (n) (a)
(n) (a) 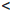 0, то
0, то  (x)
(x) 
 (a), ∀x ∈ (a – δ0, a + δ0) {a}, и
(a), ∀x ∈ (a – δ0, a + δ0) {a}, и имеет в точке a локальный максимум. Если n — нечетное число, то функция (x – a)n имеет противоположные знаки по разные стороны от точки a, то есть разность
имеет в точке a локальный максимум. Если n — нечетное число, то функция (x – a)n имеет противоположные знаки по разные стороны от точки a, то есть разность  (x) –
(x) –  (a) меняет знак при переходе через точку a. Последнее означает, что a не является точкой экстремума функции
(a) меняет знак при переходе через точку a. Последнее означает, что a не является точкой экстремума функции  .
.
Замечание. Очевидно, что теорема 4.25 является следствием теоремы 4.26.
С задачей локального экстремума тесно связана задача о наибольшем и наименьшем значении непрерывной функции на промежутке. Для функции  (x), непрерывной на отрезке [a, b], согласно 2-ой теореме Вейерштрасса существует точка p ∈ [a, b], в которой эта функция принимает наибольшее значение, и точка q ∈ [a, b], в которой функция принимает наименьшее значение. Если p ∈ (a, b), то точка p является точкой локального максимума функции, а если q ∈ (a, b), то q является точкой локального минимума функции. Поэтому наибольшее (sup{
(x), непрерывной на отрезке [a, b], согласно 2-ой теореме Вейерштрасса существует точка p ∈ [a, b], в которой эта функция принимает наибольшее значение, и точка q ∈ [a, b], в которой функция принимает наименьшее значение. Если p ∈ (a, b), то точка p является точкой локального максимума функции, а если q ∈ (a, b), то q является точкой локального минимума функции. Поэтому наибольшее (sup{ (x) : x ∈ [a, b]}) и наименьшее (inf {
(x) : x ∈ [a, b]}) и наименьшее (inf { (x) : x ∈ [a, b]}) значения функция
(x) : x ∈ [a, b]}) значения функция  на [a, b] может принимать либо в критических точках, лежащих в интервале (a, b), либо в точках a, b.
на [a, b] может принимать либо в критических точках, лежащих в интервале (a, b), либо в точках a, b.
Если  (x) непрерывна на интервале (a, b), то вместо значений функции в точках a, b, следует рассматривать
(x) непрерывна на интервале (a, b), то вместо значений функции в точках a, b, следует рассматривать
 ,
,
если такие пределы существуют (конечные или бесконечные). Точно также следует поступать и на промежутках [a, b) и (a, b].
В прикладных задачах при нахождении наибольшего (наименьшего) значения функции на промежутке X часто встречается ситуация, когда функция непрерывна на X и имеет на нем единственную критическую точку. Можно доказать, что, если x0 — точка локального максимума, то  (x0) = sup{
(x0) = sup{ (x), x ∈ X}, а если x0 — точка локального минимума, то
(x), x ∈ X}, а если x0 — точка локального минимума, то  (x0) = inf {
(x0) = inf { (x), x ∈ X}.
(x), x ∈ X}.
- Заказать решение задач по высшей математике
Пример №9
Исследовать на экстремум  (x) = xe-x, x ∈ [0, +∞).
(x) = xe-x, x ∈ [0, +∞).
Функция  непрерывна и дифференцируема на [0, +∞), причем
непрерывна и дифференцируема на [0, +∞), причем
 /(x) = e -x — xe -x = e -x(1 — x);
/(x) = e -x — xe -x = e -x(1 — x);  /(x) = 0
/(x) = 0  x = 1.
x = 1.
Таким образом, функция  имеет на (0, +∞) единственную стационарную точку. Из таблицы
имеет на (0, +∞) единственную стационарную точку. Из таблицы
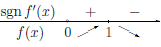
и теоремы 4.24 следует, что функция  имеет в точке x = 1 локальный максимум. При этом
имеет в точке x = 1 локальный максимум. При этом  (1) =
(1) =  .
.
Направление выпуклости графика функции
Будем считать, что функция  дифференцируема на интервале (a, b), то есть график Γ
дифференцируема на интервале (a, b), то есть график Γ функции
функции  имеет в каждой точке невертикальную касательную.
имеет в каждой точке невертикальную касательную.
Определение 4.12. Говорят, что график функции  обращен выпуклостью вверх на интервале (a, b) (или функция
обращен выпуклостью вверх на интервале (a, b) (или функция  является выпуклой вверх на (a, b)), если график Γ
является выпуклой вверх на (a, b)), если график Γ функции лежит не выше касательных, проведенных в точках (x,
функции лежит не выше касательных, проведенных в точках (x,  (x)), x ∈ (a, b), к этому графику.
(x)), x ∈ (a, b), к этому графику.
Определение 4.13. Говорят, что график функции  обращен выпуклостью вниз на интервале (a, b), если на нем Γ
обращен выпуклостью вниз на интервале (a, b), если на нем Γ лежит не ниже касательных, проведенных в точках (x,
лежит не ниже касательных, проведенных в точках (x,  (x)), x ∈ (a, b), к Γ
(x)), x ∈ (a, b), к Γ .
.
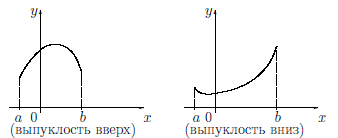
Теорема 4.27. Пусть функция  дважды дифференцируема на интервале (a, b). Если
дважды дифференцируема на интервале (a, b). Если  //(x) ≤ 0 (
//(x) ≤ 0 ( //(x) ≥ 0) на (a, b), то график Γ
//(x) ≥ 0) на (a, b), то график Γ обращен выпуклостью вверх (соответственно, вниз) на (a, b).
обращен выпуклостью вверх (соответственно, вниз) на (a, b).
Пусть f//(x) ≥ 0, ∀ x ∈ (a, b), и c — некоторая точка интервала (a, b). Уравнение касательной, проведенной к Γ в точке (c,
в точке (c,  (c)) имеет вид y =
(c)) имеет вид y =  (c) +
(c) +  / (c)(x – c). Поскольку функция
/ (c)(x – c). Поскольку функция  дважды дифференцируема на (a, b), то из формулы Тейлора с остаточным членом в форме Лагранжа следует, что ∀ x ∈ (a, b) ∃ ηx, лежащая между (c, x), такая, что
дважды дифференцируема на (a, b), то из формулы Тейлора с остаточным членом в форме Лагранжа следует, что ∀ x ∈ (a, b) ∃ ηx, лежащая между (c, x), такая, что
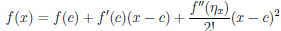 .
.
Поэтому 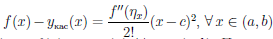 . Так как
. Так как  //(x) ≥ 0 для всех x ∈ (a, b), то
//(x) ≥ 0 для всех x ∈ (a, b), то  (x) ≥ yκac(x), ∀ x ∈ (α,b). Поскольку c — произвольная точка интервала (a, b), то Γ
(x) ≥ yκac(x), ∀ x ∈ (α,b). Поскольку c — произвольная точка интервала (a, b), то Γ обращен выпуклостью вниз на (a, b).
обращен выпуклостью вниз на (a, b).
Следствие. Если функция  // непрерывна и положительна (отрицательна) в точке c, то существует такая окрестность Uc точки c, в которой график Γ
// непрерывна и положительна (отрицательна) в точке c, то существует такая окрестность Uc точки c, в которой график Γ обращен выпуклостью вниз (соответственно, вверх).
обращен выпуклостью вниз (соответственно, вверх).
Замечание 1. Если на интервале (a, b)  //(x) = 0, то
//(x) = 0, то  (x) = kx+c и можно считать, что график функции обращен на (a, b) как выпуклостью вверх, так и вниз.
(x) = kx+c и можно считать, что график функции обращен на (a, b) как выпуклостью вверх, так и вниз.
Замечание 2. Из определений 4.12 и 4.13 следует, что если график Γ обращен выпуклостью вверх, то всякая хорда, соединяющая две различные точки графика функции, лежит под соответствующей дугой Γ
обращен выпуклостью вверх, то всякая хорда, соединяющая две различные точки графика функции, лежит под соответствующей дугой Γ , а для функции, выпуклой вниз, она лежит над соответствующей дугой Γ
, а для функции, выпуклой вниз, она лежит над соответствующей дугой Γ . Это свойство часто берется в качестве определения выпуклости Γ
. Это свойство часто берется в качестве определения выпуклости Γ вверх и, ответственно, вниз.
вверх и, ответственно, вниз.
Пример №10
Пусть  (x) = x2/3. Функция
(x) = x2/3. Функция  непрерывна на
непрерывна на  , дважды дифференцируема на
, дважды дифференцируема на  {0} и
{0} и  //(x)=
//(x)=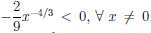 . Поэтому на интервалах (-∞, 0) и (0, +∞) график функции обращен выпуклостью вверх.
. Поэтому на интервалах (-∞, 0) и (0, +∞) график функции обращен выпуклостью вверх.
Точки перегиба
Определение 4.14. Пусть функция  непрерывна на интервале (a, b), c ∈ (a, b). Точку c называют точкой перегиба функции
непрерывна на интервале (a, b), c ∈ (a, b). Точку c называют точкой перегиба функции  (или графика функции), если существует такая окрестность Uc(δ) точки c, что на интервалах (c – δ, c) и (c, c + δ) график Γ
(или графика функции), если существует такая окрестность Uc(δ) точки c, что на интервалах (c – δ, c) и (c, c + δ) график Γ имеет различные направления выпуклости.
имеет различные направления выпуклости.
Теорема 4.28 (необходимое условие точки перегиба). Пусть c — точка перегиба функции  и
и  имеет в точке c конечную вторую производную. Тогда
имеет в точке c конечную вторую производную. Тогда  //(c) = 0.
//(c) = 0.
Для простоты доказательства будем считать, что функция  дважды дифференцируема в некоторой окрестности Uc(δ0) точки c и
дважды дифференцируема в некоторой окрестности Uc(δ0) точки c и  //(x) непрерывна в точке c.
//(x) непрерывна в точке c.
Предположим, что  //(c)
//(c)  0. Тогда в силу непрерывности функции
0. Тогда в силу непрерывности функции  //(x) в точке c существует такое δ ∈ (0, δ0), что на интервале Uc(δ)
//(x) в точке c существует такое δ ∈ (0, δ0), что на интервале Uc(δ)  //(x) сохраняет знак. По теореме 4.27 Γ
//(x) сохраняет знак. По теореме 4.27 Γ обращен выпуклостью вверх, если
обращен выпуклостью вверх, если  // (c)
// (c)  0, и вниз, если
0, и вниз, если  //(c) > 0, на интервале Uc(δ). Но тогда c не является точкой перегиба функции
//(c) > 0, на интервале Uc(δ). Но тогда c не является точкой перегиба функции  . Следовательно,
. Следовательно,  //(c) = 0.
//(c) = 0.
Замечание. Условие  //(c) = 0 является необходимым, но не достаточным условием наличия у функции f в точке c перегиба. Подтверждением может служить функция
//(c) = 0 является необходимым, но не достаточным условием наличия у функции f в точке c перегиба. Подтверждением может служить функция  (x) = x4.
(x) = x4.
Как и при рассмотрении необходимых условий экстремума функции, можно показать, что точки перегиба непрерывной на интервале (a, b) функции  следует искать среди тех точек c ∈ (a, b), в которых либо функция дважды дифференцируема и
следует искать среди тех точек c ∈ (a, b), в которых либо функция дважды дифференцируема и  //(c) = 0, либо функция
//(c) = 0, либо функция  не является дважды дифференцируемой.
не является дважды дифференцируемой.
Теорема 4.29 (1-ое достаточное условие перегиба). Пусть функция  непрерывна на интервале (a, b) и функция
непрерывна на интервале (a, b) и функция  дважды дифференцируема в некоторой окрестности точки c ∈ (a, b), кроме, быть может, точки c. Если
дважды дифференцируема в некоторой окрестности точки c ∈ (a, b), кроме, быть может, точки c. Если  //(c) = 0 или f00(c) не существует, а функция
//(c) = 0 или f00(c) не существует, а функция  //(x) в этой окрестности по разные стороны от точки c имеет противоположные знаки, то c — точка перегиба функции
//(x) в этой окрестности по разные стороны от точки c имеет противоположные знаки, то c — точка перегиба функции  .
.
Пусть, например, на интервале (c – δ, c)  //(x) > 0, а на интервале (c, c + δ)
//(x) > 0, а на интервале (c, c + δ)  //(x)
//(x)  0. Тогда по теореме 4.27 функция
0. Тогда по теореме 4.27 функция  на интервале (c – δ, c) обращена выпуклостью вниз, а на интервале (c, c+δ) — вверх. Поэтому c — точка перегиба функции
на интервале (c – δ, c) обращена выпуклостью вниз, а на интервале (c, c+δ) — вверх. Поэтому c — точка перегиба функции .
.
Пример №11
Исследовать на перегиб функцию  (x) = x5/3.
(x) = x5/3.
Функция  непрерывна на
непрерывна на  и
и  //(x) =
//(x) = 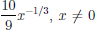 . Тогда на интервале (-∞, 0)
. Тогда на интервале (-∞, 0)  // (x)
// (x)  0 и график Γ
0 и график Γ обращен выпуклостью вверх, а на интервале (0, +∞)
обращен выпуклостью вверх, а на интервале (0, +∞)  //(x) > 0 и график Γ
//(x) > 0 и график Γ обращен выпуклостью вниз, поэтому точка x = 0 — точка перегиба функции
обращен выпуклостью вниз, поэтому точка x = 0 — точка перегиба функции  .
.
Теорема 4.30 (2-ое достаточное условие перегиба). Пусть функция  трижды дифференцируема в точке c и
трижды дифференцируема в точке c и  //(c) = 0, а
//(c) = 0, а  (3) (c)
(3) (c)  0. Тогда c — точка перегиба функции
0. Тогда c — точка перегиба функции  .
.
Так как функция  трижды дифференцируема в точке c, то функция
трижды дифференцируема в точке c, то функция //(x) дифференцируема в точке c, поэтому в силу формулы Тейлора с остаточным членом в форме Пеано
//(x) дифференцируема в точке c, поэтому в силу формулы Тейлора с остаточным членом в форме Пеано
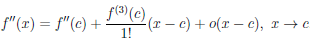 .
.
Но  // (c) = 0, поэтому
// (c) = 0, поэтому
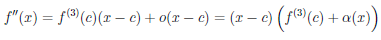
где α(x) → 0 при x → c, и, значит, найдется δ > 0 такое, что для всех x ∈ (δ)
(δ)
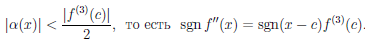
Следовательно, в 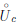 (δ) по разные стороны от точки c функция
(δ) по разные стороны от точки c функция  //(x) имеет противоположные знаки. С учетом теоремы 4.29 получаем, что c — точка перегиба функции
//(x) имеет противоположные знаки. С учетом теоремы 4.29 получаем, что c — точка перегиба функции  .
.
Например, x = 0 — точка перегиба функции  (x) = sin x, так как
(x) = sin x, так как  //(0) = 0, а
//(0) = 0, а  (3) (0)
(3) (0) 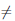 0.
0.
Асимптоты графика функции
Определение 4.15. Пусть функция  определена на промежутке X, a — левосторонняя (правосторонняя) предельная точка множества X. Прямая x = a называется вертикальной асимптотой функции
определена на промежутке X, a — левосторонняя (правосторонняя) предельная точка множества X. Прямая x = a называется вертикальной асимптотой функции  или графика Γ
или графика Γ при x → a – 0 (соответственно, при x → a + 0), если
при x → a – 0 (соответственно, при x → a + 0), если 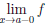 (x)= +∞ или -∞ x→a-0 (соответсвенно,
(x)= +∞ или -∞ x→a-0 (соответсвенно, 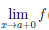 (x) = +∞ или -∞).
(x) = +∞ или -∞).
Пример №12
Пусть  (x) = ln x. Тогда D(
(x) = ln x. Тогда D( ) = (0, +∞) и функциям
) = (0, +∞) и функциям  непрерывна на D(
непрерывна на D( ). Точка x = 0 является правосторонней предельной точкой области определения функции и
). Точка x = 0 является правосторонней предельной точкой области определения функции и 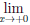
 (x) = -∞. Поэтому прямая x = 0 является вертикальной асимптотой функции
(x) = -∞. Поэтому прямая x = 0 является вертикальной асимптотой функции  при x → +0.
при x → +0.
Пример №13
Пусть  (x) = e-1/x. Тогда D(
(x) = e-1/x. Тогда D( ) =
) = 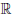 {0}, функция
{0}, функция  непрерывна на D(
непрерывна на D( ),
), 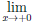
 (x) = 0 и
(x) = 0 и 
 (x) = +∞. Значит, прямая x = 0 является вертикальной асимптотой графика Γ
(x) = +∞. Значит, прямая x = 0 является вертикальной асимптотой графика Γ при x → -0.
при x → -0.
Определение 4.16. Пусть функция  определена на промежутке X и X ⊃ (a, +∞) (или X ⊃ (-∞, a)), a ∈
определена на промежутке X и X ⊃ (a, +∞) (или X ⊃ (-∞, a)), a ∈  . Прямую y = kx + b называют наклонной (невертикальной) асимптотой функции
. Прямую y = kx + b называют наклонной (невертикальной) асимптотой функции  или графика Γ
или графика Γ при x → +∞ (соответственно, при x → -∞), если ∃
при x → +∞ (соответственно, при x → -∞), если ∃ 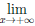 (
( (x) – (kx + b)) = 0 (соответственно,
(x) – (kx + b)) = 0 (соответственно,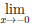 (
( (kx + b))=0).
(kx + b))=0).
Если k = 0, то асимптоту называют горизонтальной.
Пример №14
Найти асимптоты функций
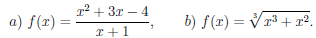
a) Функция  непрерывна на
непрерывна на  {-1}. Так как
{-1}. Так как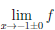 (x) =
(x) = , то прямая x = -1 является вертикальной асимптотой Γ
, то прямая x = -1 является вертикальной асимптотой Γ при x → -1+0 и при x → -1-0. Разделим числитель x2 + 3x- 4 на знаменатель x + 1 по правилу деления многочленов :
при x → -1+0 и при x → -1-0. Разделим числитель x2 + 3x- 4 на знаменатель x + 1 по правилу деления многочленов :
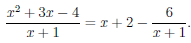
Так как 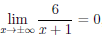 , то прямая y = x + 2 является наклонной асимптотой функции
, то прямая y = x + 2 является наклонной асимптотой функции
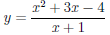 при x → +∞ и при x → -∞.
при x → +∞ и при x → -∞.
b) Функция непрерывна на  и потому не имеет вертикальных асимптот. Заметим, что для x
и потому не имеет вертикальных асимптот. Заметим, что для x  0
0
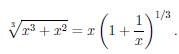
В силу формулы Тейлора с остаточным членом в форме Пеано
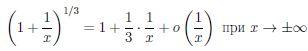 .
.
Следовательно, 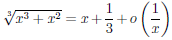 при x → ±∞, а поэтому прямая у =
при x → ±∞, а поэтому прямая у =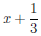 является наклонной асимптотой функции
является наклонной асимптотой функции 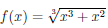 при x → +∞ и при x → -∞.
при x → +∞ и при x → -∞.
Теорема 4.31. Для того, чтобы прямая y = kx+b была наклонной асимптотой графика функции y =  (x) при x → +∞, необходимо и достаточно, чтобы существовали конечные пределы
(x) при x → +∞, необходимо и достаточно, чтобы существовали конечные пределы
 . (4.23)
. (4.23)
Необходимость. Если y = kx + b — асимптота Γ при x → +∞, то по определению 4.16
при x → +∞, то по определению 4.16
 (x) = kx + b + α(x), (4.24)
(x) = kx + b + α(x), (4.24)
где α(x) → 0 при x → +∞. Разделим обе части полученного равенства на x и получим
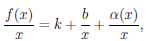
откуда следует существование предела 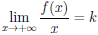 . Но (см. (4.24))
. Но (см. (4.24))
 (x) — kx = b + α(x), где α(x) → 0 при x → +∞.
(x) — kx = b + α(x), где α(x) → 0 при x → +∞.
Поэтому 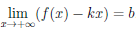
Достаточность. Если существуют конечные пределы, перечисленные в 4.23,
то  (x) — (kx+b) = α(x), где α(x) → 0 при x → +∞, а поэтому по определению 4.16 прямая y = kx + b является наклонной асимптотой Γ
(x) — (kx+b) = α(x), где α(x) → 0 при x → +∞, а поэтому по определению 4.16 прямая y = kx + b является наклонной асимптотой Γ при x → +∞.
при x → +∞.
Аналогично формулируется и доказывается критерий существования наклон
ной асимптоты графика Γ при x → -∞.
при x → -∞.
Построение графика функции
Для построения графика функции y =  (x) нужно последовательно выполнить следующие операции:
(x) нужно последовательно выполнить следующие операции:
- Найти область определения функции
 , изучить функцию на четность (нечетность), периодичность.
, изучить функцию на четность (нечетность), периодичность. - Исследовать функцию на непрерывность, указать точки разрыва, найти асимптоты.
- Найти
 /(x), исследовать функцию на экстремум, указать промежутки монотонности.
/(x), исследовать функцию на экстремум, указать промежутки монотонности. - Найти
 //(x), исследовать функцию на перегиб, указать промежутки выпуклости вверх (вниз) графика функции.
//(x), исследовать функцию на перегиб, указать промежутки выпуклости вверх (вниз) графика функции. - Дать характеристику поведения функции на каждом из полученных промежутков.
- Нарисовать график.
Пример №15
Построить график функции (x) =
(x) =  .
.
Решение:
1. D( ) =
) = 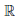 ; функция является функцией общего вида (иными словами: функция не является четной, не является нечетной), так как
; функция является функцией общего вида (иными словами: функция не является четной, не является нечетной), так как
Функция не является периодической, так как обращается в нуль только в двух точках x = 0 и x = —1.
2.  (x) ∈ C (
(x) ∈ C ( ), поэтому Γ
), поэтому Γ не имеет вертикальных асимптот. Прямая y =
не имеет вертикальных асимптот. Прямая y = 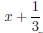 наклонная асимптота Γ
наклонная асимптота Γ при x → ±∞ .
при x → ±∞ .
3. Для всех x ∈ (-∞, —1) S(—1, 0) S(0, +∞)
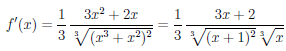 .
.
Так как
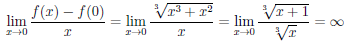 ,
,
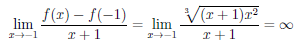 ,
,
то функция имеет в точках x = —1 и x = 0 бесконечные производные, а значит Γ имеет в соответствующих точках (—1, 0) и (0, 0) вертикальные касательные и эти точки являются критическими.
имеет в соответствующих точках (—1, 0) и (0, 0) вертикальные касательные и эти точки являются критическими.
Далее,  /(x) = 0
/(x) = 0  x =
x = 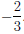 . Поэтому x =
. Поэтому x = 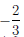 стационарная точка функции. Поскольку sgn
стационарная точка функции. Поскольку sgn  /(x) = sgnx (3x + 2), ∀x
/(x) = sgnx (3x + 2), ∀x 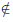 {—1; 0}, то
{—1; 0}, то
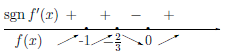
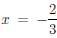 точка локального максимума и
точка локального максимума и 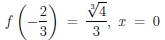 точка локального минимума и
точка локального минимума и  (0)=0. На 2/3], [0, +∞) функция возрастает, а на [—2/3, 0] — убывает.
(0)=0. На 2/3], [0, +∞) функция возрастает, а на [—2/3, 0] — убывает.
4. Так как
 //(x) = –
//(x) = – (x + 1)-5/3x-4/3, ∀x ∈ (-∞, -1)
(x + 1)-5/3x-4/3, ∀x ∈ (-∞, -1)  (-1,0)
(-1,0) (0, +∞),
(0, +∞),
то  //(x)
//(x)  0 на указанном множестве и x = -1, x = 0 — точки возможного перегиба Γ
0 на указанном множестве и x = -1, x = 0 — точки возможного перегиба Γ . Но sgn
. Но sgn  //(x) = – sgn (x + 1), ∀x
//(x) = – sgn (x + 1), ∀x 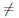 0, -1, а значит
0, -1, а значит
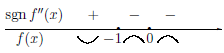
очка x = -1 — точка перегиба заданной функции.
Полученные результаты объединим в таблицу и нарисуем график:
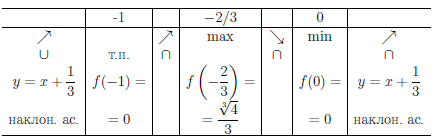
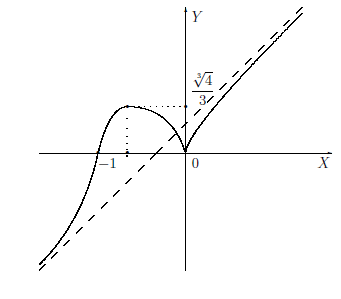
Свойства дифференцируемых функций
Определение 12.1. Функция y=f(x) называется возрастающей в точке 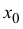 , если
, если 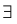 окрестность
окрестность 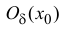 этой точки такая, что
этой точки такая, что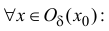
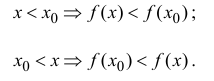
Аналогично определяется убывающая в точке 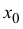 функция.
функция.
Точка 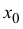 называется точкой локального максимума (минимума) функции
называется точкой локального максимума (минимума) функции
y=f(x), если  окрестность
окрестность 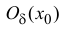 этой точки такая, что
этой точки такая, что 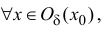
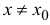 .
.
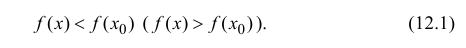
Точки локального максимума и минимума называются точками локального экстремума. Если знаки неравенств в соотношениях (12.1) нестрогие, то говорят о нестрогом локальном максимуме (минимуме).
Теорема 12.1. (теорема Ферма). Пусть функция y=f(x) определена в некоторой окрестности 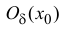 точки
точки 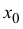 , дифференцируема в этой точке и имеет в ней локальный экстремум. Тогда
, дифференцируема в этой точке и имеет в ней локальный экстремум. Тогда 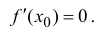
Доказательство
Равенство 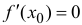 в теореме 12.1 означает, что касательная к графику
в теореме 12.1 означает, что касательная к графику
функции y=f(x) в точке 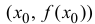 горизонтальна.
горизонтальна.
Теорема 12.2. Пусть функция y=f(x) дифференцируема в точке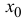 и
и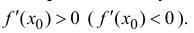 . Тогда f(x) возрастает (убывает) в точке
. Тогда f(x) возрастает (убывает) в точке 
Доказательство
Докажем для случая 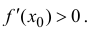 По формуле (6.4)
По формуле (6.4)
 окрестность
окрестность  такая что
такая что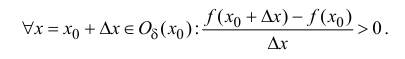
Если 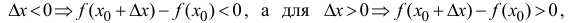 следовательно условия возрастания функции в точке (см. определение 12.1) выполнены.
следовательно условия возрастания функции в точке (см. определение 12.1) выполнены.
Теорема 12.3 (теорема Ролля). Пусть функция y=f(x):
1) непрерывна на отрезке  ;
;
2) дифференцируема на интервале (a ,b );
3) f(a)=f(b).
Тогда 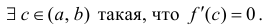
Доказательство
По теореме 11.1 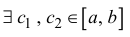 такие, что
такие, что
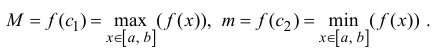
Если M = m, то f( x) – постоянная функция поэтому
поэтому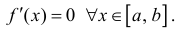
Если 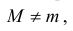 , то либо max, либо min достигается на ( a,b ). Пусть, например,
, то либо max, либо min достигается на ( a,b ). Пусть, например,
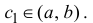 . Тогда точка
. Тогда точка 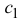 удовлетворяет условиям теоремы 12.1, и поэтому
удовлетворяет условиям теоремы 12.1, и поэтому
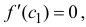 , что и требовалось доказать.
, что и требовалось доказать.
Теорема 12.4 (теорема Лагранжа).
Пусть функция y=f(x):
1) непрерывна на отрезке [a,b];
2) дифференцируема на интервале ( a,b ).
Тогда 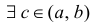 такая, что
такая, что 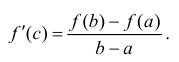 (12.4)
(12.4)
Доказательство
Рассмотрим функцию 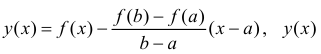 – непрерывна на отрезке [a, b] и дифференцируема на интервале ( a,b );
– непрерывна на отрезке [a, b] и дифференцируема на интервале ( a,b ); 
Поэтому y(x) удовлетворяет условиям теоремы 12.3, то есть 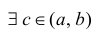 такая, что
такая, что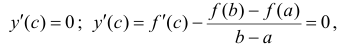 что и требовалось доказать.
что и требовалось доказать.
Угловой коэффициент прямой L, проходящей через точки  равен
равен
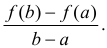 Поэтому формула (12.4) означает, что
Поэтому формула (12.4) означает, что 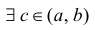 такая, что касательная к графику функции y=f(x) в точке
такая, что касательная к графику функции y=f(x) в точке 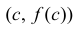 параллельна прямой L, рис. 12.1.
параллельна прямой L, рис. 12.1.
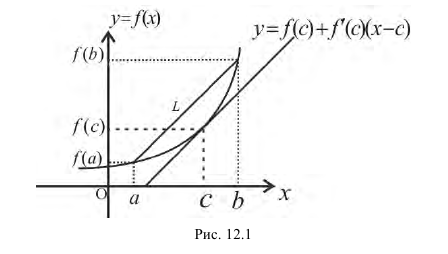
Если х задает время и y=f(x) – путь, пройденный телом при движении по прямой за время х, то 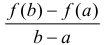 – средняя скорость движения тела на промежутке времени [a b] и согласно (12.4)
– средняя скорость движения тела на промежутке времени [a b] и согласно (12.4) 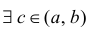 такая, что мгновенная скорость
такая, что мгновенная скорость 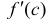 тела в момент времени с равна средней скорости.
тела в момент времени с равна средней скорости.
Пример №16
Дана кривая  и точки A(0;1) и B(6; 37) на кривой. На интервале (0; 6) найти точку с, удовлетворяющую условию (12.4). Написать уравнение касательной в точке (c,f(c)). Сделать чертеж.
и точки A(0;1) и B(6; 37) на кривой. На интервале (0; 6) найти точку с, удовлетворяющую условию (12.4). Написать уравнение касательной в точке (c,f(c)). Сделать чертеж.
Решение:
Подставив точки А и В в формулу (12.4), получим
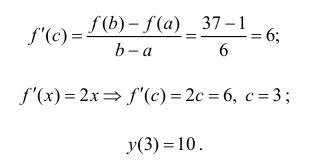
Уравнение касательной к кривой 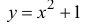
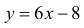 (см. пример 9.9), рис. 12.2.
(см. пример 9.9), рис. 12.2.
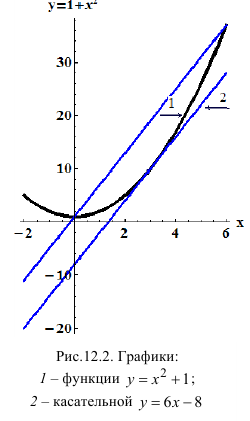
Теорема 12.5. (терема Коши). Пусть функции y=f(x) и y=g(x):
1) непрерывны на отрезке [a b];
2) дифференцируемы на интервале ( a,b ), причем 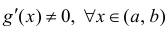 и
и 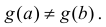 . Тогда
. Тогда 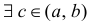 такая, что
такая, что
Доказательство
Рассмотрим функцию
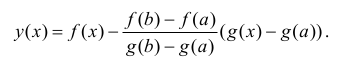
y(x) удовлетворяет условиям теоремы 12.3, и далее доказательство аналогично доказательству теоремы 12.4.
- Техника дифференцирования
- Дифференциальная геометрия
- Логарифмическая функция, её свойства и график
- Логарифмические выражения
- Применение производной к исследованию функции
- Приложения производной
- Производные высших порядков
- Дифференциал функции
Производная функции, согласно ее математического определения (1.5) и (1.6) – это некий предел. Но, как и всякий предел, он может оказаться:
А) конечным; б) бесконечным; в) вообще не существовать.
Если для данного X имеет место вариант (а), то есть если при заданном X производная ![]() функции
функции ![]() Существует и конечна, то эта функция называется Дифференцируемой в точке x.
Существует и конечна, то эта функция называется Дифференцируемой в точке x.
Функция, дифференцируемая в Каждой точке X некоторого промежутка оси Ох (например, интервала (A; B) или отрезка [A; B]) называется Дифференцируемой на этом промежутке. Кстати, сама процедура вычисления производной функции называется ее Дифференцированием (продифференцировать функцию – это значит найти ее производную).
 Из геометрического смысла производной функции, определяемого равенством (1.11) и рис. 4.5, вытекают следующие два наглядные необходимые и достаточные условия дифференцируемости заданной функции
Из геометрического смысла производной функции, определяемого равенством (1.11) и рис. 4.5, вытекают следующие два наглядные необходимые и достаточные условия дифференцируемости заданной функции ![]() в заданной точке X:
в заданной точке X:
1) Существование касательной к графику функции в его точке с абсциссой X.
2) Невертикальность этой касательной (ибо ![]() не существует).
не существует).
Например, функция ![]() , график которой изображен на рис. 4.7, не дифференцируема в точках X1, X2 и X3.
, график которой изображен на рис. 4.7, не дифференцируема в точках X1, X2 и X3.
Действительно, точке X1 соответствует на графике функции точка M1 с вертикальной касательной. Точке X2 (точке максимума функции) соответствует остроконечная вершина M2, касательная в которой не существует. Точке X3 соответствует точка M3 – точка излома графика функции, в которой тоже касательная не существует.
Во всех же остальных точках M графика функции касательную к графику провести можно, и она невертикальна. Значит, для всех остальных X, отличных от (X1; X2; X3), существует производная функции. То есть во всех остальных точках X функция ![]() дифференцируема.
дифференцируема.
| < Предыдущая | Следующая > |
|---|
Дифференцируемость функции многих переменных
9 разделов
от теории до практики
4 примера
Примеры решения задач
видео
Примеры решения задач
-
Частные производные.
Начать изучение
-
Дифференцируемость функции многих переменных в точке.
Начать изучение
-
Необходимое условие дифференцируемости функции в точке.
Начать изучение
-
Достаточные условия дифференцируемости функции в точке.
Начать изучение
-
Дифференцируемость сложной функции.
Начать изучение
-
Дифференциал. Инвариантность формы первого дифференциала. Правила дифференцирования.
Начать изучение
-
Формула конечных приращений Лагранжа.
Начать изучение
-
Касательная плоскость к графику функции двух переменных. Геометрический смысл дифференциала.
Начать изучение
-
Производная по направлению. Градиент.
Начать изучение
Частные производные.
Пусть функция
$$
f(x) = f(x_{1}, ldots, x_{n})nonumber
$$
определена в окрестности точки (x^{0} = (x_{1}^{0}, ldots, x_{n}^{0})). Рассмотрим функцию одной переменной
$$
varphi (x_{1}) = f(x_{1},x_{2}^{0}, ldots, x_{n}^{0})nonumber
$$
Функция (varphi (x_{1})) может иметь производную в точке (x_{1}^{0}). По определению такая производная называется частной производной (frac{partial f}{partial x_{1}}(x^{0})).
Таким образом,
$$
frac{partial f}{partial x_{1}}(x^{0}) = frac{partial f}{partial x_{1}}(x_{1}^{0}, ldots, x_{n}^{0}) = lim_{substack{vartriangle x_{1}longrightarrow 0}}frac{f(x_{1},x_{2}^{0}, ldots, x_{n}^{0}) — f(x_{1}^{0}, ldots, x_{n}^{0})}{vartriangle x_{1}}nonumber
$$
где (vartriangle x_{1} = x_{1} — x_{1}^{0}).
Аналогично определяются частные производные (первого порядка)
$$
frac{partial f}{partial x_{i}}(x_{1}^{0}, ldots, x_{n}^{0}), i = overline{2, n}.nonumber
$$
Употребляются и другие обозначения для частных производных первого порядка:
$$
frac{partial f}{partial x_{1}}(x^{0}) = f_{x_{i}}(x^{0}) = D_{i}f(x^{0}) = f_{x_{i}}^{‘}(x^{0}) = frac{partial f}{partial x_{i}}f(x^{0}) = frac{partial f(x^{0})}{partial x_{i}}.nonumber
$$
Функция двух переменных может иметь в точке (x^{0}, y^{0}) две частные производные первого порядка
$$
frac{partial f}{partial x}(x^{0}, y^{0}),quad frac{partial f}{partial y}(x^{0}, y^{0}).nonumber
$$
Для функции трех переменных — три частные производные первого порядка
$$
frac{partial f}{partial x}(x^{0}, y^{0}, z^{0}),quad frac{partial f}{partial y}(x^{0}, y^{0}, z^{0}),quad frac{partial f}{partial z}(x^{0}, y^{0}, z^{0})nonumber
$$
Поскольку при вычислении частных производных все переменные, кроме одной, фиксируются, то техника вычисления частных производных такая же, как техника вычисления производных функции одной переменной.
Например,
$$
frac{partial}{partial x}sqrt{x^{2} + y^{2}} = frac{1}{2{sqrt{x^{2} + y^{2}}}}frac{partial}{partial x}(x^{2} + y^{2}) = frac{x}{sqrt{x^{2} + y^{2}}}.nonumber
$$
Дифференцируемость функции многих переменных в точке.
Дадим определение дифференцируемости функции в точке.
Определение.
Функция (f(x) = f(x_{1}, ldots, x_{n})) называется дифференцируемой в точке (x^{0} = (x_{1}^{0}, ldots, x_{n}^{0})), если она определена в некоторой окрестности этой точки и существуют такие числа (A_{1}, ldots, A_{n}), что
$$
f(x) — f(x^{0}) = sum_{substack{i=1} }^{substack{n}}A_{i}(x_{i} — x_{i}^{0}) + o(rho(x, x^{0})),quad при x rightarrow x^{0}.label{ref1}
$$
Теорема 1.
Функция (f(x)) дифференцируема в точке (x^{0}) в том и только том случае, когда в некоторой окрестности точки (x^{0}) функция (f(x)) может быть представлена в следующем виде:
$$
f(x) = f(x^{0}) + sum_{i=1}^{n}f_{i}(x)(x_{i} — x_{i}^{0})label{ref2}
$$
где функции (f_{i}(x)) непрерывны в точке (x^{0}).
Доказательство.
(circ) Пусть функция (f(x)) дифференцируема в точке (x^{0}). Тогда выполнено условие (1). Заметим, что равенство (psi(x) = o(rho(x, x^{0}))) при (x longrightarrow x^{0}) означает, что (psi(x) = varepsilon(x)rho(x, x^{0})), где (displaystylelim_{substack{x longrightarrow x^{0}}}varepsilon(x) = 0).
Тогда
$$
psi(x) = dfrac{varepsilon(x)}{rho(x, x^{0})} sum_{substack{i=1} }^{substack{n}}(x_{i} — x_{i}^{0})^{2} = sum_{substack{i=1} }^{substack{n}}varepsilon_{i}(x)(x_{i} — x_{i}^{0}),label{ref3}
$$
где (varepsilon_{i}(x) = varepsilon(x)dfrac{(x_{i} — x_{i}^{0})}{rho(x, x^{0})}), (displaystylelim_{substack{x longrightarrow x^{0}}}varepsilon(x) = 0), так как (0 leq dfrac{|(x_{i} — x_{i}^{0})|}{rho(x, x^{0})} leq 1).
Доопределим функции (varepsilon_{i}(x)) в точке (x^{0}) по непрерывности, полагая (displaystylelim_{substack{x longrightarrow x^{0}}}varepsilon_{i}(x) = varepsilon_{i}(x^{0}) = 0).
Тогда из eqref{ref1} и eqref{ref3} получаем
$$
f(x) = f(x^{0}) + sum_{substack{i=1} }^{substack{n}}A_{i}(x_{i} — x_{i}^{0}) + sum_{substack{i=1} }^{substack{n}}varepsilon_{i}(x)(x_{i} — x_{i}^{0}) =\= f(x^{0}) + sum_{substack{i=1} }^{substack{n}}f_{i}(x)(x_{i} — x_{i}^{0}),quad f_{i}(x) = A_{i} + varepsilon_{i}(x).nonumber
$$
Так как функции (varepsilon_{i}(x)) непрерывны в точке (x^{0}), то и функции (f_{i}(x)) непрерывны в точке (x^{0}) и (f_{i}(x^{0}) = A_{i}), (i = overline{1, n}).
Пусть выполнено eqref{ref2}. Тогда, воспользовавшись непрерывностью функции (f_{i}(x)) в точке (x^{0}), положим
$$
A_{i} = f_{i}(x^{0}),quad f_{i}(x) = A_{i} + varepsilon_{i}(x),quad lim_{substack{x longrightarrow x^{0}}}varepsilon_{i}(x) = 0.nonumber
$$
Получаем
$$
f(x) — f(x^{0}) = sum_{substack{i=1} }^{substack{n}}A_{i}(x_{i} — x_{i}^{0}) + sum_{substack{i=1} }^{substack{n}}varepsilon_{i}(x)(x_{i} — x_{i}^{0}) =\= sum_{substack{i=1} }^{substack{n}}A_{i}(x_{i} — x_{i}^{0}) + o(rho(x, x^{0})),nonumber
$$
так как
$$
frac{displaystyleleft|sum_{i=1}^{n}varepsilon_{i}(x)(x_{i} — x_{i}^{0})right|}{rho(x, x^{0})} leq sum_{i=1}^{n}vertvarepsilon_{i}(x)vert rightarrow 0quad при x rightarrow x^{0}. bulletnonumber
$$
Пример 1.
Показать, что функция
$$
f(x, y) = sqrt [3] {x^{3} + y^{4}}nonumber
$$
дифференцируема в точке ((0,0)).
Решение.
(vartriangle) Покажем, что существует число (C > 0) такое, что для любых (x in boldsymbol {R}) и (y in boldsymbol {R}) справедливо неравенство
$$
|sqrt [3] {x^{3} + y^{4}} — x| leq C |y|^{4/3}label{ref4}
$$
Если (y = 0), то неравенство eqref{ref4} справедливо при любом (C). Пусть (y neq 0). Положим (t = xy^{-4/3}). Тогда неравенство eqref{ref4} эквивалентно неравенству (vert psi(t) vert < C), где (psi(t) =displaystyle sqrt [3] {1 + t^{3}} — t).
Так как функция (psi(t)) непрерывна на (R) и (psi(t) rightarrow 0) при (t rightarrow infty), то (psi(t)) есть ограниченная функция на (R).
Итак, неравенство eqref{ref4} установлено. Так как
$$
left|frac{y^{4/3}}{sqrt{x^{2} + y^{2}}}right| = |y|^{1/3}frac{|y|}{sqrt{x^{2} + y^{2}}} leq |y|^{1/3},nonumber
$$
то
$$
y^{4/3} = o (sqrt{x^{2} + y^{2}}),quad при (x, y) rightarrow (0, 0).nonumber
$$
и, следовательно,
$$
sqrt [3] {x^{3} + y^{4}} = x + o (sqrt{x^{2} + y^{2}}),quad при (x, y) rightarrow (0, 0).nonumber
$$
то есть функция (f(x, y)) дифференцируема в точке ((0,0)). (blacktriangle)
Пример 2.
Показать, что функция
$$
f(x, y) = sqrt [3] {x^{3} + y^{3}}nonumber
$$
недифференцируема в точке (0,0).
Решение.
(triangle) Первый способ. Пусть функция дифференцируема в точке ((0,0)), тогда, согласно определению, существуют числа (A) и (B) такие, что
$$
f(x, y) — f(0, 0) = Ax + By + o(rho),quad rho = sqrt{x^{2} + y^{2}},nonumber
$$
где (f(x, y) = sqrt [3] {x^{3} + y^{3}}, f(0, 0) = 0, A =displaystyle frac{partial f(0, 0)}{partial x} = 1, B = frac{partial f(0, 0)}{partial y} = 1).
Поэтому
$$
sqrt [3] {x^{3} + y^{3}} = x + y + o(sqrt{x^{2} + y^{2}}).nonumber
$$
Пусть (x = y > 0), тогда
$$
sqrt [3] {2} x = 2x + o(x)nonumber
$$
или ((sqrt [3] {2} — 2) x = o(x)) при (x rightarrow 0), что противоречит определению символа (o(x)). Следовательно, функция (sqrt [3] {x^{3} + y^{3}}), недифференцируема в точке ((0, 0)).
Второй способ. Если функция (f(x, y)) дифференцируема в точке ((0,0)), то ее можно в некоторой окрестности этой точки, согласно теореме 1, представить в следующем виде:
$$
sqrt [3] {x^{3} + y^{3}} = x varphi (x, y) + y psi (x, y),label{ref5}
$$
где функции (varphi (x, y)) и (psi (x, y)) непрерывны в точке ((0,0)).
Пусть (k) — произвольное число. Положим в eqref{ref5} (y = kx). Тогда
$$
sqrt[3]{1 + k^{3}}=varphi(x,kx)+kpsi(x,kx).nonumber
$$
Переходя к пределу при (x rightarrow 0) и пользуясь непрерывностью функций (varphi (x, y)) и (psi (x, y)) в точке ((0,0)), получаем, что при любом (k) выполняется равенство
$$
sqrt [3] {1 + k^{3}} = varphi (0, 0) + k psi (0, 0) = a + kb.nonumber
$$
Это неверно, так как функция (sqrt [3] {1 + k^{3}}) не есть линейная функция (ее вторая производная по (k) не обращается тождественно в нуль). (blacktriangle)
Необходимое условие дифференцируемости функции в точке.
Теорема 2.
Если функция (f(x)) дифференцируема в точке (x^{0} in R^{n}), то она имеет в точке (x^{0}) все частные производные (displaystylefrac{partial f}{partial x_{i}}(x^{0}), i = overline{1, n}), и
$$
f(x) — f(x^{0}) = sum_{substack{i=1} }^{substack{n}}frac{partial f}{partial x_{i}}(x^{0})(x_{i} — x_{i}^{0}) + o(rho(x, x^{0}))quad при x rightarrow x^{0}.label{ref6}
$$
Доказательство.
(circ) Пусть функция (f(x)) дифференцируема в точке (x^{0}). Тогда найдутся такие числа (A_{1}, ldots, A_{n}), что при (x rightarrow x^{0}) будет выполнено равенство eqref{ref1}. Пусть в этом равенстве (x_{1} neq x_{1}^{0}), а (x_{2} = x_{2}^{0}, ldots, x_{n} = x_{n}^{0}). Тогда равенство eqref{ref1} принимает следующий вид:
$$
f(x_{1}, x_{2}^{0}, ldots, x_{n}^{0}) — f(x_{1}^{0}, ldots, x_{n}^{0}) = A_{1} (x_{1} — x_{1}^{0}) + o (|Delta x_{1}|)nonumber
$$
при (x_{1} — x_{1}^{0} = Delta x_{1} longrightarrow 0).
Следовательно, существует предел:
$$
A_{1} = lim_{substack{Delta x_{1} rightarrow 0}} dfrac{f(x_{1}, x_{2}^{0}, ldots, x_{n}^{0}) — f(x_{1}^{0}, ldots, x_{n}^{0})}{Delta x_{1}} = frac{partial f}{partial x_{1}}(x^{0}).nonumber
$$
Аналогично доказывается, что у функции (f(x)) в точке (x^{0}) существуют и остальные частные производные и что
$$
A_{i} = frac{partial f}{partial x_{i}}(x^{0}), i = overline{2, n}.nonumber
$$
Подставляя эти выражения в равенство eqref{ref1}, получаем eqref{ref6}. (bullet)
Функция примера 2 имеет в точке ((0, 0)) обе частные производные первого порядка:
$$
frac{partial f}{partial x}(0,0) = lim_{substack{x rightarrow 0}}frac{f(x, 0) — f (0,0)}{x} = lim_{substack{x rightarrow 0}}frac{sqrt[3]{x^{3}}}{x} = 1, frac{partial f}{partial y}(0,0) = 1.nonumber
$$
Так как функция (f(x, y) = sqrt [3] {x^{3} + y^{3}}) примера 2 недифференцируема в точке ((0,0)), то этот пример показывает, что из существования частных производных в точке не следует дифференцируемость функции в этой точке. Существование частных производных функции в точке не гарантирует даже непрерывности функции в этой точке. Так, функция
$$
f(x, y) = begin{cases}
displaystylefrac{2xy}{x^{2} + y^{2}} & text{при (x^{2} + y^{2} > 0)}\
0 & text{при (x = y = 0)}
end{cases}nonumber
$$
не имеет предела при (x, y) rightarrow (0, 0)), а поэтому и не является непрерывной в точке ((0,0)). Тем не менее у этой функции в точке ((0,0)) существуют обе частные производные:
$$
frac{partial f}{partial x}(0,0) = lim_{substack{x rightarrow 0}}frac{f(x, 0) — f (0,0)}{x} = 0,quad frac{partial f}{partial y}(0,0) = 0.nonumber
$$
Достаточные условия дифференцируемости функции в точке.
Теорема 3.
Если все частные производные (frac{partial f}{partial x_{i}}(x), i = overline{1, n}), определены в окрестности точки (x^{0} in R^{n}) и непрерывны в точке (x^{0}), то функция (f(x)) дифференцируема в точке (x^{0}).
Доказательство.
(circ) Рассмотрим случай функции трех переменных. Общий случай рассматривается аналогично. Пусть функции (displaystyle frac{partial f}{partial x}(x, y, z), frac{partial f}{partial y}(x, y, z), frac{partial f}{partial z}(x, y, z)), определены в некотором шаре (S_{varepsilon}(x^{0}, y^{0}, z^{0})) и непрерывны в центре шара ((x^{0}, y^{0}, z^{0})).
Запишем приращение функции в следующем виде:
$$
f(x, y, z) — f(x^{0}, y^{0}, z^{0}) = f(x, y, z) — f(x^{0}, y, z) +\+ f(x^{0}, y, z) — f(x^{0}, y^{0}, z) + f(x^{0}, y^{0}, z) — f(x^{0}, y^{0}, z^{0}).nonumber
$$
Пусть (x^{0} < x). Рассмотрим функцию одной переменной (psi (t) = int (l, y, z)) при (l in [x^{0}, x]). На этом отрезке функция (psi (l)) имеет производную
$$
psi’ (t) = frac{partial f}{partial x}(t, y, z).nonumber
$$
Применяя формулу конечных приращений Лагранжа для функции (psi (t)) на отрезке ([x^{0}, x]), получаем
$$
psi (x) — psi (x^{0}) = psi’ (x^{0} + theta (x — x^{0}))(x^{0}),quad 0 < theta < 1.nonumber
$$
Если подставить в эту формулу выражение для (psi (t)), то
$$
begin{array}{c}f(x, y, z) — f(x^{0}, y, z) = f_{1}(x, y, z)(x — x^{0}),\displaystyle f_{1}(x, y, z) = frac{partial f}{partial x}(x^{0} + theta (x — x^{0}, y, z)).end{array}label{ref7}
$$
Так как частная производная (displaystylefrac{partial f}{partial x}(x, y, z)) непрерывна в точке ((x^{0}, y^{0}, z^{0})), то существует
$$
lim_{substack{(x, y, z) longrightarrow (x^{0}, y^{0}, z^{0})}} f_{1}(x, y, z) = frac{partial f}{partial x}(x^{0}, y^{0}, z^{0}).nonumber
$$
Аналогично,
$$
begin{array}{c}f(x^{0}, y, z) — f(x^{0}, y^{0}, z) = f_{2}(x, y, z)(y — y^{0}),\f(x^{0}, y^{0}, z) — f(x^{0}, y^{0}, z^{0}) = f_{3}(x, y, z)(z — z^{0}),end{array}label{ref8}
$$
где функции (f_{2}(x, y, z)) и (f_{3}(x, y, z)) имеют конечные пределы при ((x, y, z) rightarrow (x^{0}, y^{0}, z^{0})). Доопределяя эти функции в точке ((x^{0}, y^{0}, z^{0})) предельными значениями, получим, что функции (f_{i}(x, y, z), i = overline{1, 3}), непрерывны в точке ((x^{0}, y^{0}, z^{0})). Таким образом,
$$
f(x, y, z) — f(x^{0}, y^{0}, z^{0}) =\= (x — x^{0})f_{1}(x, y, z) + (y — y^{0})f_{2}(x, y, z) + (z — z^{0})f_{3}(x, y, z).nonumber
$$
Из непрерывности функций (f_{1}(x, y, z)), (f_{2}(x, y, z)) и (f_{3}(x, y, z)) в точке ((x^{0}, y^{0}, z^{0})) и теоремы 1 следует дифференцируемость функции (f(x, y, z)) в точке ((x^{0}, y^{0}, z^{0})). (bullet)
Непрерывность частных производных в точке не является необходимым условием дифференцируемости функции в этой точке.
Функция
$$
f(x, y) = begin{cases}
(x^{2} + y^{2} sin frac{1}{sqrt{x^{2} + y^{2}}}), & text{(x^{2} + y^{2} > 0)}\
0, & text{при (x = y = 0)}
end{cases}nonumber
$$
дифференцируема в точке ((0,0)), так как
$$
f(x, y) = 0 cdot x + 0 cdot y + o(sqrt{x^{2} + y^{2}})nonumber
$$
при ((x, y) rightarrow (0, 0)).
Но при (x^{2} + y^{2} > 0) частная производная
$$
frac{partial f}{partial x}(x, y) = 2x sin frac{1}{sqrt{x^{2} + y^{2}}} — frac{x}{sqrt{x^{2} + y^{2}}} cos frac{1}{sqrt{x^{2} + y^{2}}}nonumber
$$
не имеет предела при ((x, y) rightarrow (0, 0)) и, следовательно, не является непрерывной функцией в точке ((0,0)). Чтобы в этом убедиться, достаточно показать, что (displaystylefrac{partial f (x, 0)}{partial x}) не имеет предела при (x rightarrow 0).
Дифференцируемость сложной функции.
Теорема 4.
Пусть функции (varphi_{1} (x), ldots, varphi_{m} (x)) дифференцируемы в точке (x^{0} = (x_{1}^{0}, ldots, x_{n}^{0}) in R^{n}, y^{0} = (varphi_{1} (x^{0}), ldots, varphi_{m} (x^{0})) in R^{n}) и функция (f(y) = f(y_{1}, ldots, y_{m})) дифференцируема в точке (y^{0}).
Тогда сложная функция
$$
Phi (x) = f(varphi_{1} (x), ldots, varphi_{m} (x))nonumber
$$
дифференцируема в точке (x^{0}), причем при (x rightarrow 0)
$$
begin{array}{c}Phi (x) — Phi (x^{0}) = displaystyle sum_{substack{i=1} }^{substack{n}}A_{i}(x_{i} — x_{i}^{0}) + o(rho(x, x^{0})),\displaystyle A_{i}frac{partial Phi}{partial x_{i}}(x^{0}) = sum_{substack{y=1} }^{substack{m}}frac{partial f}{partial y_{i}}(y^{0})frac{partial varphi_{j}}{partial x_{i}}(x^{0}), i = overline{1, n}.end{array}label{ref9}
$$
Доказательство.
(circ) Так как функция (f(y)) дифференцируема в точке (y^{0}), то в силу теоремы 1 найдутся функции (f_{i}(y), y = overline{1, m}), непрерывные в точке (y^{0} = (y_{1}^{0}, ldots, y_{m}^{0})) и такие, что
$$
f(y) — f(y^{0}) = sum_{substack{y=1} }^{substack{m}}f_{i}(y)(y_{i} — y_{i}^{0}),quad f_{i}(y^{0}) = frac{partial f}{partial y_{i}}(y^{0}).label{ref10}
$$
Воспользовавшись тем, что дифференцируемая в точке функция непрерывна в этой точке, а также теоремой о непрерывности сложной функции, получаем, что функции
$$
psi_{i} (x) = f_{i}(varphi_{1} (x), ldots, varphi_{m} (x)),quad j = overline{1, m},label{ref11}
$$
непрерывны в точке (x^{0}), причем
$$
psi_{i} (x^{0}) = f_{i}(varphi_{1} (x^{0}), ldots, varphi_{m} (x^{0})) = f_{i}(y^{0}) = frac{partial f}{partial y_{i}}(y^{0}).label{ref12}
$$
Подставив в eqref{ref10} (y_{1} = varphi_{1} (x), ldots, y_{m} = varphi_{m} (x)) и воспользовавшись обозначениями eqref{ref11}, получаем
$$
Phi (x) — Phi (x^{0}) = sum_{substack{y=1} }^{substack{m}}psi_{i}(x)(varphi_{i} (x^{0}) — varphi_{i} (x^{0})).label{ref13}
$$
Но функции (varphi_{i} (x^{0}), j = overline{1, m}), дифференцируемы в точке (x^{0}), поэтому найдутся такие непрерывные в точке (x^{0}) функции (varphi_{ij}(x)), что
$$
begin{array}{c}
displaystyle varphi_{j} (x) — varphi_{j} (x^{0}) = sum_{substack{i=1} }^{substack{n}}varphi_{ij}(x)(x_{i} — x_{i}^{0}),quad varphi_{ij}(x^{0})=frac{partial varphi_{j}}{partial x_{i}}(x^{0}),\ i = overline{1, n},quad j = overline{1, m}.
end{array}label{ref14}
$$
Подставляя выражения eqref{ref14} в eqref{ref13}, получаем
$$
Phi (x) — Phi (x^{0}) = sum_{substack{i=1} }^{substack{n}}Phi_{i}(x)(x_{i} — x_{i}^{0}),quad Phi_{i}(x) = sum_{substack{j=1} }^{substack{m}}varphi_{ij}(x) psi_{j}(x).label{ref15}
$$
Так как функции (psi_{j}(x)) и (varphi_{ij}(x)) непрерывны в точке (x^{0}), то и функции (Phi_{i}(x)) непрерывны в точке (x^{0}). А это означает, что сложная функция (Phi(x)) дифференцируема в точке (x^{0}) (теорема 1).
Дифференцируемая функция (Phi(x)) может быть записана в виде eqref{ref9} с коэффициентами (A_{i}), равными, в силу eqref{ref12} и eqref{ref14},
$$
A_{i} = Phi_{i} (x^{0}) = sum_{substack{j=1} }^{substack{m}}varphi_{ij}(x) psi_{j}(x) = sum_{substack{j=1} }^{substack{m}}frac{partial f}{partial y_{i}}(y^{0})frac{partial varphi_{i}}{partial x_{i}}(x^{0}) = frac{partial Phi}{partial x_{i}}(x^{0}). bulletnonumber
$$
Замечание.
Вторая из формул eqref{ref9} дает правило нахождения частных производных сложной функции, аналогичное соответствующему правилу для функций одной переменной.
Пример 3.
Пусть функция (f(x, y)) дифференцируема во всех точках пространства (R^{2}). Перейти к полярным координатам и найти выражения для (displaystylefrac{partial f}{partial r}) и (displaystylefrac{partial f}{partial varphi}).
Решение.
(vartriangle) Пусть (F(r, varphi) = f(r cos varphi, r sin varphi), x = r cos varphi, y = r sin varphi). Тогда, пользуясь правилом eqref{ref9}, получаем
$$
frac{partial F}{partial r} = frac{partial f}{partial x}frac{partial x}{partial r} + frac{partial f}{partial y}frac{partial y}{partial r} = cos frac{partial f}{partial x} + sin varphi frac{partial f}{partial y} = frac{1}{sqrt{x^{2} + y^{2}}}left(x frac{partial f}{partial x} + y frac{partial f}{partial y}right),nonumber
$$
$$
frac{partial F}{partial varphi} = frac{partial f}{partial x}frac{partial x}{partial varphi} + frac{partial f}{partial y}frac{partial y}{partial varphi} = -r sin varphi frac{partial f}{partial x} + r cos varphi frac{partial f}{partial y} = -y frac{partial f}{partial x} + x frac{partial f}{partial y}. blacktrianglenonumber
$$
Дифференциал. Инвариантность формы первого дифференциала. Правила дифференцирования.
Пусть функция (f(x)) дифференцируема в точке (x^{0}). Тогда при (x rightarrow x^{0}) ее можно записать в виде eqref{ref5}:
$$
f(x) = f(x^{0}) + sum_{substack{i=1} }^{substack{n}}frac{partial f(x^{0})}{partial x_{i}}(x^{0})(x_{i} — x_{i}^{0}) + o(rho(x, x^{0})).nonumber
$$
Положим по определению
$$
dx_{i} = Delta x_{i} = x_{i} — x_{i}^{0}.nonumber
$$
Если функция (f(x)) дифференцируема в точке (x^{0}), то линейную форму относительно приращений независимых переменных
$$
df(x^{0}) = sum_{substack{i=1} }^{substack{n}}frac{partial f}{partial x_{i}}(x^{0})dx_{i}label{ref16}
$$
назовем дифференциалом функции (f(x)) в точке (x^{0}). Тогда
$$
f(x) = f(x^{0}) + d f(x^{0}) + o(rho(x, x^{0})) mbox{при} x rightarrow x^{0}.nonumber
$$
Иногда выражение eqref{ref16} называют первым дифференциалом функции (f(x)) в точке (x^{0}).
Найдем теперь дифференциал сложной функции. Пусть функции (varphi_{1} (x), ldots, varphi_{m}(x)) дифференцируемы в точке (x^{0}), а функция (f(y_{1}, ldots, y_{m})) дифференцируема в точке (y^{0} = (varphi_{1} (x^{0}), ldots, varphi_{m}(x^{0}))). Тогда в силу теоремы 3 сложная функция (Phi (x) = f(varphi_{1} (x), ldots, varphi_{m}(x))) дифференцируема в точке (x^{0}). Используя формулы eqref{ref9}, получаем
$$
d Phi (x^{0}) = d f(varphi_{1} (x^{0}), ldots, varphi_{m}(x^{0})) = sum_{substack{i=1} }^{substack{n}}frac{partial Phi}{partial x_{i}}(x^{0})dx_{i} =\= sum_{substack{i=1} }^{substack{n}}sum_{substack{j=1} }^{substack{m}}frac{partial f}{partial y_{i}}(y^{0})frac{partial varphi_{i}}{partial x_{i}}(x^{0})dx_{i} =\= sum_{substack{j=1} }^{substack{m}}frac{partial f}{partial y_{i}}(y^{0})dy_{i}(x^{0}),quad dy_{i}(x^{0}) = sum_{substack{i=1} }^{substack{n}}frac{partial varphi_{i}}{partial x_{i}}(x^{0})dx_{i}.nonumber
$$
Итак,
$$
df(y_{1} (x^{0}), ldots, y_{m}(x^{0})) = sum_{substack{j=1} }^{substack{m}}frac{partial f}{partial y_{i}}(y^{0})dy_{i}(x^{0}).label{ref17}
$$
Если бы (y_{1}, ldots, y_{m}) были независимыми переменными, то (df(y^{0})) отличался бы от дифференциала сложной функции eqref{ref17} только тем, что в выражении eqref{ref17} (dy_{i}(x^{0})) — дифференциалы функций (varphi_{i}), а в
$$
df(y^{0}) = sum_{substack{j=1} }^{substack{m}}frac{partial f}{partial y_{j}}(y^{0})dy_{j}nonumber
$$
(dy_{j}) — дифференциалы независимых переменных. Формальная запись дифференциала в обоих случаях одинакова. Говорят, что форма первого дифференциала инвариантна относительно замены переменных.
Инвариантность формы первого дифференциала является весьма удобным его свойством. При записи (df(y^{0})) в виде eqref{ref17} мы можем не задумываться о том, являются ли переменные (y_{1}, ldots, y_{m}) независимыми. Заметим, что во многих прикладных задачах часто бывает затруднительно выяснить вопрос о независимости переменных.
Пусть функция (f(x)) дифференцируема во всех точках некоторого открытого множества (G subset R^{n}). Тогда в каждой точке (x in G) можно вычислить дифференциал
$$
df(x) = sum_{substack{i=1} }^{substack{n}}frac{partial f}{partial x_{i}}(y^{0})dx_{i}.nonumber
$$
Он будет функцией (2n) переменных (x_{1}, ldots, x_{n}), (dx_{1}, ldots, dx_{n}), причем при фиксированных (x_{1}, ldots, x_{n}) дифференциал есть линейная функция (dx_{1}, ldots, dx_{n}). Правила дифференцирования такие же, как и для функций одной переменной:
- (d(u + v) = du + dv);
- (d(uv) = u dv + v du);
- (d(frac{u}{v}) = displaystyle frac{v du — u dv}{v^{2}}, v neq 0).
Докажем, например, что (d(uv) = u dv + v du).
(circ) Прежде всего заметим, что из теоремы о дифференцируемости сложной функции следует, что функция (u(x)v(x)) дифференцируема, если дифференцируемы функции (u(x)) и (v(x)). Далее, имеем
$$
d(uv) = sum_{substack{i=1} }^{substack{n}}frac{partial (uv)}{partial x_{i}}dx_{i} = sum_{substack{i=1} }^{substack{n}}left(u frac{partial v}{partial x_{i}} + v frac{partial u}{partial x_{i}}right)dx_{i} =\= u sum_{substack{i=1} }^{substack{n}}frac{partial v}{partial x_{i}}dx_{i} + v sum_{substack{i=1} }^{substack{n}}frac{partial u}{partial x_{i}}dx_{i} = u dv + v du. bulletnonumber
$$
Пример 4.
Найти дифференциал функции (displaystyleoperatorname{arctg}frac{y}{x}).
Решение.
(vartriangle) Пусть (u =displaystyle frac{y}{x}), тогда
$$
dleft(operatorname{arctg}frac{y}{x}right) = d(operatorname{arctg} u) = frac{du}{1 + u^{2}}=\=frac{d(y/x)}{1 + (y/x)^{2}} = frac{x^{2}}{x^{2} + y^{2}}frac{x dy — y dx}{x^{2}} = frac{x dy — y dx}{x^{2} + y^{2}}. blacktrianglenonumber
$$
Формула конечных приращений Лагранжа.
Пусть функция (f(x)) дифференцируема в выпуклой области (G subset R^{n}). Напомним, что выпуклая область есть открытое множество, любые две точки которого можно соединить отрезком, лежащим в области. Тогда для любых двух точек (x = (x_{1}, ldots, x_{n}) in G, y = (y_{1}, ldots, y_{n}) in G) найдется число (theta in (0, 1)) такое, что
$$
f(y) — f(x) = sum_{substack{i=1} }^{substack{n}}frac{partial f}{partial y_{i}}(x + theta(y — x))(y_{i} — x_{i}).label{ref18}
$$
Формула eqref{ref18} называется формулой конечных приращений Лагранжа. Докажем ее.
(circ) Пусть точки (x, y in G). Так как область (G) выпукла, то отрезок, соединяющий точки (x) и (y), лежит в области (G). Поэтому определена функция одной переменной
$$
varphi (t) = f(x_{1} + t(y_{1} — x_{1}), ldots, x_{n} + t(y_{n} — x_{n})), 0 leq t leq 1.label{ref19}
$$
Очевидно, что (varphi (0) = f(x), varphi (1) = f(y)) и что функция (varphi (t)) дифференцируема на отрезке [0,1]. По правилу нахождения производной сложной функции имеем
$$
varphi'(t) = sum_{substack{i=1} }^{substack{n}}frac{partial f}{partial x_{i}}(x_{1} + t(y_{1} — x_{1}), ldots, x_{n} + t(y_{n} — x_{n}))(y_{i} — x_{i}).label{ref20}
$$
Применим к функции (varphi (t)) формулу конечных приращений Лагранжа для функции одной переменной. Получаем, что найдется число (theta in (0, 1)) такое, что (varphi (1) — varphi (0) = varphi’ (theta)). Используя формулы eqref{ref19} и eqref{ref20}, теперь легко получаем формулу eqref{ref18}. (bullet)
Касательная плоскость к графику функции двух переменных. Геометрический смысл дифференциала.
Пусть функция (f(x, y)) дифференцируема на открытом множестве (G subset R^{2}). Рассмотрим ее график
$$
operatorname{Gr} f = {(x, y, z): z = f(x, y), (x, y) in G}.nonumber
$$
Пусть точка (P(x_{0}, y_{0}, z_{0})) лежит на (operatorname{Gr} f), то есть (z_{0} = f(x_{0}, y_{0})), и пусть гладкая кривая
$$
Gamma = {x = x(t), y = y(t), z = z(t), alpha leq t leq beta}nonumber
$$
лежит на графике и проходит через точку ((x_{0}, y_{0}, z_{0})). Это означает, что
$$
z(t) = f(x(t), y(t)); (x(t_{0}), y(t_{0}), z(t_{0}) = (x_{0}, y_{0}, z_{0}), t_{0} in (alpha, beta).label{ref21}
$$
Дифференцируя тождество eqref{ref21} в точке (t_{0}) и пользуясь инвариантностью формы первого дифференциала, получаем
$$
dz = frac{partial f}{partial x}(x_{0}, y_{0})dx + frac{partial f}{partial y}(x_{0}, y_{0})dy.label{ref22}
$$
Вектор (d tau = (dx, dy, dz)) есть касательный вектор к кривой (Gamma) в точке ((x_{0}, y_{0}, z_{0})). Введем вектор
$$
textbf{N} = left(- frac{partial f}{partial x}(x_{0}, y_{0}), — frac{partial f}{partial y}(x_{0}, y_{0}), 1right).label{ref23}
$$
Условие eqref{ref22} означает, что вектор (textbf{N}) ортогонален к касательной к кривой (Gamma) в точке ((x_{0}, y_{0}, z_{0})). Говорят, что вектор (textbf{N}) ортогонален к кривой (Gamma) в точке (P). Но (Gamma) — любая гладкая кривая, лежащая на (operatorname{Gr} f) и проходящая через точку (P). Поэтому вектор (textbf{N}) ортогонален к любой кривой, лежащей на (operatorname{Gr} f) и проходящей через точку (P). Он называется вектором нормали к (operatorname{Gr} f) в точке (P).
Плоскость, проходящая через точку (P) и ортогональная вектору нормали (textbf{N}), называется касательной плоскостью к (operatorname{Gr} f) в точке (P). Ее уравнение есть
$$
Z — f(x_{0}, y_{0}) = frac{partial f}{partial x}(x_{0}, y_{0})(X — x_{0}) + frac{partial f}{partial y}(x_{0}, y_{0})(Y — y_{0}).label{ref24}
$$
Прямая, проходящая через точку (P) и параллельная вектору (N), называется нормалью к (operatorname{Gr} f) в точке (P). Ее уравнение —
$$
frac{X — x_{0}}{- f_{x}(x_{0}, y_{0})} = frac{Y — y_{0}}{- f_{y}(x_{0}, y_{0})} = Z — f(x_{0}, y_{0}).
$$
Найдем значение аппликаты касательной плоскости, построенной в точке (P(x_{0}, y_{0}, z_{0}) in operatorname{Gr} f).
Из eqref{ref24} получаем
$$
Z — f(x_{0}, y_{0}) = frac{partial f}{partial x}(x_{0}, y_{0})(x — x_{0}) + frac{partial f}{partial y}(x_{0}, y_{0})(y — y_{0}) = d f(x_{0}, y_{0}).nonumber
$$
Таким образом, (d f(x_{0}, y_{0})) есть приращение аппликаты касательной плоскости (рис. 26.1).
Производная по направлению. Градиент.
Пусть функция (f(x, y, z)) определена в области (G subset R^{3}), и пусть точка (P(x_{0}, y_{0}, z_{0}) in G). Рассмотрим луч, проходящий через точку и параллельный направлению
$$
textbf{l} = (cos alpha, cos beta, cos gamma),nonumber
$$
где
$$
cos^{2} alpha + cos^{2} beta + cos^{2} gamma = 1.nonumber
$$
Так как (P) — внутренняя точка (G), то найдется число (t_{0}) такое, что отрезок
$$
x = x_{0} + tcos alpha, y = y_{0} + tcos beta, z = z_{0} + tcos gamma,quad -t_{0} leq t leq t_{0},nonumber
$$
лежит в области (G). Производной функции (f(x, y, z)) в точке ((x_{0}, y_{0}, z_{0})) в направлении (textbf{l}) назовем
$$
frac{partial f}{partial l}(x_{0}, y_{0}, z_{0}) = lim_{substack{t rightarrow +0}}frac{f(x_{0} + tcos alpha, y_{0} + tcos beta, z_{0} + tcos gamma) — f(x_{0}, y_{0}, z_{0})}{t}.nonumber
$$
Теорема 5.
Если функция (f(x, y, z)) дифференцируема в точке (P(x_{0}, y_{0}, z_{0}) in G), то производную по направлению (textbf{l}) в этой точке можно вычислить при помощи следующей формулы:
$$
frac{partial f}{partial l}(x_{0}, y_{0}, z_{0}) = left.frac{d}{dt}f(x_{0} + tcos alpha, y_{0} + tcos beta, z_{0} + tcos gamma)right|_{t = 0} =\= frac{partial f}{partial x}(x_{0}, y_{0}, z_{0}) cos alpha + frac{partial f}{partial y}(x_{0}, y_{0}, z_{0}) cos beta + frac{partial f}{partial z}(x_{0}, y_{0}, z_{0}) cos gamma.label{ref25}
$$
Доказательство.
(circ) Формула eqref{ref25} есть простое следствие правила нахождения производной сложной функции. (bullet)
Обозначим через (operatorname{grad} f(x_{0}, y_{0}, z_{0})) вектор
$$
operatorname{grad} f(x_{0}, y_{0}, z_{0}) = left(frac{partial f}{partial x}(x_{0}, y_{0}, z_{0}), frac{partial f}{partial y}(x_{0}, y_{0}, z_{0}), frac{partial f}{partial z}(x_{0}, y_{0}, z_{0}right).
$$
Тогда равенство eqref{ref25} можно записать в следующем виде:
$$
frac{partial f}{partial l}(x_{0}, y_{0}, z_{0}) = (textbf{l}, operatorname{grad} f(x_{0}, y_{0}, z_{0})).nonumber
$$
Если ввести символический вектор (оператор Гамильтона)
$$
nabla = textbf{i}frac{partial}{partial x} + textbf{j}frac{partial}{partial y} + textbf{k}frac{partial}{partial z}label{ref26}
$$
и договориться, что векторы, стоящие слева от (nabla), перемножаются с (nabla) по правилам векторной алгебры, а на величины, стоящие справа, (nabla) действует как дифференциальный оператор, то
$$
(textbf{l}, nabla) =cos alpha frac{partial}{partial x} + cos beta frac{partial}{partial y} + cos gamma frac{partial}{partial z}.nonumber
$$
Тогда формулу eqref{ref25} можно записать через оператор Гамильтона
$$
frac{partial f}{partial l}(x_{0}, y_{0}, z_{0}) = (textbf{l}, nabla)f(x_{0}, y_{0}, z_{0}).nonumber
$$
Что такое дифференцируемость?
Однажды восприняв теорию эволюции, вы начинаете видеть природу с позиций конкуренции и выживания. Вы понимаете, почему микробы становятся резистентными к лекарственным препаратам (выживание наиболее приспособленных). Или, например, почему нас тянет к сладкой и жирной пище (поощрение природой потребления высококалорийных продуктов на случай дефицита).
Аналогичным образом изучение математического анализа подобно просветлению. В школьном курсе мы изучаем приведенные ниже формулы в различных разделах геометрии, получаем их как данность. Но разве они не связаны каким-то образом? Математический анализ показывает, что одно следует из другого. Сегодня мы будем двигаться относительно приведенного изображения справа налево. Как бы расщепляя природу объектов, подменяя их более простыми сущностями, дифференцируя.
Понятие «дифференцируемость» лежит в основании математического анализа. Изначально этот курс так и назывался: интегральное и дифференциальное исчисление. Что подразумевают математики, когда говорят, что функция дифференцируема в точке?
В учебниках по математическому анализу даётся следующее определение (не пугайтесь, далее мы будем излагать мысли более простым языком). Функция f дифференцируема в точке x, если её приращение в этой точке представимо в виде:
Здесь A – постоянная, не зависящая от приращения аргумента Δx. Обозначение
соответствует бесконечно малой функция более высокого порядка, чем Δx.
Далее в учебниках доказывается, что для дифференцируемости функции f в точке x необходимо и достаточно существование в этой точке предела.
который называется производной функции f в точке x .
Потом обычно устанавливаются правила дифференцирования, арифметические свойства, доказываются основные теоремы дифференциального исчисления и т.п.
Однако за этим нагромождением нередко пропадает основная идея понятия дифференцируемости. Если функция y = f(x) дифференцируема в точке x и вычислимо значение f(x+ Δx), то ее можно представить в виде линейной функции y = AΔx + B, с “хорошей степенью точности”.
Перейдем к примерам
Рассмотрим примеры различных функций. Исходя из обозначенной главной идеи, будем задаваться при рассмотрении каждой зависимости вопросом: можно ли представить исследуемую функцию f(x) в виде прямой линии вблизи точек x? Обсудим, что именно мы под этим подразумеваем, на ряде конкретных примеров.
Синусоидальная функция
Начнем с простой степенной функции – синусоидальная функция f(x) = sin*x.
Здесь и далее на анимациях сверху изображается график исследуемой функции на заданном отрезке (сплошная линия), а также хорда (оранжевый пунктир), соединяющая точки зависимости, соответствующие концам выбранного числового отрезка.
Одновременно снизу строится функция модуля разности между исходной функцией и описывающей хорду линейной зависимостью.
Синусоидальная функция дифференцируема на всей числовой прямой. На gif-изображении ниже можно видеть, что после нескольких приближений к точке x=0 график функции сливается с хордой, превращаясь в прямую линию. Соответствующая разность с каждой итерацией на всем выбранном отрезке становится все ближе к нулю. Эта ситуация соответствует устремлению приращения к нулю.
Модуль гармонической функции
Существует бесконечное число примеров, когда подобного приближения указанной разности к нулю представить нельзя. То есть нельзя говорить и о дифференцируемости функции.
Возьмем, например, функцию модуля гармонической функции f(x) = |sinx|. Легко доказать, что эта функция не дифференцируема во всех точках, в которых значение синуса обращается в ноль.
Пусть x = 0. На анимации ниже заметно, что какой бы малый отрезок вокруг этой точки мы ни брали, рассматриваемая разность не устремляется к нулю.
Композиции степенных и гармонических функций
Указанный подход позволяет визуализировать и более сложные примеры композиций нескольких функций.
Рассмотрим две родственные функции:
и
Первая функция дифференцируема при x=0, вторая – нет. Это хорошо видно на анимациях ниже.
Обсудим теперь поведение подобных функций с немного другой точки зрения. Для этого рассмотрим функцию
, домноженную на степенные функции с различным показателем.
Простейший вариант –
Эта функция имеет разрыв в x=0. Проиллюстрируем ситуацию точкой, движущейся по графику данной функции.
При приближении к началу координат рассматриваемая точка начинает скакать и дёргаться, то есть не стремится к какому-то определенному значению. Функция
терпит в x=0 разрыв.
Следующая функция
уже непрерывна в нуле, но, как было понятно из вышеприведенной анимации, она не дифференцируема в этой точке.
Проиллюстрируем это, нарисовав хорду. Угловой коэффициент этой хорды сильно осциллирует при подходе движущейся точки к началу координат. Отсюда видно, что функция не является дифференцируемой в точке x=0
Рассмотрим далее функцию:
Угловой коэффициент хорды стабилизируется при подходе к 0, но касательная беспорядочно меняет своё положение (постоянно меняется её угловой коэффициент). Это происходит из-за того, что функция
не является непрерывно дифференцируемой, т.е. её производная терпит разрыв в точке x=0.
В заключение рассмотрим функцию:
Эта функция непрерывно дифференцируема в точке x=0. Изобразим на графике этой функции движущуюся точку, хорду и касательную. На нижеприведённой анимации видно, что здесь стабилизируется и хорда, и касательная.
Заключение
Таким образом, на наглядных примерах гармонических, степенных функций и их композиций мы рассмотрели природу дифференцируемости различных числовых функций. При этом мы опирались на на стандартные подходы рассмотрения взятия производной в окрестностях точек различного вида, а на «практическом» подходе, при котором производная решает вопрос замены оригинальной функции ее упрощенным линейным представлением.
Выражаем большую признательность за работу Алексею Никитину, Матвею Грицаеву и Алексею Карпову
Другие материалы по теме
- 9 гифок, наглядно иллюстрирующих числовые последовательности
- Математика для программиста: советы, разделы, литература
- Математика для программистов: 7 крутых YouTube-каналов
- В уме и на пальцах: 7 простых математических трюков
- Иллюстративный курс по математическому анализу

