Как найти точки для графика онлайн

Точки пересечения функций

Примеры кривых

Указанные выше примеры содержат также:

• модуль или абсолютное значение: absolute(x) или |x|
• квадратные корни sqrt(x),
  кубические корни cbrt(x)
• тригонометрические функции:
  синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
• показательные функции и экспоненты exp(x)
• обратные тригонометрические функции:
  арксинус asin(x), арккосинус acos(x), арктангенс atan(x),
  арккотангенс acot(x)
• натуральные логарифмы ln(x),
  десятичные логарифмы log(x)
• гиперболические функции:
  гиперболический синус sh(x), гиперболический косинус ch(x),
  гиперболический тангенс и котангенс tanh(x), ctanh(x)
• обратные гиперболические функции:
  гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x),
  гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x)
• другие тригонометрические и гиперболические функции:
  секанс sec(x), косеканс csc(x), арксеканс asec(x),
  арккосеканс acsc(x), гиперболический секанс sech(x),
  гиперболический косеканс csch(x), гиперболический арксеканс asech(x),
  гиперболический арккосеканс acsch(x)
• функции округления:
  в меньшую сторону floor(x), в большую сторону ceiling(x)
• знак числа:
  sign(x)
• для теории вероятности:
  функция ошибок erf(x) (интеграл вероятности),
  функция Лапласа laplace(x)
• Факториал от x:
  x! или factorial(x)
• Гамма-функция gamma(x)
• Функция Ламберта LambertW(x)
• Тригонометрические интегралы: Si(x),
  Ci(x),
  Shi(x),
  Chi(x)

Правила ввода

Можно делать следующие операции

2*x

– умножение

3/x

– деление

x^2

– возведение в квадрат

x^3

– возведение в куб

x^5

– возведение в степень

x + 7

– сложение

x – 6

– вычитание

Действительные числа

вводить в виде 7.5, не 7,5

Постоянные

pi

– число Пи

e

– основание натурального логарифма

i

– комплексное число

oo

– символ бесконечности

Данный калькулятор предназначен для определения точек пересечения графика функции с осями координат.
В точке пересечения функции с осью Ox координата y всегда равна нулю, а в точке пересечения с осью Oy координата x=0.
Для того чтобы найти точки пересечения графика функции с осью ординат (Oy), необходимо подставить в уравнения функции x=0 , тем самым, найти y. Аналогично, чтобы найти точки пересечения графика функции с осью абсцисс (Ox), необходимо подставить в уравнение функции y=0 и найти x.

Нахождение координат точек пересечения функции с осями используется для анализа функции и построения ее графика.
Для того чтобы получить ответ, введите функцию в ячейку. Основные примеры ввода функций для данного калькулятора указаны ниже.

Для получения полного хода решения нажимаем в ответе Step-by-step.

При проведении исследования функции, возникает задача нахождения точек пересечения этой функции с осями координат. Рассмотрим на конкретном примере алгоритм решения такой задачи. Для простоты будем работать с функцией одной переменной:

График данной функции представлен на рисунке:

Как следует из рисунка, наша функция пересекает ось

в двух точках, а ось

– в одной.

Сначала найдём точки пересечения функции

с осью
. Сразу отметим, что в этих точках координата
. Поэтому для их поиска, нам нужно
решить уравнение:

Это
квадратное уравнение
имеет два корня:

Таким образом, мы нашли две точки пересечения нашей функции с осью абсцисс:

и
. Стоит отметить, что задача поиска пересечений функции с осью

эквивалентна задаче нахождения
нулей функции.

Теперь найдём точку пересечения с осью ординат. В этой точке координата
. Поэтому для их поиска, просто подставляем значение

в нашу функцию:

Таким образом, мы нашли точку пересечения нашей функции с осью ординат
.

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

на главную

Построить график функции онлайн

Поддержать сайт

←Вернуться в «Калькуляторы онлайн»

	y =
	y =

Здесь будет анализ функции…

Инструкции

Чтобы построить график функции онлайн:
• укажите функцию в поле выше в виде «y = x² – 3»;
• нажмите кнопку «Построить график функции»;
• ожидайте результат анализа функции (точки пересечения с осями координат) и график функции под полем задания функции.

При необходимости вы можете построить одновременно графики двух функций онлайн. Для этого нажмите кнопку
«Добавить функцию».

В случае построения двух графиков функции будут показаны их точки пересечения.

Таблица обозначений для задания функций

Математическая операция	Символ	Пример использования
Десятичная дробь	Можно и через точку, и через запятую.	«2,789» или «2.879»
Сложение	«+»	x + 1
Вычитание	«-»	x – 2.5
Умножение	«*»(shift + 8)	2 * x Коэффициент при «x» можно записывать без знака умножения. Например: «2x». Но при умножении скобок обязательно использовать символ «*». Правильно: «(2x – 1) * (6.7 – x)».
Деление	«/» (знак вопроса на английской раскладке)	(x – 1) / 2
Дробь	Кнопка	x – 2 10   – 1 2
Модуль	Кнопка	|x – 2.3|
Возведение в степень	Кнопка 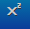или «^»(shift + 6)	При нажатой кнопке символы попадают в степень. Чтобы вернуться к обычному набору символу, нужно отжать кнопку . Другой способ задания степени через знак «^». Например: «x^(2)».
Корень	Кнопка	2 √(x – 2)    — квадратный корень    3 √(2x – 1)    — кубический корень
Синус	Кнопка	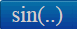sin(x + 1)
Косинус	Кнопка	cos(x)
Тангенс	Кнопка	tg(2.5 – x)
Число π (пи)	Кнопка	sin(x + π) + 2
Логарифм	Кнопка	log2(2x – 1,4)
Натуральный логарифм	Кнопка	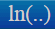ln(x) – 2
Десятичный логарифм	Кнопка	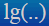lg(2.3 – x)
Основание натурального логарифма (число Эйлера)	Кнопка	ex

---

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

20 апреля 2023 в 6:08

Илья Костромин

Профиль
Благодарили: 0

Сообщений: 1

Илья Костромин
Профиль
Благодарили: 0

Сообщений: 1

0
Спасибо
Ответить

---