п.1. Алгоритм исследования и построения графика функции
1. Найти область определения функции, классифицировать точки разрыва
2. Исследовать функцию на четность и периодичность
3. Провести анализ асимптотического поведения функции (наличие вертикальных, горизонтальных и наклонных асимптот) (см. §41 данного справочника)
4. Взять первую производную. Определить критические точки, интервалы монотонности, точки экстремума
5. Взять вторую производную. Определить критические точки 2-го порядка, интервалы выпуклости и точки перегиба
6. Найти точки пересечения функции с осями координат (если уравнение (f(x)=0) не имеет аналитического решения, указать количество точек пересечения с осью OX)
7. Построить график функции
п.2. Примеры
Пример 1. Постройте график функции (y=2x^3-6x^2-18x+7)
1) Область определения (xinmathbb{R})
Точек разрыва нет
2) Четность begin{gather*} f(-x)=2(-x)^3-6(-x)^2-18(-x)+7ne left[ begin{array}{l} f(x)\ -f(x) end{array} right. end{gather*} Функция ни четная, ни нечетная.
Периодичность: функция не периодическая
3) Асимптоты
1. Вертикальных асимптот нет, т.к. нет точек разрыва 2-го рода
2. Горизонтальные асимптоты: begin{gather*} b_1=lim_{xrightarrow -infty}2x^3-6x^2-18x+7=-infty\ b_2=lim_{xrightarrow +infty}2x^3-6x^2-18x+7=+infty\ end{gather*} Пределы бесконечны, горизонтальных асимптот нет.
3. Наклонные асимптоты: begin{gather*} k_1=lim_{xrightarrow -infty}frac{2x^3-6x^2-18x+7}{x}=+infty\ k_2=lim_{xrightarrow +infty}frac{2x^3-6x^2-18x+7}{x}=+infty\ end{gather*} Пределы бесконечны, наклонных асимптот нет.
4) Первая производная begin{gather*} f'(x)=2cdot 3x^2-6cdot 2x-18cdot 1+0=6x^2-12x-18=6(x^2-2x-3)=\ =6(x-3)(x+1)\ f'(x)=0 text{при} left[ begin{array}{l} x=3\ x=-1 end{array} right. end{gather*} Критические точки: (x=-1) и (x=3)
Составляем таблицу:
| (x) | ((-infty;-1)) | -1 | (-1;3) | 3 | ((3;+infty)) |
| (f'(x)) | >0 | 0 | <0 | 0 | >0 |
| (f(x)) | (nearrow) | max | (searrow) | min | (nearrow) |
Функция возрастает при (xin(-infty;-1)cup(3;+infty))
Функция убывает при (xin(-1;3))
Точка максимума (x=-1; y_{max}=f(-1)=-2-6+18+7=17)
Точка минимума (x=3; y_{min}=f(3)=54-54-54+7=-47)
5) Вторая производная: begin{gather*} f”(x)=(6x^2-12x-18)’=6cdot 2x-12cdot 1-0=12x-12=12(x-1)\ f”(x)=0 text{при} x=1 end{gather*} Критическая точка 2-го порядка: (x=1)
Составляем таблицу:
| (x) | ((-infty;1)) | 1 | ((1;+infty)) |
| (f”(x)) | <0 | 0 | >0 |
| (f(x)) | (cap) | перегиб | (cup) |
Функция выпуклая вверх при (xin(-infty;1))
Функция выпуклая вниз при (xin(1;+infty))
Точка перегиба (x=1; f(1)=2-6-18+7=-15)
6) Точки пересечения с осями координат
Пересечение с осью OY: (x=0, y=7)
Пересечение с осью OX: $$ 2x^3-6x^2-18x+7=0 $$ У кубической параболы точка максимума (-1;17), точка минимума (3;-47).
Т.к. (y_{max}gt 0, y_{min}lt 0) кубическая парабола пересекает ось OX в трех точках: $$ x_1lt -1, -1lt x_2lt 3, x_3gt 3 $$
7) График
Пример 2. Постройте график функции (y=frac3x+frac x3)
1) Область определения
ОДЗ: (xne 0)
(x=0) – точка разрыва. Исследуем односторонние пределы: begin{gather*} lim_{xrightarrow -0}left(frac 3x+frac x3right)=frac{3}{-0}+0=-infty, lim_{xrightarrow +0}left(frac 3x+frac x3right)=frac{3}{+0}+0=+infty end{gather*} Пределы не равны и бесконечны. (x=0) – точка разрыва 2-го рода.
2) Четность $$ f(-x)=frac{3}{-x}+frac{-x}{3}=-left(frac 3x+frac x3right)=-f(x) $$ Функция нечётная.
Периодов нет. Функция не периодическая.
3) Асимптоты
1. Вертикальная асимптота (x=0) – точка разрыва 2-го рода
2. Горизонтальные асимптоты begin{gather*} b_1=lim_{xrightarrow -infty}left(frac 3x+frac x3right)=0+(-infty)=-infty\ b_2=lim_{xrightarrow +infty}left(frac 3x+frac x3right)=0+(+infty)=+infty end{gather*} Пределы бесконечны, горизонтальных асимптот нет.
3. Наклонные асимптоты: begin{gather*} k_1=frac1x lim_{xrightarrow -infty}left(frac 3x+frac x3right)=lim_{xrightarrow -infty}left({3}{x^2}+frac13right)=0+frac13=frac13\ k_1=frac1x lim_{xrightarrow +infty}left(frac 3x+frac x3right)=lim_{xrightarrow +infty}left({3}{x^2}+frac13right)=0+frac13=frac13\ k=k_1=k_2=frac13 end{gather*} Ищем b: $$ b=lim_{xrightarrow infty}(y-kx)=lim_{xrightarrow infty}left(frac3x+frac x3-frac x3right)=lim_{xrightarrow infty}frac 3x=0 $$ Есть одна наклонная асимптота (y=frac 3x)
Кривая стремится к ней на минус и плюс бесконечности.
4) Первая производная: begin{gather*} f'(x)=-frac{3}{x^2}+frac13=frac{x^2-9}{3x^2}=frac{(x+3)(x-3)}{3x^2}\ f'(x)=0 text{при} x=pm 3 end{gather*} Критические точки: (x=left{0;pm 3right})
Составляем таблицу:
| (x) | ((-infty;-3)) | -3 | (-3;0) | 0 | ((0;3)) | 3 | ((3+infty)) |
| (f'(x)) | >0 | 0 | <0 | (varnothing) | <0 | 0 | >0 |
| (f(x)) | (nearrow) | max | (searrow) | (varnothing) | (searrow) | min | (nearrow) |
Функция возрастает при (xin(-infty;-3)cup(-3;+infty))
Функция убывает при (xin(-3;0)cup(0;3))
Точка максимума (x=-3; y_{max}=f(-3)=-1-1=-2)
Точка минимума (x=3; y_{min}=f(3)=1+1=2)
5) Вторая производная: begin{gather*} f”(x)=frac13left(1-frac{9}{x^2}right)’=frac13left(0+frac{9cdot 2}{x^3}right)=frac{6}{x^3} end{gather*} Вторая производная нулей не имеет.
Критическая точка 2-го порядка: (x=0)
Составляем таблицу:
| (x) | ((-infty;0)) | 0 | ((0;+infty)) |
| (f”(x)) | <0 | (varnothing) | >0 |
| (f(x)) | (cap) | (varnothing) | (cup) |
Функция выпуклая вверх при (xin(-infty;0))
Функция выпуклая вниз при (xin(0;+infty))
Точек перегиба нет.
6) Точки пересечения с осями
Пересечение с осью OY: (x=0notin D) – не входит в ОДЗ, пересечений с OY нет
Пересечение с осью OX:
(frac3x+frac x3=0Rightarrow frac{9+x^2}{3x}=0Rightarrow xin varnothing) – решений нет, пересечений с OX нет
7) График
Пример 3*. Постройте график функции (y=frac{x^3-4}{(x-1)^3})
Сколько корней имеет уравнение (frac{x^3-4}{(x-1)^3}=a)?
1) Область определения
ОДЗ: (xne 1)
(x=1) – точка разрыва. Исследуем односторонние пределы: begin{gather*} lim_{xrightarrow 1-0}frac{x^3-4}{(x-1)^3}=frac{1-4}{(1-0-1)^3}=frac{-3}{-0}=+infty\ lim_{xrightarrow 1+0}frac{x^3-4}{(x-1)^3}=frac{1-4}{(1+0-1)^3}=frac{-3}{+0}=-infty end{gather*} Пределы не равны и бесконечны. (x=1) – точка разрыва 2-го рода.
2) Четность $$ f(-x)=frac{(-x)^3-4}{(-x-1)^3}ne left[ begin{array}{l} f(x)\ -f(x) end{array} right. $$ Функция ни четная, ни нечетная.
Периодичность: функция не периодическая
3) Асимптоты
1. Вертикальная асимптота (x=1) – точка разрыва 2-го рода
2. Горизонтальные асимптоты begin{gather*} b_1=lim_{xrightarrow -infty}frac{x^3-4}{(x-1)^3}=left[frac{infty}{infty}right]=lim_{xrightarrow -infty}frac{x^3left(1-frac{4}{x^3}right)}{x^3left(1-frac{1}{x^3}^3right)}=frac{1-0}{(1-0)^3}=1\ b_2=lim_{xrightarrow +infty}frac{x^3-4}{(x-1)^3}=left[frac{infty}{infty}right]=lim_{xrightarrow +infty}frac{x^3left(1-frac{4}{x^3}right)}{x^3left(1-frac{1}{x^3}^3right)}=frac{1-0}{(1-0)^3}=1\ b=b_1=b_2=1 end{gather*} Одна горизонтальная асимптота: (y=1)
Функция стремится к ней на минус и плюс бесконечности.
3. Наклонные асимптоты: begin{gather*} k_1=lim_{xrightarrow infty}frac{x^3-4}{x(x-1)^3}=left[frac{infty}{infty}right]=lim_{xrightarrow infty}frac{x^4left(frac1x-frac{4}{x^4}right)}{x^4left(1-frac{1}{x^3}^3right)}=frac{0-0}{(1-0)^3}=0 end{gather*} Угловой коэффициент (k=0). Наклонных асимптот нет.
4) Первая производная: begin{gather*} f'(x)=left(frac{x^3-4}{(x-1)^3}right)’=frac{3x^2(x-1)^3-(x^3-4)cdot 3(x-1)^2}{(x-1)^6}=frac{3x^2(x-1)-3(x^3-4)}{(x-1)^4}=\ =frac{3x^3-3x^2-3x^3+12}{(x-1)^4}=frac{-3(x^2-4)}{(x-1)^4}=frac{-3(x-2)(x+2)}{(x-1)^4}\ f'(x)=0 text{при} x=pm 2 end{gather*} Критические точки: (x=left{1;pm 2right})
Составляем таблицу:
| (x) | ((-infty;-2)) | -2 | (-2;1) | 1 | ((1;2)) | 2 | ((2+infty)) |
| (f'(x)) | <0 | 0 | >0 | (varnothing) | >0 | 0 | <0 |
| (f(x)) | (searrow) | min | (nearrow) | (varnothing) | (nearrow) | max | (searrow) |
Функция возрастает при (xin(-2;1)cup(1;2))
Функция убывает при (xin(-infty;-2)cup(2;+infty))
Точка максимума (x=2; y_{max}=f(2)=frac{2^3-4}{(2-1)^3}=4)
Точка минимума (x=-2; y_{min}=f(-2)=frac{(-2)^3-4}{(-2-1)^3}=frac{-12}{-27}=frac49)
5) Вторая производная: begin{gather*} f”(x)=left(frac{-3(x^2-4)}{(x-1)^4}right)’=-3left(frac{2x(x-1)^4-(x^2-4)cdot 4(x-1)^3}{(x-1)^8}right)=\ =-3left(frac{2x(x-1)-4(x^2-4)}{(x-1)^5}right)=-3left(frac{2x^2-2x-4x^2+16}{(x-1)^5}right)=\ =-3left(frac{-2x^2-2x+16}{(x-1)^5}right)=frac{6(x^2+x-8)}{(x-1)^5}=frac{6(x-x_1)(x-x_2)}{(x-1)^5}\ D=1^2-4cdot (-8)=33, x_{1,2}=frac{-1pm sqrt{33}}{2}= left[ begin{array}{l} approx -3,37\ approx 2,37 end{array} right.\ f”(x)=0, text{при} x=x_{1,2} end{gather*} Критические точки 2-го порядка: (x=left{1;frac{-1pm sqrt{33}}{2}right})
| (x) | ((-infty;x_1)) | (x_1) | ((x_1;1)) | 1 | ((1;x_2)) | (x_2) | ((x_2;+infty)) |
| (f”(x)) | <0 | 0 | >0 | (varnothing) | <0 | 0 | >0 |
| (f(x)) | (cap) | перегиб | (cup) | (varnothing) | (cap) | перегиб | (cup) |
Функция выпуклая вверх при (xin(-infty;x_1)cup(1;x_2))
Функция выпуклая вниз при (xin(x_1;1)cup (x_2;++infty))
Точки перегиба: $$ begin{cases} x=frac{-1-sqrt{33}}{2}approx -3,37\ yapprox 0,51 end{cases}, begin{cases} x=frac{-1+sqrt{33}}{2}approx 2,37\ yapprox 3,62 end{cases} $$
6) Точки пересечения с осями
Пересечение с OY: (x=0, y=frac{0^3-4}{(0-1)^3}=4)
Пересечение с осью OX:
(frac{x^3-4}{(x-1)^3}=0Rightarrow x=sqrt[3]{4}, y=0)
7) График
Чтобы узнать количество корней уравнения (frac{x^3-4}{(x-1)^3}=a), нужно снизу вверх двигать горизонталь (y=a) и считать количество точек её пересечения с графиком функции.
Последовательно, получаем:
(altfrac{12}{27}) – один корень
(a=frac49) – два корня
(frac49lt alt 1) – три корня
(a=1) – два корня
(1lt alt 4) – три корня
(a=4) – два корня
(agt 4) – один корень
Ответ:
(altfrac49cup agt 4), один корень
(a=left{frac49;1;4right}), два корня
(frac{12}{27}lt 1lt 1cup 1lt alt 4), три корня
Пример 4*. Постройте график функции (y=sin^4x+cos^4x), используя правила преобразования тригонометрических функций и с помощью стандартной процедуры исследования функции
1) Область определения (xinmathbb{R})
2) Четность $$ f(-x)=sin^4(-x)+cos^4(-x)=sin^4x+cos^4x=f(x) $$ Функция четная.
Чтобы найти период, преобразуем тригонометрическое выражение, применяя формулы понижения степени (см. §15 данного справочника): begin{gather*} sin^4x+cos^4x=left(frac{1-cos2x}{2}right)^2+left(frac{1+cos2x}{2}right)^2=\ =frac14(1-2cos2x+cos^2 2x+1+2cos2x+cos^2 2x)=frac{1+cos^2 2x}{2}=\ =frac12left(1+frac{1+cos4x}{2}right)=frac{3+cos4x}{4} end{gather*} Функция периодическая с периодом (T=frac{2pi}{4}=frac pi 2)
Исходя из полученного выражения и применяя правила преобразования графиков тригонометрических функций (см. §8 данного справочника), можно сразу получить результат. $$ y=frac{3+cos4x}{4}=frac34+frac14 cos4x $$ Цепочка преобразований: $$ x xrightarrow1 4xxrightarrow2 cos4x xrightarrow3 frac14xrightarrow4 frac34+frac14 cos4x $$ Пошагово получаем:
1. Умножение аргумента на 4 приводит к уменьшению периода в 4 раза (T=fracpi 2)
2. Косинус – функция четная, при (x=0, cos4x=1), остальные единицы будут через период: (x=frac{pi k}{2}, cos4x=1). Соответственно: (x=fracpi 4+frac{pi k}{2}0 ,cos4x=-1).
Нули функции: (x=fracpi 8+frac{pi k}{4}, cos4x=0).
3. Умножение на (frac14) уменьшает амплитуду косинусоиды в 4 раза: (-frac14leqfrac14 cos4xleq frac14)
4. Прибавление (frac34) перемещает график на (frac34) вверх: (frac12leqfrac34+frac14 cos4xleq 1)
Получаем график:
Продолжим стандартное исследование функции.
3) Асимптоты
1. Вертикальных асимптот нет, т.к. нет точек разрыва 2-го рода.
2. Горизонтальных асимптот нет, т.к. нет пределов на бесконечности.
3. Наклонных асимптот нет, т.к. на бесконечности отношение ограниченной тригонометрической функции к бесконечному x дает (k=0).
4) Первая производная:
Исследуем промежуток, равный одному периоду (T=fracpi 2, 0leq xleqfracpi 2) begin{gather*} f'(x)=(sin^4 x+cos^4 x)’=left(frac{3+cos4x}{4}right)’=0-frac14cdot 4cdot sin4x=-sin4x\ sin4x=0Rightarrow 4x=pi kRightarrow x=frac{pi k}{4} end{gather*} Критические точки: (x=frac{pi k}{4}). На периоде (T=fracpi 2) получаем три точки (x=left{0;fracpi 4;fracpi 2right})
| (x) | 0 | (left(0;fracpi 4right)) | (fracpi 4) | (left(fracpi 4;fracpi 2right)) | (fracpi 2) |
| (f'(x)) | 0 | <0 | 0 | >0 | 0 |
| (f(x)) | 1 max |
(searrow) | (frac12) min |
(nearrow) | 1 max |
Функция убывает при (xinleft(frac{pi k}{2};fracpi 4+frac{pi k}{2}right))
Функция возрастает при (xinleft(fracpi 4+frac{pi k}{2};fracpi 2+frac{pi k}{2}right))
Точки минимума (x=fracpi 4+frac{pi k}{2}; y_{min}=frac12)
Точки максимума (x=frac{pi k}{2}; y_{max}=1)
5) Вторая производная: begin{gather*} f”(x)=(-sin4x)’=-4cos4x\ cos4x=0Rightarrow 4x=fracpi 2+pi kRightarrow x=fracpi 8+frac{pi k}{4} end{gather*} Критические точки 2-го порядка: (x=fracpi 8+frac{pi k}{4}).
На периоде (T=fracpi 2) получаем две точки (x=left{fracpi 8;frac{3pi}{8}right})
| (x) | (left(0;fracpi 8right)) | (fracpi 8) | (left(fracpi 8;frac{3pi}{8}right)) | (frac{3pi}{8}) | (left(frac{3pi}{8};fracpi 2right)) |
| (f”(x)) | <0 | 0 | >0 | 0 | <0 |
| (f(x)) | (cap) | перегиб | (cup) | перегиб | (cap) |
Функция выпуклая вниз при (xinleft(fracpi 8+frac{pi k}{2};frac{3pi}{8}+frac{pi k}{2}right))
Функция выпуклая вверх при (xinleft(-fracpi 8+frac{pi k}{2};fracpi 8+frac{pi k}{2}right))
Точки перегиба: ( x=fracpi 8+frac{pi k}{4}, y=frac{3+cos4cdot left(fracpi 8+frac{pi k}{4}right)}{4}=frac{3+0}{4}=frac34 )
6) Точки пересечения с осями
Пересечение с OY: (x=0, y_{max}=1)
Пересечение с осью OX: т.к. функция ограничена (frac12leq yleq 1), пересечений с OX нет.
7) График
График тот же, что и полученный с помощью правил преобразований графиков тригонометрических функций. Добавились только точки перегиба.
Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют
функцией в математике.
Если вы прочно закрепите общие знания о функции (способы задания, понятие графика)
дальнейшее изучение других
видов функций будет даваться значительно легче.
Что называют квадратичной функцией
Запомните!
![]()
Квадратичная функция — это функция вида
y = ax2 + bx + c,
где a,
b и с — заданные числа.
Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень,
в которой стоит «x» — это «2»,
то перед нами квадратичная функция.
Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты «a»,
«b» и «с».
| Квадратичная функция | Коэффициенты |
|---|---|
| y = 2x2 − 7x + 9 |
|
| y = 3x2 − 1 |
|
| y = −3x2 + 2x |
|
Как построить график квадратичной функции
Запомните!
![]()
График квадратичной функции называют параболой.
Парабола выглядит следующим образом.
Также парабола может быть перевернутой.
Существует четкий алгоритм действий при построении графика квадратичной функции.
Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.
Чтобы было проще понять этот алгоритм, сразу разберем его на примере.
Построим график квадратичной функции «y = x2 −7x + 10».
- Направление ветвей параболы
Запомните!

Если «a > 0», то ветви направлены вверх.

Если «a < 0», то ветви направлены вниз.

В нашей функции «a = 1», это означает, что ветви параболы направлены вверх.

- Координаты вершины параболы
Запомните!

Чтобы найти «x0»
(координата вершины по оси «Ox»)
нужно использовать формулу:Найдем «x0» для нашей функции «y = x2 −7x + 10».
Теперь нам нужно найти «y0»
(координату вершины по оси «Oy»).
Для этого нужно подставить найденное значение «x0» в исходную функцию.
Вспомнить, как найти значение функции можно в уроке
«Как решать задачи на функцию» в подразделе
«Как получить значение функции».y0(3,5) =
(3,5)2 − 7 ·3,5 + 10 = 12,25 − 24,5 + 10 =−12,25 + 10 = −2,25
Выпишем полученные координаты вершины параболы.
(·) A (3,5; −2,25) — вершина параболы.
Отметим вершину параболы на системе координат.
Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график
относительно оси «Oy».
- Нули функции
Для начала давайте разберемся, что называют нулями функции.
Запомните!

Нули функции — это точки пересечения графика функции с осью «Ox»
(осью абсцисс).Наглядно нули функции на графике выглядят так:
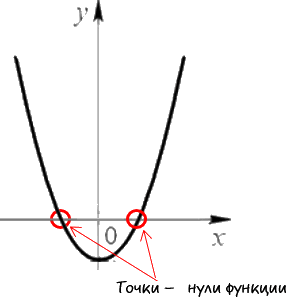
Свое название нули функции получили из-за того, что у этих точек координата
по оси «Oy» равна нулю.Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.
Запомните!

Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо
«y = 0».Подставим в заданную функцию «y = x2 −7x + 10»
вместо «y = 0» и решим полученное
квадратное уравнение
относительно
«x» .0 = x2 −7x + 10
x2 −7x + 10 = 0x1;2 =
7 ±
√49 − 4 · 1 · 102 · 1 x1;2 =
x1;2 =
x1 = x2 =
x1 = x2 =
x1 = 5 x2 = 2
Мы получили два корня в уравнении, значит, у нас две точки пересечения
с осью «Ox».
Назовем эти точки и выпишем их координаты.- (·) B (5; 0)
- (·) C (2; 0)
Отметим полученные точки («нули функции») на системе координат.

- Дополнительные точки для построения графика
Возьмем четыре произвольные числовые значения для «x».
Целесообразно брать целые числовые значения на оси «Ox»,
которые наиболее близки к оси
симметрии. Числа запишем в таблицу в порядке возрастания.x 1 3 4 6 y Для каждого выбранного значения «x»
рассчитаем «y».- y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 =
4 -
y(3) = 32 − 7 · 3 + 10 = 9 − 21 + 10 =
−2 -
y(4) = 42 − 7 · 4 + 10 = 16 − 28 + 10 =
−2 -
y(6) = 62 − 7 · 6 + 10 = 36 − 42 + 10 =
4
Запишем полученные результаты в таблицу.
x 1 3 4 6 y 4 −2 −2 4 Отметим полученные точки графика на системе координат (зеленые точки).
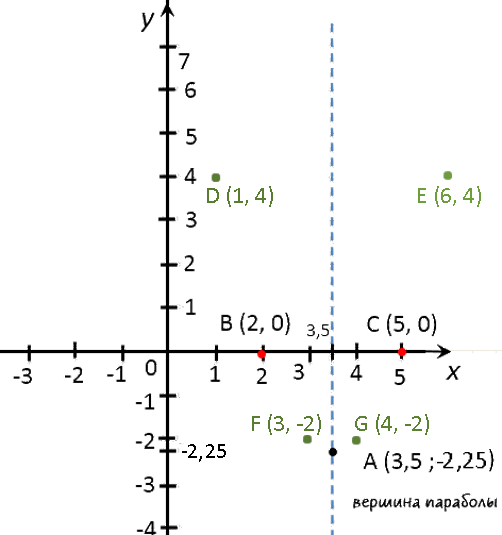
Теперь мы готовы построить график.
На забудьте после построения подписать график функции.
- y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 =
Краткий пример построения параболы
Рассмотрим другой пример построения графика квадратичной функции.
Только теперь запишем алгоритм построения коротко без подробностей.
Пусть требуется построить график функции
«y = −3x2 − 6x − 4».
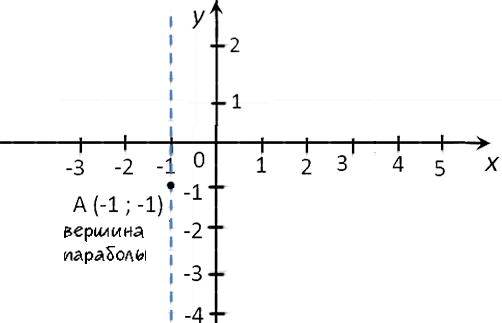
- Направление ветвей параболы
- Координаты вершины параболы
x0 =
x0 = == −1
y0(−1) = (−3) · (−1)2 − 6 · (−1) − 4 =
−3 · 1 + 6 − 4 = −1(·) A (−1; −1)
— вершина параболы.
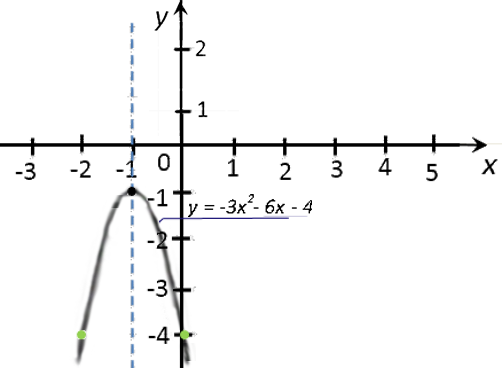
- Нули функции
Точки пересечения с осью «Ox» (y = 0).
0 = −3x2 − 6x − 4
−3x2 − 6x − 4 = 0 |·(−1)
3x2 + 6x + 4 = 0
x1;2 =
−6 ±
√62 − 4 · 3 · 42 · 1 x1;2 =
x1;2 =
Ответ: нет действительных корней.Так как корней нет, значит, график функции не пересекает ось
«Ox». - Вспомогательные точки для: «x = −3»;
«x = −2»;
«x = 0»;
«x = 1». Подставим в исходную функцию
«y = −3x2 − 6x − 4».- y(−3) = −3 · (−3)2 − 6 · (−3) − 4
= −3 · 9 + 18 − 4 = −27 + 14 = −13 -
y(−2) = −3 · (−2)2 − 6 · (−2) − 4
= −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4 -
y(0) = −3 · 02 − 6 · 0 − 4
= −4 -
y(1) = −3 · 12 − 6 · 1 − 4
= −3 −6 − 4 = −13
x −3 −2 0 1 y −13 −4 −4 −13 - y(−3) = −3 · (−3)2 − 6 · (−3) − 4
«a = −3» — ветви параболы направлены вниз.

Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые
не выходят за масштаб нашей системы координат, то есть точки
«(−2; −4)» и «(0; −4)».
Построим и подпишем график функции.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Для многих учащихся, тема “Графики” и все что с ними связано, очень сложна и почти все как один говорит, что не понимает их. А на самом деле, все легко. Достаточно уметь выполнять простые арифметические действия. Если сравнивать задания из второй части ОГЭ по математике, то решить текстовую задачу, чаще бывает сложнее, чем построить график и ответить на вопрос. Сложность заключается в том, что задача требует размышления, правильного прочтения текста, и составление математической модели. При выполнения заданий на построение графиков, нужно всего лишь следовать алгоритму построения. Что можно описать конкретными шагами, то всегда легко.
Разберем построение следующего графика функции и определим шаги для выполнения таких заданий.
Напишем алгоритм построения:
1) Находим ОДЗ функции, т.е. находим такие значения, при которых знаменатель дроби может превратится в ноль.
Как видим, функция не может принимать значения при х=0, х=2/9 и х=-2/9.
2) Упрощаем дробное выражение:
В итоге мы получаем простую функцию, которая называется – обратная пропорциональная зависимость (гипербола).
3) Применяем свойство модуля.
Когда мы выполнили раскрытие модуля, содержащего в функции, и нашли координаты точек для построения графика, можем уже построить график на координатной плоскости.
4) Строим график функции
Если на графике не будут указаны выколотые точки (черные пустые точки на графике), то график будет считаться не верным
5) Отвечаем на вопрос задания, находим параметр по графику. В данном задании нужно было ответить на следующий вопрос:
Поскольку график функции y=kx, это график прямой пропорциональности, то он проходит через координату (0;0). Что бы прямая y=kx не имела с нашим графиком общих точек, то она должна проходить через выколотые точки, как это показано на рисунке красными линиями
Осталось найти значения параметра K. Для этого, в прямую y=kx подставим координаты выколотых точек (2/9; -9/2) и (-2/9; -9/2).
В ответе получаем три значения параметра К. Третье значение К=0 соответствует прямой которая совпадает с осью Ох.
Итак, в алгоритме у нас получилось 5 шагов:
1) Находим ОДЗ функции.
2) Упрощаем дробное выражение функции
3)Раскрываем модуль по его свойству и находи точки для построения графика.
4) Строим график по точкам, которые нашли в пункте 3.
5) Находим параметр.
Так же разбор этого задания, вы можете посмотреть ниже:
Спасибо, что прочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
Download Article
Download Article
A graph of a function is a visual representation of a function’s behavior on an x-y plane. Graphs help us understand different aspects of the function, which would be difficult to understand by just looking at the function itself. You can graph thousands of equations, and there are different formulas for each one. That said, there are always ways to graph a function if you forget the exact steps for the specific type of function.
-

1
-

2
Use the constant to mark your y-intercept. The y-intercept is where the function crosses the y-axis on your graph. In other words, it is the point where
. So, to find it, you simply set x to zero, leaving the constant in the equation alone. For the earlier example,
, your y-intercept is 5, or the point (0,5). On your graph, mark this spot with a dot.[2]
Advertisement
-

3
Find the slope of your line with the number right before the variable. In your example,
, the slope is “2.” That is because 2 is right before the variable in the equation, the “x.” Slope is how steep a line is, or how high the line goes before going to the right or left. Bigger slopes mean steeper lines.
-

4
Break the slope into a fraction. Slope is about steepness, and steepness is simply the difference between movement up and down and movement left and right. Slope is a fraction of rise over run. How much does the line “rise” (go up) before it “runs” (goes to the side)? For the example, the slope of “2” could be read as
.[3]
- If the slope is negative, that means the line goes down as you move to the right.
-

5
Starting at your y-intercept, follow your “rise” and “run” to graph more points. Once you know your slope, use it to plot out your linear function. Start at your y-intercept, here (0,5), and then move up 2, over 1. Mark this point (1,7) as well. Find 1-2 more points to create an outline of your line.[4]
-

6
Use a ruler to connect your dots and graph your linear function. To prevent mistakes or rough graphs, find and connect at least three separate points, though two will do in a pinch. This is the graph of your linear equation![5]
Advertisement
-

1
Determine the function. Get the function of the form like f(x), where y would represent the range, x would represent the domain, and f would represent the function. As an example, we’ll use y = x+2, where f(x) = x+2.[6]
-

2
Draw two lines in a + shape on a piece of paper. The horizontal line is your x axis. The vertical line is your y axis.
-

3
Number your graph. Mark both the x axis and the y axis with equally-spaced numbers. For the x axis, the numbers are positive on the right side and negative on the left side. For the y axis, the numbers are positive on the upper side and negative on the lower side.[7]
-

4
Calculate a y value for 2-3 x values. Take your function f(x) = x+2. Calculate a few values for y by putting the corresponding values for x visible on the axis into the function. For more complicated equations, you may want to simplify the function by getting one variable isolated first.[8]
- -1: -1 + 2 = 1
- 0: 0 +2 = 2
- 1: 1 + 2 = 3
-

5
Draw the graph point for each pair. Simply sketch imaginary lines vertically for each x axis value and horizontally for each y axis value. The point where these lines intersect is a graph point.[9]
-

6
Remove the imaginary lines. Once you have drawn all the graph points, you can erase the imaginary lines. Note: the graph of f(x) = x would be a line parallel to this one passing through the origin (0,0), but f(x) = x+2 is shifted two units up (along the y-axis) on the grid because of the +2 in the equation.[10]
Advertisement
-

1
-

2
Find any zeros first. Zeros, also called x-intercepts, are the points where the graph crosses the horizontal line on the graph. While not all graphs even have zeros, most do, and it is the first step you should take to get everything on track. To find zeros, simply the entire function to zero and solve. For example:
-

3
Find and mark any horizontal asymptotes, or places where it is impossible for the function to go, with a dotted line. This is usually points where the graph does not exist, like where you are dividing by zero. If your equation has a variable in a fraction, like
, start by setting the bottom of the fraction to zero. Any places where it equals zero can be dotted off (in this example, a dotted line at x=2 and x=-2), since you cannot ever divided by zero. Fractions, however, are not the only places you can find asymptotes. Usually, all you need is some common sense:
-

4
Plug in and graph several points. Simply pick a few values for x and solve the function. Then graph the points on your graph. The more complicated the graph, the more points you’ll need. In general, -1, 0, and 1 are the easiest points to get, though you’ll want 2-3 more on either side of zero to get a good graph.[13]
- For the equation
, you might plug in -1,0,1, -2, 2, -10, and 10. This gives you a nice range of numbers to compare.
- Be smart selecting numbers. In the example, you’ll quickly realize that having a negative sign doesn’t matter — you can stop testing -10, for example, because it will be the same as 10.
- For the equation
-

5
Map the end behavior of the function to see what happens when it is really huge. This gives you an idea of the general direction of a function, usually as a vertical asymptote. For example — you know that eventually,
gets really, really big. Just one additional “x” (one million vs. one million and one) makes y much bigger. There are a few ways to test end behavior, including:
-

6
Connect the dots, avoiding asymptotic and following the end behavior to graph an estimate of the function. Once you have 5-6 points, asymptotes, and a general idea of end behavior, plug it all in to get an estimated version of the graph.[15]
-

7
Get perfect graphs using a graphing calculator. Graphing calculators are powerful pocket computers that can give exact graphs for any equation. They allow you to search exact points, find slope lines, and visualize difficult equations with ease. Simply input the exact equation into the graphing section (usually a button labeled “F(x) = “) and hit graph to see your function at work.
Advertisement
Add New Question
-
Question
How do I sketch a graph of a square root function?

The process is the same as shown in the article above except, of course, it involves calculating (or estimating) the square roots of certain values.
-
Question
How do I graph function y = -2 sin(2/3x)?

Choose a value for x. Find 2/3 of that value. Then use a trigonometry table to find the sine of that last value. Then multiply the sine by -2. That gives you the value of y that corresponds to the chosen value of x. Do this again for other x values, and you will then have several x-y pairs to form the graph of the function.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
If you are ever completely lost with what to do, start plugging in points. You could technically graph the entire function like this if you tried infinite combinations of numbers.
-
Graphing calculators are a great way to practice. Try to graph by hand, then use the calculator to get a perfect image of the graph and see how you did.
Advertisement
References
About This Article
Article SummaryX
To graph a function, start by plugging in 0 for x and then solving the equation to find y. Then, mark that spot on the y-axis with a dot. Next, find the slope of the line, which is the number that’s right before the variable. Once you know your slope, write it as a fraction over 1 and then use the rise over run to plot the rest of the points from the spot you marked on the y-axis. Finally, use a ruler to draw a line connecting all of the points on your graph. To learn how to graph complicated functions by hand, scroll down!
Did this summary help you?
Thanks to all authors for creating a page that has been read 138,689 times.
Did this article help you?
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Декартова система координат
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) – горизонтальная ось.
Ось ординат (ось y ) – вертикальная ось.

Функция
Функция – это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.
Прямая
Линейная функция – функция вида y = a x + b где a и b – любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :
Если a > 0 , прямая будет проходить через I и III координатные четверти.
b – точка пересечения прямой с осью y .

Если a < 0 , прямая будет проходить через II и IV координатные четверти.
b – точка пересечения прямой с осью y .

Если a = 0 , функция принимает вид y = b .

Отдельно выделим график уравнения x = a .
Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».

Парабола
Графиком функции y = a x 2 + b x + c является парабола.
Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a , b , c :
- Коэффициент a указывает на то, куда направлены ветки параболы.
- Если a > 0 , ветки параболы направлены вверх.
- Если a < 0 , ветки параболы направлены вниз.
- Коэффициент c указывает, в какой точке парабола пересекает ось y.
- Коэффициент b помогает найти x в – координату вершины параболы.
x в = − b 2 a
- Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .
- Если D > 0 – две точки пересечения.
- Если D = 0 – одна точка пересечения.
- Если D < 0 – нет точек пересечения.




Гипербола
Графиком функции y = k x является гипербола.
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
Ось x – горизонтальная асимптота гиперболы
Ось y – вертикальная асимптота гиперболы.
На графике асимптоты отмечены зелёной пунктирной линией.
Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.

Если k < 0, ветви гиперболы проходят через II и IV четверти.

Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .


Квадратный корень
Функция y = x имеет следующий график:

Возрастающие/убывающие функции
Функция y = f ( x ) возрастает на интервале, если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Примеры возрастающих функций:

Функция y = f ( x ) убывает на интервале, если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.

Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.

Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.
Скачать домашнее задание к уроку 5.
