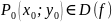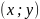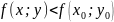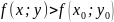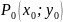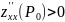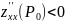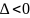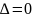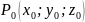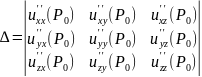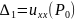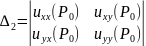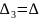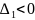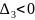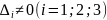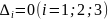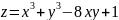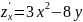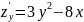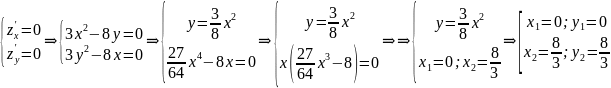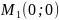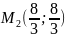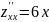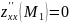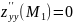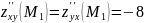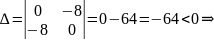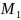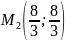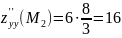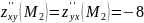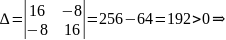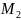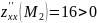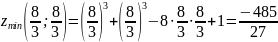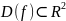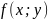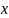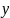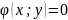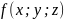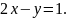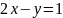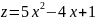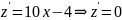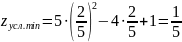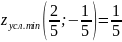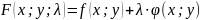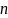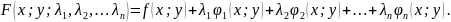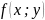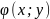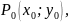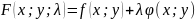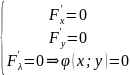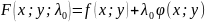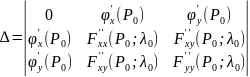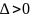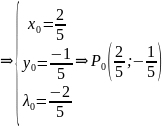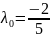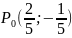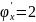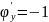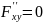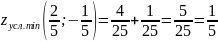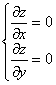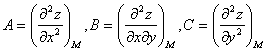Как найти точки экстремума с двумя переменными - Сайт, где вы сможете решить свои вопросы

Уважаемые студенты!
Заказать задачи по физике, информатике, экономике, праву, химии, теормеху, сопромату и другим предметам можно здесь всего за 10 минут.

Экстремум функции двух переменных

Как найти?

Постановка задачи

Найти экстремум функции двух переменных $ z = z(x,y) $

План решения

Экстремумы функции двух переменных возможны в стационарных точках функции. Стационарными точками называются точки $ M(x_1,y_1), M(x_2,y_2)… $, в которых первые частные производные функции равны нулю: $ z(x,y) = 0 $

Для нахождения стационарных точек (подозрительных на экстремум) составляем систему:

$$ begin{cases} z’_x = 0 \ z’_y = 0 end{cases} $$

Решая систему получаем точки $ M(x_1,y_1), M(x_2,y_2)… $, каждую из которых нужно проверить на экстремум.

Проверку осуществляется с помощью подстановки точек в выражение, называемое достаточным условием существования экстремума:

$$ A = z”_{xx} cdot z”_{yy} – (z”_{xy})^2 $$

Если в точке $ M(x_1,y_1) $:

$ A>0 $ и $ z”_{xx} > 0 $, то $ M(x_1,y_1) $ точка минимума
$ A >0 $ и $ z”_{xx} < 0 $, то $ M(x_1,y_1) $ точка максимума
$ A < 0 $, то $ M(x_1,y_1) $ не является точкой экстремума
$ A = 0 $, то требуется дополнительное исследование (по определению)

Итак, необходимо выполнить действия:

Найти частные производные первого порядка. Приравнять их к нулю и решить систему уравнений. Получить точки $ M(x_1,y_1), M(x_2,y_2),… $
Найти частные производные второго порядка в точках $ M(x_1,y_1), M(x_2,y_2),… $
Используя достаточное условие существования экстремума делаем вывод о наличии экстремума в точках $ M(x_1,y_1), M(x_2,y_2),… $

Примеры решений

Пример 1

Найти экстремумы функции двух переменных $ z = x^2 -xy +y^2 $

Решение

Находим частные производные первого порядка:

$$ z’_x = 2x – y $$ $$ z’_y = -x + 2y $$

Приравниваем полученные выражения к нулю и решаем систему двух уравнений:

$$ begin{cases} 2x-y = 0 \ -x + 2y = 0 end{cases} $$

Решив систему получаем стационарную точку (подозрительные на экстремум):

$$ M (0,0) $$

Далее вычисляем значения частных производных второго порядка в точке $ M $:

$$ z”_{xx} Big |_M = 2 $$ $$ z”_{yy} Big |_M= 2 $$ $$ z”_{xy} Big |_M = -1 $$

Подставляя найденные значения в достаточное условие экстремума функции, проводим исследование знаков:

$$ A = Big |_M = z”_{xx} Big |_M cdot z”_{yy} Big |_M – (z”_{xy} Big |_M)^2 = 2 cdot 2 – (-1)^2 = 3 $$

Так как получили $ A > 0 $ и $ z”_{xx} > 0 $, то получается $ M(0,0) $ точка минимума.

Наименьшее значение находится в минимуме и равно:

$$ z_{min} (0,0) = 0^2 – 0 cdot 0 + 0^2 = 0 $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

В точке $ M(0,0) $ находится минимум функции; $ z_{min} = 0 $

Пример 2

Найти экстремумы функции двух переменных $ z = x^3 + y^3 – 15xy $

Решение

Составляем систему уравнений из частных производных первого порядка:

$$ begin{cases} z’_x = 3x^2 – 15y = 0 \ z’_y = 3y^2 – 15x =0 end{cases} $$

Получаем стационарные точки $ M_1(0,0) $ и $ M_2(5,5) $, которые необходимо проверить через достаточное условие экстремума.

Вычисляем значение частных прозводных второго порядка в точке $ M_1 $:

$$ z”_{xx} Big |_{M_1} = 6x Big |_{M_1} = 0 $$

$$ z”_{yy} Big |_{M_1} = 6y Big |_{M_2} = 6y Big |_{M_2} = 0 $$

$$ z”_{xy} Big |_{M_1} = -15 $$

Подставляем данные значения в формулу достаточного условия экстремума:

$$ A Big |_{M_1} = 0 cdot 0 – (-15)^2 = -225 $$

Так как $ A < 0 $, то в точке $ M_1(0,0) $ экстремума нет.

Получаем значения частных производных 2 порядка в $ M_2 $:

$$ z”_{xx} Big |_{M_2} = 6x Big |_{M_2} = 6 cdot 5 = 30 $$

$$ z”_{yy} Big |_{M_2} = 6y Big |_{M_2} = 6 cdot 5 = 30 $$

$$ z”_{xy} Big |_{M_2} = -15 $$

Вычисляем значение выражения достаточного условия экстремума:

$$ A = 30 cdot 30 – (-15)^2 = 900 – 225 = 675 $$

Получили $ A > 0 $ и $ z”_{xx} > 0 $, то значит, $ M_2(5,5) $ точка минимума.

Наименьшее значение функции $ z = x^3 + y^3 – 15xy $ равно:

$$ z_{min} |_{M_2} = 5^3 + 5^3 – 15 cdot 5 cdot 5 = 125 + 125 – 375 = -125 $$

Ответ

В $ M_1 (0,0) $ экстремума нет, в $ M_2(5,5) $ минимум функции $ z_{min}=-125 $

Источник

Экстремум функции двух переменных. Примеры исследования функций на экстремум.

Пусть функция $z=f(x,y)$ определена в некоторой окрестности точки $(x_0,y_0)$. Говорят, что $(x_0,y_0)$ – точка (локального) максимума, если для всех точек $(x,y)$ некоторой окрестности точки $(x_0,y_0)$ выполнено неравенство $f(x,y)< f(x_0,y_0)$. Если же для всех точек этой окрестности выполнено условие $f(x,y)> f(x_0,y_0)$, то точку $(x_0,y_0)$ называют точкой (локального) минимума.

Точки максимума и минимума часто называют общим термином – точки экстремума.

Если $(x_0,y_0)$ – точка максимума, то значение функции $f(x_0,y_0)$ в этой точке называют максимумом функции $z=f(x,y)$. Соответственно, значение функции в точке минимума именуют минимумом функции $z=f(x,y)$. Минимумы и максимумы функции объединяют общим термином – экстремумы функции.

Алгоритм исследования функции $z=f(x,y)$ на экстремум

Найти частные производные $frac{partial z}{partial x}$ и $frac{partial z}{partial y}$. Составить и решить систему уравнений $
left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$. Точки, координаты которых удовлетворяют указанной системе, называют стационарными.
Найти $frac{partial^2z}{partial x^2}$, $frac{partial^2z}{partial xpartial y}$, $frac{partial^2z}{partial y^2}$ и вычислить значение $Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2$ в каждой стационарной точке. После этого использовать следующую схему:
1. Если $Delta > 0$ и $frac{partial^2z}{partial x^2} > 0$ (или $frac{partial^2z}{partial y^2} > 0$), то в исследуемая точка есть точкой минимума.
2. Если $Delta > 0$ и $frac{partial^2z}{partial x^2} < 0$ (или $frac{partial^2z}{partial y^2} < 0$), то в исследуемая точка есть точкой максимума.
3. Если $Delta < 0$, то в расматриваемой стационарной точке экстремума нет.
4. Если $Delta = 0$, то ничего определённого про наличие экстремума сказать нельзя; требуется дополнительное исследование.

Примечание (желательное для более полного понимания текста): показатьскрыть

Пример №1

Исследовать на экстремум функцию $z=4x^2-6xy-34x+5y^2+42y+7$.

Решение

Будем следовать указанному выше алгоритму. Для начала найдём частные производные первого порядка:

$$
frac{partial z}{partial x}=8x-6y-34; frac{partial z}{partial y}=-6x+10y+42.
$$

Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:

$$
left { begin{aligned}
& 8x-6y-34=0;\
& -6x+10y+42=0.
end{aligned} right.
$$

Сократим каждое уравнение этой системы на $2$ и перенесём числа в правые части уравнений:

$$
left { begin{aligned}
& 4x-3y=17;\
& -3x+5y=-21.
end{aligned} right.
$$

Мы получили систему линейных алгебраических уравнений. Мне в этой ситуации кажется наиболее удобным применение метода Крамера для решения полученной системы.

$$ begin{aligned}
& Delta=left| begin{array} {cc} 4 & -3\ -3 & 5 end{array}right|=4cdot 5-(-3)cdot (-3)=20-9=11;\
& Delta_x=left| begin{array} {cc} 17 & -3\ -21 & 5 end{array}right|=17cdot 5-(-3)cdot (-21)=85-63=22;\
& Delta_y=left| begin{array} {cc} 4 & 17\ -3 & -21 end{array}right|=4cdot (-21)-17cdot (-3)=-84+51=-33.end{aligned} \
x=frac{Delta_{x}}{Delta}=frac{22}{11}=2; ; y=frac{Delta_{y}}{Delta}=frac{-33}{11}=-3.
$$

Значения $x=2$, $y=-3$ – это координаты стационарной точки $(2;-3)$. Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:

$$
frac{partial^2 z}{partial x^2}=8; frac{partial^2 z}{partial y^2}=10; frac{partial^2 z}{partial x partial y}=-6.
$$

Вычислим значение $Delta$:

$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
8cdot 10-(-6)^2=80-36=44.
$$

Так как $Delta > 0$ и $frac{partial^2 z}{partial x^2} > 0$, то согласно алгоритму точка $(2;-3)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $(2;-3)$:

$$
z_{min}=z(2;-3)=4cdot 2^2-6cdot 2 cdot (-3)-34cdot 2+5cdot (-3)^2+42cdot (-3)+7=-90.
$$

Ответ: $(2;-3)$ – точка минимума; $z_{min}=-90$.

Пример №2

Исследовать на экстремум функцию $z=x^3+3xy^2-15x-12y+1$.

Решение

Будем следовать указанному выше алгоритму. Для начала найдём частные производные первого порядка:

$$
frac{partial z}{partial x}=3x^2+3y^2-15; frac{partial z}{partial y}=6xy-12.
$$

Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:

$$
left { begin{aligned}
& 3x^2+3y^2-15=0;\
& 6xy-12=0.
end{aligned} right.
$$

Сократим первое уравнение на 3, а второе – на 6.

$$
left { begin{aligned}
& x^2+y^2-5=0;\
& xy-2=0.
end{aligned} right.
$$

Если $x=0$, то второе уравнение приведёт нас к противоречию: $0cdot y-2=0$, $-2=0$. Отсюда вывод: $xneq 0$. Тогда из второго уравнения имеем: $xy=2$, $y=frac{2}{x}$. Подставляя $y=frac{2}{x}$ в первое уравнение, будем иметь:

$$
x^2+left(frac{2}{x} right)^2-5=0;\
x^2+frac{4}{x^2}-5=0;\
x^4-5x^2+4=0.
$$

Получили биквадратное уравнение. Делаем замену $t=x^2$ (при этом имеем в виду, что $t > 0$):

$$
t^2-5t+4=0;\
begin{aligned}
& D=(-5)^2-4cdot 1 cdot 4=9;\
& t_1=frac{-(-5)-sqrt{9}}{2}=frac{5-3}{2}=1;\
& t_2=frac{-(-5)+sqrt{9}}{2}=frac{5+3}{2}=4.end{aligned}
$$

Если $t=1$, то $x^2=1$. Отсюда имеем два значения $x$: $x_1=1$, $x_2=-1$. Если $t=4$, то $x^2=4$, т.е. $x_3=2$, $x_4=-2$. Вспоминая, что $y=frac{2}{x}$, получим:

begin{aligned}
& y_1=frac{2}{x_1}=frac{2}{1}=2;\
& y_2=frac{2}{x_2}=frac{2}{-1}=-2;\
& y_3=frac{2}{x_3}=frac{2}{2}=1;\
& y_4=frac{2}{x_4}=frac{2}{-2}=-1.
end{aligned}

Итак, у нас есть четыре стационарные точки: $M_1(1;2)$, $M_2(-1;-2)$, $M_3(2;1)$, $M_4(-2;-1)$. На этом первый шаг алгоритма закончен.

Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:

$$
frac{partial^2 z}{partial x^2}=6x; frac{partial^2 z}{partial y^2}=6x; frac{partial^2 z}{partial x partial y}=6y.
$$

Найдём $Delta$:

$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
6xcdot 6x-(6y)^2=36x^2-36y^2=36(x^2-y^2).
$$

Теперь будем вычислять значение $Delta$ в каждой из найденных ранее стационарных точек. Начнём с точки $M_1(1;2)$. В этой точке имеем:

$$Delta(M_1)=36(1^2-2^2)=-108.$$

Так как $Delta(M_1) < 0$, то согласно алгоритму в точке $M_1$ экстремума нет.

Исследуем точку $M_2(-1;-2)$. В этой точке имеем:

$$Delta(M_2)=36((-1)^2-(-2)^2)=-108.$$

Так как $Delta(M_2) < 0$, то согласно алгоритму в точке $M_2$ экстремума нет.

Исследуем точку $M_3(2;1)$. В этой точке получим:

$$
Delta(M_3)=36(2^2-1^2)=108;;; left.frac{partial^2 z}{partial x^2}right|_{M_3}=6cdot 2=12.
$$

Так как $Delta(M_3) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_3} > 0$, то согласно алгоритму $M_3(2;1)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_3$:

$$
z_{min}=z(2;1)=2^3+3cdot 2cdot 1^2-15cdot 2-12cdot 1+1=-27.
$$

Осталось исследовать точку $M_4(-2;-1)$. В этой точке получим:

$$
Delta(M_4)=36((-2)^2-(-1)^2)=108;;; left.frac{partial^2 z}{partial x^2}right|_{M_4}=6cdot (-2)=-12.
$$

Так как $Delta(M_4) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_4} < 0$, то согласно алгоритму $M_4(-2;-1)$ есть точкой максимума функции $z$. Максимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_4$:

$$
z_{max}=z(-2;-1)=(-2)^3+3cdot (-2)cdot (-1)^2-15cdot (-2)-12cdot (-1)+1=29.
$$

Исследование на экстремум завершено. Осталось лишь записать ответ.

Ответ:

$(2;1)$ – точка минимума, $z_{min}=-27$;
$(-2;-1)$ – точка максимума, $z_{max}=29$.

Примечание

Вычислять значение $Delta$ в общем случае нет необходимости, потому что нас интересует лишь знак, а не конкретное значение данного параметра. Например, для рассмотренного выше примера №2 в точке $M_3(2;1)$ имеем $Delta=36cdot(2^2-1^2)$. Здесь очевидно, что $Delta > 0$ (так как оба сомножителя $36$ и $(2^2-1^2)$ положительны) и можно не находить конкретное значение $Delta$. Правда, для типовых расчётов это замечание бесполезно, – там требуют довести вычисления до числа 🙂

Пример №3

Исследовать на экстремум функцию $z=x^4+y^4-2x^2+4xy-2y^2+3$.

Решение

Будем следовать алгоритму. Для начала найдём частные производные первого порядка:

$$
frac{partial z}{partial x}=4x^3-4x+4y; frac{partial z}{partial y}=4y^3+4x-4y.
$$

Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:

$$
left { begin{aligned}
& 4x^3-4x+4y=0;\
& 4y^3+4x-4y=0.
end{aligned} right.
$$

Сократим оба уравнения на $4$:

$$
left { begin{aligned}
& x^3-x+y=0;\
& y^3+x-y=0.
end{aligned} right.
$$

Добавим к второму уравнению первое и выразим $y$ через $x$:

$$
y^3+x-y+(x^3-x+y)=0;\
y^3+x^3=0; y^3=-x^3; y=-x.
$$

Подставляя $y=-x$ в первое уравнение системы, будем иметь:

$$
x^3-x-x=0;\
x^3-2x=0;\
x(x^2-2)=0.
$$

Из полученного уравнения имеем: $x=0$ или $x^2-2=0$. Из уравнения $x^2-2=0$ следует, что $x=-sqrt{2}$ или $x=sqrt{2}$. Итак, найдены три значения $x$, а именно: $x_1=0$, $x_2=-sqrt{2}$, $x_3=sqrt{2}$. Так как $y=-x$, то $y_1=-x_1=0$, $y_2=-x_2=sqrt{2}$, $y_3=-x_3=-sqrt{2}$.

Первый шаг решения окончен. Мы получили три стационарные точки: $M_1(0;0)$, $M_2(-sqrt{2},sqrt{2})$, $M_3(sqrt{2},-sqrt{2})$.

Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:

$$
frac{partial^2 z}{partial x^2}=12x^2-4; frac{partial^2 z}{partial y^2}=12y^2-4; frac{partial^2 z}{partial x partial y}=4.
$$

Найдём $Delta$:

$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
(12x^2-4)(12y^2-4)-4^2=\
=4(3x^2-1)cdot 4(3y^2-1)-16=16(3x^2-1)(3y^2-1)-16=16cdot((3x^2-1)(3y^2-1)-1).
$$

Теперь будем вычислять значение $Delta$ в каждой из найденных ранее стационарных точек. Начнём с точки $M_1(0;0)$. В этой точке имеем:

$$Delta(M_1)=16cdot((3cdot 0^2-1)(3cdot 0^2-1)-1)=16cdot 0=0.$$

Так как $Delta(M_1) = 0$, то согласно алгоритму требуется дополнительное исследование, ибо ничего определённого про наличие экстремума в рассматриваемой точке сказать нельзя. Оставим покамест эту точку в покое и перейдём в иным точкам.

Исследуем точку $M_2(-sqrt{2},sqrt{2})$. В этой точке получим:

begin{aligned}
& Delta(M_2)=16cdot((3cdot (-sqrt{2})^2-1)(3cdot (sqrt{2})^2-1)-1)=16cdot 24=384;\
& left.frac{partial^2 z}{partial x^2}right|_{M_2}=12cdot (-sqrt{2})^2-4=24-4=20.
end{aligned}

Так как $Delta(M_2) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_2} > 0$, то согласно алгоритму $M_2(-sqrt{2},sqrt{2})$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_2$:

$$
z_{min}=z(-sqrt{2},sqrt{2})=(-sqrt{2})^4+(sqrt{2})^4-2(-sqrt{2})^2+4cdot (-sqrt{2})sqrt{2}-2(sqrt{2})^2+3=-5.
$$

Аналогично предыдущему пункту исследуем точку $M_3(sqrt{2},-sqrt{2})$. В этой точке получим:

begin{aligned}
& Delta(M_3)=16cdot((3cdot (sqrt{2})^2-1)(3cdot (-sqrt{2})^2-1)-1)=16cdot 24=384;\
& left.frac{partial^2 z}{partial x^2}right|_{M_3}=12cdot (sqrt{2})^2-4=24-4=20.
end{aligned}

Так как $Delta(M_3) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_3} > 0$, то согласно алгоритму $M_3(sqrt{2},-sqrt{2})$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_3$:

$$
z_{min}=z(sqrt{2},-sqrt{2})=(sqrt{2})^4+(-sqrt{2})^4-2(sqrt{2})^2+4cdot sqrt{2}(-sqrt{2})-2(-sqrt{2})^2+3=-5.
$$

Настал черёд вернуться к точке $M_1(0;0)$, в которой $Delta(M_1) = 0$. Согласно алгоритму требуется дополнительное исследование. Под этой уклончивой фразой подразумевается “делайте, что хотите” :). Общего способа разрешения таких ситуаций нет, – и это понятно. Если бы такой способ был, то он давно бы вошёл во все учебники. А покамест приходится искать особый подход к каждой точке, в которой $Delta = 0$. Ну что же, поисследуем поведение функции в окрестности точки $M_1(0;0)$. Сразу отметим, что $z(M_1)=z(0;0)=3$. Предположим, что $M_1(0;0)$ – точка минимума. Тогда для любой точки $M$ из некоторой окрестности точки $M_1(0;0)$ получим $z(M) > z(M_1) $, т.е. $z(M) > 3$. А вдруг любая окрестность содержит точки, в которых $z(M) < 3$? Тогда в точке $M_1$ уж точно не будет минимума.

Рассмотрим точки, у которых $y=0$, т.е. точки вида $(x,0)$. В этих точках функция $z$ будет принимать такие значения:

$$
z(x,0)=x^4+0^4-2x^2+4xcdot 0-2cdot 0^2+3=x^4-2x^2+3=x^2(x^2-2)+3.
$$

В всех достаточно малых окрестностях $M_1(0;0)$ имеем $x^2-2 < 0$, посему $x^2(x^2-2) < 0$, откуда следует $x^2(x^2-2)+3 < 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z < 3$, посему точка $M_1(0;0)$ не может быть точкой минимума.

Но, может быть, точка $M_1(0;0)$ – точка максимума? Если это так, то для любой точки $M$ из некоторой окрестности точки $M_1(0;0)$ получим $z(M) < z(M_1) $, т.е. $z(M) < 3$. А вдруг любая окрестность содержит точки, в которых $z(M) > 3$? Тогда в точке $M_1$ точно не будет максимума.

Рассмотрим точки, у которых $y=x$, т.е. точки вида $(x,x)$. В этих точках функция $z$ будет принимать такие значения:

$$
z(x,x)=x^4+x^4-2x^2+4xcdot x-2cdot x^2+3=2x^4+3.
$$

Так как в любой окрестности точки $M_1(0;0)$ имеем $2x^4 > 0$, то $2x^4+3 > 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z > 3$, посему точка $M_1(0;0)$ не может быть точкой максимума.

Точка $M_1(0;0)$ не является ни точкой максимума, ни точкой минимума. Вывод: $M_1$ вообще не является точкой экстремума.

Ответ: $(-sqrt{2},sqrt{2})$, $(sqrt{2},-sqrt{2})$ – точки минимума функции $z$. В обеих точках $z_{min}=-5$.

Источник

Экстремумы функций двух и трёх переменных

Определение
1

Точка

называется
точкой максимума функции

,
если
для любых точек

,
принадлежащих
окрестности точки

,
выполняется неравенство:

.

Определение
2

Точка

называется
точкой минимума функции

,
если
для любых точек

,
принадлежащих окрестности точки

,
выполняется
неравенство:

.

Определение
3

Точки
максимума и минимума называются
точками
экстремума
функции.

Теорема
1 (необходимое условие экстремума)

Если
точка

является точкой экстремума функции

,
то её частные производные в точке

равны нулю или не существуют.

При
доказательстве теоремы 1 используются
определения частных производных и
теорема о необходимых условиях экстремума
функции одной переменной.

Замечание
1.
Аналогично формулируются определения
1 и 2 и теорема 1 для функции трёх и более
переменных.

Теорема
2
(достаточные
условия экстремума функции двух
переменных)

Если
функция

дважды дифференцируема в критической
точке

и её окрестности и определитель

,
то в точке

есть экстремум. Причём, если

,
то точка

является точкой минимума функции, а
если

,
то точка

является точкой максимума.
Замечание
2.
Если определитель

,
то в точке

нет экстремума, при этом точку

называют седловой точкой. Если

,
то вопрос об экстремуме в точке

остаётся нерешённым, нужны исследования
функции

по её производным более высокого порядка.

Теорема
3
(достаточные
условия экстремума функции трёх
переменных)

Пусть
функция

дважды дифференцируема в
критической точке

и её окрестности. Определитель

имеет все главные диагональные миноры

положительные, то

–точка минимума функции

.
Если

,

, то точка

– точка максимума функции

Замечание
3.
Если


критическая точка функции

и

,
но не выполняются условия теоремы 3, то
в точке

нет экстремума, при этом точка

называется седловой точкой. Если все

,
то вопрос об экстремуме в точке

решается с помощью производных более
высокого порядка.

Пример
1.
Найти экстремумы функции:

.

Решение.

;

Получили
две точки

;

а)
Исследуем точку

;

Тогда

точка

не является точкой экстремума.

б)
Исследуем точку

:

;

Тогда

точка

является точкой экстремума. Причём так
как

,
то точка

является точкой минимума функции:

Ответ:

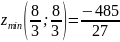
Условный экстремум

Пусть
задана функция

на множестве

.
Требуется найти экстремумы функции

,
если

связаны некоторым условием

,
называемым уравнением
связи.

Определение
4.
Точка

называется точкой
условного экстремума
функции

при выполнении дополнительных условий

– уравнений связи.

Для
нахождения точек условного экстремума
существует два метода: метод прямого
отыскания и метод Лагранжа. Прямой
метод состоит в том, что из уравнения
связи

выражается одна из переменных через
другую, и её подставляют в функцию

.
Получают функцию одной переменной, для
которой и решают задачу нахождения
обычного экстремума. Такой метод
применяют тогда, когда удаётся из
уравнения связи выразить одну переменную
через другую.

Пример
2.
Найти условный экстремум функции

при
условии

Решение.
Используем метод прямого отыскания
точек условного экстремума. Из условия

выразим

и подставим его в функцию

.
Тогда

Найдём
для функции

обычный экстремум.

– +
x

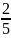
Следовательно,

– точка минимума функции

Подставляем

в функцию

и получим:

Ответ:

Определение
5.
Функция

называется функцией
Лагранжа,
а коэффициент λ
–
множителем
Лагранжа.

Замечание
4.
Если связи не одно уравнение, а несколько
(например,

),
то функция Лагранжа для функции

записывается с

множителями Лагранжа:

Теорема
4
(необходимое
условие поиска условного экстремума)

Пусть
функции

и

,
дифференцируемые в точке

является точкой условного экстремума
функции

при условии

.
Тогда найдется такое число

,
при котором точка

является критической для функции
Лагранжа

.

Метод
Лагранжа
поиска условного экстремума состоит в
следующем:

1)
составляют функцию Лагранжа

;

2)
находят её частные производные по

;

3)
приравнять частные производные к нулю
и решают систему уравнений

;

4)
исследуют найденную в результате решения
системы точку

при найденном значении

и решают задачу обычного экстремума
для

.

Теорема
5 (достаточное условие поиска условного
экстремума для случая одного уравнения
связи)

Пусть
точка

найдены из решения системы

.

Пусть
определитель

Если

,
то функция

имеет в точке

условный максимум.

Если

,
то функция

имеет в точке

условный минимум.

Пример
3.
Методом Лагранжа найти условный экстремум
для функции

при условии

.
Решение.
Составим функцию Лагранжа

Найдём
её частные производные по

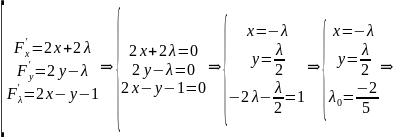
при

Выясним
характер точки

по теореме 5:

;

Составим
определитель:

Так
как

,
то

– точка условного минимума.

Ответ:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Экстремум функции двух переменных

Назначение сервиса. Онлайн-калькулятор используется для нахождения в онлайн режиме наибольшего и наименьшего значения функции двух переменных (см. пример). Решение оформляется в формате Word.

Решение онлайн
Видеоинструкция
Оформление Word

Для функции трех переменных можно использовать матрицу Гессе.

Алгоритм исследования функции двух переменных на экстремум

Функция z = f(x,y) имеет максимум в точке M₀(x₀;y₀), если f(x₀;y₀) > f(x;y) для всех точек (x;y), достаточно близких к точке (x₀;y₀) и отличных от неё. Функция z = f(x,y) имеет минимум в точке M₀(x₀;y₀), если f(x₀;y₀) < f(x;y) для всех точек (x;y), достаточно близких к точке (x₀;y₀) и отличных от неё. Максимум и минимум функции называются экстремумами функции.

Исследование функции двух переменных на экстремум проводят по следующей схеме.

1. Находят частные производные dz/dx и dz/dy.

2. Решают систему уравнений:

и таким образом находят критические точки функции.

3. Находят частные производные второго порядка:

4. Вычисляют значения этих частных производных второго порядка в каждой из найденных в п.2 критических точках M(x₀;y₀).

5. Делаю вывод о наличии экстремумов:

а) если AC – B² > 0 и A < 0 , то в точке M имеется максимум;

б) если AC – B² > 0 и A > 0 , то в точке M имеется минимум;

в) если AC – B² < 0, то экстремума нет;

г) если AC – B² = 0, то вопрос о наличии экстремума остается открытым;

Пример №1. Найти экстремумы функции f(x,y)=x³+xy²+x²+y² и определить по критерию Сильвестра их тип.

Решение.

1. Найдем первые частные производные.

2. Решим систему уравнений.

3x²+2x+y²=0

2xy+2y=0

Получим:

а) Из первого уравнения выражаем x и подставляем во второе уравнение:

x = -1

y²+1=0

Данная система уравнений не имеет решения.

б) Из первого уравнения выражаем y и подставляем во второе уравнение:

или

или

Откуда x₁ = -2/3; x₂ = 0; x₃ = -2/3; x₄ = 0

Данные значения x подставляем в выражение для y. Получаем: y₁ = 0; y₂ = 0; y₃ = 0; y₄ = 0

Количество критических точек равно 2: M₁(-2/3;0), M₂(0;0)

3. Найдем частные производные второго порядка.

4. Вычислим значение этих частных производных второго порядка в критических точках M(x₀;y₀).

Вычисляем значения для точки M₁(-2/3;0)

AC – B² = -4/3 < 0, то глобального экстремума нет.

Вычисляем значения для точки M₂(0;0)

AC – B² = 4 > 0 и A > 0 , то в точке M₂(0;0) имеется минимум z(0;0) = 0

Вывод: В точке M₂(0;0) имеется минимум z(0;0) = 0

Пример №2. Исследовать функцию на экстремум классическим методом: Z=8x²+2xy-5x+6.

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Источник

Содержание:

Экстремум функции двух переменных
Экстремумы функции двух переменных и производная по направлению
Достаточные условия экстремума функции двух переменных
Производная по направлению
Градиент

Экстремум функции двух переменных

Для функции двух переменных, как и для функции одной переменной, можно ввести понятие экстремума. Считают, что в точке М₀ (х₀, у₀) функция z = f (x, y) достигает локального максимума, если в окрестности точки М₀ выполняется неравенство f (x, y) ≤. f(х₀, у₀). Аналогично, в точке М₀ (х₀, у₀) функция z = f (x, y) достигает локального минимума, если в окрестности этой точки выполняется неравенство f (x, y) ≤. f (х₀, у₀).
На рис. 10 функция достигает максимума, а на рис. 11 — минимума.

Рис. 10. Рис. 11.

Точки локального минимума и максимума называются точками экстремума функции z = f (x, y).

Для нахождения экстремальных значений функции двух переменных используются необходимые и достаточные условия экстремума.

ТЕОРЕМА 2. (Необходимое условие экстремума функции). Если в точке М₀ (х₀; у₀) функция z = f (x, y) достигает экстремума, то ее частные производные первого порядка в этой точке равны нулю, то есть

Доказательство. Пусть в точке М₀ (х₀; у₀) функция z = f (x; y) достигает экстремума. Для конкретности предположим, что это max. Зафиксируем значение y = y₀ и рассмотрим функцию z = f (x; y₀). Как функция одной переменной, эта функция при x = x0 достигает максимума, поэтому должно выполняться необходимое условие экстремума: производная при x = x0 обращается в нуль. Но производная от f (x; y₀) по x есть ни что иное, как частная производная функции z = f (x; y) по x в точке М₀ (х₀; у₀). Итак,

Аналогично, зафиксируем значение x = x0 и рассмотрим функцию z = f (x_о; y). При y = y₀ эта функция достигает max, поэтому должна превращаться в ноль, если y = y₀.
Отсюда следует, что Теорема доказана.

Фактически мы получаем систему уравнений для нахождения координат точки М₀ (х₀, у₀). Таких точек может быть несколько или не существовать вовсе. Точки, в которых частные производные первого порядка превращаются в ноль, называются точками, подозрительными на экстремум, или критическими точками. Пусть в точке М₀ (х₀, у₀) выполняется условие и существуют частные производные второго порядка. Введем следующие обозначения:

и рассмотрим число D = AC – B².

ТЕОРЕМА 3. (Достаточное условие экстремума функции).
Если D > 0, то в точке М₀ (х₀, у₀) функция z = f (x, y) имеет экстремум, если D < 0, то экстремума нет. Если D > 0 и A > 0, то функция достигает минимума, если D > 0 и A < 0, то функция достигает максимума.

Доказательство. Пусть точка М₀ (х₀, у₀) является критической точкой, то есть и Допустим, что существуют другие частные производные и . Составим из чисел A, B, C определитель Рассмотрим приращение функции z = f (x; y) в точке М₀ (х₀, у₀)

где ε → 0, если

Последняя запись вытекает из формулы Тейлора для функций двух переменных. Очевидно, что основной вклад в приращение Δz задается квадратичной формой относительно Δx и Δy.
Рассмотрим матрицу:

а) Допустим теперь, что и A > 0. Тогда автоматически следует, что C > 0. Поскольку выражение представляет собой квадратичную форму, то по условию теоремы Рауса-Гурвица, квадратичная форма является положительно-определенной, то есть

б) Допустим, что D > 0, A < 0. Тогда автоматически C < 0. В данном случае квадратичная форма является отрицательно-определенной, следовательно
Теорема доказана.

Замечание 1. Если D < 0, то функция не достигает ни минимума, ни максимума, следовательно экстремума нет. Это можно продемонстрировать для случая седловидной точки поверхности, например, для функции в точке O (0; 0).

Из рис. 6 видно, что по переменной x функция достигает min, а по переменной y достигает min, а экстремума в точке O (0; 0) не существует.

Замечание 2. Случай D = 0 не рассматриваем, так как в этом случае экстремум может быть, а может не быть. С помощью частных производных второго порядка исследовать функцию на экстремумы невозможно. Например, z = x⁴ + y⁴.

Пример 1. Исследовать на экстремум функцию z = x² + xy + y² + 2x – 2y + 3.

Решение. Находим частные производные первого порядка:
Приравниваем их к нулю:

Находим частные производные второго порядка:

Тогда D = 2 ⋅ 2 — 1² = 3 > 0. Следовательно, в точке M₀ (–2; 2) функция достигает экстремума. Поскольку A = 2 > 0, то имеем минимум. Находим z_min = -5.

Пример 2. Исследовать на экстремум функцию .
Решение. Находим частные производные:

Из системы уравнений
находим, что x = 0; y = 0.
Дальше Тогда
Отсюда следует, что экстремум функции не существует.

Пример 3. Исследовать на экстремум функцию z = 2 x³ + 2 y³ – 36 xy + 430.

Решение. Найдем

Решим систему уравнений
то есть или

Из первого уравнения имеем Подставив это значение во второе уравнение, получим Последнее уравнение можно записать так:
x⁴ – 216 x = x (x³ – 216) = x (x – 6) (x² + 6 x + 36) = 0.

Отсюда следует, что x₁ = 0, x₂ = 6. Корни уравнения x² + 6 x + 36 = 0 комплексные, которые нас не интересуют.

Подставив полученные значения x в равенство , получим: y₁ = 0, y₂ = 6. Таким образом, имеем две пары решений предыдущей системы уравнений: 1) x₁ = 0, y₁ = 0; 2) x₂ = 6, y₂ = 6.

Для нахождения D определим

Подставляя сюда сначала первую пару решений, а затем вторую, вычислим A, B, C. Для первой пары решений:

то есть D = AC – B² = –362 < 0. Поскольку D < 0, то при x = 0; y = 0 функция не имеет экстремума. Для второй пары решений:

Поскольку число D = AC – B² = 72 ⋅ 72 – (–36)² = 3888, положительное, то экстремум при x = 6; y = 6 существует, причем минимум (A > 0).

Для нахождения минимального значения функции подставим x = 6; y = 6 и получим

Пример 4. Малое предприятие производит товары вида A и B. Общие ежедневные затраты на производство x единиц товара A и y единиц товара B задаются функцией
V = 620 – 14 x – 10 y + 0,2 x² + 0,1 y².
Определить количество единиц товаров A и B, при которых общие расходы предприятия будут минимальными.

Решение. Чтобы найти количество единиц x и y товаров A и B, необходимо исследовать на экстремум функцию V = 620 – 14 x – 10 y + 0,2 x² + 0,1 y².

Находим частные производные первого порядка

Приравнивая их к нулю, получим систему уравнений:

Находим частные производные второго порядка

Находим D = AC – B² = 0,4 ⋅ 0,2 – 0² = 0,08 > 0. Поскольку A > 0, то имеем минимум. Следовательно, функция затрат V (x; y) при x = 35, y = 50 достигает минимума. V_min = 125 (ден. ед.)

Экстремумы функции двух переменных и производная по направлению

Рассмотрим функцию , которая определена и непрерывна в некоторой окрестности точки .

Определение 1. Точка называется точкой локального максимума (минимума) функции , если существует такая окрестность точки , в которой для любой точки из этой окрестности выполняется неравенство .

Точки локального максимума и локального минимума называются точками локального экстремума или просто точками экстремума.

Теорема 1 (необходимое условие экстремума). Если функция имеет частные производные первого порядка в точке локального экстремума , то

Доказательство. Рассмотрим сначала функцию одной переменной . Производная этой функции совпадает с частной производной , а сама функция имеет локальный экстремум в точке . По теореме 3.17 (необходимое условие локального экстремума функции одной переменной) производная функция в точке равна нулю, т.е. . Аналогично функция одной переменной имеет локальный экстремум в точке . Следовательно, ее производная в этой точке равна нулю, т.е. . Теорема доказана.

Итак, «подозрительными» на экстремум являются те точки , в которых все частные производные первого порядка обращаются в нуль. Как и в случае функции одной переменной, такие точки называются стационарными (при этом требуется, чтобы функция была дифференцируемой в точке ). Стационарные точки функции можно найти, решив систему уравнений

(1)

Пример №76

Найти стационарные точки функции .

Решение:

Система (1) имеет вид

Из первого уравнения находим . Из второго уравнения находим . Следовательно, функция (рис. 1.21, а) имеет шесть стационарных точек: (1; 0), (1; -1), (1; 1), (-1; 0), (-1; -1), (-1; 1).

Достаточные условия экстремума функции двух переменных

Условия теоремы 1 не являются достаточными условиями существования экстремума.

Например, для функции (рис. 1, б) частные производные первого порядка равны нулю в точке (0; 0), однако эта точка не является точкой локального экстремума. Действительно, в любой окрестности точки (0; 0) существуют точки вида (; 0), в которых . Поэтому (0; 0) не является точкой локального максимума. Аналогично в любой окрестности точки (0; 0) существуют точки вида (0; ), в которых . Поэтому (0; 0) не является точкой локального минимума.

Теорема 2 (достаточные условия экстремума). Пусть функция имеет непрерывные частные производные второго порядка в некоторой окрестности стационарной точки . Положим

Тогда:

1) если , то в точке функция имеет локальный экстремум, причем при – локальный максимум, а при – локальный минимум;

2) если <0, то в точке нет экстремума;

3) если = 0, то в точке экстремум может быть, а может и не быть, и необходимы дополнительные исследования.

Пример №77

Найти экстремумы функции

Решение:

Найдем частные производные первого порядка

, .

Стационарные точки найдем, решая систему уравнений

Сложив уравнения системы, получим , откуда . Подставив в первое уравнение системы, придем к уравнению . Получим корни: =0, . =, . Отсюда следует, что = 0, , . Итак, наша функция имеет три стационарные точки:

(0; 0), , .

Чтобы найти определитель , рассчитаем частные производные второго порядка:

, , .

Получим

Вычислим величину в стационарных точках:

, , .

Так как и , то, согласно теореме 2, – точка локального минимума (как и точка ).

Рассчитаем значение функции (рис. 2) в этих точках:

, .

Так как , поэтому в точке , теорему 2 применить нельзя. Убедимся, что в этой точке экстремум отсутствует. Действительно, если = 0, то в окрестности точки . Если , то . Итак, в окрестности точки значения могут быть как положительные, так и отрицательные, а это означает, что точка не является экстремальной. Отметим, что других экстремумов заданная функция не имеет, поскольку точки, в которых производные и не существуют, отсутствуют.

Производная по направлению

Пусть функция определена и непрерывна в некоторой окрестности точки ; – единичный вектор; – направленная прямая, проходящая через точку ; – точка на прямой (рис. 3); -величина отрезка ; – приращение функции в точке .

Рис. 3. Иллюстрация производной но направлению

Определение 2. Предел отношения при , если он существует, называется производной функции в точке по направлению вектора (кратко – производная по направлению) и обозначается:

Производная по направлению вычисляется по формуле:

где и – направляющие косинусы вектора . Ее физический смысл – скорость изменения функции в точке по направлению вектора . Действительно, если =(1; 0), то , и . Если же =(0; 1), то = . Т.о., производная по направлению обобщает понятие частной производной.