Точки пересечения графиков функций
В алгебре и начале анализа можно встретить множество задач на поиск точек пересечения графиков функций с помощью их построения или другими методами. Благодаря определенному алгоритму действий, найти ответ достаточно просто. В большинстве случаев решение заключается в определении корней различного вида уравнений.
График функции (y = f(x)) является множеством точек ((x; y)), координаты которых связаны соотношением (y = f(x).)
Равенство (y = f(x)) называют уравнением данного графика. Таким образом, график функции представляет собой множество точек (x; y), где x — является аргументом, а y — определяется как значение функции, соответствующее данному аргументу.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В том случае, когда графики пересекаются в какой-то точке, можно сделать вывод о существовании общего решения системы уравнений. Определить координаты точки можно с помощью графического или аналитического метода. В первом случае требуется построить график уравнения с переменной. Аналитический метод поиска координат точек, в которых графики функций пересекаются, подразумевает решение уравнения, а найденные корни и являются искомыми точками.
Как найти координаты, примеры решения
Существует несколько способов решения подобных задач:
- Поиск точек пересечения графиков функций заключается в приравнивании обеих функций друг к другу. При этом все члены с х переносят в левую сторону, а оставшиеся – в правую. Затем остается найти корни уравнения, которое получилось после преобразований.
- Второй метод состоит в записи системы уравнения для ее последующего решения с помощью подстановки одной функции в другую.
- Третий способ подразумевает построение графиков функций, чтобы определить точки их пересечения визуально.
В качестве примера можно рассмотреть две линейные функции:
(f(x) = k_1 x+m_1)
(g(x) = k_2 x + m_2)
Данные функции являются прямыми. Их можно графически изобразить, если принять какие-либо два значения (x_1) и (x_2) и найти (f(x_1)) и ((x_2)). Далее действия необходимо повторить с функцией (g(x)). Затем достаточно легко определить визуально координаты точки пересечения рассматриваемых функций.
Важно отметить, что для линейных функций характерна лишь одна точка пересечения только в том случае, когда (k_1 neq k_2). В противном случае (k_1=k_2), а функции будут параллельными друг другу, в связи с тем, что k является коэффициентом угла наклона. При( k_1 neq k_2) и (m_1=m_2) точка пересечения будет соответствовать (M(0;m)). Данная закономерность упрощает решение многих подобных задач.
Задача № 1
Имеются функции: (f(x) = 2x-5)
(g(x)=x+3)
Требуется определить координаты точки, в которой пересекаются графики рассматриваемых функций.
Решение
В первую очередь стоит отметить, что функции являются линейными. Важно обратить внимание на коэффициент угла наклона рассматриваемых функций:
(k_1 = 2)
(k_2 = 1)
Заметим, что:
(k_1 neq k_2)
По этой причине имеется лишь одна точка пересечения графиков функций. Определить ее можно путем решения уравнения:
(f(x)=g(x))
(2x-5 = x+3)
Необходимо перенести члены с x в левую часть, а остальные – в правую:
(2x – x = 3+5)
(x = 8)
В результате удалось найти x=8, что соответствует абсциссе точки пересечения графиков. Требуется определить ординату y с помощью подстановки x = 8 в любое из уравнений – в (f(x)), либо в (g(x)):
(f(8) = 2cdot 8 – 5 = 16 – 5 = 11)
Таким образом, M (8;11) – представляет собой точку, в которой пересекаются графики пары линейных функций.
Ответ: M (8;11)
Задача № 2
Записаны две функции: (f(x)=2x-1)
(g(x) = 2x-4.)
Необходимо определить точки, в которых графики рассматриваемых функций пересекаются.
Решение
Угловые коэффициенты:
(k_1 = k_2 = 2)
Таким образом, линейные функции параллельны между собой, что объясняет отсутствие точек пересечения их графиков.
Ответ: графики функций параллельны, точки пересечения отсутствуют.
Задача № 3
Требуется определить координаты точки, в которой пересекаются графики следующих функций: (f(x)=x^2-2x+1)
(g(x)=x^2+1)
Решение
В данном случае функции являются нелинейными. Поэтому алгоритм решения задачи будет несколько отличаться от предыдущих примеров. В первую очередь следует приравнять уравнения:
(x^2-2x+1=x^2+1)
Далее необходимо разнести в разные стороны уравнения члены с x и без него:
(x^2-2x-x^2=1-1)
(-2x=0)
(x=0)
Таким образом, будет определена абсцисса искомой точки. Затем необходимо найти ординату у. Для этого нужно подставить (x = 0) в какое-либо из двух начальных уравнений. К примеру:
(f(0)=0^2-2cdot 0 + 1 = 1)
M (0;1) является точкой, в которой пересекаются графики функций.
Ответ: M (0;1)
Приравнивание функций друг к другу и нахождение корней
Выяснить, имеют ли точки пересечения графики функций, можно путем сравнения соответствующих тождеств и решения уравнения. Однако при этом допускается получение различных равенств с неизвестными. Тогда целесообразно воспользоваться специальными методиками.
Когда уравнение относится к первой степени или является линейным, решение получить достаточно просто. Метод заключается в переносе переменных величин в одну часть уравнения, а известных – в другую. Алгоритм действий:
- раскрытие скобок, приведение подобных коэффициентов;
- перенос членов с неизвестными в одну сторону, а с известными – в другую;
- математические преобразования;
- определение корня.
Квадратные уравнения решают с помощью одного из способов:
- разложение на множители;
- выделение полного квадрата;
- поиск дискриминанта;
- теорема Виета.
В первом случае представляется возможным понизить степень при неизвестной величине. Второй метод заключается в выделении квадрата по одной из формул сокращенного умножения. Каждая из этих методик реализуема при наличии знаний соответствующих тождеств, в том числе правил разложения на множители.
Третий способ состоит в поиске корней через дискриминант (Д), который является дополнительным параметром, позволяющим сразу решить задачу. Дискриминант определяется с помощью формулы:
((-S)^2-4PU)
В том случае, когда Д>0, переменная может иметь пару значений, которые превращают равенство в справедливое тождество. Если Д=0, то корень является единственным. Когда Д<0, искомое тождество с неизвестными не имеет решений.
Квадратные уравнения решают таким образом:
- выполнение необходимых алгебраических преобразований, в том числе раскрытие скобок и приведение подобных слагаемых;
- выбор наиболее оптимального способа решения и его реализация;
- проверка корней с помощью их подстановки в начальное выражение.
Примечание
Распространенной ошибкой является пренебрежение проверкой результатов решения. Некорректные действия могут привести к образованию ложных корней.
Существует несколько методик решения тождеств кубического и биквадратного типов:
- понижение степени, то есть разложение на множители;
- замена переменной.
Первый вариант решения подразумевает выполнение преобразований для последующего применения одной из формул сокращенного умножения. Такой способ применяют нечасто. Второй способ состоит в том, что при решении необходимо ввести переменную с более низкой степенью, которая упрощает выражение. Порядок действий при этом следующий:
- выполнение математических преобразований;
- выражение переменной через другую;
- решение квадратного или линейного уравнения;
- подстановка промежуточных корней, которые получилось найти на третьем шаге, во второй;
- вычисление искомых корней;
- проверка;
- исключение ложных решений;
- запись ответа.
Путем составления системы уравнений
Данный метод определения точек пересечения графиков функций предполагает запись системы уравнения. К примеру:
Решение системы уравнений представляет собой пару чисел (х, у), являющуюся одновременно решением для первого и второго уравнения системы. Решить систему уравнений – значит, отыскать все ее решения, либо установить их отсутствие.
Порядок действий при решении системы уравнений можно рассмотреть на примере:
Решение будет иметь следующий вид:
Данные уравнения являются линейными, поэтому график каждого из них представляет собой прямую. График первого уравнения проходит через точки (0; 1) и (-1; 0). График второго уравнения проходит через точки (0; -1) и (-1; 0). Прямые пересекаются в точке (-1; 0), это и является решением системы уравнений.
Решение системы представляет сбой единственную пару чисел:
Если подставить данные числа в любое из уравнений, то получится справедливое равенство. Таким образом, имеется единственное решение линейной системы. Можно записать отчет: (-1;0).
В процессе решения линейной системы можно столкнуться с разными ситуациями:
- система обладает единственным решением, прямые пересекаются;
- решения системы отсутствуют. прямые параллельны;
- система обладает бесчисленным множеством решений, прямые совпадают.
При рассмотрении частного случая системы p(x; y) и q(x; y) являются линейными выражениями от x и y.
В задачах нередко требуется решить нелинейную систему уравнений. К примеру, необходимо решить следующую систему:
Решение имеет следующий вид:
График первого уравнения будет иметь вид прямой, а второго – являться окружностью. Можно построить первый график по точкам:
Центр окружности в точке О(0; 0), радиус равен 1.
Графики пересекаются в точке А(0; 1) и в точке В(-1; 0).
Ответ: (0; 1); (-1; 0).
Можно решить систему графическим способом:
В первую очередь необходимо построить график первого уравнения, который будет представлять собой окружность с центром в точке О (0; 0) и радиусом 2. График второго уравнения является параболой, которая смещена относительно начала координат на 2 вверх, то есть ее вершина – точка (0; 2).
Графики обладают одной общей точкой А(0; 2). Данная точка является решением системы. Если подставить два числа в уравнение, можно проверить корректность ответа и записать его. Ответ: (0; 2).
В качестве еще одного примера можно решить следующую систему:
Первым шагом является построение графика первого уравнения, который будет представлять собой окружность с центром в точке О (0; 0) и радиусом 1.
Далее необходимо построить график функции:
График будет являться ломанной:
Далее следует сместить ее на 1 вниз по оси oy. В результате получится график функции:
При помещении обоих графиков в одну систему координат получится следующая ситуация:
Таким образом, получились три точки пересечения: А(1; 0), т. В(-1; 0), т. С(0; -1)
Нахождение через графическое построений функций
Любой определенный график задают с помощью соответствующей функции. Найти точки, в которых пересекаются графики, можно путем решения уравнения, имеющего вид:
(f1(x)=f2(x))
Решение данного уравнения будет являться искомой точкой.
Построить график можно с помощью бумаги и ручки. В процессе необходимо обратить внимание на то, что количество точек пересечения пары графиков определяется видом функции. Линейные функции обладают лишь одной точкой пересечения, линейная и квадратная – двумя, квадратные – двумя, либо четырьмя.
В общем случае двух линейных функций можно предположить, что:
(y1=k1x+b1)
(y2=k2x+b2)
Для поиска точки пересечения графиков необходимо решить уравнение:
(y1=y2 или k1x+b1=k2x+b2)
После преобразований получится, что:
(k1x-k2x=b2-b1.)
Далее нужно выразить x:
(x=(b2-b1)/(k1-k2).)
При известной координате точки по оси абсцисс следует определить координату по оси ординат. Таким образом, можно найти координаты точки пересечения графиков:
(((b2-b1)/(k1-k2); k1(b2-b1)/(k1-k2)+b2))
График функции y = f (х) представляет собой множество точек плоскости, координаты (х, у) которых соответствуют выражению y = f(x). График функции наглядно иллюстрирует поведение и свойства функции. Для построения графика определяют несколько значений довода х и для них рассчитывают соответствующие значения функции y=f(x). Для больше точного и наглядного построения графика следует обнаружить его точки пересечения с осями координат.
С целью определить точку пересечения графика функции с осью y, нужно определить значение функции при х=0, то есть обнаружить f(0). В качестве примера можно рассмотреть график линейной функции, изображенной на рисунке:
В данном случае при х=0 ((y=a*0+b)) функция равна b. Таким образом, график пересекает ось ординат (ось Y) в точке (0,b). Когда пересекается ось абсцисс (ось Х) функция равна 0, то есть (y=f(x)=0). Для того чтобы определить х, следует решить уравнение (f(x)=0). В случае линейной функции получаем уравнение (ax+b=0), откуда и находим (x=-b/a). В результате можно сделать вывод, что ось Х пересекается в точке ((-b/a,0).)
При наличии квадратичной зависимости y от х, уравнение (f(x)=0) обладает двумя корнями. Таким образом, ось абсцисс пересекается два раза. В случае периодической зависимости y от х, например, (y=sin(x)), график функции обладает бесконечным количеством точек пересечения с осью Х. Проверить корректность расчета координат точек, в которых пересекаются графики функций, можно с помощью подстановки найденных значений х в выражение f(x). Значение выражения при любом из вычисленных х должно быть равно 0.
Принадлежит ли графику функции точка
Как определить, принадлежит ли графику функции точка? Это можно сделать, не выполняя построения графика.
График функции проходит через точку, если координаты этой точки обращают формулу функции в верное числовое равенство.
Таким образом, чтобы выяснить, принадлежит ли графику функции точка, надо подставить координаты точки в формулу функции. Если получится верное числовое равенство, точка лежит на графике.
1) Принадлежат ли графику функции y=10x-3 точки A(-2; 17) и B(1; 7)?
График функции проходит через точки A и B, если их координаты обращают формулу y=10x-3 в верное числовое равенство.
Подставляем в формулу функции вместо y ординату точки A (y=17), а вместо x — абсциссу (x=-2). Имеем:
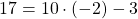
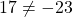
Значит, точка A графику функции y=10x-3 не принадлежит.
Ординату 7 точки B подставляем в формулу функции y=10x-3 вместо y, абсциссу 1 — вместо x. Имеем:
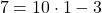
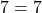
Следовательно, точка B принадлежит графику функции y=10x-3.
Ответ: точка B принадлежит графику функции, точка A — не принадлежит.
2) Какие из точек A(2;15), B(-1;-15), C(-10; 243) принадлежат графику функции y=3x²+5x-7?
В формулу функции y=3x²+5x-7 вместо y подставляем ординату точки, вместо каждого x — абсциссу.
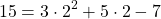
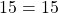
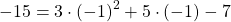
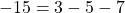
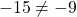
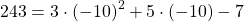
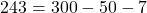
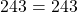
Верные равенства получили для точек A и C. Значит, эти точки принадлежат графику функции y=3x²+5x-7, а точка B — не принадлежит.
Ответ: точки A и C принадлежат графику функции.
Построение графиков функций

О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — наглядно.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида  область определения выглядит так
область определения выглядит так
- х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).

Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:

Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
- стационарные и критические точки;
- точки экстремума;
- нули функции;
- точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке: 
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.

Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
- Найти область определения функции.
- Найти область допустимых значений функции.
- Проверить не является ли функция четной или нечетной.
- Проверить не является ли функция периодической.
- Найти нули функции.
- Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
- Найти асимптоты графика функции.
- Найти производную функции.
- Найти критические точки в промежутках возрастания и убывания функции.
- На основании проведенного исследования построить график функции.
У нас есть отличные курсы по математике для учеников с 1 по 11 классы!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции 
Упростим формулу функции:
 при х ≠ -1.
при х ≠ -1.
График функции — прямая y = x — 1 с выколотой точкой M (-1; -2).
Задача 2. Построим график функции
Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции 

Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины  , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
, т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
Ветви вниз, следовательно, a 0.
Координата вершины  , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b
, т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b

Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.

k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.

k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.

k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 5. Построить график функции 
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:

Задача 6. Построить графики функций:
б) 
г) 
д) 
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а) 
Преобразование в одно действие типа f(x) + a.

Сдвигаем график вверх на 1:

б)
Преобразование в одно действие типа f(x — a).

Сдвигаем график вправо на 1:

В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.

Сдвигаем график вправо на 1:

Сдвигаем график вверх на 2:

г) 
Преобразование в одно действие типа 

Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:


д) 
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.



Сжимаем график в два раза вдоль оси абсцисс:


Сдвигаем график влево на 1/2 вдоль оси абсцисс:


Отражаем график симметрично относительно оси абсцисс:
Как определить a, b и c по графику параболы
Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.
1 способ – ищем коэффициенты на графике
Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.
Коэффициент (a) можно найти с помощью следующих фактов:
— Если (a>0), то ветви параболы направленных вверх, если (a 1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.

Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:

Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.
Решаем систему.
Пример:
Вычтем из второго уравнения первое:
Подставим (9a) вместо (b):
Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:
Подставим в первое уравнение (a):
Получается квадратичная функция: (y=-x^2-9x-15).

Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).

Таким образом имеем систему:
Сложим 2 уравнения:
Подставим во второе уравнение:
Теперь найдем точки пересечения двух функций:
Теперь можно найти ординату второй точки пересечения:
3 способ – используем преобразование графиков функций
Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.
Главный недостаток этого способа — вершина должна иметь целые координаты.
Сам способ базируется на следующих идеях:
График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).

– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.

– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
— График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц.

График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.

У вас наверно остался вопрос — как этим пользоваться? Предположим, мы видим такую параболу:

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).

То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:

Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:
Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).

Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).
Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).
источники:
http://skysmart.ru/articles/mathematic/postroenie-grafikov-funkcij
http://cos-cos.ru/ege/zadacha203/378/
Решение уравнений с помощью графиков
Решение линейных уравнений
Как ты уже знаешь, графиком линейного уравнения является прямая линия, отсюда и название данного вида.
Линейные уравнения достаточно легко решать алгебраическим путем – все неизвестные переносим в одну сторону уравнения, все, что нам известно – в другую и вуаля! Мы нашли корень.
Сейчас же я покажу тебе, как это сделать графическим способом.
Итак, у тебя есть уравнение: ( displaystyle 2{x} -10=2)
Как его решить?
Вариант 1, и самый распространенный – перенести неизвестные в одну сторону, а известные в другую, получаем:
( displaystyle 2x=2+10)
( displaystyle 2x=12)
Обычно дальше мы делим правую часть на левую, и получаем искомый корень, но мы с тобой попробуем построить левую и правую части как две различные функции в одной системе координат.
Иными словами, у нас будет:
( displaystyle {{y}_{1}}=2x)
( displaystyle {{y}_{2}}=12)
А теперь строим. Что у тебя получилось?
Как ты думаешь, что является корнем нашего уравнения? Правильно, координата ( displaystyle x) точки пересечения графиков:
Наш ответ: ( displaystyle x=6)
Вот и вся премудрость графического решения. Как ты с легкостью можешь проверить, корнем нашего уравнения является число ( displaystyle 6)!
Вариант 1. Напрямую
Просто строим параболу по данному уравнению: ( displaystyle {{x}^{2}}+2{x} -8=0)
Чтобы сделать это быстро, дам тебе одну маленькую подсказку: удобно начать построение с определения вершины параболы. Определить координаты вершины параболы помогут следующие формулы:
( displaystyle x=-frac{b}{2a})
( displaystyle y=-frac{{{b}^{2}}-4ac}{4a})
Ты скажешь «Стоп! Формула для ( displaystyle y) очень похожа на формулу нахождения дискриминанта» да, так оно и есть, и это является огромным минусом «прямого» построения параболы, чтобы найти ее корни.
Тем не менее, давай досчитаем до конца, а потом я покажу, как это сделать намного (намного!) проще!
Посчитал? Какие координаты вершины параболы у тебя получились? Давай разбираться вместе:
( displaystyle x=frac{-2}{2}=-1)
( displaystyle y=-frac{{{2}^{2}}-4cdot left( -8 right)}{4}=-frac{4+32}{4}=-9)
Точно такой же ответ? Молодец!
И вот мы знаем уже координаты вершины, а для построения параболы нам нужно еще … точек. Как ты думаешь, сколько минимум точек нам необходимо? Правильно, ( displaystyle 3).
Ты знаешь, что парабола симметрична относительно своей вершины, например:
Соответственно, нам необходимо еще две точки по левой или правой ветви параболы, а в дальнейшем мы эти точки симметрично отразим на противоположную сторону:
Возвращаемся к нашей параболе.
Для нашего случая точка ( displaystyle Aleft( -1;-9 right)). Нам необходимо еще две точки, соответственно, ( displaystyle x) можно взять положительные, а можно взять отрицательные? Какие точки тебе удобней?
Мне удобней работать с положительными, поэтому я рассчитаю при ( displaystyle x=0) и ( displaystyle x=2).
При ( displaystyle x=0):
( displaystyle y={{0}^{2}}+0-8=-8)
При ( displaystyle x=2):
( displaystyle y={{2}^{2}}+2cdot 2-8=0)
Теперь у нас есть три точки, и мы спокойно можем построить нашу параболу, отразив две последние точки относительно ее вершины:
Как ты думаешь, что является решением уравнения?
Правильно, точки, в которых ( displaystyle y=0), то есть ( displaystyle x=2) и ( displaystyle x=-4). Потому что ( displaystyle {{x}^{2}}+2{x} -8=0).
И если мы говорим, что ( displaystyle y={{x}^{2}}+2{x} -8), то значит, что ( displaystyle y) тоже должен быть равен ( displaystyle 0), или ( displaystyle y={{x}^{2}}+2{x} -8=0).
Просто? Это мы закончили с тобой решение уравнения сложным графическим способом, то ли еще будет!
Конечно, ты можешь проверить наш ответ алгебраическим путем – посчитаешь корни через теорему Виета или Дискриминант.
Что у тебя получилось? То же самое?
Вот видишь! Теперь посмотрим совсем простое графическое решение, уверена, оно тебе очень понравится!
Решение смешанных неравенств
Теперь перейдем к более сложным неравенствам!
Как тебе такое:
( displaystyle 4x<{{x}^{3}})?
Жуть, правда? Честно говоря, я понятия не имею, как решить такое алгебраически… Но, оно и не надо. Графически ничего сложного в этом нет! Глаза боятся, а руки делают!
Первое, с чего мы начнем, – это с построения двух графиков:
( displaystyle {{y}_{1}}=4x)
( displaystyle {{y}_{2}}={{x}^{3}})
Я не буду расписывать для каждого таблицу – уверена, ты отлично справишься с этим самостоятельно (еще бы, столько прорешать примеров!).
Расписал? Теперь строй два графика.
Сравним наши рисунки?
У тебя так же? Отлично!
Теперь расставим точки пересечения и цветом определим, какой график у нас по идее должен быть больше, то есть ( displaystyle {{y}_{2}}={{x}^{3}}).
Смотри, что получилось в итоге:
А теперь просто смотрим, в каком месте у нас выделенный график находится выше, чем график ( displaystyle {{y}_{1}}=4x)? Смело бери карандаш и закрашивай данную область! Она и будет решением нашего сложного неравенства!
На каких промежутках по оси ( displaystyle Ox) у нас ( displaystyle {{y}_{2}}={{x}^{3}}) находится выше, чем ( displaystyle {{y}_{1}}=4x)? Верно, ( displaystyle xin left( -2;0 right)cup left( 2;+infty right)).
Это и есть ответ!
Ну вот, теперь тебе по плечу и любое уравнение, и любая система, и уж тем более любое неравенство!
Подведём итоги наших знаний о графиках функций.
Нами были изучены методы построения таких функций, как:
(y =b) (график — прямая, параллельная оси (x));
(y = kx) (график — прямая, которая проходит через начало координат);
(y = kx + m) (график — прямая);
(график — парабола).
При необходимости мы сможем преобразовать аналитическую модель на графическую. Допустим, аналитическую модель
y=x2
трансформировать в графическую модель в виде параболы, расположенной в прямоугольной системе координат.
Этот приём полезен при решении уравнений. Продемонстрируем это на примерах.
Пример:
решить уравнение
x2=2x+8
.
Рассмотрим две функции:
y=x2
, (y = 2x + 8) — выполним построение графиков этих функций в одной системе координат, чтобы найти их точки пересечения.

Парабола
y=x2
и прямая (y = 2x + 8) пересекаются в точках (A (- 2; 4)) и (B (4; 16)).
Корни уравнения
x2=2x+8
— значения (x), при которых выражения
x2
и (2x + 16) принимают одинаковые значения. Это первые координаты точек (A) и (B) пересечения графиков:
x1=−2;x2=4
.
Алгоритм графического решения уравнений
1. Преобразовать уравнение так, чтобы в левой и правой части стояли известные функции.



2. В одной системе координат начертить графики этих функций.
3. Определить точки пересечения полученных графиков.
4. Взять из них значения абсцисс.



Уравнением линии на плоскости называют уравнение с двумя переменными 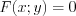 или
или  , которому удовлетворяют координаты
, которому удовлетворяют координаты  (абсцисса) и
(абсцисса) и  (ордината) любой точки данной линии.
(ордината) любой точки данной линии.
Уравнение окружности
Рассмотрим расположение окружности на координатной плоскости:
1) если уравнение окружности имеет вид 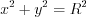 , то ее центр находится в точке
, то ее центр находится в точке  , а радиус равен
, а радиус равен  (рис. 2.51);
(рис. 2.51);
2) если уравнение окружности имеет вид  , то ее центр находится в точке
, то ее центр находится в точке  , а радиус равен
, а радиус равен  (рис. 2.52).
(рис. 2.52).

Заметим, что неравенству  удовлетворяют координаты всех точек плоскости, лежащих внутри окружности
удовлетворяют координаты всех точек плоскости, лежащих внутри окружности  , а неравенству
, а неравенству  удовлетворяют координаты всех точек, лежащих вне этой окружности. Неравенству
удовлетворяют координаты всех точек, лежащих вне этой окружности. Неравенству  удовлетворяют координаты всех точек плоскости, лежащих внутри окружности
удовлетворяют координаты всех точек плоскости, лежащих внутри окружности  и на ее границе.
и на ее границе.
Уравнение квадрата
Рассмотрим расположение квадрата на координатной плоскости:
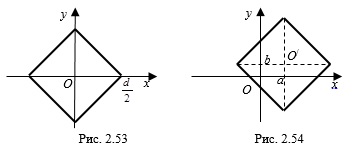
1) если уравнение квадрата имеет вид  , то точка
, то точка  – точка пересечения диагоналей квадрата,
– точка пересечения диагоналей квадрата,  – длина диагонали квадрата (рис. 2.53);
– длина диагонали квадрата (рис. 2.53);
2) если уравнение квадрата имеет вид  , то точка
, то точка  – точка пересечения диагоналей квадрата,
– точка пересечения диагоналей квадрата,  – длина диагонали квадрата (рис. 2.54).
– длина диагонали квадрата (рис. 2.54).
Пересечение линий на плоскости
Рассмотрим две линии, заданные уравнениями  и
и  . Чтобы найти точку пересечения этих линий необходимо решить систему уравнений
. Чтобы найти точку пересечения этих линий необходимо решить систему уравнений 
Графическое решение уравнений и неравенств
1. Рассмотрим уравнение  . Это уравнение можно решить графически, если построить в одной системе координат графики функций
. Это уравнение можно решить графически, если построить в одной системе координат графики функций  ,
,  и найти их точки пересечения. Абсциссы точек пересечения и будут корнями уравнения
и найти их точки пересечения. Абсциссы точек пересечения и будут корнями уравнения  .
.
2. Использование монотонности функций при решении уравнений: если функция  строго возрастает, а функция
строго возрастает, а функция  строго убывает на некотором множестве, то графики этих функций имеют не более одной точки пересечения, а уравнение
строго убывает на некотором множестве, то графики этих функций имеют не более одной точки пересечения, а уравнение  на этом множестве имеет не более одного решения. Поэтому, чтобы решить такие уравнения можно подобрать (если это удается) число, которое является их корнем. На рисунке 2.55 число
на этом множестве имеет не более одного решения. Поэтому, чтобы решить такие уравнения можно подобрать (если это удается) число, которое является их корнем. На рисунке 2.55 число  – корень уравнения
– корень уравнения  . Аналогично решаются уравнения, если функция
. Аналогично решаются уравнения, если функция  имеет вид
имеет вид 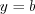 (эта прямая параллельна оси абсцисс) (рис. 2.56).
(эта прямая параллельна оси абсцисс) (рис. 2.56).
Например, число  является единственным корнем уравнения
является единственным корнем уравнения  , так как левая часть этого уравнения представлена строго убывающей функцией, а правая – строго возрастающей.
, так как левая часть этого уравнения представлена строго убывающей функцией, а правая – строго возрастающей.
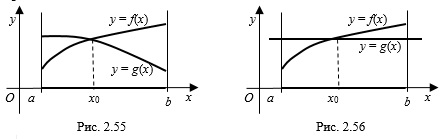
3. Использование монотонности функций при решении неравенств: если функция  строго возрастает на некотором отрезке
строго возрастает на некотором отрезке ![[a;b] LaTeX formula: [a;b]](https://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png) , а функция
, а функция  строго убывает на этом отрезке и
строго убывает на этом отрезке и  – корень уравнения
– корень уравнения  , то решением неравенства
, то решением неравенства 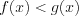 является промежуток
является промежуток  , а решением неравенства
, а решением неравенства 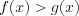 является промежуток
является промежуток ![(x_{0};b] LaTeX formula: (x_{0};b]](https://helpy.quali.me/uploads/formulas/402673c7d0139142c651324cae3880d5bb511595.1.1.png) (рис. 2.57).
(рис. 2.57).
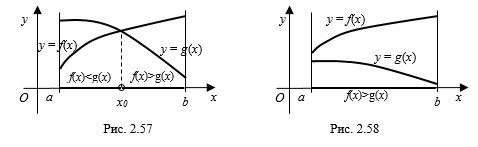
Графики функций на заданном отрезке могут и не пересекаться. Например, на рисунке 2.58 неравенство 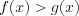 выполняется на всем отрезке
выполняется на всем отрезке ![[a;b] LaTeX formula: [a;b]](https://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png) .
.
Пример 1. Найдите площадь фигуры, ограниченной прямыми  ,
,  и
и  .
.
Решение. Построим на координатной плоскости данные прямые (рис. 2.59).

Прямая  (1) параллельна оси ординат и проходит через точку
(1) параллельна оси ординат и проходит через точку  . Чтобы построить прямую
. Чтобы построить прямую  (2), необходимо знать две точки, принадлежащие этой прямой. Например, можно построить точки
(2), необходимо знать две точки, принадлежащие этой прямой. Например, можно построить точки  ,
,  и провести через них прямую (2). Чтобы построить прямую
и провести через них прямую (2). Чтобы построить прямую  (3), можно построить точки
(3), можно построить точки  и
и  , принадлежащие этой прямой, и провести через них прямую (3).
, принадлежащие этой прямой, и провести через них прямую (3).
Из рисунка 2.59 видим, что треугольник  ограничен данными прямыми. Площадь полученного треугольника найдем по формуле
ограничен данными прямыми. Площадь полученного треугольника найдем по формуле 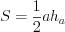 , а в нашем случае
, а в нашем случае  .
.
Найдем координаты точек пересечения прямых.
1. Найдем координаты точки  , решая систему уравнений
, решая систему уравнений  Получим точку
Получим точку  .
.
2. Найдем координаты точки  , решая систему уравнений
, решая систему уравнений  Получим точку
Получим точку  .
.
3. Найдем координаты точки 

 , решая систему уравнений
, решая систему уравнений  Получим точку
Получим точку  .
.
Найдем длину отрезка  , вычитая из ординаты точки
, вычитая из ординаты точки  ординату точки
ординату точки  . Получим
. Получим  . Найдем длину отрезка
. Найдем длину отрезка  , вычитая из абсциссы точки
, вычитая из абсциссы точки  абсциссу точки
абсциссу точки  :
:  . Найдем площадь треугольника
. Найдем площадь треугольника  :
:  .
.
Ответ:  .
.
Пример 2. Найдите площадь фигуры, заданной на координатной плоскости системой неравенств 
Решение. Построим гранич-ные прямые, соответствующие неравенствам заданной системы:  (1),
(1),  (2),
(2),  (3),
(3),  (4) (рис. 2.60). Система неравенств задает на координатной плоскости трапецию
(4) (рис. 2.60). Система неравенств задает на координатной плоскости трапецию  , площадь которой найдем по формуле
, площадь которой найдем по формуле  .
.
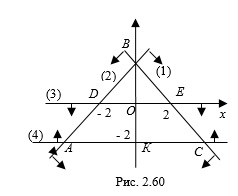
Согласно рисунку 2.60 запишем:  ,
,  .
.
Найдем координаты точки  , решая систему уравнений
, решая систему уравнений  Получим
Получим  . Аналогично найдем координаты точки
. Аналогично найдем координаты точки  . Получим
. Получим  . Тогда
. Тогда  .
.
Найдем площадь трапеции:  .
.
Ответ:  .
.
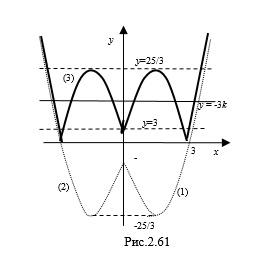
Пример 3. Найдите все целые значений параметра  , при которых уравнение
, при которых уравнение  имеет шесть корней.
имеет шесть корней.
Решение. Заменим данное уравнение равносильной системой уравнений 
Построим схематически график функции  , предварительно построив графики функций
, предварительно построив графики функций  и
и  .
.
1. Графиком функции  является парабола, ветви которой направлены вверх. Найдем координаты вершины параболы.
является парабола, ветви которой направлены вверх. Найдем координаты вершины параболы.
Согласно формулам  ,
,  получим:
получим:  ,
,  . Найдем нули функции (точки пересечения графика с осью абсцисс), решая уравнение
. Найдем нули функции (точки пересечения графика с осью абсцисс), решая уравнение  . Получим
. Получим  ,
,  . Найдем точку пересечения графика с осью ординат:
. Найдем точку пересечения графика с осью ординат:  . Построим график (1) (рис. 2.61).
. Построим график (1) (рис. 2.61).
2. Рассмотрим функцию  . Поскольку
. Поскольку  , то запишем
, то запишем  . Построим график (2) этой функции, выполняя следующее преобразование: часть графика функции
. Построим график (2) этой функции, выполняя следующее преобразование: часть графика функции  правее оси
правее оси  оставим и ее же отразим симметрично этой оси (рис. 2.61).
оставим и ее же отразим симметрично этой оси (рис. 2.61).
3. Построим график (3) функции  , выполняя следующее преобразование: часть графика функции
, выполняя следующее преобразование: часть графика функции  , расположенной над осью
, расположенной над осью  оставим, а ту, что под осью
оставим, а ту, что под осью  , отразим симметрично этой оси (рис. 2.61).
, отразим симметрично этой оси (рис. 2.61).
Рассмотрим линейную функцию  . Построим семейство прямых, параллельных оси
. Построим семейство прямых, параллельных оси  так, чтобы они пересекали график функции
так, чтобы они пересекали график функции  в шести точках. Это возможно при условии, что
в шести точках. Это возможно при условии, что  или
или  . Очевидно, что промежутку
. Очевидно, что промежутку  принадлежит одно целое значение
принадлежит одно целое значение  .
.
Ответ: 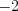 .
.
Пример 4. Найдите все значения параметра  , при которых уравнение
, при которых уравнение  имеет один корень.
имеет один корень.
Решение. Решим уравнение графически, заменив его равносильной системой уравнений 
1. Построим схематически график функции  (рис. 2.62). Для этого найдем нули функции под знаком модуля:
(рис. 2.62). Для этого найдем нули функции под знаком модуля:  ,
,  и раскроем модуль на полученных промежутках, учитывая при этом, что
и раскроем модуль на полученных промежутках, учитывая при этом, что  – точка разрыва функции.
– точка разрыва функции.
Рассмотрим два случая:
1) если  , то
, то  или
или  ;
;
2) если  , то
, то  или
или  .
.
2. Построим схематически график функции  , предварительно построив параболу
, предварительно построив параболу  .
.
Парабола  и прямая
и прямая  имеют две общие точки. Так как согласно условию задачи графики функций
имеют две общие точки. Так как согласно условию задачи графики функций  и
и  должны иметь только одну точку пересечения, то, выполняя параллельный перенос параболы
должны иметь только одну точку пересечения, то, выполняя параллельный перенос параболы  на
на  единичных отрезка влево, заметим, что при
единичных отрезка влево, заметим, что при  парабола
парабола  и прямая
и прямая  имеют одну точку пересечения, а при
имеют одну точку пересечения, а при  уже не имеют общих точек. Следовательно, если
уже не имеют общих точек. Следовательно, если  принимает значения из промежутка
принимает значения из промежутка  , то графики функций
, то графики функций  и
и  имеют одну общую точку, а уравнение
имеют одну общую точку, а уравнение  имеет одно решение.
имеет одно решение.
Ответ:  .
.
Построим прямую  так, чтобы она имела с графиком функции
так, чтобы она имела с графиком функции  бесконечно много общих точек. Очевидно, что это возможно в том случае, если
бесконечно много общих точек. Очевидно, что это возможно в том случае, если  , откуда
, откуда ![a=-2sqrt[3]{2} LaTeX formula: a=-2sqrt[3]{2}](https://helpy.quali.me/uploads/formulas/1da946b3ee73655d5d103a1df7688b9505e43c78.1.1.png) .
.
Ответ: ![a=-2sqrt[3]{2} LaTeX formula: a=-2sqrt[3]{2}](https://helpy.quali.me/uploads/formulas/1da946b3ee73655d5d103a1df7688b9505e43c78.1.1.png) .
.
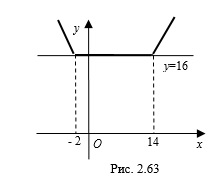
Пример 6. Найдите все значения параметра  , при которых система уравнений
, при которых система уравнений 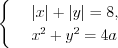 имеет четыре решения.
имеет четыре решения.
Решение. Имеем уравнение квадрата  и уравнение окружности
и уравнение окружности  .
.
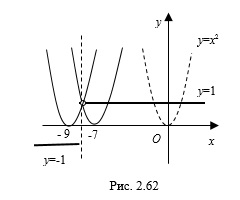
1. Построим квадрат с центром в точке  и диагональю
и диагональю  (рис. 2.64).
(рис. 2.64).

Площадь квадрата найдем по формуле  . Получим:
. Получим: 
 . С другой стороны площадь квадрата можно вычислить по формуле
. С другой стороны площадь квадрата можно вычислить по формуле  , где
, где  – сторона квадрата. Тогда
– сторона квадрата. Тогда  и
и  .
.
2. Построим окружность с центром в точке  и радиусом
и радиусом  (рис. 2.64). Поскольку система уравнений
(рис. 2.64). Поскольку система уравнений 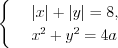 имеет четыре решения, то окружность должна быть вписана в квадрат, тогда ее радиус
имеет четыре решения, то окружность должна быть вписана в квадрат, тогда ее радиус  или
или  , откуда
, откуда  или описана около квадрата, тогда радиус окружности
или описана около квадрата, тогда радиус окружности  или
или  , откуда
, откуда  .
.
Ответ:  ;
;  .
.
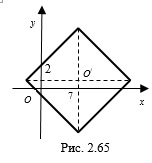
Пример 7. Найдите площадь и периметр фигуры, заданной неравенством  .
.
Решение. Данному неравенству удовлетворяют координаты всех точек плоскости, расположенных внутри квадрата  и на его границе.
и на его границе.
Построим квадрат с центром в точке  и диагональю
и диагональю  (рис. 2.65). Найдем площадь квадрата. Согласно формуле
(рис. 2.65). Найдем площадь квадрата. Согласно формуле  получим
получим  .
.
С другой стороны площадь квадрата находят по формуле  , где
, где  – сторона квадрата.
– сторона квадрата.
Тогда  ,
,  . Найдем периметр квадрата:
. Найдем периметр квадрата:  .
.
Ответ:  ,
,  .
.
Решая уравнение или систему уравнений графически, точное решение найти бывает достаточно сложно, а то и вовсе не возможно. Поэтому этот метод чаще всего применяют в случае, когда необходимо определить количество корней уравнения или найти их приближенное значение.



