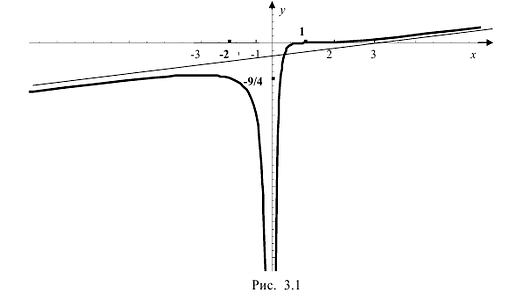
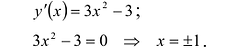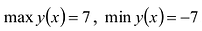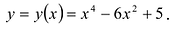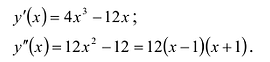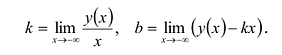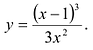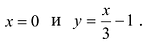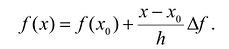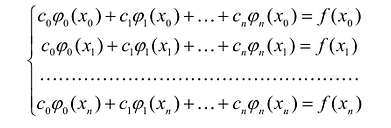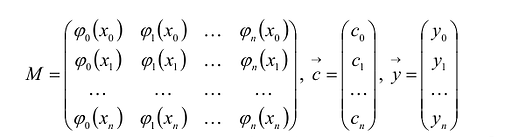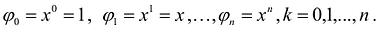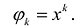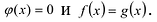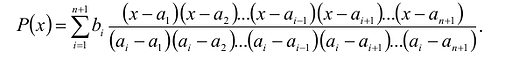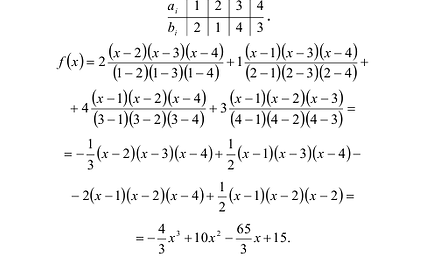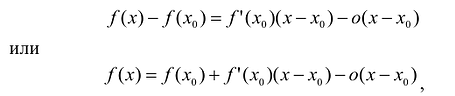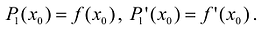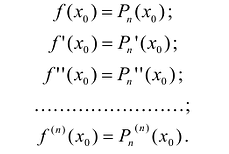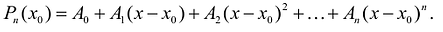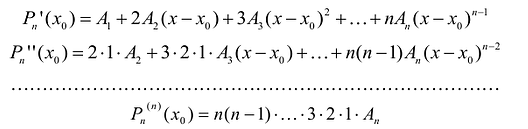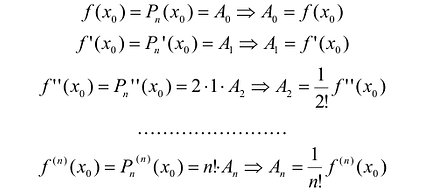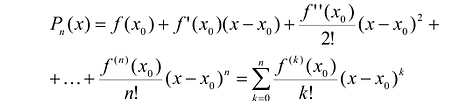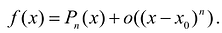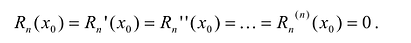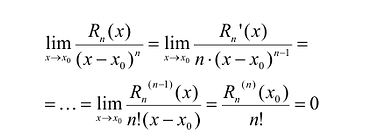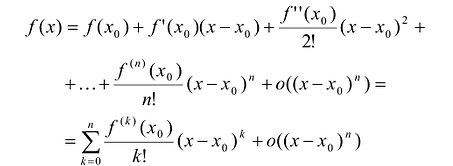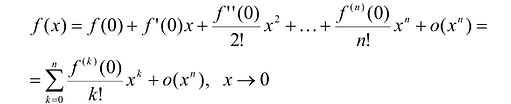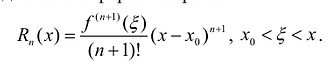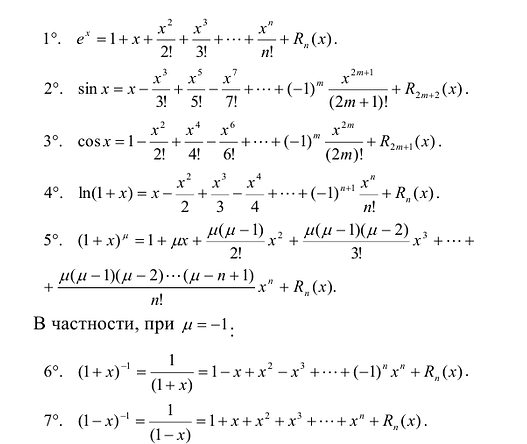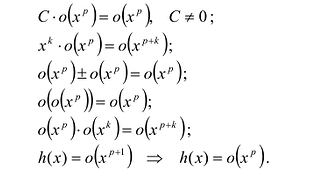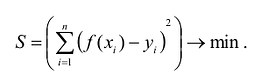Пример 1
Дана функция:
Нужно построить ее график на промежутке [-5;5] с шагом равным 1.
Создание таблицы
Создадим таблицу, первый столбец назовем переменная x (ячейка А1), второй — переменная y (ячейка В1). Для удобства в ячейку В1 запишем саму функцию, чтобы было понятно, какой график будем строить. Введем значения -5, -4 в ячейки А2 и А3 соответственно, выделим обе ячейки и скопируем вниз. Получим последовательность от -5 до 5 с шагом 1.
Вычисление значений функции
Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).
Важно: для возведения в степень используется знак ^, который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).
Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.
Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.
Построение графика
Выделим диапазон значений переменной x и функции y. Перейдем на вкладку Вставка и в группе Диаграммы выберем Точечная (можно выбрать любую из точечных диаграмм, но лучше использовать вид с гладкими кривыми).
Мы получили график данной функции. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графика.
Пример 2
Даны функции:
и y=50x+2. Нужно построить графики этих функций в одной системе координат.
Создание таблицы и вычисление значений функций
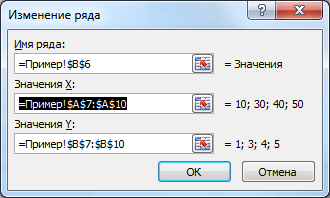
Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.
Мы получили таблицу значений переменной х и обеих функций в этих точках.
Построение графиков
Для построения графиков выделяем значения трёх столбцов, на вкладке Вставка в группе Диаграммы выбираем Точечная.
Мы получили графики функций в одной системе координат. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графиков.
Последний пример удобно использовать, если нужно найти точки пересечения функций с помощью графиков. При этом можно изменить значения переменной x, выбрать другой промежуток или взять другой шаг (меньше или больше, чем 1). При этом столбцы В и С менять не нужно, диаграмму тоже. Все изменения произойдут сразу же после ввода других значений переменной x. Такая таблица является динамической.
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Точки пересечения графиков в Excel
Как найти точки пересечения графиков в Excel? Например, есть графики, отображающие несколько показателей. Далеко не всегда они будут пересекаться непосредственно на поле диаграммы. Но пользователю нужно показать те значения, в которых линии рассматриваемых явлений пересекаются. Рассмотрим на примере.
Строим графики с точками пересечений
Имеются две функции, по которым нужно построить графики:
Выделяем диапазоны данных, на вкладке «Вставка» в группе «Диаграммы» подбираем нужный тип графика. Как:
- Нужно найти точки пересечения графиков со значением Х, поэтому столбчатые, круговые, пузырьковые и т.п. диаграммы не выбираем. Это должны быть прямые линии.
- Для поиска точек пересечения необходима ось Х. Не условная, на которой невозможно задать другое значение. Должна быть возможность выбирать промежуточные линии между периодами. Обычные графики не подходят. У них горизонтальная ось – общая для всех рядов. Периоды фиксированы. И манипулировать можно только с ними. Выберем точечную диаграмму с прямыми отрезками и маркерами.
Для данного типа диаграммы между основными периодами 0, 2, 4, 6 и т.д. можно использовать и промежуточные. Например, 2,5.
Находим точку пересечения графиков в Excel
В табличном редакторе Excel нет встроенной функции для решения подобной задачи. Линии построенных графиков не пересекаются (см. рисунок), поэтому даже визуально точку пересечения найти нельзя. Ищем выход.
Первый способ. Найти общие значения в рядах данных для указанных функций.
В таблице с данными таковых значений пока нет. Так как мы решали уравнения с помощью формул в полуавтоматическом режиме, с помощью маркера автозаполнения продолжим ряды данных.
Значения Y одинаковые при Х = 4. Следовательно, точка пересечения двух графиков имеет координаты 4, 5.
Изменим график, добавив новые данные. Получим две пересекающиеся линии.
Второй способ. Применение для решения уравнений специального инструмента «Поиск решения». Кнопка вызова инструмента должна быть на вкладке «Данные». Если нет, нужно добавить из «Надстроек Excel».
Преобразуем уравнения таким образом, чтобы неизвестные были в одной части: y – 1,5 х = -1; y – х = 1. Далее для неизвестных х и y назначим ячейки в Excel. Перепишем уравнения, используя ссылки на эти ячейки.
Вызываем меню «Поиск решения» — заполняем условия, необходимые для решения уравнений.
Нажимаем «Выполнить» — инструмент предлагает решение уравнений.
Найденные значения для х и y совпадают с предыдущим решением с помощью составления рядов данных.
Точки пересечения для трех показателей
Существует три показателя, которые измерялись во времени.
По условию задачи показатель В имеет постоянную величину на протяжении всех периодов. Это некий норматив. Показатель А зависит от показателя С. Он то выше, то ниже норматива. Строим графики (точечную диаграмму с прямыми отрезками и маркерами).
Точки пересечения имеются только у показателей А и В. Но их точные координаты нужно еще определить. Усложним задачу – найдем точки пересечения показателя C с показателями А и В. То есть в какие временные периоды и при каких значениях показателя А линия показателя С пересекает линию норматива.
Точек у нас будет две. Их рассчитаем математическим путем. Сначала найдем точки пересечения показателя А с показателем В:
На рисунке видно, какие значения использовались для расчета. По такой же логике находим значение х для второй точки.
Теперь рассчитаем точки, найденных значений по оси Х с показателем С. Используем близкие формулы:
На основе новых данных построим точечные диаграммы на том же поле (где наши графики).
Получается такой рисунок:
Для большей информативности и эстетики восприятия добавим пунктирные линии. Их координаты:
Добавим подписи данных – значения показателя C, при которых он пересечет линию норматива.
Можно форматировать графики по своему усмотрению – делать их более выразительными и наглядными.
Особенности построения при неравномерном шаге по Х
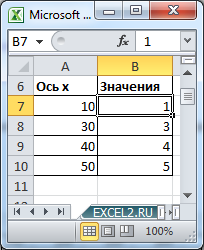
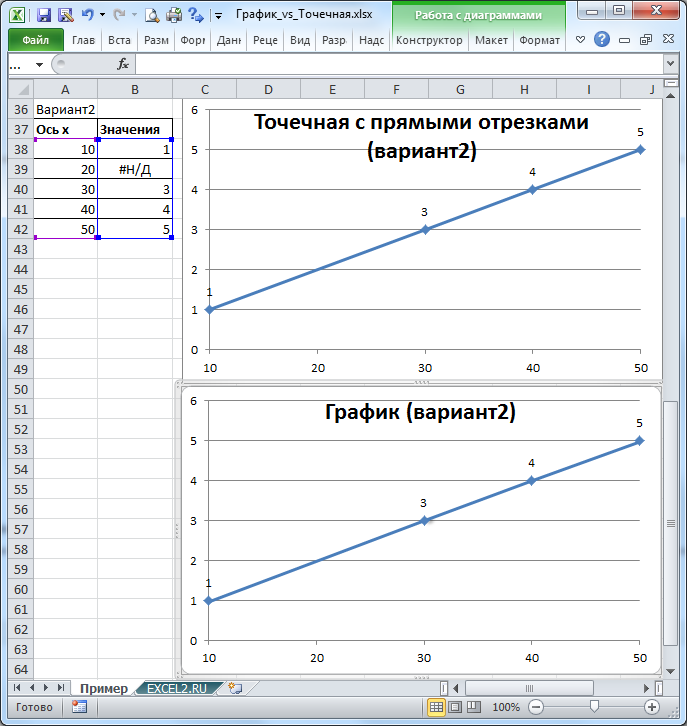
Пусть дана таблица с исходными данными (значения в исходной таблице расположены по оси Х равномерно с шагом 10, но точка с х=20 отсутствует).
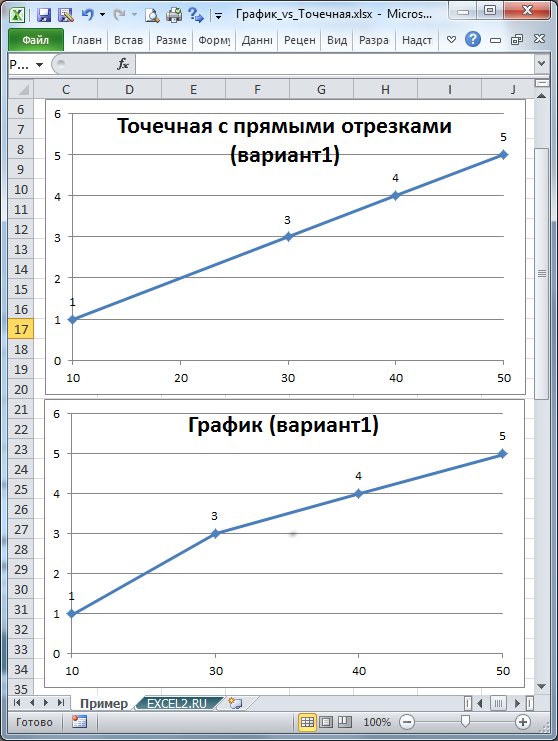
Построим График и Точечную диаграмму с прямыми отрезками используя одну и туже таблицу.
Точечная диаграмма использует все данные из исходной таблицы: как значения х, так и y.
Диаграмма График откладывает значения по оси х равномерно (значения из столбца Ось х не используются для построения).
Значения из столбца Ось х используются в Диаграмме График только для подписей данных по оси х (значения из столбца Ось х никак не влияют на расположение точек). Это часто используется для гибкой настройки подписей по оси х (можно в качестве подписей указать любые, в том числе и текстовые значения).
Вывод : если значения по оси х расположены неравномерно (в исходной таблице нет точки с х=20, поэтому кривая на Диаграмме График имеет излом), то использование Точечной диаграммы предпочтительней.
В случае, если данные расположены по оси х равномерно (с определенным шагом), то можно использовать оба типа диаграммы — линии на диаграмме будут выглядеть одинаково. Но если некоторые значения по оси Х пропущены, то для настройки диаграммы типа График нужно изменить таблицу с исходными данными. Можно использовать функцию НД() см. статью Функция НД() в MS EXCEL . Эта функция позволяет сделать кривую на диаграмме График аналогичной кривой на Точечной диаграмме (вариант2).
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
Построение графика функции на плоскости
Элементарные функции (y=sin(x), y=x 2 ) удовлетворяют условию однозначности функции: одному значению Х соответствует единственное значение Y (горизонтальная линия, параллельная оси ординат, не может пересекать график функции более чем в одной точке). Поэтому, Диаграмма типа График, как и диаграмма типа Точечная, годятся для построения графика функции на плоскости.
Построим график функции y=sin(x) с использованием обоих типов диаграмм.
- подписи Оси Х: на диаграмме График на оси Х указаны фактические значения Х (могут также быть указаны любые подписи, даже текст), а на Точечной — цены основных и промежуточных делений вычислены автоматически. Т.е. подписи на этих типах диаграмм не обязательно совпадают (но можно добиться, чтобы совпадали).
- шаг вертикальной сетки: основные линии сетки на Графике проходят строго через точки значений, а на Точечной — шаг выбирается автоматически (точно предсказать не возможно, т.к. шаг зависит от размера самой диаграммы, диапазона изменения по Х и др.)
Эти графики построены в файле примера .
Построение плоских алгебраических кривых
Кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли можно построить только с помощью диаграммы типа Точечная, т.к. эти кривые НЕ удовлетворяют условию однозначности функции: одному значению Х могут соответствовать несколько значений Y. Эти графики построены в этой статье.
Построение диаграммы рассеяния
Диаграммы рассеяния используются для анализа временных рядов и в статистическом анализе. Про построение этой диаграммы (возможно использовать только Точечную) см. эту статью.
Инструменты прогнозирования в Microsoft Excel
Прогнозирование – это очень важный элемент практически любой сферы деятельности, начиная от экономики и заканчивая инженерией. Существует большое количество программного обеспечения, специализирующегося именно на этом направлении. К сожалению, далеко не все пользователи знают, что обычный табличный процессор Excel имеет в своем арсенале инструменты для выполнения прогнозирования, которые по своей эффективности мало чем уступают профессиональным программам. Давайте выясним, что это за инструменты, и как сделать прогноз на практике.
Процедура прогнозирования
Целью любого прогнозирования является выявление текущей тенденции, и определение предполагаемого результата в отношении изучаемого объекта на определенный момент времени в будущем.
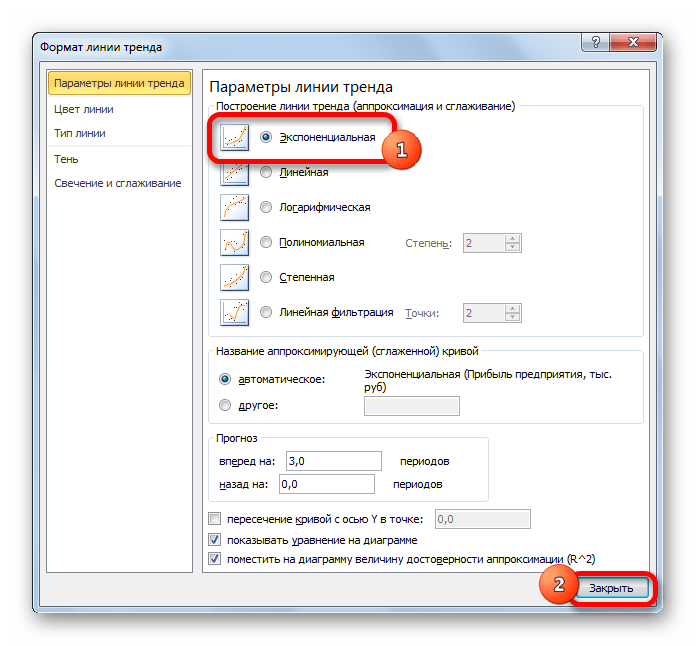
Способ 1: линия тренда
Одним из самых популярных видов графического прогнозирования в Экселе является экстраполяция выполненная построением линии тренда.
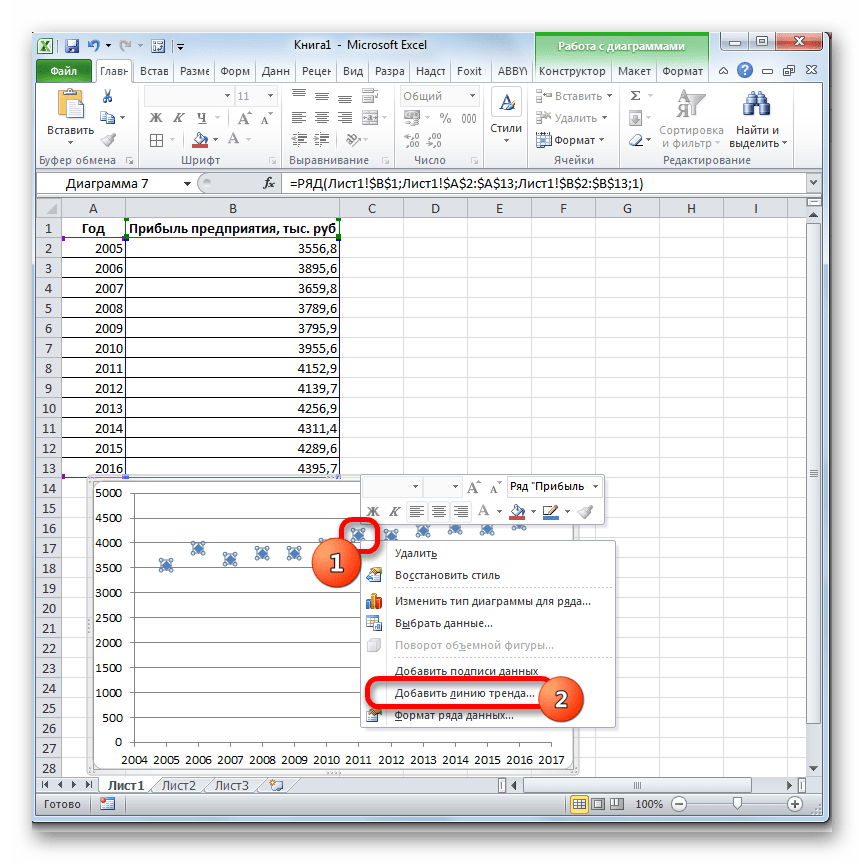
Попробуем предсказать сумму прибыли предприятия через 3 года на основе данных по этому показателю за предыдущие 12 лет.
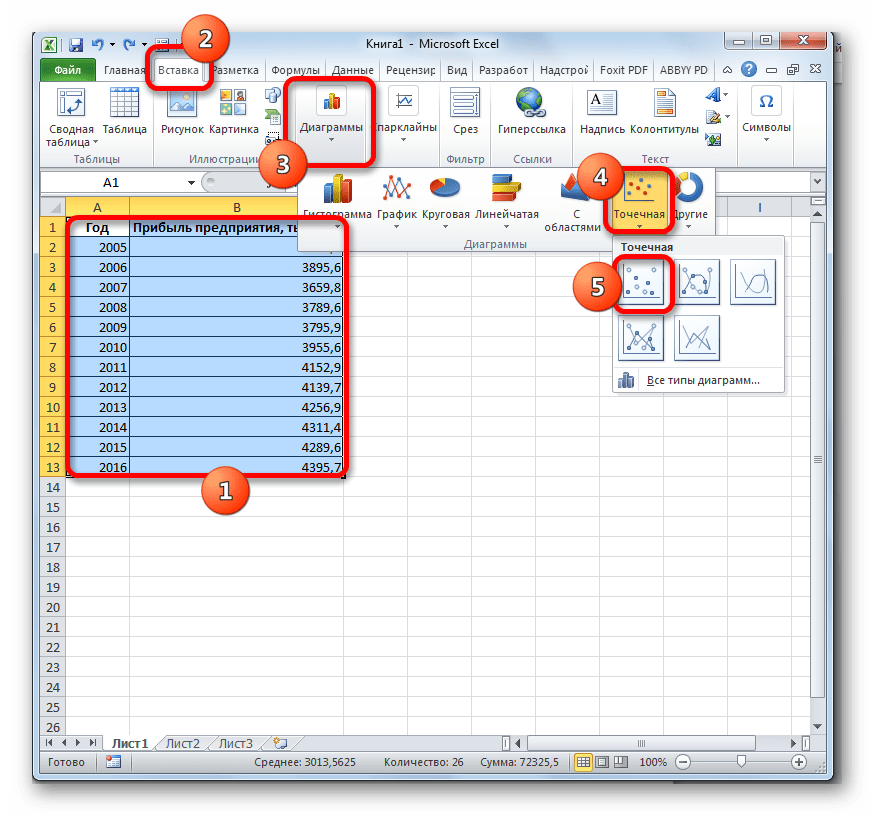
- Строим график зависимости на основе табличных данных, состоящих из аргументов и значений функции. Для этого выделяем табличную область, а затем, находясь во вкладке «Вставка», кликаем по значку нужного вида диаграммы, который находится в блоке «Диаграммы». Затем выбираем подходящий для конкретной ситуации тип. Лучше всего выбрать точечную диаграмму. Можно выбрать и другой вид, но тогда, чтобы данные отображались корректно, придется выполнить редактирование, в частности убрать линию аргумента и выбрать другую шкалу горизонтальной оси.
- Линейная;
- Логарифмическая;
- Экспоненциальная;
- Степенная;
- Полиномиальная;
- Линейная фильтрация.
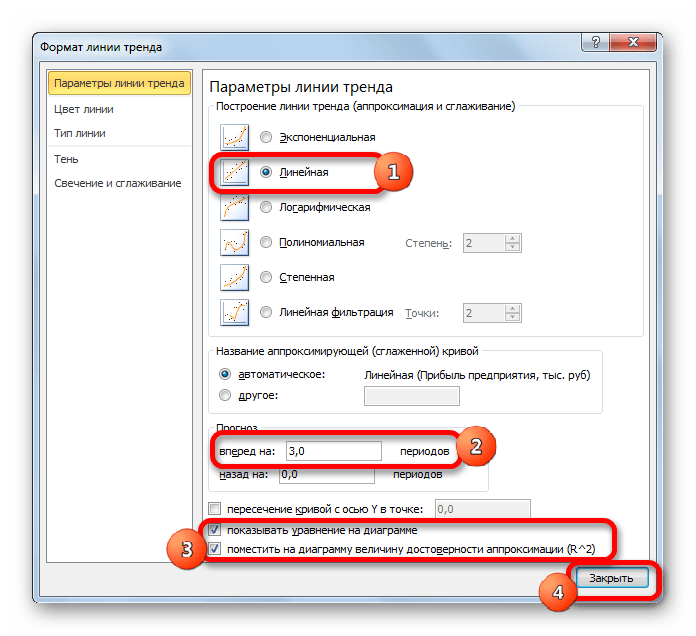
Давайте для начала выберем линейную аппроксимацию.
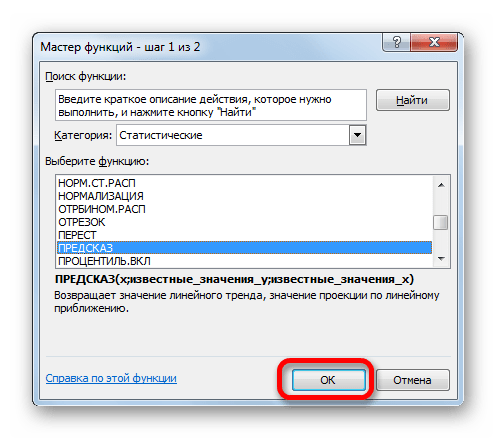
Способ 2: оператор ПРЕДСКАЗ
Экстраполяцию для табличных данных можно произвести через стандартную функцию Эксель ПРЕДСКАЗ. Этот аргумент относится к категории статистических инструментов и имеет следующий синтаксис:
«X» – это аргумент, значение функции для которого нужно определить. В нашем случае в качестве аргумента будет выступать год, на который следует произвести прогнозирование.
«Известные значения y» — база известных значений функции. В нашем случае в её роли выступает величина прибыли за предыдущие периоды.
«Известные значения x» — это аргументы, которым соответствуют известные значения функции. В их роли у нас выступает нумерация годов, за которые была собрана информация о прибыли предыдущих лет.
Естественно, что в качестве аргумента не обязательно должен выступать временной отрезок. Например, им может являться температура, а значением функции может выступать уровень расширения воды при нагревании.
При вычислении данным способом используется метод линейной регрессии.
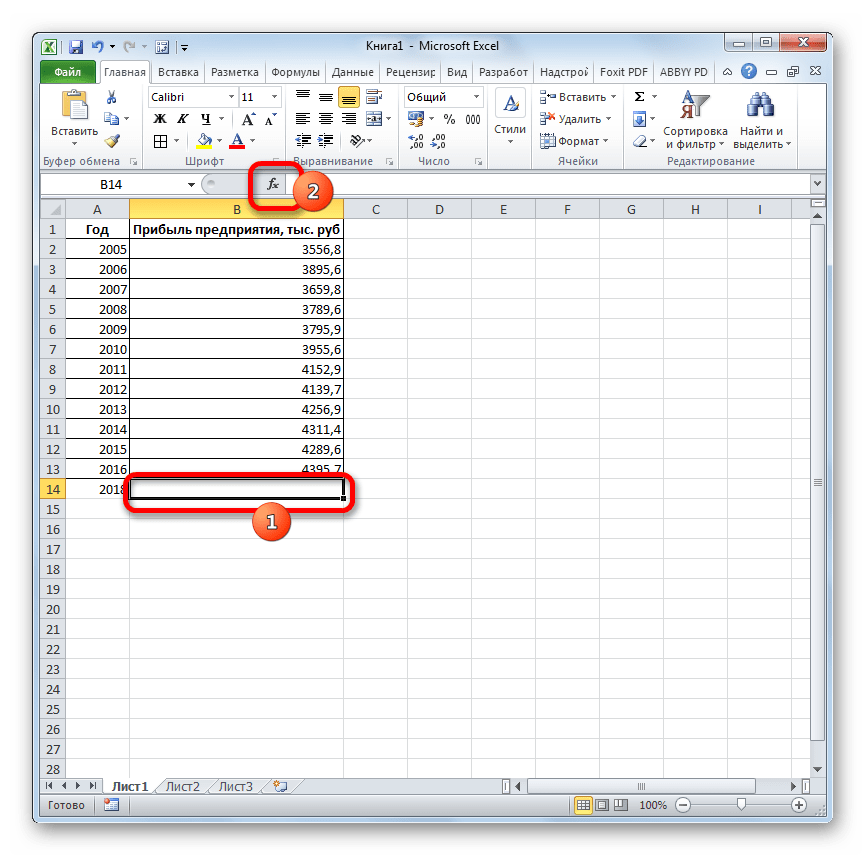
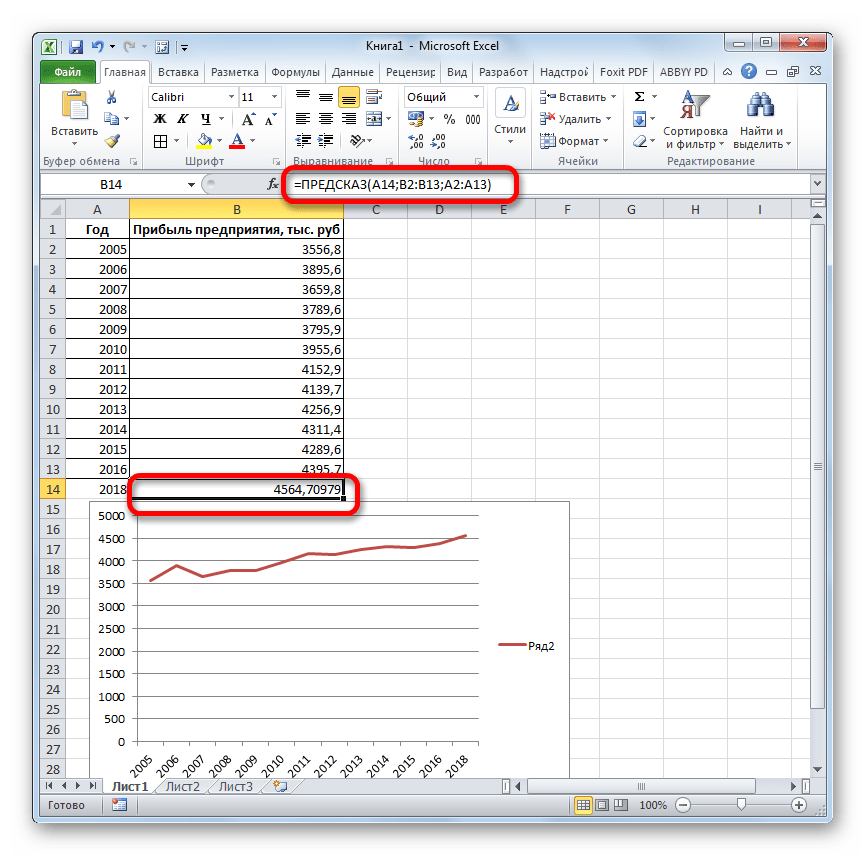
Давайте разберем нюансы применения оператора ПРЕДСКАЗ на конкретном примере. Возьмем всю ту же таблицу. Нам нужно будет узнать прогноз прибыли на 2018 год.
- Выделяем незаполненную ячейку на листе, куда планируется выводить результат обработки. Жмем на кнопку «Вставить функцию».
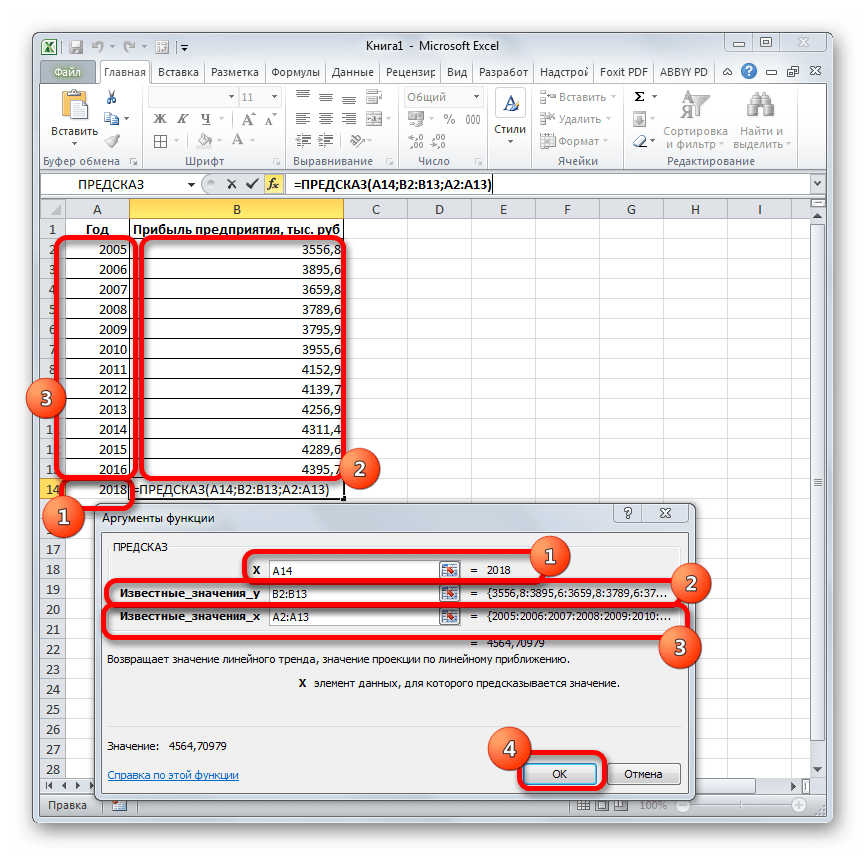
В поле «Известные значения y» указываем координаты столбца «Прибыль предприятия». Это можно сделать, установив курсор в поле, а затем, зажав левую кнопку мыши и выделив соответствующий столбец на листе.
Аналогичным образом в поле «Известные значения x» вносим адрес столбца «Год» с данными за прошедший период.
Но не стоит забывать, что, как и при построении линии тренда, отрезок времени до прогнозируемого периода не должен превышать 30% от всего срока, за который накапливалась база данных.
Способ 3: оператор ТЕНДЕНЦИЯ
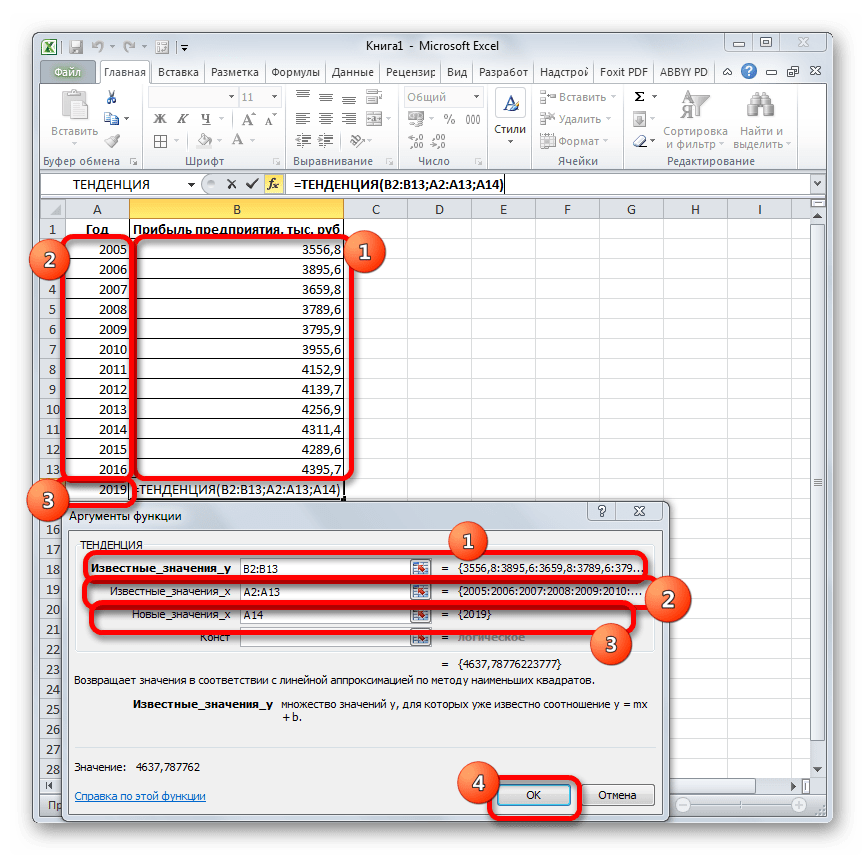
Для прогнозирования можно использовать ещё одну функцию – ТЕНДЕНЦИЯ. Она также относится к категории статистических операторов. Её синтаксис во многом напоминает синтаксис инструмента ПРЕДСКАЗ и выглядит следующим образом:
=ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы «Известные значения y» и «Известные значения x» полностью соответствуют аналогичным элементам оператора ПРЕДСКАЗ, а аргумент «Новые значения x» соответствует аргументу «X» предыдущего инструмента. Кроме того, у ТЕНДЕНЦИЯ имеется дополнительный аргумент «Константа», но он не является обязательным и используется только при наличии постоянных факторов.
Данный оператор наиболее эффективно используется при наличии линейной зависимости функции.
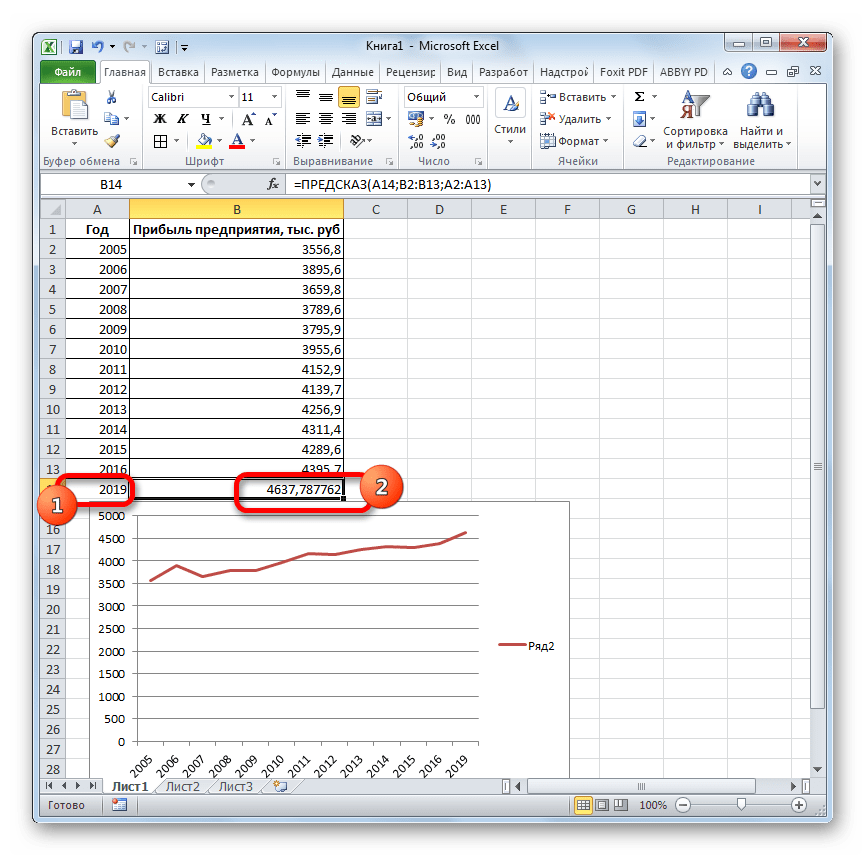
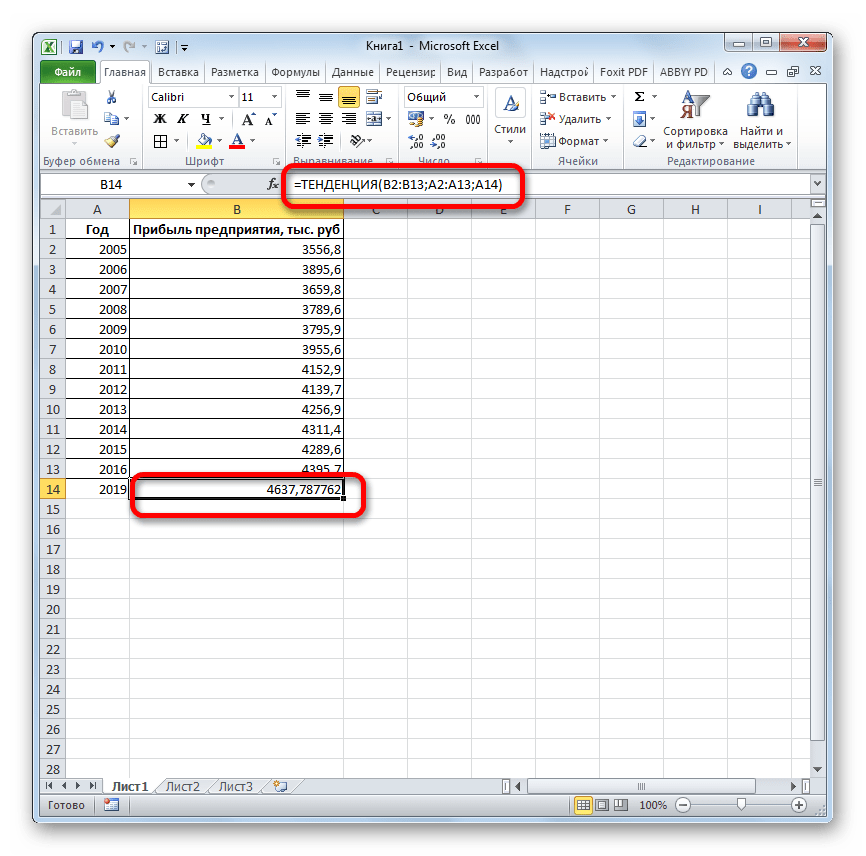
Посмотрим, как этот инструмент будет работать все с тем же массивом данных. Чтобы сравнить полученные результаты, точкой прогнозирования определим 2019 год.
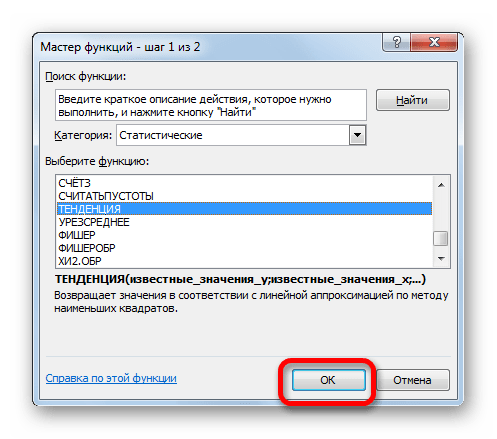
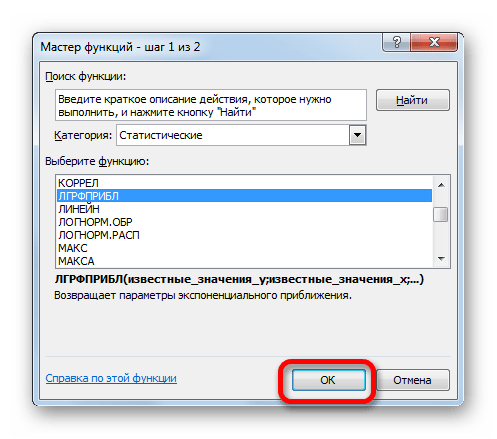
- Производим обозначение ячейки для вывода результата и запускаем Мастер функций обычным способом. В категории «Статистические» находим и выделяем наименование «ТЕНДЕНЦИЯ». Жмем на кнопку «OK».
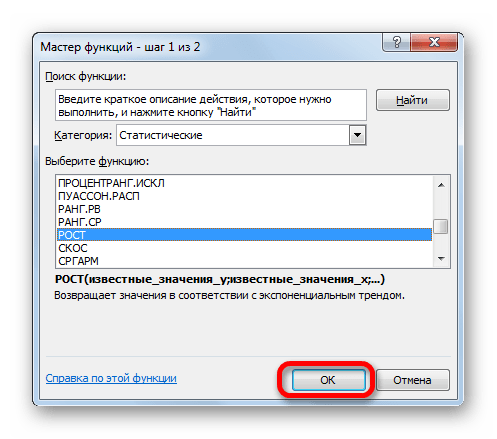
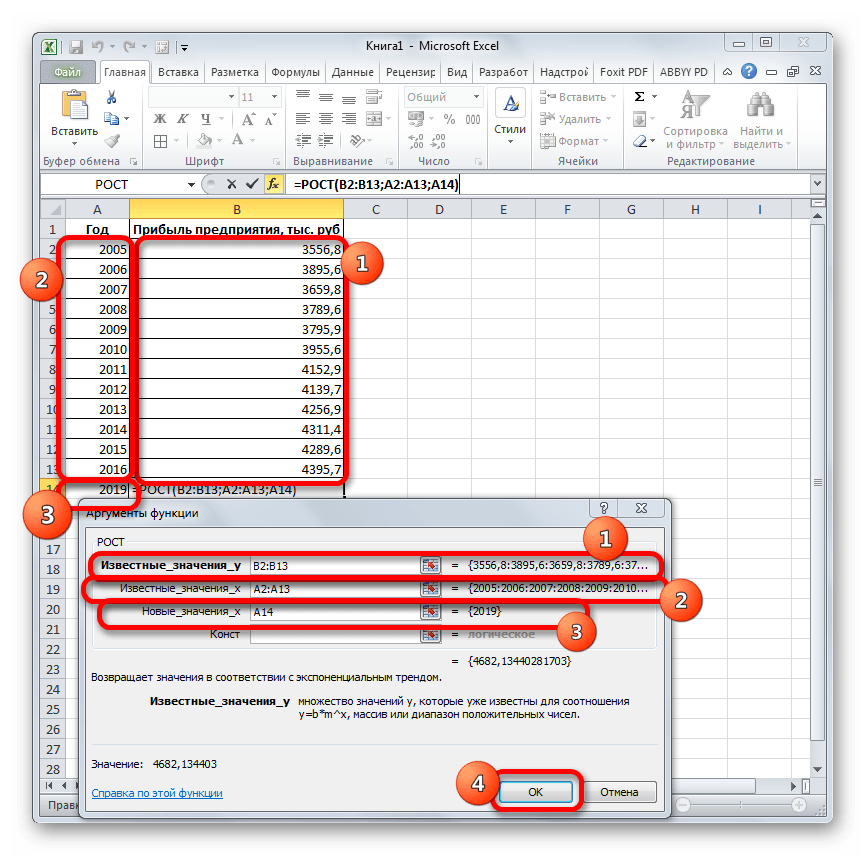
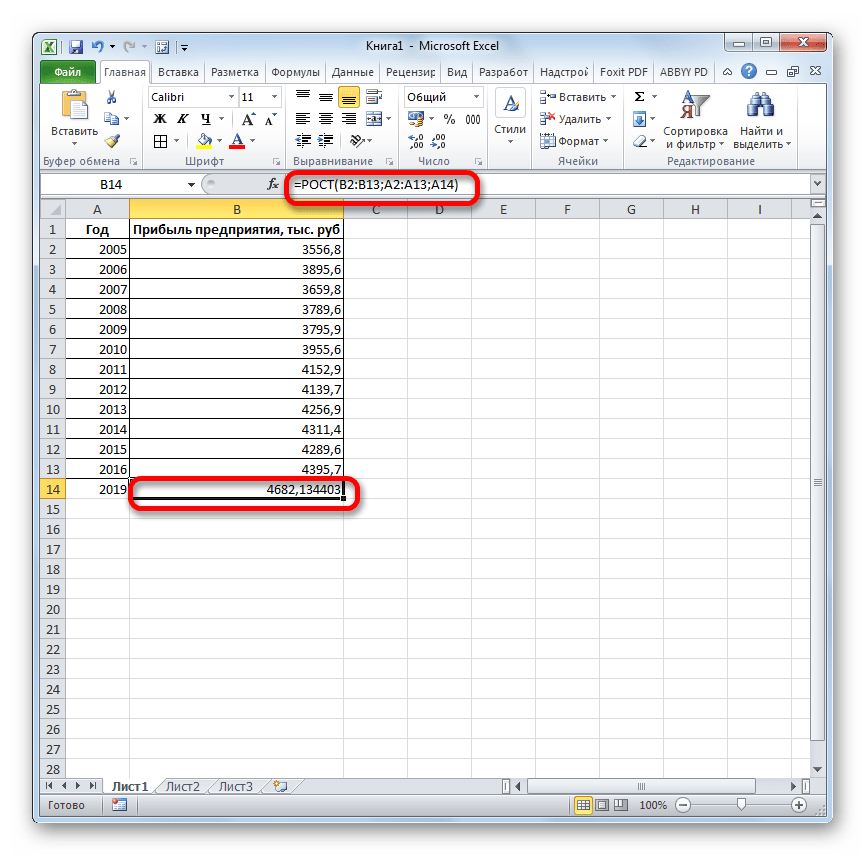
Способ 4: оператор РОСТ
Ещё одной функцией, с помощью которой можно производить прогнозирование в Экселе, является оператор РОСТ. Он тоже относится к статистической группе инструментов, но, в отличие от предыдущих, при расчете применяет не метод линейной зависимости, а экспоненциальной. Синтаксис этого инструмента выглядит таким образом:
=РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы у данной функции в точности повторяют аргументы оператора ТЕНДЕНЦИЯ, так что второй раз на их описании останавливаться не будем, а сразу перейдем к применению этого инструмента на практике.
- Выделяем ячейку вывода результата и уже привычным путем вызываем Мастер функций. В списке статистических операторов ищем пункт «РОСТ», выделяем его и щелкаем по кнопке «OK».
Способ 5: оператор ЛИНЕЙН
Оператор ЛИНЕЙН при вычислении использует метод линейного приближения. Его не стоит путать с методом линейной зависимости, используемым инструментом ТЕНДЕНЦИЯ. Его синтаксис имеет такой вид:
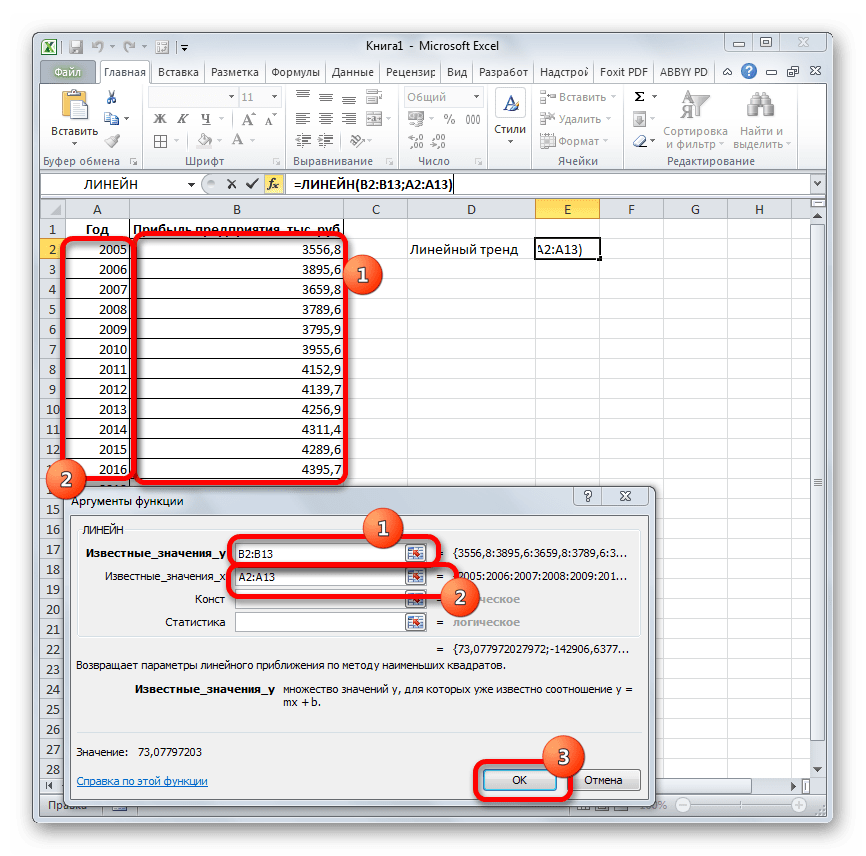
=ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
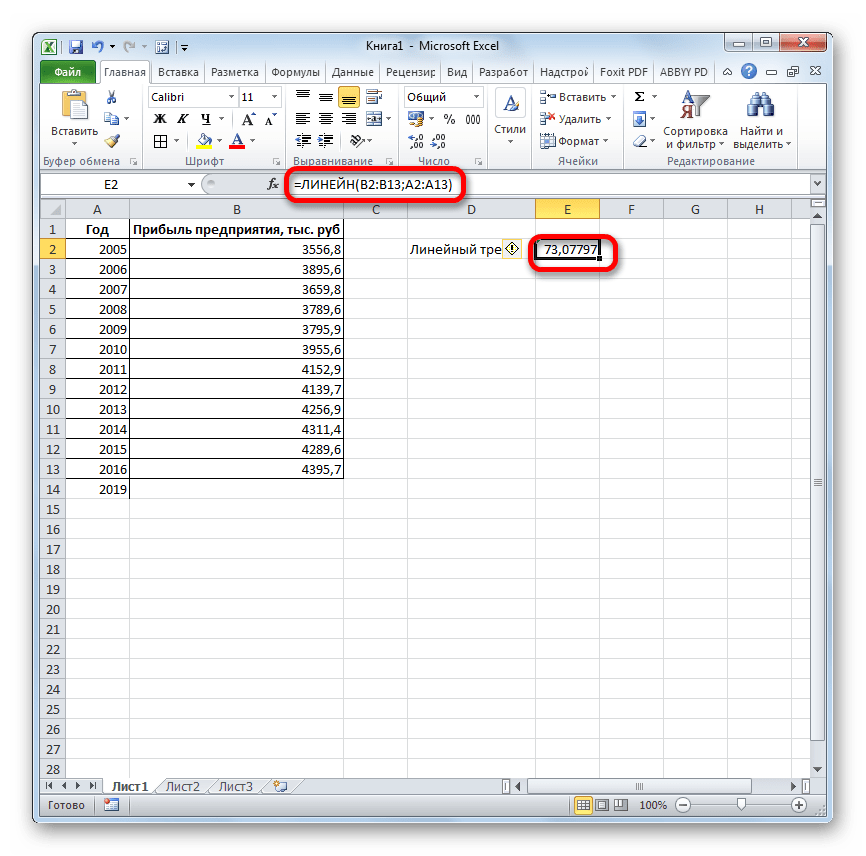
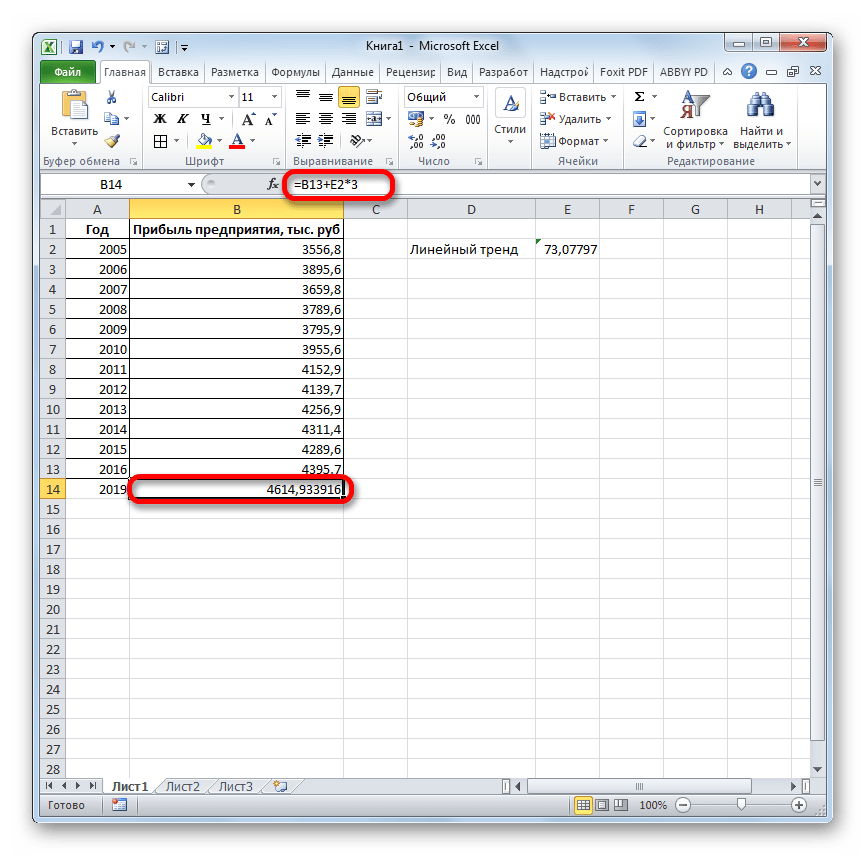
Последние два аргумента являются необязательными. С первыми же двумя мы знакомы по предыдущим способам. Но вы, наверное, заметили, что в этой функции отсутствует аргумент, указывающий на новые значения. Дело в том, что данный инструмент определяет только изменение величины выручки за единицу периода, который в нашем случае равен одному году, а вот общий итог нам предстоит подсчитать отдельно, прибавив к последнему фактическому значению прибыли результат вычисления оператора ЛИНЕЙН, умноженный на количество лет.
- Производим выделение ячейки, в которой будет производиться вычисление и запускаем Мастер функций. Выделяем наименование «ЛИНЕЙН» в категории «Статистические» и жмем на кнопку «OK».
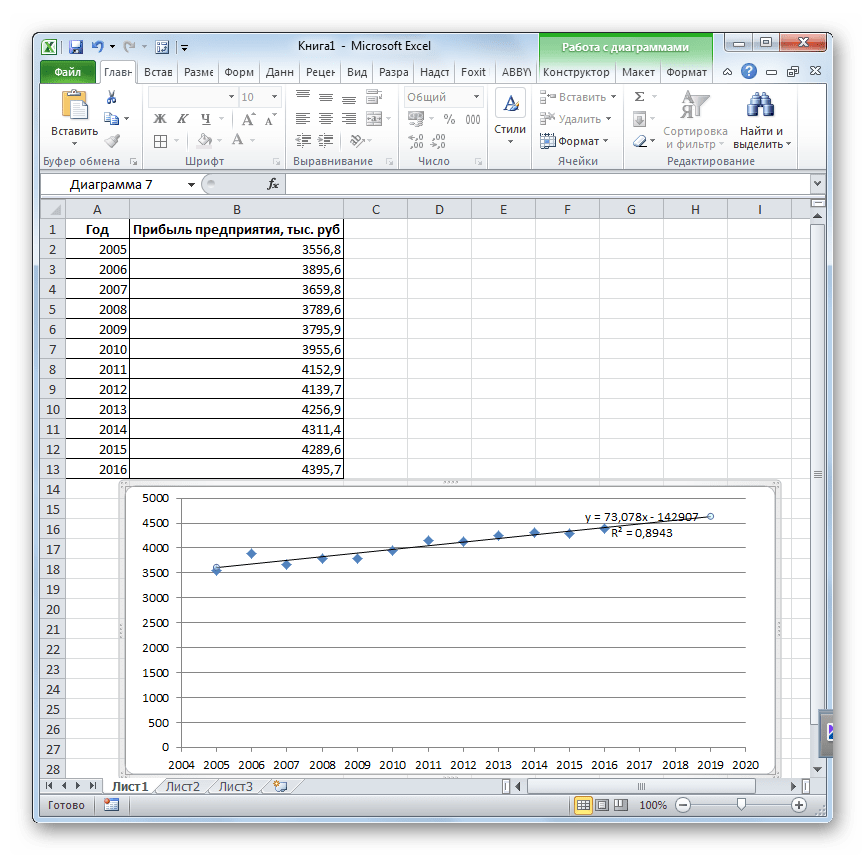
Как видим, прогнозируемая величина прибыли, рассчитанная методом линейного приближения, в 2019 году составит 4614,9 тыс. рублей.
Способ 6: оператор ЛГРФПРИБЛ
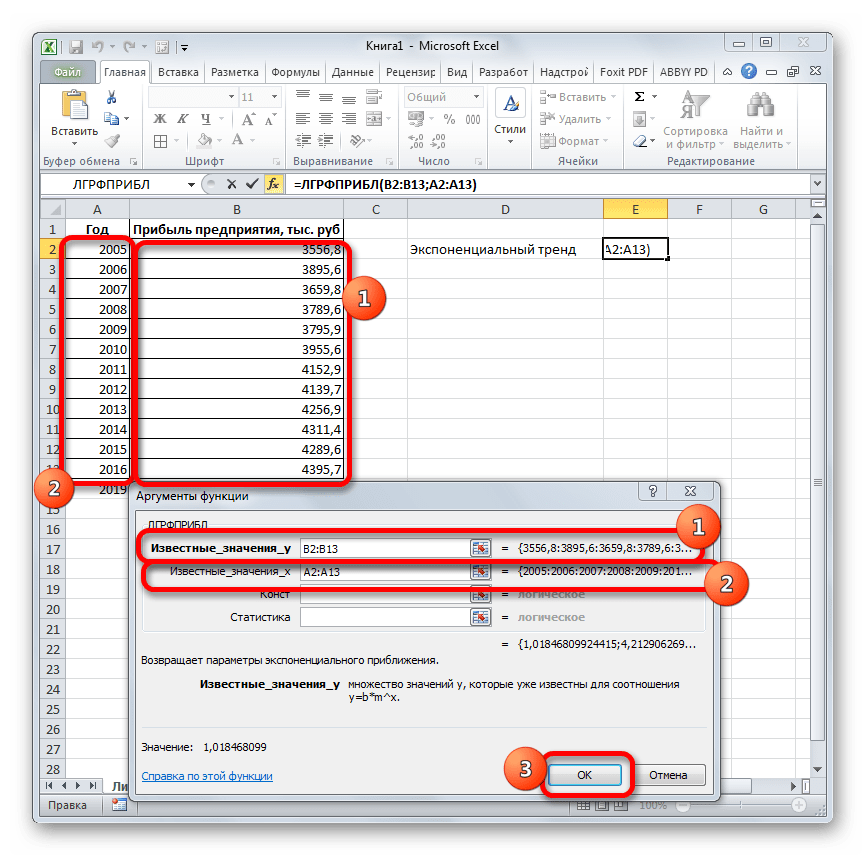
Последний инструмент, который мы рассмотрим, будет ЛГРФПРИБЛ. Этот оператор производит расчеты на основе метода экспоненциального приближения. Его синтаксис имеет следующую структуру:
= ЛГРФПРИБЛ (Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
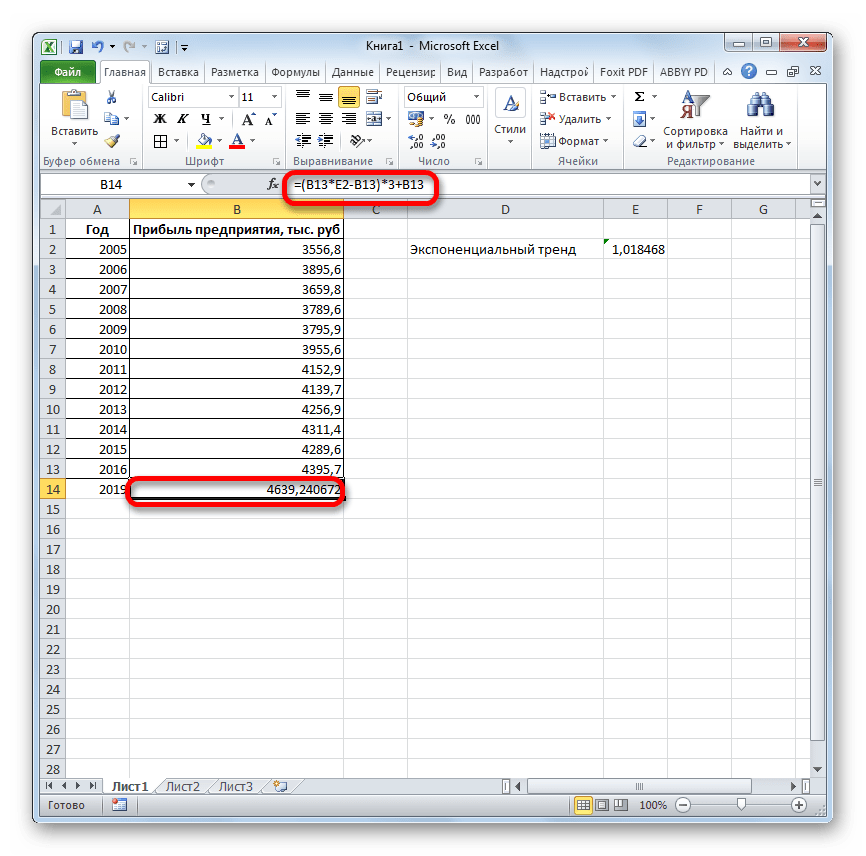
Как видим, все аргументы полностью повторяют соответствующие элементы предыдущей функции. Алгоритм расчета прогноза немного изменится. Функция рассчитает экспоненциальный тренд, который покажет, во сколько раз поменяется сумма выручки за один период, то есть, за год. Нам нужно будет найти разницу в прибыли между последним фактическим периодом и первым плановым, умножить её на число плановых периодов (3) и прибавить к результату сумму последнего фактического периода.
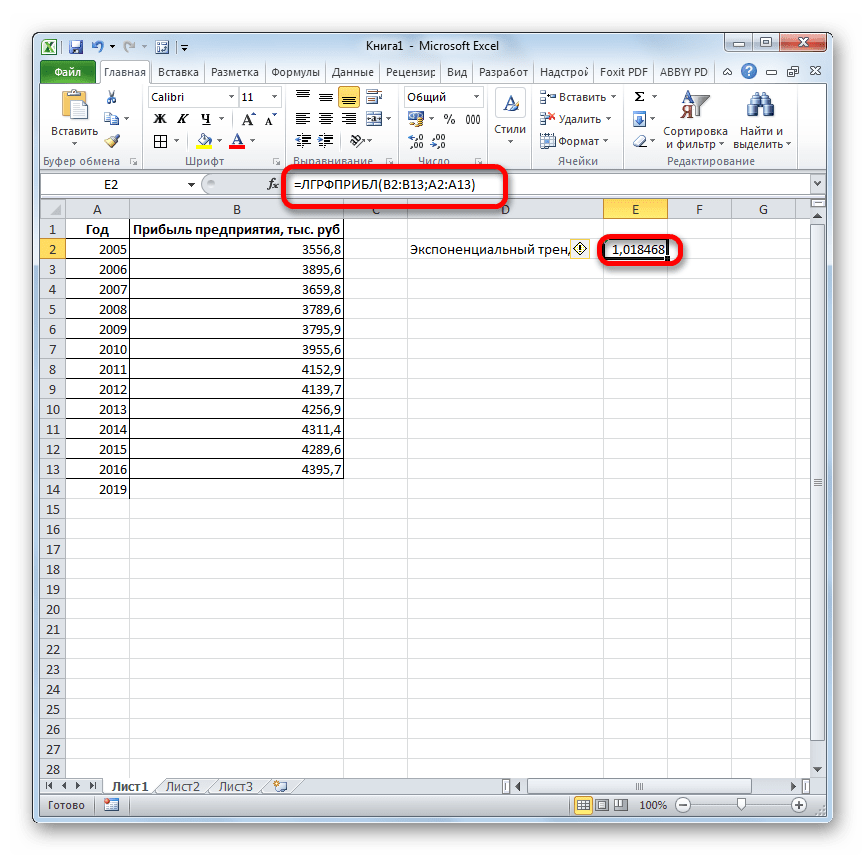
- В списке операторов Мастера функций выделяем наименование «ЛГРФПРИБЛ». Делаем щелчок по кнопке «OK».
Прогнозируемая сумма прибыли в 2019 году, которая была рассчитана методом экспоненциального приближения, составит 4639,2 тыс. рублей, что опять не сильно отличается от результатов, полученных при вычислении предыдущими способами.
Мы выяснили, какими способами можно произвести прогнозирование в программе Эксель. Графическим путем это можно сделать через применение линии тренда, а аналитическим – используя целый ряд встроенных статистических функций. В результате обработки идентичных данных этими операторами может получиться разный итог. Но это не удивительно, так как все они используют разные методы расчета. Если колебание небольшое, то все эти варианты, применимые к конкретному случаю, можно считать относительно достоверными.

Содержание
- Как по графику определить функцию в excel
- Часть 10. Подбор формул по графику. Линия тренда
- Найти функцию по ее графику (аппроксимация)
- Решение
- Как по графику в экселе определить значение точки
- Точки пересечения графиков в Excel
- Строим графики с точками пересечений
- Находим точку пересечения графиков в Excel
- Точки пересечения для трех показателей
- Особенности построения при неравномерном шаге по Х
- Построение графика функции на плоскости
- Построение плоских алгебраических кривых
- Построение диаграммы рассеяния
- Инструменты прогнозирования в Microsoft Excel
- Процедура прогнозирования
- Способ 1: линия тренда
- Способ 2: оператор ПРЕДСКАЗ
- Способ 3: оператор ТЕНДЕНЦИЯ
- Способ 4: оператор РОСТ
- Способ 5: оператор ЛИНЕЙН
- Способ 6: оператор ЛГРФПРИБЛ
Как по графику определить функцию в excel
Часть 10. Подбор формул по графику. Линия тренда
Для рассмотренных выше задач удавалось построить уравнение или систему уравнений. Но во многих случаях при решении практических задач имеются лишь экспериментальные (результаты измерений, статистические, справочные, опытные) данные. По ним с определенной мерой близости пытаются восстановить эмпирическую формулу (уравнение), которая может быть использована для поиска решения, моделирования, оценки решений, прогнозов.
Процесс подбора эмпирической формулы P(x) для опытной зависимости F(x) называется аппроксимацией (сглаживанием). Для зависимостей с одним неизвестным в Excel используются графики, а для зависимостей со многими неизвестными – пары функций из группы Статистические ЛИНЕЙН и ТЕНДЕНЦИЯ, ЛГРФПРИБЛ и РОСТ .
В настоящем разделе рассматривается аппроксимация экспериментальных данных с помощью графиков Excel: на основе данных стоится график, к нему подбирается линия тренда, т.е. аппроксимирующая функция, которая с максимальной степенью близости приближается к опытной зависимости.
Степень близости подбираемой функции оценивается коэффициентом детерминации R 2 . Если нет других теоретических соображений, то выбирают функцию с коэффициентом R 2 , стремящимся к 1. Отметим, что подбор формул с использованием линии тренда позволяет установить как вид эмпирической формулы, так и определить численные значения неизвестных параметров.
Excel предоставляет 5 видов аппроксимирующих функций:
1. Линейная – y=cx+b. Это простейшая функция, отражающая рост и убывание данных с постоянной скоростью.
2. Полиномиальная – y=c0+c1x+c2x 2 +…+c6x 6 . Функция описывает попеременно возрастающие и убывающие данные. Полином 2-ой степени может иметь один экстремум (min или max), 3-ей степени – до 2-х экстремумов, 4-ой степени – до 3-х и т.д.
3. Логарифмическая – y=clnx+b. Эта функция описывает быстро возрастающие (убывающие) данные, которые затем стабилизируются.
4. Степенная – y=cx b , (х>0и y>0). Функция отражает данные с постоянно увеличивающейся (убывающей) скоростью роста.
5. Экспоненциальная – y=ce bx , (e – основание натурального логарифма). Функция описывает быстро растущие (убывающие) данные, которые затем стабилизируются.
Для всех 5-ти видов функций используется аппроксимация данных по методу наименьших квадратов (см. справку по F1 «линия тренда»).
В качестве примера рассмотрим зависимость продаж от рекламы, заданную следующими статистическими данными по некоторой фирме:
| Реклама (тыс. руб.) | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 |
| Продажи (тыс. руб.) |
Необходимо построить функцию, наилучшим образом отражающую эту зависимость. Кроме того, необходимо оценить продажи для рекламных вложений в 6 тыс. руб.
Приступим к решению. В первую очередь введите эти данные в Excel и постройте график, как на рис. 38. Как видно, график построен на основании диапазона B2:J2. Далее, щелкнув правой кнопкой мыши по графику, добавьте линию тренда, как показано на рис. 38.
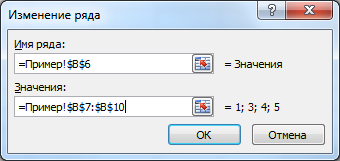
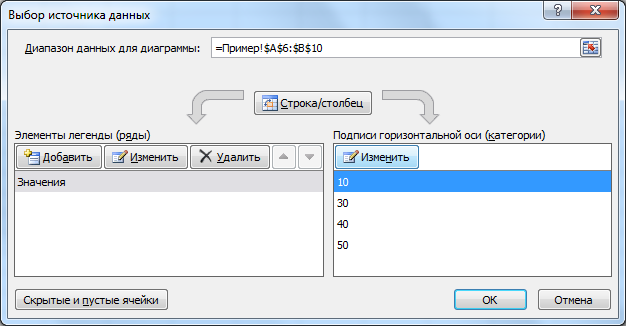
Чтобы подписать ось Х соответствующими значениями рекламы (как на рис. 38), следует в ниспадающем меню (рис. 38) выбрать пункт Исходные данные. В открывшемся одноименном окне, в закладке Ряд, в поле Подписи оси Х, укажите диапазон ячеек, где записаны значения Х (здесь $B$1:$K$1):
В открывшемся окне настройки (рис. 39), на закладке Тип выберите для аппроксимации логарифмическую линию тренда (по виду графика). На закладке Параметры установите флажки, отображающие на графике уравнение и коэффициент детерминации.
После нажатия ОК Вы получите результат, как на рис. 40. Коэффициент детерминации R 2 =0.9846, что является неплохой степенью близости. Для подтверждения правильности выбранной функции (поскольку других теоретических соображений нет) спрогнозируйте развитие продаж на 10 периодов вперед. Для этого щелкните правой кнопкой по линии тренда – измените формат – после этого в поле Прогноз: вперед на: установите 10 (рис. 41).
После установки прогноза Вы увидите изменение кривой графика на 10 периодов наблюдения вперед, как на рис. 42. Он с большой долей вероятности отражает дальнейшее увеличение продаж с увеличением рекламных вложений.
Вычисление по полученной формуле =237,96*LN(6)+5,9606 в Excel дает значение 432 тыс. руб.
В Excel имеется функция ПРЕДСКАЗ(), которая вычисляет будущее значение Y по существующим парам значений X и Y значениям с использованием линейной регрессии. Функция Y по возможности должна быть линейной, т.е. описываться уравнением типа c+bx. Функция предсказания для нашего примера запишется так: =ПРЕДСКАЗ(K1;B2:J2;B1:J1). Запишите – должно получится значение 643,6 тыс. руб.
Часть11. Контрольные задания
Найти функцию по ее графику (аппроксимация)
Дано:
Два параметра, зависящих друг от друга (X; Y). На их основании построен график.
Задача: найти функцию, отражающую (приблизительно) зависимость между параметрами.
Я эту задачу пытаюсь решить с помощью инструмента в экселе (построение тренда; полиноминальная линия тренда 6й степени).
Эксель подсказывает мне формулу функции, но по факту эта формула выдает не верные параметры (т.е. «Y» по данному формуле рассчитывается не правильно).
Помощь в написании контрольных, курсовых и дипломных работ здесь.
расчет.xlsx (15.9 Кб, 22 просмотров)
Аппроксимация к графику
Здравствуйте! Проблема такая, приходится работать с данными с осциллографа и с помощью программы.
Найти функцию по графику(парабола)
Нужно найти функцию по графику(только параболу), пробовал по формулам с википедии, но что то не.
Нужно найти функцию по графику
Вот собственно график и из него надо получить функцию для того чтобы написать программу на паскале.
найти функцию сигнала по графику
Доброго времени суток, как по графику сигнала найти его изображение (ну или сначала оригинал.
расчет (1).xlsx (16.1 Кб, 55 просмотров)
Сообщение было отмечено p1111 как решение
Решение
Как, оказывается, было просто.
Спасибо огромное, очень выручили.
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Нужно найти функцию по графику
Здравствуйте, у меня есть данные для построения кусочка ВАХ-электрической дуги. Мне нужно найти.
Вывести функцию по графику
Процесс предполагается обратный от привычного, имея график, построить функцию. Как это сделать.
Написать функцию по графику
Помогите пожалуйста! По данному графику нужна функция (формула), чтобы я потом через if смог.
Составить функцию по графику.
Привет всем, помогите составить функцию, по графику, график приложен снизу функция в каком-то.
Источник
Как по графику в экселе определить значение точки
Точки пересечения графиков в Excel
Как найти точки пересечения графиков в Excel? Например, есть графики, отображающие несколько показателей. Далеко не всегда они будут пересекаться непосредственно на поле диаграммы. Но пользователю нужно показать те значения, в которых линии рассматриваемых явлений пересекаются. Рассмотрим на примере.
Строим графики с точками пересечений
Имеются две функции, по которым нужно построить графики:
Выделяем диапазоны данных, на вкладке «Вставка» в группе «Диаграммы» подбираем нужный тип графика. Как:
- Нужно найти точки пересечения графиков со значением Х, поэтому столбчатые, круговые, пузырьковые и т.п. диаграммы не выбираем. Это должны быть прямые линии.
- Для поиска точек пересечения необходима ось Х. Не условная, на которой невозможно задать другое значение. Должна быть возможность выбирать промежуточные линии между периодами. Обычные графики не подходят. У них горизонтальная ось – общая для всех рядов. Периоды фиксированы. И манипулировать можно только с ними. Выберем точечную диаграмму с прямыми отрезками и маркерами.
Для данного типа диаграммы между основными периодами 0, 2, 4, 6 и т.д. можно использовать и промежуточные. Например, 2,5.
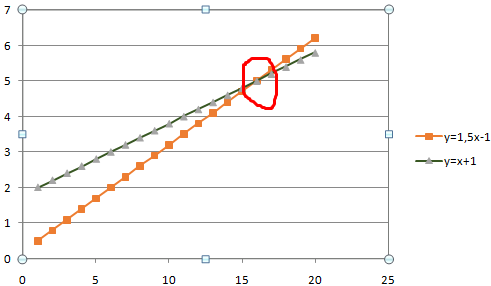
Находим точку пересечения графиков в Excel
В табличном редакторе Excel нет встроенной функции для решения подобной задачи. Линии построенных графиков не пересекаются (см. рисунок), поэтому даже визуально точку пересечения найти нельзя. Ищем выход.
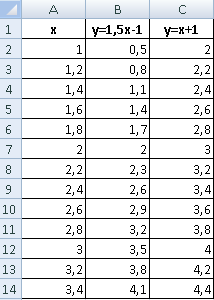
Первый способ. Найти общие значения в рядах данных для указанных функций.
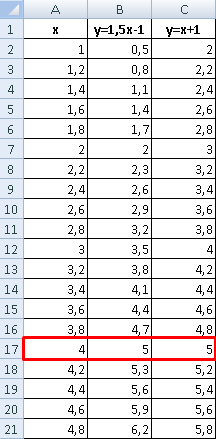
В таблице с данными таковых значений пока нет. Так как мы решали уравнения с помощью формул в полуавтоматическом режиме, с помощью маркера автозаполнения продолжим ряды данных.
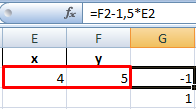
Значения Y одинаковые при Х = 4. Следовательно, точка пересечения двух графиков имеет координаты 4, 5.
Изменим график, добавив новые данные. Получим две пересекающиеся линии.
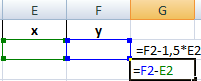
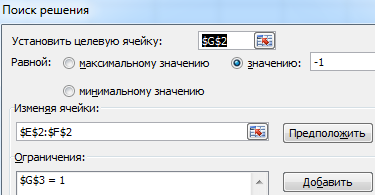
Второй способ. Применение для решения уравнений специального инструмента «Поиск решения». Кнопка вызова инструмента должна быть на вкладке «Данные». Если нет, нужно добавить из «Надстроек Excel».
Преобразуем уравнения таким образом, чтобы неизвестные были в одной части: y – 1,5 х = -1; y – х = 1. Далее для неизвестных х и y назначим ячейки в Excel. Перепишем уравнения, используя ссылки на эти ячейки.
Вызываем меню «Поиск решения» — заполняем условия, необходимые для решения уравнений.
Нажимаем «Выполнить» — инструмент предлагает решение уравнений.
Найденные значения для х и y совпадают с предыдущим решением с помощью составления рядов данных.
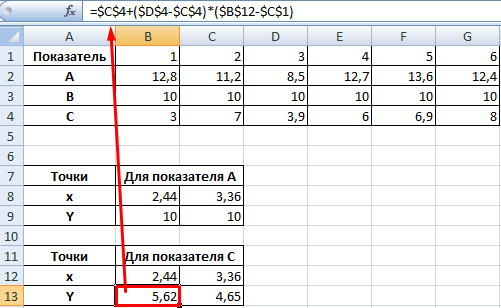
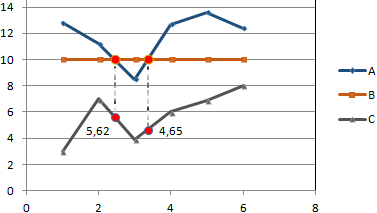
Точки пересечения для трех показателей
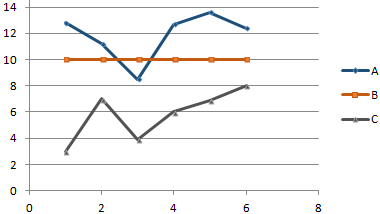
Существует три показателя, которые измерялись во времени.
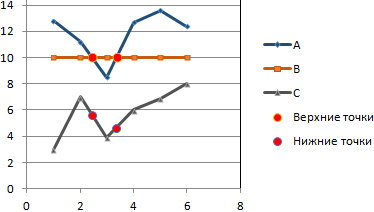
По условию задачи показатель В имеет постоянную величину на протяжении всех периодов. Это некий норматив. Показатель А зависит от показателя С. Он то выше, то ниже норматива. Строим графики (точечную диаграмму с прямыми отрезками и маркерами).
Точки пересечения имеются только у показателей А и В. Но их точные координаты нужно еще определить. Усложним задачу – найдем точки пересечения показателя C с показателями А и В. То есть в какие временные периоды и при каких значениях показателя А линия показателя С пересекает линию норматива.
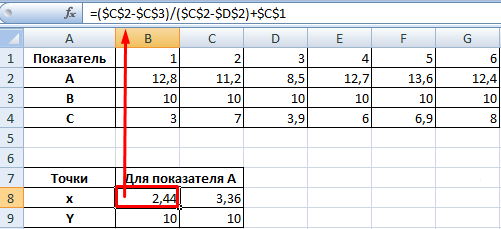
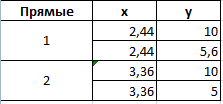
Точек у нас будет две. Их рассчитаем математическим путем. Сначала найдем точки пересечения показателя А с показателем В:
На рисунке видно, какие значения использовались для расчета. По такой же логике находим значение х для второй точки.
Теперь рассчитаем точки, найденных значений по оси Х с показателем С. Используем близкие формулы:
На основе новых данных построим точечные диаграммы на том же поле (где наши графики).
Получается такой рисунок:
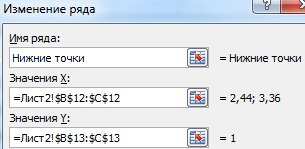
Для большей информативности и эстетики восприятия добавим пунктирные линии. Их координаты:
Добавим подписи данных – значения показателя C, при которых он пересечет линию норматива.
Можно форматировать графики по своему усмотрению – делать их более выразительными и наглядными.
Особенности построения при неравномерном шаге по Х
Пусть дана таблица с исходными данными (значения в исходной таблице расположены по оси Х равномерно с шагом 10, но точка с х=20 отсутствует).
Построим График и Точечную диаграмму с прямыми отрезками используя одну и туже таблицу.
Точечная диаграмма использует все данные из исходной таблицы: как значения х, так и y.
Диаграмма График откладывает значения по оси х равномерно (значения из столбца Ось х не используются для построения).
Значения из столбца Ось х используются в Диаграмме График только для подписей данных по оси х (значения из столбца Ось х никак не влияют на расположение точек). Это часто используется для гибкой настройки подписей по оси х (можно в качестве подписей указать любые, в том числе и текстовые значения).
Вывод : если значения по оси х расположены неравномерно (в исходной таблице нет точки с х=20, поэтому кривая на Диаграмме График имеет излом), то использование Точечной диаграммы предпочтительней.
В случае, если данные расположены по оси х равномерно (с определенным шагом), то можно использовать оба типа диаграммы — линии на диаграмме будут выглядеть одинаково. Но если некоторые значения по оси Х пропущены, то для настройки диаграммы типа График нужно изменить таблицу с исходными данными. Можно использовать функцию НД() см. статью Функция НД() в MS EXCEL . Эта функция позволяет сделать кривую на диаграмме График аналогичной кривой на Точечной диаграмме (вариант2).
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
Построение графика функции на плоскости
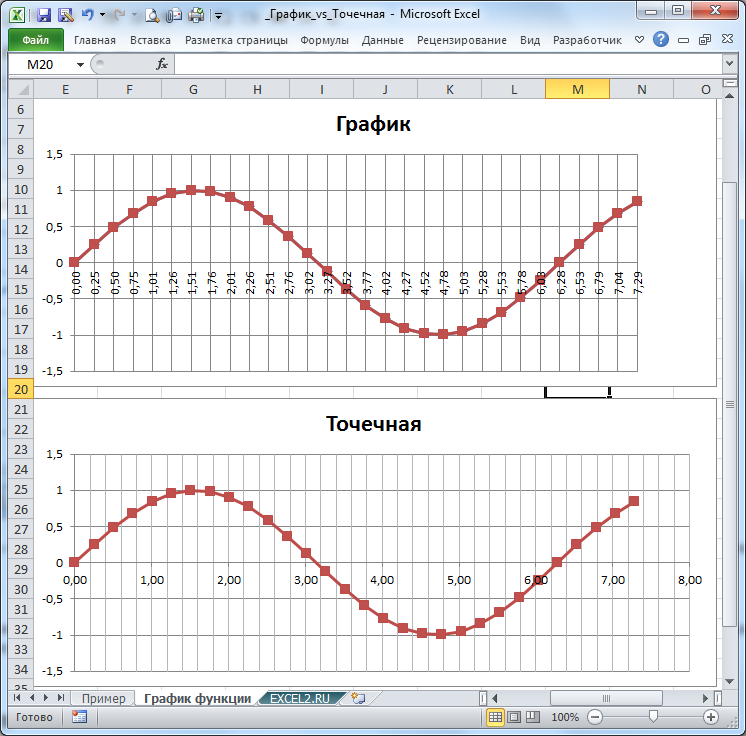
Элементарные функции (y=sin(x), y=x 2 ) удовлетворяют условию однозначности функции: одному значению Х соответствует единственное значение Y (горизонтальная линия, параллельная оси ординат, не может пересекать график функции более чем в одной точке). Поэтому, Диаграмма типа График, как и диаграмма типа Точечная, годятся для построения графика функции на плоскости.
Построим график функции y=sin(x) с использованием обоих типов диаграмм.
- подписи Оси Х: на диаграмме График на оси Х указаны фактические значения Х (могут также быть указаны любые подписи, даже текст), а на Точечной — цены основных и промежуточных делений вычислены автоматически. Т.е. подписи на этих типах диаграмм не обязательно совпадают (но можно добиться, чтобы совпадали).
- шаг вертикальной сетки: основные линии сетки на Графике проходят строго через точки значений, а на Точечной — шаг выбирается автоматически (точно предсказать не возможно, т.к. шаг зависит от размера самой диаграммы, диапазона изменения по Х и др.)
Эти графики построены в файле примера .
Построение плоских алгебраических кривых
Кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли можно построить только с помощью диаграммы типа Точечная, т.к. эти кривые НЕ удовлетворяют условию однозначности функции: одному значению Х могут соответствовать несколько значений Y. Эти графики построены в этой статье.
Построение диаграммы рассеяния
Диаграммы рассеяния используются для анализа временных рядов и в статистическом анализе. Про построение этой диаграммы (возможно использовать только Точечную) см. эту статью.
Инструменты прогнозирования в Microsoft Excel
Прогнозирование – это очень важный элемент практически любой сферы деятельности, начиная от экономики и заканчивая инженерией. Существует большое количество программного обеспечения, специализирующегося именно на этом направлении. К сожалению, далеко не все пользователи знают, что обычный табличный процессор Excel имеет в своем арсенале инструменты для выполнения прогнозирования, которые по своей эффективности мало чем уступают профессиональным программам. Давайте выясним, что это за инструменты, и как сделать прогноз на практике.
Процедура прогнозирования
Целью любого прогнозирования является выявление текущей тенденции, и определение предполагаемого результата в отношении изучаемого объекта на определенный момент времени в будущем.
Способ 1: линия тренда
Одним из самых популярных видов графического прогнозирования в Экселе является экстраполяция выполненная построением линии тренда.
Попробуем предсказать сумму прибыли предприятия через 3 года на основе данных по этому показателю за предыдущие 12 лет.
- Строим график зависимости на основе табличных данных, состоящих из аргументов и значений функции. Для этого выделяем табличную область, а затем, находясь во вкладке «Вставка», кликаем по значку нужного вида диаграммы, который находится в блоке «Диаграммы». Затем выбираем подходящий для конкретной ситуации тип. Лучше всего выбрать точечную диаграмму. Можно выбрать и другой вид, но тогда, чтобы данные отображались корректно, придется выполнить редактирование, в частности убрать линию аргумента и выбрать другую шкалу горизонтальной оси.
Давайте для начала выберем линейную аппроксимацию.
Способ 2: оператор ПРЕДСКАЗ
Экстраполяцию для табличных данных можно произвести через стандартную функцию Эксель ПРЕДСКАЗ. Этот аргумент относится к категории статистических инструментов и имеет следующий синтаксис:
«X» – это аргумент, значение функции для которого нужно определить. В нашем случае в качестве аргумента будет выступать год, на который следует произвести прогнозирование.
«Известные значения y» — база известных значений функции. В нашем случае в её роли выступает величина прибыли за предыдущие периоды.
«Известные значения x» — это аргументы, которым соответствуют известные значения функции. В их роли у нас выступает нумерация годов, за которые была собрана информация о прибыли предыдущих лет.
Естественно, что в качестве аргумента не обязательно должен выступать временной отрезок. Например, им может являться температура, а значением функции может выступать уровень расширения воды при нагревании.
При вычислении данным способом используется метод линейной регрессии.
Давайте разберем нюансы применения оператора ПРЕДСКАЗ на конкретном примере. Возьмем всю ту же таблицу. Нам нужно будет узнать прогноз прибыли на 2018 год.
- Выделяем незаполненную ячейку на листе, куда планируется выводить результат обработки. Жмем на кнопку «Вставить функцию».
В поле «Известные значения y» указываем координаты столбца «Прибыль предприятия». Это можно сделать, установив курсор в поле, а затем, зажав левую кнопку мыши и выделив соответствующий столбец на листе.
Аналогичным образом в поле «Известные значения x» вносим адрес столбца «Год» с данными за прошедший период.
Но не стоит забывать, что, как и при построении линии тренда, отрезок времени до прогнозируемого периода не должен превышать 30% от всего срока, за который накапливалась база данных.
Способ 3: оператор ТЕНДЕНЦИЯ
Для прогнозирования можно использовать ещё одну функцию – ТЕНДЕНЦИЯ. Она также относится к категории статистических операторов. Её синтаксис во многом напоминает синтаксис инструмента ПРЕДСКАЗ и выглядит следующим образом:
=ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы «Известные значения y» и «Известные значения x» полностью соответствуют аналогичным элементам оператора ПРЕДСКАЗ, а аргумент «Новые значения x» соответствует аргументу «X» предыдущего инструмента. Кроме того, у ТЕНДЕНЦИЯ имеется дополнительный аргумент «Константа», но он не является обязательным и используется только при наличии постоянных факторов.
Данный оператор наиболее эффективно используется при наличии линейной зависимости функции.
Посмотрим, как этот инструмент будет работать все с тем же массивом данных. Чтобы сравнить полученные результаты, точкой прогнозирования определим 2019 год.
- Производим обозначение ячейки для вывода результата и запускаем Мастер функций обычным способом. В категории «Статистические» находим и выделяем наименование «ТЕНДЕНЦИЯ». Жмем на кнопку «OK».
Способ 4: оператор РОСТ
Ещё одной функцией, с помощью которой можно производить прогнозирование в Экселе, является оператор РОСТ. Он тоже относится к статистической группе инструментов, но, в отличие от предыдущих, при расчете применяет не метод линейной зависимости, а экспоненциальной. Синтаксис этого инструмента выглядит таким образом:
=РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы у данной функции в точности повторяют аргументы оператора ТЕНДЕНЦИЯ, так что второй раз на их описании останавливаться не будем, а сразу перейдем к применению этого инструмента на практике.
- Выделяем ячейку вывода результата и уже привычным путем вызываем Мастер функций. В списке статистических операторов ищем пункт «РОСТ», выделяем его и щелкаем по кнопке «OK».
Способ 5: оператор ЛИНЕЙН
Оператор ЛИНЕЙН при вычислении использует метод линейного приближения. Его не стоит путать с методом линейной зависимости, используемым инструментом ТЕНДЕНЦИЯ. Его синтаксис имеет такой вид:
=ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Последние два аргумента являются необязательными. С первыми же двумя мы знакомы по предыдущим способам. Но вы, наверное, заметили, что в этой функции отсутствует аргумент, указывающий на новые значения. Дело в том, что данный инструмент определяет только изменение величины выручки за единицу периода, который в нашем случае равен одному году, а вот общий итог нам предстоит подсчитать отдельно, прибавив к последнему фактическому значению прибыли результат вычисления оператора ЛИНЕЙН, умноженный на количество лет.
- Производим выделение ячейки, в которой будет производиться вычисление и запускаем Мастер функций. Выделяем наименование «ЛИНЕЙН» в категории «Статистические» и жмем на кнопку «OK».
Как видим, прогнозируемая величина прибыли, рассчитанная методом линейного приближения, в 2019 году составит 4614,9 тыс. рублей.
Способ 6: оператор ЛГРФПРИБЛ
Последний инструмент, который мы рассмотрим, будет ЛГРФПРИБЛ. Этот оператор производит расчеты на основе метода экспоненциального приближения. Его синтаксис имеет следующую структуру:
= ЛГРФПРИБЛ (Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Как видим, все аргументы полностью повторяют соответствующие элементы предыдущей функции. Алгоритм расчета прогноза немного изменится. Функция рассчитает экспоненциальный тренд, который покажет, во сколько раз поменяется сумма выручки за один период, то есть, за год. Нам нужно будет найти разницу в прибыли между последним фактическим периодом и первым плановым, умножить её на число плановых периодов (3) и прибавить к результату сумму последнего фактического периода.
- В списке операторов Мастера функций выделяем наименование «ЛГРФПРИБЛ». Делаем щелчок по кнопке «OK».
Прогнозируемая сумма прибыли в 2019 году, которая была рассчитана методом экспоненциального приближения, составит 4639,2 тыс. рублей, что опять не сильно отличается от результатов, полученных при вычислении предыдущими способами.
Мы выяснили, какими способами можно произвести прогнозирование в программе Эксель. Графическим путем это можно сделать через применение линии тренда, а аналитическим – используя целый ряд встроенных статистических функций. В результате обработки идентичных данных этими операторами может получиться разный итог. Но это не удивительно, так как все они используют разные методы расчета. Если колебание небольшое, то все эти варианты, применимые к конкретному случаю, можно считать относительно достоверными.

Источник
Цели урока:
- научить строить графики элементарных
математических функций с помощью табличного
процессора Excel; - показать возможности использования программы
Excel для решения задач по математике; - закрепить навыки работы с Мастером диаграмм.
Задачи урока:
- образовательная – знакомство учащихся с
основными приемами построения графиков функций
в программе Excel; - развивающие – формирование у учащихся
логического и алгоритмического мышления;
развитие познавательного интереса к предмету;
развитие умения оперировать ранее полученными
знаниями; развитие умения планировать свою
деятельность; - воспитательные – воспитание умения
самостоятельно мыслить, ответственности за
выполняемую работу, аккуратности при выполнении
работы.
Тип урока:
- комбинированный
Учебники:
Информатика. Базовый курс 2-е издание/Под ред.
С.В. Симоновича. – СПб.: Питер, 2004.-640с.:ил.
Технические и программные средства:
- Персональные компьютеры;
- Приложение Windows – электронные таблицы Excel.
- Проектор
Раздаточный материал:
- Карточки с индивидуальными заданиями на
построение графиков функций.
План урока.
- Организационный момент – 3 мин.
- Проверка домашнего задания –10 мин.
- Объяснение нового материала –20 мин.
- Применение полученных знаний –20 мин.
- Самостоятельная работа. – 20 мин
- Подведение итогов урока. Домашнее задание – 7
мин.
Ход урока
Организационный момент
Проверка готовности учащихся к уроку, отметка
отсутствующих, объявление темы и цели урока
Проверка домашнего задания. (фронтальный
опрос)
Вопросы для проверки
- Что представляет собой рабочая область
программы Excel? - Как определяется адрес ячейки?
- Как изменить ширину столбца, высоту строки?
- Как ввести формулу в Excel?
- Что такое маркер заполнения и для чего он нужен?
- Что такое относительная адресация ячеек?
- Что такое абсолютная адресация ячеек? Как она
задается? - Что такое колонтитулы? Как они задаются?
- Как задать поля печатного документа? Как
изменить ориентацию бумаги? - Что такое функциональная зависимость у = f(х)?
Какая переменная является зависимой, а какая
независимой? - Как ввести функцию в Excel?
- Что такое график функции у = f(х)?
- Как построить диаграмму в Excel?
Объяснение нового материала.
При объяснении нового материала может быть
использован файл Excel с шаблонами задач (Приложение 1), который
выводится на экран с помощью проектора
Сегодня мы рассмотрим применение табличного
процессора Excel для графиков функций. На
предыдущих практических вы уже строили
диаграммы к различным задачам, используя Мастер
диаграмм. Графики функций, так же как и диаграммы
строятся с помощью Мастера диаграмм программы
Excel.
Рассмотрим построение графиков функций на
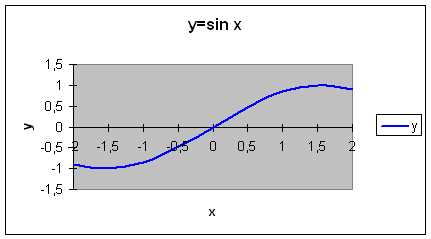
примере функции у = sin x.
Вид данного графика хорошо известен вам по
урокам математики, попробуем построить его
средствами Excel.
Программа будет строить график по точкам: точки
с известными значениями будут плавно
соединяться линией. Эти точки нужно указать
программе, поэтому, сначала создается таблица
значений функции у = f(х).
Чтобы создать таблицу, нужно определить
- отрезок оси ОХ, на котором будет строиться
график. - шаг переменной х, т.е. через какой промежуток
будут вычисляться значения функции.
Задача 1.Построить график функции у = sin
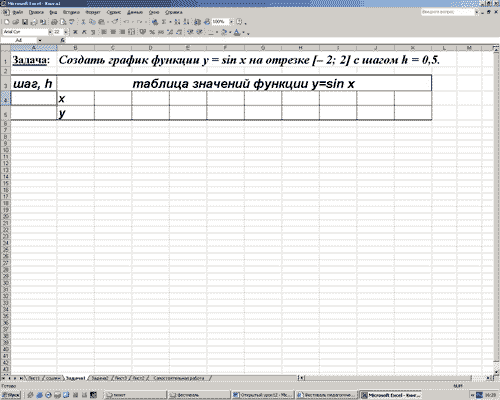
x на отрезке [– 2; 2] с шагом h = 0,5.
1. Заполним таблицу значений функции. В ячейку С4
введем первое значение отрезка: – 2
2. В ячейку D4 введем формулу, которая будет
добавлять к лево-стоящей ячейки шаг: = В4 + $A$4
3. Маркером заполнения ячейки D4 заполним влево
ячейки строки 4, до тех пор, пока получим значение
другого конца отрезка: 2.
4. Выделим ячейку С5, вызовем Мастер функций, в
категории математические выберем функцию SIN, в
качестве аргумента функции выберем ячейку С4.
5. Маркером заполнения распространим эту формулу
в ячейках строки 5 до конца таблицы.
Таким образом, мы получили таблицу аргументов
(х) и значений (у) функции у = sin x на отрезке [-2;2] с
шагом h = 0,5 :
| x | -2 | -1,75 | -1,5 | -1,25 | -1 | -0,75 | -0,5 | -0,25 | 0 | 0,25 | 0,5 | 0,75 | 1 | 1,25 | 1,5 | 1,75 | 2 |
| y | -0,9092 | -0,9839 | -0,9974 | -0,9489 | -0,8414 | -0,6816 | -0,4794 | -0,2474 | 0 | 0,2474 | 0,4794 | 0,6816 | 0,8414 | 0,9489 | 0,9974 | 0,9839 | 0,9092 |
6. Следующий шаг. Выделим таблицу и вызовем
Мастер диаграмм. На первом шаге выберем во
вкладке Нестандартные Гладкие графики.
7. На втором шаге во вкладке Ряд выполним:
В поле Ряд необходимо выделить ряд х и нажать на
кнопку “Удалить” (график изменений х нам не
нужен. График функции – это график изменения
значений у)
В поле Подписи оси Х нажать на кнопку.
Выделить в таблице ячейки со значениями х и
нажмите на кнопку . Подписи по горизонтальной оси
станут такими, как у нас в таблице.
8. На третьем шаге заполним вкладку Заголовки.
9. Пример полученного графика.
На самом деле пока это мало похоже на график
функции в нашем привычном понимании.
Для форматирования графика:
- Вызовем контекстное меню оси ОУ. Затем, выберем
пункт Формат оси…. Во вкладке Шкала установим:
цена основного деления: 1. Во вкладке Шрифт
установим размер шрифта 8пт. - Вызовем контекстное меню оси ОХ. Выберем пункт
Формат оси….
Во вкладке Шкала установим: пересечение с осью
ОУ установите номер категории 5 (чтобы ось ОУ
пересекала ось ОХ в категории с подписью 0, а это
пятая по счету категория).
Во вкладке шрифт установите размер шрифта 8пт.
Нажмите на кнопку ОК.
Остальные изменения выполняются аналогично.
Для закрепления рассмотрим еще одну задачу на
построение графика функций. Эту задачу
попробуйте решить самостоятельно, сверяясь с
экраном проектора.
Применение полученных знаний.
Пригласить к проектору студента и
сформулировать следующую задачу.
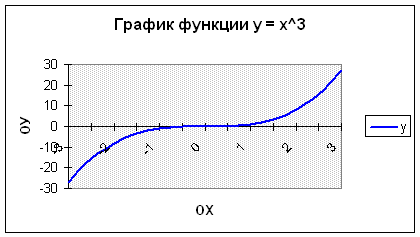
Задача 2. Построить график функции у = х3
на отрезке [– 3; 3] с шагом h = 0,5.
1. Создать следующую таблицу: Создать таблица
значений функции у = f(х).
2. В ячейку С4 ввести первое значение отрезка: –3
3. В ячейку D4 ввести формулу, которая будет
добавлять к лево-стоящей ячейки шаг: = В4 + $A$4
4. Маркером заполнения ячейки D3 заполнить влево
ячейки строки 3, до тех пор, пока не будет получено
значение другого конца отрезка: 3.
5. В ячейку С5 ввести формулу вычисления значения
функции: = С4^3
6. Маркером заполнения скопировать формулу в
ячейки строки 5 до конца таблицы.
Таким образом, должна получиться таблица
аргументов (х) и значений (у) функции у = х3 на
отрезке [–3;3] с шагом h = 0,5:
| х | -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
| y | -27 | -15,625 | -8 | -3,375 | -1 | -0,125 | 0 | 0,125 | 1 | 3,375 | 8 | 15,625 | 27 |
7. Выделить таблицу и вызвать мастер диаграмм.
На первом шаге выбрать во второй вкладке Гладкие
графики.
8. На втором шаге во вкладке Ряд выполнить:
9. На третьем шаге заполнить вкладку Заголовки.
10. Пример полученного графика:
11. Оформить график.
12. Установить параметры страницы и размеры
диаграмм таким образом, что бы все поместилось на
одном листе альбомной ориентации.
13. Создать колонтитулы для данного листа (Вид
Колонтитулы…):
14. Верхний колонтитул слева: график функции у = x3
Сохранить документ своей папке под именем
График.
Самостоятельная работа.
Работа по карточкам с индивидуальными
заданиями. (Приложение 2)
Пример карточки, с задачей в общем виде,
выводится на экран с помощью проектора.
1. Построить график функции y=f(x) на отрезке [a;b] с
шагом h=c
2. Установить параметры страницы и размеры
графика таким образом, что бы все поместилось на
одном листе альбомной ориентации.
3. Создать колонтитулы для данного листа (Вид
Колонтитулы…):
- Верхний колонтитул слева: график функции y=f(x)
- Нижний колонтитул в центре: ваши Ф.И.О. и дата
4. Сохранить в своей папке под именем “Зачетный
график”
5. Вывести документ на печать.
После выполнения задания правильность каждого
варианта проверяется с помощью проектора.
Подведение итогов.
Домашнее задание.
Оценки за урок.
Содержание:
Полная схема исследования функции:
- Найти область определения функции.
- Исследовать функцию на чётность и периодичность.
- Найти точки пересечения графика функции с осями координат.
- Найти интервалы знакопостоянства.
- Найти первую производную, промежутки возрастания и убывания, точки экстремума и экстремумы функции.
- Найти вторую производную. Определить интервалы выпуклости графика функции и точки перегиба.
- Исследовать поведение функции на концах промежутков определения.
- Найти асимптоты графика функции.
- Построить график функции.
Пример:
Исследуйте функцию
Решение:
1) Область определения функции:
2) Функция ни чётная, ни нечётная, ни периодическая.
3) 
4)
5) Чтобы найти производную функции, запишем её в виде
Поскольку в точке 
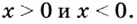
Функция имеет две критические точки:
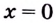
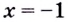
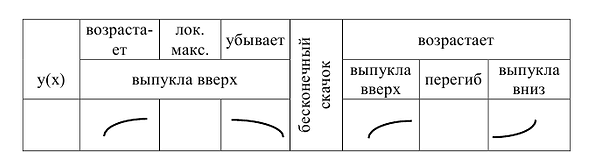
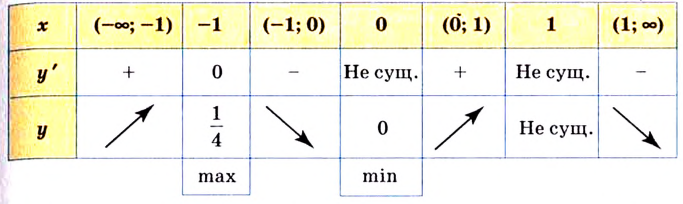
Составим и заполним таблицу для первой производной
Из таблицы видно, что функция возрастает на промежутках 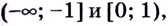
Первая производная при переходе через точку 
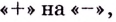
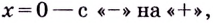
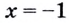
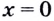
6) Найдём вторую производную:
Функция имеет две критические точки второго рода: 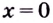

Составим и заполним таблицу для второй производной
Как видим из таблицы, кривая выпуклая на промежутке 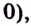
Вторая производная при переходе через точку 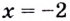

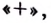
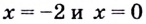
7) Исследуем поведение заданной функции на концах промежутков определения:
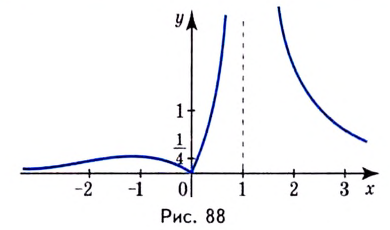
8) Найдём асимптоты. Функция не определена в точке
Поскольку 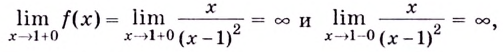
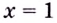
Поскольку 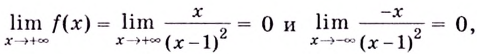
9) Используя полученные данные, построим график функции {рис. 88).
Пример:
Найдите интервалы выпуклости, вогнутости и точки перегиба кривых:
Решение:
1) Область определения функции —
2) Найдём первую и вторую производные. Имеем: 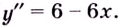
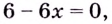
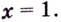
3) Определим знак второй производной на каждом из интервалов 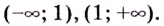
Если 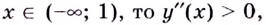
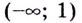
Если 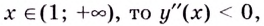
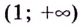
Точка 
Следовательно, 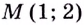
1) Область определения функции—
2) Найдём критические точки второго рода:
Как видим, вторая производная существует на множестве всех действительных чисел и ни в одной точке в ноль не превращается. А потому критических точек второго рода нет. Следовательно, нет и точек перегиба. На всей области определения 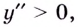
Пример:
Найдите асимптоты кривой
Решение:
Область определения функции — 
Найдем наклонную асимптоту:
Следовательно, прямая 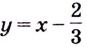
Исследование функций
Процесс управления требует от менеджера компактного представления разносторонних знаний из разных областей хозяйственной, управленческой, налоговой, коммерческой и других видов деятельности в виде разнообразных функциональных зависимостей.
В процессе такой деятельности перед менеджером возникают задачи тактического и стратегического планирования, оценки возможностей предприятия и конкурентов, оптимального распределения ресурсов, разумного реагирования на налоговую политику, выбора ценовой и инвестиционной политики и др.
Важную роль при этом играет исследование функций, используемых при построении математической модели рассматриваемой проблемы. Такое исследование проводится с учетом свойств конкретных функций и позволяет уточнить сформулированную математическую задачу, решая которую (с учетом выбранного метода решения), рассчитывают получить определенный результат, требующий в дальнейшем интерпретации в терминах исследуемой проблемы.
Все это связано с выявлением таких свойств функций, используемых в модели, как характер изменения (монотонность), наличие точек с особыми свойствами (стационарные точки, экстремумы), геометрические свойства (выпуклость графика функции) и другие.
Настоящий раздел посвящен исследованию функций методами дифференциального исчисления и использованию полученных навыков для решения задач.
Монотонность функции
Функция y = y (x) называется возрастающей на промежутке l, если 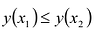
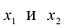
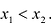
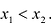
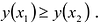
Теорема. Если функция у = f(x) непрерывна на отрезке [a,b], дифференцируема на интервале (a,b), то для того, чтобы f(x) была возрастающей (убывающей) необходимо и достаточно, чтобы 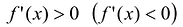
Дифференцируемая функция является возрастающей на промежутке l тогда и только тогда, когда
Пример:
Найти промежутки возрастания и убывания функции
Вычислим:
Точки 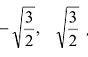
Производная 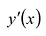
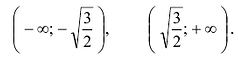
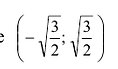
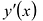
Локальный экстремум
Точка 
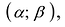

Точка 
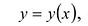
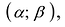

Точки локального минимума и локального максимума называются точками локального экстремума.
Необходимым условием локального экстремума дифференцируемой функции является выполнение равенства 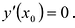
Решения этого уравнения называют стационарными точками.
Исследование стационарных точек
I правило. Если при возрастании .v при переходе через стационарную точку х0 производная у'(х) меняет знак с + на – , то 
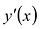

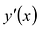

II правило. Если вторая производная 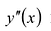


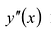


Точками локального экстремума функции могут быть такие точки, в которых производная не существует или обращается в бесконечность. Исследовать такие точки можно по I правилу. Экстремум в такой точке называется острым экстремумом.
Пример:
Найти экстремум функции 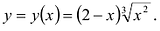
Функция имеет стационарную точку 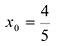
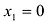
Поскольку 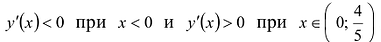
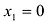
Это будет острый минимум.
При переходе через стационарную точку 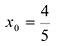
Глобальный экстремум
Непрерывная на отрезке [a;b] функция у = y(x) принимает свое наибольшее значение 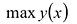
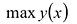
- Находят стационарные точки
функции;
- Находят точки
в которых производная у'(x) не существует или обращается в бесконечность;
- Вычисляют значения:
– и выбирают среди этих чисел наибольшее и наименьшее.
Это и будут 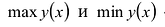
Пример:
Найти наибольшее и наименьшее значения функции 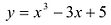
Вычисляем 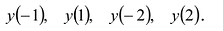
Выпуклость и перегибы графика функции
Графиком функции у = у(х), заданной на множестве X, называют множество точек плоскости с координатами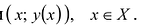
Если на промежутке l вторая производная у'(х) положительна, то график является выпуклым вниз на этом промежутке. Если .у “(x) < 0 на промежутке l, то график является выпуклым вверх на промежутке l.
Точка М(с;у{с)) может быть точкой перегиба только в том случае, когда у'(x) = 0, либо у”(x) не существует – необходимое условие перегиба. Однако равенство нулю или не существование второй производной в точке с не означает еще, что в точке 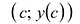
Пример:
Найти промежутки выпуклости и точки перегиба графика функции
Вычислим вторую производную .
Точки -1 и 1 разбивают числовую прямую на три промежутка: 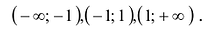
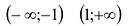
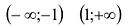
В точках 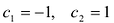
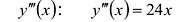
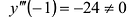
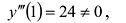
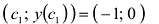
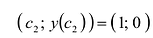
Исследование функции и построение графика
График функции у = у(х)у заданной на множестве X, т.е. множество точек плоскости с координатами 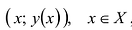
Для построения графика функции у = у{х) выясняют особенности поведения функции. Существенную роль при этом играют характерные точки: концевые точки промежутков задания функции, точки разрыва, стационарные точки и точки недифференцируемости функции и се производной и т.д. По этим точкам выделяются участки однообразного поведения функции, а именно: промежутки ее непрерывности; промежутки, на которых у'(х) и y”(x) сохраняют знак, что позволяет изучить характер монотонности функции и направление ее выпуклости.
Построение графика функции может быть осуществлено по следующему плану.
Если функция задана аналитическими выражениями, то выясняют естественную область определения функции, т.е. множество значений аргумента х, при которых y(x) имеет смысл.
Если функция периодическая, то находят ее период, т.е. число 
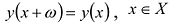
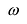
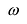
Для четной функции: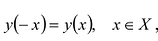
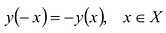
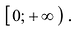
Используя симметричное отражение относительно оси Oy для четной функции и относительно точки О – для нечетной функции.
Находят точки разрыва и промежутки, на которых она непрерывна. Выясняют характер точек разрыва. Вычисляют предельные значения функции в граничных точках множества X (если таковые имеются). Находят вертикальные асимптоты (в точках бесконечного скачка). Если X ограничено, то вычисляют пределы функции при 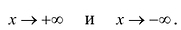
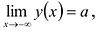
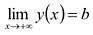
Аналогично находят коэффициенты правосторонней асимптоты (нужно вычислить пределы при 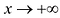
Вычисляют производную 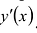
Вычисляют вторую производную . Находят критические точки производной 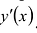
Исследуя стационарные точки функции у(х), находят точки локального экстремума и локальные экстремальные значения функции. Для этого можно изучить поведение производной 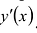
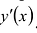
Опираясь на характерные точки функции, строят таблицу, в которую вносят все особенности функции.
На координатную плоскость в выбранном масштабе наносят характерные точки функции, асимптоты и строят график, руководствуясь п. 1-6. Если нужно, строят дополнительно несколько точек графика
Пример:
Построить график функции
I. Область определения
Функция не является периодической, четной, нечетной.
II. Поскольку 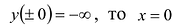
Так как 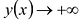
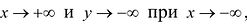
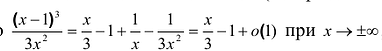
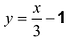
3. 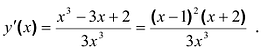
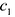
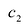
IV. 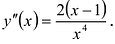
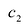
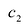
V. Строим таблицу, в которой выделены промежутки однообразного поведения функции и ее характерные точки.
VI. На координатной плоскости отмечаем точки локального максимума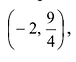
Строим схематично график функции с учетом выясненных ранее особенностей ее поведения.
Интерполяция и аппроксимация функций
При табличной форме задания функции часто возникает ситуация, когда аргумент функции задан с большей точностью, чем позволяет таблица. В этом случае приходится прибегнуть к интерполяции (или интерполированию) – приближенному нахождению неизвестных значений функций по известным ее значениям в заданных точках.
Наиболее простым является линейное интерполирование, при котором допускается, что приращение функции пропорционально приращению аргумента. Если заданное значение д: лежит между приведенными в таблице значениями 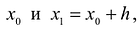
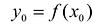
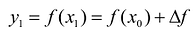
Если по заданным значениям функции необходимо найти приближенное значение аргумента, то такая операция называется обратным интерполированием.
В общем виде интерполяционная задача состоит в построении обобщенного многочлена Р(х), принимающего значения исследуемой функции у = f(x) на конечном множестве 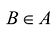
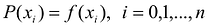
В частности, если A = [a,b] а множество 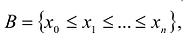
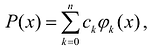
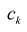
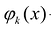
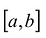
Условия интерполирования 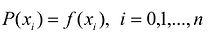
К системе можно применить векторно-матричную форму записи 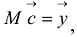
Если семейство функций 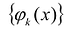
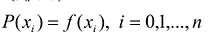
- Заказать решение задач по высшей математике
Интерполяционный полином Лагранжа
Примером наипростейшей базисной системы функций можно считать систему
Утверждение 1. Если два многочлена степени 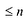
Пусть многочлены P(x) и Q(x) степени n, 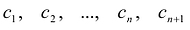
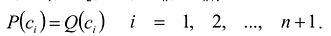
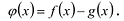
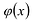
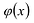
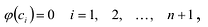
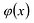
Это утверждение позволяет доказать следующую теорему.
Теорема. Для каждого натурального числа n существует один и только один многочлен степени 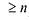
Пусть 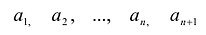
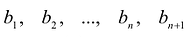
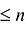
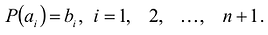
Степень 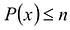
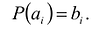
Пример. Построить интерполяционный многочлен Лагранжа по заданной таблице значений:
Формула Тейлора
Задача аппроксимации (приближенного вычисления) функции в окрестности данной точки, которую часто называют рабочей точкой, является одной из основных задач математического анализа. Для дифференцируемых функций эта задача решается с помощью формулы Тейлора.
Поскольку функция дифференцируема, то ее приращение представимо в виде:
т.е. существует многочлен первой степени 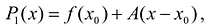
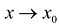
В более общем виде задачу можно сформулировать следующим образом. Пусть функция определена в некоторой окрестности точки 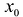
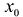
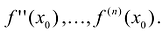
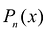
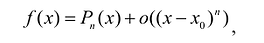
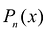
Предположим, что искомый аппроксимационный многочлен имеет вид:
Тогда:
Тогда, с учетом условий (5), можно получить:
Таким образом, если в аппроксимационый полином подставить полученные значения коэффициентов, то полином можно записать следующим образом:
Этот многочлен называется многочленом Тейлора функции f. Можно показать, что он удовлетворяет условию
Рассмотрим функцию 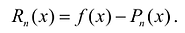
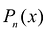
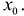
Для того, чтобы убедиться, что 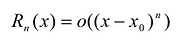
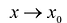
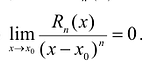
Полученные выводы можно сформулировать в виде теоремы.
Теорема. Пусть функция f определена в некоторой окрестности точки 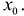
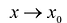
Полученный многочлен называется формулой Тейлора n -го порядка с остаточным членом в форме Пеано.
Если 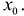
Для остаточного члена формулы Тейлора существуют и другие представления. Так, если функция f имеет производную n-го порядка в окрестности точки 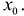
Основные разложения
Используя основные разложения можно получать формулы Тейлора для других функций. При этом используют то, что:
Понятие об эмпирических формулах
На практике часто возникает задача аппроксимации данных о зависимости между двумя переменными у их, полученных опытным путем и представленных в табличной форме. Это могут быть результаты опыта, наблюдений, статистической обработки результатов и т.д. При этом необходимо зависимость между этими переменными представить в виде аналитического выражения функции у = f(x) так, чтобы эта формула наилучшим образом отражала общую тенденцию зависимости у от fx, исключив при этом случайные отклонения, связанные с неизбежными погрешностями измерений или статистических наблюдений.
Формулы, служащие для аналитического представления опытных данных, называются эмпирическими. Задача нахождения эмпирических формул выполняется в два этапа:
- Установление вида зависимости у = f(x);
- Определение неизвестных параметров этой функции.
При определении вида эмпирической функции у-f{x)
обычно предполагается, что это наиболее гладкая кривая, согласованная с экспериментальными данными. Кроме того, для выбора этой функции привлекаются дополнительные соображения, как правило, не математического характера (теоретические модели, опыт предшествующих исследований, и т.п.).
Эта задача может быть решена в ходе регрессионного анализа, который изучается в курсе теории вероятностей, но решить ее можно и математическими методами. Согласно наиболее распространенному и теоретически обоснованному методу наименьших квадратов, в качестве неизвестных параметров функции у = f (х) выбираются такие значения, которые соответствуют минимальному значению суммы квадратов отклонений эмпирических значений у. от значений функции 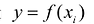
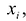
Разность 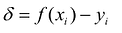
В ходе решения задачи отыскания оптимальных параметров аппроксимационной функции y = f(x) возникает необходимость поиска экстремума функции нескольких переменных, поэтому, прежде чем решать эту задачу для конкретных эмпирический функций, необходимо рассмотреть свойства функций нескольких переменных.
- Пространство R”
- Неопределённый интеграл
- Методы интегрирования неопределенного интеграла
- Определённый интеграл
- Квадратичные формы – определение и понятие
- Системы линейных уравнений с примерами
- Линейное программирование
- Дифференциальное исчисление функций одной переменной



















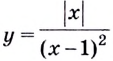
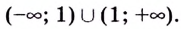
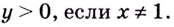
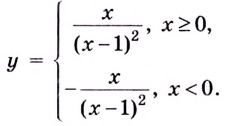
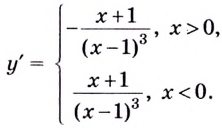
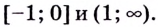
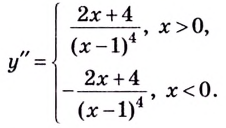

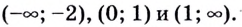
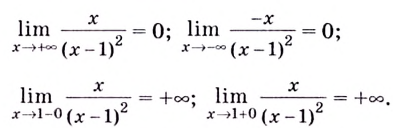
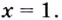
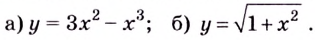
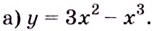
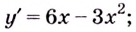
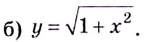
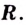
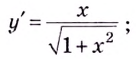
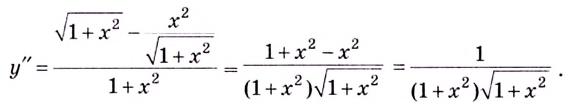
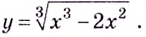
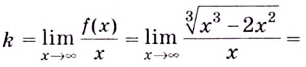
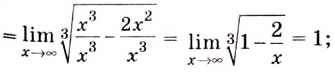

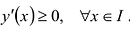
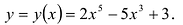
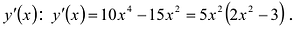
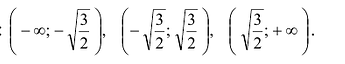
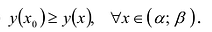
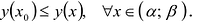
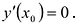
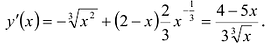
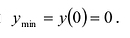
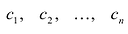 функции;
функции;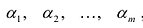 в которых производная у'(x) не существует или обращается в бесконечность;
в которых производная у'(x) не существует или обращается в бесконечность;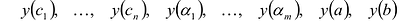 – и выбирают среди этих чисел наибольшее и наименьшее.
– и выбирают среди этих чисел наибольшее и наименьшее.