Как найти точки касания вписанной окружности

Как найти точки касания вписанной окружности

Окружность, вписанная в треугольник. Основное свойство биссектрисы угла

Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла

Определение 1 . Биссектрисой угла называют луч, делящий угол на две равные части.

Теорема 1 (Основное свойство биссектрисы угла) . Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).

Доказательство . Рассмотрим произвольную точку D , лежащую на биссектрисе угла BAC , и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE , а гипотенуза AD – общая. Следовательно,

что и требовалось доказать.

Теорема 2 (обратная теорема к теореме 1) . Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).

Доказательство . Рассмотрим произвольную точку D , лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE , а гипотенуза AD – общая. Следовательно,

что и требовалось доказать.

Определение 2 . Окружность называют окружностью, вписанной в угол , если она касается касается сторон этого угла.

Теорема 3 . Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.

Доказательство . Пусть точка D – центр окружности, вписанной в угол BAC , а точки E и F – точки касания окружности со сторонами угла (рис.3).

Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности ), а гипотенуза AD – общая. Следовательно

что и требовалось доказать.

Замечание . Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных , проведенных к окружности из одной точки, равны.

Определение 3 . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.

Теорема 4 . В любом треугольнике все три биссектрисы пересекаются в одной точке.

Доказательство . Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC , и обозначим точку их пересечения буквой O (рис. 4).

Опустим из точки O перпендикуляры OD , OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC , то в силу теоремы 1 справедливо равенство:

Поскольку точка O лежит на биссектрисе угла ACB , то в силу теоремы 1 справедливо равенство:

Следовательно, справедливо равенство:

откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC . Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать

Определение 4 . Окружностью, вписанной в треугольник , называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности .

Следствие . В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.

Формулы для радиуса окружности, вписанной в треугольник

Формулы, позволяющие найти радиус вписанной в треугольник окружности , удобно представить в виде следующей таблицы.

a, b, c – стороны треугольника,
S – площадь,
r – радиус вписанной окружности,
p – полупериметр

.

a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Фигура Рисунок Формула Обозначения
Произвольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Прямоугольный треугольник

где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр
.

где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр
.

где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Произвольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Прямоугольный треугольник
Произвольный треугольник

где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр
.

где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр
.

Равнобедренный треугольник

Равносторонний треугольник

где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Прямоугольный треугольник

Вывод формул для радиуса окружности, вписанной в треугольник

Теорема 5 . Для произвольного треугольника справедливо равенство

где a, b, c – стороны треугольника, r – радиус вписанной окружности, – полупериметр (рис. 6).

с помощью формулы Герона получаем:

что и требовалось.

Теорема 6 . Для равнобедренного треугольника справедливо равенство

где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).

то, в случае равнобедренного треугольника, когда

что и требовалось.

Теорема 7 . Для равностороннего треугольника справедливо равенство

где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).

то, в случае равностороннего треугольника, когда

что и требовалось.

Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.

Теорема 8 . Для прямоугольного треугольника справедливо равенство

Доказательство . Рассмотрим рисунок 9.

Поскольку четырёхугольник CDOF является прямоугольником прямоугольником , у которого соседние стороны DO и OF равны, то этот прямоугольник – квадрат квадрат . Следовательно,

В силу теоремы 3 справедливы равенства

Следовательно, принимая также во внимание теорему Пифагора, получаем

что и требовалось.

Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.

Please wait.

We are checking your browser. mathvox.ru

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6cfef275ba737b5f • Your IP : 85.95.179.65 • Performance & security by Cloudflare

Вписанная окружность

Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.

Окружность, точно можно вписать в такие геометрические фигуры, как:

  • Треугольник
  • Выпуклый, правильный многоугольник
  • Квадрат
  • Равнобедренная трапеция
  • Ромб

В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.

Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.

Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.

Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.

Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.

Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.

Свойства вписанной окружности

В треугольник

  1. В любой треугольник может быть вписана окружность, причем только один раз.
  2. Центр вписанной окружности — точка пересечения биссектрис треугольника.
  3. Вписанная окружность касается всех сторон треугольника.
  4. Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac<1><2>(a+b+c) cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

  • Центр окружности вписанной в треугольник равноудален от всех сторон.
  • Точка касания — это точка, в которой соприкасается
    окружность и любая из сторон треугольника.
  • От центра вписанной окружности можно провести
    перпендикуляры к любой точке касания.
  • Вписанная в треугольник окружность делит стороны
    треугольника на 3 пары равных отрезков.
  • Вписанная и описанная около треугольника окружность тесно взаимосвязаны.
    Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:

    с — расстояние между центрами вписанной и описанной окружностей треугольника.
    R — радиус описанной около треугольника.
    r — радиус вписанной окружности треугольника.

    В четырехугольник

    1. Не во всякий четырехугольник можно вписать окружность.
    2. Если у четырехугольника суммы длин его противолежащих
      сторон равны, то окружность, может быть, вписана (Теорема Пито).
    3. Центр вписанной окружности и середины двух
      диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона).
    4. Точка пересечения биссектрис — это центр вписанной окружности.
    5. Точка касания — это точка, в которой соприкасается
      окружность и любая из сторон четырехугольника.
    6. Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:

    [ S = frac<1><2>(a+b+c+d)cdot r = pr ]

    p — полупериметр четырехугольника.
    r — радиус вписанной окружности четырехугольника.

  • Точка касания вписанной окружности, которая лежит на любой из сторон,
    равноудалены от этой конца и начала этой стороны, то есть от его вершин.

    • Примеры вписанной окружности

    Примеры описанного четырехугольника:
    равнобедренная трапеция, ромб, квадрат.

    Примеры описанного треугольника:
    равносторонний    , равнобедренный,
    прямоугольный треугольники.

    Верные и неверные утверждения

    1. Радиус вписанной окружности в треугольник и радиус вписанной
      в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
    2. Любой параллелограмм можно вписать в окружность. Неверное утверждение.
    3. В любой четырехугольник можно вписать окружность. Неверное утверждение.
    4. В любой ромб можно вписать окружность. Верное утверждение.
    5. Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
    6. Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
    7. Угол вписанный в окружность равен соответствующему центральному
      углу опирающемуся на ту же дугу. Неверное утверждение.
    8. Радиус вписанной окружности в прямоугольный треугольник равен
      половине разности суммы катетов и гипотенузы. Верное утверждение.
    9. Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
    10. Вписанная окружность в треугольник имеет в общем
      три общие точки со всеми сторонами треугольника. Верное утверждение.

    Окружность вписанная в угол

    Окружность вписанная в угол — это окружность, которая
    лежит внутри этого угла и касается его сторон.

    Центр окружности, которая вписана в угол,
    расположен на биссектрисе этого угла.

    К центру окружности вписанной в угол, можно провести,
    в общей сложности два перпендикуляра со смежных сторон.

    Длина диаметра, радиуса, хорды, дуги вписанной окружности
    измеряется в км, м, см, мм и других единицах измерения.

    [spoiler title=”источники:”]

    http://mathvox.ru/geometria/treugolniki/glava-13/tochki-kasaniya-vpisannoi-okrujnosti-svoistvo-2/

    http://colibrus.ru/vpisannaya-okruzhnost/

    [/spoiler]

    Источник

    Для решения задач повышенной сложности часто требуются знания решений некоторых вспомогательных задач. Эти задачи, как правило, в учебнике Л.С. Атанасяна не входят в основной параграф и идут как разобранные (решенные) номера.

    В этой статье разберем одну такую задачу, а в следующий раз рассмотрим ее применение для решения задания повышенной сложности.

    ЗАДАЧА:

    В треугольнике со сторонами BC=a, CA=b, AB=c найдите расстояния от вершин треугольника до точек касания вписанной в него окружности.

    Вспомогательная задача по геометрии. Вписанная окружность. Расстояние от вершин до точек касания.

    Условие можно кратко записать так:

    BC=a, CA=b, AB=c, окр О вписана в △АВС, K,L,M – точки касания.

    Найти: СК, АК, CL,BL,CM,BM.

    Решение:

    Т.к. K,L,M – точки касания, то по свойству отрезков касательных AK=AL, BL=BM, CK=CM.

    Вспомогательная задача по геометрии. Вписанная окружность. Расстояние от вершин до точек касания.

    Тогда

    ВС=СМ+MB

    или

    ВС=СK+BL.

    C другой стороны СК=AC-AK и BL=AB-AL.

    ВС=(AC-AK)+(AB-AL)=AC+AB-AK-AL.

    Учтем, что AK=AL.

    BC=AC+AB-2AK

    AK=(AC+AB-BC)/2

    AK=(b+c-a)/2

    Немного доработав это выражение, получим универсальную формулу:

    AK=AL=(b+c+a-2a)/2

    Значит отрезок АК= AL=p-a, где р- полупериметр.

    Аналогично получается

    BL=BM=p-b

    CK=CM=p-c

    Словами это можно сформулировать так:

    Расстояние от вершины до точки касания вписанной в треугольник окружности равно разности полупериметра и длины противолежащей стороны.

    Если вы знаете того, кто готовится к ОГЭ не забудьте поделиться с ним этой информацией. Всегда пригодится.

    Продолжение следует…

    Не забудь нажать на пальчик вверх после прочтения и подписаться. За это отдельная благодарность

    (✿◠‿◠)

    Источник

    Треугольник (чёрный) с вписанной окружностью (синей), инцентр (I), вневписанными окружностями (оранжевые), эксцентры (JA,JB,JC), внутренние биссектрисы (красные) и внешние биссектрисы (зелёные)

    Вписанная в треугольник окружность — окружность внутри треугольника, касающаяся всех его сторон; наибольшая окружность, которая может находиться внутри треугольника. Центр этой окружности является точкой пересечения биссектрис треугольника и называется инцентром треугольника.

    Вневписанная окружность треугольника — окружность, лежащая вне треугольника и касающаяся одной стороны треугольника и продолжения двух других сторон[en]. Любой треугольник имеет три различные вневписанные окружности, каждая из которых касается своей стороны треугольника.
    Центром вневписанной окружности является пересечение биссектрисы одного внутреннего угла[en] и биссектрис двух других внешних углов[en]. Поскольку биссектриса внутреннего угла перпендикулярна биссектрисе смежного внешнего угла, центр вписанной окружности вместе с тремя центрами вневписанных окружностей образуют ортоцентричную систему[en][1].

    Не все многоугольники с числом сторон более трёх имеют вписанную окружность. Те, которые имеют, называются описанными.

    Связь с площадью треугольника[править | править код]

    Радиусы вписанных и вневписанных окружностей имеют тесную связь с площадью треугольника[2].

    Вписанная окружность[править | править код]

    Вики вписанная окружность7.png

    Пусть triangle ABC имеет вписанную окружность радиуса r с центром I.
    Пусть a — длина BC, b — длина AC, а c — длина AB.
    Пусть вписанная окружность касается AB в некоторой точке C′, тогда
    angle AC'I является прямым.
    Тогда радиус C’I будет высотой треугольника
    triangle IAB.
    Таким образом,
    triangle IAB
    имеет основание длины c и высоту r, а следовательно, его площадь равна
    {tfrac {1}{2}}cr.
    Подобным же образом
    triangle IAC
    имеет площадь
    {tfrac {1}{2}}br
    и
    triangle IBC
    имеет площадь {tfrac {1}{2}}ar.
    Поскольку эти три треугольника разбивают triangle ABC, получаем, что

    {displaystyle Delta ={frac {1}{2}}(a+b+c)r=pr,}

    где Delta  — площадь triangle ABC, а {displaystyle p={frac {1}{2}}(a+b+c)} — его полупериметр.

    Чтобы получить альтернативную формулу, рассмотрим triangle IC'A. Это прямоугольный треугольник, у которого один из катетов равен r, а другой равен {displaystyle rcdot mathrm {ctg} {frac {angle A}{2}}}. То же самое верно для triangle IB'A. Весь треугольник состоит из 6 таких треугольников, и общая площадь составляет:

    {displaystyle Delta =r^{2}cdot (mathrm {ctg} {frac {angle A}{2}}+mathrm {ctg} {frac {angle B}{2}}+mathrm {ctg} {frac {angle C}{2}})}

    Вневписанные окружности[править | править код]

    Пусть вневписанная окружность, касающаяся стороны AB, касается продолжения стороны AC в точке G, и пусть радиус этой окружности равен r_{c}, а её центр — I_{c}. Тогда I_{c}G является высотой треугольника triangle ACI_{c},
    так что triangle ACI_{c} имеет площадь {tfrac {1}{2}}br_{c}. По тем же причинам
    triangle BCI_{c}
    имеет площадь
    {tfrac {1}{2}}ar_{c},
    а triangle ABI_{c}
    имеет площадь
    {tfrac {1}{2}}cr_{c}.
    Тогда

    {displaystyle Delta ={frac {1}{2}}(a+b-c)r_{c}=(p-c)r_{c}}.

    Таким образом, ввиду симметрии,

    {displaystyle Delta =pr=(p-a)r_{a}=(p-b)r_{b}=(p-c)r_{c}}.

    По теореме косинусов получаем

    cos A={frac {b^{2}+c^{2}-a^{2}}{2bc}}

    Комбинируя это с тождеством sin ^{2}A+cos ^{2}A=1, получим

    sin A={frac {sqrt {-a^{4}-b^{4}-c^{4}+2a^{2}b^{2}+2b^{2}c^{2}+2a^{2}c^{2}}}{2bc}}

    Но Delta ={tfrac {1}{2}}bcsin A, так что

    {displaystyle {begin{aligned}Delta &={frac {1}{4}}{sqrt {-a^{4}-b^{4}-c^{4}+2a^{2}b^{2}+2b^{2}c^{2}+2a^{2}c^{2}}}\&={frac {1}{4}}{sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}\&={sqrt {p(p-a)(p-b)(p-c)}},end{aligned}}}

    и это формула Герона вычисления площади треугольника по его сторонам.

    Комбинируя формулу Герона с {displaystyle pr=Delta }, получим

    {displaystyle r^{2}={frac {Delta ^{2}}{p^{2}}}={frac {(p-a)(p-b)(p-c)}{p}}}.

    Аналогично, {displaystyle (p-a)r_{a}=Delta } даёт

    {displaystyle r_{a}^{2}={frac {p(p-b)(p-c)}{p-a}}}.

    Из этих формул видно, что вневписанные окружности всегда больше вписанной и наибольшая окружность соответствует самой длинной стороне, а самая наименьшая из вневписанных окружностей соответствует самой маленькой стороне. Дальнейшее комбинирование формул приводит к:[3]

    Delta ={sqrt {rr_{a}r_{b}r_{c}}}.

    Отношение площади вписанной окружности к площади треугольника меньше или равно {frac {pi }{3{sqrt {3}}}}, и равенство достигается только на правильных треугольниках[4].

    Связанные построения[править | править код]

    Окружность девяти точек и точка Фейербаха[править | править код]

    • Теорема Эйлера об окружности Эйлера. Середины отрезков высот от ортоцентра до вершин треугольника называются точками Эйлера. Основания медиан, основания высот и точки Эйлера лежат на одной окружности, называемой окружностью девяти точек[5].
    • Теорема Фейербаха. Окружность девяти точек касается всех трёх вневписанных окружностей, а также вписанной окружности в четырёх разных точках. Одна из них – точка касания окружности Эйлера и вписанной окружности известна как точка Фейербаха.

    Треугольник и точка Жергонна[править | править код]

    Треугольник ΔABC с вписанной окружностью (синяя), и её центр (синий, I), треугольник точек касания (красный, ΔTaTbTc) и точка Жергонна (зелёная, Ge)

    Треугольник Жергонна (для треугольника ABC) определяется тремя точками касания вписанной окружности на трёх сторонах.
    Эти вершины обозначим TA, и т. д..
    Точка TA лежит напротив вершины A.

    Этот треугольник Жергонна TATBTC известен также как треугольник касаний треугольника ABC.

    Три прямые ATA, BTB и CTC пересекаются в одной точке — точке Жергонна и обозначается Ge — X(7). Точка Жергонна лежит внутри открытого ортоцентроидного круга[en] с выколотым центром[6].

    Интересно, что точка Жергонна треугольника является точкой пересечения симедиан треугольника Жергонна. Полный набор свойств точки Жергонна можно найти в статье Декова[7].

    Трилинейные координаты вершин треугольника касаний задаются формулами

    • вершина A=0:sec ^{2}left({frac {B}{2}}right):sec ^{2}left({frac {C}{2}}right)
    • вершина B=sec ^{2}left({frac {A}{2}}right):0:sec ^{2}left({frac {C}{2}}right)
    • вершина C=sec ^{2}left({frac {A}{2}}right):sec ^{2}left({frac {B}{2}}right):0

    Трилинейные координаты точки Жергонна

    sec ^{2}left({frac {A}{2}}right):sec ^{2}left({frac {B}{2}}right):sec ^{2}left({frac {C}{2}}right),

    или, эквивалентно, по теореме синусов,

    {frac {bc}{b+c-a}}:{frac {ca}{c+a-b}}:{frac {ab}{a+b-c}}.

    Точка Жергонна является изотомическим сопряжением точки Нагеля.

    Треугольник и точка Нагеля[править | править код]

    Треугольник Нагеля (см. рис. выше) для треугольника ABC определяется вершинами TA, TB и TC, которые являются точками касания вневписанных окружностей треугольника ABC и точка XA противоположна стороне A, и т. д. Описанная вокруг треугольника TATBTC окружность называется окружностью Мандарта (частный случай эллипса Мандарта). Три прямые ATA, BTB и CTC делят периметр пополам и пересекаются в одной точке Нагеля Na — X(8).

    Трилинейные координаты точек касания треугольника вневписанными окружностями задаются формулами

    • вершина A=0:csc ^{2}left({frac {B}{2}}right):csc ^{2}left({frac {C}{2}}right)
    • вершина B=csc ^{2}left({frac {A}{2}}right):0:csc ^{2}left({frac {C}{2}}right)
    • вершина C=csc ^{2}left({frac {A}{2}}right):csc ^{2}left({frac {B}{2}}right):0

    Трилинейные координаты точки Нагеля задаются формулами

    csc ^{2}left({frac {A}{2}}right):csc ^{2}left({frac {B}{2}}right):csc ^{2}left({frac {C}{2}}right),

    или, эквивалентно, по теореме синусов,

    {frac {b+c-a}{a}}:{frac {c+a-b}{b}}:{frac {a+b-c}{c}}.

    Точка Нагеля является изотомическим сопряжением точки Жергонна.

    Трилинейные координаты вписанных треугольников[править | править код]

    Трилинейные координаты вершин треугольника, образованного основаниями биссектрис, задаются формулами

    • вершина A=0:1:1
    • вершина B=1:0:1
    • вершина C=1:1:0

    Трилинейные координаты треугольника, образованного точками касания сторон внеописанными окружностями, задаются формулами

    • вершина A=-1:1:1
    • вершина B=1:-1:1
    • вершина C=1:-1:-1

    Уравнения окружностей[править | править код]

    Пусть x : y : z — координаты точки в трилинейных координатах, и пусть u = cos2(A/2), v = cos2(B/2), w = cos2(C/2). Четыре окружности, описанные выше, можно задать любым из двух указанных способов[8]:

    • Вписанная окружность:
    u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}-2vwyz-2wuzx-2uvxy=0
    pm {sqrt {x}}cos {frac {A}{2}}pm {sqrt {y}}cos {frac {B}{2}}pm {sqrt {z}}cos {frac {C}{2}}=0
    • A-внешневписанная:
    u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}-2vwyz+2wuzx+2uvxy=0
    pm {sqrt {-x}}cos {frac {A}{2}}pm {sqrt {y}}cos {frac {B}{2}}pm {sqrt {z}}cos {frac {C}{2}}=0
    • B-внешневписанная:
    u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}+2vwyz-2wuzx+2uvxy=0
    pm {sqrt {x}}cos {frac {A}{2}}pm {sqrt {-y}}cos {frac {B}{2}}pm {sqrt {z}}cos {frac {C}{2}}=0
    • C-внешневписанная:
    u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}+2vwyz+2wuzx-2uvxy=0
    pm {sqrt {x}}cos {frac {A}{2}}pm {sqrt {y}}cos {frac {B}{2}}pm {sqrt {-z}}cos {frac {C}{2}}=0

    Другие свойства вписанной окружности[править | править код]

    Некоторые формулы с радиусом вписанной окружности[править | править код]

    • Радиус вписанной окружности не больше одной девятой суммы высот треугольника[9].
    • Неравенство Эйлера: радиус вписанной окружности не превосходит половины радиуса описанной окружности и равенство имеет место лишь для равностороннего треугольника[10].
    • Предположим, что точки касания вписанной окружности делят стороны на отрезки длиной x и y, y и z, z и x. Тогда вписанная окружность имеет радиус[11]
    r={sqrt {frac {xyz}{x+y+z}}}

    и площадь треугольника равна

    K={sqrt {xyz(x+y+z)}}.
    • Если высоты, опущенные на стороны a, b и c есть ha, hb и hc, то радиус вписанной окружности r равен одной трети гармонического среднего этих высот, то есть
    r={frac {1}{h_{a}^{-1}+h_{b}^{-1}+h_{c}^{-1}}}.
    • Произведение радиуса вписанной окружности r и радиуса описанной окружности R треугольника со сторонами a, b и c равен[1]
    rR={frac {abc}{2(a+b+c)}}.
    • Некоторые связи сторон, радиусов вписанной окружности и описанной окружностей[12]:
    ab+bc+ca=s^{2}+(4R+r)r,
    a^{2}+b^{2}+c^{2}=2s^{2}-2(4R+r)r.
    • Любая прямая, проходящая через треугольник и делящая площадь треугольника и периметр пополам, проходит через центр вписанной окружности. Таких прямых может существовать три, две или одна[13].
    • Перпендикуляры, восставленные к сторонам треугольника в точках касания вневписанных окружностей, пересекаются в одной точке. Эта точка симметрична центру вписанной окружности относительно центра описанной окружности[14].

    Формулы для расстояний до центра вписанной или вневписанной окружностей[править | править код]

    Теорема Эйлера[править | править код]

    Теорема Эйлера утверждает, что в треугольнике[10]:

    (R-r_{in})^{2}=d^{2}+r_{in}^{2},

    где R и rin являются радиусами описанной и вписанной окружностей соответственно, а d — расстояние между центрами этих окружностей.

    Для вневписанных окружностей уравнение выглядит похоже:

    (R+r_{ex})^{2}=d^{2}+r_{ex}^{2},

    где rex — радиус одной из вневписанных окружностей, а d — расстояние между центрами описанной и вневписанной окружностей[15][16][17]

    • Возводя в квадрат и приводя подобные из первой формулы Эйлера выше имеем:

    Квадрат расстояния от центра вписанной окружности I до центра описанной O задаётся уравнением[18]

    OI^{2}=d^{2}=R(R-2r_{in}),
    {displaystyle OI^{2}={frac {abc,}{a+b+c}}left[{frac {abc,}{(a+b-c),(a-b+c),(-a+b+c)}}-1right]}

    Аналогично для второй формулы:

    d^{2}=R(R+2r_{ex}).

    Другие формулы для расстояний до центра вписанной или вневписанной окружностей[править | править код]

    • Расстояние от центра вписанной окружности до центра N окружности девяти точек равно[18]
    IN={frac {1}{2}}(R-2r)<{frac {1}{2}}R.
    • Расстояние от вершины до точек касания вписанной окружности на прилегающих сторонах равно полусумме длин прилегающих сторон минус половина противолежащей стороны[19]. Так, для вершины B и прилежащих точек касания TA и TC,
    BT_{A}=BT_{C}={frac {BC+AB-AC}{2}}.
    • Если обозначить центр вписанной окружности треугольника ABC буквой I, мы получим[20]
    {frac {IAcdot IA}{CAcdot AB}}+{frac {IBcdot IB}{ABcdot BC}}+{frac {ICcdot IC}{BCcdot CA}}=1

    и[21]

    IAcdot IBcdot IC=4Rr^{2}.
    • Теорема Мансиона (составная часть Теоремы о трезубце). Середины трёх отрезков, соединяющих центр вписанной окружности с центрами вневписанных окружностей лежат на описанной окружности[10].

    • Теорема Харкорта. Пусть треугольник задан своими вершинами A, B и C, противоположные вершинам стороны имеют длины a, b и c, площадь равна K и прямая касается вписанной в треугольник окружности в произвольной точке. Обозначим расстояния от вершин треугольника до прямой через a ‘, b ‘ и c ‘, при этом, если вершина и центр окружности лежат по разные стороны от прямой, расстояние считается отрицательным. Тогда
    aa^{prime }+bb^{prime }+cc^{prime }=2K..

    Другие свойства вневписанных окружностей[править | править код]

    • Следующее отношение выполняется для радиуса r вписанной окружности, радиуса R описанной окружности, полупериметра s и радиусов вневписанных окружностей ra, rb, rc[12]:
    r_{a}+r_{b}+r_{c}=4R+r,
    r_{a}r_{b}+r_{b}r_{c}+r_{c}r_{a}=s^{2},
    r_{a}^{2}+r_{b}^{2}+r_{c}^{2}=(4R+r)^{2}-2s^{2},
    • Окружность, проходящая через центры вневписанных окружностей, имеет радиус 2R[12].
    • Если H — ортоцентр треугольника ABC, то[12]
    r_{a}+r_{b}+r_{c}+r=AH+BH+CH+2R,
    r_{a}^{2}+r_{b}^{2}+r_{c}^{2}+r^{2}=AH^{2}+BH^{2}+CH^{2}+(2R)^{2}.
    • Вершины A, B и C треугольника ABC являются основаниями высот треугольника JAJB,JC,

    где JAJB,JC — центры вневписанных окружностей[10].

    • Перпендикуляры, восставленные к сторонам треугольника в точках касания вневписанных окружностей, пересекаются в одной точке. Эта точка симметрична центру вписанной окружности относительно центра описанной окружности[14].
    • Центр Шпикера треугольника является радикальным центром его вневписанных окружностей[22]. Если из центра Шпикера треугольника провести 6 касательных к 3 вневписанным окружностям треугольника, то все их длины будут равны между собой.

    Окружность Аполлония[править | править код]

    Определение окружности Аполлония[править | править код]

    Точка Аполлония и окружность Аполлония

    Пусть дан треугольник ABC. Пусть вневписанные окружности треугольника ABC, противоположные вершинам A, B и C, есть соответственно EA, EB, EC (см. рисунок). Тогда окружность Аполлония E (на рис. справа показана зеленым цветом) касается внутренним образом сразу трех вневписанных окружностей треугольника ABC в точках соответственно EA, EB и EC (см. рисунок)[23].

    Радиус окружности Аполлония[править | править код]

    Радиус окружности Аполлония равен {frac {r^{2}+s^{2}}{4r}}, где r — радиус вписанной окружности и s — полупериметр треугольника[24].

    Определение точки Аполлония Ap[править | править код]

    • Точка Аполлония Ap в Энциклопедии центров треугольника у Кларка Кимберлинга (Encyclopedia of Triangle Centers (ETC)) именуется как центр треугольника под именем X(181).
    • Точка Аполлония Ap или X(181) определяется следующим образом:

    Пусть A’ , B’ и C’ есть точки касания окружности Аполлония E с соответствтвующими вневписанными окружностями. Тогда прямые AA’ , BB’ и CC’ пересекаются в одной точке Ap, которую называют точкой Аполлония треугольника ABC.

    Изогональное сопряжение[править | править код]

    Изогональное сопряжение имеет ровно четыре неподвижные точки (то есть точки, которые сопряжены самим себе): центр вписанной окружности и центры вневписанных окружностей треугольника[25].

    Ортоцентр треугольника изогонально сопряжён центру описанной окружности этого треугольника[25].

    Обобщение на другие многоугольники[править | править код]

    • Некоторые (но не все) четырёхугольники имеют вписанную окружность. Они называются описанными четырёхугольниками. Среди свойств этих четырёхугольников наиболее важным является то, что суммы противоположных сторон равны. Это утверждение называется теоремой Пито.
    • Некоторые (но не все) четырёхугольники имеют вневписанную окружность. Они называются внеописанными четырёхугольниками. Среди свойств этих четырёхугольников наиболее важное свойство отмечает теорема Уркхарта. Она утверждает:
    • Если противоположные стороны выпуклого четырёхугольника ABCD пересекаются в точках E и F, то
    {displaystyle AB+BC=AD+DCquad Leftrightarrow quad AE+EC=AF+FC.}

    См. также[править | править код]

    • Вневписанная окружность
    • Внеописанный четырёхугольник
    • Вписанная окружность
    • Вписанные и описанные фигуры для треугольника
    • Вписанное коническое сечение[en]
    • Вписанная сфера
    • Высота треугольника
    • Замечательные точки треугольника
    • Инцентр или Центр вписанной окружности
    • Окружность
    • Описанная окружность
    • Описанный четырёхугольник
    • Ортоцентр
    • Степень точки относительно окружности
    • Теорема Мансиона
    • Теорема о трезубце
    • Теорема Тебо 2 и 3
    • Теорема Харкорта
    • Точки Аполлония
    • Степень точки относительно окружности
    • Центр Шпикера
    • Центроид
    • Центроид треугольника
    • Эллипс Мандарта
    • Эллипс Штейнера

    Примечания[править | править код]

    1. ↑ 1 2 Roger A. Johnson. Advanced Euclidean Geometry. — Dover, 2007 (оригинал — 1929).. — С. 189, #298(d).
    2. ↑ H.S.M. Coxeter. Introduction to Geometry. — 2. — Wiley, 1961..
    3. ↑ Marcus Baker. A collection of formulae for the area of a plane triangle. — January 1885. — Т. part 1, vol. 1(6). — С. 134-138.. См. также часть 2 в томе. 2(1), Сентябрь 1885, 11-18.)
    4. ↑ D. Minda, S. Phelps. Triangles, ellipses, and cubic polynomials // American Mathematical Monthly. — October 2008. — Вып. 115. — С. 679-689: Theorem 4.1..
    5. ↑ С. И. Зетель. Новая геометрия треугольника. — Москва: УЧПЕДГИЗ, 1962. — С. 52-53 Глава III.
    6. ↑ Christopher J. Bradley, Geoff C. Smith. The locations of triangle centers // Forum Geometricorum. — 2006. — Вып. 6. — С. 57-70..
    7. ↑ Deko Dekov. Computer-generated Mathematics : The Gergonne Point // Journal of Computer-generated Euclidean Geometry. — 2009. — Т. 1. — С. 1–14.. Архивировано 5 ноября 2010 года.
    8. ↑ William Allen Whitworth. Trilinear Coordinates and Other Methods of Modern Analytical Geometry of Two Dimensions. — 2012. — С. 210-215. — (Forgotten Books).
    9. ↑ Alfred S. Posamentier, Ingmar Lehmann. The Secrets of Triangles. — Prometheus Books, 2012. — С. 289.
    10. ↑ 1 2 3 4 А. Д. Куланин, С. Н. Федин. Геометрия треугольника в задачах. — М.: Книжный дом «ЛИБРОКОМ», 2009. — ISBN 978-5-397-00786-3.
    11. ↑ Thomas Chu. The Pentagon. — Spring, 2005. — С. 45, задача 584..
    12. ↑ 1 2 3 4 Amy Bell. Hansen’s right triangle theorem, its converse and a generalization // Forum Geometricorum. — 2006. — Вып. 6. — С. 335–342.
    13. ↑ Dimitrios Kodokostas. Triangle Equalizers // Mathematics Magazine. — 2010. — Вып. 83, April. — С. 141-146..
    14. ↑ 1 2 Мякишев, 2002, с. 11, п. 5.
    15. ↑ Roger Nelson. Euler’s triangle inequality via proof without words // Mathematics Magazine. — February 2008. — Вып. 81(1). — С. 58-61.
    16. ↑ R. A. Johnson. Modern Geometry. — Boston: Houghton Mifflin, 1929. — С. 187.
    17. ↑ Lev Emelyanov, Tatiana Emelyanova. Euler’s formula and Poncelet’s porism // Forum Geometricorum. — 2001. — Вып. 1. — С. 137–140..
    18. ↑ 1 2 3 William N. Franzsen. The distance from the incenter to the Euler line // Forum Geometricorum. — 2011. — Т. 11. — С. 231–236..
    19. ↑ Mathematical Gazette, July 2003, 323—324.
    20. ↑ Patricia R. Allaire, Junmin Zhou, Haishen Yao. Proving a nineteenth century ellipse identity // Mathematical Gazette. — 2012. — Вып. 96, March. — С. 161-165..
    21. ↑ Nathan Altshiller-Court. College Geometry. — Dover Publications, 1980. — С. 121,#84.
    22. ↑ Odenhal, 2010, с. 35—40.
    23. ↑ Darij Grinberg, Paul Yiu. The Apollonius Circle as a Tucker Circle // Forum Geometricorum. — 2002. — Вып. 2. — С. 175-182.
    24. ↑ Milorad R. Stevanovi´c. The Apollonius circle and related triangle centers // Forum Geometricorum. — 2003. — Вып. 3. — С. 187-195..
    25. ↑ 1 2 В. В. Прасолов. Точки Брокара и изогональное сопряжение. — М.: МЦНПО, 2000. — (Библиотека «Математическое просвещение»). — ISBN 5-900916-49-9.

    Литература[править | править код]

    • Мякишев А.Г. Элементы геометрии треугольника. — М.: МЦНМО, 2002.
    • Clark Kimberling. Triangle Centers and Central Triangles // Congressus Numerantium. — 1998. — Вып. 129. — С. i-xxv, 1-295.
    • Sándor Kiss. The Orthic-of-Intouch and Intouch-of-Orthic Triangles // Congressus Numerantium. — 2006. — Вып. 6. — С. 171—177.
    • Boris Odenhal. Some triangle centers associated with the circles tangent to the excircles // Forum Geometricorum. — 2010. — Т. 10.

    Ссылки[править | править код]

    • Derivation of formula for radius of incircle of a triangle
    • Weisstein, Eric W. Incircle (англ.) на сайте Wolfram MathWorld.

    Сайты с интерактивным содержанием[править | править код]

    • Triangle incenter Triangle incircle Incircle of a regular polygon With interactive animations
    • Constructing a triangle’s incenter / incircle with compass and straightedge An interactive animated demonstration
    • Equal Incircles Theorem at cut-the-knot
    • Five Incircles Theorem at cut-the-knot
    • Pairs of Incircles in a Quadrilateral at cut-the-knot
    • An interactive Java applet for the incenter
    Источник

    Что такое окружность, вписанная в треугольник? Какие у вписанной окружности свойства?

    Определение.

    Окружность называется вписанной в треугольник, если она касается всех его сторон.

    Общие точки окружности и треугольника называются точками касания.

    Okruzhnost vpisannaya v treugolnik Запись окр. (O; r) читают: «Окружность с центром в точке O и радиусом r».

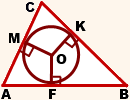
    На рисунке окр. (O; r) — вписанная в треугольник ABC.

    M, K, F- точки касания.

    Свойства вписанной в треугольник окружности.

    Vpisannaya v treugolnik okruzhnost

    1) Центр вписанной в треугольник окружности является точкой пересечения биссектрис этого треугольника.

    AO, BO, CO — биссектрисы треугольника ABC.

    Svoystva vpisannoy v treugolnik okruzhnosti

    2) Отрезки соединяющие центр вписанной окружности с точками касания, перпендикулярны сторонам треугольника (как радиусы, проведенные в точку касания):

        [OM bot AC,]

        [OK bot BC,]

        [OF bot AB.]

    Svoystva vpisannoy okruzhnosti

    3) Вписанная в треугольник окружность делит стороны треугольника на 3 пары равных отрезков.

        [AM = AF,]

        [BK = BF,]

        [CK = CF]

    (как отрезки касательных, проведенные из одной точки).

    Источник

    Вписанная окружность — это окружность, которая вписана
    в геометрическую фигуру и касается всех его сторон.

    Окружность, точно можно вписать в такие геометрические фигуры, как:

    • Треугольник
    • Выпуклый, правильный многоугольник
    • Квадрат
    • Равнобедренная трапеция
    • Ромб

    В четырехугольник, можно вписать окружность,
    только при условии, что суммы длин
    противоположных сторон равны.

    Во все вышеперечисленные фигуры
    окружность, может быть вписана, только один раз.

    Окружность невозможно вписать в прямоугольник
    и параллелограмм, так как окружность не будет
    соприкасаться со всеми сторонам этих фигур.

    Геометрические фигуры, в которые вписана окружность,
    называются описанными около окружности.

    Описанный треугольник — это треугольник, который описан
    около окружности и все три его стороны соприкасаются с окружностью.

    Описанный четырехугольник — это четырехугольник, который описан
    около окружности и все четыре его стороны соприкасаются с окружностью.

    Содержание

    1. Свойства вписанной окружности
    2. В треугольник
    3. В четырехугольник
    4. Примеры вписанной окружности
    5. Верные и неверные утверждения
    6. Окружность вписанная в угол

    Свойства вписанной окружности

    В треугольник

    1.  В любой треугольник может быть вписана окружность, причем только один раз.
    2.  Центр вписанной окружности — точка пересечения биссектрис треугольника.
    3.  Вписанная окружность касается всех сторон треугольника.
    4.  Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

      [ S = frac{1}{2}(a+b+c) cdot r = pr ]

      p —  полупериметр четырехугольника.
      r — радиус вписанной окружности четырехугольника.

    5.  Центр окружности вписанной в треугольник равноудален от всех сторон.
    6.  Точка касания — это точка, в которой соприкасается
      окружность и любая из сторон треугольника.
    7.  От центра вписанной окружности можно провести
      перпендикуляры к любой точке касания.
    8.  Вписанная в треугольник окружность делит стороны
      треугольника на 3 пары равных отрезков.
    9.  Вписанная и описанная около треугольника окружность тесно взаимосвязаны.
      Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:

      [ с = sqrt{R^2 — 2Rr} ]

      с — расстояние между центрами вписанной и описанной окружностей треугольника.
      R — радиус описанной около треугольника.
      r — радиус вписанной окружности треугольника.

    В четырехугольник

    1. Не во всякий четырехугольник можно вписать окружность.
    2. Если у четырехугольника суммы длин его противолежащих
      сторон равны, то окружность, может быть, вписана (Теорема Пито).
    3. Центр вписанной окружности и середины двух
      диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона).
    4. Точка пересечения биссектрис — это центр вписанной окружности.
    5. Точка касания — это точка, в которой соприкасается
      окружность и любая из сторон четырехугольника.
    6. Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:

      [ S = frac{1}{2}(a+b+c+d)cdot r = pr ]

      p —  полупериметр четырехугольника.
      r — радиус вписанной окружности четырехугольника.

    7. Точка касания вписанной окружности, которая лежит на любой из сторон,
      равноудалены от этой конца и начала этой стороны, то есть от его вершин.

    Примеры вписанной окружности

    Примеры описанного четырехугольника:
    равнобедренная трапеция, ромб, квадрат.

    Примеры описанного треугольника:
    равносторонний    , равнобедренный,
    прямоугольный треугольники.

    Верные и неверные утверждения

    1. Радиус вписанной окружности в треугольник и радиус вписанной
      в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
    2. Любой параллелограмм можно вписать в окружность. Неверное утверждение.
    3. В любой четырехугольник можно вписать окружность. Неверное утверждение.
    4. В любой ромб можно вписать окружность. Верное утверждение.
    5. Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
    6. Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
    7. Угол вписанный в окружность равен соответствующему центральному
      углу опирающемуся на ту же дугу. Неверное утверждение.
    8. Радиус вписанной окружности в прямоугольный треугольник равен
      половине разности суммы катетов и гипотенузы. Верное утверждение.
    9. Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
    10. Вписанная окружность в треугольник имеет в общем
      три общие точки со всеми сторонами треугольника. Верное утверждение.

    Окружность вписанная в угол

    Окружность вписанная в угол — это окружность, которая
    лежит внутри этого угла и касается его сторон.

    Центр окружности, которая вписана в угол,
    расположен на биссектрисе этого угла.

    К центру окружности вписанной в угол, можно провести,
    в общей сложности два перпендикуляра со смежных сторон.

    Центральный угол вписанной окружности – это угол, вершина
    которого лежит в центре вписанной окружности.

    Вписанный угол вписанной окружности – это угол,
    вершина которого лежит на вписанной окружности.

    Длина диаметра, радиуса, хорды, дуги вписанной окружности
    измеряется в км, м, см, мм и других единицах измерения.

    Так-же читайте статью про треугольник вписанный в окружность.

    Источник

    Добавить комментарий