Как найти точки минимума задание 7 - Сайт, где вы сможете решить свои вопросы

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.

Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

– Производная положительна там, где функция возрастает.
– Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после – производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.

(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.

(- 9): функция возрастает, а потом убывает – максимум.

(-7): минимум.

(3): максимум.

Все вышесказанное можно обобщить следующими выводами:

– Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
– Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

Найдите производную функции (f'(x)).
Найдите корни уравнения (f'(x)=0).
Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
Определите знак производной в каждом промежутке (методом интервалов).
Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
– если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
– если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
– если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.

Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:

(15x^4-60x^2=0) (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0) (x^2-4=0)
(x=±2)

3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является (-2).

Ответ. (-2).

Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов

Скачать статью

Источник

Производная положительна только тогда, когда функция возрастает. То есть, нам необходимо найти точки, в которых функция растет. Смотрим на график нашей функции: функция растет на промежутках: от (x=-7) до (x=0) и от (x = 6) до (x=12).

Так как по условию нам нужны только ЦЕЛЫЕ точки, в которых производная положительна, то это будут: (x=—6); (x=-5), (x=-4), (x=-3), (x=-2), (x=-1), (x=7), (x=8), (x=9), (x=10), (x=11). Всего точек получилось (11). Я отметил их зеленым цветом.

Обратите внимание, что точки (x=-7), (x=0), (x=6), (x=12) мы не считаем, так как в этих точках у нас будут минимумы и максимумы функции, а в них производная равна нулю, то есть не положительна.

Ответ: (11.)

Пример 2
На рисунке 6 изображен график функции, определенной на промежутке ((-10;12)). Найдите количество точек, в которых производная функции равна нулю.

Источник

было в ЕГЭ

в условии
в решении
в тексте к заданию
в атрибутах

Категория

Атрибут

Всего: 229 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Найдите точку минимума функции

Найдите наименьшее значение функции на отрезке [−2,5; 0].

Найдите наименьшее значение функции на отрезке

Найдите точку минимума функции

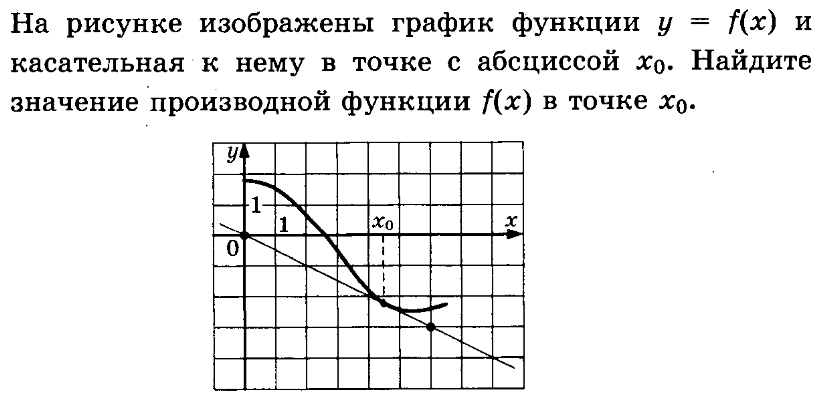
На рисунке изображен график функции y=f(x), определенной на интервале (−3; 9). Найдите количество точек, в которых касательная к графику функции параллельна прямой y  =  12 или совпадает с ней.

Найдите наименьшее значение функции на отрезке

Найдите точку минимума функции

Найдите наименьшее значение функции на отрезке [−2,5; 0].

Всего: 229 1–20 | 21–40 | 41–60 | 61–80 …

Источник

В (11) задании ЕГЭ нужно уметь находить точки минимума и максимума функции, определять наибольшее и наименьшее значения функции на отрезке.

За правильное выполнение задания даётся (1) первичный балл.

Пример:

найди точку минимума функции

y=(x+5)2(x−1)+7

Алгоритм выполнения задания

1. Определи тип задания:

найди точку максимума (минимума);
найди точку максимума (минимума) на отрезке;
найди максимальное (минимальное) значение функции;
найди максимальное (минимальное) значение функции на отрезке.

2. Вычисли производную (f’(x)).

3. Реши уравнение (f’(x)=0).

4. Выполни действия в соответствии с типом задания, сделай вывод.

5. Запиши в ответе значение, которое требуется найти.

Как решить задание из примера?

1. В задании нужно найти точку максимума.

2. Производная функции:

y′=2(x+5)(x−1)+x+52=(x+5)(2x−2+x+5)=3(x+5)(x+1).

3. Приравняем производную к нулю и найдём корни уравнения:

4. Найдём промежутки возрастания и убывания функции (рис. (1)). В точке (-1) функция меняет знак с минуса на плюс, значит, это точка минимума.

Рис. (1). Промежутки возрастания и убывания функции

5. Запишем ответ (непосредственно в самом задании — без точки в конце).

Ответ: (-1).

Обрати внимание!

В заданиях «Как на ЕГЭ» ответы записывай в виде целого числа или десятичной дроби без пробелов и точки в конце.

Если получилась обыкновенная дробь и её нельзя перевести в конечную десятичную дробь — ищи ошибку в решении!

Источники:

Источник

Задание №7 (ЕГЭ)

Как работать если

на рисунке изображен график функции y = f(x), надо ответить на вопросы, связанные с производной,
или на рисунке изображен график первообразной y = F(x) (это график функции), надо ответить на вопросы, связанные с функцией y = f(x) (это производная y = F(x)),
или изображен график пройденного расстояния S = S(t) (это формула функции), надо ответить на вопросы, связанные со скоростью (производная пути).

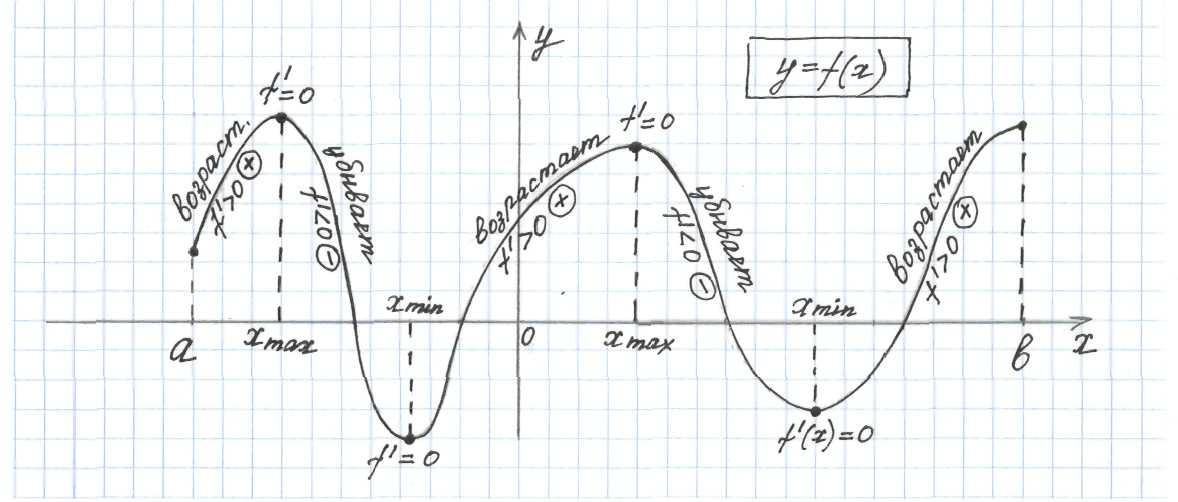
Если график задан на промежутке [a; b], то через числа a и b провести вертикальные пунктирные линии.
Жирно выделить часть графика на этом отрезке.
Обводить график слева направо.
Если поднимаемся вверх, то над графиком записать функция возрастает, под графиком f ‘(x) 0 (производная положительная «+»).
Если опускаемся вниз, то над графиком записать функция убывает, под графиком f ‘(x) (производная отрицательная « – »).
Если слева на право, функция меняет возрастание на убывание, то это точка максимума и производная в этой точке равна нулю (f ‘(x) = 0).
Если слева на право, функция меняет убывание на возрастание, то это точка минимума и производная в этой точке равна нулю (f ‘(x) = 0).

Внимание!!!

Если изображен график функции и несколько чисел на оси OX, просят найти наименьшее или наибольшее значение производной, то

Если наибольшее: выбрать числа, где производная положительная, через точки касания провести касательную и луч параллельный оси OX (вправо), где угол больше там и производная больше.

Если наименьшее: выбрать числа, где производная отрицательная, через точки касания провести касательную и луч параллельный оси OX (вправо), где угол меньше там и производная меньше.

Задание №7 (ЕГЭ)

Как дать правильный ответ, если сказано:

На рисунке изображен график производной функции f(x). Значит, изображен график y = f ‘(x).

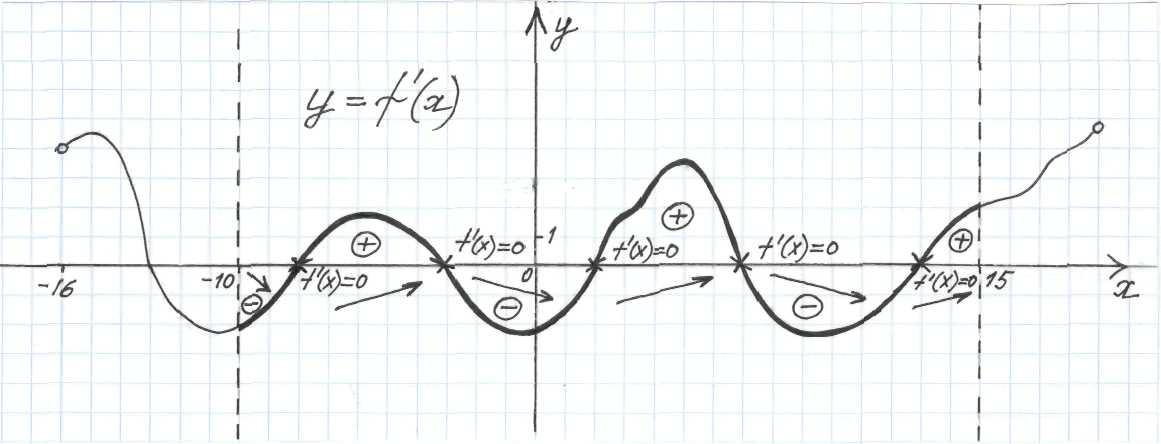
На рисунке изображен график производной функции f(x) на интервале (-16; 19). Отвечать на вопросы на отрезке [-10; 15].

Через концы заданного отрезка (найти числа на оси OX) провести вертикальные линии (это пунктирные).

Жирно выделить часть графика на этом отрезке.

Крестиком отметить точки пересечения графика с осью OX, здесь производная равна нулю. На чертеже около крестика записать f ‘(x) = 0.

Ось Ox (горизонтальная) делит график производной функции на части:

Если часть графика лежит выше оси Ox, здесь производная положительная (вверху поставить знак плюс «+», внизу нарисовать стрелку вверх (это значит, функция возрастает)).

Если часть графика лежит ниже оси Ox, здесь производная отрицательная (внизу поставить знак «-»), здесь внизу изобразить стрелку вниз (это значит, функция убывает).

Если двигаться по оси Ox от левого конца заданного отрезка (левый пунктирный конец) к правому концу, то:

Если при переходе через точку, где производная равна нулю (это крестик) производная меняет знак с минуса «-» на плюс «+», а функция убывание на возрастание , то эта точка (смотрят какой у этой точки x) минимума.

Если до точки (слева) стоял знак производной плюс «+», а после этой точки знак производной минус «-», при переходе через эту точку функция меняет возрастание на убывание , то эта точка (смотрим какой у этой точки x) максимума.

Если просят найти точки экстремума: это точки максимума и минимума вместе.

Если по графику производной надо выяснить, в какой точке заданного отрезка функция принимает наибольшее или наименьшее значение, то надо посмотреть на график и выделить вертикальными пунктирными линиями отрезок.

Если производная на этом отрезке отрицательная «-», а функция убывает , то наибольшее значение будет в левой точке, наименьшее в правой точке заданного отрезка.

Если производная положительная «+», а функция возрастает , то наименьшее значение в левой точке, наибольшее значение в правой точке заданного отрезка.

Если просят найти количество точек, в которых касательная параллельна прямой y = a (y =6; y =-2; и т.д.), формула без x (нет x), это значит угловой коэффициент (число перед x, его нет так как нет x) равен нулю. k = 0, но k = f ‘(x) = tgα. Если k = 0, то f ‘(x) = 0 (производная равна нулю). Тогда считаем точки, где производная равна нулю (крестики).

Если просят найти количество точек, в которых касательная параллельна заданной прямой y = kx +m (у = -2 x + 4; y = 3 x -6) тогда надо обвести кружком число, стоящее перед x вместе со знаком (угловой коэффициент), записать k = -2 или k = 3. Но k = f ‘(x), значит, производная равна этому числу f ‘(x) = -2; f ‘(x) = 3. Дальше на оси Oy найти это число и через него провести прямую, параллельную оси Ox. Посчитать количество точек пересечения, проведенной прямой с жирно выделенным графиком, это число записать в ответ.

Внимание!!!

Несколько раз внимательно прочитайте задание, жирно обведите вопрос, постарайтесь понять, что Вас просят найти, а дальше ищите и не забывайте записать ответ, проверив три раза!!!

Задание №7 (ЕГЭ)

I способ

Знаем!!! f ‘(x₀) = tgα = k

Чтобы найти f ‘(x₀) найдем tgα. tgα =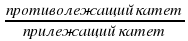

Если прямая убывающая (имеет вид ), то f ‘(x₀) = – tgα

На прямой найти две жирные точки. Если таких нет, то на прямой надо выделить жирно две точки, которые будут вершиной клетки (узловые точки).

Через верхнею точку, провести вертикальную (параллельную оси Oy) прямую.

Через нижнею точку горизонтальную (параллельную оси Ox) прямую.

Проведенные прямые вместе с касательной образуют прямоугольный треугольник, его нужно жирно выделить.

В прямоугольном треугольнике выделить острый угол около горизонтального катета, обозначить его буквой α.

Записать tgα = 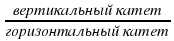(длины катетов посчитать по клеткам).

Полученную дробь заменить десятичной.

Записать ответ f ‘(x₀) = – tgα

Перенести в бланк ответов.

Задание №7 (ЕГЭ)

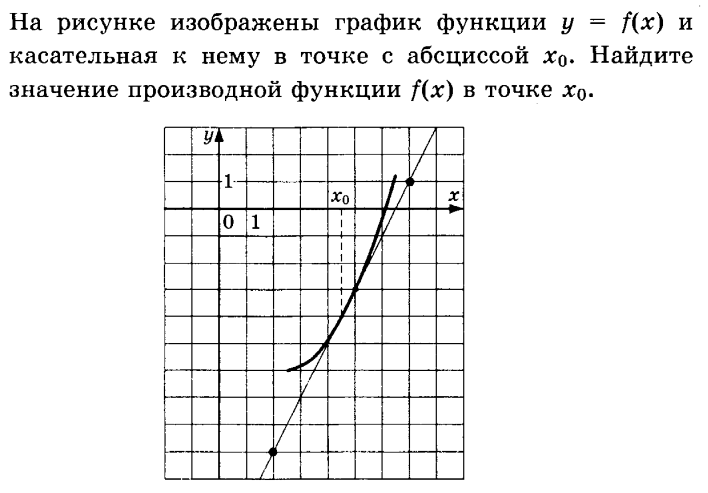
I способ

Знаем!!! f ‘(x₀) = tgα = k

Чтобы найти f ‘(x₀) найдем tgα. tgα =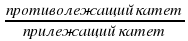

Если прямая возрастающая (имеет вид ), то f ‘(x₀) = tgα

На прямой найти две жирные точки. Если таких нет, то на прямой надо выделить жирно две точки, которые будут вершиной клетки (узловые точки).

Через верхнею точку, провести вертикальную (параллельную оси Oy) прямую.

Через нижнею точку горизонтальную (параллельную оси Ox) прямую.

Проведенные прямые вместе с касательной образуют прямоугольный треугольник, его нужно жирно выделить.

В прямоугольном треугольнике выделить острый угол около горизонтального катета, обозначить его буквой α.

Записать tgα = 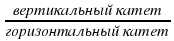(длины катетов посчитать по клеткам).

Полученную дробь заменить десятичной.

Записать ответ f ‘(x₀) = tgα (без минуса)

Перенести в бланк ответов.

Задание №7 (ЕГЭ)

II способ

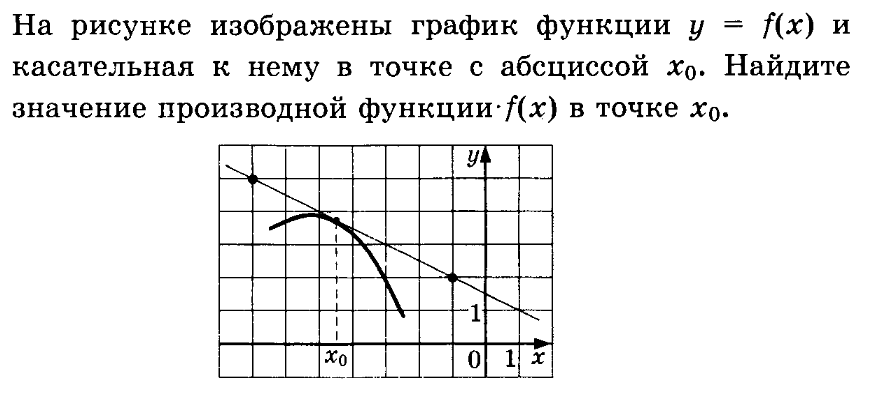
Знаем, что f ‘(x₀) = tgα = k , где k – угловой коэффициент касательной

Записать уравнение прямой y = k∙x + m

На касательной выбрать две точки А (-7; 5) и В (-1; 2)

В уравнение прямой подставить координаты точек

y = k∙x + m А (-7; 5) x =-7; y = 5 5 = k∙(-7) + m

y = k∙x + m В (-1; 2) x =-1; y = 2 2 = k∙(-1) + m

Составить систему

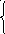
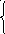-7∙k + m = 5, -6∙k = 3, k = –

-1∙k + m = 2; -1∙k + m = 2;

Т.к. k = f ‘(x₀), то f ‘(x₀) = –

Источник

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Минимумы и максимумы вместе именуют экстремумами функции.

В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

– Производная положительна там, где функция возрастает. – Производная отрицательна там, где функция убывает.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Вам также может понравиться

Книга как составить духи

Как найти карандаш в френ боу

Сумма ндфл за месяц как найти

Добавить комментарий Отменить ответ

В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.

– Производная положительна там, где функция возрастает.
– Производная отрицательна там, где функция убывает.