Ниже приведены некоторые примеры построений в прямоугольных изометрической и диметрической проекциях.
I. Проекция сферы. На рис. 473 сверху дано изображение сферы в изометрической и диметрической проекциях.
В обоих случаях сфера показана с вырезом одной восьмой части.
Окружности, представляющие собой очерк проекции, проведены: для
изометрической проекции радиусом, равным
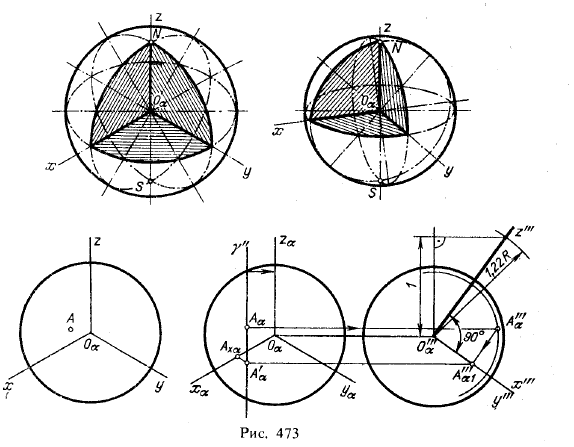
1,22R, для диметрической проекции радиусом 1,06R, где R — радиус
сферы. Эллипсы в обоих случаях соответствуют экваториальному и двум
меридиональным сечениям.
На рис, 473 внизу слева дано изображение сферы в изометрической
проекции; на видимой стороне сферы дана точка А. Справа показано
построение вторичной проекции А’α (см, рис, 449) и трехзвенной
координатной ломаной линии АαА’αАхαОα, что дает возможность определить прямоугольные координаты точки А в
пространстве. Построение выполнено в предположении, что плоскость
изометрических проекций занимает фронтальное положение и что
равнонаклоненнью к ней оси х, у, z прямоугольных координат спроецированы
не только на эту плоскость, но и на дополнительную профильную плоскость
π3. Получается система плоскостей проекций α, π3
и проекции Аα и А'”α заданной точки А, причем А'”α получена при помощи сечения сферы пл. γ. Вторичная проекция точки А также изображена двумя проекциями: А'”α1 и А’α
2. Линии пересечения цилиндра и конуса плоскостью. На рис, 474 и 475
показано построение в изометрической проекции линий пересечения цилиндра
и конуса фронтально-проецирующими плоскостями 1). В рассматриваемых случаях линии пересечения представляют собой эллипсы.
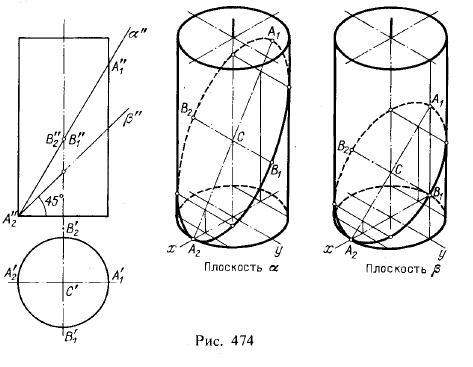
Прежде всего, руководствуясь чертежом, наносим по координатам точек А1 и А2 линии наклона ллоскостей α и β. Для построения точек эллипсов берем вспомогательные секущие плоскости: для цилиндра — параллельно его
образующим и плоскости yOz, для конуса — про-
1) Построение выполнено в приведенных коэффициентах искажения.
ходящие через его вершину параллельно оси у. Эти плоскости задаются
их следами, параллельными оси у, на плоскостях оснований цилиндра и
конуса.
При таком выборе вспомогательных плоскостей прямые, по которым они
пересекаются с плоскостями α и β, получаются параллельными оси γ. В
пересечении этих прямых с образующими цилиндра и конуса получаются точки
эллипса.
В первую очередь следует найти такие характерные точки, как отмеченные на чертежах буквами А1, А2. В1 и В2,
а также получаемые на очерковых линиях изометрической проекции. Малая
полуось получаемого в сечении эллипса, равная С’В’1, сохраняет свою
величину и в изометрической проекции (С’В’1 = СВ1). Но свое значение
малой оси для эллипса в изометрической проекции отрезок В1В2 сохраняет лишь при пл. β, т. е. при указанном на рисунке угле наклона этой плоскости, равном 45°.
Действительно, в этом случае отрезок В1В2 будучи параллельным оси у, остается и в изометрической проекции перпендикулярным к A1A2, следовательно, отрезки A1A2 и В1В2 сохраняют свое значение осей эллипса. В случае же иного наклона плоскости, как это показано на цилиндре для пл. α, отрезки А1А2 и В1В2 в изометрической проекции не являются осями эллипса, а лишь его сопряженными диаметрами.
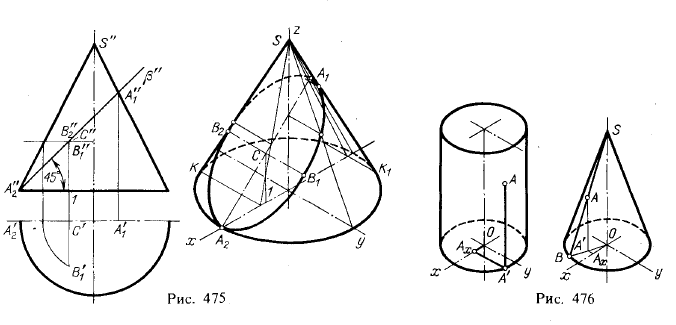
3. Построение координатных отрезков для точки, заданной на
поверхности цилиндра и конуса вращения в аксонометрической проекции. На
рис. 476 даны примеры для цилиндра и конуса в изометрической проекции.
Во всех случаях начало координат взято в центре основания (точка О).
Через заданную на цилиндре точку А проведена прямая параллельно оси
z, и из вторичной проекции А’ проведена прямая шраллельно оси γ до
пересечения с осью х. Отрезки 0Аx, АxА’ и А’А позволяют определить координаты точки А в данной системе осей координат.
Через заданную на конусе точку А проведена образующая и построена
вторичная проекция (ОВ) этой образующей. Проводя из точки А
перпендикуляр до пересечения с ОВ, получаем вторичную проекцию точки А.
Дальнейшее ясно из чертежа.
На рис. 477 показано построение координатных отрезков для точки,
заданной на поверхности усеченного конуса вращения в изометрической
проекции (рис. 411, а). Положим, что мы имеем сечение конуса плоскостью,
проходящей через ось
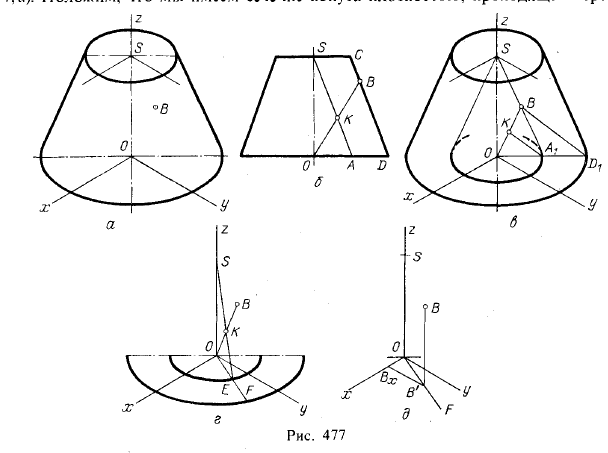
конуса и точку В (рис. 477,6). В полученной трапеции проведена прямая
SA || CD и пересекающая ее в точке К прямая ОВ. Получаем OK : KB = OA : AD. Но эта пропорция сохранится в изометрической проекции. Построим
конус с вершиной в точке S и с образующей, параллельной образующей
усеченного конуса (рис. 477, в). От
ношение OA1: A1D1 повторяет
отношение OA : AD, содержащееся в указанной выше пропорции. Теперь можно
получить точку К на ОВ на рис. 477, в. Образующая, проведенная через
точки S и Е, определяет точку К (рис. 477, г) и проекцию OF образующей,
на которой находится точка В. Отсюда мы получаем возможность получить
вторичную проекцию В’ (рис. 477, д) и координатные отрезки ВВ’, В’Вx и ОВх, определяющие координаты z, у и х.
Указанное построение дается на случай, если нельзя достроить
усеченный конус до полного. Если достроить можно, то построение
производится, как показано для конуса на рис. 477,6.
4. Примеры построения линий пересечения цилиндрических и конических
поверхностей вращения между собой. Линии пересечения строят по точкам;
эти точки находят или по их координатам, взятым с ортогональных
проекций, или способом вспомогательных секущих плоскостей
непосредственно в аксонометрических проекциях. Последнее показано на
рис. 478, а — г.
Вспомогательные секущие плоскости пересекают данные цилиндры и конусы
по образующим линиям. На рис; 478, а оси цилиндров пересекаются, на
рис. б) скрещиваются. Если на рис. а) точки А и А1 определялись при помощи секущей плоскости, проходящей через оси обоих цилиндров, то на рис. б) надо учесть смещение на
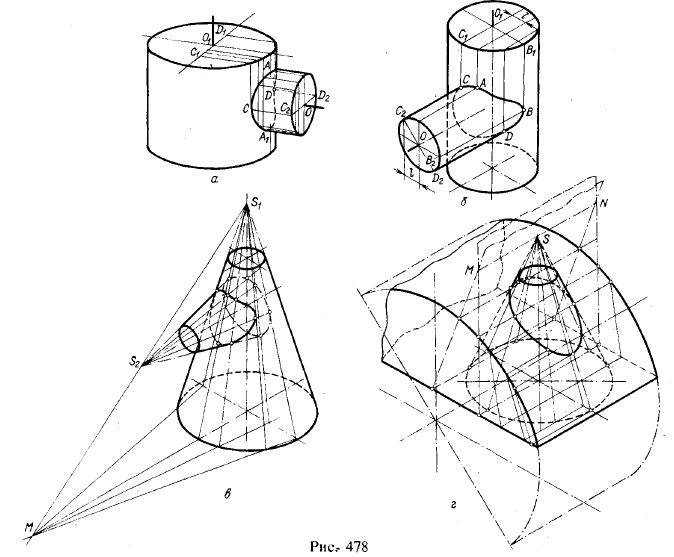
l 1). На рис. 478,в секущие плоскости проходят через прямую S1S2, а их следы на плоскости основания конуса с вершиной S1 проходят через след прямой S1S2 на этой плоскости. На рис. 478, г плоскости проходят через прямую MN, проведенную через вершину конуса — точку S — параллельно образующей цилиндра.
1) Разметка точек буквами произведена лишь для пояснении.
5. Построение точек касания окружности — очерка проекции сферы — с
эллипсом — проекцией окружности, получаемой на сфере при пересечении ее
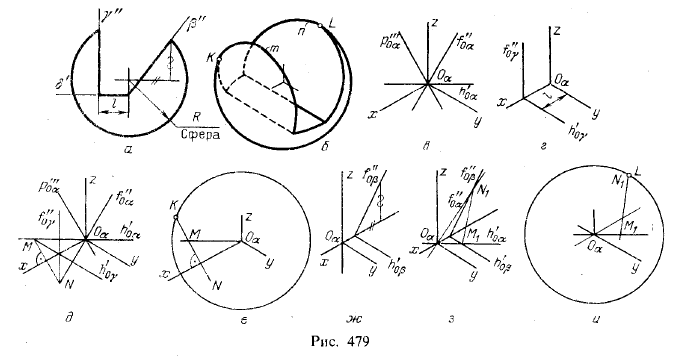
плоскостью. На рис. 479, а показана сфера, срезанная тремя плоскостями – профильной
(γ), горизонтальной (δ) и фронтально-проецирующей (β). По этому чертежу
построена: изометрическая проекция (рис. 479,6) в приведенных
коэффициентах искажения. Эллипс m построен так, как было показано на
рис. 469, а эллипс n — как на рис. 465. Проекция сферы дана очерком —
окружностью радиуса равного 1,22R. Эта окружность касается эллипса m в
точке К, эллипса n — в точке L.
Рассмотрим, как найдена точка К. Она получена на окружности — очерке
проекции сферы, т. е. в плоскости изометрической проекции (α), и в то же
время на эллипсе m т. е. в пл. γ, пересекающей сферу. Но если точка
принадлежит одновременно двум плоскостям, то она принадлежит линии
пересечения этих плоскостей.
Плоскость изометрической проекции, как известно, равнонаклонна к π1, π2 и π3. Треугольник следов этой плоскости равносторонний (см. рис. 457). Отнеся пл. α к точке Оα, т. е. к началу осей и центру сферы, помучим положение следов, указанное на рис. 479, в.
Пл. γ в системе тех же осей изобразится в следах, как показано на
рис. 479,г. Совместим рис. в) и г) и построим линию пересечения
плоскостей α и γ (рис. 479, е): прямая MN проходит через точку M
пересечения горизонтальных следов параллельно следу р”‘0α, так как γ||π3 (при этом р”‘0α⊥OαX. следовательно, MN⊥Оαх).
Теперь остается найти точку К в пересечении прямой MN с окружностью — изометрической проекцией сферы (рис. 479, е).
Для определения положения точки L (см. рис. 479, б) надо изобразить в
системе изометрических осей фронтально-проецирующую пл. β (рис. 479,.ж),
а затем найти прямую пересечения плоскостей α и β (рис. 479, з), эта
прямая проходит через точку M1 пересечения следов h’0β и h’0α и через точку N1 пересечения следов f”0β и f”0α. Искомая точка L получается в пересечении прямой M1N1 с окружностью — изометрической проекцией сферы (рис. 479, и).
Печатать книгу
Укажите способы построения аксонометрических проекций и их особенности. Как строят аксонометрические проекции плоских фигур? - Вы узнаете: как построить прямоугольные изометрические проекции геометрических тел, как найти точки на их поверхностях.
- Вы научитесь: выполнять прямоугольные изометрические проекции геометрических тел, находить точки на их поверхностях.
| Сайт: | Профильное обучение |
| Курс: | Черчение. 10 класс |
| Книга: | § 19. Аксонометрические проекции геометрических тел. Нахождение точек, лежащих на поверхности геометрических тел |
| Напечатано:: | Гость |
| Дата: | Вторник, 16 Май 2023, 14:06 |
Оглавление
- Вступление
- Аксонометрические проекции многогранников
- Аксонометрические проекции поверхностей вращения
- Проверим знания
- Вопросы и задания повышенной сложности
- Практическая работа № 10. Аксонометрические проекции геометрических тел
- Практическая работа №10.1. Чертеж аксонометрической проекции.
- Практическая работа №10.2. Аксонометрическая проекция по чертежу.
Вступление
Геометрические тела правильной формы (многогранники и поверхности вращения) часто встречаются в конструкции деталей машин и механизмов. Правильные геометрические тела характеризуются наличием в них различных осей и плоскостей симметрии, что позволяет строить аксонометрические изображения этих тел по принципу симметрии.
Построение аксонометрических проекций геометрических тел начинают с построения горизонтальной проекции его нижнего основания, к которому достраиваются другие его элементы (грани, ребра, верхнее основание).
Аксонометрические проекции многогранников
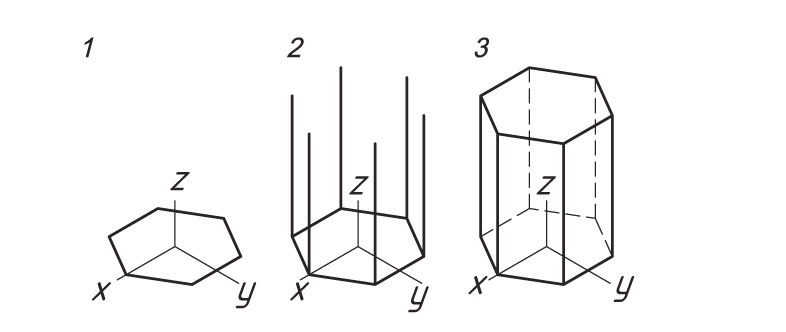Прямоугольная изометрическая проекция призмы. Основание призмы — правильный многоугольник (например, шестиугольник). Высота призмы совпадает с осью z, а основание расположено в плоскости осей x и y. Размеры призмы определяются их высотой и размерами фигуры основания.
1. Проводят оси изометрической проекции. Затем строят нижнее основание призмы.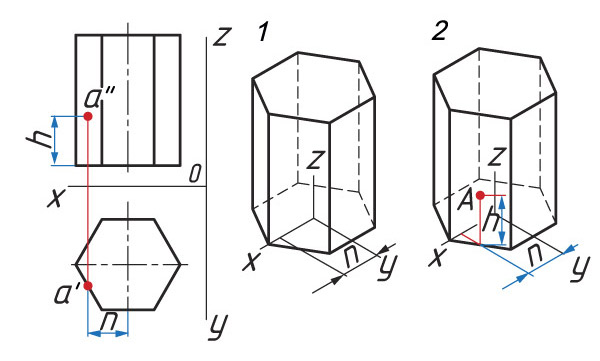
2. Из каждой вершины проводят перпендикуляры, на которых откладывают отрезки, равные высоте призмы.
3. Через полученные точки проводят прямые, параллельные ребрам основания. Определяют видимость ребер.
Определение расположения точки А:
1. От центра основания по оси х проводят прямую хА = n. Из точки n проводят прямую, параллельную оси у, до пересечения с основанием призмы.
2. Из полученной точки параллельно оси z проводят прямую
zА = h.
Определите последовательность построения проекции точки, расположенной на ребре призмы.
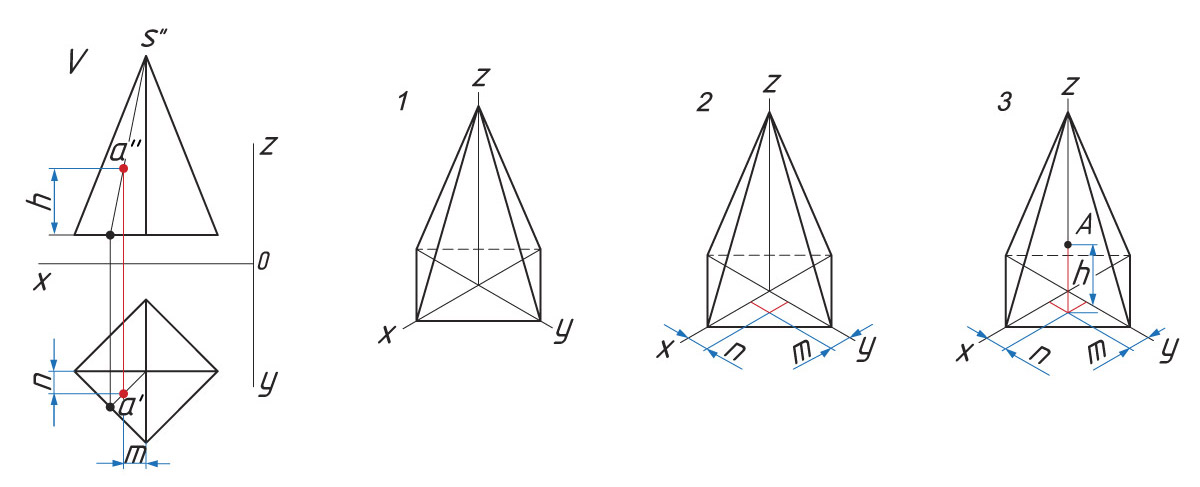
Прямоугольная изометрическая проекция пирамиды (например, четырехгранной). Основание пирамиды — ромб. Высота пирамиды (OS) совпадает с осью z, а основание расположено в плоскости осей x и y.
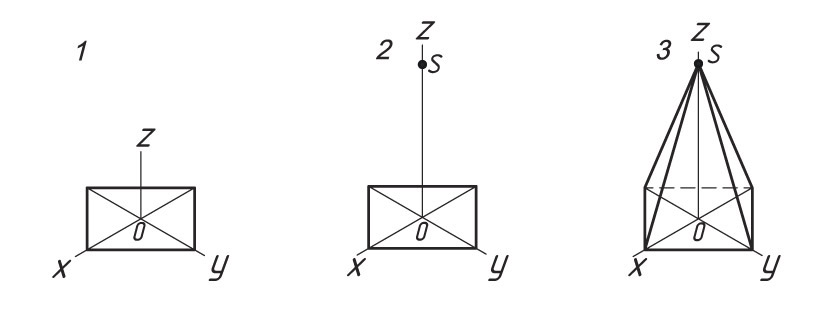
1. Проводят оси изометрической проекции. Размеры пирамиды определяются размерами ее основания и высотой. Затем строят нижнее основание пирамиды, параллельное горизонтальной плоскости.
2. Из центра основания О восстанавливают перпендикуляр, на котором откладывают высоту пирамиды.
3. Соединяют полученную точку S с вершинами основания. Определяют видимость ребер.
Определение расположения точки А
1. От центра основания О по оси х откладывают расстояние хА = m.
2. На оси у откладывают расстояние уА = n.
3. Параллельно оси z проводят отрезок zA = h.
Аксонометрические проекции поверхностей вращения
Окружности, лежащие в основаниях цилиндра и конуса, расположены параллельно горизонтальной плоскости проекций. Построение проекций цилиндра и конуса начинают с проведения осей симметрий и построения нижнего основания. Нижнее основание аксонометрических проекций цилиндра и конуса — эллипс.
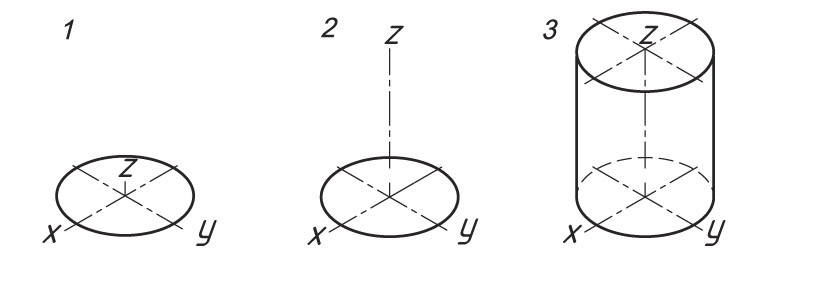
Прямоугольная изометрическая проекция цилиндра. Основание цилиндра — эллипс. Высота цилиндра совпадает с осью z, а основание расположено в плоскости осей x и y. Размеры определяются высотой и диаметром основания.
1. Проводят оси изометрической проекции. Затем строят нижнее основание цилиндра.
2. Из центра основания восстанавливают перпендикуляр и откладывают высоту цилиндра. Строят верхнее основание (эллипс).
3. Проводят боковые образующие цилиндрической поверхности, определяют видимость нижнего основания.
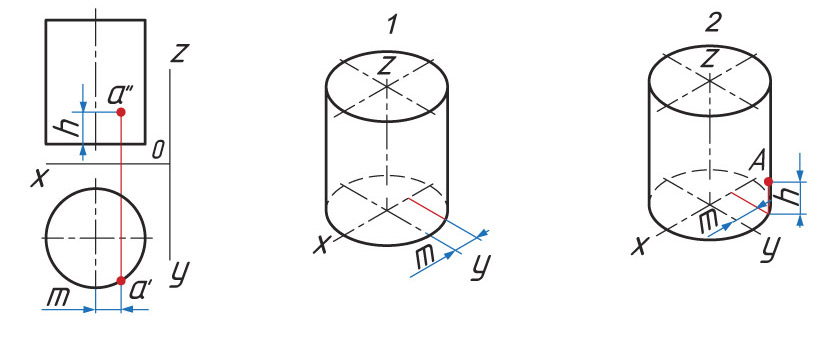
Определение расположения точки А
1. От центра основания по оси х проводят прямую хА= m. Из точки m проводят прямую, параллельную оси у до пересечения с основанием.
2. Из полученной точки параллельно оси z проводят прямую zА= h
Составьте алгоритм нахождения точки на поверхности цилиндра, учитывая тот факт, что точка расположена на нижнем основании цилиндра.
Прямоугольная изометрическая проекция конуса. Основание конуса — эллипс. Построение проекции конуса схоже с построением проекции цилиндра. Определение расположения точек на поверхности конуса подобно построениям точек на пирамиде.
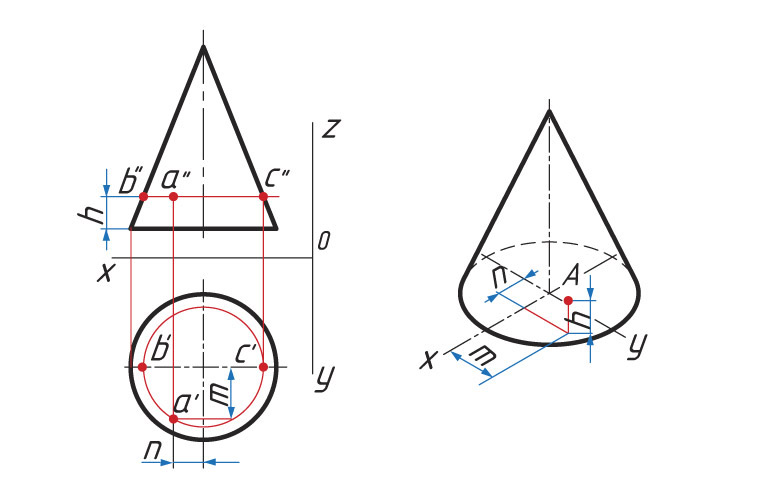
Используя ранее изученный материал, укажите способ нахождения положения точек В и С, изображенный на рисунке.
Проверим знания
1. Что такое показатель (коэффициент) искажения? Какие виды аксонометрии вы знаете? Как располагаются оси прямоугольной изометрии?
2. В какой последовательности выполняют аксонометрическую проекцию геометрического тела?
3. Приведите примеры использования аксонометрических проекций в различных сферах профессиональной деятельности.
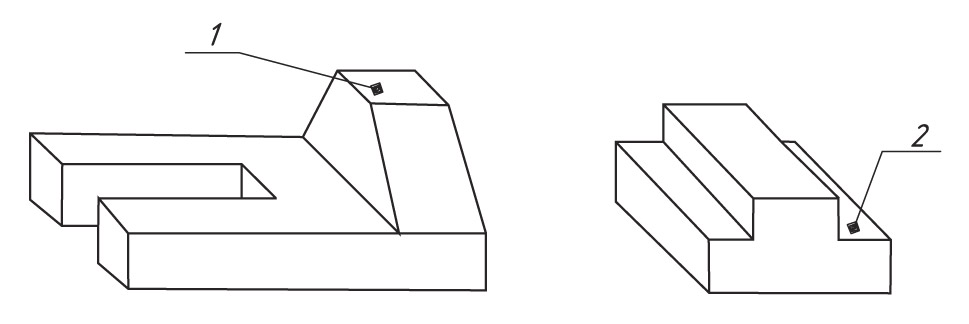
4. Мысленно удалите элемент 1, заменив его на элемент 2. Выполните изометрическую проекцию получившейся детали.
Вопросы и задания повышенной сложности
1. Назовите общие для фронтальной диметрической и изометрической проекций этапы построения цилиндра.
2. Постройте в изометрической проекции правильные треугольную и шестиугольную призмы. Основания призмы расположены горизонтально, длина сторон основания 30 мм, высота 60 мм.
Практическая работа № 10. Аксонометрические проекции геометрических тел
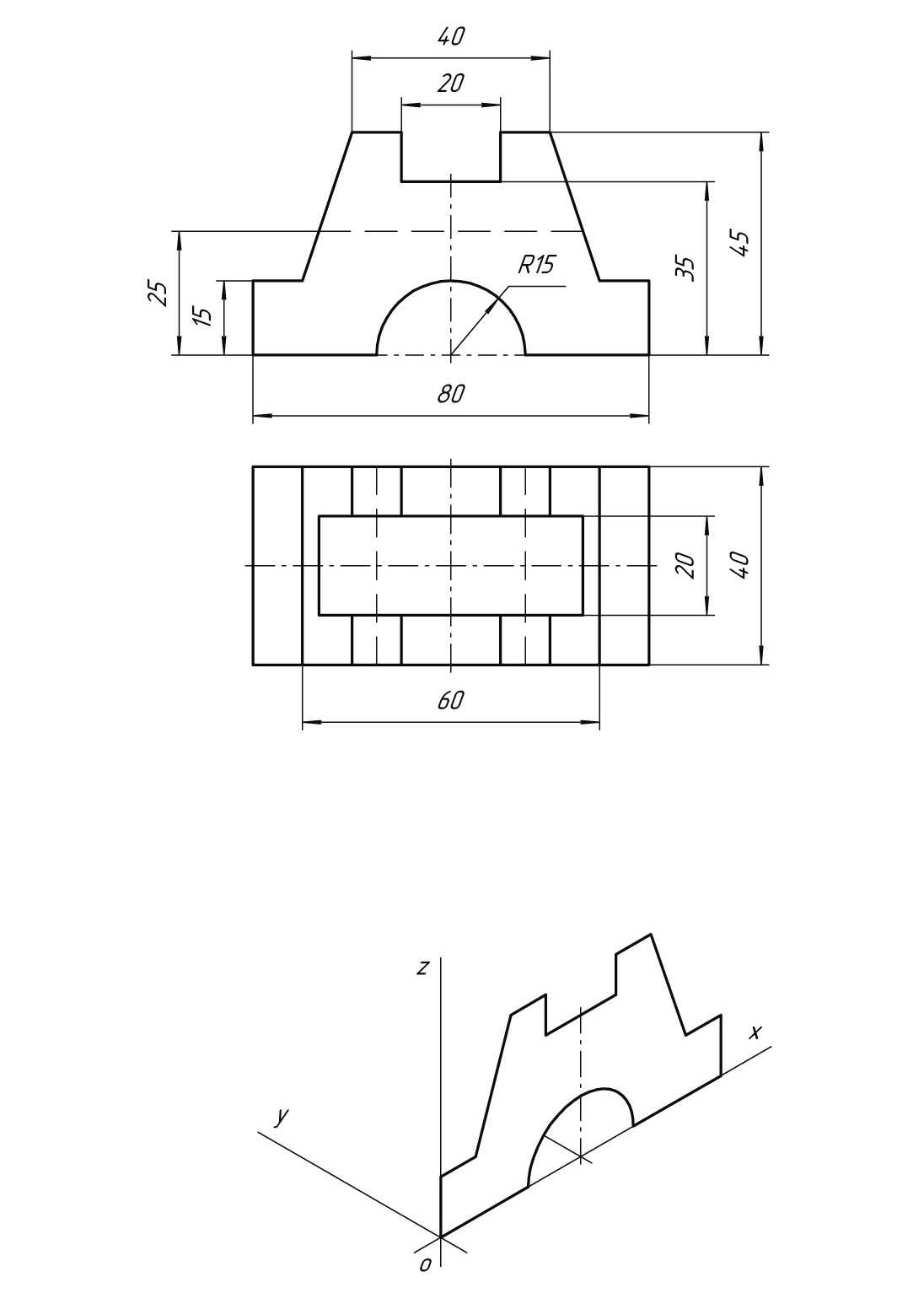
В рабочей тетради выполните по чертежу изометрическую проекцию детали в масштабе 2,5:1. На аксонометрической проекции определите расположение точек А, Б и В.
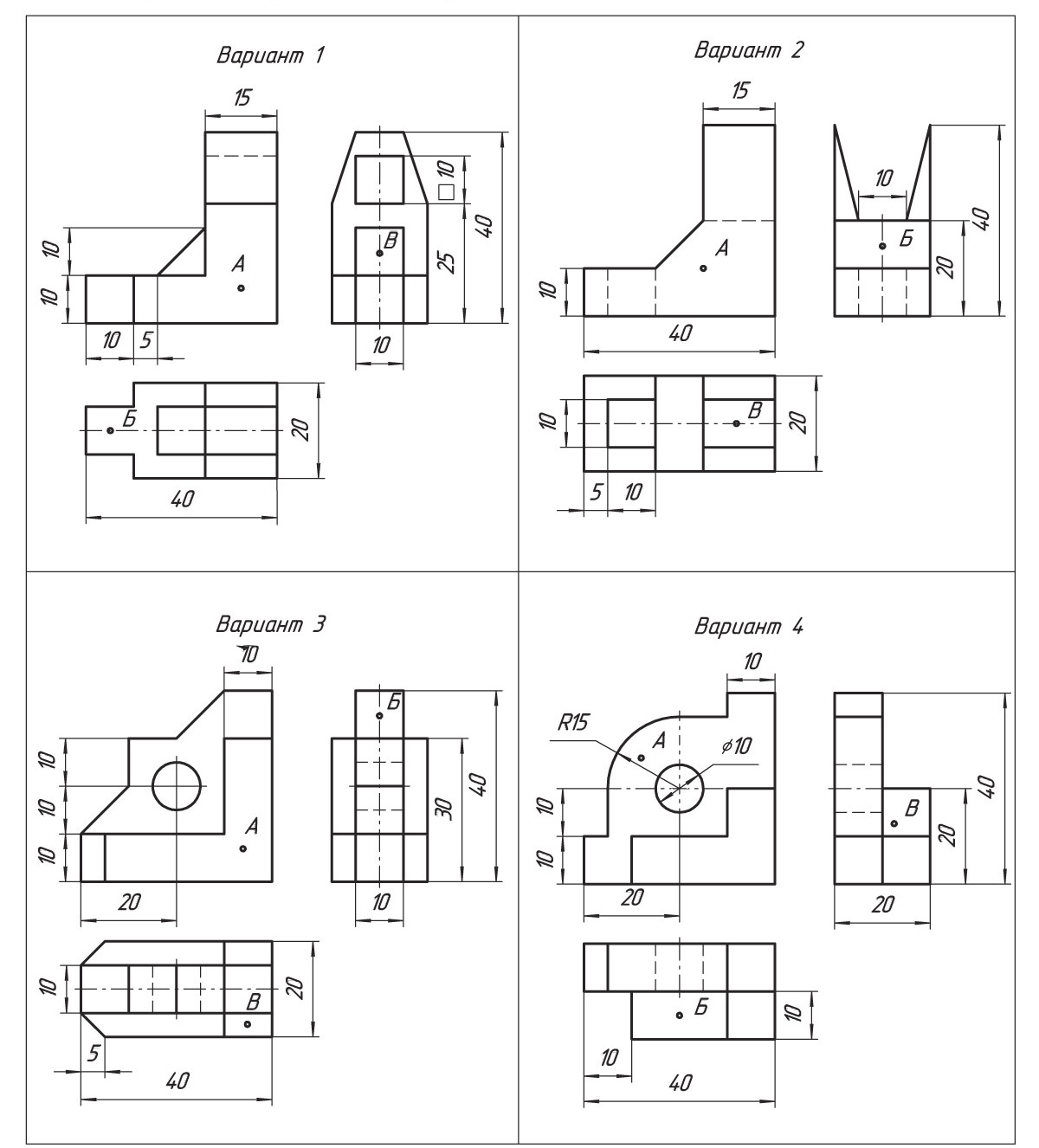
Практическая работа №10.1. Чертеж аксонометрической проекции.
На формате А4 выполнить чертеж детали и аксонометрическую проекцию детали. На аксонометрической проекции покажите точки А, Б, В, Г.
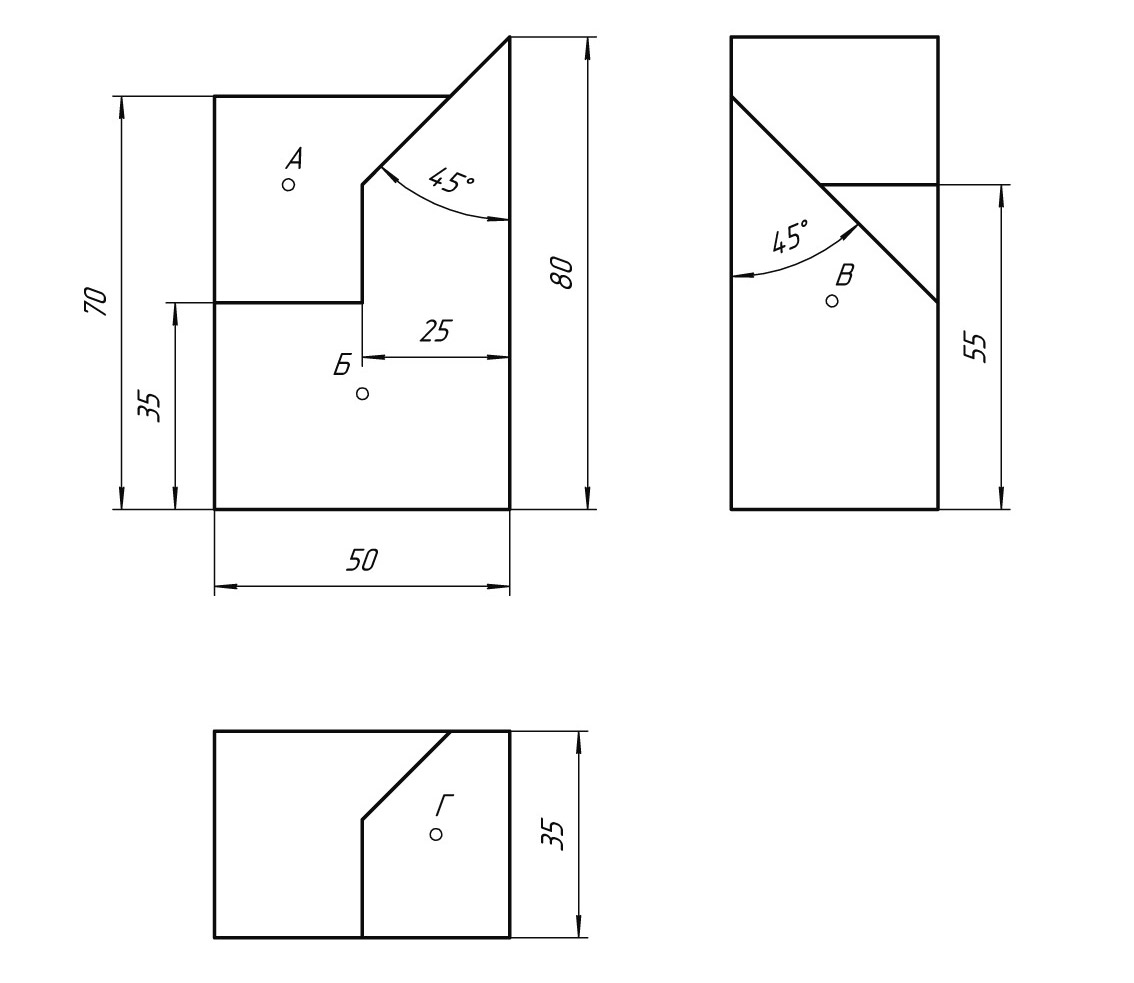
Практическая работа №10.2. Аксонометрическая проекция по чертежу.
Руководствуясь двумя видами на формате А4, выполните чертеж детали в трех проекциях, закончите построение аксонометрической проекции.
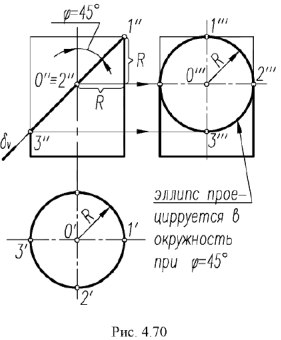
Нахождение проекций точек на поверхности конуса
Для нахождения недостающих проекций точек на поверхности конуса могут применяться следующие линии, принадлежащие поверхности конуса: окружность — параллель конуса (рис. 2.7, а), прямая — образующая конуса (рис. 2.7, б). Рассмотрим оба способа.
Пример 2.1. На поверхности конуса заданы проекции А2 и В, (см. рис. 2.7). Найдите недостающие проекции точек Ли В на поверхности конуса.
Рис. 2.7. Нахождение проекций точек на поверхности конуса
Способ 1. На рис. 2.7, а точка А задана проекцией А. Для нахождения недостающих проекций точки А воспользуемся вышеизложенным алгоритмом.
- 1. Через заданную проекцию точки Аг проводим линию, принадлежащую поверхности конуса — параллель.
- 2. Строим проекции параллели на других изображениях конуса. Па виде сверху она представляет собой окружность радиусом Rvна виде слева — отрезок.
- 3. На проекциях линии находим соответствующие проекции точек.
- 4. На пересечении окружности радиусом Л., с вертикальной линией связи, опущенной из А2, отмечаем проекцию Л,.
- 5. На виде сверху измеряем координату от проекции А, до горизонтальной оси и откладываем ее на проведенной линии связи на виде слева — получаем проекцию Л3.
- 6. Отмечаем проекцию А.л как невидимую. Проекция А., задана как видимая, следовательно, точка лежит в той части конической поверхности, которая обращена к наблюдателю (на виде сверху это часть, расположенная ниже горизонтальной оси). Таким образом, на виде слева ее проекция не видна.
Способ 2. Па рис. 2.7, 6 точка В задана проекцией В,. Построение недостающих проекций аналогично построению проекций точки А, за исключением того, что вместо окружности используется образующая конуса, пересекающая его основание в точке 1.
Коническая поверхность вращения
Коническая поверхность вращения — это линейчатая поверхность, образованная вращением прямолинейной образующей, которая пересекает криво-линейную направляющую (окружность) и проходит через неподвижную точку оси вращения, называемую вершиной.
Конусом называют геометрическое тело, ограниченное конической поверхностью и плоскостью основания, пересекающего все его образующие.
Конус называют прямым, если ось вращения перпендикулярна его основанию. Конус называют круговым, так как направляющей является окружность Конус с двумя параллельными основаниями, т.е. конус со срезанной вершиной, называют усеченным.
Построение проекций прямого кругового конуса
На рис. 4.71 показан пример построения проекций прямою кругового конуса с горизонтально-проецирующей осью вращения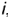 
, заданной высотой 
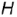и основанием радиусом 
.
Для построения проекций конуса требуется выполнить графо-аналитические действия в следующем порядке:
1-е действие. По заданному условию построить горизонтальную проекцию очерка прямого кругового конуса, которая представляет собой окружность заданного радиуса с вершиной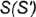 
, совпадающей с осью вращения 
.
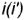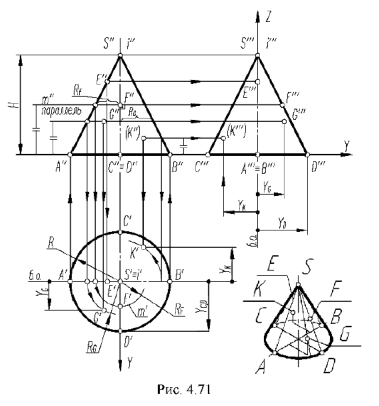
2-е действие. Выполнить графический анализ построенной горизонтальной проекции конуса:
- Круг радиуса является невидимой проекцией основания конуса.
- Круг радиуса с вершиной конуса 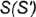является видимой проекцией боковой поверхности конуса.
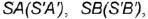
- Обозначить на горизонтальной проекции характерные образующие конуса 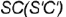и которые будут определять очерки фронтальной и профильной проекций конуса.
и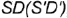 
которые будут определять очерки фронтальной и профильной проекций конуса.3-е действие. Построить фронтальную проекцию (очерк) конуса, которая представляет собой треугольник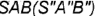 
заданной высоты 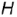, ограниченный:
4-е действие. Построить профильную проекцию (очерк) конуса:
- ‘Задать на окружности горизонтальной проекции конуса положение базовой линии (б.о.), совпадающей с горизонтальной линией оси этой окружности.
- Выбрать положение базовой оси 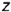(б.о.), которая будет совпадать с вертикальной осью 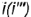вращения на профильной проекции конуса.
- Профильная проекция конуса представляет собой треугольник ограниченный:
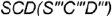ограниченный:слева и справа очерковыми образующим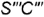и 
и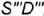 
построенными по координате 
:
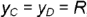вершиной 
, лежащей на базовой оси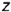 
; горизонтальным отрезком проекцией основания;
профильными проекциями характерных образующих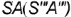 
и 
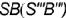, которые совпадают с осью вращения конуса 
.
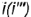. Запомните характерные признаки очерков прямого круговою конуса на чертеже — окружность основания и два треугольника.
. Характерные признаки очерков прямого кругового усеченного конуса окружность основания и две равнобокие трапеции.
Построение проекции точек, лежащих на поверхности конуса
Принадлежность точки поверхности конуса определяется ее принадлежностью образующей поверхности и принадлежностью круговым параллелям (окружностям), по которой точка вращается вокруг оси конуса. Следовательно, проекции точки можно строить либо по принадлежности образующей, либо по принадлежности круговой параллели.
На рис. 4.71 показан пример построения горизонтальных и профильных проекций точек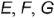 
и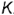 
, заданных фронтальными проекциям 
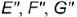и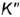 
но их принадлежности круговым параллелям.
Посфоение горизонтальных проекций заданных точек:
горизонтальные проекции точек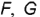 
и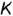 
построены на вспомогательных круговых параллелях, проведенных через заданные фронтальные проекции точек.
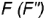
Рассмотрим графический алгоритм для построения горизонтальных проекции точек, лежащих на боковой поверхности конуса (на примере заданной точки , по их при надежности круговым параллелям:
Графический алгоритм I:
1-е действие. Провести фронтальную проекцию вспомогательной круговой параллели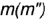 
через заданную фронтальную проекцию точки 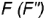: проекция параллели — это прямая, перпендикулярная оси конуса и параллельная его основанию.
2-е действие. Провести окружность горизонтальной проекции параллели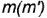 
полученным радиусом 
.
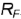3-е действие. Построить по вертикальной линии связи горизонтальную проекцию точки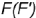 
на горизонтальной проекции параллели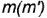
Повторить действия графического алгоритма 1 и построить аналогично горизонтальные проекци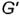и 
и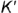 
точек 
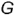и .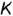
Построение профильных проекций заданных точек. Точки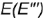 
и 
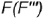построены по принадлежности характерным образующим:
точка 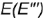лежит на видимой характерной образующей 
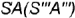, совпадающей с осью конуса;
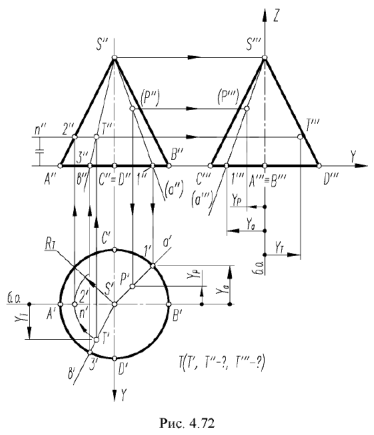
На рис. 4.72 показан пример построения горизонтальной и профильной проекции точки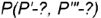 
по ее принадлежности образующей 
.
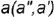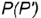
- Построение горизонтальной проекции точки по принадлежности образующей выполняется по графическому алгоритму II:
1-е действие. Провести через вершину конуса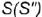 
и заданную невидимую фронтальную проекцию точки 
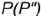вспомогательную образующую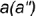 
2-е действие. Построить горизонтальную проекцию образующей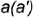 
проходящей через вершину конуса 
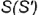и вспомогательную точку 
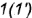, лежащую на основании конуса.
3-е действие. Построить по вертикальной линии связи горизонтальную проекцию точки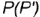 
по ее принадлежности образующей .
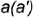- Построение профильной проекции невидимой точки выполняется по принадлежности образующей , построенной но координате .
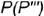выполняется по принадлежности образующей 
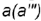, построенной но координате 
.
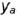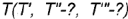
На рис. 4.72 показано построение фронтальной и профильной проекции точки по ее заданной горизонтальной проекции. Построение выполнено по приведенным алгоритмам I и II, но в обратном порядке:
1-е действие. Провести на горизонтальной проекции конуса радиусом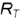 
окружность вспомогательной параллели 
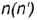или вспомогательную образующую 
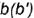, на которых лежит горизонтальная проекция точки 
.
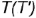2-е действие. Построить фронтальные проекции вспомогательной параллели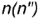 
или вспомогательной образующей 
:
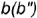параллель 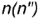провести через вспомогательную точку 
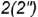на образующей 
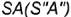параллельно основанию конуса;
образующую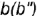 
провести через вспомогательную точку 
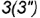на основании конуса и вершину конуса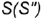 
3-е действие. Построить по вертикальной линии связи фронтальную проекцию точки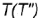 
по ее принадлежности либо параллели 
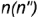, либо образующей .
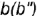Конические сечения
Рассмотрим пять возможных случаев расположения секущей плоскости относительно оси конуса и его образующих, определяющих форму линии ее пересечения с поверхностью конуса (математические доказательства не приводятся):
1-й случаи. Гели секущая плоскость проходит через вершину конуса, то эта плоскость пересекает коническую поверхность по двум образующим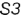 
(фронтально-проецирующая плоскость 
, рис. 4.73).
2-й случай. Если секущая плоскость расположена перпендикулярно оси конуса, то эта плоскость пересекает коническую поверхность но окружности (горизонтальная плоскость рис. 4.73).
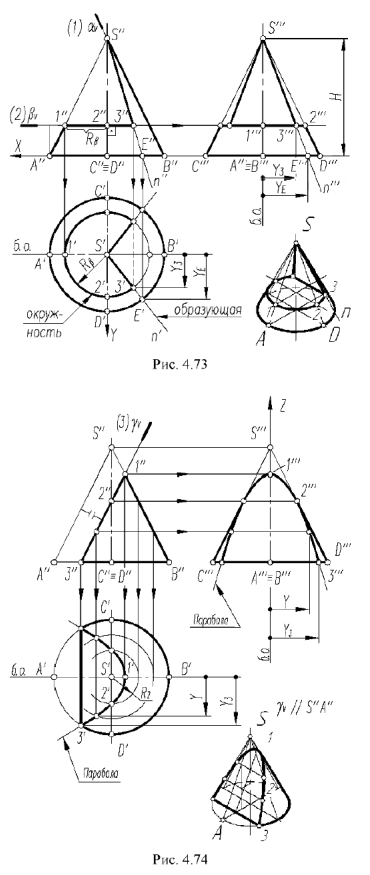
3-й случай. Если секущая плоскость расположена параллельно одной образующей конуса, то эта плоскость пересекает коническую поверхность по параболе (фронтально-проецирующая плоскость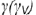 
параллельна одной образующей 
, рис.4.74).
4-и случай. Если секущая плоскость расположена параллельно двум образующим конуса, то эта плоскость пересекает коническую поверхность по гиперболе (фронтальная плоскость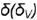 
параллельна двум образующим — и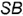 
, рис.4.75).
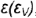
5-й случай. Если плоскость пересекает все образующие конуса под углом, отличным от прямого (или иначе, не параллельна ни одной образующей конуса), то эта плоскость пересекает коническую поверхность по эллипсу (фронтально-проецирующая плоскость ), рис 4.76).
Рассмотрим построение на проекциях конуса линии пересечения для всех пяти случаев сечений.
1-й и 2-й случаи. На рис. 4.73 показано построение проекций прямого кругового конуса с вырезом, образованным сечениями конической поверхности фронтально-проецирующей плоскостью , проходящей через вершину конуса (1-й случай), и горизонтальной плоскостью , расположенной перпендикулярно оси конуса (2-й случай).
Плоскость 
пересекает поверхность конуса по образующим 
, горизонтальные и профильные проекции которых строятся с помощью вспомогательной точки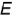 
лежащей на основании конуса.
Плоскость пересекает поверхность конуса по окружности радиуса ограниченной линией 3-3 пересечения плоскостей выреза.
Построение горизонтальной и профильной проекций конуса с вырезом и оформление очерков этих проекций видно из чертежа.
3-й случай. На рис. 4.74 показано построение проекций конуса со срезом фронтально-проецирующей плоскостью 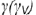, расположенной параллельно одной образующей конуса .
Плоскость пересекает поверхность конуса по параболе, горизонтальная и профильная проекции которой строятся по отмеченным характерным точкам 1, 2 и 3 и промежуточной точке (не обозначена)
Построение проекций этих точек выполнено по их принадлежности:
- проекции промежуточной точки построены по ее принадлежности соответствующей параллели (профильные проекции — по координате ).
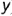).Оформление очерков проекций видно из чертежа.
4-й случай. На рис. 4.75 показано построение проекций конуса со срезом фронтальной плоскостью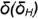 
, расположенной параллельно двум образующим конуса 
и 
.
Плоскость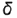 
пересекает поверхность конуса по гиперболе, фронтальная проекция которой строится по отмеченным точкам 1. 2 и 3 по их принадлежности параллелям (обратный алгоритм I), а профильная проекция гиперболы проецируется в вертикальную линию и совпадает с вырожденной проекцией плоскости среза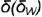 
Оформление очерков проекций видно из чертежа.
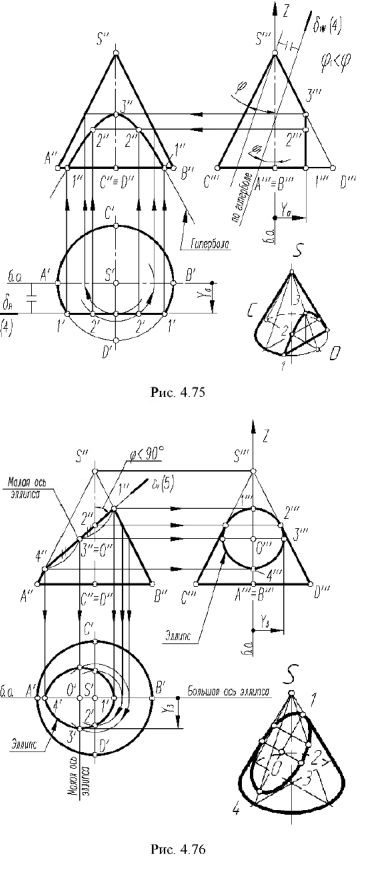
На рис 4 75 на профильной проекции конуса показано положение секущей плоскости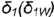 
под углом 
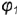к оси конуса. При 
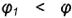плоскость пересекает поверхность конуса также по гиперболе.
5-й ыучай. На рис. 4.76 показано построение проекции конуса со срезом фронтально-проецирующей плоскостью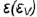 
пересекающей все образующие конуса под углом 
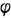к оси, отличным от прямого.
Плоскость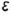 
пересекает поверхность конуса по эллипсу, горизонтальная и профильная проекции которого построены по проекциям отмеченных характерных точек 1, 2, 4 и про-межуточных точек 3, взятых на середине отрезка 1-4, который является совпадающей проекцией эллипса и его большой оси. Почки 3 определяют проекции малой оси эллипса и построены на горизонтальной проекции конуса по радиусу параллели, а на профильной проекции но координате 
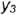(алгоритм I).
Оформление очерков проекций видно из чертежа.
. Количество взятых промежуточных точек должно быть минимальным, но достаточным, чтобы построить на проекциях конуса формы кривых второго порядка (параболы, гиперболы и эллипса), которые выполняют на чертеже по построенным характерным и промежуточным точкам с помощью лекала.
Построении проекции прямого конуса со срезами плоскостями частного положения
На рис. 4.77 показан пример построения проекций прямого круговою конуса со срезами фронтально-проецирующей плоскостью и профильной плоскостью .
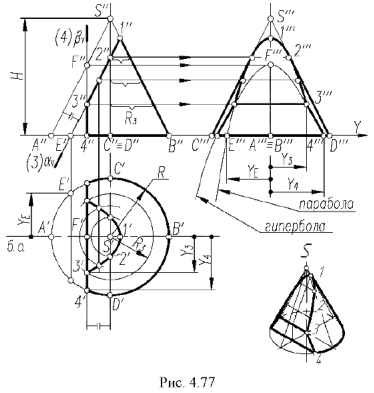
Для построения проекций конуса со срезами следует выполнить графический алгоритм, определяющий порядок действий при решении всех подобных задач.
1-е действие. Построить на чертеже тонкими линиями по заданному радиусу основания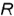 
и высоте 
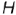фронтальную, горизонтальную и профильную проекции конуса без срезов, а затем выполнить на его фронтальной проекции заданные срезы фронтально-проецирующей плоскостью и профильной плоскостью ;
2-е действие. Обозначить на фронтальной проекции характерные точки пересечения плоскостей срезов с образующими и основанием конуса и выпол-иить графический анализ сечений:
1. Фронтально-проецирующая плоскость параллельна одной образующей конуса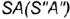 
и пересекает его поверхность по участку параболы 
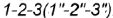, которая проецируется в отрезок и ограничена вырожденной в точку фронтально-проецирующей линией пересечения 
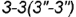плоскостей срезов и .
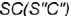- Профильная плоскость параллельна двум образующим конуса и 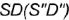и пересекает его поверхность по участку гиперболы 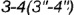, которая проецируется в отрезок и ограничена вырожденными в точки фронтально-проецирующими линиями пересечения плоскостей срезов и 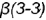и плоскости с основанием конуса (4-4).
и 
и пересекает его поверхность по участку гиперболы 
, которая проецируется в отрезок и ограничена вырожденными в точки фронтально-проецирующими линиями пересечения плоскостей срезов 
и плоскости 3-е действие. Достроить горизонтальную проекцию конуса со срезами, построив проекции плоскостей срезов по горизонтальным проекциям обозначенных точек и определить видимость плоскостей срезов:
1. Плоскость среза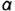 
определяет видимая горизонтальная проекция участка параболы 
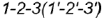построенной по горизонтальным проекциям обозначенных точек:
- Плоскость среза определяет вертикальный видимый отрезок вырожденной в линию проекции профильной плоскости, точки которой лежат на очерковой окружности основания конуса.
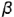определяет вертикальный видимый отрезок 
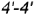вырожденной в линию проекции профильной плоскости, точки 
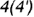которой лежат на очерковой окружности основания конуса.. Поскольку горизонтальная проекция имеет вертикальную симметрию, точки обозначены на одной ее половине (нижней).
4-е действие. Выполнить графический анализ построенной горизонтальной проекции конуса для определения ее очерка и внутреннего контура:
- Горизонтальный очерк определяют участок окружности и отрезок .
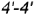- Внутренний контур определяет видимый участок параболы .
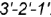.5-е действие. Достроить профильную проекцию конуса со срезами, пост-роив проекции плоскостей срезов по профильным проекциям обозначенных точек, и определить видимость плоскостей срезов:
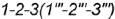
1. Плоскость среза а определяет видимый участок параболы , построенный по профильным проекциям обозначенных точек:
- Плоскость среза 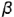определяют видимые участки гиперболы , ограниченные видимым отрезком (построен) и видимым отрезком . точки которого построены но координате .
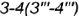, ограниченные видимым отрезком 
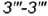(построен) и видимым отрезком 
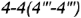. точки которого построены но координате 
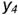.6-е действие. Выполнить графический анализ построенной профильной проекции конуса для определения ее очерка и внутреннего контура.
- Профильный очерк определяют:
- Внутренний контур определяют:
7-е действие. Оформить чертеж конуса, выполнив толстыми сплошными линиями очерки и видимый внутренний контур каждой его проекции (оставить сплошными тонкими линиями полные очерки проекций и линии построения).
Эта теория взята со страницы задач по начертательной геометрии:
Возможно эти страницы вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Сечение поверхности конуса плоскостью общего положения
При пересечении прямого кругового конуса с плоскостью могут образовываться следующие кривые второго порядка: окружность, эллипс, гипербола и парабола. Вид этих кривых зависит от угла наклона секущей плоскости к оси конической поверхности.
Ниже мы рассмотрим задачу, в которой требуется построить проекции и натуральную величину сечения конуса ω плоскостью α . Начальные данные представлены на рисунке ниже.
Определение высшей и низшей точки сечения. Границы видимости
Построение линии пересечения следует начинать с нахождения её характерных точек. Они определяют границы сечения и его видимость по отношению к наблюдателю.
Через ось конической поверхности проведем вспомогательную плоскость γ, параллельную П2. Она пересекает конус ω по двум образующим, а плоскость α по фронтали fγ. Точки 1 и 2 пересечения fγ с образующими являются граничными точками. Они делят сечение на видимую и невидимую части.
Определим высшую и низшую точки линии пересечения. Для этого через ось конуса перпендикулярно h0α введем дополнительную секущую плоскость β. Она пересекает коническую поверхность по образующим SL и SK, а плоскость α по прямой MN. Искомые точки 3 = SL ∩ MN и 4 = SK ∩ MN определяют большую ось эллипса. Его центр находится в точке O, которая делит отрезок 3–4 пополам.
Определение промежуточных точек и построение проекций эллипса
Чтобы построить проекции сечения наиболее точно, найдем ряд дополнительных точек. В случае с эллипсом целесообразно определить величину его малого диаметра. Для этого через центр O проводим вспомогательную горизонтальную плоскость δ. Она пересекает коническую поверхность по окружности диаметром AB, а плоскость α – по горизонтали hδ. Строим горизонтальные проекции окружности и прямой hδ. Их пересечение определяет точки 5′ и 6′ малого диаметра эллипса.
Для построения промежуточных точек 7 и 8 вводим вспомогательную горизонтальную плоскость ε. Проекции 7′ и 8′ определяются аналогично 5′ и 6′, как это показано на рисунке.
Соединив найденные точки плавной кривой, мы получили контур эллиптического сечения. На рисунке он обозначен красным цветом. Фронтальная проекция контура меняет свою видимость в точках 1 и 2, как это было отмечено выше.
Построение натуральной величины сечения методом совмещения
Чтобы найти натуральную величину сечения, повернем плоскость α до совмещения её с горизонтальной плоскостью. В качестве оси вращения будем использовать след h0α. Его положение в процессе преобразований останется неизменным.
Построение начинается с определения направления фронтального следа f1α. На прямой f0α возьмем произвольную точку E и определим её проекцию E’. Из E’ опустим перпендикуляр к h0α. Пересечение данного перпендикуляра с окружностью радиусом XαE» определяет положение точки E’1. Через Xα и E’1 проводим f1α.
Строим проекцию горизонтали h’1δ ∥ h0α, как это показано на рисунке. Точки O’1 и 5′1, 6′1 лежат на пересечении h’1δ с прямыми, проведенными перпендикулярно h0α из O’ и 5′, 6′. Аналогично на горизонтали h’1ε находим 7′1 и 8′1.
Строим проекции фронталей f’1γ ∥ f1α, f’3 ∥ f1α и f’4 ∥ f1α. Точки 1′1, 2′1, 3′1 и 4′1 лежат на пересечении этих фронталей с перпендикулярами, восстановленными к h0α из 1′, 2′, 3′ и 4′ соответственно.
