Как найти точки на координатной окружности

Числовая окружность

В этой статье мы очень подробно разберем определение числовой окружности, узнаем её главное свойство и расставим числа 1,2,3 и т.д. Про то, как отмечать другие числа на окружности (например, (frac<π><2>, frac<π><3>, frac<7π><4>, 10π, -frac<29π><6>)) разбирается в этой статье .

Числовой окружностью называют окружность единичного радиуса, точки которой соответствуют действительным числам , расставленным по следующим правилам:

1) Начало отсчета находится в крайней правой точке окружности;

2) Против часовой стрелки – положительное направление; по часовой – отрицательное;

3) Если в положительном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (t);

4) Если в отрицательном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (–t).

Почему окружность называется числовой?
Потому что на ней обозначаются числа. В этом окружность похожа на числовую ось – на окружности, как и на оси, для каждого числа есть определенная точка.

Зачем знать, что такое числовая окружность?
С помощью числовой окружности определяют значение синусов, косинусов, тангенсов и котангенсов. Поэтому для знания тригонометрии и сдачи ЕГЭ на 60+ баллов, обязательно нужно понимать, что такое числовая окружность и как на ней расставить точки.

Что в определении означают слова «…единичного радиуса…»?
Это значит, что радиус этой окружности равен (1). И если мы построим такую окружность с центром в начале координат, то она будет пересекаться с осями в точках (1) и (-1).

Ее не обязательно рисовать маленькой, можно изменить «размер» делений по осям, тогда картинка будет крупнее (см. ниже).

Почему радиус именно единица? Так удобнее, ведь в этом случае при вычислении длины окружности с помощью формулы (l=2πR) мы получим:

Длина числовой окружности равна (2π) или примерно (6,28).

А что значит «…точки которой соответствуют действительным числам»?
Как говорили выше, на числовой окружности для любого действительного числа обязательно найдется его «место» – точка, которая соответствует этому числу.

Зачем определять на числовой окружности начало отсчета и направления?
Главная цель числовой окружности – каждому числу однозначно определить свою точку. Но как можно определить, где поставить точку, если неизвестно откуда считать и куда двигаться?

Тут важно не путать начало отсчета на координатной прямой и на числовой окружности – это две разные системы отсчета! А так же не путайте (1) на оси (x) и (0) на окружности – это точки на разных объектах.

Какие точки соответствуют числам (1), (2) и т.д?

Помните, мы приняли, что у числовой окружности радиус равен (1)? Это и будет нашим единичным отрезком (по аналогии с числовой осью), который мы будем откладывать на окружности.

Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.

Чтобы отметить на окружности точку соответствующую числу (2), нужно пройти расстояние равное двум радиусам от начала отсчета, чтобы (3) – расстояние равное трем радиусам и т.д.

При взгляде на эту картинку у вас могут возникнуть 2 вопроса:
1. Что будет, когда окружность «закончится» (т.е. мы сделаем полный оборот)?
Ответ: пойдем на второй круг! А когда и второй закончится, пойдем на третий и так далее. Поэтому на окружность можно нанести бесконечное количество чисел.

2. Где будут отрицательные числа?
Ответ: там же! Их можно так же расставить, отсчитывая от нуля нужное количество радиусов, но теперь в отрицательном направлении.

К сожалению, обозначать на числовой окружности целые числа затруднительно. Это связано с тем, что длина числовой окружности будет равна не целому числу: (2π). И на самых удобных местах (в точках пересечения с осями) тоже будут не целые числа, а доли числа (π) : ( frac<π><2>),(-frac<π><2>),(frac<3π><2>), (2π). Поэтому при работе с окружностью чаще используют числа с (π). Обозначать такие числа гораздо проще (как это делается можете прочитать в этой статье ).

Главное свойство числовой окружности

Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.

Такая вот математическая полигамия.

И следствие из этого правила:

Все значения одной точки на числовой окружности можно записать с помощью формулы:

Если хотите узнать логику этой формулы, и зачем она нужна, посмотрите это видео .

В данной статье мы рассмотрели только теорию о числовой окружности, о том как расставляются точки на числовой и окружности и принципе, как с ней работать вы можете прочитать здесь .

Что надо запомнить про числовую окружность:

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.

Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .

Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.

Формула для расстояния между двумя точками координатной плоскости

Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

| A1A2| 2 = = ( x2 – x1) 2 + ( y2 – y1) 2 .

(1)

что и требовалось доказать.

Уравнение окружности на координатной плоскости

Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A₀ (x₀ ; y₀) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

Единичная числовая окружность на координатной плоскости

п.1. Понятие тригонометрии

Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., – спроектирован с использованием тригонометрии.

Базовым объектом изучения в тригонометрии является угол.

Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.

п.2. Числовая окружность

Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.

Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0). Точка с координатами (1;0) является началом отсчета , ей соответствует угол, равный 0. Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным ; по часовой стрелке – отрицательным .

Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90°, –120°, –180°.

п.3. Градусная и радианная мера угла

Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).

В целом, более обоснованной и естественной для измерения углов является радианная мера.

Найдем радианную меру прямого угла ∠AOB=90°. Построим окружность произвольного радиуса r с центром в вершине угла – точке O. Длина этой окружности: L=2πr. Длина дуги AB: (l_=frac<4>=frac<2pi r><4>=frac<pi r><2>.) Тогда радианная мера угла: $$ angle AOB=frac>=frac<pi r><2cdot r>=frac<pi> <2>$$

30°	45°	60°	90°	120°	135°	150°	180°	270°	360°
(frac<pi><6>)	(frac<pi><4>)	(frac<pi><3>)	(frac<pi><2>)	(frac<2pi><3>)	(frac<3pi><4>)	(frac<5pi><6>)	(pi)	(frac<3pi><2>)	(2pi)

п.4. Свойства точки на числовой окружности

Построим числовую окружность. Обозначим O(0;0), A(1;0)

Каждому действительному числу t на числовой окружности соответствует точка Μ(t). При t=0, M(0)=A. При t>0 двигаемся по окружности против часовой стрелки, описывая дугу ⌒ AM=t. Точка M – искомая. При t Например:

Отметим на числовой окружности точки, соответствующие (frac<pi><6>, frac<pi><4>, frac<pi><2>, frac<2pi><3>, pi), а также (-frac<pi><6>, -frac<pi><4>, -frac<pi><2>, -frac<2pi><3>, -pi) Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности.

Отметим на числовой окружности точки, соответствующие (frac<pi><6>, frac<13pi><6>, frac<25pi><6>), и (-frac<11pi><6>). Все четыре точки совпадают, т.к. begin Mleft(frac<pi><6>right)=Mleft(frac<pi><6>+2pi kright)\ frac<pi><6>-2pi=-frac<11pi><6>\ frac<pi><6>+2pi=frac<13pi><6>\ frac<pi><6>+4pi=frac<25pi> <6>end

п.5. Интервалы и отрезки на числовой окружности

Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.

Числовой промежуток	Соответствующая дуга числовой окружности
Отрезок
$$ -frac<pi> <6>lt t lt frac<pi> <3>$$ а также, с учетом периода $$ -frac<pi><6>+2pi klt tltfrac<pi><3>+2pi k $$
Интервал
$$ -frac<pi> <6>leq t leq frac<pi> <3>$$ а также, с учетом периода $$ -frac<pi><6>+2pi kleq tleqfrac<pi><3>+2pi k $$
Полуинтервал
$$ -frac<pi> <6>leq t ltfrac<pi> <3>$$ а также, с учетом периода $$ -frac<pi><6>+2pi kleq tltfrac<pi><3>+2pi k $$

п.6. Примеры

Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?

Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin BE=30^<circ>=frac<pi><6>.\ EC=60^<circ>=frac<pi><3>.\ AE=EC+CD=90^<circ>+30^<circ>=120^<circ>=frac<2pi><3>.\ ED=EC+CD=60^<circ>+90^<circ>=150^<circ>=frac<5pi><6>. end

Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac<pi><2>; frac<3pi><4>; frac<7pi><6>; frac<7pi><4>).

Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. begin -frac<pi><2>=-90^<circ>, frac<3pi><4>=135^<circ>\ frac<7pi><6>=210^<circ>, frac<7pi><4>=315^ <circ>end

Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac<11pi><2>; 5pi; frac<17pi><6>; frac<27pi><4>).

Выделяем из дроби целую часть, отнимаем/прибавляем один или больше полных оборотов (2πk – четное количество π), чтобы попасть в промежуток от 0 до 2π. Далее – действуем, как в примере 2. begin -frac<11pi><2>=frac<-12+1><2>cdotpi=-6pi+frac<pi><2>rightarrow frac<pi><2>=90^<circ>\ 5pi=4pi+pirightarrow pi=180^<circ>\ frac<17pi><6>=frac<18-1><6>pi=3pi-frac<pi><6>rightarrow pi-frac<pi><6>=frac<5pi><6>\ frac<27pi><4>=frac<28-1><4>pi=7pi-frac<pi><4>rightarrow pi-frac<pi><4>=frac<3pi> <4>end

Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.

Сравниваем каждое число с границами четвертей: begin 0, fracpi2approxfrac<3,14><2>=1,57, piapprox 3,14\ 3pi 3cdot 3,14\ frac<3pi><2>approx frac<3cdot 3,14><2>=4,71, 2piapprox 6,28 end

(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти
(pilt 4lt frac<3pi> <2>Rightarrow ) угол 4 радиана находится в 3-й четверти
(frac<3pi><2>lt 5lt 2pi Rightarrow ) угол 5 радиана находится в 4-й четверти
(7gt 2pi), отнимаем полный оборот: (0lt 7-2pilt fracpi2Rightarrow) угол 7 радиан находится в 1-й четверти.

Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb)), запишите количество полученных базовых точек.

Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.

[spoiler title=”источники:”]

http://www.resolventa.ru/demo/him/diagege.htm

http://reshator.com/sprav/algebra/10-11-klass/edinichnaya-chislovaya-okruzhnost-na-koordinatnoj-ploskosti/

[/spoiler]

Сегодня поговорим об единичной окружности 🧑‍🏫

 

Можно ли найти точку (её координаты) на окружности, зная координаты центра окружности, её радиус и угол поворота?🤔

Ну, конечно, можно! Записывай и запоминай общую формулу для нахождения координат точки:

x=x0+r⋅cos δ

y=y0+r⋅sin δ

x0,y0 — координаты центра окружности;

r — радиус окружности;

δ —угол поворота радиуса вектора.

В этой статье мы очень подробно разберем определение числовой окружности, узнаем её главное свойство и расставим числа 1,2,3 и т.д. Про то, как отмечать другие числа на окружности (например, (frac<π><2>, frac<π><3>, frac<7π><4>, 10π, -frac<29π><6>)) разбирается в этой статье .

Числовой окружностью называют окружность единичного радиуса, точки которой соответствуют действительным числам , расставленным по следующим правилам:

1) Начало отсчета находится в крайней правой точке окружности;

2) Против часовой стрелки — положительное направление; по часовой – отрицательное;

3) Если в положительном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (t);

4) Если в отрицательном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (–t).

Почему окружность называется числовой?
Потому что на ней обозначаются числа. В этом окружность похожа на числовую ось – на окружности, как и на оси, для каждого числа есть определенная точка.

Зачем знать, что такое числовая окружность?
С помощью числовой окружности определяют значение синусов, косинусов, тангенсов и котангенсов. Поэтому для знания тригонометрии и сдачи ЕГЭ на 60+ баллов, обязательно нужно понимать, что такое числовая окружность и как на ней расставить точки.

Что в определении означают слова «…единичного радиуса…»?
Это значит, что радиус этой окружности равен (1). И если мы построим такую окружность с центром в начале координат, то она будет пересекаться с осями в точках (1) и (-1).

Ее не обязательно рисовать маленькой, можно изменить «размер» делений по осям, тогда картинка будет крупнее (см. ниже).

Почему радиус именно единица? Так удобнее, ведь в этом случае при вычислении длины окружности с помощью формулы (l=2πR) мы получим:

Длина числовой окружности равна (2π) или примерно (6,28).

А что значит «…точки которой соответствуют действительным числам»?
Как говорили выше, на числовой окружности для любого действительного числа обязательно найдется его «место» — точка, которая соответствует этому числу.

Зачем определять на числовой окружности начало отсчета и направления?
Главная цель числовой окружности — каждому числу однозначно определить свою точку. Но как можно определить, где поставить точку, если неизвестно откуда считать и куда двигаться?

Тут важно не путать начало отсчета на координатной прямой и на числовой окружности – это две разные системы отсчета! А так же не путайте (1) на оси (x) и (0) на окружности – это точки на разных объектах.

Какие точки соответствуют числам (1), (2) и т.д?

Помните, мы приняли, что у числовой окружности радиус равен (1)? Это и будет нашим единичным отрезком (по аналогии с числовой осью), который мы будем откладывать на окружности.

Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.

Чтобы отметить на окружности точку соответствующую числу (2), нужно пройти расстояние равное двум радиусам от начала отсчета, чтобы (3) – расстояние равное трем радиусам и т.д.

При взгляде на эту картинку у вас могут возникнуть 2 вопроса:
1. Что будет, когда окружность «закончится» (т.е. мы сделаем полный оборот)?
Ответ: пойдем на второй круг! А когда и второй закончится, пойдем на третий и так далее. Поэтому на окружность можно нанести бесконечное количество чисел.

2. Где будут отрицательные числа?
Ответ: там же! Их можно так же расставить, отсчитывая от нуля нужное количество радиусов, но теперь в отрицательном направлении.

К сожалению, обозначать на числовой окружности целые числа затруднительно. Это связано с тем, что длина числовой окружности будет равна не целому числу: (2π). И на самых удобных местах (в точках пересечения с осями) тоже будут не целые числа, а доли числа (π) : ( frac<π><2>),(-frac<π><2>),(frac<3π><2>), (2π). Поэтому при работе с окружностью чаще используют числа с (π). Обозначать такие числа гораздо проще (как это делается можете прочитать в этой статье ).

Главное свойство числовой окружности

Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.

Такая вот математическая полигамия.

И следствие из этого правила:

Все значения одной точки на числовой окружности можно записать с помощью формулы:

Если хотите узнать логику этой формулы, и зачем она нужна, посмотрите это видео .

В данной статье мы рассмотрели только теорию о числовой окружности, о том как расставляются точки на числовой и окружности и принципе, как с ней работать вы можете прочитать здесь .

Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам.

Единичной окружностью называют окружность радиуса 1.

Общий вид числовой окружности.

1) Ее радиус принимается за единицу измерения.

2) Горизонтальный и вертикальный диаметры делят числовую окружность на четыре четверти (см.рисунок). Их соответственно называют первой, второй, третьей и четвертой четвертью.

3) Горизонтальный диаметр обозначают AC, причем А – это крайняя правая точка.
Вертикальный диаметр обозначают BD, причем B – это крайняя верхняя точка.
Соответственно:

первая четверть – это дуга AB

вторая четверть – дуга BC

третья четверть – дуга CD

четвертая четверть – дуга DA

4) Начальная точка числовой окружности – точка А.

Отсчет по числовой окружности может вестись как по часовой стрелке, так и против часовой стрелки.
Отсчет от точки А против часовой стрелки называется положительным направлением.
Отсчет от точки А по часовой стрелке называется отрицательным направлением.

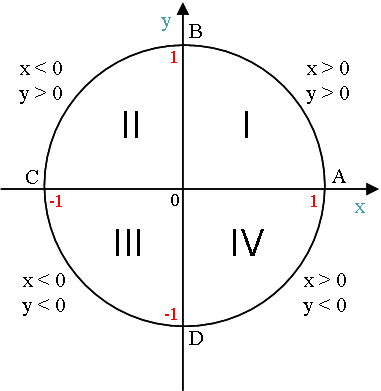Числовая окружность на координатной плоскости.

Центр радиуса числовой окружности соответствует началу координат (числу 0).

Горизонтальный диаметр соответствует оси x, вертикальный – оси y.

Начальная точка А числовой окружности находится на оси x и имеет координаты (1; 0).

Значения x и y в четвертях числовой окружности:

x 0, y Основные величины числовой окружности:

Величина
в радианах

Величина
в радиусах

Имена и местонахождение основных точек числовой окружности:

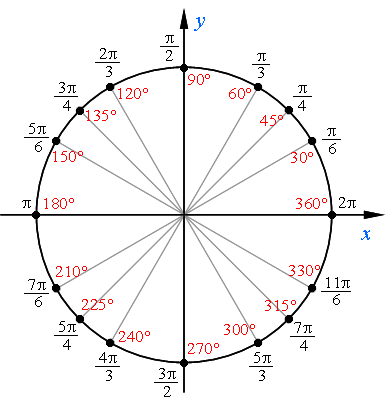
Как запомнить имена числовой окружности.

Есть несколько простых закономерностей, которые помогут вам легко запомнить основные имена числовой окружности.

Перед тем как начать, напомним: отсчет ведется в положительном направлении, то есть от точки А (2π) против часовой стрелки.

1) Начнем с крайних точек на осях координат.

Начальная точка – это 2π (крайняя правая точка на оси х, равная 1).

Как вы знаете, 2π – это длина окружности. Значит, половина окружности – это 1π или π. Ось х делит окружность как раз пополам. Соответственно, крайняя левая точка на оси х, равная -1, называется π.

Крайняя верхняя точка на оси у, равная 1, делит верхнюю полуокружность пополам. Значит, если полуокружность – это π, то половина полуокружности – это π/2.

Одновременно π/2 – это и четверть окружности. Отсчитаем три таких четверти от первой до третьей – и мы придем в крайнюю нижнюю точку на оси у, равной -1. Но если она включает три четверти – значит имя ей 3π/2.

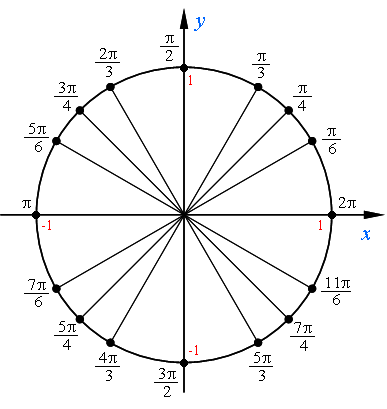
2) Теперь перейдем к остальным точкам. Обратите внимание: все противоположные точки имеют одинаковый числитель – причем это противоположные точки и относительно оси у, и относительно центра осей, и относительно оси х. Это нам и поможет знать их значения точек без зубрежки.

Надо запомнить лишь значение точек первой четверти: π/6, π/4 и π/3. И тогда мы «увидим» некоторые закономерности:

— Относительно оси у в точках второй четверти, противоположных точкам первой четверти, числа в числителях на 1 меньше величины знаменателей. К примеру, возьмем точку π/6. Противоположная ей точка относительно оси у тоже в знаменателе имеет 6, а в числителе 5 (на 1 меньше). То есть имя этой точки: 5π/6. Точка, противоположная π/4, тоже имеет в знаменателе 4, а в числителе 3 (на 1 меньше, чем 4) – то есть это точка 3π/4.
Точка, противоположная π/3, тоже имеет в знаменателе 3, а в числителе на 1 меньше: 2π/3.

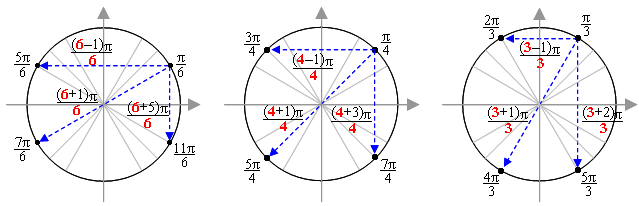— Относительно центра осей координат все наоборот: числа в числителях противоположных точек (в третьей четверти) на 1 больше значения знаменателей. Возьмем опять точку π/6. Противоположная ей относительно центра точка тоже имеет в знаменателе 6, а в числителе число на 1 больше – то есть это 7π/6.

Точка, противоположная точке π/4, тоже имеет в знаменателе 4, а в числителе число на 1 больше: 5π/4.
Точка, противоположная точке π/3, тоже имеет в знаменателе 3, а в числителе число на 1 больше: 4π/3.

— Относительно оси х (четвертая четверть) дело посложнее. Здесь надо к величине знаменателя прибавить число, которое на 1 меньше – эта сумма и будет равна числовой части числителя противоположной точки. Начнем опять с π/6. Прибавим к величине знаменателя, равной 6, число, которое на 1 меньше этого числа – то есть 5. Получаем: 6 + 5 = 11. Значит, противоположная ей относительно оси х точка будет иметь в знаменателе 6, а в числителе 11 – то есть 11π/6.

Точка π/4. Прибавляем к величине знаменателя число на 1 меньше: 4 + 3 = 7. Значит, противоположная ей относительно оси х точка имеет в знаменателе 4, а в числителе 7 – то есть 7π/4.
Точка π/3. Знаменатель равен 3. Прибавляем к 3 на единицу меньшее число – то есть 2. Получаем 5. Значит, противоположная ей точка имеет в числителе 5 – и это точка 5π/3.

3) Еще одна закономерность для точек середин четвертей. Понятно, что их знаменатель равен 4. Обратим внимание на числители. Числитель середины первой четверти – это 1π (но 1 не принято писать). Числитель середины второй четверти – это 3π. Числитель середины третьей четверти – это 5π. Числитель середины четвертой четверти – это 7π. Получается, что в числителях середин четвертей – четыре первых нечетных числа в порядке их возрастания:
(1)π, 3π, 5π, 7π.
Это тоже очень просто. Поскольку середины всех четвертей имеют в знаменателе 4, то мы уже знаем их полные имена: π/4, 3π/4, 5π/4, 7π/4.

Особенности числовой окружности. Сравнение с числовой прямой.

Как вы знаете, на числовой прямой каждая точка соответствует единственному числу. К примеру, если точка А на прямой равна 3, то она уже не может равняться никакому другому числу.

На числовой окружности все иначе, поскольку это окружность. К примеру, чтобы из точки А окружности прийти к точке M, можно сделать это, как на прямой (только пройдя дугу), а можно и обогнуть целый круг, а потом уже прийти к точке M. Вывод:

Пусть точка M равна какому-то числу t. Как мы знаем, длина окружности равна 2π. Значит, точку окружности t мы можем записать двояко: t или t + 2π. Это равнозначные величины.
То есть t = t + 2π. Разница лишь в том, что в первом случае вы пришли к точке M сразу, не делая круга, а во втором случае вы совершили круг, но в итоге оказались в той же точке M. Таких кругов можно сделать и два, и три, и двести. Если обозначить количество кругов буквой k, то получим новое выражение:
t = t + 2πk.

Отсюда формула:

Если точка M числовой окружности равна числу t, то она равна и числу вида t + 2πk, где k – любое целое число:

M(t) = M(t + 2πk),

где k ∈ Z.

Число k называется параметром.

Уравнение числовой окружности
(второе уравнение – в разделе «Синус, косинус, тангенс, котангенс»):

Числовая окружность
Изучая курс алгебры 7—9-го классов, мы до сих пор имели дело с алгебраическими функциями, т.е. функциями, заданными аналитически выражениями, в записи которых использовались алгебраические операции над числами и переменной (сложение, вычитание, умножение, деление, возведение в степень, извлечение квадратного корня). Но математические модели реальных ситуаций часто бывают связаны с функциями другого типа, не алгебраическими. С первыми представителями класса неалгебраических функций — тригонометрическими функциями — мы познакомимся в этой главе. Более детально изучать тригонометрические функции и другие виды неалгебраических функций (показательные и логарифмические) вам предстоит в старших классах.
Для введения тригонометрических функций нам понадобится новая математическая модель — числовая окружность, с которой вы до сих пор не встречались, зато хорошо знакомы с числовой прямой. Напомним, что числовая прямая — это прямая, на которой заданы начальная точка О, масштаб (единичный отрезок) и положительное направление. Любое действительное число мы можем сопоставить с точкой на прямой и обратно.

Как по числу х найти на прямой соответствующую точку М? Числу 0 соответствует начальная точка О. Если х > 0, то, двигаясь по прямой из точки 0 в положительном направлении, нужно пройти п^ть длиной х; конец этого пути и будет искомой точкой М(х). Если х 0, то, двигаясь из точки А в направлении против часовой стрелки (положительное направление обхода окружности), опишем по окружности путь длиной и конечная точка М этого пути и будет искомой точкой: М = М(x);

Мы выбрали положительный корень уравнения, так как абсцисса точки (M) больше нуля.

Аналогично можно получить координаты и других точек первого макета числовой окружности, учитывая только знаки координат в каждой четверти.

Полученные результаты запишем в таблицу.

Абсциссу (x) точки (M) найдём, решив уравнение:

x2=1−122=1−14=34;x=32.

При решении учитываем, что абсцисса точки (M) положительна.

	π6	π3	2π3	5π6	7π6	4π3	5π3	11π6
Абсцисса (x)	32	12	−12	−32	−32	−12	12	32
Ордината (y)	12	32	32	12	−12	−32	−32	−12

Дата публикации: 09 апреля 2017.

Урок и презентация на тему: “Числовая окружность на координатной плоскости”

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.

---

Скачать:
Числовая окружность на координатной плоскости (PPTX)

---

Что будем изучать:
1. Определение.
2. Важные координаты числовой окружности.
3. Как искать координату числовой окружности?
4. Таблица основных координат числовой окружности.
5. Примеры решения задач.

Определение числовой окружности на координатной плоскости

Расположим числовую окружность в координатной плоскости так, чтобы центр окружности совместился с началом координат, а её радиус принимаем за единичный отрезок. Начальная точка числовой окружности A совмещена с точкой (1;0).

Каждая точка числовой окружности имеет в координатной плоскости свои координаты х и у, причем:
1) при $x > 0$, $у > 0$ – в первой четверти;
2) при $х < 0$, $у > 0$ – во второй четверти;
3) при $х < 0$, $у < 0$ – в третьей четверти;
4) при $х > 0$, $у < 0$ – в четвертой четверти.

Для любой точки $М(х; у)$ числовой окружности выполняются неравенства: $-1 < x < 1$; $-1 < у < 1$.

Запомните уравнение числовой окружности: $x^2 + y^2 = 1$.

Нам важно научиться находить координаты точек числовой окружности, представленных на рисунке.

Найдем координату точки $frac{π}{4}$

Точка $М(frac{π}{4})$ – середина первой четверти. Опустим из точки М перпендикуляр МР на прямую ОА и рассмотрим треугольник OMP.Так как дуга АМ составляет половину дуги АВ, то $∠MOP=45°$.
Значит, треугольник OMP – равнобедренный прямоугольный треугольник и $OP=MP$, т.е. у точки M абсцисса и ордината равны: $x = y$.
Так как координаты точки $M(х;y)$ удовлетворяют уравнению числовой окружности, то для их нахождения нужно решить систему уравнений:
$begin {cases} x^2 + y^2 = 1, \ x = y. end {cases}$
Решив данную систему, получаем: $y = x =frac{sqrt{2}}{2}$.
Значит, координаты точки M, соответствующей числу $frac{π}{4}$, будут $M(frac{π}{4})=M(frac{sqrt{2}}{2};frac{sqrt{2}}{2})$.
Аналогичным образом рассчитываются координаты точек, представленных на предыдущем рисунке.

Координаты точек числовой окружности

Рассмотрим примеры

Пример 1.
Найти координату точки числовой окружности: $Р(45frac{π}{4})$.

Решение:
Т.к. числам $t$ и $t+2π*k$, где k-целое число, соответствует одна и та же точка числовой окружности то:
$45frac{π}{4} = (10 + frac{5}{4}) * π = 10π +5frac{π}{4} = 5frac{π}{4} + 2π*5$.
Значит, числу $45frac{π}{4}$ соответствует та же точка числовой окружности, что и числу $frac{5π}{4}$. Посмотрев значение точки $frac{5π}{4}$ в таблице, получаем:
$P(frac{45π}{4})=P(-frac{sqrt{2}}{2};-frac{sqrt{2}}{2})$.

Пример 2.
Найти координату точки числовой окружности: $Р(-frac{37π}{3})$.

Решение:

Т.к. числам $t$ и $t+2π*k$, где k-целое число, соответствует одна и та же точка числовой окружности то:
$-frac{37π}{3} = -(12 + frac{1}{3})*π = -12π –frac{π}{3} = -frac{π}{3} + 2π*(-6)$.
Значит, числу $-frac{37π}{3}$ соответствует та же точка числовой окружности, что и числу $–frac{π}{3}$, а числу –$frac{π}{3}$ соответствует та же точка, что и $frac{5π}{3}$. Посмотрев значение точки $frac{5π}{3}$ в таблице, получаем:
$P(-frac{37π}{3})=P(frac{{1}}{2};-frac{sqrt{3}}{2})$.

Пример 3.
Найти на числовой окружности точки с ординатой $у =frac{1}{2}$ и записать, каким числам $t$ они соответствуют?

Решение:

Прямая $у =frac{1}{2}$ пересекает числовую окружность в точках М и Р. Точка М соответствует числу $frac{π}{6}$ (из данных таблицы). Значит, и любому числу вида: $frac{π}{6}+2π*k$. Точка Р соответствует числу $frac{5π}{6}$, а значит, и любому числу вида $frac{5π}{6} +2 π*k$.
Получили, как часто говорят в таких случаях, две серии значений:
$frac{π}{6} +2 π*k$ и $frac{5π}{6} +2π*k$.
Ответ : $t=frac{π}{6} +2 π*k$ и $t=frac{5π}{6} +2π*k$.

Пример 4.
Найти на числовой окружности точки с абсциссой $x≥-frac{sqrt{2}}{2}$ и записать, каким числам $t$ они соответствуют.

Решение:

Прямая $x =-frac{sqrt{2}}{2}$ пересекает числовую окружность в точках М и Р. Неравенству $x≥-frac{sqrt{2}}{2}$ соответствуют точки дуги РМ. Точка М соответствует числу $3frac{π}{4}$ (из данных таблицы). Значит, и любому числу вида $-frac{3π}{4} +2π*k$. Точка Р соответствует числу $-frac{3π}{4}$, а значит, и любому числу вида $-frac{3π}{4} +2π*k$.

Тогда получим $-frac{3π}{4} +2 π*k ≤t≤frac{3π}{4} +2πk$.

Ответ : $-frac{3π}{4} +2 π*k ≤t≤frac{3π}{4} +2πk$.

Задачи для самостоятельного решения

1) Найти координату точки числовой окружности: $Р(frac{61π}{6})$.
2) Найти координату точки числовой окружности: $Р(-frac{52π}{3})$.
3) Найти на числовой окружности точки с ординатой $у = -frac{1}{2}$ и записать, каким числам $t$ они соответствуют.
4) Найти на числовой окружности точки с ординатой $у ≥ -frac{1}{2}$ и записать, каким числам $t$ они соответствуют.
5) Найти на числовой окружности точки с абсциссой $x≥-frac{sqrt{3}}{2}$ и записать, каким числам $t$ они соответствуют.