Точка принадлежит
поверхности сферы, если она принадлежит
линии этой поверхности.
В качестве линии
берется параллель, проходящая через
данную точку. Радиус параллели R
замеряют от оси вращения до образующей
сферы (рис.57).
Рис.57
7.9 Построение проекций точки На поверхности сферы
R
1 Случай
Дано:
– сфера
А
Построить
недостающие проекции точки А.
Точка А – опорная
точка, т.к. принадлежит очерку поверхности
сферы, поэтому для построения проекций
точки не требуется дополнительных
линий.
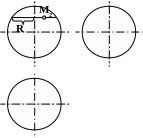
1. Через точку М
проведите параллель.
2.
Замерьте радиус параллели.
Фронтальная
проекция точки принадлежит фронтальному
меридиану.
Спроецируйте
точку А на горизонтальную и профильную
проекции фронтального меридиана (А1,
А3).
2 Случай
Дано:
– сфера
M
Построить
недостающие проекции точки M.
M2
1. Через точку М
проведите параллель.
2. Замерьте радиус
параллели.
3. На горизонтальной
проекции сферы проведите окружность
радиусом R.
Это будет горизонтальная проекция
параллели.
4. Спроецируйте
точку М на горизонтальную проекцию
параллели. Получится две проекции М1,
М1I
M2
М1
М1I
М3
М3I
5. Для того, чтобы
получить профильную проекцию точки М3
необходимо замерить расстояние от оси
Х до проекции М1
на горизонтальной проекции сферы и
отложить это расстояние от оси Z
вправо на профильной проекции сферы
(показано фигурными скобками).
6. Аналогично
постройте проекцию М3I.
7.10 Поверхность тора
Тор образуется
вращением окружности l,
вокруг оси i,
не проходящей через ее центр.
На (рис.58)
представлен открытый
тор, так
как ось вращения не пересекает эту
окружность.
Рис.58
Рис.59
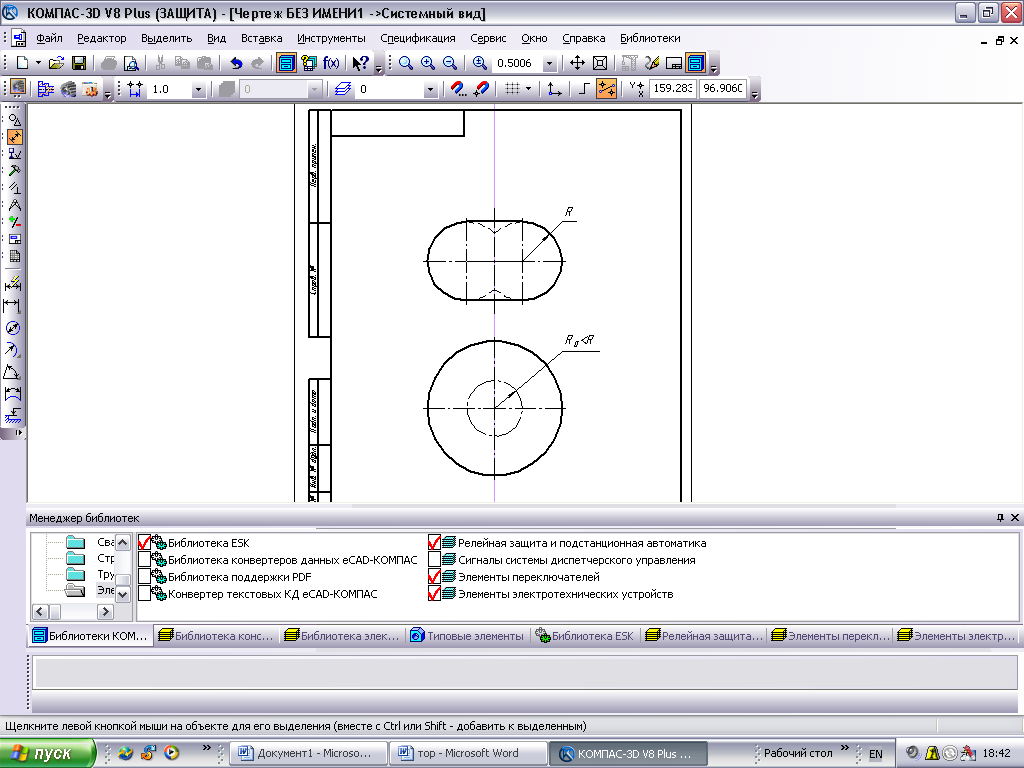
Если ось вращения
тора перпендикулярна горизонтальной
плоскости проекций, то проекция тора
на эту плоскость изображается двумя
концентрическими окружностями (рис.59).
Радиус малой
окружности (рис.57) равен расстоянию от
оси вращения до точки 1.
Радиус большой
окружности равен расстоянию от оси
вращения до точки 2.
На фронтальной
плоскости проекций тор изображается
двумя образующими окружностями,
соединенными сверху и снизу прямыми
линиями. Половины окружностей будут
не видны.
Тор называется
закрытым
(рис.60), если ось вращения пересекает
или касается окружности.
Рис.60
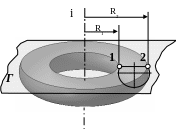
Если через
поверхность тора провести секущую
плоскость Г, перпендикулярно оси
вращения, то в сечении получатся две
окружности – параллели (рис.61). Радиус
меньшей параллели R1
замеряют от оси вращения до точки 1
образующей окружности. Радиус большой
параллели равен расстоянию от оси
вращения до точки 2 образующей окружности.
Рис.61
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
$begingroup$
Let $S$ be a sphere with origin at $(0,0,0)$.
Let $P$ be a point in $S$ surface, whose $y$ coordinate is a given $y_0$.
Let $(x_0, 0, z_0)$ be any point of the line from $(0,0,0)$ to the “shadow” of $P$ (projection of $P$ in the plane $y=0$).
How can I find $P$ ?
asked Feb 19, 2018 at 23:08
$endgroup$
0
$begingroup$
By spherical coordinates, exchanging y and z with respect to the usual convention in the following image
$$R=y_0 cos phiimpliescos phi=frac{R}{y_0}impliessin phi=pmsqrt{1-cos phi}$$
Note: the sign depends upon the sign of $y_0$
From $x_0$ and $z_0$ we can obtain
- $cos theta = frac{x_0}{sqrt{x_0^2+z_0^2}}$
- $sin theta = frac{z_0}{sqrt{x_0^2+z_0^2}}$
then we can calculate
- $x=Rsin phi cos theta$
- $z=Rsin phi sin theta$
therefore we can determine $P(x,y_0,z)$.
answered Feb 19, 2018 at 23:14
useruser
147k12 gold badges74 silver badges138 bronze badges
$endgroup$
7
$begingroup$
Let $u = frac{(x_0,0,z_0)}{|(x_0,0,z_0)|}$. Then, $langle u, Prangle = (p_1, 0, p_3)$ where $p_1$ is the x-coordinate of $P$ and $p_3$ is the z-coordinate of $P$. Since you know the $y$ coordinate, we have $P=(p_1, y_0, p_3) = u+(0,y_0,0)$.
answered Feb 19, 2018 at 23:13
mordecai iwazukimordecai iwazuki
7,0752 gold badges19 silver badges46 bronze badges
$endgroup$
3
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
7.1. Поверхности. Образование и задание поверхности на чертеже
Поверхности составляют широкое многообразие объектов трехмерного пространства. Инженерная деятельность человека связана непосредственно с проектированием, конструированием и изготовлением различных поверхностей. Большинство задач прикладной геометрии сводится к автоматизации проектно-конструкторского процесса и воспроизведения сложных поверхностей. Способы формообразования и отображения поверхностей составляют основу инструментальной базы трехмерного моделирования современных систем автоматизированного проектирования.
Рассматривая поверхности как непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением вида F(x,y,z)=0, можно выделить алгебраические поверхности (F(x,y,z)— многочлен n-ой степени и трансцендентные (F(x,y,z)— трансцендентная функция.
Если алгебраическая поверхность описывается уравнением n-й степени, то поверхность считается поверхностью n-го порядка. Произвольно расположенная секущая плоскость пересекает поверхность по кривой того же порядка (иногда распадающейся или мнимой), какой имеет исследуемая поверхность. Порядок поверхности может быть определен также числом точек её пересечения с произвольной прямой, не принадлежащей целиком поверхности, считая все точки (действительные и мнимые).
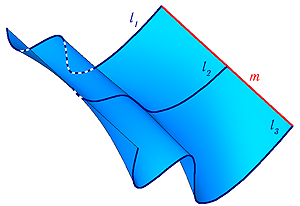
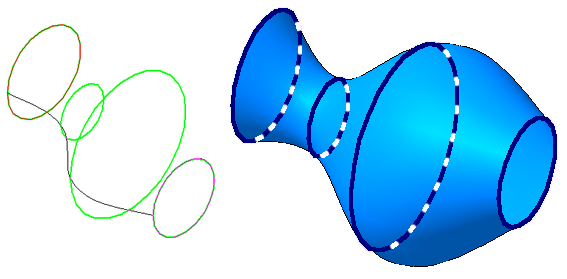
Поверхность можно рассматривать, как совокупность последовательных положений l1,l2… линии l перемещающейся в пространстве по определенному закону (Рисунок 7.1). В процессе образования поверхности линия l может оставаться неизменной или менять свою форму — изгибаться или деформироваться. Для наглядности изображения поверхности на эпюре Монжа закон перемещения линии l целесообразно задавать графически в виде одной линии или целого семейства линий (m, n, p…).
Подвижную линию принято называть образующей (li), неподвижные – направляющими (m). Такой способ образования поверхности принято называть кинематическим.
Примером такого способа могут служить все технологические процессы обработки металлов режущей кромкой, когда поверхность изделия несёт на себе «отпечаток» режущей кромки резца, т.е. её поверхность можно рассматривать как множество линий конгруэнтных профилю резца.
Рисунок 7.1 — Кинематическая поверхность
По виду образующей различают поверхности линейчатые и нелинейчатые, образующая первых – прямая линия, вторых – кривая.
Линейчатые поверхности в свою очередь разделяют на развертывающиеся, которые можно без складок и разрывов развернуть на плоскость и неразвертывающиеся.
Значительный класс поверхностей формируется движением окружности постоянного или переменного радиуса. Такие поверхности носят название циклические (Рисунок 7.2).
Рисунок 7.2 — Циклическая поверхность
Если группировать поверхности по закону движения образующей линии, то большинство встречающихся в технике поверхностей можно разделить на:
- поверхности вращения;
- винтовые поверхности;
- поверхности с плоскостью параллелизма;
- поверхности параллельного переноса.
Особое место занимают такие нелинейные поверхности, образование которых, не подчинено ни какому закону. Оптимальную форму таких поверхностей определяют теми физическими условиями, в которых они работают и устанавливают форму экспериментально (поверхности лопастей турбин, обшивка каркасов морских судов и самолетов).
Для графического изображения поверхности на чертеже используется её каркас.
Множество линий, заполняющих поверхность так, что через каждую точку поверхности проходит в общем случае одна линия этого множества, называется каркасом поверхности.
Поверхность может быть задана и конечным множеством точек, которое принято называть точечным каркасом.
Проекции каркаса могут быть построены, если задан определитель поверхности – совокупность условий, задающих поверхность в пространстве и на чертеже.
Различают две части определителя: геометрическую и алгоритмическую.
Геометрическая часть определителя представляет собой набор постоянных геометрических элементов (точек, прямых, плоскостей и т.п.), которые могут и не входить в состав поверхности.
Вторая часть – алгоритмическая (описательная) – содержит перечень операций, позволяющий реализовать переход от фигуры постоянных элементов к непрерывному каркасу.
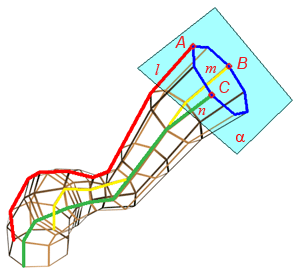
Например, циклическая поверхность, каркас которой состоит из восьмиугольников (Рисунок 7.3), может быть задан следующим образом:
- Геометрическая часть определителя: три направляющих l, m, n.
- Алгоритмическая часть: выбираем плоскость α; находим точки А, В, С, в которых α пересекает соответственно направляющие l, m, n. Строим восьмиугольник, определяемый тремя найденными точками. Переходим к следующей плоскости и повторяем построение
Рисунок 7.3 –Образование циклической поверхности
7.2. Поверхности вращения
Поверхностями вращения называются поверхности, полученные вращением образующей вокруг неподвижной оси (Рисунок 7.5).
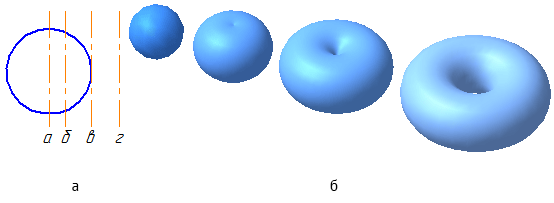
Цилиндрическая и коническая поверхности бесконечны (т.к. бесконечны образующие); сферическая, торовая поверхности — конечны.
Сферическая поверхность – частный случай торовой поверхности. При вращении окружности вокруг осей б, в, г (Рисунок 7.4, а) получим торовую поверхность (Рисунок 7.4, б), а вокруг оси а – сферическую.
Рисунок 7.4 – Образование поверхностей вращения
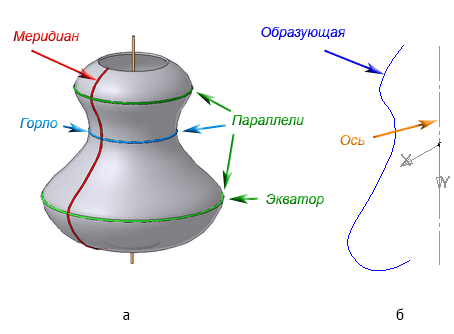
Рисунок 7.5 – Элементы поверхности вращения
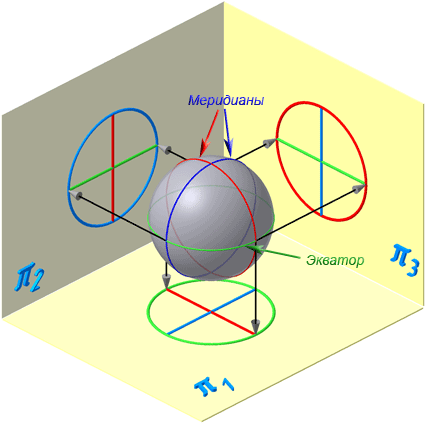
Каждая точка образующей линии при вращении вокруг оси описывает окружность, которая располагается в плоскости, перпендикулярной оси вращения. Эти окружности называются параллелями (Рисунок 7.5).
Наименьшая параллель называется горлом, наибольшая – экватором.
Линия пересечения поверхности вращения плоскостью, проходящей через ось, называется меридианом.
Линия пересечения поверхности вращения плоскостью, проходящая через ось, параллельно фронтальной плоскости проекций, называется главным меридианом.
7.3. Цилиндрическая поверхность
Цилиндрическая поверхность образуется движением прямой линии, которая в любом своём положении параллельна данному направлению и пересекает криволинейную направляющую (Рисунок 7.6).
Цилиндр – геометрическое тело, ограниченное замкнутой цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими все образующие данной поверхности.
Взаимно параллельные плоские фигуры, ограниченные цилиндрической поверхностью, называются основаниями цилиндра.
Если нормальное сечение (плоскость сечения перпендикулярна образующим) имеет форму окружности, то цилиндрическая поверхность называется круговой.
Если образующие цилиндрической поверхности перпендикулярны к основаниям, то цилиндр называется прямым, в противном случае – наклонным.
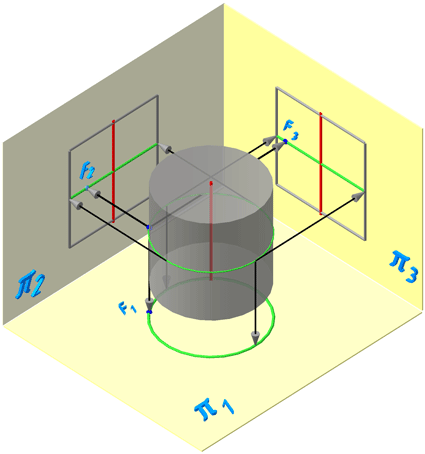
Рассмотрим проецирование прямого кругового цилиндра и принадлежащей ему точки F.
Условимся, что фронтальная проекция точки F – невидима (Рисунок 7.6).
Рисунок 7.6 – Проецирование цилиндра на плоскости проекций
Горизонтальная и профильная проекции точки F будут видимы.
При определении видимости, образующие, которые находятся на части, обращённой к наблюдателю и обозначенной на π1 сплошной зелёной линией – на плоскости проекции π2 видны, а которые находятся на части, обозначенной толстой штриховой линией – видны на π3.
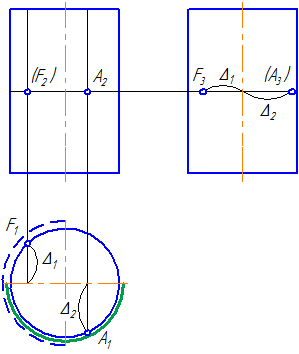
Пусть точка А на π2 видима (Рисунок 7.7). Тогда на π1 она будет видима, а на π3 невидима.
Рисунок 7.7 – Эпюр прямого кругового цилиндра и принадлежащих ему точек
7.4. Пересечение прямой с поверхностью прямого кругового цилиндра
Для построения точек пересечения прямой линии с поверхностью прямого кругового цилиндра не требуется дополнительных построений. На горизонтальной плоскости проекций точки пересечения (1 и 2) находятся сразу. Фронтальные проекции строим по линиям связи.
Но в общем случае, алгоритм решения рассмотрим на следующем упражнении.
Рисунок 7.8 – Пересечение прямой с поверхностью прямого кругового цилиндра
Упражнение
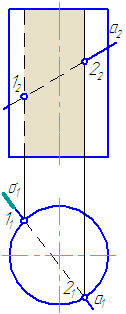
Заданы: прямой круговой цилиндр с осью вращения, перпендикулярной плоскости проекций π1 и прямая а общего положения (Рисунок 7.8).
Построить точки пересечения прямой а с поверхностью цилиндра.
Решение:
Для построения точек пересечения прямой с поверхностью цилиндра необходимо:
- Заключить прямую во вспомогательную секущую плоскость частного положения σ (горизонтально-проецирующую).
- Построить фигуру пересечения поверхности цилиндра горизонтально-проецирующей плоскостью: результат пересечения — четырехугольник (на π2 условно заштрихован).
- Найти точки «входа» и «выхода» прямой: на пересечении её фронтальной проекции с фронтальными проекциями сторон четырёхугольника (они же — проекции образующей цилиндра);
Прямая а пересекается со сторонами сечения в двух точках – 1 и 2.
Определим видимость участков прямой: очевидно, что между точками 1-2 прямая невидима, а на плоскости проекций π2 будет ещё невидим участок прямой от точки 1 до левой крайней образующей.
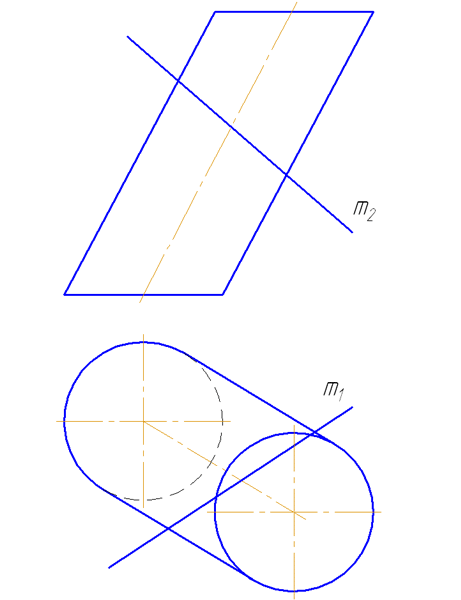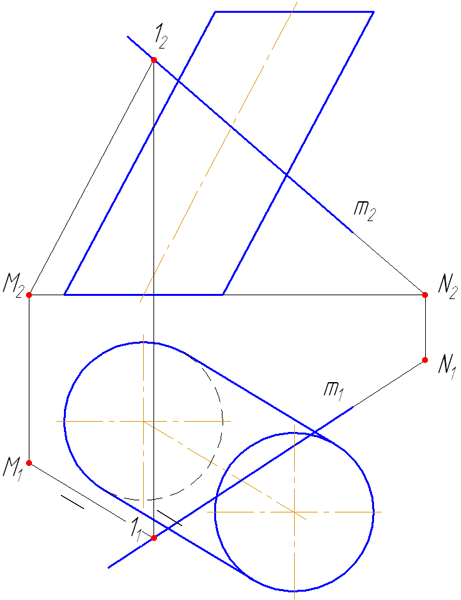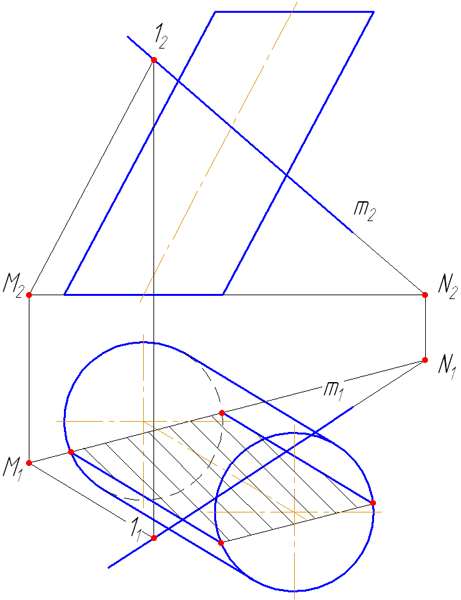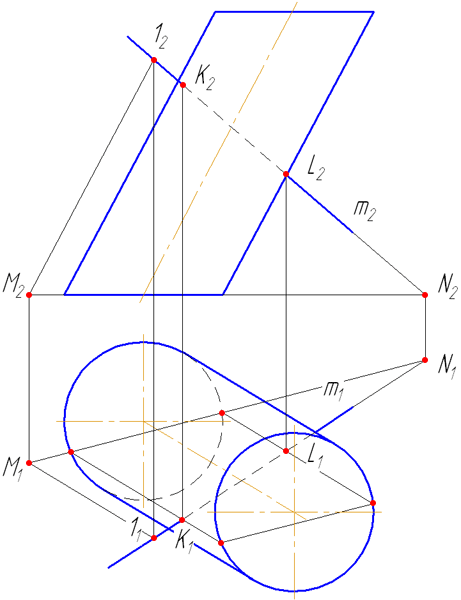
7.5. Пересечение прямой с поверхностью наклонного цилиндра
Упражнение
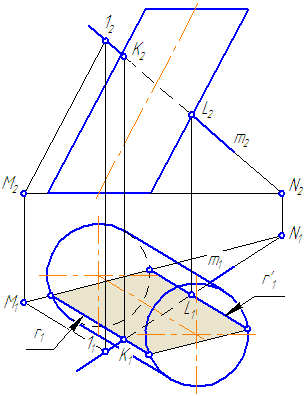
Заданы: наклонный круговой цилиндр с осью вращения, наклонной к плоскости проекций π1 и прямая mобщего положения (Рисунок 7.9).
Построить точки пересечения прямой mс поверхностью цилиндра.
Решение:
Для построения точек пересечения прямой с поверхностью цилиндра необходимо:
Рисунок 7.9 – Пересечение прямой с наклонным цилиндром
- Заключить прямую m во вспомогательную плоскость σ, дающую в сечении наиболее простую фигуру – четырехугольник (σ параллельна оси цилиндра или образующим). Эту плоскость зададим двумя пересекающимися прямыми m∩(1M);
- Построить горизонтальный след плоскости σ (прямую пересечения σ с плоскостью проекций π1) как проходящую через горизонтальные следы прямых m и (1M) (точки пересечения прямых с плоскостью проекций π1 (основания)) – (MN);
- Найти точки пересечения MN с окружностью основания цилиндра. Через эти точки провести образующие r, по которым плоскость σ пересекает боковую поверхность цилиндра:
На анимации ниже представлена последовательность построения точек пересечения прямой с наклонным цилиндром.
7.6. Сферическая поверхность
Сферическая поверхность – поверхность, образованная вращением окружности вокруг отрезка, являющегося её диаметром.
Шаром называется тело, ограниченное сферической поверхностью.
Экватор – это окружность, которая получается пересечением сферы горизонтальной плоскостью, проходящей через ее центр (Рисунок 7.10).
Меридиан – это окружность, которая получается пересечением сферы плоскостью, перпендикулярной плоскости экватора и проходящей через центр сферы.
Параллелями называются окружности, которые получаются пересечением сферы плоскостями, параллельными плоскости экватора.
Рисунок 7.10 – Проецирование сферической поверхности
Прямоугольная проекция шара (сферы) на любую плоскость – есть окружность, которую часто называют очерковой.
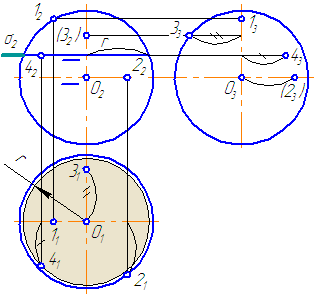
Рисунок 7.11 – Эпюр сферы и принадлежащих ей точек
Упражнение
Заданы: сферическая поверхность тремя проекциями (Рисунок 7.11) и фронтальные проекции точек 1, 2, 3, 4.
Необходимо построить горизонтальные и профильные проекции заданных точек.
Решение.
- Проанализируем их расположение на поверхности сферы. Точки 1, 2, 3 лежат на очерковых образующих сферы.
- Точка 1 принадлежит главному меридиану (очерковой окружности на π2), проекция которого на π1 совпадает с проекцией горизонтальной оси, на π3 – с проекцией вертикальной оси.
- Недостающие проекции точки 1 находим посредством линий проекционной связи. Все проекции точки 1 видимы.
- Рассмотрим положение точки 2. Точка 2 принадлежит экватору (очерковой окружности на π1), проекции которого на π2 и π3 совпадают с проекцией горизонтальной оси. Горизонтальная проекция точки 2 строится посредством линии проекционной связи, для построения профильной проекции необходимо измерить расстояние, отмеченное дугой, и отложить его по линии связи от точки О3 вправо. Профильная проекция точки 2 невидима.
- Точка 3 принадлежит очерковой окружности на π3, которая также является меридианом, проекции которого на π2 и π1 совпадают с проекцией вертикальной оси. Профильная проекция точки строится посредством линии проекционной связи. Для построения горизонтальной проекции точки 3 необходимо расстояние, отмеченное на π3 двумя засечками, отложить на π1 вверх от точки О1. Горизонтальная и профильная проекции точки 3 видимы.
- Для построения проекций точки 4 необходимо ввести вспомогательную секущую плоскость (зададим плоскость σ//π1 и σ⊥π2). Плоскость σ пересекает поверхность сферы по окружности радиусом r. На π1 строим данное сечение и по линии проекционной связи находим 41. Для построения профильной проекции необходимо расстояние, отмеченное засечкой, отложить по линии проекционной связи на π3 вправо от оси. Все проекции точки 4 видимы.
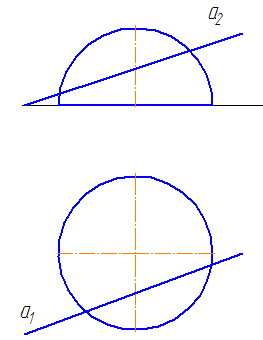
7.7. Пересечение прямой с поверхностью сферы
Упражнение
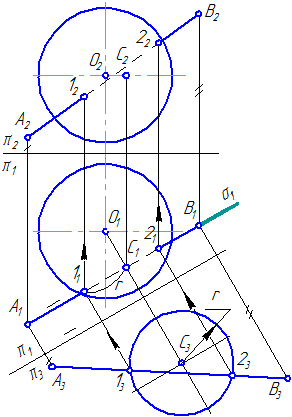
Заданы: сфера и прямая общего положения АВ.
Найти: точки пересечения прямой с поверхностью сферы (точки «входа» и «выхода»).
Чтобы найти точки пересечения прямой с поверхностью сферы необходимо:
- Заключить прямую во вспомогательную плоскость, пересекающую поверхность сферы так, чтобы получались простые фигуры (например, круг, ограниченный окружностью);
- Построить фигуру пересечения сферы вспомогательной плоскостью;
- Найти общие точки прямой и контура фигуры (окружность): так как прямая и окружность лежат в одной плоскости, то они, пересекаясь, образуют точки, общие для прямой и сферы, которые и будут являться искомыми точками (Рисунок 7.12).
Решение
- Через прямую проводим плоскость σ. Пусть σ⊥π1 и пересекает сферу по окружности радиусом r. С – центр окружности сечения ОС⊥σ:
Рисунок 7.12 – Пересечение прямой с поверхностью сферы
- Введём π3⊥π1 и π3//σ1. Построим проекцию окружности сечения на π3 и проекцию А3В3.
- Находим точки их пересечения 12 и 23.
- Определим видимость участков прямой.
- На π1 точки 1 и 2 находятся на переднем полушарии, следовательно, на π2 они видимы.
7.8. Коническая поверхность
Коническая поверхность образуется движением прямой линии (образующей), которая в любом своем положении проходит через неподвижную точку и пересекает криволинейную направляющую (имеет две полости).
Тело, ограниченное замкнутой конической поверхностью вершиной и плоскостью, называется конусом.
Плоская фигура, ограниченная конической поверхностью, называется основанием конуса.
Часть конической поверхности, ограниченная вершиной и основанием, называется боковой поверхностью конуса.
Если основание конуса является кругом, то конус называется круговым.
Если вершина конуса расположена на перпендикуляре к основанию, восстановленному из его центра, то конус называется прямым круговым.
Перемещая точку A» — можно изменять диаметр основания конуса;
перемещая точку O’ — можно менять положение точки на поверхности конуса.
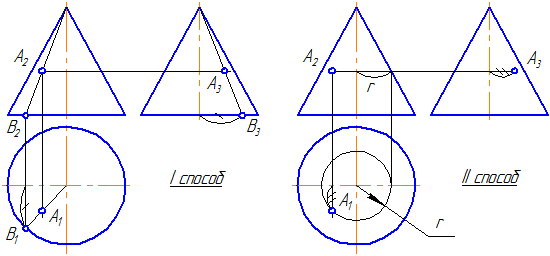
Рисунок 7.13 – Принадлежность точки конической поверхности
Рассмотрим вопрос принадлежности точки А поверхности конуса.
Дана фронтальная проекция точки А и она видима (Рисунок 7.13).
1 способ. Для построения ортогональных проекций точки, расположенной на поверхности конуса, построим проекции образующей, проходящей через данную точку. При таком положении точки А все её проекции – видимы.
2 способ. Точка А лежит на параллели конуса радиусом r. На π1 строим проекцию окружности (параллели) и по линии проекционной связи находим А1. По двум проекциям точки строим третью.
7.9. Пересечение прямой с поверхностью конуса
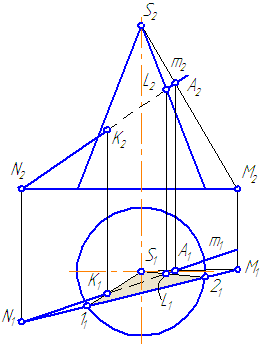
Пусть задан прямой круговой конус и прямая общего положения m (Рисунок 7.14). Найти точки «входа» и «выхода» прямой с поверхностью конуса.
- Через прямую m проводим вспомогательную секущую плоскость σ, дающую в сечении наиболее простую фигуру.
- Применение в качестве вспомогательной секущей плоскости проецирующей плоскости в данном случае нецелесообразно, так как в сечении получится кривая второго порядка, которую нужно строить по точкам.
Наиболее простая фигура – треугольник. Для этого секущая плоскость σ должна пройти через вершину S. Плоскость зададим с помощью двух пересекающихся прямых σ=SM∩MN или, что, то же самое, (σ=SM∩m).
- Возьмем на прямой m точку А и соединим её с вершиной. Прямая SA пересечёт плоскость основания в точке М.
- Построим горизонтальные проекции этих объектов.
- Продлим фронтальную проекцию прямой m до пересечения с плоскостью основания в точке N.
Рисунок 7.14 – Построение точек пересечения прямой с поверхностью конуса
- Построим её горизонтальную проекцию.
- Соединим точки M1N1, на пересечении с окружностью основания получим точки 1 и 2.
- Строим треугольник сечения конуса плоскостью σ, соединив точки 1 и 2 с вершиной S.
- На пересечении образующих 1-S и 2-S с прямой m получим искомые точки K и L.
- Определим видимость прямой относительно поверхности конуса.
На анимации ниже представлена последовательность построения точек пересечения прямой с поверхностью конуса.
7.10. Пересечение цилиндра плоскостью
Пусть плоскость сечения γ – фронтально-проецирующая (Рисунок 7.15).
- Если плоскость сечения γ параллельна оси цилиндра, то она пересекает цилиндр по четырехугольнику.
- Если плоскость сечения γ перпендикулярна оси цилиндра, то она пересекает цилиндр по окружности.
- Если плоскость сечения γ не параллельна и не перпендикулярна оси цилиндра в сечении эллипс.
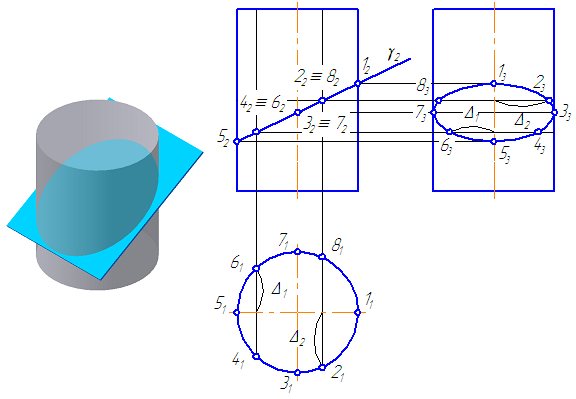
Рассмотрим алгоритм построения сечения – эллипс (Рисунок 7.15):
Рисунок 7.15 – пересечение цилиндра плоскостью
- Находим и строим характерные точки (точки, не требующие дополнительных построений) – в нашем случае, точки принадлежащие крайним образующим – 1, 3, 5, 7. Одновременно с этим, данные точки определяют величину большой и малой оси эллипса.
- Для построения участка эллипса необходимо построить не менее 5-ти точек (так как лекальная кривая второго порядка определяется как минимум пятью точками). Для построения точек 2, 4, 6, 8 возьмем на π1 произвольно расположенные образующие цилиндра, которые проецируются на данную плоскость проекции в точки.
- Построим вторые проекции данных образующих. Из точек пересечения вторых проекций образующих с проекцией плоскости сечения γ проводим линии связи к π3. Для построения третьей проекции, например, точки 6 измеряем расстояние Δ1 и откладываем его по соответствующей линии связи на π3. Симметрично ей, относительно оси вращения, строим точку 4. Аналогично строятся другие точки.
7.11. Пересечение сферы плоскостью
Плоскость пересекает поверхность сферы всегда по окружности. Задачу пересечения плоскости со сферой мы рассматривали при решении задачи построения точек пересечения прямой с поверхностью сферы (см. выше).
7.12. Пересечение конуса плоскостью
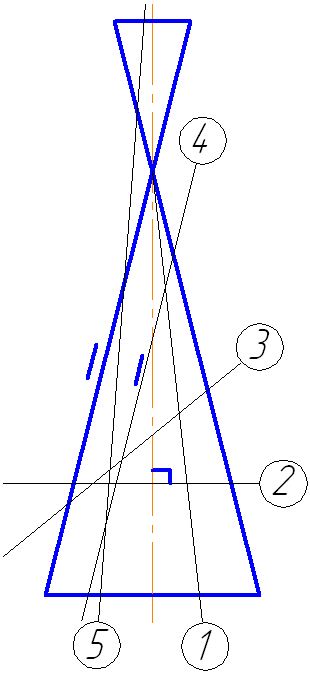
Рассмотрим пять возможных вариантов расположения плоскости относительно поверхности прямого кругового конуса. Пусть плоскость сечения перпендикулярна плоскости проекций π2 (Рисунок 7.16).
Рисунок 7.16
- Если плоскость проходит через вершину (1) – в сечении две образующие и прямая пересечения с плоскостью основания.
- Если плоскость перпендикулярна оси вращения конуса (2) – в сечении окружность.
- Если плоскость не параллельна ни одной образующей (пересекает все образующие (3)) – в сечении эллипс.
- Если плоскость параллельна одной образующей конуса – в сечении парабола (на примере – плоскость сечения (4) параллельна крайней образующей конуса).
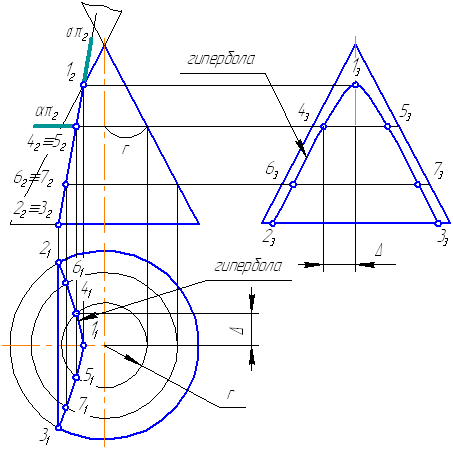
- Если плоскость параллельна двум образующим (пересекает обе полости конической поверхности (5)) – в сечении гипербола (рисунок 7.17).
Рисунок 7.17. Плоскость сечения параллельна двум образующим конуса
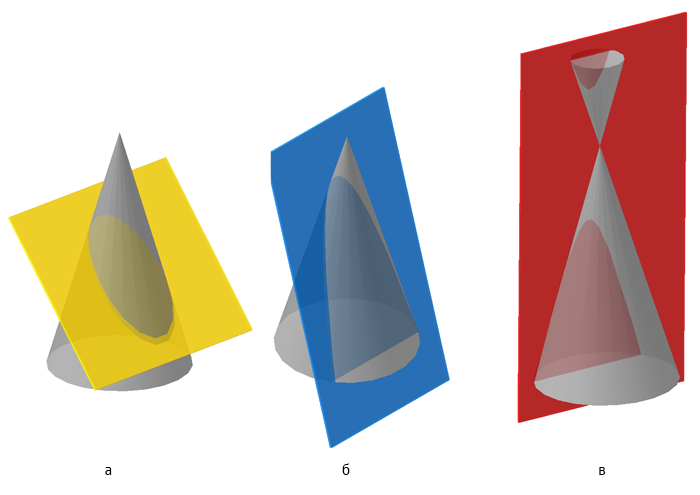
Ниже, на моделях, представлены варианты положения секущей плоскости относительно поверхности конуса, при которых получаются сечения в виде эллипса, параболы и гиперболы.
Рисунок 7.18 – Сечение конической поверхности плоскостью (а — эллипс, б — парабола, в — гипербола)
Рассмотрим пример построения сечения конической поверхности плоскостью.
Рисунок 7.19 – Построение пересечения конической поверхности плоскостью
Пусть задана секущая проецирующая плоскость σ⊥π2 (Рисунок 7.19). Если продлить коническую поверхность и проекцию плоскости, то видно, что плоскость пересекает вторую ветвь конической поверхности, следовательно, в сечении получится гипербола.
- Построим характерные точки. Это точки, лежащие на крайних образующих и на окружности основания конуса (1, 2, 3). Их проекции строятся по линиям проекционной связи.
- Для построения промежуточных точек, воспользуемся методом вспомогательных секущих плоскостей. Введём плоскость α⊥π2 и перпендикулярно оси вращения, что даст в сечении окружность радиусом r. Строим эту окружность на π1. Плоскость α пересекает и заданную плоскость сечения по прямой, проекции которой на π1 и π3 совпадают с линиями проекционной связи.
- На пересечении этих двух сечений на плоскости проекций π1 строим точки 4, 5. Профильные проекции этих точек строим по линии проекционной связи, откладывая расстояние от оси вращения конуса, равное Δ.
- Аналогично строим точки 6, 7. Плавно соединим построенные точки, образуя гиперболу.
- Обведём то, что осталось от конуса после такого среза с определением видимости. В нашем примере все проекции построенной кривой будут видимы.
На анимации ниже представлена последовательность построения пересечения конической поверхности плоскостью.
7.13. Задачи для самостоятельной работы
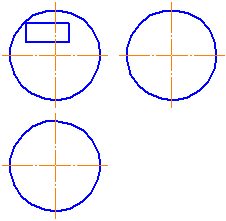
1. Достроить проекции сферы с заданным вырезом (Рисунок 7.20).
Рисунок 7.20
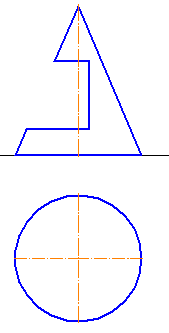
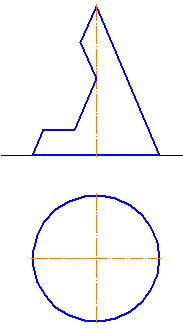
2-3. Построить три проекции конуса с призматическим отверстием (Рисунки 7.21, 7.22).
Рисунок 7.21
Рисунок 7.22
4. Построить точки «входа» и «выхода» прямой при пересечении её с поверхностью полусферы (Рисунок 7.23).
Рисунок 7.23
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
Сферическая поверхность — шар
При вращении окружности вокруг ее диаметра образуется поверхность вращения, называемая сферой. Сферическая поверхность — геометрическое место точек, равноудаленных от ее центра. Сфера — единственная геометрическая поверхность, которая имеет бесконечное число осей, проходящих через ее центр, что удобно использовать при построении проекций точек на ее поверхности и при решении различных позиционных задач с геометрическими формами, в образование которых входит сфера.
Геометрическое тело, ограниченное сферой, называют шаром.
Проекции шара и проекции его очерковых окружностей
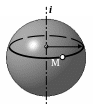
Все три очерка шара — фронтальный, горизонтальный и профильный -представляют собой окружности одного диаметра с центром в точке 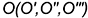
Каждая точка на поверхности шара описывает вокруг соответствующей оси окружности, называемые параллелями.
Фронтальный очерк шара — окружность 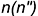
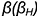
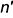
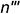
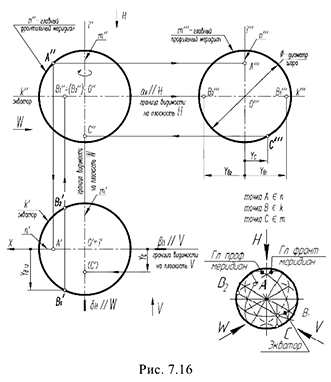
Горизонтальный очерк шара — это окружность 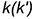
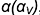
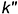
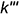
Профильный очерк шара — это окружность 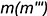
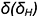
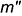
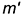
!!! Запомните характерные признаки шара на чертеже — три очерковые окружности одного диаметра.
Построение проекций точек на поверхности шара
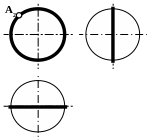
На рис. 7.16 показаны примеры построения проекций точек, лежащих на характерных очерковых окружностях шара.
Точка 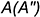
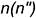
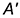
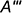
Точки 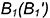
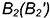
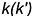
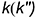
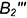
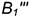
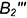
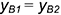
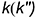
Точка 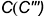
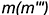
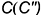
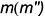
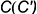
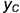
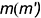
!!! Видимость проекций точки на проекциях шара определяется видимостью той части поверхности шара, на которой лежит точка, и определяется указанными границами видимости при взгляде на каждую плоскость проекций.
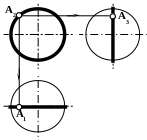
На рис. 7.17 показаны примеры построения проекций точек 
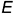
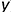
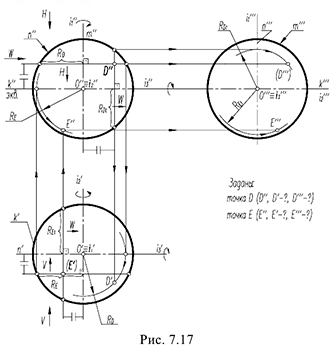
Точка 
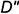
Для построения ее горизонтальной проекции 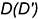
1-е действие. Провести через фронтальную проекцию точки 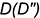
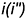
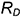

2-е действие. Провести горизонтальную проекцию этой параллели: окружность радиусом 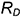
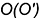
3-е действие. Построить по линии связи горизонтальную (видимую) проекцию точки 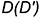
Точка 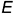
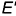
Для построения ее фронтальной проекции 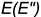
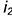
1-е действие. Провести через горизонтальную проекцию точки 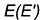
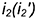
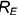
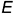
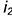
2-е действие. Провести фронтальную проекцию этой параллели: окружность радиусом 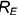
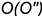
3-е действие. Построить по вертикальной линии связи фронтальную видимую проекцию точки 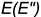
Для построения профильных проекций заданных точек 
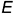
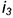
1-е действие. Провести через фронтальную проекцию точки 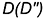
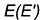
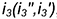
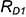
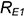

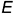
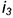
2-е действие. Провести профильные проекции этих параллелей: окружности радиусами 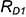
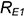
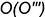
3-е действие. Построить по горизонтальным линиям связи профильные проекции точек 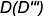
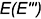
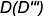
Построение проекций шара со срезами плоскостями частного положения
Всякая плоскость пересекает поверхность шара по окружностям (круговым параллелям). В зависимости от расположения секущих плоскостей относительно плоскостей проекций 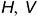
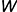
На рис. 7.18 показан пример построения проекций шара со срезами горизонтальной плоскостью 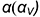
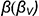
Окружность сечения шара горизонтальной плоскостью 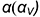
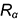
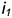
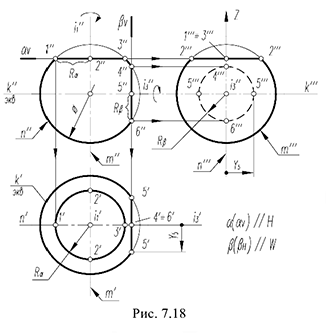
Окружность сечения шара профильной плоскостью 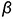
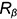
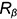
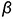
На этом же рисунке показано расположение проекции характерных точек 1,2, 3, 4, 5 и б, лежащих в плоскостях сечений на характерных очерковых окружностях шара:
- точки 1, 3, 4 и 6 лежат на главном фронтальном меридиане шара
и их проекции определяются на проекциях этого меридиана;
- точки 5 лежат на экваторе шара
и их проекции определяются на проекциях экватора;
- точки 2 лежат на профильном меридиане
и их проекции определяются на проекциях этого меридиана.
Оформление очерков проекций ясно из чертежа.
На рис. 7.19 показан пример построения проекций шара со срезом фронтально-проецирующей плоскостью 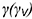
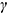
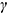
Проекции шара со срезом построены по проекциям точек, обозначенных на фронтальной проекции сечения
Горизонтальная проекция шара со срезом в виде эллипса построена по горизонтальным проекциям обозначенных точек:
-точки 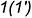
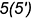
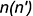
-точки 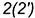
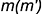
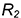
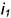
Построенные видимые горизонтальные проекции точек соединить плавной кривой эллипса с помощью лекала.
Очерк горизонтальной проекции определяет его экватор вправо от точек 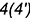
Профильная проекция шара со срезом в виде эллипса построена по профильным проекциям обозначенных точек:
Построенные видимые проекции точек соединить плавной кривой эллипса.
Очерк профильной проекции определяет профильный меридиан 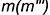
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
|
Статистика |
Координаты на сфереКоординаты на сфереПоложение точки на сфере удобнее всего задавать так, как это делается в географии. На данной сфере радиуса R выберем какие-нибудь две диаметрально противоположные точки, одну из них N назовем условно северным полюсом, другую S — южным. Какой-нибудь из «меридианов» (кратчайший путь по сфере из S в N) назовем начальным меридианом; проходящую через центр О сферы и перпендикулярную оси SN плоскость назовем экваториальной, а пересечение ее со сферой — экватором, на экваторе изберем направление, скажем против часовой стрелки, если смотреть из N. Положение любой точки М на сфере определяется двумя координатами, одна из них, назовем ее долготой,—угол φ между плоскостью начального меридиана и плоскостью, проходящей через М и ось SN (угол должен отсчитываться в направлении, соответствующем выбранному на экваторе). Широтой точки М будем называть угол θ между радиусом ОМ и плоскостью экватора (θ считается положительным для точек северного полушария и отрицательным для южного). Будем писать: М < φ ; θ>, ставя на первое место долготу, на второе — широту. Пример. Проверьте правильность координатного обозначения точек на рис. 21.
Все точки с одинаковой долготой φ0 заполняют меридиан, уравнение которого поэтому φ=φ0. Все точки с одинаковой широтой θ0 заполняют параллель θ=θ0. Уравнение, связывающее текущие координаты φ и θ, определяет, как и в плоской геометрии, кривую; неравенство, соответствующее этому уравнению, определяет одну или несколько областей, на которые эта кривая разделяет сферу. Так, неравенство θ< 0 определяет южную полусферу,θ>0—северную;θ=0 есть уравнение экватора. Если сферу отнести к декартовым координатам в пространстве, приняв центр О сферы за начало, ось SN — за ось z, ось х направив через точку <0; 0>, ось у — через<90°; 0>, то декартовы координаты х, y, z любой точки М сферы легко выразить через долготу и широту этой точки. Для этого выразим сначала координаты ее проекции М1 на плоскость Оху, где обычным образом расположим полярную систему координат. Из рис. 21 видно, что для М1(х; у; 0) полярный радиус r=Rcosθ, а полярный угол φ совпадает с долготой точки М. Кроме того, z=Rsinθ. Приняв во внимание формулы (11), получим: По этим формулам вычисляют декартовы координаты точки М (х; у; z), если известны ее координаты φ и θ на сфере. На эти же формулы можно взглянуть и с другой точки зрения. Будем считать со и 6 переменными, придавая им всевозможные значения в естественных пределах 0≤ φ<360°, -90°≤ θ≤+90°; тогда точка М<φ;θ> будет перемещаться по сфере, занимая всевозможные положения. Это напоминает параметрические уравнения линии, в которых декартовы координаты х, y, z выражены через один переменный параметр t. Разница лишь в том, что теперь х, у, z выражены через два параметра, поэтому получается не линия (одномерное образование), а поверхность (образование двумерное). Подобные уравнения называют параметрическими уравнениями поверхности; переменные параметры чаще всего здесь обозначают буквами и и v. Итак, уравнения сферы запишем в виде:
Если из этих уравнений исключить параметры и, v (для этого проще всего возвести (13) в квадрат и сложить; к сожалению, исключение переменных не всегда так просто), получим обычное ее уравнение x2 + y2+z2=R2.
|














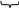




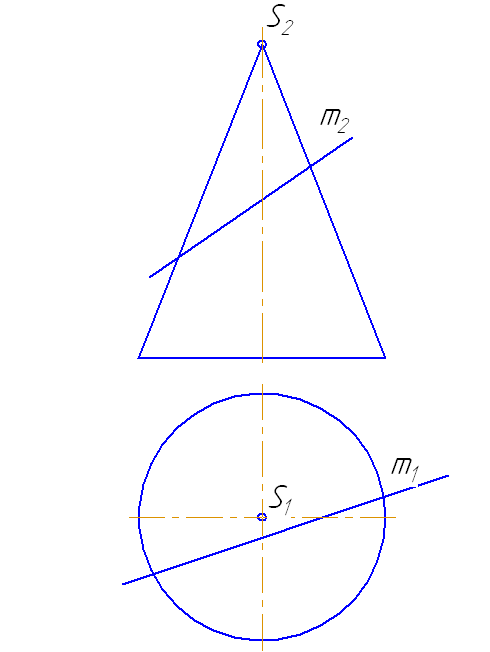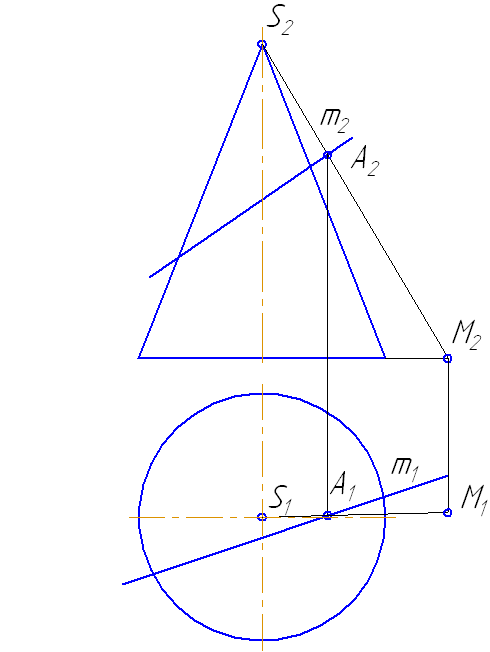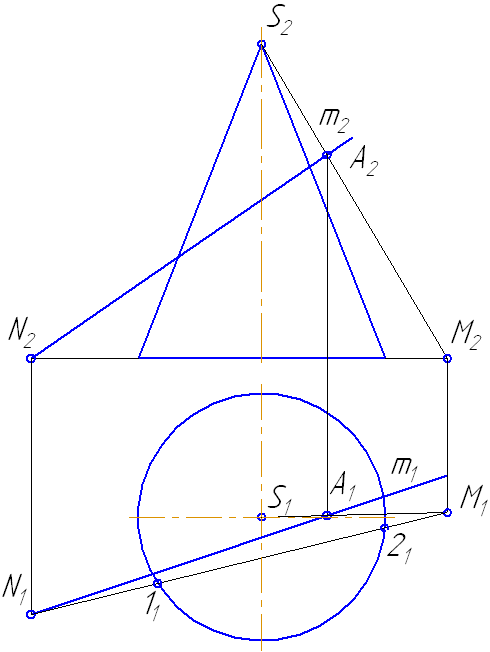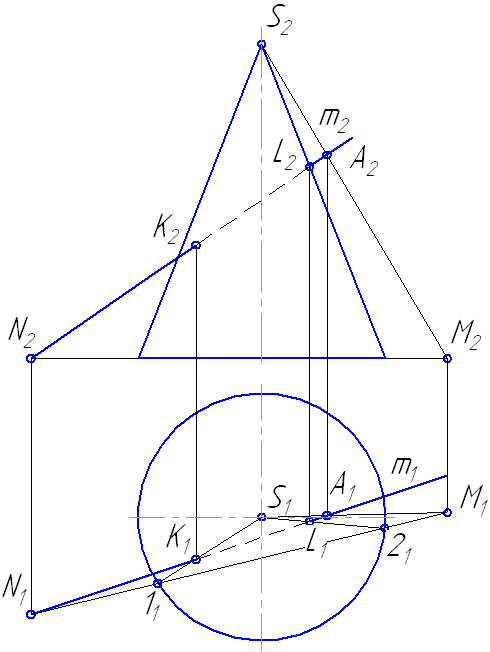

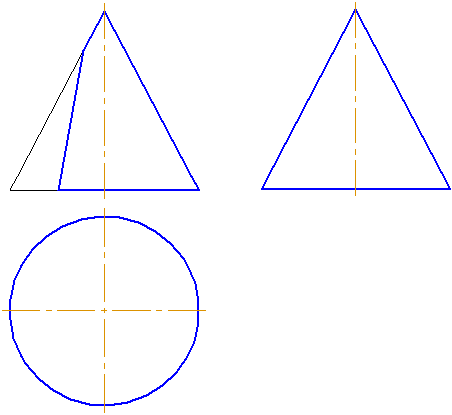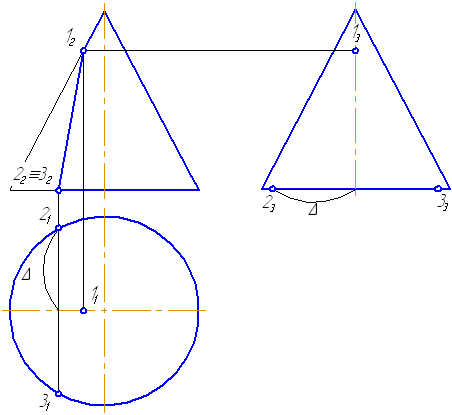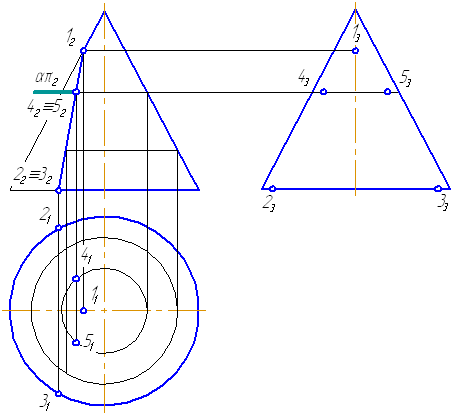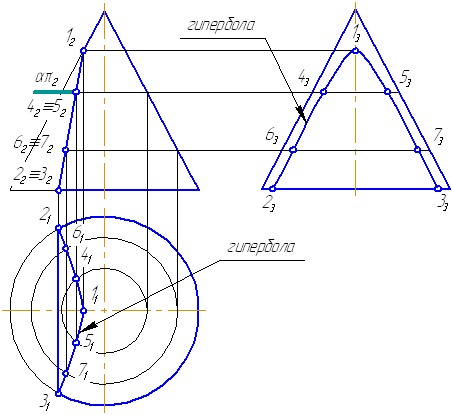

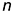 и их проекции определяются на проекциях этого меридиана;
и их проекции определяются на проекциях этого меридиана;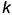 и их проекции определяются на проекциях экватора;
и их проекции определяются на проекциях экватора;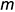 и их проекции определяются на проекциях этого меридиана.
и их проекции определяются на проекциях этого меридиана.



