Как найти точки пересечения двух сфер - Сайт, где вы сможете решить свои вопросы

Для отыскания условия пересечения двух сфер примем прямую, соединяющую их центры, за ось х. Пусть точка — центр первой сферы, — ее радиус. Точка — центр второй сферы, а — ее радиус. Уравнениями сфер будут

Решая эту систему, можно прийти к выводу:

Т.4.1. Линия пересечения двух сфер есть окружность.

Пример. Радиусы шаров равны 25 и расстояние между их центрами Найти длину линии, по которой пересекаются их поверхности.

Решение. Рассмотрим на плоскости отрезок длиной и две окружности с центрами в точках О и радиусами 25 и Если А — одна из точек пересечения этих окружностей (рис. 202), то радиус окружности пересечения данных в условии задачи сфер (поверхностей данных шаров) равен высоте треугольника и его можно найти, предварительно вычислив площадь по формуле Герона

. С другой стороны, откуда

Длина окружности пересечения сфер равна .

Источник

Пересечение двух сфер рассмотрим на примере, представленное ниже. А для начало необходимо ознакомиться с заданием. Как видите, даны две сферы, у которых центры смещены друг от друга.

Задание на пересечение двух сфер.

Алгоритм пересечение двух сфер:

1.) Чертится первоначальный вид геометрических фигур согласно заданию.

2.) Вид линии пересечения будем определять методом секущих плоскостей, и обозначим a, b, m.

Как видно из нижнего изображения, часть секущей плоскости «а» и обозначил синим цветом. Затем провел из крайних точек двух фигур прямые до осевых линий и начертил синим цветом дополнительные окружности, они пересекаются в точке.

3.) Рассмотрим секущую плоскость «b», часть ее имеет сиреневый цвет. Из крайних точек фигур опускаем линии до осей на вид сверху и чертим окружности, которые пересекаются в 2 точках.

4.) Секущая «m» также делит сферы на окружности, крайние точки которых переносим на вид сверху, точнее на осевые линии и чертим окружности (имеют зеленый цвет), пересекающие в 2 точках.

5.) У основания, точки находятся аналогичным путем как и в предыдущих 3-х пунктах.

6.) Найденные точки, описанные в пунктах 2,3 и 4, необходимо перенести на вид спереди (фронталь).

Я не зря обозначил разными цветами, это поможет лучше понять как чертить.

Сначала построим точки,показывающие линию с видимой передней стороны. Все точки с вида сверху переносятся на вид спереди.

От точки синего цвета ведется прямая до секущей плоскости «a»(часть имеет также синий цвет) и в месте пересечения указывается точка.

От точек сиреневого цвета ведутся линии вверх до пересечения с плоскостью «b» и вместе их пересечения ставятся точки.

От точек зеленого цвета ведутся прямые до пересечения с плоскостью «m», в месте пересечения ставятся точки.

Точки оснований проще перенести. Проводятся линии от вида сверху до вида спереди, которые имеют место пересечения в точках (имеют черный цвет).

8.) Последним шагом является удаление дополнительных линий построения. А также, если это необходимо, обозначают точки согласно расположениям в проекциях.

Просмотрели 302

Источник

Скачать материал

без ожидания

Скачать материал

без ожидания

Сейчас обучается 962 человека из 80 регионов

Сейчас обучается 35 человек из 26 регионов

Сейчас обучается 76 человек из 34 регионов

Описание презентации по отдельным слайдам:

1 слайд

Урок геометрии в 11 классе
.

Полушина Елена Владимировна
учитель математики Зудиловской школы Алтайского края
2 слайд

Истинное знание состоит не в знакомстве с фактами, которые делают человека лишь педантом, а в использовании фактов, которые делают его философом.
Г. Боклъ
4 слайд

Что называется сферой, шаром?
Что называется радиусом и диаметром шара?
Какие точки называются диаметрально противоположными?
Какая фигура образуется при пересечении шара с плоскостью, сферы с плоскостью?
Где лежит центр этой окружности?
Какая плоскость называется диаметральной плоскостью шара?
Какая плоскость называется касательной плоскостью сферы?
5 слайд

Пересечение двух сфер
6 слайд

Теорема: линия пересечения двух сфер есть окружность
7 слайд

Теорема: линия пересечения двух сфер есть окружность
8 слайд

Теорема: линия пересечения двух сфер есть окружность
Дано: сфера (О1, R), сфера (О2, R), А – точка пересечения
9 слайд

Теорема: линия пересечения двух сфер есть окружность
Дано: сфера (О1, R), сфера (О2, R), А – точка пересечения
Доказать: линия пересечения – окружность
Доказательство:
10 слайд

Теорема: линия пересечения двух сфер есть окружность
,
Дано: сфера (О1 , R), сфера (О2 , R), А – точка пересечения
Доказать: линия пересечения – окружность
Доказательство:
1. через А проведем α перпендикулярную О1О2
11 слайд

Теорема: линия пересечения двух сфер есть окружность
Дано: сфера (О1, R), сфера (О2 , R), А – точка пересечения
Доказать: линия пересечения – окружность
Доказательство:
1. через А проведем α перпендикулярную О1О2 ,
2. α∩сферы по окружности (В,АВ),
12 слайд

Теорема: линия пересечения двух сфер есть окружность
Дано: сфера (О1 , R), сфера (О2 , R), А и В – точки пересечения сфер
Доказать: линия пересечения – окружность
Доказательство:
1. через А проведем α перпендикулярную О1О2 ,
2. α∩сферы по окружности (В,АВ),
3. т.о. окружность (В,АВ)- линия пересечения сфер.
13 слайд

Задача1. два равных шара радиуса R расположены так, что центр одного лежит на поверхности другого. Найти длину линии, по которой пересекаются их поверхности.
14 слайд

Задача1. два равных шара радиуса R расположены так, что центр одного лежит на поверхности другого. Найти длину линии, по которой пересекаются их поверхности
Дано: сфера (О, R) пересекает сферу (О1 , R)
15 слайд

Задача1. два равных шара радиуса R расположены так, что центр одного лежит на поверхности другого. Найти длину линии, по которой пересекаются их поверхности
Дано: сфера (О, R) пересекает сферу (О1 , R)
Найти: длину линии пересечения.
16 слайд

Задача1. два равных шара радиуса R расположены так, что центр одного лежит на поверхности другого. Найти длину линии, по которой пересекаются их поверхности.
Дано: сфера (О, R) пересекает сферу (О1 , R)
Найти: длину линии пересечения.
Решение: 1. проведем сечение через центры шаров,
17 слайд

Задача1. два равных шара радиуса R расположены так, что центр одного лежит на поверхности другого. Найти длину линии, по которой пересекаются их поверхности
Дано: сфера (О, R) пересекает сферу (О1 , R)
Найти: длину линии пересечения.
Решение: 1. проведем сечение через центры шаров,
2. по теореме 20.6 сферы пересекаются по окружности,
18 слайд

Задача1. два равных шара радиуса R расположены так, что центр одного лежит на поверхности другого. Найти длину линии, по которой пересекаются их поверхности
Дано: сфера (О, R) пересекает сферу (О1 , R)
Найти: длину линии пересечения.
Решение: 1. проведем сечение через центры шаров,
2. по теореме 20.6 сферы пересекаются по окружности,
3. ∆АО1О2 – равносторонний,
19 слайд

Задача1. два равных шара радиуса R расположены так, что центр одного лежит на поверхности другого. Найти длину линии, по которой пересекаются их поверхности
Дано: сфера (О, R) пересекает сферу (О1 , R)
Найти: длину линии пересечения.
Решение: 1. проведем сечение через центры шаров,
2. по теореме 20.6 сферы пересекаются по окружности,
3. ∆АО1О2 – равносторонний,
4. радиус окружности равен высоте ∆А О1О2 ,
20 слайд

Задача1. два равных шара радиуса R расположены так, что центр одного лежит на поверхности другого. Найти длину линии, по которой пересекаются их поверхности
Дано: сфера (О, R) пересекает сферу (О1 , R)
Найти: длину линии пересечения.
Решение: 1. проведем сечение через центры шаров,
2. по теореме 20.6 сферы пересекаются по окружности,
3. ∆АО1О2 – равносторонний,
4. радиус окружности равен высоте ∆А О1О2 ,
5. h =½R√3
6. C = π R√3
21 слайд

Задача 2. Две сферы, радиусы которых 15 и 20, пересекаются по окружности, радиус которой равен 12. Найти расстояние между центрами сфер, если они находятся по разные стороны от линии пересечения.

Дано: сфера (О1,R1 ), сфера (О2, R2), R1 = 20, R2 = 15
Найти: О1 О2
Решение: 1. АО =12,
2. О1О = √400-144 = 16,
3. ОО2 = √225 – 144 = 9,
4. О1 О2 = 16 + 9 = 25
О
22 слайд

Задача 2. Две сферы, радиусы которых 15 и 20, пересекаются по окружности, радиус которой равен 12. Найти расстояние между центрами сфер, если они находятся по одну сторону от линии пересечения.
Дано: сфера (О1,R1 ), сфера (О2, R2), R1 = 20, R2 = 15
Найти: О1 О2
Решение: 1. АО =12,
2. О1О = √400-144 = 16,
3. ОО2 = √225 – 144 = 9,
4. О1 О2 = 16 – 9 = 7

О
23 слайд

Задача 4. Найти радиус окружности пересечения двух сфер, если радиусы сфер равны R, а расстояние между их центрами равно
1,6 R.

Дано: сфера (О1,R ),
сфера (О2, R),О1 О2 =1,6 R
Найти: АВ
Решение: 1. АО1 =R,
АО2 =R, О1 О2 = 1,6 R
24 слайд

Задача 4. Найти радиус окружности пересечения двух сфер, если радиусы сфер равны R, а расстояние между их центрами равно
1,6 R.
Дано: сфера (О1,R ),
сфера (О2, R),О1 О2 =1,6 R
Найти: АВ
Решение: 1. АО1 =R,
АО2 =R, О1 О2 = 1,6 R
2. ∆АО1О2 – равнобедренный,
АВ – высота→медиана
25 слайд

Задача 4. Найти радиус окружности пересечения двух сфер, если радиусы сфер равны R, а расстояние между их центрами равно
1,6 R.
Дано: сфера (О1,R ),
сфера (О2, R),О1 О2 =1,6 R
Найти: АВ
Решение: 1. АО1 =R,
АО2 =R, О1 О2 = 1,6 R
2. ∆АО1О2 – равнобедренный,
АВ – высота→медиана
3. О1В = 0,8 R
4. АВ = √ R2 -0,64 R2,=0,6R
26 слайд

Итог урока
1. Мы доказали, что линия пересечения двух сфер есть окружность

2. Научились практически применять теорему при решении задач.
3. Проверили свой уровень знаний
27 слайд

Домашнее задание:
Повторить п. 187-190
Выучить теорему 20.6 (существование окружности ) п.191
Самостоятельно доказать единственность окружности
Решить задачу № 45
28 слайд

Критерий оценивания

25 – 27 баллов – «5»
21 – 24 балла – «4»
15 – 20 баллов – «3»
29 слайд

Дорогу осилит идущий, а геометрию – мыслящий.
30 слайд

На этом наш урок закончен
Спасибо за работу

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 258 559 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Материал подходит для УМК

«Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Погорелов А.В.

Тема

62. Пересечение двух сфер

Больше материалов по этой теме

Другие материалы

Зачетная работа по теме “Пирамида. Конус.”

Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Погорелов А.В.
Тема: 47. Пирамида

28.01.2018
1017
4

Тест по теме “Аксиомы стереометрии”

Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Погорелов А.В.
Тема: 1. Аксиомы стереометрии

22.01.2018
2271
1

Вам будут интересны эти курсы:

Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Использование активных методов обучения в вузе в условиях реализации ФГОС»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Организация деятельности помощника-референта руководителя со знанием иностранных языков»
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Курс профессиональной переподготовки «Организация технической поддержки клиентов при установке и эксплуатации информационно-коммуникационных систем»
Курс повышения квалификации «Мировая экономика и международные экономические отношения»
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
Курс профессиональной переподготовки «Организация и управление службой рекламы и PR»
Курс повышения квалификации «Информационная этика и право»

Источник

Гипермаркет знаний>>Математика>>Математика 11 класс>>Математика:Пересечение двух сфер

Пересечение двух сфер

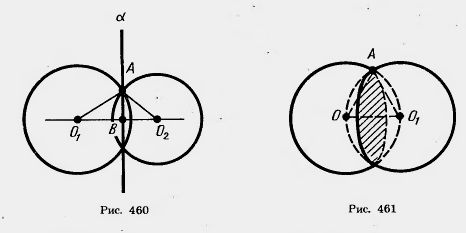
Теорема 20.6. Линия пересечения двух сфер есть окружность.

Доказательство. Пусть О₁ и О₂ — центры сфер и А — их точка пересечения (рис. 460). Проведем через точку А плоскость , перпендикулярную прямой О₁О₂.

Обозначим через В точку пересечения плоскости с прямой О₁О₂. По теореме 20.3 плоскость пересекает обе сферы по окружности К с центром В, проходящей через точку А. Таким образом, окружность К принадлежит пересечению сфер.

Покажем теперь, что сферы не имеют других точек пересечения, кроме точек окружности К. Допустим, точка X пересечения сфер не лежит на окружности К. Проведем плоскость через точку X и прямую О₁О₂. Она пересечет сферы по окружностям с центрами О₁ и О₂. Эти окружности пересекаются в двух точках, принадлежащих окружности К, да еще в точке X. Но две окружности не могут иметь больше двух точек пересечения. Мы пришли к противоречию. Итак, пересечение наших сфер есть окружность (К). Теорема доказана.

Задача (44). Два равных шара радиуса R расположены так, что центр одного лежит на поверхности другого. Найдите длину линии, по которой пересекаются их поверхности.

Решение. Проведем сечение через центры шаров (рис. 461). Линия, о которой идет речь в задаче, есть окружность (теорема 20.6). Ее радиус равен высоте равностороннего треугольника ОАО₁ со сторонами, равными R.

Высота равна

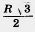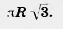
Следовательно, длина линии равна

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь – Образовательный форум.

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов –
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других “взрослых” тем.

Разработка – Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email:

Источник

Линия пересечения двух сфер есть окружность.

Доказательство

Пусть O1 и O2 – центры сфер и A – их точка пересечения. Проведем через точку A плоскость α, перпендикулярную прямой O1O2.
Обозначим через B точку пересечения плоскости α с прямой O1O2. По теореме сечение шара плоскостью плоскость α пересекает обе сферы по окружности K с центром B, проходящей через точку A. Таким образом, окружность K принадлежит пересечению сфер.
Докажем, что сферы не имеют других точек пересечения, кроме точек окружности K. Допустим, точка X пересечения сфер не лежит на окружности K. Проведем плоскость через точку X и прямую O1O2. Она пересечет сферы по окружностям с центрами O1 и O2. Эти окружности пересекаются в двух точках, принадлежащих окружности K, да еще в точке X. Но две окружности не могут иметь больше двух точек пересечения. Следовательно, пересечение сфер есть окружность. Теорема доказана

Источник

Алгоритм пересечение двух сфер:

Описание презентации по отдельным слайдам:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Материал подходит для УМК

Тема

Другие материалы

Вам будут интересны эти курсы:

Вам также может понравиться

Как найти задание борьба за искупление

800b0109 ошибка обновления windows 7 как исправить ошибку

Как найти модуль от числа в python

Добавить комментарий Отменить ответ