Как найти точку пересечения двух линейных функций, не строя графиков?
Иванова Ирина
Знаток
(309),
закрыт
8 лет назад
Лучший ответ
Роман Сергеевич
Искусственный Интеллект
(167571)
10 лет назад
Приравниваете обе функции к друг другу, решаете полученное уравнение и в результате получаетте значения х где функции равны.
Остальные ответы
Zellandia@bk _
Мыслитель
(5889)
10 лет назад
Здесь понадобится система уравнений.
Максим Головченко
Профи
(941)
10 лет назад
Решить систему уравнений этих функций
Например
y=2x
y=x+2
2x=x+2
2x-x=2
x=2
Два графика пересекаются в точке (2;4)
Похожие вопросы
Решение на Задание 1074 из ГДЗ по Алгебре за 7 класс: Макарычев Ю.Н.
Условие
Решение 1
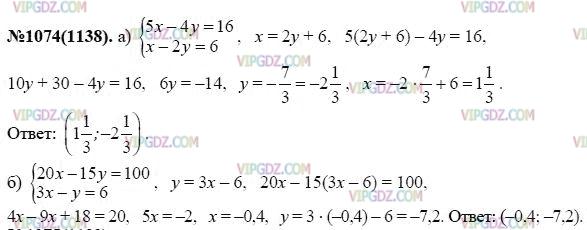
Решение 2

Поиск в решебнике
Популярные решебники
Издатель: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2013г.
Издатель: А.Г. Мордкович, 2013г.
Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2015г.
Как найти точки пересечения графиков функций — алгоритмы и примеры правила и методики
Существует определенный класс задач по дисциплине «Алгебра и начало анализа», в которых нужно найти точки пересечения графиков функций без их построения. Решать такие задания довольно просто, когда известна определенная методика нахождения координат по оси абсцисс и ординат. Однако для этого необходимо научиться правильно находить корни уравнений различных типов.

Общие сведения

Функция — некоторое выражение, описывающее зависимость между двумя величинами. Следует отметить, что последних может быть несколько. Параметр, который не зависит от других элементов, называется аргументом, а зависимое тождество — значением функции.
Точка пересечения графиков означает, что у системы уравнений существует общее решение. Следует отметить, что для их нахождения можно воспользоваться графическим и аналитическим методом. Первый подразумевает построение графического представления выражения с переменной.
Чтобы найти пересечение графиков функций аналитическим способом, необходимо решить уравнение, корни которого являются искомыми точками. Для их нахождения специалисты рекомендуют получить базовые понятия о равенствах с переменными, а также о методах их решения.
Классификация уравнений
Уравнение — тождество, содержащее неизвестные величины (переменные), которые следует найти при помощи определенного алгоритма. Последний зависит от типа выражений. Тождества классифицируются на несколько типов:
Линейными являются уравнения, содержащие единичную степень, т. е. 2t=4. Квадратные — тождества, у которых переменная возведена в квадрат. Они имеют следующий вид: Pt^2+St+U=0, где Р и S — коэффициенты при неизвестных, а U — свободный член.
Кубическое — уравнение вида Ot^3+Pt^2+St+U=0, где O, Р и S — коэффициенты при переменных, а U — константа. Последний вид — равенства, в которых при переменной присутствует четвертая степень (Nt^4+Ot^3+Pt^2+St+U=0).
Равносильные тождества

При выполнении математических операций каждое выражение может быть заменено на эквивалентное, т. е. равносильное. Иными словами, равносильными называются уравнения, различные по составляющим их элементам, но имеющие одинаковые корни. Следует отметить, что ими являются также выражения, не имеющие решений. Математики выделяют три свойства: симметричность, транзитивность и разложение на множители.
Формулировка первого: когда I уравнение равносильно II, то значит, и II равносильно I. Суть транзитивности состоит в том, что если I равносильно II, а II — III, то значит I эквивалентно III. Второе свойство имеет такую формулировку: произведение двух элементов, содержащих переменные, равное нулевому значению, эквивалентно двум выражениям, которые можно приравнять к 0. Математическая запись утверждения имеет такой вид: R(t)*S(t)=0 .
Математические преобразования
Для решения уравнения необходимо выполнить некоторые математические преобразования. Они должны выполняться грамотно, поскольку любая ошибка приводит к образованию ложных корней. Допустимыми операциями являются следующие:

Специалисты рекомендуют избегать операций, при которых сокращаются неизвестные величины. Следствием этого могут стать ложные корни. Кроме того, делитель не должен иметь значения, при которых его значение равно 0. Последнее условие следует всегда проверять, а при решении ни один корень уравнения не должен соответствовать значению переменной при нахождении окончательных корней.
Иными словами, в выражении (t+2)^2=0 для упрощения можно разделить обе части на (t+2) при условии, что t не равно -2, т. к. [(t+2)^2]/(t+2)=0/(t+2).
Однако при решении (t+2)=0 получается, что t=-2, а это недопустимо. Следовательно, вышеописанный метод не всегда подходит.
Разложение на множители
Для решения уравнений при выполнении математических преобразований могут потребоваться специальные формулы разложения на множители. Их еще называют тождествами сокращенного умножения. К ним относятся следующие:
В некоторых случаях можно воспользоваться сразу двумя соотношениями, т. е. выделить квадрат суммы, а затем из первого — разность квадратов. Выделение первого осуществляется группировкой посредством скобок в выражении, а затем введение положительного и отрицательного элементов, т. е. s^2+4s-5=s^2+4s+4-4-5=(s^2+4s+4)-4-5=(s+2)^2 -9. Для получения всех элементов формулы «p+r)^2=p^2+2pr+r^2» нужно прибавить, а затем отнять 4. При этом значение равенства не изменится, поскольку 4-4=0.
Следует отметить, что математические преобразования выражения (s+2)^2 -9 не заканчиваются, поскольку его можно представить в виде разности квадратов, т. е. (s+2-9)(s+2+9)=(s-7)(s+11). Кроме того, формулы сокращенного умножения рекомендуется применять при понижении степени.
Методики нахождения точек
Чтобы узнать, пересекаются ли графики функций, нужно приравнять соответствующие тождества, а затем решать уравнение. Однако при такой операции могут получиться различные равенства с неизвестными. В этом случае требуется обратить внимание на нижеописанные методики решения для каждого вида.
Первой и второй степени
Уравнение первой степени, или линейное, решается очень просто. Для этого необходимо перенести переменные величины в одну, а известные — в другую сторону. Методика решения имеет следующий вид:
Сложнее решается квадратное уравнение. Существует несколько способов нахождения его корней:

Первый способ применяется довольно часто, поскольку с его помощью можно понижать степень при неизвестной величине. Второй подразумевает выделение квадрата по одной из формул сокращенного умножения. Чтобы воспользоваться одним из двух методов, необходимо знать соответствующие тождества (правила разложения на множители).
Однако не всегда можно быстро решить квадратное уравнение при помощи первых двух методов. Еще один вариант — нахождение корней через дискриминант (Д), т. е. дополнительный параметр, позволяющий сразу находить решения. Он находится по следующей формуле: Д=(-S)^2 -4PU.

Следует отметить, что при Д>0 переменная принимает два значения, которые превращают равенство в истину. Если Д=0, то корень только один. Когда Д
![]()
Учитель физики, информатики и вычислительной техники. Победитель конкурса лучших учителей Российской Федерации в рамках Приоритетного Национального Проекта “Образование”.
Как найти координаты точек пересечения графика функции: примеры решения
Вы будете перенаправлены на Автор24
В практике и в учебниках наиболее распространены нижеперечисленные способы нахождения точки пересечения различных графиков функций.
Первый способ
Первый и самый простой – это воспользоваться тем, что в этой точке координаты будут равны и приравнять графики, а из того что получится можно найти $x$. Затем найденный $x$ подставить в любое из двух уравнений и найти координату игрек.
Найдём точку пересечения двух прямых $y=5x + 3$ и $y=x-2$, приравняв функции:
Теперь подставим полученный нами икс в любой график, например, выберем тот, что попроще — $y=x-2$:
$y=-frac<1> <2>– 2 = – 2frac12$.
Точка пересечения будет $(-frac<1><2>;- 2frac12)$.
Второй способ
Второй способ заключается в том, что составляется система из имеющихся уравнений, путём преобразований одну из координат делают явной, то есть, выражают через другую. После это выражение в приведённой форме подставляется в другое.
Узнайте, в каких точках пересекаются графики параболы $y=2x^2-2x-1$ и пересекающей её прямой $y=x+1$.
Решение:
Второе уравнение проще первого, поэтому подставим его вместо $y$:
Вычислим, чему равен x, для этого найдём корни, превращающие равенство в верное, и запишем полученные ответы:
Подставим наши результаты по оси абсцисс по очереди во второе уравнение системы:
$y_1= 2 + 1 = 3; y_2=1 – frac<1> <2>= frac<1><2>$.
Точки пересечения будут $(2;3)$ и $(-frac<1><2>; frac<1><2>)$.
Третий способ
Готовые работы на аналогичную тему
Перейдём к третьему способу — графическому, но имейте в виду, что результат, который он даёт, не является достаточно точным.
Для применения метода оба графика функций строятся в одном масштабе на одном чертеже, и затем выполняется визуальный поиск точки пересечения.
Данный способ хорош лишь в том случае, когда достаточно приблизительного результата, а также если нет каких-либо данных о закономерностях рассматриваемых зависимостей.
Найдите точку пересечения графиков на общем рисунке.
Рисунок 1. Точка пересечения двух функций. Автор24 — интернет-биржа студенческих работ
Решение:
Тут всё просто: ищем точки пересечения пунктиров, опущенных с графиков с осями абсцисс и ординат и записываем по порядку. Здесь точка пересечения равна $(2;3)$.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 07.05.2021
[spoiler title=”источники:”]
http://kupuk.net/uroki/algebra/kak-naiti-tochki-peresecheniia-grafikov-fynkcii-algoritmy-i-primery-pravila-i-metodiki/
http://spravochnick.ru/matematika/kak_nayti_koordinaty_tochek_peresecheniya_grafika_funkcii_primery_resheniya/
[/spoiler]
Как определить точку пересечения функций без построения графика?
На этой странице находится вопрос Как определить точку пересечения функций без построения графика?. Здесь же – ответы на него,
и похожие вопросы в категории Алгебра, которые можно найти с помощью
простой в использовании поисковой системы. Уровень сложности вопроса
соответствует уровню подготовки учащихся 5 – 9 классов. В комментариях,
оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С
ними можно обсудить тему вопроса в режиме on-line. Если ни один из
предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой
строке, расположенной вверху, и нажмите кнопку.
Содержание
- – Как найти точки пересечения графиков функций?
- – Как узнать пересекаются ли графики функций или нет?
- – Как понять что графики функций параллельны?
- – В каком случае графики двух линейных функций пересекаются?
- – Как определить что графики параллельны?
- – В каком случае прямые пересекаются?
- – Как найти точку пересечения параболы с осью Y?
- – Как найти вершину параболы квадратичной функции?
Можно точки пересечения находить без построения графиков – аналитически. Для этого приравнивают правые части обоих уравнений и решают получившееся уравнение. Итак, запишем уравнение из правых частей заданных функций: 2х – 1 = 5 – х.
Как найти точки пересечения графиков функций?
Чтобы найти координаты точки пересечения графиков функций нужно приравнять обе функции друг к другу, перенести в левую часть все члена, содержащие x , а в правую остальные и найти корни, полученного уравнения. Третий способ подразумевает графическое построение функций и визуальное определение точки пересечения.
Как узнать пересекаются ли графики функций или нет?
Если две линейные функции имеют различные и k и m, то они пересекаются в какой-то точке, которую можно найти графическим способом. Сначала на координатной плоскости чертится одна прямая, затем вторая, далее находится их точка пересечения.
Как понять что графики функций параллельны?
Графики линейных функций по отношению друг к другу на плоскости могут быть параллельны, если угловые коэффициенты k1 и k2 равны, а коэффициенты m1 и m2 различны. Могут пересекаться в случае, когда угловые коэффициенты k1 и k2 не равны.
В каком случае графики двух линейных функций пересекаются?
Если угловые коэффициенты прямых, являющихся графиками двух линейных функций, различны, то эти прямые пересекаются, а если угловые коэффициенты одинаковы, то прямые параллельны.
Как определить что графики параллельны?
Графики этих двух линейных функций параллельны, когда соблюдается равенство k=t, то есть коэффициент при х первой функции равен коэффициенту при х второй функции. Графики линейных функций совпадают, когда помимо k=t соблюдается равенство b=j.
В каком случае прямые пересекаются?
Пересекающимися называются две прямые лежащие в одной плоскости и имеющие одну общую точку. Если прямые пересекаются, то точки пересечения их одноименных проекций находится на одной линии связи (рис. … Если одна из прямых параллельна какой-либо из плоскостей проекций, например, профильной (рис.
Как найти точку пересечения параболы с осью Y?
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
Как найти вершину параболы квадратичной функции?
Формулы вершины параболы получаются при преобразовании квадратичной функции к виду y = f(x + l) + m. Делается это методом выделения полного квадрата.
Интересные материалы:
Как подключить IMO?
Как подключить инстаграм к фейсбуку через компьютер?
Как подключить инстаграм к фейсбуку?
Как подключить Инстаграм к странице в Фейсбуке?
Как подключить Инстаграм к ВК 2020?
Как подключить инстаграм на компьютер?
Как подключить инстаграм на ноутбук?
Как подключить интеллектуальный пульт к телевизору самсунг?
Как подключить интеллектуальный пульт самсунг?
Как подключить интерактивное телевидение Ростелеком к телевизору?
Математика
Мироныч
21 апреля, 22:00
Как найти точки пересечения графиков двух функции, не строя эти графики?
+1
Ответы (1)
-

Валерьянка
21 апреля, 23:50
0
X+Y=Z
X – вертикально
Y – горизонтально
Z – точка
- Комментировать
- Жалоба
- Ссылка
Знаешь ответ?
Не уверен в ответе?
Найди верный ответ на вопрос ✅ «Как найти точки пересечения графиков двух функции, не строя эти графики? …» по предмету 📙 Математика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Новые вопросы по математике
2 тыс=. Дес 2 дес. тыс.=тысяч. 5 сот тысяч=дес. тыс 3 дес. тыс=сот тысяч 10 дес=ед 20 дес. тыс=сот тысяч
Ответы (3)
В треугольнике авс сторона ав=корень из 43, вс=корень из 59, ас=4. Найдите величину наибольшего угла
Ответы (1)
Сколько существует различных расположений 15 монеток, в которых нет 2 подряд идущих орлов?
Ответы (2)
Стороны треугольника равны 3/8 м, 1/2 м, 5/6 м. Найти периметр.
Ответы (2)
Всем привет. В магазине в 1 день продали 35%, во 2 – 28%всеховощей, А в 3 – оставшиеся 333 кг. Сколько кг овощейбыло в магазине первоначально?
Ответы (3)
Главная » Математика » Как найти точки пересечения графиков двух функции, не строя эти графики?
