Построение линии пересечения плоскостей, заданных различными способами
Две плоскости пересекаются друг с другом по прямой линии. Чтобы её построить, необходимо определить две точки, принадлежащие одновременно каждой из заданных плоскостей. Рассмотрим, как это делается, на следующих примерах.
Задача
Найдем линию пересечения плоскостей общего положения α и β для случая, когда пл. α задана проекциями треугольника ABC, а пл. β – параллельными прямыми d и e. Решение этой задачи осуществляется путем построения точек L1 и L2, принадлежащих линии пересечения.
Решение
- Вводим вспомогательную горизонтальную плоскость γ1. Она пересекает α и β по прямым. Фронтальные проекции этих прямых, 1”C” и 2”3”, совпадают с фронтальным следом пл. γ1. Он обозначен на рисунке как f0γ1 и расположен параллельно оси x.
- Определяем горизонтальные проекции 1’C’ и 2’3′ по линиям связи.
- Находим горизонтальную проекцию точки L1 на пересечении прямых 1’C’ и 2’3′. Фронтальная проекция точки L1 лежит на фронтальном следе плоскости γ.
- Вводим вспомогательную горизонтальную плоскость γ2. С помощью построений, аналогичных описанным в пунктах 1, 2, 3, находим проекции точки L2.
- Через L1 и L2 проводим искомую прямую l.
Стоит отметить, что в качестве пл. γ удобно использовать как плоскости уровня, так и проецирующие плоскости.
Пересечение плоскостей, заданных следами
Найдем линию пересечения плоскостей α и β, заданных следами. Эта задача значительно проще предыдущей. Она не требует введения вспомогательных плоскостей. Их роль выполняют плоскости проекций П1 и П2.
Алгоритм построения
- Находим точку L’1, расположенную на пересечении горизонтальных следов h0α и h0β. Точка L”1 лежит на оси x. Её положение определяется при помощи линии связи, проведенной из L’1.
- Находим точку L”2 на пересечении фронтальных следов пл. α и β. Точка L’2 лежит на оси x. Её положение определяется по линии связи, проведенной из L”2.
- Проводим прямые l’ и l” через соответствующие проекции точек L1 и L2, как это показано на рисунке.
Таким образом, прямая l, проходящая через точки пересечения следов плоскостей, является искомой.
Пересечение плоскостей треугольников
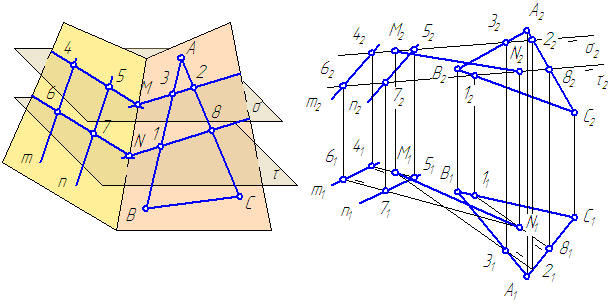
Рассмотрим построение линии пересечения плоскостей, заданных треугольниками ABC и DEF, и определение их видимости методом конкурирующих точек.
Алгоритм построения
- Через прямую DE проводим фронтально-проецирующую плоскость σ: на чертеже обозначен ее след f0σ. Плоскость σ пересекает треугольник ABC по прямой 35. Отметив точки 3”=A”B”∩f0σ и 5”=A”С”∩f0σ, определяем положение (∙)3′ и (∙)5′ по линиям связи на ΔA’B’C’.
- Находим горизонтальную проекцию N’=D’E’∩3’5′ точки N пересечения прямых DE и 35, которые лежат во вспомогательной плоскости σ. Проекция N” расположена на фронтальном следе f0σ на одной линии связи с N’.
-
Через прямую BC проводим фронтально-проецирующую плоскость τ: на чертеже обозначен ее след f0τ. С помощью построений, аналогичных тем, что описаны в пунктах 1 и 2 алгоритма, находим проекции точки K.
- Через N и K проводим искомую прямую NK – линию пересечения ΔABC и ΔDEF.
Определение видимости
Фронтально-конкурирующие точки 4 и 5, принадлежащие ΔDEF и ΔABC соответственно, находятся на одной фронтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π2. Так как (∙)5′ находится ближе к наблюдателю, чем (∙)4′, то отсек ΔABC с принадлежащей ему (∙)5 является видимым в проекции на пл. π2. С противоположной стороны от линии N”K” видимость треугольников меняется.
Горизонтально-конкурирующие точки 6 и 7, принадлежащие ΔABC и ΔDEF соответственно, находятся на одной горизонтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π1. Так как (∙)6” находится выше, чем (∙)7”, то отсек ΔABC с принадлежащей ему (∙)6 является видимым в проекции на пл. π1. С противоположной стороны от линии N’K’ видимость треугольников меняется.
Дополнительные материалы:
- Способы задания плоскости на чертеже
- Точка пересечения прямой и плоскости
Пересечение двух плоскостей
Пересечение двух плоскостей общего положения представляет собой прямую линию, поэтому для ее определения достаточно найти две
точки, принадлежащие одновременно каждой из двух заданных плоскостей – так называемые общие точки.
Чтобы найти общие точки, достаточно ввести одну или две вспомогательные секущие плоскости γ1
и γ2.
Найти пересечение двух плоскостей общего положения линию l, если плоскости заданны пересекающимися прямыми b c и
параллельными прямыми d e.
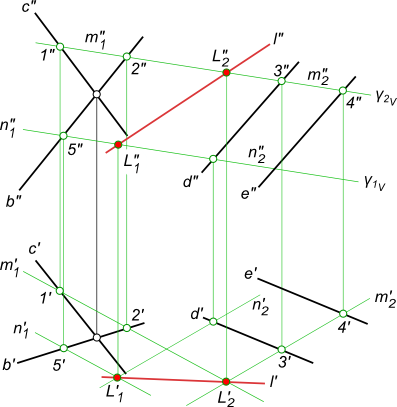
Пересечение двух плоскостей
Вспомогательная плоскость γ1 пересекает заданные плоскости по прямым n1 и n2, которые пересекаясь между собой дают первую точку искомой линии.
Вспомогательная плоскость γ2 пересекает заданные плоскости по прямым m1 и m2, которые пересекаясь между собой дают вторую точку искомой линии.
Проведя через найденные точки L1 и L2 прямую линию получаем искомое, пересечение двух плоскостей – линию l.
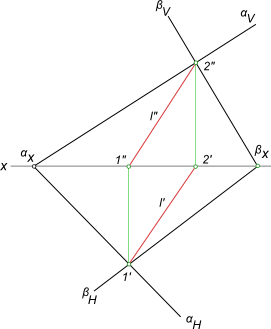
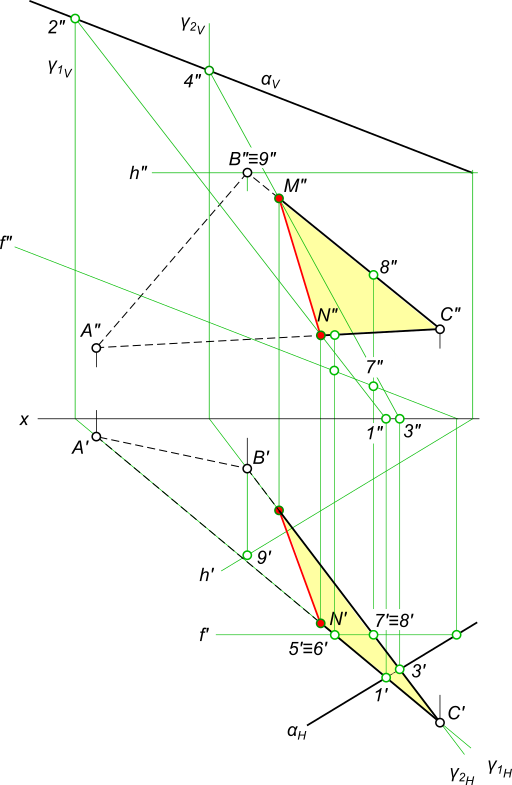
Определить линию пересечения l плоскостей заданных следами αH,
αV и βH, βV.
Пересечение двух плоскостей
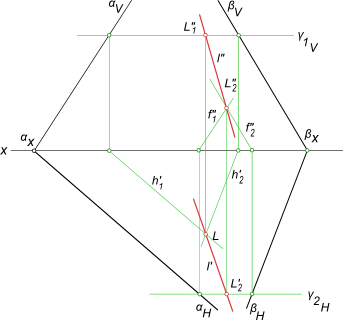
Задача на пересечение плоскостей заданных следами αH,
αV и βH, βV.
Пересечение двух плоскостей
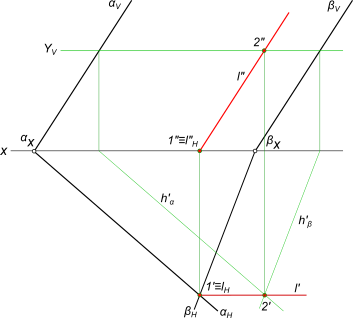
Задача на пересечение плоскостей заданных следами αH,
αV и βH, βV причем αV ║ βV.
Пересечение двух плоскостей
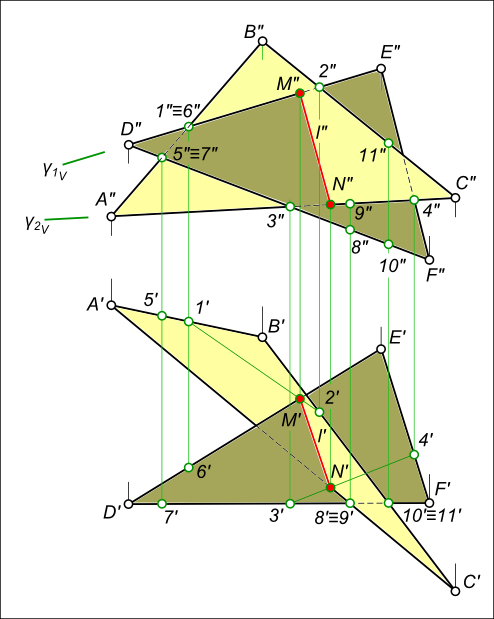
Пересечение двух плоскостей, заданных треугольниками ABC и DEF.
Пересечение двух плоскостей
Вспомогательная плоскость γ1 пересекает заданные плоскости по прямым 1-2 и DE, которые пересекаясь между собой дают первую точку искомой линии – точка M.
Вспомогательная плоскость γ2 пересекает заданные плоскости по прямым 3-4 и AC, которые пересекаясь между собой дают вторую точку искомой линии – точка N.
Соединяем точки MN прямой линией получаем искомую линию l пересечения двух плоскостей.
Определение видимости пересекающихся плоскостей на плоскостях проекций выполняем, используя Конкурирующие точки:
на фронтальной плоскости проекций – 1″≡6″; 1`, 6` и 5″≡ 7″; 5`, 7` – будет видна вершина D с прилегающими сторонами до линии пересечения.
на горизонтальной плоскости проекций – 8`≡9`; 8″, 9″ и 10`≡ 11`; 10″, 11″ – будет видна вершина C с прилегающими сторонами до линии пересечения.
Построить линию пересечения двух плоскостей треугольник ABC и α(αH, αV)
Пересечение двух плоскостей
Графическая работа 1 представляет задачу на пересечение двух плоскостей заданных треугольником и ромбом
+
§11. Построение линии пересечения двух плоскостей. (Вторая позиционная задача).
Результатом пересечения двух плоскостей является прямая . Для построения этой прямой достаточно найти две точки, принадлежащие обеим плоскостям и провести через них прямую линию.
Если мы возьмем прямую, принадлежащую одной плоскости и найдем точку ее пересечения с другой плоскостью, то эта точка будет общей для обеих плоскостей. Таким образом, построение линии пересечения двух плоскостей сводится к решению первой позиционной задачи, повторенному дважды.
Задача 11.1. Построить линию пересечения плоскости α, заданной треугольником АВС, и плоскости β, заданной двумя пересекающимися прямыми МЕ и МК (рисунок 11.1). Определить видимость плоскостей.
Решение.
1. Возьмем прямую АВ, принадлежащую плоскости α, и найдем точку ее пересечения с плоскостью β. Для этого заключим ее в проецирующую плоскость и найдем точку пересечения, используя алгоритм для решения первой позиционной задачи (см. §7).
На рисунке 11.2 продемонстрирован этот этап решения – точка N является точкой пересечения прямой АВ и плоскости β(МК, МЕ). В данном случае мы заключили прямую в фронтально-проецирующую плоскость ФП, прямая 1-2 является результатом пересечения плоскости ФП и плоскостиβ.
Не нужно забывать о том, что все точки на чертеже отображены в проекциях. Так, например, на рисунке 11.2. точка N представлена проекциями N1 и N2.
2. Возьмем прямую МК, принадлежащую плоскости β, и найдем точку ее пересечения с плоскостью α. Заключив ее в горизонтально-проецирующую плоскость, и проведя аналогичные построения, найдем точку L (рисунок 11.3).
3. Проведем прямую NL, являющуюся линией пересечения плоскостей α и β (рисунок 11.4).
4. Определяем видимость плоскостей (рисунок 11.5).
Применяем метод конкурирующих точек – для определения видимости на фронтальной проекции берем конкурирующие точки, проекции которых совпадают с точкой 22, для определения видимости на горизонтальной проекции берем точки с проекцией в 41. Конкурирующие точки 22 принадлежат фронтальной проекции АВ и МК. Пройдя по стрелке взгляда вниз, видим, что точка, лежащая на прямой АВ находится ближе к наблюдателю, так как у нее координата у больше, поэтому в районе проекции прямая АВ видимая, а МК – невидимая. Следовательно, проекция М2К2 в точке 22 меняет свой вид с видимой на невидимую.
Точка 41 лежит на горизонтальной проекции ВС и МК. Видимой будет та прямая, которая по стрелке взгляда находится выше на фронтальной проекции, в данном случае это прямая ВС.
Нужно обратить внимание на то, что прямые АВ и ВС меняют видимость в точках пересечения с прямой NL. Линия пересечения плоскостей всегда видимая.
На рисунке 11.6 показано окончательное решение задачи, для наглядности плоскости затонированы.
Задача 11.2. Построить линию пересечения плоскостей α и β, заданных следами (рисунок 11.7). Определить видимость плоскостей.
Решение.
Поскольку следы плоскости – это прямые, принадлежащие этой плоскости, а точки пересечения 1 и 2 одноименных проекций следов являются общими для обеих плоскостей, то очевидно, что результат пересечения плоскостей – это прямая, проходящая через эти точки. На эпюре Монжа определяем фронтальные и горизонтальные проекции точек 1 и 2 (рисунок 11.8).
Как видно на рисунке 11.8, горизонтальная проекция точки 1, являющейся точкой пересечения фронтальных следов α и β, а также фронтальная проекция точки 2 – лежат она оси х, поскольку сами прямые принадлежат плоскостям проекций. Соединив одноименные проекции точек 1 и 2, получим линию пересечения плоскостей (рисунок 11.9).
Определив видимость плоскостей в проекциях, получим окончательное решение задачи (рисунок 11.10)
3.1. Способы задания плоскости на ортогональных чертежах
Положение плоскости в пространстве определяется:
- тремя точками, не лежащими на одной прямой;
- прямой и точкой, взятой вне прямой;
- двумя пересекающимися прямыми;
- двумя параллельными прямыми;
- плоской фигурой.
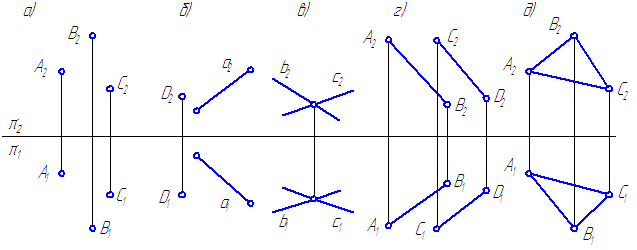
В соответствии с этим на эпюре плоскость может быть задана:
- проекциями трёх точек, не лежащих на одной прямой (Рисунок 3.1,а);
- проекциями точки и прямой (Рисунок 3.1,б);
- проекциями двух пересекающихся прямых (Рисунок 3.1,в);
- проекциями двух параллельных прямых (Рисунок 3.1,г);
- плоской фигурой (Рисунок 3.1,д);
- следами плоскости;
- линией наибольшего ската плоскости.
Рисунок 3.1 – Способы задания плоскостей
Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.
Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.
Плоскость общего положения может иметь три следа: горизонтальный – απ1, фронтальный – απ2 и профильный – απ3, которые она образует при пересечении с известными плоскостями проекций: горизонтальной π1, фронтальной π2 и профильной π3 (Рисунок 3.2).
Рисунок 3.2 – Следы плоскости общего положения
3.2. Плоскости частного положения
Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.
Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.
Свойство проецирующей плоскости: все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).
Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС
Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).
Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).
Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.
Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.
Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).
Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).
Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).
Рисунок 3.4 – Эпюры плоскостей частного положения
3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости
Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5). Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).
Рисунок 3.5 – Принадлежность точки плоскости
α = m // n D ∈ n ⇒ D ∈ α
Рисунок 3.6 – Принадлежность прямой плоскости
left.begin{array}{l}alpha=mparallel n,\Dinalpha\Cinalpha\end{array}right} Longrightarrow CDinalpha
Упражнение
Дана плоскость, заданная четырехугольником (Рисунок 3.7, а). Необходимо достроить горизонтальную проекцию вершины С.
Рисунок 3.7 – Решение задачи
Решение:
- ABCD – плоский четырехугольник, задающий плоскость.
- Проведём в нём диагонали AC и BD (Рисунок 3.7, б), которые являются пересекающимися прямыми, также задающими ту же плоскость.
- Согласно признаку пересекающихся прямых, построим фронтальную проекцию точки пересечения этих прямых — K: A2C2 ∩ B2D2=K2.
- Восстановим линию проекционной связи до пересечения с горизонтальной проекцией прямой BD: на проекции диагонали B1D1 строим К1.
- Через А1К1 проводим проекцию диагонали А1С1.
- Точку С1 получаем, посредством линии проекционной связи до пересечения её с горизонтальной проекцией продолженной диагонали А1К1.
3.4. Главные линии плоскости
В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).
Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.
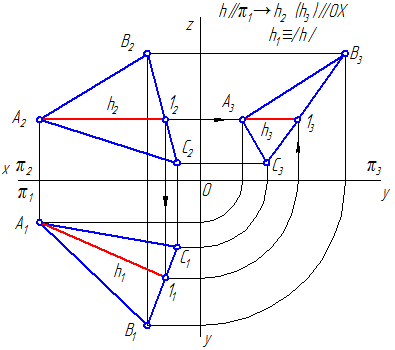
Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π1) (Рисунок 3.8, а; 3.9).
Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π2) (Рисунок 3.8, б; 3.10).
Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π3) (Рисунок 3.8, в; 3.11).
Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником
Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником
Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником
Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами
Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами
Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами
3.5. Взаимное положение прямой и плоскости
Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.
3.5.1. Параллельность прямой плоскости
Признак параллельности прямой плоскости: прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).
alpha=mcap n\left.begin{array}{l}a_2parallel m_2\a_1parallel m_1\end{array}right} Rightarrow aparallelalpha
Рисунок 3.12 – Параллельность прямой плоскости
3.5.2. Пересечение прямой с плоскостью
Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:
- Заключить прямую а во вспомогательную плоскость β (в качестве вспомогательной плоскости следует выбирать плоскости частного положения);
- Найти линию пересечения вспомогательной плоскости β с заданной плоскостью α;
- Найти точку пересечения заданной прямой а с линией пересечения плоскостей MN.
Рисунок 3.13 – Построение точки встречи прямой с плоскостью
Упражнение
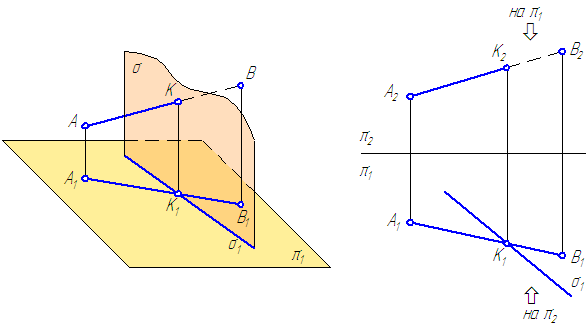
Заданы: прямая АВ общего положения, плоскость σ⊥π1. (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.
Решение:
-
- Точка К должна принадлежать прямой АВ ⇒ К1∈А1В и заданной плоскости σ ⇒ К1∈σ, следовательно, К1 находится в точке пересечения проекций А1В1 и σ1;
- Плоскость σ – горизонтально-проецирующая, следовательно, горизонтальной проекцией плоскости σ является прямая σ1 (горизонтальный след плоскости);
- Фронтальную проекцию точки К находим посредством линии проекционной связи: К2∈А2В2.
Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения
Упражнение
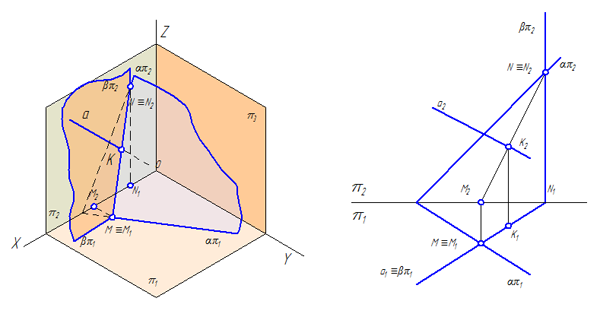
Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).
Требуется построить точку пересечения прямой EF с плоскостью σ.
Рисунок 3.15 – Пересечение прямой с плоскостью
Решение:
- Заключим прямую EF во вспомогательную плоскость, в качестве которой воспользуемся горизонтально-проецирующей плоскостью α (Рисунок 3.15, а);
- Если α⊥π1, то на плоскость проекций π1 плоскость α проецируется в прямую (горизонтальный след плоскости απ1 или α1), совпадающую с E1F1;
- Найдём прямую пересечения (1-2) проецирующей плоскости α с плоскостью σ (решение подобной задачи будет рассмотрено ниже);
- Прямая (1-2) и заданная прямая EF лежат в одной плоскости α и пересекаются в точке K.
Алгоритм решения задачи (Рисунок 3.15, б): Через EF проведем вспомогательную плоскость α:
- left.begin{array}{l}alpha perp pi_1\alphain EF\end{array}right} Longrightarrow alpha_1in E_1F_1
- alphacapsigma=(1-2)left.begin{array}{l}|alpha_1cap A_1C_1=1_1longrightarrow 1_2\|alpha_1cap A_1B_1=2_1longrightarrow 2_2\end{array}right.
- (1_2-2_2)cap E_2F_2=K_2\left.begin{array}{l}Kin EF\Kin (1-2)Rightarrow Kinsigma\end{array}right}Longrightarrow K=EFcap (sigma =triangle ABC)
3.6. Определение видимости методом конкурирующих точек
При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π1 или π2.
Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций.
Необходимо отдельно определить видимость на каждой плоскости проекций.
Видимость на π2 (рис. 3.15)
Выберем точки, конкурирующие на π2 – точки 3 и 4. Пусть точка 3∈ВС∈σ, точка 4∈EF.
Чтобы определить видимость точек на плоскости проекций π2 надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π2.
Направление взгляда на π2 показано стрелкой.
По горизонтальным проекциям точек 3 и 4, при взгляде на π2, видно, что точка 41 располагается ближе к наблюдателю, чем 31.
41∈E1F1 ⇒ 4∈EF ⇒ на π2 будет видима точка 4, лежащая на прямой EF, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K – точки пересечения прямой с плоскостью σ.
Видимость на π1.
Для определения видимости выберем точки, конкурирующие на π1 – точки 2 и 5.
Чтобы определить видимость точек на плоскости проекций π1 надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π1.
Направление взгляда на π1 показано стрелкой.
По фронтальным проекциям точек 2 и 5, при взгляде на π1, видно, что точка 22 располагается ближе к наблюдателю, чем 52.
22∈А2В2 ⇒ 2∈АВ ⇒ на π1 будет видима точка 2, лежащая на прямой АВ, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.
Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.
3.7. Перпендикулярность прямой плоскости
Признак перпендикулярности прямой плоскости: прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.
Рисунок 3.16 – Задание прямой, перпендикулярной плоскости
Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)
Теорема доказывается через теорему о проецировании прямого угла в частном случае.
Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).
Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K.
- Построим горизонталь и фронталь в плоскости σ=ΔАВС : σ=ΔАВС : A-1∈σ; A-1//π1; С-2∈σ; С-2//π2.
- Восстановим из точки K перпендикуляр к заданной плоскости: p1⊥h1 и p2⊥f2, или p1⊥απ1 и p2⊥απ2.
3.8. Взаимное положение двух плоскостей
3.8.1. Параллельность плоскостей
Две плоскости могут быть параллельными и пересекающимися между собой.
Признак параллельности двух плоскостей: две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
Упражнение
Задана плоскость общего положения α=ΔАВС и точка F∉α (Рисунок 3.17).
Через точку F провести плоскость β, параллельную плоскости α.
Рисунок 3.17 – Построение плоскости, параллельной заданной
Решение: В качестве пересекающихся прямых плоскости α возьмем, например, стороны треугольника АВ и ВС.
- Через точку F проводим прямую m, параллельную, например, АВ.
- Через точку F, или же через любую точку, принадлежащую m, проводим прямую n, параллельную, например, ВС, причём m∩n=F.
- β = m∩n и β//α по определению.
3.8.2. Пересечение плоскостей
Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.
Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.
Упражнение
Две плоскости α и β заданы следами (Рисунок 3.18). Построить линию пересечения плоскостей.
Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами
Порядок построения линии пересечения плоскостей:
- Найти точку пересечения горизонтальных следов — это точка М (её проекции М1 и М2, при этом М1=М, т.к. М – точка частного положения, принадлежащая плоскости π1).
- Найти точку пересечения фронтальных следов — это точка N (её проекции N1 и N2, при этом N2=N, т.к. N – точка частного положения, принадлежащая плоскости π2).
- Построить линию пересечения плоскостей, соединив одноименные проекции полученных точек: М1N1 и М2N2.
МN – линия пересечения плоскостей.
Упражнение
Задана плоскость σ = ΔАВС, плоскость α – горизонтально- проецирующая (α⊥π1) ⇒α1 – горизонтальный след плоскости (Рисунок 3.19). Построить линию пересечения этих плоскостей.
Решение:
Так как плоскость α пересекает стороны АВ и АС треугольника АВС, то точки пересечения K и L этих сторон с плоскостью α являются общими для обеих заданных плоскостей, что позволит, соединив их, найти искомую линию пересечения.
Точки могут быть найдены как точки пересечения прямых с проецирующей плоскостью: находим горизонтальные проекции точек K и L, то есть K1 и L1 , на пересечении горизонтального следа (α1) заданной плоскости α с горизонтальными проекциями сторон ΔАВС: А1В1 и A1C1. После чего посредством линий проекционной связи находим фронтальные проекции этих точек K2 и L2 на фронтальных проекциях прямых АВ и АС. Соединим одноимённые проекции: K1 и L1; K2 и L2. Линия пересечения заданных плоскостей построена.
Алгоритм решения задачи:
left.begin{array}{l}ABcapsigma=K\ACcapsigma=L\end{array}right} left.begin{array}{l}Rightarrow A_1B_1capsigma_1=K_1 rightarrow K_2\Rightarrow A_1C_1cap sigma_1=L_1 rightarrow L_2\end{array}right.
KL – линия пересечения ΔАВС и σ (α∩σ = KL).
Рисунок 3.19 – Пересечение плоскостей общего и частного положения
Упражнение
Заданы плоскости α = m//n и плоскость σ = ΔАВС (Рисунок 3.20). Построить линию пересечения заданных плоскостей. Решение:
- Чтобы найти точки, общие для обеих заданных плоскостей и задающие линию пересечения плоскостей α и β, необходимо воспользоваться вспомогательными плоскостями частного положения.
- В качестве таких плоскостей выберем две вспомогательные плоскости частного положения, например: σ // τ; σ⊥π2; τ⊥π2.
- Вновь введённые плоскости пересекаются с каждой из заданных плоскостей α и β по прямым, параллельным друг другу, так как σ // τ:
— результатом пересечения плоскостей α, σ и τ являются прямые (4-5) и (6-7); — результатом пересечения плоскостей β, σ и τ являются прямые (3-2) и (1-8).
- Прямые (4-5) и (3-2) лежат в плоскости σ; точка их пересечения М одновременно лежит в плоскостях σ и β, то есть на прямой пересечения этих плоскостей;
- Аналогично находим точку N, общую для плоскостей σ и β.
- Соединив точки M и N, построим прямую пересечения плоскостей σ и β.
Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)
Алгоритм решения задачи:
left.begin{array}{l}alphacapsigma=(4-5)\betacapsigma=(3-2)\end{array}right}\left.begin{array}{l}alphacaptau=(6-7)\betacaptau=(1-8)\end{array}right}left.begin{array}{l}(4_1-5_1)cap(3_1-2_1)=M_1rightarrow M_2\(6_1-7_1)cap(1_1-8_1)=N_1rightarrow N_2\end{array}right}rightarrow\left.begin{array}{l}M_1N_1\M_2N_2\end{array}right}Rightarrowalphacapbeta=MN
Упражнение
Заданы плоскости α = ΔАВС и β = a//b. Построить линию пересечения заданных плоскостей (Рисунок 3.21).
Рисунок 3.21 Решение задачи на пересечение плоскостей
Решение: Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π2, заключив прямую a во вспомогательную плоскость σ (σ∈a). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а. Следовательно (1-2)∩а=K. Точка К принадлежит обеим плоскостям α и β. Следовательно, точка K, является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β. Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π2 (τ∈b). Соединив точки K и L, получим прямую пересечения плоскостей α и β.
3.8.3. Взаимно перпендикулярные плоскости
Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.
Упражнение
Задана плоскость σ⊥π2 и прямая общего положения – DE (Рисунок 3.22)
Требуется построить через DE плоскость τ⊥σ.
Решение.
Проведём перпендикуляр CD к плоскости σ – C2D2⊥σ2 (на основании теоремы о проецировании прямого угла).
Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости
По теореме о проецировании прямого угла C1D1 должна быть параллельна оси проекций. Пересекающиеся прямые CD∩DE задают плоскость τ. Итак, τ⊥σ. Аналогичные рассуждения, в случае плоскости общего положения.
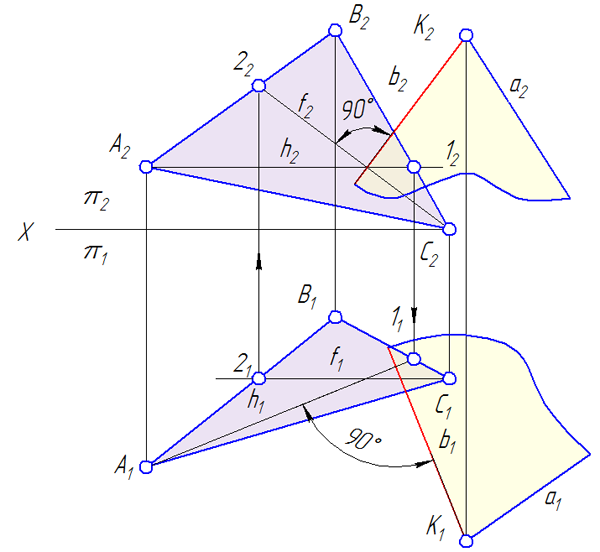
Упражнение
Задана плоскость α = ΔАВС и точка K вне плоскости α. Требуется построить плоскость β⊥α, проходящую через точку K. Алгоритм решения (Рисунок 3.23):
- Построим горизонталь h и фронталь f в заданной плоскости α = ΔАВС;
- Через точку K проведём перпендикуляр b к плоскости α (по теореме о перпендикуляре к плоскости: если прямая перпендикулярна плоскости, то её проекции перпендикулярны к наклонным проекциям горизонтали и фронтали, лежащих в плоскости: b2⊥f2; b1⊥h1;
- Задаём плоскость β любым способом, например, β = a∩b, таким образом, плоскость, перпендикулярная к заданной, построена: α⊥β.
Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС
3.9. Задачи для самостоятельного решения
1. Задана плоскость α = m//n (Рисунок 3.24). Известно, что K∈α.
Постройте фронтальную проекцию точки К.
Рисунок 3.24
2. Постройте следы прямой, заданной отрезком CB, и определите квадранты, через которые она проходит (Рисунок 3.25).
Рисунок 3.25
3. Постройте проекции квадрата, принадлежащего плоскости α⊥π2, если его диагональ MN //π2 (Рисунок 3.26).
Рисунок 3.26
4. Построить прямоугольник ABCD с большей стороной ВС на прямой m, исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).
Рисунок 3.27
5. Задана плоскость α=a//b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.
Рисунок 3.28
6. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D плоскость β⊥α и β⊥π1.
7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE//α и DE//π1.
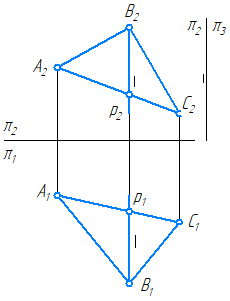
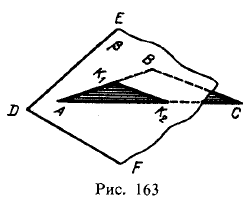
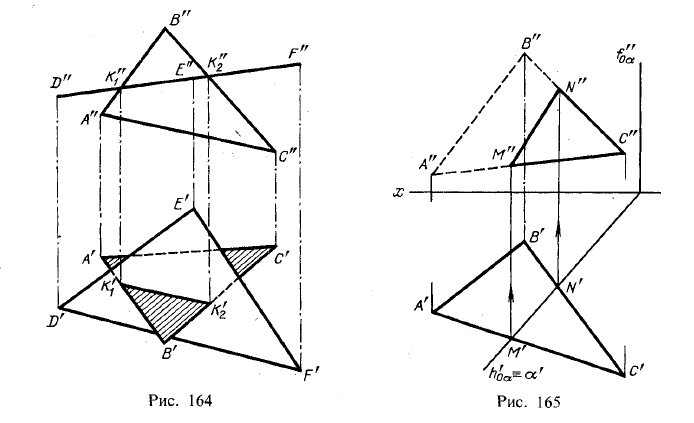
Прямая линия, получаемая при взаимном пересечении двух плоскостей, вполне определяется двумя точками, из которых каждая принадлежит обеим плоскостям. Так, прямая K1К2 (рис. 163), по которой пересекаются между собой плоскость, заданная треугольником АВС, и пл. β, заданная прямыми DE и DF, проходит через точки K1 и K2; но в этих точках прямые АВ и АС первой плоскости пересекают пл. β т. е. точки К1 и К2 принадлежат обеим плоскостям.
Следовательно, в общем случае для построения линии пересечения двух плоскостей надо найти какие-либо две точки, каждая из которых принадлежит обеим плоскостям; эти точки определяют линию пересечения плоскостей.
Для нахождения каждой из таких двух точек обычно приходится выполнять специальные построения. Но если хотя бы одна из пересекающихся плоскостей перпендикулярна к плоскости проекций, то построение проекций линии пересечения упрощается. Начнем с такого случая.
На рис. 164 показано пересечение двух плоскостей, из которых одна (заданная треугольником DEF) расположена перпендикулярно к пл. π2. Так как треугольник DEF проецируется на пл.π2 в виде прямой линии (D”F”), то фронтальная проекция отрезка прямой, по которому пересекаются оба треугольника, представляет собой отрезок К”1К”2 на проекции D”F”. Дальнейшее построение ясно из чертежа.
Другой пример дан на рис. 165. Горизонтально-проецирующая плоскость α пересекает плоскость треугольника АВС. Горизонтальная проекция линии пересечения этих плоскостей — отрезок M’N’ — определяется на следе α’.
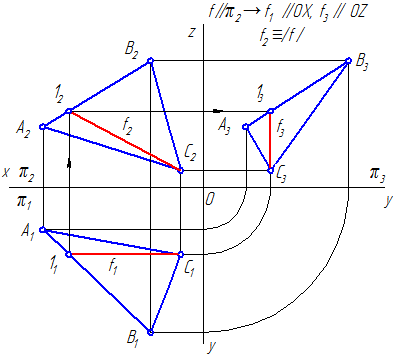
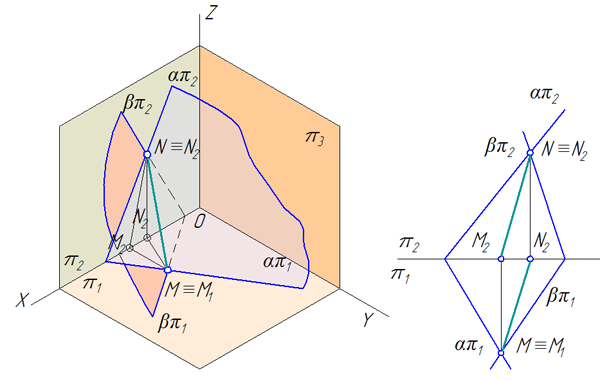
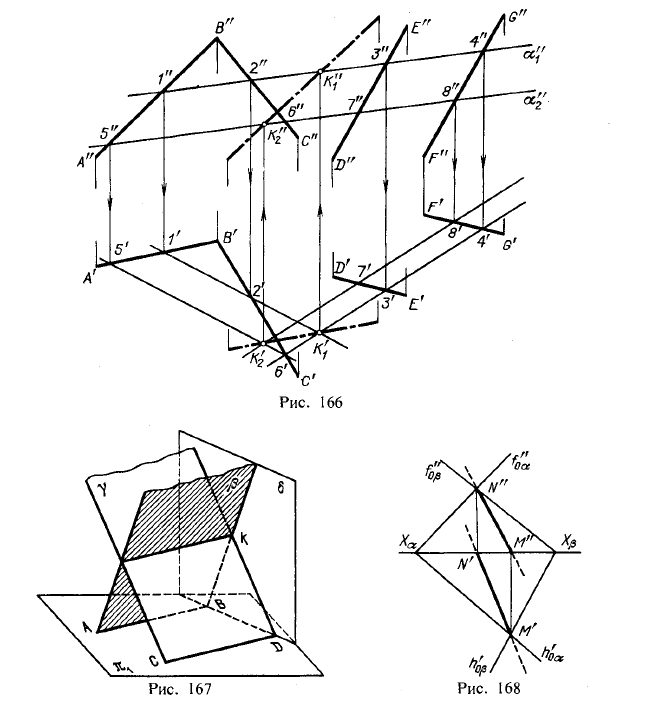
Теперь рассмотрим общий случай построения линии пересечения двух плоскостей. Пусть одна из плоскостей, β, задана двумя пересекающимися прямыми, а другая, γ,— двумя параллельными прямыми. Построение показано на рис. 166. В результате взаимного пересечения плоскостей β и γ получена прямая K1K2. Выразим это записью: β × γ = К1K2.
Для определения положения точек K1 и К2 возьмем две вспомогательные фронтально-проецирующие плоскости (α1, и α2), пересекающие каждую из плоскостей β и γ. При пересечении плоскостей β и γ плоскостью α1. получаем прямые с проекциями 1″2″, 1’2′ и 3″4″, 3’4′. Эти прямые, расположенные в пл. α1, в своем пересечении определяют первую точку, К1, линии пересечения плоскостей β и γ.
Введя, далее, ил. α2, получаем в ее пересечении с β и γ прямые с проекциями 5″6″, 5’6′ и 7″8″, 7’8′. Эти прямые, расположенные в пл. α2, в своем пересечении определяют вторую точку, К2, общую для β и γ.
Получив проекции К’1 и К’2 находим на следах и α”1 и α”2 проекции К”1 и К”2. Этим определяются проекции К’1К’2 и К”1К”2 искомой прямой пересечения плоскостей β и γ(проекции проведены штрихпунктирной линией).
При построении можно иметь в виду следующее: так как вспомогательные секущие плоскости α1 и α2 взаимно параллельны, то, построив проекции 1’2′ и 3’4′ следует для проекций 5’6′ и 7’8′ взять по одной точке, хотя бы 5 и 8, так как 5’6’||1’2′ и 7’8’||3’4′.
В рассмотренном построении были взяты в качестве вспомогательных две фронгально- проецирующие плоскости. Конечно, можно было взять и иные плоскости, например две горизонтальные или одну горизонтальную, другую фронтальную и т. д. Сущность построений от этого не меняется. Однако может встретиться такой случай. Положим, что были взяты в качестве вспомогательных две горизонтальные плоскости и полученные при пересечении ими
плоскостей β и γ горизонтали оказались взаимно параллельными. Но рис. 167 показывает, что β и γ пересекаются между собой, хотя их горизонтали параллельны. Следовательно, получив взаимно параллельные горизонтальные проекции горизонталей АВ и CD и зная, что плоскости при этом не обязательно параллельны, а могут пересекаться (по общей для них горизонтали), надо испытать плоскости β и γ при помощи хотя бы, горизонгально-проецирующей плоскости (см. рис. 167); если прямые, по которым эта вспомогательная плоскость σ, пересечет β и γ, также оказались бы параллельны одна другой, то плоскости β и γ не пересекаются, а параллельны одна другой. На рис. 167 эти прямые пересекаются в точке К, через которую и проходит линия пересечения плоскостей β и γ параллельно прямым ВА и CD.
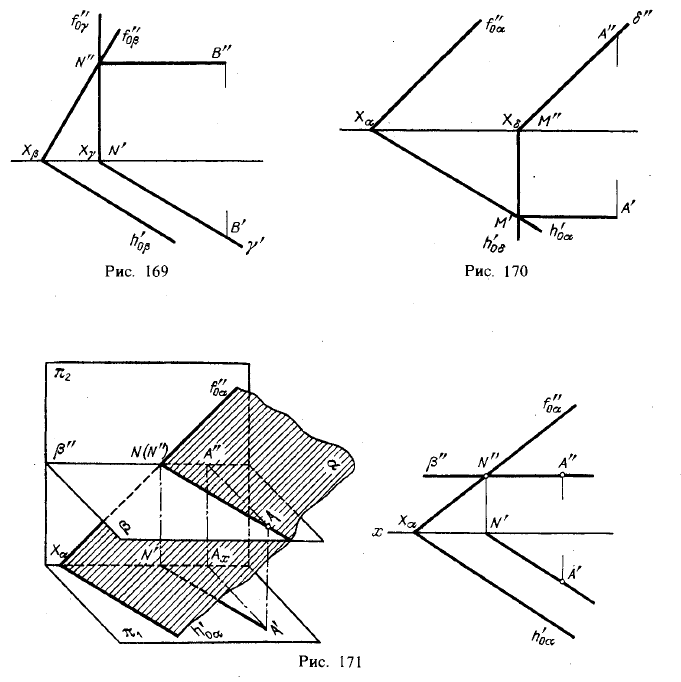
Если плоскости заданы их следами на плоскостях проекций, то естественно искать точки, определяющие прямую пересечения плоскостей, в точках пересечения одноименных следов плоскостей (рис. 168): прямая, проходящая через эти точки, является общей для обеих плоскостей, т. е. их линией пересечения.
Схему построения линии пересечения двух плоскостей (см. рис. 166) можно, конечно, распространить и на случай задания плоскостей их следами. Здесь роль вспомогательных секущих плоскостей исполняют сами плоскости проекций:
α × π1=h’0α; β× π1=h’0β; h’0α × h’0β=M;
α × π2=f”0α; β× π2=f”0β; f”0α × f”0β=N.
Точки пересечения одноименных следов плоскостей являются следами линии пересечения этих плоскостей. Поэтому для построения проекций линии пересечения плоскостей α и β (рис. 168) надо: 1) найти точку М’ в пересечении следов h’0α и h’0β
и точку N” в пересечении f”0α и f”0β, а по ним — проекции М” и N’; 2) провести прямые линии M”N” и M’N’,
На рис. 169—171 показаны случаи, когда известно направление линии пересечения. Поэтому достаточно иметь лйшь одну точку от пересечения следов и далее провести через эту точку прямую, исходя из положения плоскостей и их следов.
Вопросы к §§ 22-24
- Какое взаимное положение могут занимать две плоскости?
- Каков признак параллельности двух плоскостей?
- Как взаимно располагаются фронтальные следы двух параллельных между собой фронтально-проецирующих плоскостей?
- Как взаимно располагаются горизонтальные следы двух параллельных между собой горизонтально-проецирующих плоскостей?
- Как взаимно располагаются одноименные следы двух параллельных между собой плоскостей?
- Служит ли признаком взаимного пересечения двух плоскостей пересечение хотя бы одной пары их одноименных следов?
- Как установить взаимное положение прямой и Плоскости?
- Как строится точка пересечения прямой линии с плоскостью, перпендикулярной к одной или к двум плоскостям проекций?
- Какая точка из числа расположенных на общем перпендикуляре к а) пл. π1 б) пл. π2 считается видимой соответственно на π1, на π2?
- Как строится линия пересечения двух плоскостей, из которых хотя бы одна перпендикулярна к пл. π1 или к пл. π2?
- В чем заключается общий способ построения линии пересечения двух плоскостей?