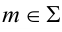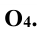Возможны три варианта расположения
прямой относительно поверхности. Прямая
может:
-
пересекать поверхность;
-
касаться поверхности;
-
не пересекать поверхность.
Частные случаи:
Пример 1.
Пересекаются прямая общего положения
l
с проецируюей поверхностью .
Если задана проецирующая поверхность,
то одна из проекций искомых точек
пересечения определяется сразу, исходя
из принадлежности их этой проецирующей
поверхности.
В данном примере призма является
горизонтально-проецирующей поверхностью,
следовательно, горизонтальные проекции
точек пересечения лежат на пересечении
горизонтальной проекции прямой lи горизонтального очерка призмы.
.
Рис. 6.10
Вторая проекция точек определяется
исходя из принадлежности их непроецирующей
прямой l.
.
Пример 2. Пересекаются проецирующая
прямая i с
поверхностью конуса .
Рис. 6.11
В этом случае одна
из проекций искомой точки также
изначально определена на чертеже. Она
совпадает с вырожденной проекцией
прямой.
.
Вторая
проекция точки определяется из условия
принадлежности ее образующей поверхности.
.
Общий случай:
Пересекаются
непроецирующая поверхность и прямая
общего положения.
В
этом случае, чтобы найти точки пересечения
прямой с поверхностью, необходимо:
-
Заключить
прямую в дополнительную (вспомогательную)
плоскость. -
Построить
линию пересечения вспомогательной
плоскости с поверхностью. -
Определить
точки пересечения полученного сечения
с заданной прямой.
Эти точки являются
искомыми.
В
качестве вспомогательной плоскости
выбирают плоскость общего или частного
положения, дающую наиболее простую
линию сечения поверхности (ломаную или
окружность).
Пример:
Построить точки пересечения прямой l
с трехгранной пирамидой SABC.
Определить видимость прямой относительно
поверхности.
Рис. 6.12
Видимость
прямой определяется по принадлежности
точек пересечения граням пирамиды.
Видима та часть прямой, которая исходит
из точки, лежащей на видимой грани
многогранника.
Пример:
Построить
точки пересечения прямой l
с конусом.
В
данном примере в качестве дополнительной
плоскости выбирается плоскость общего
положения, проходящая через вершину
конуса и пересекающая его боковую
поверхность по образующим.
Видимость
прямой определяется по принадлежности
точек пересечения той или иной образующей.
Видна та часть прямой, которая исходит
из точки, принадлежащей видимой
образующей.
Рис. 6.13
Лекция 10
6.7. Пересечение поверхности вращения плоскостью
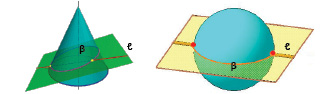
Форма сечения
поверхности вращения плоскостью зависит
от угла наклона секущей плоскости к
оси вращения поверхности.
Если секущая
плоскость:
-
перпендикулярна оси вращения, сечение
– окружность; -
наклонена к оси и пересекает все
образующие – эллипс; -
параллельна одной образующей –
парабола; -
параллельна двум образующим – гипербола;
-
проходит через вершину – две
пересекающиеся прямые; -
касается поверхности – прямая.
Вся совокупность этих линий может быть
получена при пересечении конуса
плоскостью. Поэтому их называют
коническими сечениями, или
кониками.
Рис. 6.14
Для
построения линии пересечения необходимо
найти общие точки поверхности и заданной
плоскости. Для определения этих точек
необходимо ввести дополнительные
секущие плоскости, которые дают наиболее
простые линии сечения – окружности
или ломаные прямые.
Построение
линии сечения начинают с нахожденияхарактерных
точек сечения,
к которым относятся:
-
высшая и низшая
точки; -
крайняя левая и
крайняя правая точки, в которых проекции
линии сечения касаются очерковых
образующих (точки, лежащие на границе
видимости); -
ближайшая и
наиболее удаленная точки сечения.
Пример:
Определить
линию сечения конуса плоскостью общего
положения (hf).
Построить развертку нижней отсеченной
поверхности конуса.
Анализ формы линии пересечения
Заданная плоскость пересекает только
боковую поверхность конуса, следовательно,
линией сечения qявляется эллипс.
Характерные
точки линии пересечения:
-
Высшая
и низшая точки сечения
(А, В)
определяют большую ось эллипса и лежат
на линии наибольшего наклона плоскости
к плоскости основания конуса. Эти точки
определяются с помощью дополнительной
плоскости.
О
– центр
эллипса
-
Малая
ось эллипса
(С, D)
перпендикулярна к линии наибольшего
наклона (большой оси), т.е. лежит на
горизонтали плоскости
.
-
Точки
границы видимости
(E,
F)
сечения на
лежат в плоскости
,
делящей конус на видимую и невидимую
части по отношению к фронтальной
плоскости проекций.
Рис. 6.15
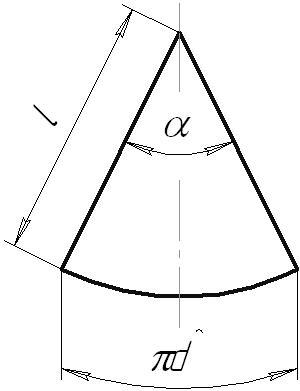
Развертка
Полная развертка
боковой поверхности конуса представляет
собой угол кругового сектора. Ее можно
построить двумя способами:
-
Нахождение
угла кругового сектора.
Рис. 6.16
где
d
– диаметр окружности основания конуса,
l
– длина образующей.
-
Способ
малых хорд.
Графическое
построение величины
осуществляется способом малых хорд,
при котором окружность основания конуса
делится на 8 или 12 равных частей и
полученная длина дуги приравнивается
ее хорде.
Разрывать
отсеченную боковую поверхность следует
по наиболее короткой или длинной
образующей, так чтобы развертка
представляла собой симметричную фигуру
и была единым целым.
Рис. 6.17
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пересечение прямой линии с поверхностью:
Для построения точки пересечения прямой с поверхностью через прямую следует провести вспомогательную плоскость и найти линию пересечения этой плоскости с поверхностью. Точка пересечения (или точка встречи заданной прямой и построенной линии или фигуры сечения) на поверхности и будет искомой точкой пересечения прямой с поверхностью. Сложность решения задачи зависит от трудоемкости нахождения линии пересечения, которая определяется следами поверхности и расположением прямой относительно как поверхности, так и плоскости проекций. Чтобы получить рациональное решение, следует пользоваться наиболее простым способом определения линии пересечения. Этого можно достичь двумя путями:
- выбором положения вспомогательной секущей плоскости;
- переводом секущей прямой в частное положение.
Вспомогательная секущая плоскость -проецирующая
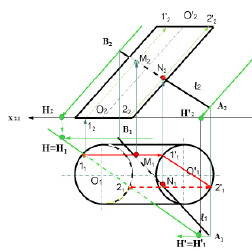
Задание: определить точки пересечения прямой m с поверхностью пирамиды SABC (рис. 12.1).
Решение: для решения задачи прямую m заключают во фронтально проецирующую плоскость Σ (
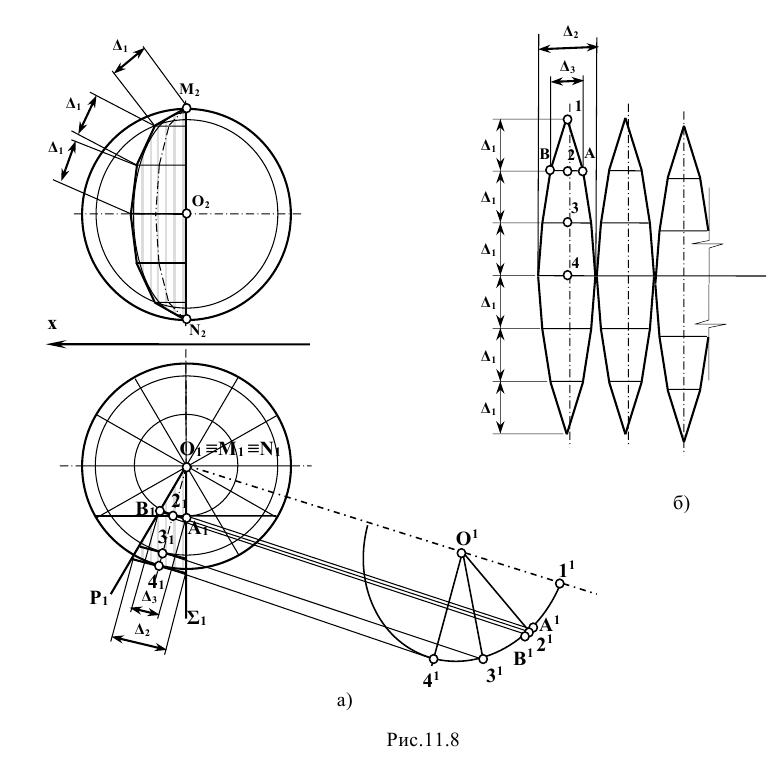
Задание: определить точки пересечения прямой m с поверхностью прямого кругового цилиндра (рис. 12.2).
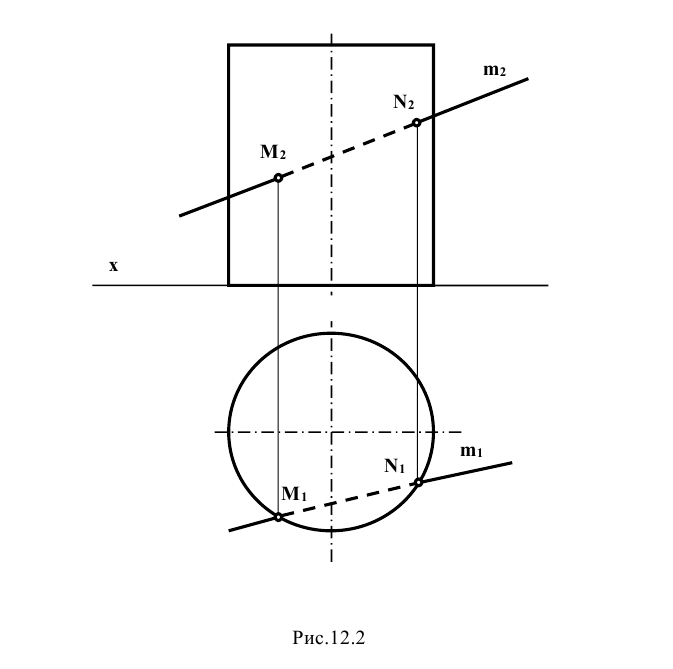
Решение: при решении задачи выделим проекции точек пересечения М и N прямой m с поверхностью цилиндра на горизонтальной проекции – точки 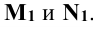
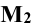
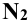
Вспомогательная секущая плоскость общего положения
Вспомогательную секущую плоскость, проводимую через прямую, при пересечении ею какой-либо поверхности, следует выбирать так, чтобы в результате получилось простейшее сечение. Например, при пересечении конической поверхности прямой линией такой плоскостью является плоскость, проходящая через вершину и пересекающая эту поверхность по прямым линиям (образующим).
При пересечении цилиндрической поверхности прямой линией вспомогательную плоскость целесообразно проводить через заданную прямую параллельно образующим цилиндра.
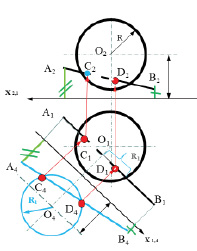
Задание: определить точки пересечения прямой m с поверхностью прямого кругового конуса (рис. 12.3).
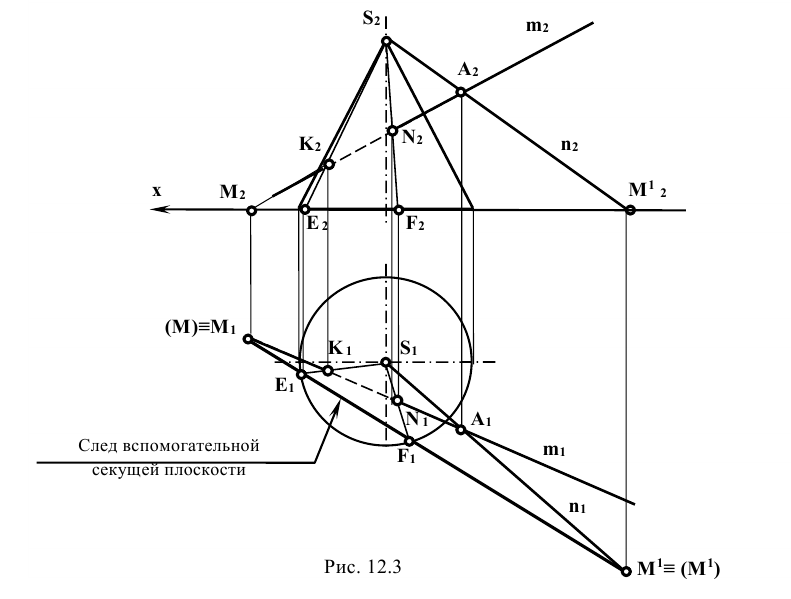
Решение: прямую m заключают в плоскость Р, проходящую через вершину конической поверхности S. Плоскость Р задана пересекающимися прямыми m и n, проходящими через точку А, которая выбирается произвольно на заданной прямой m.
Для определения горизонтального следа плоскости Р находят горизонтальные следы прямых m и n. Следы отмечают точками, например, 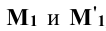
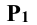
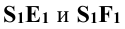
Точки 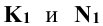
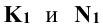
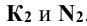
Перевод прямой общего положения, пересекающей заданную поверхность в частное положение
При пересечении поверхности сферы плоскостью в сечении получается окружность, которая проецируется на плоскости проекции в виде эллипсов или прямой и эллипса (если секущая плоскость – проецирующая). В случае, когда секущая плоскость параллельна плоскости проекции, окружность проецируется на эту плоскость проекции без искажения. Поэтому для упрощения решения задачи следует произвольно расположенную прямую перевести в положение, параллельное какой-либо плоскости проекции. Тогда прямую можно заключить в плоскость, параллельную плоскости проекции.
- Заказать чертежи
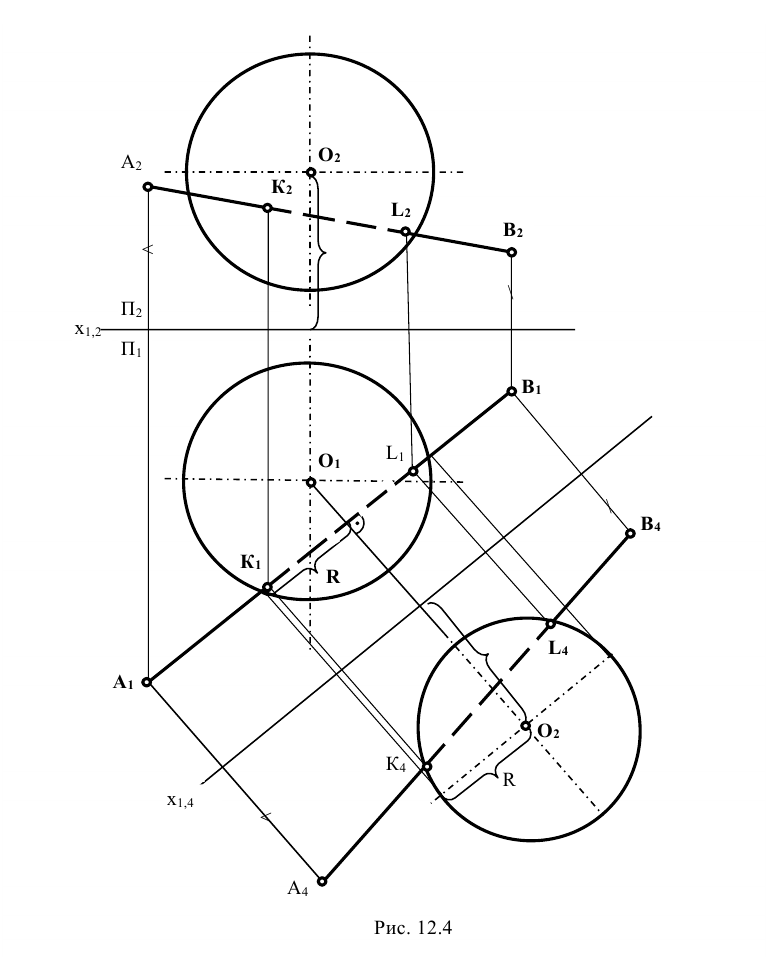
Задание: определить точки встречи прямой m, заданной отрезком АВ, с поверхностью сферы (рис. 12.4).
Решение: при решении этой задачи переводят прямую m общего положения в положение, параллельное плоскости проекции. Для этого вводят новую систему плоскостей 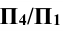
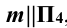
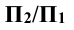
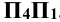
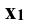
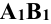
Далее от концов горизонтальной проекции прямой, точек 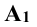
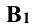
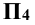
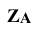
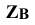
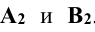
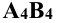
Аналогично находят и центр сферы
В новой системе горизонтально проецирующая плоскость Р 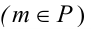
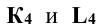
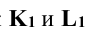
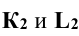
Плоскость, касательная к поверхности
Плоскость, касательная к поверхности в заданной на поверхности точке, есть множество всех прямых — касательных, проведенных к поверхности через заданную точку.
Для задания плоскости, касательной к поверхности в заданной точке, достаточно провести через эту точку две произвольные линии, принадлежащие поверхности (желательно простые по форме) и к каждой их них построить касательные в точке пересечения этих линий. Построенные прямые (касательные) определяют касательную плоскость.
Задание: построить плоскость Р, касательную к поверхности сферы и проходящую через точку К (рис. 12.5).
Решение: плоскость, касательная к сфере, перпендикулярна к радиусу, проведенному в точку касания. Поэтому, проведя радиус ОК, строят плоскость, задавая ее горизонталью КВ и фронталью КС.
При этом горизонтальная проекция 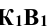
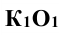
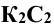
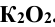
- Построение линии пересечения поверхностей
- Проецирование прямой
- Взаимное положение плоскостей, прямой линии и плоскости
- Взаимное расположение точки, прямых и плоскостей
- Проецирование точки
- Прямая в пространстве и ее изображение на чертеже
- Многогранники
- Поверхности вращения
8.1. Взаимное положение прямой и поверхности. Пересечение поверхности прямой линией
Одной из позиционных задач является определение взаимного положения прямой и поверхности.
Прямая может принадлежать поверхности и в этом случае все точки этой прямой принадлежат поверхности, а в другом случае прямая может пересекать поверхность и иметь точки входа и выхода (рис. 8.1).
а б
Рис. 8.1. Примеры пересечения прямой линией поверхностей:
а – втулки; б – диска
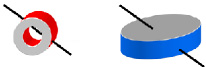
Для определения этих точек на комплексном чертеже можно использовать плоскости – посредники и использовать метод вспомогательных секущих плоскостей, сущность которого заключается в том, что через прямую ℓ проводится вспомогательная плоскость ∑ и на линииm пересечения этой плоскости с поверхностью λ находятся и точки входа и выхода А и В (рис. 8.2), принадлежащие прямой и поверхности.
Чтобы получить рациональное решение, следует использовать наиболее простой способ получения линии пересечения m. В качестве линии пересечения желательно получить либо прямую линию, либо окружность.
Рассмотрим некоторые примеры пересечения прямой линии с поверхностями.
m
Рис. 8.2. Пример определения точек входа прямой ℓ в поверхность λ
и выхода из неё
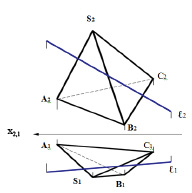
Задача 1. Найти точки входа и выхода прямой ℓ при её пересечении поверхности пирамиды SАВС (рис. 8.3).
Рис. 8.3. Графическое условие задачи на определение
точек пересечения поверхности пирамиды прямой линией
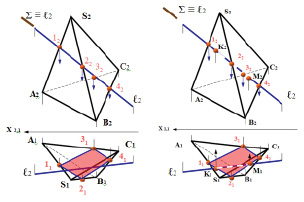
Для решения предложенной задачи (рис. 8.3), нужно поступить так же, как при нахождении точки пересечения прямой с плоскостью (рис. 3.9): через фронтальную (горизонтальную) проекцию прямой ℓ2 провести вспомогательную проецирующую плоскость ∑, определить во фронтальной (горизонтальной) плоскости проекций точки пересечения вспомогательной плоскости с поверхностью пирамиды 12223242. Затем, по принадлежности, найти горизонтальную (фронтальную) проекцию линии пересечения 11213141 плоскости с поверхностью (рис. 8.4.а).
а б
Рис.8.4. Пример определения:
а – проекции линии пересечения поверхности плоскостью; б – точек входа
и выхода прямой при пересечении поверхности пирамиды
Для определения точек входа и выхода прямой при пересечении поверхности (рис. 8.4. б) необходимо в горизонтальной плоскости проекций найти горизонтальные проекции точек пересечения (К1 и М1) горизонтальной проекции прямой ℓ1 с горизонтальной проекцией линии пересечения поверхности с плоскостью 11213141. Затем по принадлежности определить фронтальные проекции (К2 и М2)точек входа и выхода. Часть линии, находящейся в поверхности будет невидимой.
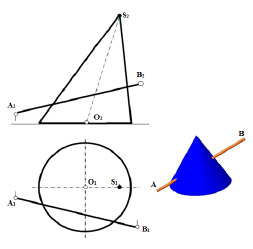
Задача 2. Найти точки входа и выхода прямой АВ при её пересечении поверхности конуса (рис. 8.5).
Рис. 8.5. Графическое условие задачи на определение точек входа и выхода
при пересечении поверхности конуса прямой линией
Для решения задачи нужно:
1) Во фронтальной плоскости проекций через прямую АВ и вершину конуса S провести вспомогательную произвольную плоскость, заданную двумя пересекающимися прямыми (SA, SB);
2) найти горизонтальный след h0 этой плоскости, для чего нужно построить два горизонтальных следа H и H’ прямых SA и SB вспомогательной плоскости (рис. 8.6).
3) Определить линию сечения поверхности вспомогательной плоскостью.
Горизонтальный след плоскости h0, пересекая основание поверхности конуса в точках 11 и 21, укажет границы проекции линии сечения (S11 21) поверхности вспомогательной плоскостью.
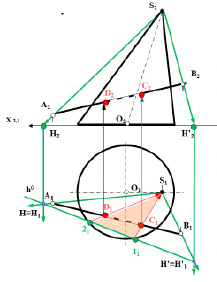
Рис. 8.6. Пример определения точек входа и выхода прямой
при пересечении поверхности конуса
4) Найти горизонтальные проекции точек входа и выхода.
Для определения точек входа и выхода прямой при пересечении поверхности конуса необходимо отметить горизонтальные проекции точек пересечения C1 и D1 горизонтальной проекции линии сечения поверхности конуса S11 21 с горизонтальной проекцией заданной прямой А1В1.
5) Определить фронтальные проекции точек входа и выхода.
Фронтальные проекции C2D2 точек входа и выхода прямой при пересечении поверхности конуса определяются по принадлежности. В соответствии с расположением прямой относительно поверхности определяется видимость элементов прямой.
Задача 3. Построить точки пересечения цилиндрической поверхности с прямой (рис. 8.7).
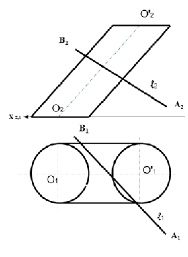
Рис. 8.7. Графическое условие задачи на пересечение поверхности цилиндра прямой линией
Для решения задачи нужно:
1) Во фронтальной плоскости проекций через прямую АВ провести произвольную вспомогательную плоскость, заданную двумя прямыми, параллельными образующим цилиндра;
2) Найти горизонтальный след h0 этой плоскости, для чего нужно построить два горизонтальных следа H и H’ параллельных прямых вспомогательной плоскости (рис. 8.8).
3) Определить проекции линии сечения.
Горизонтальный след плоскости h0, пересекая основание поверхности конуса в точках 11 и 21, укажет границы проекции линии сечения (111’1212’1) поверхности цилиндра вспомогательной плоскостью.
4) Найти горизонтальные проекции точек входа и выхода.
Для определения проекций точек входа и выхода прямой при пересечении поверхности цилиндра необходимо отметить горизонтальные проекции точек пересечения M1 и N1 горизонтальной проекции линии сечения поверхности цилиндра 111’1212’1 с горизонтальной проекцией заданной прямой А1В1.
5) Найти фронтальные проекции точек входа и выхода.
Фронтальные проекции N2M2 точек входа и выхода прямой при пересечении поверхности цилиндра определяются по принадлежности. В соответствии с расположением прямой относительно поверхности и плоскостей проекций необходимо определить видимость элементов прямой. В рассматриваемом случае фронтальная проекция точки N2 оказывается видимой, а проекция точки М2 – невидимой. Полное решение задачи представлено на рис. 8.8.
Рис. 8.8. Пример определения точек входа и выхода прямой
при пересечении поверхности цилиндра
Задача 4. Построить точки пересечения сферической поверхности с прямой (рис. 8.9).
Для решения такой задачи можно использовать способ замены плоскостей проекций. Через А1В1 провести вспомогательную горизонтально-проецирующую плоскость, которая позволит найти линию пересечения поверхность сферы.
Рис. 8.9. Пример определения точек пересечения прямой
с поверхностью сферы на комплексном чертеже
Линия пересечения пройдёт по окружности радиуса R1. Натуральную величину линии сечения можно получить на плоскости проекций П4, параллельной вспомогательной плоскости сечения. Проекции точек входа и выхода прямой С4D4 в поверхности сферы окажутся на пересечении проекций линии сечения и прямой А4В4. По принадлежности находятся горизонтальные и фронтальные проекции точек С и D. Затем определяется видимость элементов прямой.
а б
Рис. 8.10. Примеры пересечения кривых поверхностей с прямыми линиями:
а – конуса; б – сферы
CLIMATE_JUSTICE писал(а):
Как записать уравнение данной прямой в параметрическом виде?
Надо открыть учебник и посмотреть, как перейти от общего уравнения прямой к его параметрическому виду.
[math]begin{gathered}frac{x-4}{2}=frac{y+6}{-3}= frac{z+2}{-2}=t~~Rightarrow~,begin{cases} x=4+2t,\ y=-6-3t,\z=-2-2t.end{cases}hfill\ frac{x^2}{16} + frac{y^2}{12} + frac{z^2}{4} = 1,hfill\[2pt] frac{(4 + 2t)^2}{16} + frac{(-6 – 3t)^2}{12} + frac{(-2-2t)^2}{4} = 1,hfill\[2pt] frac{16 + 16t + 4t^2}{16} + frac{36 + 36t + 9t^2}{12} + frac{4 + 8t + 4t^2}{4} = 1,hfill\[2pt] 1+t+frac{t^2}{4}+3+3t + frac{3t^2}{4} + 1 + 2t +t^2=1,hfill\[2pt] 2t^2+ 6t + 4 = 0,hfill\[2pt] t^2+3t+2=0,hfill\[2pt] t_1=-1,~~t_2=-2.hfill\[5pt] t_1=- 1colon,begin{cases}x_1=4-2 = 2,\ y_1=-6+3=-3,\ z_1=-2+2=0;end{cases}quad t_2=-2colon,begin{cases}x_2=4-4 = 0,\y_2=-6+6 = 0,\z_2=-2+4=2.end{cases}hfillend{gathered}[/math]
– это прямая, не параллельная (и не перпендикулярная) ни одной из плоскостей проекций.
Все задачи на пересечение прямой общего положения с поверхностью решаются с помощью вспомогательных секущих плоскостей-посредников.
При пересечении прямой с поверхностью получаются две точки, одновременно принадлежащие как прямой, так и поверхности. Эти точки называются точками входа и выхода.
Следовательно, такие задачи сводятся к поиску этих двух точек. Для их нахождения в общем случае поступают так:
a) проводят через данную прямую вспомогательную проецирующую плоскость;
b) находят фигуру сечения данной плоскостью;
c) определяют точки пересечения с контуром сечения.
Примеры задач:
Задача 1: Построить точки пересечения прямой l с поверхностью конуса и определить видимость прямой.
рис.1
Решение:
Проводим вспомогательную секущую плоскость I. Её удобнее всего провести через заданную прямую l и вершину конуса S. Она пересечет поверхность конуса по его образующим.
Найдем линию пересечения горизонтальной плоскости со вcпомогательной I. Для этого выполним следующие действия: обозначим через точку 3”-точку пересечения прямой l с горизонтальной плоскостью. Затем выберем произвольную точку 1”, взятую на верхней части прямой l” (см.рис.2). Проведем через вершину конуса S” и эту точку прямую n”, она пересечет горизонтальную плоскость в точке 2”. Соединив точки 3” и 2” получим искомый горизонтальный след плоскости I.
Спроецируем точки 3” и 1” на прямую l’, проведем через вершину конуса S’ и точку 1′ прямую n’. Спроецируем на нее точку 2”. А затем, соединив точки 2′ и 3′, получим горизонтальную проекцию-m’ прямой m.
Прямая m проходит через основание конуса в точках A и B.
Таким
образом, в сечении конуса вспомогательной
секущей плоскостью I получается треугольник ABS.
Для определения точек пересечения прямой с поверхностью конуса соединяем вершину конуса S’ с точками A’ и B’, обозначив точки пересечения прямых A’S’ и B’S’ с прямой l’ D’ и E’ соответственно.
И, так как полученный треугольник и прямая l лежат в одной плоскости, то точки их пересечения D’ и E’ и есть точки пересечения прямой l с поверхностью конуса.
Спроецировав эти точки на прямую l”, получим проекцию точек D и E в плоскости П”.
Таким образом, искомые точки пересечения найдены. Далее определить видимость прямой l не составляет труда: она будет невидима только на отрезке DE, что видно из рисунка (рис.2).
рис.2
Задача 2. Построить точки пересечения прямой l с поверхностью цилиндра. Определить видимость прямой.
рис.3
Решение:
Проведем произвольную прямую m”, параллельную образующей цилиндра. Отметим точку 1” – точку пересечения прямых l” и m” и спроецируем ее на l’. Проведем прямую m’, параллельную образующей цилиндра и пересекающей прямую l’ в точке 1′.
Спроецируем точку пересечения m’ с горизонтальной плоскостью на прямую m”, обозначив ее как A”. Точка A” – след прямой m на П”.
Аналогично точку пересечения l’ с горизонтальной плоскостью спроецируем на l”. Обозначим ее как B”. Это фронтальный след прямой l на П”.
Соединяем точки A” и B”, проводим вспомогательную секущую плоскость I и находим точки пересечения прямой AB с поверхностью цилиндра. Через эти точки проводим прямые k” и n”, параллельные образующим цилиндра. Точки пересечения этих прямых и прямой l’ – C” и D” – искомые точки. Спроецируем их на прямую l”. Отмечаем видимость прямой l’, которая невидима на отрезке CD.
рис. 4