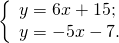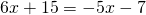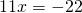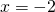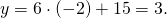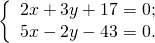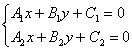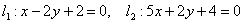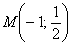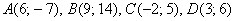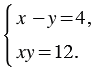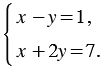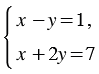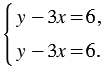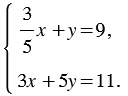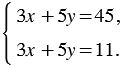Графическое решение системы уравнений: как найти координаты точки пересечения линий
Графическое решение системы уравнений – это один из методов решения системы из двух линейных уравнений с двумя неизвестными. Суть его заключается в построении на координатной плоскости двух прямых, соответствующих уравнениям системы, и определении их точки пересечения.
Как найти координаты точки пересечения линий
-
Запишите систему из двух линейных уравнений в общем виде:
ax + by = c dx + ey = f -
Решите первое уравнение относительно
y:y = (c - ax) / b -
Постройте эту функцию на координатной плоскости, используя найденные значения
a,bиc. -
Решите второе уравнение относительно
y:y = (f - dx) / e -
Постройте эту функцию на координатной плоскости, используя найденные значения
d,eиf. -
Найдите координаты точки пересечения двух линий, которые вы построили на шагах 3 и 5. Эта точка будет решением системы уравнений.
Пример решения системы уравнений
Для наглядного примера рассмотрим систему из двух линейных уравнений:
2x + 3y = 8
-4x + 5y = 7
-
Решаем первое уравнение относительно
y:y = (8 - 2x) / 3 -
Строим эту функцию на координатной плоскости:
-
Решаем второе уравнение относительно
y:y = (7 + 4x) / 5 -
Строим эту функцию на координатной плоскости:
-
Находим точку пересечения двух линий:
Координаты точки пересечения:
(1, 2).Значит, решение системы уравнений равно
x = 1,y = 2.
Выводы
Графическое решение системы уравнений является простым и наглядным методом для нахождения решения системы из двух линейных уравнений. Однако, этот метод не всегда эффективен для систем с большим количеством уравнений и переменных, поэтому часто используется более сложные алгоритмы решения систем уравнений.
Графический метод решения системы линейных уравнений
- Расположение графиков и количество решений системы линейных уравнений
- Алгоритм графического метода решения системы линейных уравнений
- Примеры
Расположение графиков и количество решений системы линейных уравнений
Рассмотрим систему двух уравнений: $ {left{ begin{array}{c} 3x-y = 5 \ 3x+2y = 8end{array} right.}$
Построим график каждого из уравнений и найдём точку пересечения.
Подставим координаты точки пересечения в уравнение:
$ {left{ begin{array}{c}3 cdot 2-1 ≡ 5\ 3cdot2+2cdot1 ≡ 8end{array} right.} Rightarrow$ (2;1) – решение системы
Таким образом, точка пересечения графиков уравнений является решением системы.
Графики двух уравнений системы могут пересекаться, быть параллельными и совпадать. Получаем разное количество решений системы в зависимости от соотношения коэффициентов уравнений:
$ frac{a_1}{a_2} neq frac{b_1}{b_2} $
$ frac{a_1}{a_2} = frac{b_1}{b_2} neq frac{c_1}{c_2} $
$ frac{a_1}{a_2} = frac{b_1}{b_2} = frac{c_1}{c_2} $
Прямые пересекаются
Прямые параллельны
Прямые совпадают
Одно решение
Нет решений
Бесконечное множество решений
Алгоритм графического метода решения системы линейных уравнений
1. Построить графики уравнений системы в одной координатной плоскости.
2а. Если $ frac{a_1}{a_2} neq frac{b_1}{b_2} $ найти точку пересечения – единственное решение системы.
2б. Если $ frac{a_1}{a_2} = frac{b_1}{b_2} neq frac{c_1}{c_2} $ прямые параллельны и решений нет.
2в. Если $ frac{a_1}{a_2} = frac{b_1}{b_2} = frac{c_1}{c_2} $ прямые совпадают, решений бесконечное множество.
Примеры
Пример 1. Решите графически систему уравнений. Сколько решений вы получили в зависимости от соотношения коэффициентов?
а)$ {left{ begin{array}{c} 5x+2y = 3 \ x-y = 4end{array} right.}$
Точка пересечения (1;-1)
Одно решение: $ frac{5}{1} neq frac{2}{-1}$
б) $ {left{ begin{array}{c}2x+y = 3 \ 4x+2y = 1end{array} right.}$
Прямые параллельны, решений нет:
$ frac{2}{4} = frac{1}{2} neq frac{3}{1}$
в) $ {left{ begin{array}{c}4x-y = 2 \ x+y = 3end{array} right.}$
Точка пересечения (1;2)
Одно решение: $ frac{4}{1} neq frac{-1}{1}$
г) $ {left{ begin{array}{c}2x-3y = 5 \ 4x-6y = 10end{array} right.}$
Прямые совпадают, бесконечное множество решений:
$ frac{2}{4} = frac{-3}{-6} = frac{5}{10} $
Пример 2*. Решите графически систему уравнений:
а)$ {left{ begin{array}{c} |x|-y = 0 \ x+3y = 4end{array} right.}$
В первом уравнении y всегда положительный: $y ge 0,∀x$
$ {left{ begin{array}{c}y(x) = |x| = {left{ begin{array}{c} x, x ge 0 \ -x, x lt 0 end{array} right.} \ x+3y = 4 end{array} right.} $
Два решения: (-2;2) и (1;1)
б)$ {left{ begin{array}{c} x-|y| = 0 \ 3x+y = 4end{array} right.}$
В первом уравнении x всегда положительный: $x ge 0,∀x$
$ {left{ begin{array}{c}y(x) = |y| = {left{ begin{array}{c} y, y ge 0 \ -y, y lt 0 end{array} right.} \ 3x+y = 4 end{array} right.} $
Два решения: (2;-2) и (1;1)
в)$ {left{ begin{array}{c} x^2-4y^2 = 0 \ 3|x|-2y = 8end{array} right.}$
$ {left{ begin{array}{c} (x-2y)(x+2y) = 0 \ y = 1,5|x|-4end{array} right.}$
$ {left{ begin{array}{c} left[ begin{array}{cc} y = frac{1}{2} x \ y = -frac{1}{2} x end{array} right. \ y = {left{ begin{array}{c} 1,5x-4,x ge 0 \ -1,5x-4,x lt 0 end{array} right.} end{array} right.} $
Из первого уравнения получаем две прямых, из второго – ломаную.
Четыре решения:
(-4;2);(-2;-1);(2;-1);(4;2)
г)$ {left{ begin{array}{c}|y-x| = 4 \ |x+y| = 2end{array} right.}$
$ {left{ begin{array}{c} left[ begin{array}{cc} y-x = 4 \ y-x = -4 end{array} right. \ left[ begin{array}{cc} x+y = 2 \ x+y = -2 end{array} right. end{array} right.}$
$ {left{ begin{array}{c} left[ begin{array}{cc} y = x+4 \ y = x-4 end{array} right. \ left[ begin{array}{cc} y = -x+2 \ y = -x-2 end{array} right. end{array} right.}$
Из первого уравнения получаем одну пару параллельных прямых, из второго уравнения – вторую пару параллельных прямых.
Четыре решения:
(-3;1);(-1;3);(3;-1);(1;-3)
Рейтинг пользователей
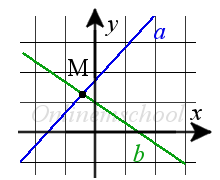
Пересечение прямых. Точка пересечения двух прямых
Если точка M, является точкой пересечения двух прямых, то она должна принадлежать этим прямым, а ее координаты удовлетворять уравнения этих прямых.
Точка пересечения двух прямых на плоскости
Если система уравнений:
- имеет единственное решение, то прямые пересекаются;
- имеет бесконечное множество решений, то прямые совпадают;
- не имеет решений, то прямые не пересекаются (прямые параллельны между собой)
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
y = 2 x — 1 y = -3 x + 1
Вычтем из первого уравнения второе
y — y = 2 x — 1 — (-3 x + 1) y = -3 x + 1 => 0 = 5 x — 2 y = -3 x + 1
Из первого уравнения найдем значение x
5 x = 2 y = -3 x + 1 => x = 2 5 = 0.4 y = -3 x + 1
Подставим значение x во второе уравнение и найдем значение y
x = 0.4 y = -3·(0.4) + 1 = -1.2 + 1 = -0.2
Ответ. Точка пересечения двух прямых имеет координаты (0.4, -0.2)
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
y = 2 x — 1 x = 2 t + 1 y = t
В первое уравнение подставим значения x и y из второго и третьего уравнений.
t = 2·(2 t + 1) — 1 x = 2 t + 1 y = t => t = 4 t + 1 x = 2 t + 1 y = t =>
-3 t = 1 x = 2 t + 1 y = t => t = — 1 3 x = 2 t + 1 y = t
Подставим значение t во второе и третье уравнение
t = — 1 3 x = 2·(- 1 3 ) + 1 = — 2 3 + 1 = 1 3 y = — 1 3
Ответ. Точка пересечения двух прямых имеет координаты ( 1 3 , — 1 3 )
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
2 x + 3 y = 0 x — 2 3 = y 4
Из второго уравнения выразим y через x
2 x + 3 y = 0 y = 4· x — 2 3
Подставим y в первое уравнение
2 x + 3·4· x — 2 3 = 0 y = 4· x — 2 3 => 2 x + 4·( x — 2) = 0 y = 4· x — 2 3 =>
2 x + 4 x — 8 = 0 y = 4· x — 2 3 => 6 x = 8 y = 4· x — 2 3 =>
x = 8 6 = 4 3 y = 4· x — 2 3 => x = 8 6 = 4 3 y = 4· 4/3 — 2 3 = 4· -2/3 3 = — 8 9
Ответ. Точка пересечения двух прямых имеет координаты ( 4 3 , — 8 9 )
Решение: Обе прямые заданы уравнениями с угловым коэффициентом. Так как k 1 = k 2 = 2, то прямые параллельны. Так как эти прямые не совпадают то точек пересечения нет.
Решим также эту задачу используя систему уравнений:
y = 2 x — 1 y = 2 x + 1
Вычтем из первого уравнения второе
y — y = 2 x — 1 — (2 x + 1) y = -3 x + 1 => 0 = -2 y = -3 x + 1
В первом уравнении получили противоречие (0 ≠ -2), значит система не имеет решений — отсутствуют точки пересечения прямых (прямые параллельны).
Ответ. Прямые не пересекаются (прямые параллельны).
Решение: Подставим координаты точки N в уравнения прямых.
Ответ. Так как оба уравнения превратились в тождества, то точка N — точка пересечения этих прямых.
Точка пересечения двух прямых в пространстве
Если система уравнений:
- имеет единственное решение, то прямые пересекаются;
- имеет бесконечное множество решений, то прямые совпадают;
- не имеет решений, то прямые не пересекаются (прямые параллельны или скрещиваются между собой)
Решение: Составим систему уравнений
x — 1 = a y — 1 = a z — 1 = a x — 3 -2 = b 2 — y = b z = b => x = a + 1 y = a + 1 z = a + 1 x — 3 -2 = b 2 — y = b z = b =>
Подставим значения x , y , z из 1, 2, 3 уравнений в 4, 5, 6 уравнения
x = a + 1 y = a + 1 z = a + 1 a + 1 — 3 -2 = b 2 — ( a + 1) = b a + 1 = b => x = a + 1 y = a + 1 z = a + 1 a — 2 -2 = b 1 — a = b a + 1 = b
К шестому уравнению добавим пятое уравнение
x = a + 1 y = a + 1 z = a + 1 a — 2 -2 = b 1 — a = b a + 1 + (1 — a ) = b + b => x = a + 1 y = a + 1 z = a + 1 a — 2 -2 = b 1 — a = b b = 1
Подставим значение b в четвертое и пятое уравнения
x = a + 1 y = a + 1 z = a + 1 a — 2 -2 = 1 1 — a = 1 b = 1 => x = a + 1 y = a + 1 z = a + 1 a — 2 = -2 a = 0 b = 1 =>
x = a + 1 y = a + 1 z = a + 1 a = 0 a = 0 b = 1 => x = 0 + 1 = 1 y = 0 + 1 = 1 z = 0 + 1 = 1 a = 0 a = 0 b = 1
Ответ. Прямые пересекаются в точке с координатами (1, 1, 1).
Решение: Составим систему уравнений заменив во втором уравнении параметр t на a
x = 2 t — 3 y = t z = — t + 2 x = a + 1 y = 3 a — 2 z = 3
Подставим значения x , y , z из 1, 2, 3 уравнений в 4, 5, 6 уравнения
x = 2 t — 3 y = t z = — t + 2 2 t — 3 = a + 1 t = 3 a — 2 — t + 2 = 3 => x = 2 t — 3 y = t z = — t + 2 2 t = a + 4 t = 3 a — 2 t = -1 =>
Подставим значение t из шестого уравнения в остальные уравнения
x = 2·(-1) — 3 y = (-1) z = -(-1) + 2 2·(-1) = a + 4 -1 = 3 a — 2 t = -1 => x = -5 y = -1 z = 3 a = -6 a = 1 3 t = -1
Ответ. Так как -6 ≠ 1 3 , то прямые не пересекаются.
Координаты точки пересечения прямых
Две прямые на плоскости могут быть параллельными, пересекаться либо совпадать.
Чтобы найти координаты точки пересечения прямых, надо составить и решить систему уравнений, составленную из уравнений этих прямых.
Найти точку пересечения прямых заданных уравнениями:
2) 2x+3y+17=0; 5x-2y-43=0.
1) Составляем систему уравнений (здесь даны уравнения прямой с угловым коэффициентом):
Приравняем правые части уравнений:
Подставим x= -2 в уравнение первой прямой:
2) Составляем систему уравнений (здесь задано общее уравнение прямой):
Умножим 1-е уравнение системы на 2, а 2-е — на 3
2.5.3. Как найти точку пересечения прямых?
Если прямые 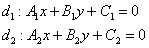
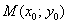
Как найти точку пересечения прямых? Решить систему.
И вот вам, кстати, геометрический смысл системы двух линейных уравнений с двумя неизвестными – это две пересекающиеся (чаще всего) прямые. И реже:
– если система несовместна (без решений), то прямые параллельны;
– если 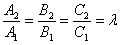
Задача 77
Найти точку пересечения прямых
Существуют два способа решения – графический и аналитический.
Графический способ состоит в том, чтобы просто начертить данные прямые и узнать точку пересечения непосредственно из чертежа: 
Для проверки следует подставить её координаты в уравнение каждой прямой, они должны подойти и там, и там. Графический способ, конечно, неплох, но существует и заметные минусы. Нет, дело не в том, что так решают семиклассники, дело в том, что на правильный и ТОЧНЫЙ чертёж уйдёт время. Кроме того, некоторые прямые построить не так-то просто, да и сама точка пересечения может находиться где-нибудь в тридесятом царстве за пределами тетрадного листа.
Поэтому точку пересечения 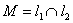
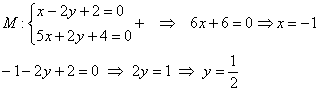
Ответ:
Проверка тривиальна – координаты точки пересечения должны удовлетворять каждому уравнению системы. К слову, этой задачей мы заодно рассмотрели графический способ решения системы двух линейных уравнений с двумя неизвестными.
Задача 78
Найти точку пересечения прямых 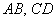
Это задача для самостоятельного решения, которое удобно разбить на несколько этапов. Анализ условия подсказывает, что нужно:
1) составить уравнение прямой 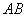
2) составить уравнение прямой 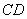
3) выяснить взаимное расположение прямых 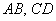
4) если прямые пересекаются, то найти точку пересечения.
Разработка алгоритма действий типична для геометрических задач, и я на этом буду неоднократно заострять внимание.
В первой части параграфа мы узнали, как построить прямую, параллельную данной, и сейчас избушка на курьих ножках разворачивается на 90 градусов:
источники:
http://www.treugolniki.ru/koordinaty-tochki-peresecheniya-pryamyx/
http://mathter.pro/angem/2_5_3_kak_nayti_tochku_peresecheniya_pryamyh_na_ploskosti.html
Не такая тривиальная задача, скажу я вам. Всякий раз, когда возникает необходимость посчитать координату пересечения пары прямых, каждая из которых задана парой точек, снова беру блокнот и вывожу пару формул. И всякий раз – блин, ну это уже когда-то было, опять надо что-то делать с параллельными прямыми, опять появляется пакостная строго вертикальна линия, когда на (x1-x2) никак не разделить и т.д.
Поэтому – в подборку теории и практики, пригодится, сэкономим блокнот, спасем дерево.
Коэффициенты А, B, C
Все помним со школы формулу:
Тоже самое, но с претензией на образование (некоторые индивидуумы утверждают, что существует такая, и только такая, и никакая другая, формулировка):
Те же фаберже, только сбоку.
В теории надо составить и решить систему уравнений для первой и второй линии, где переменными будут X и Y точки пересечения.
Загвоздка в том, что мы не знаем коэффициенты для обеих линий.
В нашем случае известны координаты двух точек, по которым проходит линия. Поэтому мне, как последователю геометрического агностицизма, более привлекательная следующая формула:
Путем несложных операций приходим к следующей записи:
Глядя на вариант в исполнении высшего образования, получаем следующие формулы для нахождения коэффициентов:
Пока все идет отлично, нигде вероятного деления на ноль не встретилось.
Итак, мы можем легко найти два набора коэффициентов для первой и второй прямых. Переходим к системе уравнений.
Система уравнений
Как правило, подобная система уравнений решается путем выражения одной переменной через другую, подстановкой во второе уравнение, получая таким образом уравнение одной переменной. Далее переменная находится, подставляется, решается. Или определяется, что система решения не имеет.
Но нас интересует метод Крамера. Потому что с помощью этого метода можно получить сразу значения для обеих переменных, без дополнительных телодвижений.
Сразу же запишем метод под нашу систему.
Имеем следующую систему:
Определители будут такими:
Исходя из метода, решение выглядит так:
Ага! Вот и возможное деление на ноль, скажете вы. И правильно! В этой, в высшей степени непозволительной ситуации, когда знаменатель равен нулю, решения нет, прямые либо параллельны, либо совпадают (что, впрочем, частный случай параллельности). В коде, естественно, этот момент надо учитывать.
Практика 1
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
//******************************************************* // Нахождение точки пересечения прямых (p1,p2) и (p3,p4) // Результат – факт пересечения //******************************************************* function CrossLines(const p1,p2,p3,p4: TxPoint; var res: TxPoint): Boolean; const Prec = 0.0001; var a1, a2: Extended; b1, b2: Extended; c1, c2: Extended; v: Extended; begin a1 := p2.y – p1.y; a2 := p4.y – p3.y; b1 := p1.x – p2.x; b2 := p3.x – p4.x; v := a1*b2 – a2*b1; Result := (abs(v) > Prec); if Result then begin c1 := p2.x*p1.y – p1.x*p2.y; c2 := p4.x*p3.y – p3.x*p4.y; res.X := –(c1*b2 – c2*b1)/v; res.Y := –(a1*c2 – a2*c1)/v; end; end; |
Частные случаи
- Прямые параллельны: ∆ab = 0
- (A1B2 – B1A2 = 0);
- Прямые совпадают: ∆ab = ∆X = ∆Y = 0
- (A1B2 – B1A2 = 0) И (A1C2 — A2C1 = 0) И (C1B2 -B1C2 = 0);
- Прямые перпендикулярны:
- (A1 A2 + B1 B2 = 0).
Принадлежность точки отрезку
В общем случае, чтобы определить принадлежность точки отрезку, надо установить две вещи:
- Точка принадлежит прямой, проходящей через конечные точки отрезка. Для этого достаточно подставить значение X и Y в уравнение прямой и проверить получившееся равенство. В нашем случае, этот пункт уже выполнен, т.к. точка пересечения априори принадлежит обеим прямым.
- Проверить факт нахождения точки между концами отрезка.
Займемся пунктом 2. Данный факт можно установить двумя способами:
- Логически, т.е. (x1 <= x <= x2) ИЛИ (x1 >= x >= x2). На случай «вертикальности» линии добавить проверку на Y:
- (y1 <= y <= y2) ИЛИ (y1 >= y >= y2).
- Арифметически. Сумма отрезков |x-x1| + |x-x2| должна быть равна длине отрезка |x1-x2|. Аналогично, на случай «вертикальности» , добавить проверку:
- |y-y1| + |y-y2| = |y1-y2|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
//***************************************************** // Проверка факта нахождения точки res между // концами отрезка (p1,p2). // Решение с помощью условных операторов и // коэффициентов A=(y2-y1) B=(x1-x2). // Выступают в качестве параметров, чтобы не тратить // время на их подсчет, т.к. в вызывающей стороне // они уже посчитаны //***************************************************** function CheckCrossPoint(const p1, p2, res: TxPoint; const A,B: Extended): Boolean; begin Result := (((B<0) and (p1.X < res.X) and (p2.X > res.X)) or ((B>0) and (p1.X > res.X) and (p2.X < res.X)) or ((A<0) and (p1.y > res.Y) and (p2.Y < res.Y)) or ((A>0) and (p1.y < res.Y) and (p2.Y > res.Y))); end; //***************************************************** // Проверить факт нахождения точки res между // концами отрезка (p1,p2) // Арифметическое решение без коэффициентов //***************************************************** function CheckCrossPoint(const p1, p2, res: TxPoint): Boolean; begin Result := (abs(p2.x–p1.x)>= abs(p2.x–res.x) + abs(p1.x–res.x)) and (abs(p2.y–p1.y)>= abs(p2.y–res.y) + abs(p1.y–res.y)); end; |
Практика показывает, что арифметический способ быстрее примерно в 3 раза. Когда-то я считал, что операции сравнения самые быстрые. Это давно уже не так.
Задача нахождения принадлежности точки P(x,y) отрезку, заданного двумя точками с координатами P1(x1, y1) и P2(x2, y2) подробно рассмотрена в отдельной статье.
Угол пересечения прямых
Угол пересечения прямых — это угол пересечения направляющих векторов. Т.е., взяв уже знакомые ранее точки p1 и p2, получим направляющий вектор V(p1,p2), и аналогично второй вектор M(p3,p4). В теории мы должны вычислить достаточно «затратную» функцию, с корнями, квадратами, дробями и арккосинусом.
Давайте не будем останавливаться на ней, она долгая, нудная и в нашем случае ненужная. Рассмотрим вектор:
α — угол наклона вектора к оси X, который можно найти, как:
α = arctan (A1 / B1)
Где расстояния:
A1 = (y1 — y2)
B1 = (x2 — x1)
Что-то знакомое? Да это ни что иное, как коэффициенты в уравнении прямой от образованных фанатов. Может они и правы в своем испепеляющем фанатизме…
Одним словом, коэффициенты (расстояния) у нас уже есть по обеим прямым.
Судя по рисунку, угол между векторами, это сумма углов наклона векторов к оси X. Ммм… не совсем так, на самом деле это разность.
По рисунку явно видно, что угол между векторам это γ = (β — α).
В предыдущем примере все правильно, просто знаки углов разные, т.к. находятся по разные стороны от оси X, а формула работает та же.
От теории к практике
Теперь в плане практического применения. Мне нужно точно знать, откуда, куда и в каком направлении этот угол. В теории, углом между прямыми считается наименьший из пары γ и (180-γ). Так вот, нам это не надо. Какой угол получится – такой нам и нужен.
Поэтому, под углом между векторами понимаем угол от вектора V(p1,p2) к вектору M(p3,p4). Если знак угла – отрицательный, понимаем, что он против часовой стрелки, иначе – по часовой стрелке.
Следует заметить, что, зная коэффициенты, для нахождения угла пересечения, координаты уже не нужны. Листинг таков:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
//********************************************************** // Посчитать угол пересечения векторов по коэфф-ам А и B //********************************************************** function CalcCrossAngle(const a1,b1: Extended; const a2,b2: Extended): Extended; var c1, c2: Extended; begin c1 := ArcTan2(a1,b1); c2 := ArcTan2(a2,b2); Result := c2–c1; if Result < –pi then Result := 2*pi + Result; if Result > pi then Result := Result – 2*pi; end; |
Тут ситуация с вертикальной прямой, т.е. когда теоретически происходит деление на ноль, явно не обрабатывается. Она корректно обрабатывается функцией ArcTan2, которая вернет в этом случае и знак, и 90 градусов.
Практика 2
В дополнение к функции нахождения точки пересечения, напишем «продвинутую» функцию, которая находит эту точку, определяет нахождение на каждом из отрезков, и определяет угол между направляющими векторами. Или же определяет, что прямые параллельны/совпадают.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 |
//********************************************************** // Тип пересечения прямых (p1,p2) и (p3,p4) //********************************************************** type TxCrossLineResult = ( xclrEqual = –32// эквивалентны ,xclrParallel = –16// параллельны ,xclrOk = 0 // как минимум пересечение есть ,xclrFirst = 1 // попадает в первый отрезок ,xclrSecond = 2 // попадает во второй отрезок ,xclrBoth = 3 // попадает в оба ,xclrPerpend = 4 // перпендикулярны // можно найти по маске через AND, но для полноты картины ,xclrFirstP = 5 // перпендикулярны и попадает в первый ,xclrSecondP = 6 // перпендикулярны и попадает в второй ,xclrBothP = 7 // перпендикулярны и попадает в оба ); //********************************************************** // Нахождение точки пересечения прямых (p1,p2) и (p3,p4) // Определяет параллельность, совпадение, // перпендикулярность, пересечение. // Определяет, каким отрезкам принадлежит. // Находит угол(рад.) от (p1,p2) к (p3,p4): // отрицательное значение – против часовой // положительное – по часовой //********************************************************** function CrossLines(const p1,p2,p3,p4: TxPoint; var res: TxPoint; var Angle: Extended): TxCrossLineResult; const Prec = 0.0001; var a1, a2: Extended; b1, b2: Extended; c1, c2: Extended; v: Extended; begin Angle := 0; a1 := p2.y – p1.y; a2 := p4.y – p3.y; b1 := p1.x – p2.x; b2 := p3.x – p4.x; c1 := p2.x*p1.y – p1.x*p2.y; c2 := p4.x*p3.y – p3.x*p4.y; v := a1*b2 – a2*b1; if abs(v) > Prec then begin Result := xclrOk; res.X := –(c1*b2 – c2*b1)/v; res.Y := –(a1*c2 – a2*c1)/v; if CheckCrossPoint(p1,p2,res) then Result := TxCrossLineResult(Integer(Result) + Integer(xclrFirst)); if CheckCrossPoint(p3,p4,res) then Result := TxCrossLineResult(Integer(Result) + Integer(xclrSecond)); if (abs(a1*a2 + b1*b2) < Prec) then Result := TxCrossLineResult(Integer(Result) + Integer(xclrPerpend)); Angle := CalcCrossAngle(a1,b1,a2,b2); end else begin Result := xclrParallel; if ((abs(c1*b2 – c2*b1) < Prec) and (abs(a1*c2 – a2*c1) < Prec)) then Result := xclrEqual; end; end; |
Исходники
Небольшие комментарии по интерфейсу.
Скачать (219 Кб): Исходники (Delphi XE 7-10)
Скачать (1.14 Мб): Исполняемый файл
При запуске генерируется случайным образом 4 точки, по две на прямую. Точки и отрезки можно перетаскивать мышкой. Также, слева присутствует панель, на которой можно ввести координаты точек или коэффициенты уравнения прямой. При нажатии «Enter» или когда элемент ввода теряет фокус, происходит перерасчет и перерисовка.
Внизу есть 4 кнопки переключения режимов отображения. Начиная со второй, помимо координат точки пересечений в верхнем левом углу будет отображаться текущий угол пересечения между направляющими векторами.
Если точка пересечений попадает в какой-либо из отрезков, соответствующий заголовок линии отрезка станет жирным. На рисунке это зеленая линия 2.
По умолчанию, рабочее поле системы координат имеет размерность [-10..10], которую можно изменить ползунком в нижнем правом углу.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Алгебра
- Системы линейных уравнений с двумя переменными
- Системы уравнений с двумя переменными. Графический метод решения системы двух линейных уравнений с двумя переменными
Рассмотрим задачу:
Разность двух чисел равна 4, а их произведение 12. Найдите эти числа.
Решение:
Обозначим первое число буквой 



Так как произведение чисел равно 12, то 
Мы составили два уравнения с двумя переменными. Чтобы ответить на вопрос задачи, надо найти такие значения переменных, которые обращают в верное равенство каждое из уравнений 


Систему уравнений записывают с помощью фигурной скобки. Поэтому, составленную нами систему уравнений, можно записать так:
Пара значений переменных 

Решением системы уравнений с двумя переменными называют пару значений переменных, обращающую каждое уравнение в верное равенство.
Решить систему уравнений – это значит найти все ее решения или убедиться, что их нет.
Для того чтобы решить систему линейных уравнений с двумя переменными, можно использовать использовать графики уравнений.
Решим систему уравнений:
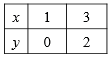
Выразив из уравнения 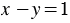


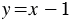
Для этого составим таблицу значений функции 

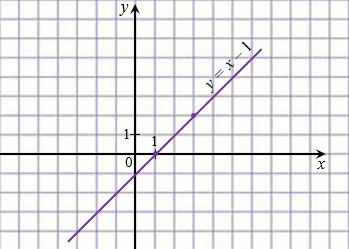
Отметим на координатной плоскости точки с координатами (1; 0) и (3; 2) и проведем через них прямую, которая является графиком линейной функции 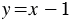
Выразив из уравнения 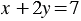



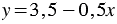
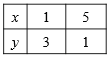
Для этого составим таблицу значений функции 

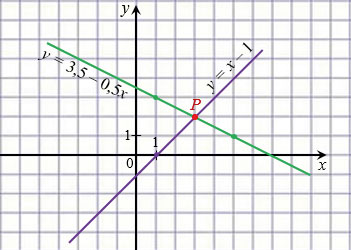
Отметим на имеющейся координатной плоскости точки с координатами (1; 3) и (5; 1) и проведем через них прямую, которая является графиком линейной функции 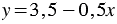
Мы получили, что прямые, которые соответствуют уравнениям 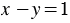
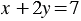


Описанный выше метод решения системы уравнений называют графическим.
Суть графического метода решения системы уравнений с двумя переменными:
1) построить на одной координатной плоскости графики уравнений, входящих в систему;
2) найти координаты всех точек пересечения построенных графиков;
3) полученные пары чисел и будут искомыми решениями.
Заметим, что графический способ обычно позволяет находить решения лишь приближенно. Поэтому графический метод эффективен в тех случаях, когда требуется определить количество решений системы.
Определим, сколько решений может иметь система двух линейных уравнений с двумя переменными.
1) Если одно из уравнений системы не имеет решения, то и вся система решений не имеет.
2) Если графиком одного из уравнений системы является вся плоскость, то система имеет бесконечно много решений.
3) Если графиками уравнений, входящих в систему линейных уравнений, являются прямые, то количество решений этой системы зависит от взаимного расположения двух прямых на плоскости:
- если прямые пересекаются, то система имеет единственное решение.
Рассмотренная нами выше система
имеет единственное решение 

- если прямые совпадают, то система имеет бесконечно много решений.
Рассмотрим систему
Если умножить обе части первого уравнения этой системы на 3, то решения этого уравнения, а значит, и всей системы не изменятся. Получим:
В полученной системе первое и второе уравнения одинаковые, значит, решения этой системы совпадают с решениями уравнения 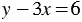
- если прямые параллельны, то система решений не имеет.
Рассмотрим систему
Если умножить обе части первого уравнения этой системы на 5, то решения этого уравнения, а значит, и всей системы не изменятся. Получим:
Очевидно, что не существует такой пары значений 

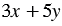
Советуем посмотреть:
Уравнения с двумя переменными
Линейное уравнение с двумя переменными и его график
Решение систем линейных уравнений методом подстановки
Решение систем линейных уравнений методом сложения
Решение задач с помощью систем линейных уравнений
Введение в алгебру
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Одночлены
Многочлены
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Функции
Системы линейных уравнений с двумя переменными
Алгебра
Правило встречается в следующих упражнениях:
7 класс
Номер 1010,
Мерзляк, Полонский, Якир, Учебник
Номер 1064,
Мерзляк, Полонский, Якир, Учебник
Номер 1079,
Мерзляк, Полонский, Якир, Учебник
Номер 1082,
Мерзляк, Полонский, Якир, Учебник
Номер 1085,
Мерзляк, Полонский, Якир, Учебник
Номер 1093,
Мерзляк, Полонский, Якир, Учебник
Номер 1098,
Мерзляк, Полонский, Якир, Учебник
Номер 1099,
Мерзляк, Полонский, Якир, Учебник
Номер 1104,
Мерзляк, Полонский, Якир, Учебник
Номер 1116,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 134,
Мерзляк, Полонский, Якир, Учебник
Номер 173,
Мерзляк, Полонский, Якир, Учебник
Номер 333,
Мерзляк, Полонский, Якир, Учебник
Номер 334,
Мерзляк, Полонский, Якир, Учебник
Номер 335,
Мерзляк, Полонский, Якир, Учебник
Номер 336,
Мерзляк, Полонский, Якир, Учебник
Номер 348,
Мерзляк, Полонский, Якир, Учебник
Номер 356,
Мерзляк, Полонский, Якир, Учебник
Номер 420,
Мерзляк, Полонский, Якир, Учебник
Номер 488,
Мерзляк, Полонский, Якир, Учебник