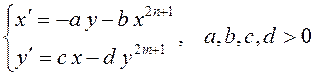Как найти точки равновесия системы

1. Главная
2. Моделирование
3. Точки равновесия для динамических систем

08 Декабрь 2011 24822

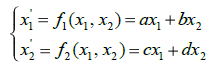
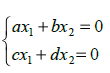
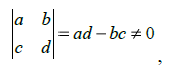
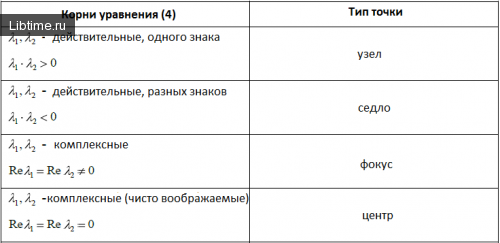
Пусть имеем линейную однородную систему дифференциальных уравнений с постоянными коэффициентами: (1) Точки равновесия системы находят из решения системы: (2) Если определитель системы этой не равен нулю (3) то система имеет единственное решение. Тип положения равновесия определяется собственными числами матрицы системы, которые находят из характеристического уравнения: (4) где: – след матрици, – детерминант. Классификация точек равновесия в случае, когда Δ ≠ 0, представленная в таблице:

Классификация точек равновесия

Характер устойчивости положений равновесия

Собственные значения матрицы системы (1) однозначно определяют характер стойкости положений равновесия:

• Устойчивый узел – если действительные части всех корней уравнения (4) отрицательны, то точка равновесия системы (1)асимптотически устойчива.
• Седло, неустойчивый узел, неустойчивый фокус – если действительная часть хотя бы одного корня уравнения (4) положительна, то точка равновесия системы (1)неустойчивая.
• Центр – если уравнение (4) имеет чисто воображаемые корни, то точка равновесия системы (1) устойчива, но не асимптотически

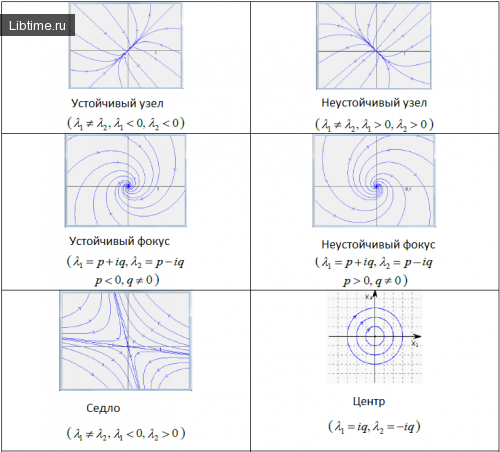
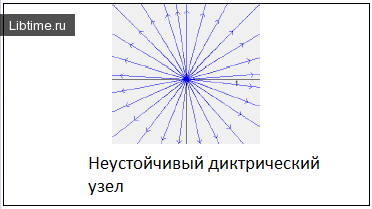
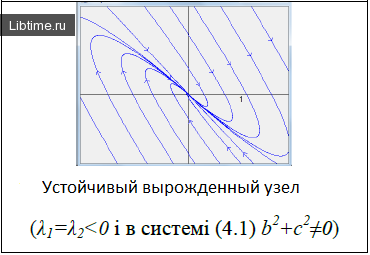
Ниже изображены фазовые портреты динамических систем для каждого типа точек равновесия. Направление стрелок на фазовой кривой указывает направление движения фазовой точки при возрастании t. Неустойчивый диктрический узел: Устойчивый вырожденный узел: Неустойчивый вырожденный узел: Бифуркационная диаграмма позволяет определить тип точки равновесия.

Рейтинг: 4,4/5 – 7
голосов

ПРИМЕР. Исследовать
на устойчивость нулевое решение системы дифференциальных уравнений  .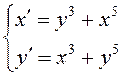  

Рассмотрим функцию . Убедимся, что она
удовлетворяет условиям 1) – 3) теоремы Четаева.  

3. Производная
в силу данной системы

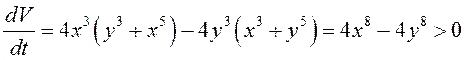
, если , то
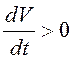
есть    во  всех  внутренних  точках  .  Поэтому  нулевое  решение  системы неустойчиво.

ЗАМЕЧАНИЕ.
Если в некоторой окрестности начала координат функция  и ее производная в силу системы  положительно определены, то все
условия теоремы Четаева выполнены, следовательно, точка покоя  неустойчива.

ЗАМЕЧАНИЕ.  Метод
функций  Ляпунова универсален и эффективен, но, недостаток метода в том, что не существует
конструктивного  алгоритма построения функции Ляпунова для произвольной системы
дифференциальных уравнений. В простейших случаях можно искать функцию
Ляпунова в виде  и т.д.. Для системы дифференциальных
уравнений вида

функция
 является функцией Ляпунова. Точка покоя  такой системы асимптотически устойчива.

ЗАМЕЧАНИЕ.
При исследовании устойчивости произвольного решения системы дифференциальных
уравнений  следует сделать замену переменной , преобразовав исходную систему к системе дифференциальных
уравнений, имеющей нулевое решение.

ПРИМЕР.
Найти все положения равновесия системы     и
исследовать их на устойчивость.

Чтобы найти все положения равновесия данной системы,
надо найти точки, в которых правые части обоих дифференциальных уравнений
одновременно обращаются в нуль:

  – положения равновесия, или точки покоя.

1) 
Исследуем на устойчивость точку .

Пусть , то есть . Подставив  в систему
дифференциальных уравнений, получим: .

Легко убедиться, что эта система имеет тривиальное
решение  Чтобы исследовать его на устойчивость,
составим систему первого приближения в соответствии с (12.11): 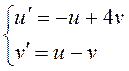. Характеристическое уравнение этой
системы: 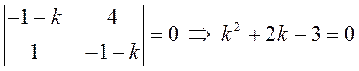. Так как , то
нулевое решение неустойчиво, а, значит, точка  –
неустойчивое положение равновесия.

2) 
Исследуем на устойчивость точку .

Аналогично,
сделав замену переменных , получим систему дифференциальных
уравнений: 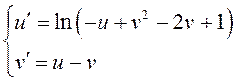, для которой система первого приближения
имеет вид: . Характеристическое уравнение этой
системы: . Все коэффициенты квадратного уравнения
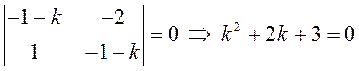
положительны, значит  и точка  –
положение устойчивого равновесия.

Библиографический список

1. 
Пискунов, Н.С. Дифференциальное и
интегральное исчисления /     Н.С. Пискунов.– М.: Интеграл–пресс, 2005.– Т.1,
2.

2. 
 Араманович 
И. Г .,
 Лунц 
 Г . Л .,
 Эльсгольц 
 Л . Э .
 Функции 
 комплексного 
 переменного .
 Операционное 
 исчисление .
 Теория 
 устойчивости .
М.: Наука, 1970.– 415 c.

3. 
Краснов М. Л .,
Киселев А.И., Макаренко Г.И. Функции комплексного переменного.  Операционное 
 исчисление .
Теория  устойчивости . М.: Наука, 1981.– 304 c.

4. 
Филиппов, А.Ф. Сборник задач по
дифференциальным уравнениям. – Ижевск: Регулярная и хаотическая динамика,
2000.–176 с.

Редактор

Компьютерная верстка, дизайн обложки

ИД № 06039 от 12.10.2001 г.

Сводный темплан 2011 г.

Подписано в печать     .  .  . Формат 60×84  ¹/₁₆.
Бумага офсетная.

Отпечатано на дупликаторе. Усл. печ. л.      .
Уч.-изд. л.          .

Тираж      . Заказ  .

______________________________________________________

Издательство ОмГТУ. 644050, г. Омск, пр-т Мира, 11

Типография ОмГТУ

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание – внизу страницы.

Рассмотрим
нелинейную систему второго порядка:

,
(1.1)

причем
будем предполагать, что функции
дважды
непрерывно дифференцируемы во всей
плоскостиXOY.

Положения равновесия
(точки покоя) системы (1.1) определяются
как решения системы уравнений:

Обозначим
эти точки через
.

Найдем
матрицу Якоби
(якобиан) системы (1.1):

и
вычислим значения
для каждой из точек покоя.
Пусть
– одна из
полученных матриц. Эта матрица задает
линейную систему

(1.2)

Пусть
– собственные значения матрицысистемы (1.2). Положение равновесия,
для которого найдена рассматриваемая
матрица, будем называтьневырожденным,
если
и.
Оказывается, что в невырожденном случае
поведение траекторий вблизи положения
равновесиядля
нелинейной системы (1.1) в существенном
совпадает с поведением траекторий
линейной системы (1.2) вблизи положения
равновесия (0,0).

За
положением равновесия
системы
(1.1) сохраним те же названия, что и за
положением равновесия системы (1.2): еслиивещественны и одного знака, то положение
равновесияузел
(– устойчивый,– неустойчивый). Еслиикомплексно-сопряженные с отрицательными
(положительными) вещественными частями,
то положение равновесия–устойчивый
(неустойчивый) фокус.
Если
ивещественны и разных знаков, то положение
равновесия –седло.

Следующие
теоремы, определяют поведение траекторий
нелинейной системы (1.1) вблизи невырожденного
положения равновесия
в зависимости от типа точки покоя системы
(1.2).

Т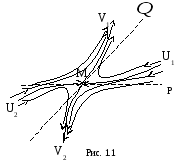еорема
1.1. Предположим,
что точка системы (1.2) является седлом.
Пусть Р – прямая, проходящая через точку
в направлении собственного вектораматрицы,
соответствующего отрицательному
собственному значению,
а Q – прямая, проходящая через точкув направлении собственного вектораматрицы,
соответствующего положительному
собственному значению,
Тогда существуют ровно две траекторииисистемы (1.1), которые приасимптотически приближаются к точке.
Эти две траектории вместе с точкой О
образуют непрерывно дифференцируемую
кривую, касающуюся прямой Р в точке.
Точно также существуют ровно две
траекториии,
которые приасимптотически приближаются к точке,
касаясь при этом прямой Q. Остальные
траектории в окрестности точкиведут себя так, как показано на рис.1. 1.

Траектории
и
–
устойчивые усы седла,траектории

и
–
неустойчивые усы седла.

Теорема
1.2. Пусть
точка
устойчивый (неустойчивый) узел, то есть.
В направлении собственного вектора,
соответствующего,
проведем через точкупрямую
Р, а в направлении собственного вектора,
соответствующего– прямую Q. Оказывается, что все траектории,
начинающиеся достаточно близко от точки,
симптотически приближаются прик точкеи имеют в этой точке касательную. При
этом только две траектории входят в
точкупо касательной к прямой Q,, а остальные
– по касательной к прямой Р (соответственно
прии)
(см. рис. 1.2).

P

Теорема
1.3.3. Пусть
точка
– фокус, то есть.
Тогда привсе траектории системы (1.1), проходящие
вблизи точки,
принаматываются на точку,
а принаматываются прина точкукак
спирали (см. рис. 1.3).

Устойчивый
фокус

Неустойчивый
фокус

Пример
1.1. Найти
особые точки системы:

(1.3)

определить
их тип. Построить схематически фазовый
портрет в окрестности каждой особой
точки.

Решение.
Для нахождения особых точек решим
систему уравнений

Итак,
особыми будут точки M₁(2,
4) и M₂(–1,–2).

Найдем
матрицу Якоби системы:
.

Для
точки M₁(2,
4) имеем
.
Для точкиM₁(-1,-2)
имеем
.

Собственные
значения матрицы– положительны, поэтому особая точкаM₁(2,
4) является точкой типа “неустойчивый
узел”.

Для
построения фазового портрета в окрестности
точки M₁(2,
4) найдем собственные векторы,
соответствующие найденным собственным
значениям матрицы А₁.
Имеем:
.
Согласно теореме 1.2, только две траектории
выходят из особой точкиM₁(2,
4) по касательной к направлению,
определяемому собственным вектором
,
а остальные выходят из нее по касательной
к направлению, определяемому вектором(рис.1.4)

Собственные
значения матрицы–
комплексно-сопряженные числа.
Поэтому состояние равновесияM₂(–1,–2)
– устойчивый фокус. Все траектории,
начинающиеся в достаточно малой
окрестности точки M₂,
спиралевидно наматываются на эту точку.

Для
определения направления закручивания
спиралей достаточно выбрать какую-либо
точку в достаточно малой окрестности
точки М₂
и найти вектор, касательный к траектории
системы в выбранной точке. Так, например,
для точки М(–1; –1,98) вектор касательной
будет таким:
.
Это означает, что спирали будут
закручиваться по ходу часовой стрелки
(рис.1.5).

Замечание
1.1. Для того,
чтобы найти особые точки уравнения
,
следует перейти к эквивалентной системе
(1.3) и рассуждать так же, как и в примере
1.1.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Точки равновесия системы дифференциальных уравнений это

МОДЕЛИ БИОЛОГИЧЕСКИХ СИСТЕМ, ОПИСЫВАЕМЫЕ

ОДНИМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЕМ ПЕРВОГО ПОРЯДКА

Модели, приводящие к одному дифференциальному уравнению. Понятие решения одного автономного дифференциального уравнения. Стационарное состояние (состояние равновесия). Устойчивость состояния равновесия. Методы оценки устойчивости. Решение линейного дифференциального уравнения Примеры: экспоненциальный рост, логистический рост.

Изучение математических моделей биологических систем начнем с систем первого порядка, которым соответствует одно дифференциальное уравнение первого порядка:

Если система автономная, то правая часть уравнений не зависит явно от времени и уравнение имеет вид:

(2.1)

Состояние таких систем в каждый момент времени характеризуется одной единственной величиной – значением переменной x в данный момент времени t.

Рассмотрим плоскость t, x. Решениями уравнения (2.1): x( t) являются кривые на плоскости t, x , называемые интегральными кривыми (рис. 2.1)

Пусть заданы начальные условия при t =0 или, иначе, пусть на плоскости t, x задана точка с координатами . Если для уравнения (2.1) выполнены условия теоремы Коши, то имеется единственное решение уравнения (2.1), удовлетворяющее этим начальным условиям, и через точку проходит одна единственная интегральная кривая x( t) .

Рис. 2.1. Интегральные кривые x ( t ); – решения уравнения f ( x ) = 0

Интегральные кривые уравнения (2.1) не могут пересекаться. Решения уравнения (2.1) не могут быть периодическими, они монотонны.

Поведение интегральных кривых на плоскости t, x можно установить, не решая в явном виде дифференциального уравнения (2.1), если известен характер движения изображающей точки на фазовой прямой.

Рассмотрим плоскость t, x , причем фазовую прямую совместим с осью x . Построим на плоскости t, x точку с абсциссой t и с ординатой, равной смещению изображающей точки по оси x в данный момент времени t. С течением времени в соответствии с уравнением (2.1) изображающая точка будет двигаться по фазовой прямой (рис. 2.2), а на плоскости t, x описывать некую кривую. Это будет интегральная кривая уравнения (2.1).

Решения одного автономного дифференциального уравнения либо уходят в бесконечность (чего не бывает в реальных системах), либо асимптотически приближаются к стационарному состоянию.

Стационарное состояние (точка покоя, особая точка, состояние равновесия)

В стационарном состоянии значения переменных в системе не меняются со временем. На языке дифференциальных уравнений это означает:

(2.2)

Если левая часть уравнения равна нулю, значит равна нулю и его правая часть:

Корни алгебраического уравнения (2.3): суть стационарные состояния дифференциального уравнения (2.1). На плоскости ( t, x) прямые – асимптоты, к которым приближаются интегральные кривые. На фазовой прямой (рис. 2.2) стационарное состояние – точка, к которой стремится величина x.

Реальные биологические системы испытывают многочисленные флуктуации, переменные при малых отклонениях возвращаются к своим стационарным значениям. Поэтому при построении модели важно знать, устойчивы ли стационарные состояния модели.

Рис. 2.3. К понятию устойчивости состояния равновесия

Устойчивость состояния равновесия

Каждый имеет интуитивное представление об устойчивости. На рис. 2.3. в обоих положениях (а и б) шарик находится в равновесии, т.к. сумма сил, действующих на него, равна нулю.

Попытайтесь ответить на вопрос : «Какое из этих состояний равновесия устойчиво?»

Скорее всего, Вы дали правильный ответ. Сказать, как Вы догадались? Вы дали шарику малое отклонение от состояния равновесия . В случае ( а) шарик вернулся. В случае ( б) покинул состояние равновесия навсегда.

Устойчивое состояние равновесия можно определить так: если при достаточно малом отклонении от положения равновесия система никогда не уйдет далеко от особой точки, то особая точка будет устойчивым состоянием равновесия, что соответствует устойчивому режиму функционирования системы.

Строгое математическое определение устойчивости состояния равновесия уравнения dx/dt = f( x) выглядит следующим образом :

Состояние равновесия устойчиво по Ляпунову, если задав сколь угодно малое положительное , всегда можно найти такое , что

для если .

Иначе говоря, для устойчивого состояния равновесия справедливо утверждение: если в момент времени отклонение от состояния равновесия мало ( ), то в любой последующий момент времени отклонение решения системы от состояния равновесия будет также мало: .

Другими словами: c тационарное состояние называется устойчивым, если малые отклонения не выводят систему слишком далеко из окрестности этого стационарного состояния. Пример — шарик в ямке (с трением или без трения).

Стационарное состояние называется асимптотически устойчивым, если малые отклонения от него со временем затухают. Пример — шарик в ямке в вязкой среде.

Стационарное состояние называется неустойчивым, если малые отклонения со временем увеличиваются. Пример: шарик на горке.

Устойчивое стационарное состояние представляет собой простейший тип аттрактора.

Аттрактором называется множество, к которому стремится изображающая точка системы с течением времени (притягивающее множество).

В нашем курсе мы рассмотрим следующие типы аттракторов:

· устойчивая точка покоя;

· предельный цикл — режим колебаний с постоянными периодом и амплитудой (начиная с размерности системы 2 );

· Области с квазистохастическим поведением траекторий в области аттрактора, например, «странный аттрактор» (начиная с размерности 3 ).

Аналитический метод исследования устойчивости стационарного состояния (метод Ляпунова). Линеаризация системы в окрестности стационарного состояния.

Метод Ляпунова приложим к широкому классу систем различной размерности, точечным системам, которые описываются обыкновенными дифференциальными уравнениями, и распределенным системам, описываемым уравнениями в частных производных, непрерывным и дискретным.

Рассмотрим метод линеаризации Ляпунова для одного автономного дифференциального уравнения первого порядка. Пусть — стационарное решение уравнения:

(2.1)

Пусть система, первоначально находившаяся в стационарном состоянии, отклонилась от него и перешла в близкую точку с координатой: , причем .

Перейдем в уравнении (2.1) от переменной x к переменной , т.е. новой переменной будет отклонение системы от стационарного состояния.

.

Учтем, что по определению стационарного состояния.

Правую часть разложим в ряд Тейлора в точке :

где

Отбросим члены порядка 2 и выше. Останется линейное уравнение:

(2.4)

которое носит название линеаризованного уравнения или уравнения первого приближения. Интеграл этого уравнения для находится сразу:

, (2.5)

где , с — произвольная постоянная.

Если SYMBOL 108 f “Symbol” s 12 l SYMBOL 60 f “Symbol” s 12 0 , то при и, следовательно, первоначальное отклонение SYMBOL 120 f “Symbol” s 12 x от состояния равновесия со временем затухает. Это означает, по определению, что состояние равновесия устойчиво.

Если же SYMBOL 108 f “Symbol” s 12 l SYMBOL 62 f “Symbol” s 12 > 0 , то при , и исходное состояние равновесия неустойчиво.

Если SYMBOL 108 f “Symbol” s 12 l =0 , то уравнение первого приближения не может дать ответа на вопрос об устойчивости состояния равновесия системы. Необходимо рассматривать члены более высокого порядка в разложении в ряд Тейлора. Такие случаи мы рассмотрим в лекции 6.

Аналогичные рассуждения проводятся при рассмотрении устойчивости стационарных состояний более сложных динамических систем.

Итак, устойчивость стационарного состояния уравнения dx/dt=f(x) определяется знаком производной правой части в стационарной точке.

В случае одного уравнения вопрос об устойчивости состояния равновесия нетрудно решить, рассматривая график функции f(x).

По определению в стационарной точке правая часть уравнения (2.1) ‑ функция f(x) обращается в нуль.

Здесь возможны три случая (рис. 2.4 а, б, в).

1. Вблизи состояния равновесия функция f(x) меняет знак с плюса на минус при возрастании x (рис. 2.4 а).

Отклоним изображающую точку системы в сторону . В этой области скорость изменения x dx/dt = f(x) положительна. Следовательно, x увеличивается, т.е. возвращается к . При скорость изменения величины x уменьшается, т.к. функция f(x) SYMBOL 60 f “Symbol” s 12 0. Следовательно, здесь x уменьшается и опять стремится к . Таким образом, отклонения от стационарного состояния в обе стороны затухают. Стационарное состояние устойчиво.

Рис. 2.4. Определение устойчивости стационарного состояния по графику функции f( x)

a – стационарное состояние устойчиво;

б, в ‑ стационарное состояние неустойчиво

2. Вблизи состояния равновесия функция f ( x) меняет знак с минуса на плюс при возрастании x ( рис. 2.4 б) .

Проведите рассуждения, аналогичные случаю 1. Поместите изображающую точку в область . Теперь в область .

В обоих случаях изображающая точка удаляется от состояния равновесия. Стационарное состояние неустойчиво.

3. Вблизи состояния равновесия функции f(x) не меняет знак ( рис 2.4 в) .

Поскольку , это означает, что изображающая точка, помещенная достаточно близко к состоянию равновесия с одной стороны, будет приближаться к нему, помещенная с другой стороны – удаляться.

Вопрос. Является ли состояние равновесия в случае 3 устойчивым?

Ответ. Нет. По определению устойчивости.

1. Рост колонии микроорганизмов

За время D t прирост численности равен:

где R – число родившихся и S – число умерших за время SYMBOL 68 f “Symbol” s 12 D t особей пропорциональные этому промежутку времени:

В дискретной форме:

.

Разделив на SYMBOL 68 f “Symbol” s 12 D t и переходя к пределу при t SYMBOL 174 f “Symbol” s 12 ® 0 , получим дифференциальное уравнение

. (2.6)

В простейшем случае, когда рождаемость и смертность пропорциональны численности:

,

(2.7)

Разделим переменные и проинтегрируем:

Переходя от логарифмов к значениям переменной x и определяя произвольную постоянную С из начальных условий, получим экспоненциальную форму динамики роста.

(2.8)

График функции (2.8) при положительных (размножение) и отрицательных (вымирание) значениях константы скорости роста представлен на рис. 2.5. Роль этой модели в развитии математической биологии и экологии мы обсудим в Лекции 3.

Рис. 2.5. Экспоненциальная форма динамики роста численности колонии микроорганизмов в соответствии с системой уравнений (2.7)

2. Вещество переходит в раствор

Пусть количество вещества, переходящего в раствор, пропорционально интервалу времени и разности между максимально возможной концентрацией Р и концентрацией x в данный момент времени: .

В форме дифференциального уравнения этот закон выглядит в

. (2.9)

Разделим в этом уравнении переменные, и проинтегрируем:

(2.10)

Здесь C ₁ — произвольная постоянная. Если x (0) = 0,

График этой функции представлен на рис. 2.6. – он представляет собой кривую с насыщением.

Рис. 2.6. Концентрация вещества х в зависимости от времени. График уравнения 2.9.

Какие дифференциальные уравнения можно решать аналитически?

Лишь для ограниченных классов дифференциальных уравнений разработаны аналитические методы решения. Подробно они изучаются в курсах дифференциальных уравнений. Отметим основные из них/

1. Уравнения с разделяющимися переменными решаются в интегралах. К ним относятся оба приведенные выше примера.

2. Линейные дифференциальные уравнения (не обязательно автономные).

3. Некоторые специальные виды уравнений.

Решение линейного уравнения

Линейным дифференциальным уравнением 1-го порядка называют уравнение, линейное относительно искомой функции и ее производной. Оно имеет вид:

. (2.11)

Здесь A, B, C — заданные непрерывные функции от t.

Пусть в некотором интервале изменения t A SYMBOL 185 f “Symbol” s 12 _ 0 . Тогда на него можно разделить все члены уравнения. При этом получим:

. (2.12)

Eсли Q=0 , уравнение (2.12) называется однородным, если Q SYMBOL 185 f “Symbol” s 12 _ 0 – неоднородным.

Решим сначала однородное уравнение.

.

Общее решение линейного однородного уравнения имеет вид:

. (2.13)

Чтобы найти решение неоднородного уравнения применим метод вариации постоянной. Будем считать С неизвестной функцией t . Подставляя правую часть выражения (2.13) в уравнение (2.12), имеем:

Теперь С находим интегрированием: . Здесь С₁ – произвольная постоянная.

Итак, общее решение линейного неоднородного уравнения первого порядка:

(2.14)

Таким образом, решение уравнения (2.12) представляет собой сумму двух слагаемых:

1) общее решение однородного уравнения (2.13) и

2) частное решение неоднородного уравнения, которое получается из общего решения, если С₁ = 0.

Рассмотрим еще один пример, который относится к классическим моделям математической экологии. Логистическое уравнение было предложено Ферхюльстом в 1838 г. Оно имеет вид:

. (2.15)

Это уравнение обладает двумя важными свойствами. При малых х численность х возрастает, при больших – приближается к определенному пределу К .

Уравнение (2.15) можно решить аналитически. Ход решения следующий. Произведем разделение переменных:

. (2.16)

Представим левую часть в виде суммы и проинтегрируем

Переходя от логарифмов к переменным, получим:

(2.17)

Здесь С – произвольная постоянная, которая определяется начальным значением численности x₀ :

; .

Подставим это значение С в формулу (2.17):

.

Отсюда получим решение – зависимость численности от времени:

. (2.18)

График функции (2.18) при разных начальных значениях численности популяции представлен на рис. 2.7.

Рис.2.7. Динамика численности в логистической модели 2.18

при разных начальных значениях численности

Если начальное значение х₀ К/2, кривая роста имеет точку перегиба. Если х₀ > К, численность со временем убывает.

В приведенных примерах в правой части уравнений стоят полиномы первой и второй степени. Если в правой части ‑ более сложная нелинейная функция, алгебраическое уравнение для стационарных значений может иметь несколько корней. Какое из этих решений реализуется в этом случае, будет зависеть от начальных условий.

В дальнейшем мы, как правило, не будем искать аналитическое решение для наших моделей. Для более сложных нелинейных уравнений это и невозможно. Однако важные заключения относительно свойств моделей можно сделать и на основании качественного их исследования, в первую очередь путем исследования устойчивости стационарных состояний и типов поведения системы вблизи этих состояний. При этом следует иметь в виду, что с помощью одного автономного дифференциального уравнения могут быть описаны только монотонные изменения переменной, и, следовательно, ни периодические, ни хаотические процессы не могут быть описаны. Для описания более сложного поведения необходимо либо переходить к системам большей размерности (2, 3 порядка и выше), либо вводить время в явном виде в правую часть уравнения. В Лекции 3 мы увидим, что дискретные уравнения и уравнения с запаздыванием могут описать и колебания, и динамический хаос.

Точки равновесия системы дифференциальных уравнений это

Рассмотрим автономную систему второго порядка:

Название автономная система оправдано тем, что решение само управляет своим изменением, поскольку производные dx₁ /dt и dx₂ /dt зависят только от x₁ и x₂ и не зависят от t.

Обозначим
и .
Пусть — решение автономной системы второго порядка. Тогда уравнения

задают в параметрической форме кривую на плоскости . Эта кривая называется фазовой кривой или фазовой траекторией системы.Плоскость, на которой расположены фазовые траектории называется фазовой плоскостью автономной системы.

Точка , в которой правая часть системы обращается в нуль, , называется положением равновесия системы. Положение равновесия называют также точкой покоя автономной системы.

Точка покоя называется устойчивой по Ляпунову, если:
1) существует такое , что для при существует решение задачи Коши с начальным условиям ;
2) для всякого существует такое , что если и , то при всех .
Устойчивая точка покоя называется асимптотически устойчивой, если
при достаточно малых .

Очевидно, что линейная автономная система

имеет единственную точку покоя: x₁(t) = 0, x₂(t) = 0, при всех . При этом характер точки покоя (0, 0) (ее устойчивость, асимптотическую устойчивость, неустойчивость) можно установить по значениям собственных чисел l₁ и l₂ матрицы системы.
А именно, пусть l₁ и l₂ — собственные значения матрицыA исследуемой системы:

• если l₁ и l₂— действительные отрицательные числа, то точка покоя устойчива и называется устойчивым узлом (пример 1);
• если l₁ и l₂ — действительные положительные числа, то точка покоя неустойчива и называется неустойчивым узлом (пример 2);
• если l₁ и l₂ — действительные числа, имеющие разные знаки, то точка покоя неустойчива и называется седлом (пример 3);
• если l₁ и l₂ — комплексные числа, l_1,2 =Rell ± Imll и Rel не превышает нуля, то точка покоя устойчива, точнее, при Rel =0 точка устойчива, но не асимптотически устойчива и называется центром (пример 4), при Rel 0, то точка покоя неустойчива и называется неустойчивым фокусом (пример 6);
• если l₁ = l₂ – отличные от нуля действительные числа, то точка покоя — узел специального вида, называемый диакритическим, устойчивым при отрицательных l₁ = l₂ и неустойчивым при положительных l₁ = l₂ (пример 7);
• если l₁ = 0 и l₂ № 0, то существует прямая, проходящая через начало координат, все точки которой являются точками покоя (пример 8);
• если l₁ = l₂ = 0, то все точки плоскости являются точками покоя.

ПРИМЕР 1. Поведение решений в окрестности устойчивого узла.

ПРИМЕР 2. Поведение решений в окрестности неустойчивого узла.

ПРИМЕР 3. Поведение решений в окрестности седла.

ПРИМЕР 4. Поведение решений в окрестности центра.

ПРИМЕР 5. Поведение решений в окрестности устойчивого фокуса.

ПРИМЕР 6. Поведение решений в окрестности неустойчивого фокуса.

ПРИМЕР 7. Поведение решений в окрестности диакритического узла.

ПРИМЕР 8. Вырожденный случай. Прямая, состоящая из точек покоя.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Digiratory

Лаборатория автоматизации и цифровой обработки сигналов

Устойчивость нелинейных систем

Анализ устойчивости систем является одним из важнейших этапов проектирования систем управления, однако при анализе нелинейных, строго говоря, нет метода отвечающего критериям необходимости и достаточности, а критерии являются, как правило только достаточным (для устойчивости). Исходя из этого, для некоторых систем невозможно однозначно говорить о неустойчивости.

В классической теории управления имеется два основных аналитических метода: первый и второй методы Ляпунова, а также достаточно большое количество модификаций второго метода, как не связанного с линеаризацией.

Рассмотрим применение классических методов Ляпунова.

Первый метод Ляпунова

Позволяет судить об устойчивости положения равновесия по линеаризованным уравнениям. Метод основан на утверждениях:

• если собственные значения линеаризованной системы имеют отрицательные действительные части (линеаризованная система асимптотически устойчива), то положение равновесия нелинейной системы устойчиво «в малом»;
• если среди собственных значений линеаризованной системы имеются «правые», то положение равновесия нелинейной системы неустойчиво;
• если имеются некратные собственные значения на мнимой оси, а остальные — «левые», то в этом критическом случае по линеаризованной модели нельзя судить об устойчивости положения равновесия нелинейной системы.

Таким образом для анализа системы по первому методу Ляпунова необходимо:

1. Найти положение равновесия системы — движений в системе нет (т.е. скорости и ускорения равны нулю) [ frac <mathrmv_><mathrmt>= <0>]
2. Линеаризовать систему в окрестности точки равновесия
3. Записать полученное линеаризованное дифференциальное уравнение в матричной форме (составить матрицу А)
4. Составить характеристический полином линеаризованной системы: [ = ]
5. Найти корни характеристического полинома. По виду корней сделать заключение о характере процессов в системе.

Основными недостатками первого метода Ляпунова являются:

• Если имеется корень на мнимой оси, то невозможно сказать о поведении процессов в системе.
• Возможно говорить только об устойчивости «в малом», т.е. при больших отклонениях от положения равновесия система может быть неустойчивой.

Пример 1.

Исследуем систему описываемую дифференциальными уравнениями:

Шаг 1. Положение равновесия:

Для нахождения точек равновесия левые части уравнений приравниваются к 0, что эквивалентно тому, что переменные состояния являются константами, а все их производные равны 0.

Шаг 2. Линеаризация для малых отклонений

Для линеаризации малых отклонений в точке равновесия старшие степени переменных, входящих в уравнения принимаются равными нулю.

Шаг 3. Линеаризованное управление в матричной форме

Преобразуем полученную линейную систему уравнений в матричный вид.

Шаг 4. Характеристический полином

Шаг 5. Корни характеристического полинома

Приравниваем характеристический полином к 0 и находим корни уравнения.

Заключение об устойчивости системы

в данном примере при линеаризации система имеет два корня с отрицательной вещественной частью, т.е. мы можем сказать, что система устойчива «в малом» (при больших отклонениях система может быть неустойчива).

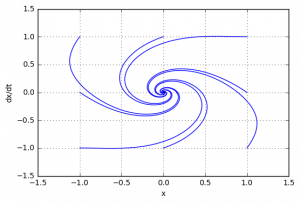
Подтвердим теоретический вывод компьютерным моделированием (построением фазового портрета)

При этом, при начальных условиях, находящиеся дальше от точки равновесия, система становится неустойчивой

Пример 2. Нелинейный осциллятор

В качестве второго примера рассмотрим нелинейный осцилятор описываемый системой дифференциальных уравнений:

Аналогично первому примеру выполняем последовательность шагов

Шаг 1. Положение равновесия:

Шаг 2. Линеаризация для малых отклонений

Шаг 3. Линеаризованное управление в матричной форме

Шаг 4. Характеристический полином

Шаг 5. Корни характеристического полинома

Заключение об устойчивости системы

Рассматриваемая система является критическим случаем о ее устойчивости невозможно судить по линеаризованным уравнениям, применяемым в первом методе Ляпунова.

Второй метод Ляпунова

Второй метод Ляпунова не связан с линеаризацией системы, поэтому также называется прямым методом.

Для начала необходимо ввести понятия знакоопределенной, знакопостоянной и знакопеременной функций. Пусть имеется функция нескольких переменных:

Функция (V ) называется знакоопределенной в некоторой области, если она во всех точках этой области вокруг начала координат сохраняет один и тот же знак и нигде не обращается в нуль, кроме только самого начала координат

[ left ( Vleft ( bar <0>right )=0 right ) ]

Функция (V ) называется знакопостоянной, если она сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках данной области.

Функция (V ) называется знакопеременной, если она в данной области вокруг начала координат может иметь разные знаки.

Теорема Ляпунова об устойчивости нелинейных систем

Если при заданных в форме

уравнениях системы n-го порядка можно подобрать такую знакоопределенную функцию Ляпунова

чтобы ее производная по времени

тоже была знакоопределенной (или знакопостоянной), но имела знак противоположный знаку (V), то данная система устойчива.

Для упрощения скажем, что функция Ляпунова должна быть положительной знакоопределенной функцией. Тогда условия теоремы Ляпунова будут выглядеть следующим образом:

Для устойчивости положения равновесия достаточно существования дифференцируемой функции

называемой функцией Ляпунова, удовлетворяющей в окрестности начала координат следующим условиям:

1. (Vleft ( v_<1>, v_<2>,…, v_right ) geq 0) причем (V=0) лишь при следующем условии, означающем что функция (V) имеет строгий минимум в начале координат. [ bar= begin v_ <1>\ vdots \ v_ end = bar <0>]
2. Производная функции по времени [ frac <mathrmVleft ( bar right )><mathrmt>=sum_^frac<partial V><partial v_>frac <mathrmv_><mathrmt>=begin frac<partial V><partial v_<1>> & frac<partial V><partial v_<2>> & cdots & frac<partial V><partial v_>endbeginfrac <mathrmv_<1>><mathrmt>\ frac <mathrmv_<2>><mathrmt>\ vdots \ frac <mathrmv_><mathrmt>end ] в силу дифференциального уравнения (frac <mathrmbar><mathrmt>=bar<varphi >left ( bar right ) ) является отрицательной знакопостоянной функцией, т.е. [ frac <mathrmVleft ( bar right )><mathrmt>=gradbarcdot frac <mathrmbar><mathrmt>=gradbarcdot bar<varphi>left ( bar right )leq 0 ] при (tgeq t_<0>)

Таким образом, условия:

1. (frac <mathrmVleft ( bar right )><mathrmt>leq 0) и функция (Vleft ( v_<1>, v_<2>,…, v_right ) ) является положительной знакоопределенной — это является достаточным условием устойчивости
2. (frac <mathrmVleft ( bar right )><mathrmt> ) — отрицательно определенная — это является достаточным условием асимптотической устойчивости.
3. (left | v right |rightarrow infty : frac <mathrmVleft ( bar right )><mathrmt>rightarrow infty ) — достаточное условие устойчивости «в целом».

Для анализа системы по второму методу Ляпунова необходимо:

1. Выбрать функцию Ляпунова от n переменных, где n- порядок системы.
2. Найти частные производные по переменным.
3. Вычислить производную функции по времени (frac <mathrmVleft ( bar right )><mathrmt>). Проанализировать полученный знак производной.

Из-за того, что второй метод Ляпунова не связан с линеаризацией, он считается универсальным. Однако он имеет ряд недостатков:

• Нет общих требований по выбору функции V
• Достаточный характер утверждения (если условия не выполняются, то об устойчивости ничего сказать нельзя, а можно посоветовать подобрать другую функцию (V ))

Пример 3. Нелинейный осциллятор

Проанализируем систему из примера (2).

Шаг 1. Функция Ляпунова

Для начала необходимо выбрать функцию Ляпунова от 2-х переменных (т.к. два вектора состояния):

Шаг 2. Частные производные

Шаг 3. Производная функции

Подставим в выражение значения исходя из ДУ:

Заключение об устойчивости системы

Исследовав систему первым методом Ляпунова мы не смогли сделать конкретный вывод об устойчивости системы, что позволил нам сделать второй метод Ляпунова. В результате мы можем сделать вывод, что система является асимптотически устойчивой.

Аналогично проверим с помощью моделирования:

Пример 4.

Рассмотрим систему, описываемую следующей системой дифференциальных уравнений:

Очевидно, что применение первого метода Ляпунова невозможно, т.к. матрица А состоит из нулей, а, следовательно, собственные значения равны нулю. Поэтому применим второй метод Ляпунова:

Шаг 1. Функция Ляпунова

Выбор функции Ляпунова второго порядка

Шаг 2. Частные производные

Шаг 3. Производная функции

При (a=3) имеет место асимптотическая устойчивость.

Заключение об устойчивости системы

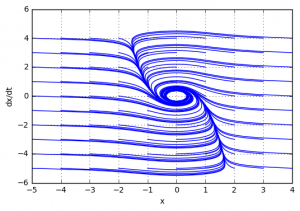
Система является устойчивой.

Фазовый портрет системы выглядит следующим образом:

[spoiler title=”источники:”]

http://old.exponenta.ru/EDUCAT/class/courses/ode/theme13/theory.asp

Устойчивость нелинейных систем

[/spoiler]

Чтобы найти положения равновесия, приравниваем производные к нулю. Получается $%y_2=y_1^2$% и $%y_1^2-y_1-2=0$%; корни $%2$% и $%-1$%. Положений равновесия получается два: $%(2;4)$% и $%(-1;1)$%. Исследуем их на устойчивость.

1) Делая замену $%z_1=y_1-2$% и $%z_2=y_2-4$%, линеаризуем систему вблизи нуля: $%z_1’=-(z_1+2)^2+(z_2+4)approx-4z_1+z_2$% и $%z_2’=lnfrac3{1-(z_1+2)+(z_1+2)^2)}=lnfrac3{3+3z_1+z_1^2}approx-z_1$% с точностью до бесконечно малых второго порядка. Матрица линеаризованной системы имеет вид $$begin{pmatrix}
-4 & 1 \
-1 & 0
end{pmatrix}.$$ Характеристическое уравнение имеет вид $%lambda^2+4lambda+1=0$%. Корни $%lambda=-2pmsqrt3$% вещественны и отрицательны. Это устойчивый узел.

2) Здесь $%z_1=y_1+1$%, $%z_2=y_2-1$%; после выделения линейных членов получается $%z_1’approx2z_1+z_2$%; $%z_2’approx z_1$%. Матрица равна $$begin{pmatrix}
2 & 1 \
1 & 0
end{pmatrix}.$$ Характеристическое уравнение имеет вид $%lambda^2-2lambda-1=0$%. Корни $%lambda=1pmsqrt2$% вещественны и имеют разные знаки. Это седло; положение равновесия неустойчивое.