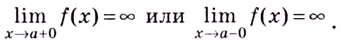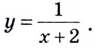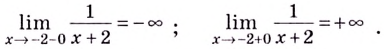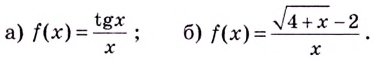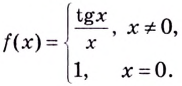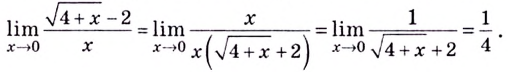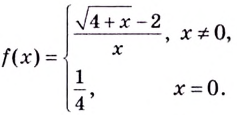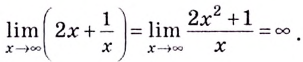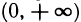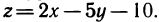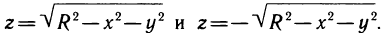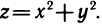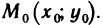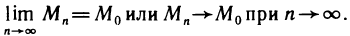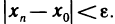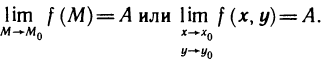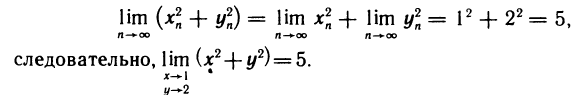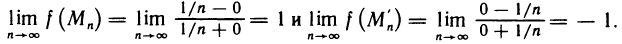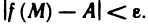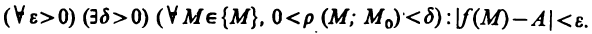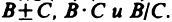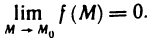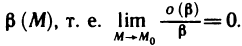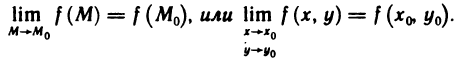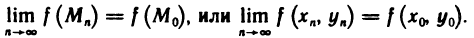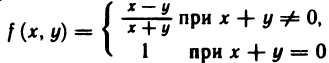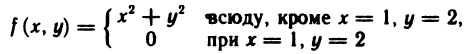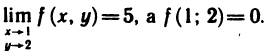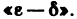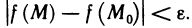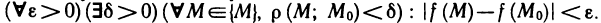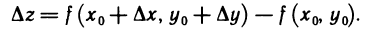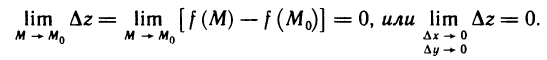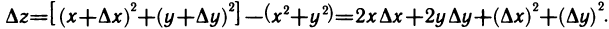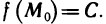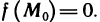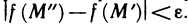Нахождение точек разрыва функции является одним из обязательных моментов исследования на непрерывность. Для кого-то это может прозвучать непонятно, а для остальных будет слишком банально.
Но и тем, и другим не стоит делать поспешные выводы: материал этой темы действительно предельно прост, но вместе с тем для успешного решения практических задач потребуется осмыслить и запомнить несколько технических приемов и нюансов.
Как минимум необходимо понимать, что за «зверь» кроется под понятием предела функции. И конечно же, нужно уметь их решать. Не менее полезным станет понимание геометрического смысла, дополненное графиком — большинство задач подобного характера требуют построения чертежа после решения.
Определение точки разрыва
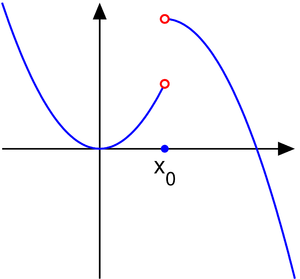
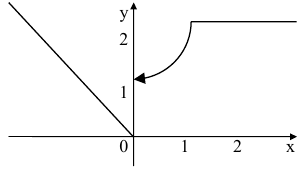
Как уже упоминалось, их поиск напрямую связан с темой непрерывности. Если говорить простым языком, то это не что иное, как координаты графика функции, в которых точки не соединяются между собой. Образуются «рваные области», которые и называют местом разрыва. Вообще, чтобы понять смысл, достаточно всего лишь взглянуть на рисунок:
Он более чем очевидно иллюстрирует определение понятия. Если функция прерывается в X0, то непрерывность в этом месте нарушена одним из двух возможных способов:
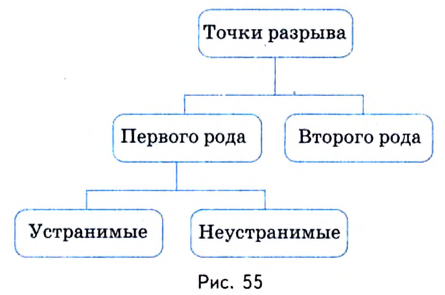
- первый род;
- второй род.
Задачи похожего типа, где необходимо находить точки разрыва, могут выступать не только, как один из этапов полного исследования на непрерывность, но и в качестве самостоятельных заданий. Чтобы определить их вид, потребуется отыскать предел для найденных значений. Поэтому, если вы еще не умеете их решать, самое время ненадолго отвлечься, чтобы изучить базовые основы.
К счастью, на практике это не так сложно — самый трудный этап заключается в приведении примера к одному из табличных. Остальные моменты легко запомнить. Не стоит забывать и о большом количестве сервисов, которые в несколько кликов выдадут значение предела любой сложности онлайн.
Классификация точек разрыва.
Точки разрыва первого и второго рода
Если функция не определена, но односторонние пределы имеют конечное значение, то ее относят к случаю первого рода. Который, в свою очередь, может иметь характеристику устранимого или конечного:
- Точки устранимого разрыва функции. Значения вычислений обоих пределов для них равны. Но также имеется возможность «исправить ситуацию»: нахождения между двумя координатами такой, левый и правый пределы которой будут одинаковы, а сама она — соединит «порванный» участок, сделав график непрерывным.
-
Точки конечного разрыва первого рода — скачок функции. Пределы могут быть вычислены, но в то же время не равны друг другу, и поэтому доопределение уравнения невозможно. Разница первого и второго называется скачком.
- Точки разрыва второго рода отличаются тем, что вычисляемые пределы не просто различны по значению, но результат хотя бы одного из них обязательно должен быть равен бесконечности или несуществующему числу.
Как найти точки разрыва функции
Если в условиях задачи не были даны координаты проверяемого отрезка, то процесс решения делится на несколько этапов. Для начала нужно найти область определенных значений, с которой в дальнейшем пойдет работа. После это вычисляются односторонние пределы функции. Полученные результаты необходимо будет сравнить, чтобы однозначно определить род и характеристику разрыва.
Рассмотрим более подробно каждый из этих моментов на примере нахождения нужных нам точек у конкретного примера f (y)=(y² – 25)/(y – 5):
- Областью определения называют множество значений, в котором существует функция. Здесь не нужны никакие сложные вычисления, достаточно взять лишь знаменатель. Если y=5, то он будет (5−5)=0 и, как всем известно, делить на него нельзя. Таким образом, получаем область допустимых y ∈ (-∞; 5) ∪ (5; +∞) и предполагаем, что наша y = 5 является точкой разрыва.
- Вычисление односторонних пределов. Это самая сложная для учеников часть, т. к. пределы не всегда бывают удобными для вычисления, да не все на них «собаку съели». Но в этом случае функцию можно значительно упростить еще до начала вычисления: f (y) = (y ²-25)/(y — 5) = ((y-5)(y+5)) /(y — 5) = y+5. Никогда не пренебрегайте такой возможностью, если она есть. Заметим, что новая функция непрерывна при любом численном значении, т. ч. по всем математическим правилам пределы будут равны: lim (y + 5) = 5 + 5 = 10.
- Проверяя совпадение результатов, мы выяснили, что левый и правый предел функции в точке y=5 одинаковые. Но вместе с тем функция f(y) не может быть определена в этой координате, иначе ее знаменатель обращается в ноль, что невозможно по условиям. Следовательно, она действительно является разрывом, а именно: устранимым и первого рода.
Видео
Из этого видео вы узнаете, как исследовать непрерывность функции.
Непрерывность функций нескольких переменных
Понятие непрерывности функции нескольких
переменных можно определить с помощью
предела.
Определение.Функцияназывается непрерывной в точке
,
если выполнены следующие три условия:
1)
определена в точке
и некоторой ее окрестности;
2) существует
;
3)
=
.
Если в точке
одно из указанных трех условий не
выполняется, то она является точкой
разрыва функции.
Для функции
двух независимых переменных точки
разрыва могут быть изолированными или
образовывать линию разрыва. Для функциитрех независимых переменных точки
разрыва могут быть изолированными,
образовывать линию или поверхность
разрыва.
Определение.Функцияназывается непрерывной на множестве
D, если она непрерывна в каждой точке
этого множества.
Пример.Найти точки разрыва функции
.
Решение.Данная функция определена
на R2всюду, кроме точки,
которая и является точкой разрыва
функции.
Пример.Найти точки разрыва функции
.
Решение.Данная функция определена
для любых,
таких, что.
Следовательно, прямаяявляется линией разрыва функции.
Пример.Найти точки разрыва функции
.
Решение.Функция
определена для любых
,
таких, что.
Следовательно, сфера с центром в
начале координат и радиусомR=3
является поверхностью разрыва функции.
Дифференцирование функций нескольких переменных
Частные и полные приращения функции
Пусть
— функция двух независимых переменных
и D—
область ее определения. Выберем
произвольную точкуD
и дадим
приращение
,
а значениеоставим неизменным. При этом функция
получит приращение
,
которое называется частным приращением
функции
по переменной
в точке
.
Аналогично, считая
постоянной и придавая
приращение
,
получаем частное приращение функциипо переменной
в точке
:
.
Полным приращением функции
в точке
называют разность
.
Замечание.В общем случае полное
приращение не равно сумме частных
приращений, т.е..
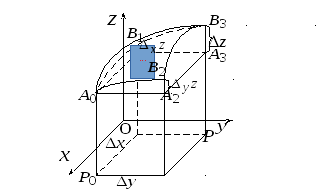
Геометрически частные и полное приращения
функции
можно изобразить отрезками
.
Пример.Найти частные и полное
приращения функциив точке
,
если=
0,2,=
0,3.
Решение.По определению найдем
частные приращения:
,
.
Найдем полное приращение функции:
.
При
=1,
=2,
=0,2,
=0,3
:
= 0,22 = 0,4,
=10,3 = 0,3,
0,4 + 0,3 +0,20,3 = 0,76,
=0,4 + 0,3 = 0,7,
0,70,76,
т.е. мы получили, что при таких условиях
.
Аналогично определяют частные и полное
приращения функции nпеременных.
Частные производные
Определение. Частной производной
функциипо переменной
в точке
называется предел отношения частного
приращения функциик соответствующему приращению аргумента
,
когда последнее произвольным образом
стремится к нулю, т.е.
.
Используются также и другие обозначения
частных производных:
,
,
.
Аналогично определяют и частную
производную функции
в точке
по переменной
:
.
Таким образом, частная производная
функции нескольких переменных определяется
как производная функции одной переменной
при фиксированных значениях остальных
переменных.
Пример. Найти частные производные
функции.
Решение. Частную производную функциивычисляем как производную данной функции
по переменной,
считаяпостоянной:
.
Аналогично.
Пример. Найти частные производные
функции.
Решение. Частную производную функциивычисляем как производную данной функции
по переменной,
считаяи
постоянными:
.
Аналогично
и
.
Геометрический смысл частных производных
функции двух переменных. Пусть графиком
функцииявляется некоторая поверхностьQ.
Возьмем точкуD
.
На этой поверхности ей соответствует
точка.
Пересечем график данной функции
плоскостью.
В сечении получим кривую(
на рисунке это кривая),
которую можно рассматривать как график
функции одной переменнойв плоскости
.
Тогда, согласно геометрическому смыслу
производной функции одной переменной,
значение частной производной
функции
в точке
равно тангенсу угла α, образованного
положительным направлением оси Ох и
касательной, проведенной в точкек линии пересечения поверхности
и плоскости
.
Аналогично трактуется и геометрический
смысл частной производной функции
по
.
Механический смысл частных производных
функции двух переменных. Частные
производныеи
характеризуют скорость изменения
функциив данной точке
,
причем частная производнаязадает скорость изменения функции в
направлении прямой,
частная производная― в направлении прямой
.
Соседние файлы в предмете Высшая математика
- #
- #
- #
- #
- #
Содержание:
Точки разрыва и их классификация
Непрерывность или разрыв функции может зависеть от конкретных условий, в которых рассматривается задача. Рассмотрим, например, численность населения земного шара как функцию времени. Она увеличивается на 1 в момент рождения каждого человека и уменьшается на 1 в момент смерти. Но рождения и смерти следуют друг за другом через бесконечно малые интервалы времени и изменение численности населения планеты на 1 настолько мало его меняет, что практически функцию можно рассматривать непрерывной. По стоит перейти от численности населения земного шара к численности населения одной квартиры, как рождение или смерть отдельного ее жителя будут так заметно менять ее численность, что функцию нельзя будет рассматривать как непрерывную.
Если хотя бы одно из условий определения непрерывности функции в точке (см. п. 3.1) не выполнено, то в данной точке функция терпит разрыв. Различают три вида точек разрыва непрерывной функции.
1. Точка
Чтобы устранить разрыв в точке 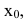
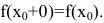
2. Точка 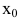
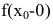
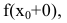
При этом величина 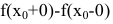
3. Если хотя бы один из односторонних пределов 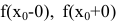
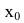
Пример №32
Исследовать функции на непрерывность. В случае устранимого разрыва доопределить функцию до непрерывной.
Решение:
1. Данная функция элементарная, т.к. получена с помощью конечного числа арифметических действий над основными элементарными функциями: экспоненциальной, постоянной и степенной. Следовательно, она непрерывна в области определения 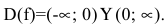
не определена и поэтому разрывна. Исследуем характер точки разрыва. Так как 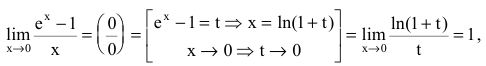
Если положить f(0)=0, то функция 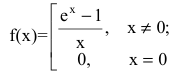
2. Функция 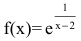
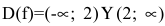
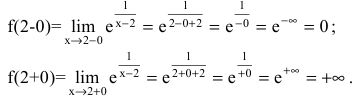
Пример №33
Исследовать функцию на непрерывность. Построить схематично график функции.
Решение:
Область определения этой функции – вся числовая прямая: 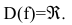
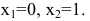
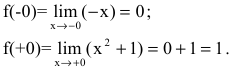
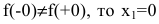
Исследуем точку
Поскольку 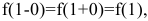
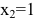
Построим график функции.
——
Точки разрыва и их классификация
Точка, в которой функция не является непрерывной, называется точкой разрыва функции, а сама функция называется разрывной в этой точке.
Точка 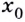
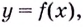
- функция в точке
не определена;
- не существует предела функции в точке
или он равен бесконечности;
- предел функции в точке
не совпадает со значением функции в этой точке.
Различают два вида точек разрыва — первого рода и второго рода (рис.55).
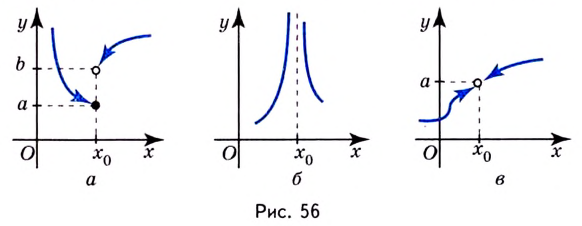
Исследуя точки разрыва, используют односторонние пределы. Это означает, что рассматривают поведение функции для значений 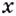
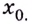
Обозначают:
Точку 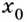
Точку 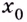
Если левосторонний и правосторонний пределы в точке 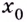
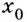
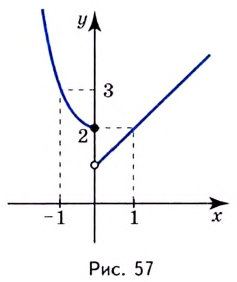
Пример №522
Найдите точки разрыва функции 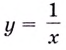
Решение:
Поскольку на ноль делить нельзя, то точкой разрыва данной функции является 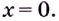
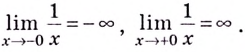
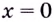
Пример №523
Исследуйте функцию 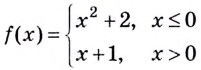
Решение:
На каждом из интервалов 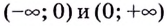
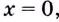
Если 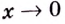
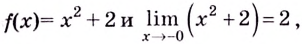
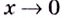
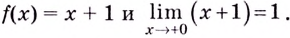
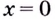
Односторонние пределы используют для нахождения вертикальных асимптот кривых.
Прямая 
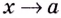
Например, ось 
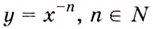
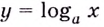
- Заказать решение задач по высшей математике
Пример №524
Найдите вертикальные асимптоты кривой
Решение:
Поскольку функция не определена в точке 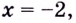
Следовательно, 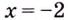
Замечание: Если 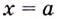
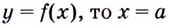
Пример №525
Исследуйте заданные функции на непрерывность и выясните характер их точек разрыва:
Решение:
Заданные в условии функции элементарные, а потому непрерывные в каждой точке области определения, а именно на множестве
а) Функция 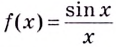
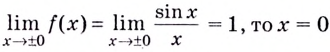
б) Функция 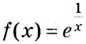

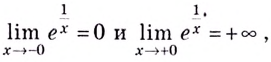
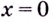
Пример №526
Заданные функции до определить в точке 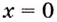
Решение:
а) Имеем 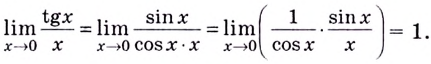
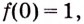
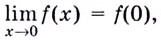

б) Вычислим предел заданной функции в точке 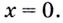
Если теперь за значение функции в точке 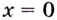
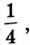
Итак,
Пример №527
Имеет ли уравнение 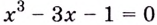
Рассмотрим функцию 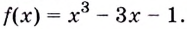
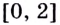
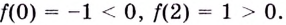
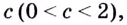
Пример №528
Имеет ли горизонтальные и вертикальные асимптоты кривая
Решение:
1) Найдём вертикальные асимптоты. Заданная функция не определена в точке 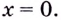
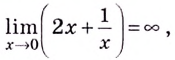

Горизонтальных асимптот нет.
- Дифференциальное исчисление
- Исследование функций с помощью производных
- Формула Тейлора и ее применение
- Интегрирование рациональных дробей
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
- Непрерывность функций и точки разрыва
Содержание:
- Определение точки разрыва
- Точка разрыва первого рода
- Точка разрыва второго рода
- Точка устранимого разрыва
- Примеры решения задач
Определение точки разрыва
Определение
Точка $a$, в которой нарушено хотя бы одно
из трех условий непрерывности функции, а именно:
- функция $f(x)$ определена в точке и ее окрестности;
- существует конечный предел функции $f(x)$
в точке $a$; - это предел равен значению функции в точке $a$,
т.е. $lim _{x rightarrow a} f(x)=f(a)$
называется точкой разрыва функции.
Пример
Функция $y=sqrt{x}$ не определена в точке
$x=-1$, а значит, эта точка является точкой
разрыва указанной функции.
Точка разрыва первого рода
Определение
Если в точке $a$ существуют конечные
пределы $f(a-0)$ и
$f(a+0)$, такие, что
$f(a-0) neq f(a+0)$, то точка
$a$ называется точкой разрыва первого рода.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Функция $f(x)=left{begin{array}{l}{0, x>1} \ {1, x leq 1}end{array}right.$ в точке
$x=1$ имеет разрыв первого рода, так как
$f(1-0)=1$, а
$f(1+0)=0$
Точка разрыва второго рода
Определение
Если хотя б один из пределов $f(a-0)$ или
$f(a+0)$ не существует или равен бесконечности, то
точка $a$ называется точкой разрыва второго рода.
Пример
Для функции $y=frac{1}{x}$ точка
$x=0$ – точка разрыва второго рода, так как
$f(0-0)=-infty$ .
Точка устранимого разрыва
Определение
Если существуют
левый и правый пределы функции в точке и они равны друг другу, но не совпадают со значением
функции $f(x)$ в точке
$a$:
$f(a) neq f(a-0)=f(a+0)$ или функция
$f(x)$ не определена в точке
$a$, то точка
$a$ называется точкой устранимого разрыва.
Пример
Рассмотрим функцию $f(x)=left{begin{array}{l}{3 x+1, x lt 0} \ {1-4 x, x>0} \ {e^{2}, x=0}end{array}right.$ .
Найдем односторонние пределы и значение функции в точке $x=0$:
$f(0)=e^{2}$
$f(0-0)=lim _{x rightarrow 0-} f(x)=lim _{x rightarrow 0-}(3 x+1)=1$
$f(0+0)=lim _{x rightarrow 0+} f(x)=lim _{x rightarrow 0+}(1-4 x)=1$
Так как $f(0-0)=f(0+0)$ и не равны значению функции в
точке, то точка $x=0$ – точка устранимого разрыва.
Примеры решения задач
Пример
Задание. Исследовать функцию $f(x)=left{begin{array}{l}{x^{2}, x lt 1} \ {(x-1)^{2}, 1 leq x leq 2} \ {3-x, x>2}end{array}right.$ на непрерывность.
Решение. Рассматриваемая функция определена и
непрерывна на промежутках
$(-infty ; 1)$,
$(1 ; 2)$ и
$(2 ;+infty)$, на которых она задана непрерывными
элементарными функциями $y_{1}(x)=x^{2}$,
$y_{2}(x)=(x-1)^{2}$ и
$y_{3}(x)=3-x$ соответственно. А тогда, разрыв возможен
только на концах указанных промежутков, то есть в точках
$x=1$ и
$x=2$ .
Найдем односторонние пределы и значение функции в каждой из точек.
1) Рассмотрим точку $x=1$ . Для нее
$f(1)=left.(x-1)^{2}right|_{x=1}=0$
$f(1-0)=lim _{x rightarrow 1-} f(x)=lim _{x rightarrow 1-} y_{1}(x)=lim _{x rightarrow 1-} x^{2}=1$
$f(1+0)=lim _{x rightarrow 1+} f(x)=lim _{x rightarrow 1+} y_{2}(x)=lim _{x rightarrow 1+}(x-1)^{2}=0$
Так как $f(1-0) neq f(1+0)$ , то в точке
$x=1$ функция терпит разрыв первого рода.
2) Для точки $x=2$ имеем:
$f(2)=left.(x-1)^{2}right|_{x=2}=1$
$f(2-0)=lim _{x rightarrow 2-} f(x)=lim _{x rightarrow 2-} y_{2}(x)=lim _{x rightarrow 2-}(x-1)^{2}=1$
$f(2+0)=lim _{x rightarrow 2+} f(x)=lim _{x rightarrow 2+} y_{3}(x)=lim _{x rightarrow 2+}(3-x)=1$
Так как односторонние пределы и значение функции в этой точке равны, то это означает, что в точке
$x=2$ функция непрерывна.
Ответ. В точке $x=1$ функция
терпит разрыв первого рода, а в точке $x=2$ непрерывна.
Пример
Задание. Исследовать функцию $y=e^{frac{1}{x-1}}$
на непрерывность в точках $x_{1}=1$ и
$x_{2}=0$ .
Решение. 1) Исследуем функцию на
непрерывность в точке
$x_{1}=1$:
$f(1-0)=lim _{x rightarrow 1-} e^{frac{1}{x-1}}=e^{-infty}=0$
$f(1+0)=lim _{x rightarrow 1+} e^{frac{1}{x-1}}=e^{+infty}=infty$
Так как один из односторонних пределов бесконечен, то точка $x_{1}=1$
– точка разрыва второго рода.
2) Для точки $x_{2}=0$ получаем:
$f(0-0)=lim _{x rightarrow 0-} e^{frac{1}{x-1}}=e^{-1}=frac{1}{e}$
$f(0+0)=lim _{x rightarrow 0+} e^{frac{1}{x-1}}=e^{-1}=frac{1}{e}$
и значение функции в точке
$f(0)=e^{frac{1}{x-1}}=frac{1}{e}$
Таким образом, в точке $x_{2}=0$ заданная
функция является непрерывной.
Ответ. $x_{1}=1$
– точка разрыва второго рода, а в точке $x_{2}=0$
функция непрерывна.
Читать дальше: основные теоремы о непрерывности функций.
До сих пор мы рассматривали функции одной переменной, т. е. функции, значения которых зависят от значений одной независимой переменной.
При рассмотрении многих вопросов естествознания приходится иметь дело с такими зависимостями между переменными величинами, в которых числовые значения одной из них полностью определяются значениями нескольких других. Так, например, температура тела в данный момент времени t может изменяться от точки к точке. Каждая точка тела определяется тремя координатами х, у и z, поэтому температура зависит от трех переменных х, у и z, а если еще учитывать зависимость температуры от времени t, то значения ее будут уже определяться значениями четырех переменных х, у, z и t. Площадь прямоугольника со сторонами, длины которых равны хну, определяется значениями двух переменных х и у, а объем прямоугольного параллелепипеда с ребрами, длины которых равны х, у, z, — значениями трех переменных х, у и z. Примеров таких зависимостей можно привести сколько угодно.
Эта часть курса и посвящается рассмотрению такого рода зависимостей. С этой целью вводится понятие функции нескольких переменных и развивается аппарат для исследования таких функций.
Определение функции двух и более переменных
Аналогично функции одной переменной вводится понятие функции двух переменных.
Определение:
Пусть X, Y и Z — некоторые числовые множества. Функцией двух переменных называется множество f упорядоченных троек чисел (х; у; z) таких, что 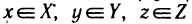
Функцию двух переменных обозначают также следующими символами: 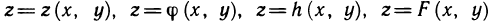
Так как каждой упорядоченной паре чисел (х; у) при фиксированной прямоугольной системе координат соответствует единственная точка М плоскости и, обратно, каждой точке М соответствует единственная упорядоченная пара чисел (х; у), то функцию двух переменных можно рассматривать как функцию точки М и вместо z=f(x; у) писать z=f(M). Областью определения функции в этом случае является некоторое множество {M} точек плоскости. В дальнейшем будем использовать эти два обозначения функции двух переменных.
Способы задания функции двух переменных, как и в случае одной переменной, могут быть различными. В примерах мы используем, как правило, аналитический способ задания, когда функция задается с помощью формулы. Областью определения функции, в этом случае считается множество всех точек плоскости, для которых эта формула имеет смысл.
Примеры функций двух переменных
1. 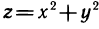
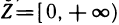
2. 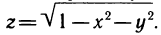
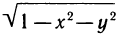
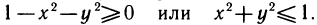
3. 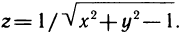
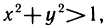
Из рассмотренных примеров следует, что областью определения функции двух переменных может быть вся плоскость Оху или ее часть.
Из аналитической геометрии известно, что множество всех упорядоченных троек чисел (х; у; z) образует координатное пространство. При этом каждой тройке (х; у; z) в пространстве соответствует точка М (х; у; z), и наоборот. Если вместо множества (М) точек плоскости взять множество {M} точек пространства, то аналогично можно дать определение функции трех переменных u=f(M) или u=f(x; y; z). Областью определения функции трех переменных является все пространство или его часть. Так, например, функция 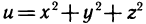
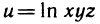
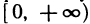
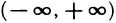
Аналогично можно дать определение функции четырех переменных u=f(x, у, z, t). В этом случае множество упорядоченных четверок чисел (х; у: z; t) образуют так называемое четырехмерное пространство, а каждая четверка (z; y; z; t) называется точкой этого пространства. Однако область определения функции четырех переменных уже не имеет наглядного геометрического истолкования. Аналогично можно ввести понятия функции пяти и вообще n переменных 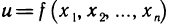
Далее подробно рассмотрены функции двух переменных; следует иметь в виду, что обобщение определений и полученных результатов на функции трех и более переменных не содержит принципиальных отличий.
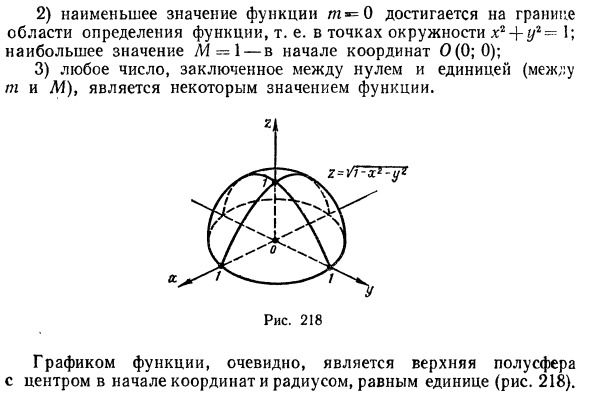
Геометрическое изображение функции двух переменных
Как известно, функция одной переменной изображается на плоскости в виде линии, определенной уравнением y=f(x). Функция двух переменных изображается в пространстве в виде поверхности, которая определяется уравнением z=f(x, у), т. е. сама формула, задающая функцию, и есть уравнение этой поверхности.
В аналитической геометрии рассматриваются различные поверхности и их уравнения. Так, например, уравнение 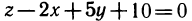
Уравнение 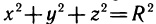
Построение графиков функций двух переменных во многих случаях представляет значительные трудности. Поэтому существует еще один способ изображения функции двух переменных, основанный на сечении поверхности z=f(x, у) плоскостями z=c, где с —любое число, т. е. плоскостями, параллельными плоскости Оху.
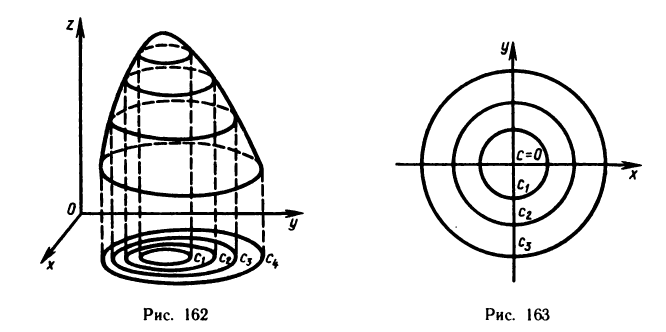
Назовем линией уровня функции z=f(x, у) множество точек (х; у) плоскости Оху, в которых функция принимает одно и то же значение с. Очевидно, при различных с получаются различные линии уровня для данной функции.
Если взять числа 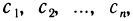
Термин «линии уровня» заимствован из картографии. Там линии уровня — это линии, на которых высота точек земной поверхности над уровнем моря постоянна. По ним можно судить не только о высоте над уровнем моря определенной точки местности, но и о характере рельефа, что особенно важно, если местность гористая.
Пример:
Построить линии уровня функции
Решение:
Линии уровня данной функции определяются уравнением 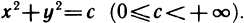
Так как в данном случае линии уровня — окружности с центрами в начале координат, то графиком данной функции должна быть поверхность вращения вокруг оси Oz. Действительно, из аналитической геометрии известно, что уравнение 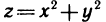
Предел функции двух переменных
Введем понятие 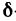
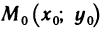
Определение:
Множество 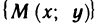
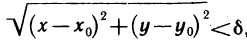
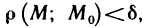
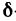
Другими словами, 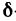
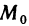
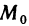
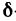
Рассмотрим последовательность точек 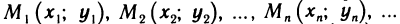
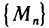
Определение:
Последовательность точек 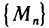
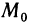

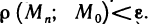
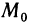
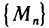
Обозначение:
Заметим, что понятие сходящейся последовательности точек плоскости является обобщением понятия сходящейся числовой последовательности. Действительно, задание последовательности 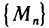
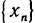
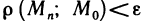
Теперь определим предел функции двух переменных. Его определение аналогично определению предела функции одной переменной.
Пусть функция z=f(M) определена на некотором множестве {М} и точка 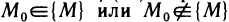
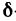
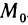
Определение:
Число А называется пределом функции z=f(М) в точке 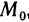
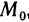
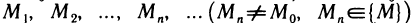
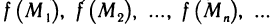
Обозначение:
Так, например, функция 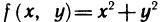
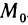
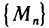
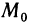
Приведем пример функции, не имеющей предела в некоторой точке. Функция 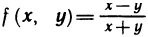
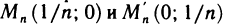
Таким образом, двум различным последовательностям точек, сходящимся к началу координат, соответствуют две последовательности значений функции, которые имеют разные пределы. Следовательно, по определению 3 данная функция не имеет предела в точке (0; 0).
Приведенное определение предела функции двух переменных дано с помощью понятия предела последовательности. Так же, как для функции одной переменной, можно дать эквивалентное определение, используя 
Определение:
Число А называется пределом функции z=f(AM) в точке 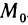

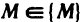
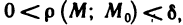
Используя логические символы, данное определение можно записать в виде
Доказательство эквивалентности определений 3 и 4 проводится точно так же, как и в случае функции одной переменной. Следует только в доказательстве теоремы 4.1 заменить последовательность 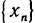
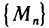
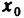
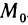
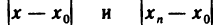
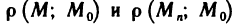
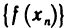
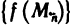
Используя определение предела функции двух переменных, можно перенести основные теоремы о пределах для функции одной переменной на функции двух переменных. Например, имеет место следующая теорема.
Теорема:
Пусть функции f(М) и g(М) определены на одном и том же множестве {M} и имеют в точке 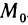
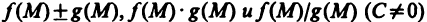
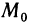
Доказательство этой теоремы аналогично доказательству теоремы 4.3 и может быть получено из него формальной заменой букв 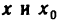
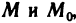
Определение:
Функция z=f(M) называется бесконечной малой в точке 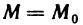
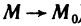
Если функция z=f(M) имеет в точке 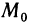
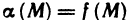
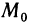
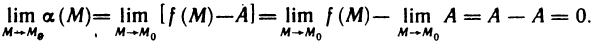
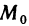
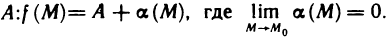

Сравнение бесконечно малых функций двух переменных производится точно так же, как и бесконечно малых функций одной переменной, причем, как и в случае одной переменной, под символом о
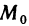

Непрерывность функции двух переменных
Понятие непрерывности функции двух переменных вводится на основе понятия предела.
Определение непрерывности функции двух переменных
Пусть на некотором множестве {M} определена функция f(M), точка 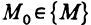
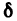

Определение:
Функция z=f(M) называется непрерывной в точке 
Согласно определению предела функции в терминах последовательностей данное определение непрерывности функции в точке 
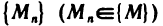
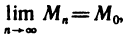
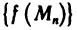
Точки, в которых функция не обладает свойством непрерывности, называются точками разрыва этой функции.
Например, функция
разрывна в точке (0; 0), так как предел этой функции при 
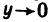
в точке (1; 2) разрывна, так как
Сформулируем определение непрерывности функции, используя определение предела функции в терминах
Определение:
Функция z=f(М) называется непрерывной в точке 

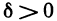
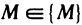
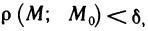
Используя символы, определение 2 можно записать в виде
Так же как для функции одной переменной, используя данные определения непрерывности и соответствующие теоремы о пределах, можно доказать, что арифметические операции над непрерывными функциями и построение сложных функций из непрерывных функций приводят к непрерывным функциям.
В дальнейшем используется определение 1 непрерывности функции, записанное в другом виде.
Назовем полным приращением функции z=f(M) в точке 
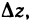
где М — любая точка из области определения функции. Пусть точки 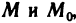
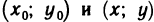
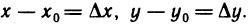
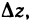
Определение 3. Функция z f (М) называется непрерывной в точке 
Это условие, очевидно, равносильно условию 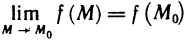
Пример:
Функция 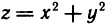
Очевидно, 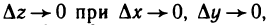
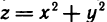
Функция z=f(М) называется непрерывной на некотором множестве {М}, если она непрерывна в каждой точке этого множества.
Основные свойства непрерывных функций двух переменных
Приведем без доказательства основные свойства непрерывных функций двух переменных, поскольку они в основном аналогичны доказательствам соответствующих свойств функций одной переменной. Предварительно введем ряд понятий для множеств {М} точек плоскости.
Определение:
Множество {М} точек плоскости называется связным, если любые две точки этого множества можно соединить непрерывной линией, состоящей из точек данного множества. Например, круг — связное множество, а множество, состоящее из двух кругов, не имеющих общих точек, не является связным.
Определение:
Точка М называется внутренней точкой множества {М}, если существует 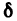
Определение:
Множество {М}, состоящее лишь из внутренних точек, называется открытым множеством.
Определение:
Связное открытое множество {М} точек называется открытой областью, или короче, областью. Простейшими областями являются: внутренность треугольника, круга, эллипса и т. п.
Определение:
Точка М называется граничной точкой области, если в любой ее 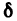
Например, для области, которая состоит из точек, лежащих внутри круга, границей является окружность.
Определение:
Множество {М} точек, образованное областью и ее границей, называется замкнутой областью.
Определение:
Множество {М} называется ограниченным, если существует круг, внутри которого оно содержится.
Отрезок и треугольник — ограниченные множества. Прямая не является ограниченным множеством.
Замкнутая ограниченная область, в которой определена функция двух переменных, является аналогом отрезка для функции одной переменной.
Теперь сформулируем основные свойства непрерывных функций двух переменных:
1°. Если функция z=f(M) непрерывна в замкнутой ограниченной области, то она ограничена в этой области, т. е. существует число k такое, что для всех точек области выполняется неравенство
2°. Если функция z=f(M) непрерывна в замкнутой ограниченной области, то она достигает в этой области своих точных граней.
3°. Если функция z=f(M) непрерывна в области, то она принимает все промежуточные значения между любыми двумя своими значениями, т. е. если 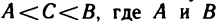

Отсюда, в частности, следует, что если 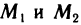

4°. Если функция z=f(M) непрерывна в замкнутой ограниченной области, то она равномерно-непрерывна в этой области, т. е. для любого 
В заключение отметим, что понятия предела, непрерывности и перечисленные свойства функций двух переменных легко обобщаются на функции трех и более переменных.
Предел функции нескольких переменных. Непрерывность функции и точки разрыва
Смотрите также:
- Решение задач по высшей математике
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
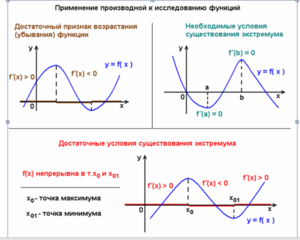
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат



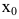
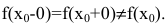
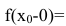
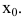
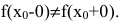
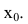
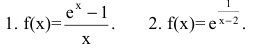
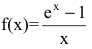
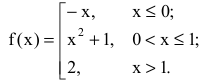
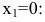
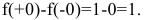
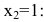
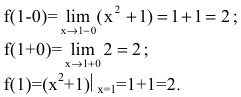
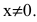
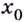 не определена;
не определена;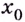 или он равен бесконечности;
или он равен бесконечности;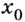 не совпадает со значением функции в этой точке.
не совпадает со значением функции в этой точке.