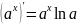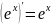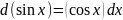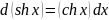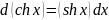Если в х-вершине (у-вершине) касательный вектор параллелен аси Оу’ (оси ОХ) и не изменяет свае направление на противоположное, то вершина кривой называется гладкой, В регулярной точке вершина всегда является гладкой, Например, кривая на рис. 44 имеет вершины в точках Мз (верхнюю н правую), Мз (левую), Ма (пижшаю), Мз (верхнюю) и Мт (правую), из которых гладкими являются только Мз, М» и Мт. Рис,44 Для кривой, заданной в полярных координатах т = г(~р), также можно найти промежутки монотонности координатных функций х(у) = г(р) саве> и у(ср) = г(юр) ашу, исследовать направление касательного вектора н найти х- и у- вершины кривой с помощью формул (7) для х'(у) и у'(~р).
Кроме того, нужна исследовать на монотонность саму функцию т(у) с помощью ее производной г'(у), Если при х с (а;,о), т'(р) > О, то при увеличении угла у от а до р” г(~р) возрастает, т. е. соответствующая точка М(<р) кривой удаляется от полюса (начала координат), а если г'(р) < О, та наоборот, приближается к нему, Точки, в которых т(р) имеет экстремум, мы будем называть г-вершинами; дальней (в случае локального максимума) и бяижией (в точке локального минимума), Если кривая т = г(у) при ~р = уо имеет г-вершину, то г'(р) либо не существует, лнба г'(у) = О. В последнем случае касательная к кривой перпендикулярна радиус- вектору г = ОМс. Очевидно, что в окрестности г-вершины кривая г = г(р) находится па одну сторону от окружности радиуса В = ОМО с центром в начале координкг.
В точках, в которых г'(<р) = аа, касательная направлена по радиус-вектору ОМО. а=из Ф 7.НАНРАВлениевыпуклости,точки ПЕРЕГИБА И ГЛАВНЫЕ ВЕРШИНЫ Рие,45 Например, если г(ф непрерывна и г'(сз,) = г~( ) — г~( (~з) = са, зибер) > О при ьз ~ (сзмсзз) и,р ~ ( “(р) ~ О “р” Р н (О’~~) р ~ (~з,~з) р > ~~,ю~~~~м~ = „( ) при увели ьенни угла из удаляется от ишиаса на участках ат Мз да Мз и от Мз до М4 и приближается к нему на участках от Мо до Мп от Мз до Мз и после точки М4, В точках Мы Мз, Мз и Мв она имеет г-вершины, причем в точках Мы Мз и М4 — гладкие, а в точке Мз касательная направлена по радиусу ОМз (см. рис.
45), Для некоторых кривых г = г(р) точное исследование знака производных х'(Оз) и у'(Зз) затруднительно (например, для спирали г = а(с). В этих случаях мохоно ограничиться исследованием только производной г'((с). Заметим, что понятие х- и у- вершины кривой инвариантно относительно параллельного переноса системы координат (но не инвариантно относительно ее поворотов), Напротив, г-вершины инвариантны относительно поворотов, но не относительно параллельных переносов системы координат. Определение. Угвовой скоростью поворота вектора г = г(1) при $ = 1о называется предел Ьу 1пп —, сп-~О Ь$ ‘ где Ь(с — ориентируемый угол между векторами г($о) и г(г), ЬФ = 1 — 1о.
Воли г(4) = х(1)1+ у(1)» и координатные функции днфференцируемы в точке 1о и г(3о) р О, та угловую скорость по- ворота ветттора г(6) при Ф = 3о вычисляют по формуле х(го) у(го) — х(зо)у(то) хз(го) + у (то) Волн точка М (8) кривой г — г(з) является регулярной ((х(1))з+ ( ‘(Г))з > О) н существуют х(3) и у($), та определена и угловая скорость ьз($) поворота касательного вектора ч(1) = У( )1+ у( )», =’$1 которую находят па формуле х(г)у(о) — У(г)у($) (11) “‘= (у(и+(в Знак дроби в (11) полностью определяется знаком ее числителя, ко- торый мы обозначим т(1) и назовем показателен выпуклости (или кривизны): х у у(1) = ху — Уу= У у’ (12) Ьд К = 1пп м-+Мо Ьв Величина т(Ф) и угловая скорость ю(ь) поворота касательного век- тора тесно связаны с кривизной КЯ кривой г = г($).
Напомним, что кривизной кривой г = г(т) в ее точке Мо называется предел где Ьв — длина дуги между точками Мс и Мы а Ьд — угол между касательными к кривой в точках Мо и М (рис.46), В любой регулярной точке М(З) кривой, в которой существуют и вторые производные координатных функций, для кривизны К(з) справедливо представление О ~ ж(з) 9(з) — ж(Ф) в(з)1 ((й(з)) + (р(з))~)~/з Рис.
46 1 Ф)! ЬйН ~ р~~ ~ц~~~з’ Точки кривой, в которых кривизна достигает экстремума, называются главными вершинами, а точки, где кривизна равна нулю, называются точками распрялтения. Пример18, Найти всевершиныкрнвойх = За+1,у = 2+4з— зз Решение. Находим ж = 2$, у = 4 — 2$; х(з) имеет минимум при З = О, соответствующая точка М1 (1; 2) — левая хвершина; р(З) имеет максимум при з = 2, соответствующая точка Мз(б;6) — верхняя р-вершина.
Далее, Ж = 2, у = -2, 7(З) = -2(21) — 2(4-2З) = — 8, 6з+Рз = 41з+(4-21) з = 8Зз-16З+ + 16 = 8(ьз — 21+ 2), К(з) 8з/ (зз — 21+ 2)з/з 2/2(Зз — 2З+ 2)з/3′ Кривизна К(Ф) имеет экстремум (максимум) при З = 1, соответствующая точка Мз(2; б) является главной вершиной (рис, 47). П Определение, Кривая г(Г) называется положительно (атрииательно) выпуклой при сь с $ < /3, если для всех 1 6 (а;,9) касательный вектор г(1) ~ О существует и при увеличении З на (а;)3) поворачивается против хода часовой стрелки (соответственно по ходу Рис. 47 часовой стрелки). Точка Мс кривой г = г($) называется точкой выпуклости, если в ней кривая не меняет знака выпуклости, и точкой перегиба, если в Мс знак выпуклости меняется, Точка возврата Мс кривой г = г(Ф) называется тачкой возврата первого рода (второго рода), если в ней знак выпуклости не меняется (соответственно меняется на противоположный), Например, кривая примера 18 всюду отрицательно выпукла, а кривая, изображенная на рис.
44, положительно выпукла до точки Мм от Мз до Мз и от Мз до Мз, отрицательно выпукла от Мз до Мз и от Мв и далее, имеет перегибы в точках М1 и Ме, точку возврата первого рода Мз и точку возврата второго рода Мз. Все остальные точки этой кривой являются точками выпуклости. Теорема 1, Если для всех 3 6 (ьх;Р) существует г(З),г(ь) ф 0 и 7(ь) > 0 (7(ь) < 0), то кривая г(3) положительно (соответственно отрицательно) выпукла при а < ь’ < ~9, Теорема 2.
Бслн кривая г = г(Х) имеет при ь’ = $с перегиб, то 7(зс) = 0 или не существует. Теорема 3. Пусть в точке Мс кривая г = г(1) имеет касательную, а значит, и нормаль, Тогда в окрестности точки Мс’. (16) а) для кривой, заданной параметрически б) для кривой в поляр- ных координатах Рие,48 у(у) = гз — 1 г” + 2(г’)2, (14) а кривизна — по формуле ) Ь()( (гя+ (,,г)2)ЗУ2′ (18) 51 50 а) в точке выпуклости кривая расположена по одну сторону от касательной н по разные — от нормали (см. рис.
48, а); б) в точке перегиба — по разные стороны от касательной и от нормали (см. рис. 48, б); в) в точке возврата 1-го рода — по одну сторону от нормали и по разные — от касательной (см. рис, 48, в), г) в тс 1ке возврата 2-го рода — по одну сторону от касательной и от нормали (см. рис. 48, г), Если кривая задана в полярных координатах т = т( р) и функция г(у) дважды дифференцнруема, то ее показатель выпуклости вычисляется по формуле где штрих означает производную по 1в. Теоремы 1,2 и 3, разумеется, справедливы и для кривых, заданных в полярных координатах с той оговоркой, что у них не бывает точек возврата второго рода.
Для того чтобы выявить точки перегиба и точки возврата кривой, надо найти ее критические точки второго порядка, т, е. для которых .г($) = 0 или не существует, Далее для каждой из найденных точек следует определить, является ли она точкой гладкости или точкой возврата н меняет лн величина Т($) в ней знак или нет, и воспользоваться определением. В заключение отметим, что точки перегиба, возврата и главные вершины инвариантны относительно параллельных переносов системы координат и ее поворотов.
Я, ТОЧКИ САМОПЕРЕСЕЧЕНИЯ Кривая, заданная параметрически ж = ж($), р = р($) нли в полярных координатах, может пересекать себя в одной или нескольких точках. Точки самопересечения (узловые точки) находят из системы уравнений (11) = к(22)’ в(11) = р(12)’ 21 ~ ~2~ г(ср1) = г(212) > 0; (Рз — 101 = 27ГЙ’, Й = ~1,~2,~3,… Отметим, что в полярных координатах полюс может быть кратной точкой, если т(у) = 0 при нескольких значениях К1 (не обязательно отличающихся на 2яй), Кроме того, если функции х(3) и д(3) имеют наименьший положительный период Т, то точки $1 и 12 следует искать на промежутке (0; Т), а в случае, если т(у) имеет период Ф = 2яи для некоторго натурального и, то и у1 и 212 также следует искать на промежутке (О; Ф).
12 Е2 1 2 1+ ~2 1+ 12 2 (1 — Й) 22(1 — 22) (11 Ф’ 22) Рнс, 50 , гр,, Зря 2+ гйп — = 2+ вш— 2 2 ~ря – ~р1 = 2яй, й Е Е О < р1 < у2 < Фг. Рнс. 49 53 Пример 19, Найти точки самопересечения кривых 12 ‘ т 13 , Зр а) я = —, и = —; б) т = 2 + е1п — (О < у < юг). 1+ Гг 1+ 12 Решение. а) Составим систему (1б): Очевидно, что $1 24 0 и 12 ф О, Разделив второе уравнение 2 на первое, получим — 1 = —, откуда 12-1 12=21-11Я ~-~ $1 12 1112(21-22)+(11 — 22)=0 ее (11-22)(1112+1) = О, ПосколькУЕ1 ф 22, то 1112+ 1 = О.
Подставив 22 =- -1/11 в первое уравнение, получим —, откуда$1 = 1 или 61 = ~1, 1+11 1+ 1/$1 Итак, 11 = 1, $2 = -1 (или наоборот). Прн этом ж(11) 1 = ю(12) = — р($1) = р(гя) = О. т1 Таким образом, 3Х~-; О) 2′ единственная точка самопересечения этой кривой, соответствующая значениям 1 = ~1 (рив. 49). б) Функция т(22) = 2 + , Зр + гйп — имеет периоды Ф„= 2 2 2ягг (и б Е), в частно- 3 сти, Фа = юг. Составим систе- мУ (17) Понятно„что гря — 221 = 2гг. Подставив (о2 = 221 + 2я, получим вш( — + 31г) = -а1п — 4е агп — =О, Зу1 .
З~Р1 . 39Р1 2 2 2 3Р1 2я”и ОтКуда — = 1ГП, 9г1 = —, П = О, 1 ИЛИ 2. ПОЛУЧИМ трн ТОЧКИ 2 ‘ 3 ‘ 2я самопересечения, отвечающих углам у1 = О и ~р2 = 2я, 221 =— 8я 4я 10я и <Р2 = — <Р1 = — и <р2 = — соответственно, Во всех трех 3 3 3 точках г(ср) = 2 (рис. 50). С) 9.
а у меня получается минимума, т.к. производная  меняет знак с минуса на плюс, наверное я что-то не так понимаю.
меняет знак с минуса на плюс, наверное я что-то не так понимаю.
Коль скоро вам заданы параметрические уравнения кривой, для нахождения минимума и максимума вам не надо брать производную  , если под минимум и максимумом вы понимаете минимальное (максимальное) значение
, если под минимум и максимумом вы понимаете минимальное (максимальное) значение  . Само значение экстремума (т.е. чему равен максимальный или минимальный игрек) не зависит от
. Само значение экстремума (т.е. чему равен максимальный или минимальный игрек) не зависит от  , в том смысле, что какое бы уравнение не определяло
, в том смысле, что какое бы уравнение не определяло  , если икс вообще существует для нужного параметра
, если икс вообще существует для нужного параметра  , минимум или максимум игрека будет равен минимуму или максимуму
, минимум или максимум игрека будет равен минимуму или максимуму  , соответственно производную от игрека можно брать по параметру, получается
, соответственно производную от игрека можно брать по параметру, получается  , имеем два корня
, имеем два корня  , вторая производная равна
, вторая производная равна  и значит в
и значит в 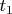 имеем максимум, а в
имеем максимум, а в  минимум (максимум
минимум (максимум
, напомню, там, где вторая производная меньше
нуля, а минимум там где больше).
Найденные 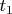 и
и  подставляем в уравнения
подставляем в уравнения  и
и  и таким образом находим координаты локальных экстремумов по игрекам (ординатам).
и таким образом находим координаты локальных экстремумов по игрекам (ординатам).
Аналогично можно найти локальные экстремумы по иксам (абсциссам).
По ним (иксам), кстати, найденные экстремумы будут в вашей задаче глобальными.
Parametric representation
$$mathbf{r}(t)=((2+cos 3t)cos 2t, (2+cos 3t)sin 2t)), tin [0,2pi ]$$
can be replaced by this (complex) one
$$mathbf{r}(t)=(2+cos 3t)e^{2it} , tin [0,2pi ]$$
Thus, we are looking for values of $t_1$ and $t_2$, $t_1 neq t_2$, such that:
$$tag{1}(2+cos 3t_1)e^{2it_1}=(2+cos 3t_2)e^{2it_2}$$
Two complex numbers are equal if and only if their modules are equal and their arguments are equal (modulo $2 pi$).
Remark:
Due to the fact that $2+cos 3t>0$ for any value of $t$ shows that $2+cos 3t_1$ and $2+cos 3t_2$ are the modules of the LHS and RHS of (1), resp.
Thus, (1) is equivalent to:
$$cases{cos(3t_1)=cos(3 t_2)\2t_1=2t_2 modulo 2 pi}$$
As $$cos(u)=cos(v) iff u=pm v+K 2pi:$$
the previous conditions are equivalent to
$$cases{3t_1= s 3 t_2+K 2pi\2t_1=2t_2+K’ 2 pi}$$
where $s=pm1$ and $K,K’$ are integers.
$$tag{2}iff cases{t_1= s t_2+K 2pi/3\t_1=t_2+K’ pi}$$
The cases where $s=1$ will not give double points (because they lead to $t_1=t_2+K”2pi$). We can thus assume $s=-1$, i.e.,
$$tag{3}iff cases{t_1= -t_2+K 2pi/3 (a)\t_1=t_2+K’ pi (b)}$$
Adding and substracting (3)(a) and (3)(b):
$$tag{4}cases{2t_1=K2pi/3+K’pi iff t_1=Kpi/3+K’pi/2 (a)\2t_2=K2pi/3-K’pi iff t_2=Kpi/3-K’pi/2 (b)}$$
with the same values of $K$ and $K’$ in (4)(a) and (4)(b).
For example, if $K=2$ and $K’=1$, $(t_1,t_2)=(7pi/6,pi/6)$, giving point $(1,sqrt{3}).$
I leave you the task to consider the different other cases (by taking different possible cases for integers $K$ and $K’$, some of them being redundant). You will end up with the three following solutions (up to an exchange between $t_1$ and $t_2$, of course):
$$(t_1,t_2)=(7pi/6,pi/6), (5pi/6,11pi/6), (pi/2,3pi/2), $$ yielding double points :
$$(1,sqrt{3}), (1,-sqrt{3}), (-2,0)$$
respectively.
Основные формулы дифференцирования элементарных функций.
|
Производная |
Дифференциал |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дифференцирование
показательно-степенных выражений:

– продифференцировать
как показательную функцию, а потом как
степенную и результаты дифференцирования
сложить.
Кривые
на плоскости и функции, заданные
параметрически. Дифференцирование
параметрически заданных функции.
Опр.
Кривой на плоскости xoy
называют всякий образ отрезка
при непрерывном отображении

.

параметрическое
задание кривых (параметризация).
Функции
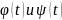
– непрерывные функции параметра

.
Непрерывность
отображения

означает, что оно либо растягивает,
либо сжимает участки
,
искривляет и помещает в

,
но не разрывает отрезок
.
При
параметризации задается начало конец
и направление движения вдоль кривой,
таким образом параметрическое задание
удобно для описания траектории движения
материальной точке.
Одну
и ту же кривую на плоскости можно задать
бесконечным множеством параметризаций.
Опр.

.
Кривые, заданные параметрически,
эквивалентны, если существует отображение
непрерывное и строго монотонное

такое, что диаграмма коммутативна, т.е.

.
Опр.
Пусть дана параметризация

прямой на плоскость. Эта параметризация
называется непрерывно дифференцируемой,
если функции

на отрезке
дифференцируемы и имеют непрерывные
производные.
В
том случае, когда параметризация

строго монотонная у нее существует
обратная функция

,
в этом случае параметризация
задает не только кривую, но и функцию,
при этом существование обратной функции

не означает, что мы сможем практически
разрешить это уравнение относительно
t,
аналогично, если строго монотонна

.
Дифференцирование
параметрически заданных функций.


Правило.
Если имеется функция, заданная
параметрически, то необходимо
продифференцировать по t
оба уравнения и поделить функцию

,
при этом производная функции запишется
в параметрическом виде следующим
образом:
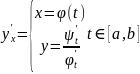
Если
функция задана параметрически, то и
производная должна быть задана
параметрически. В таком виде производная
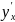
готова к новому дифференцированию.
Уравнение касательной прямой, в кривой, заданной параметрически.
3 Класса точек параметрически заданной кривой:

– в
точках I
класса обязательно существует
касательная, которая записывается
симметричным уравнением.

Уравнение
может быть записано и в виде уравнения
для I
класса.
В
данном случае не гарантированно, что
функция запишется в виде

.
Такие
точки в дальнейшем будем называть
особыми точками параметрически заданной
функции. В них одновременно обе
производные равны 0.
Оказывается,
в особых точках касательная прямая
может быть, а может ее и не быть вовсе,
это определяется старшими производными
в точке
и является предметом изучения такой
науки как дифференциальная геометрия.
Вывод.
В неособой точке параметрически заданной
кривой обязательно существует касательная
и она записывается уравнением

.
Нормальная
прямая в точке кривой, заданной на
плоскости.
Опр.
Прямую N,
проходящую через
кривой и перпендикулярную касательной
прямой, называют нормальной прямой к
кривой Г в
.

–
уравнения
нормали в

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
-
Теоретический минимум
Методы дифференциального исчисления позволяют провести достаточно полное исследование функции одной переменной, чтобы построить
её график. Такое исследование включает следующие пункты:
1. Область определения, вертикальные и горизонтальные асимптоты.
2. Характерные особенности функции (периодичность, чётность и т.п.), точки пересечения с осями координат.
3. Наклонные асимптоты.
4. Производная функции. Стационарные и критические точки.
5. Промежутки монотонности. Экстремумы.
6. Вторая производная функции. Точки перегиба. Выпуклость функции.Первые два пункта в особых комментариях не нуждаются. Только уточним, что поиск горизонтальных асимптот осуществляется нахождением
предела данной функции при![[IMG]](http://corum.mephist.ru/tex/images/6edb46e3ad2cfa15dc7368290598e389.gif) .
.Наклонные асимптоты
Наличие наклонных асимптот предполагает, что на бесконечности данная функция![[IMG]](http://corum.mephist.ru/tex/images/465a703f084c610f250f9ab50ff3f895.gif) ведёт себя линейным образом, т.е.
ведёт себя линейным образом, т.е.
имеет вид![[IMG]](http://corum.mephist.ru/tex/images/b1bac797e12f46d64cf5ea67272789c2.gif) . Запишем
. Запишем
![[IMG]](http://corum.mephist.ru/tex/images/31d9bb0feaa839a250d8019d9aee2acc.gif) ,
,
считая, что это равенство выполняется на бесконечности. Разделим обе части на![[IMG]](http://corum.mephist.ru/tex/images/8725029ea89712eed8670bae64d30e47.gif) и перейдём к пределу при
и перейдём к пределу при ![[IMG]](http://corum.mephist.ru/tex/images/6edb46e3ad2cfa15dc7368290598e389.gif) :
:
![[IMG]](http://corum.mephist.ru/tex/images/734d33beb3d0325b3221cc551ae09389.gif) .
.
Таким образом находится угловой коэффициент асимптоты. На бесконечности, кроме того,![[IMG]](http://corum.mephist.ru/tex/images/2e63a31282affc55f1c2423aef328f21.gif) . Формализуя, запишем это
. Формализуя, запишем это
![[IMG]](http://corum.mephist.ru/tex/images/a261695ef465287d9c46defb049ab1b9.gif) .
.
Если оба предела – и для![[IMG]](http://corum.mephist.ru/tex/images/a09fe38af36f6839f4a75051dc7cea25.gif) , и для
, и для ![[IMG]](http://corum.mephist.ru/tex/images/da3e61414e50aee968132f03d265e0cf.gif) существуют, то тем самым будет найдено уравнение наклонной асимптоты.
существуют, то тем самым будет найдено уравнение наклонной асимптоты.Исследование производной
Особый интерес представляют нули производной (стационарные точки) и точки, в которых производная бесконечна или не существует
(критические точки). Если при переходе через стационарную точку производная меняет знак, то это точка экстремума. Промежутки, на которых
производная положительна, соответствуют промежуткам возрастания функции; промежутки, на которых производная отрицательна – промежуткам
убывания.Критические точки бывают двух видов. Производная в них может быть бесконечна (у функции вертикальная касательная) или вовсе не существует.
Причём тут возможны варианты. У функции![[IMG]](http://corum.mephist.ru/tex/images/3b3fd3ec46a82112c2438b9dba912d14.gif) в точке
в точке ![[IMG]](http://corum.mephist.ru/tex/images/1567ccbc3aa038b2ecac14e445922a7d.gif) производная не существует, но есть правосторонняя производная.
производная не существует, но есть правосторонняя производная.
А у функции![[IMG]](http://corum.mephist.ru/tex/images/0fdc7c0b92fe1696affe027f0020f9f1.gif) в той же точке существуют обе односторонние производные, но они различны, поэтому “двусторонней” производной нет.
в той же точке существуют обе односторонние производные, но они различны, поэтому “двусторонней” производной нет.
Это т.н. точка возврата (также иногда называемую на иностранный манер каспом).Исследование второй производной
Промежутки знакопостоянства второй производной соответствуют промежуткам выпуклости и вогнутости кривой. Если вторая производная на данном
интервале положительна, то кривая вогнутая, в противном случае – выпуклая. Точка, в которой вторая производная меняет знак – точка перегиба.Функции, заданные параметрически
Построение графиков функций, заданных параметрически, содержит некоторую специфику по сравнению со случаем функций, заданных явно. Пусть
![[IMG]](http://corum.mephist.ru/tex/images/82e27e9f819cc5bf21eff809c27ff248.gif) .
.
Прежде всего, рекомендуется, построить графики зависимостей![[IMG]](http://corum.mephist.ru/tex/images/82e27e9f819cc5bf21eff809c27ff248.gif) . В первую очередь нужно обратить внимание
. В первую очередь нужно обратить внимание
на промежутки монотонного изменения функции![[IMG]](http://corum.mephist.ru/tex/images/57610e4d141a1cbaf1c0d65b0b7ed1ff.gif) . Эти промежутки задают ветви графика. Параметр сам по себе всегда
. Эти промежутки задают ветви графика. Параметр сам по себе всегда
возрастает, но при этом аргумент функции, график которой строится, может вести себя достаточно замысловато. В результате одному значению
аргумента может соответствовать не одно значение функции. А вот в пределах одной ветви исследование уже проводится довольно-таки стандартно.
Поиск асимптот осуществляется следующим образом. Если
![[IMG]](http://corum.mephist.ru/tex/images/44f8bc5ef569ef9a9e666ec6bd283a4f.gif) ,
,
то у графика есть вертикальная асимптота![[IMG]](http://corum.mephist.ru/tex/images/08f58d77ad8a71586bf5e123def5f952.gif) . Если
. Если
![[IMG]](http://corum.mephist.ru/tex/images/7b4ef2be296d921eafa68d9d5de1b85f.gif) ,
,
то у графика есть горизонтальная асимптота![[IMG]](http://corum.mephist.ru/tex/images/6446e119700759bea0ed7b72ba22bd7b.gif) . Если
. Если
![[IMG]](http://corum.mephist.ru/tex/images/e98951397db50fcbc1d044188be2915e.gif) ,
,
то проводим проверку на наличие наклонной асимптоты. Для этого вычисляем предел![[IMG]](http://corum.mephist.ru/tex/images/cfb13bd3341529dbc0d038b51e12d897.gif) . Если этот предел существует, то вычисляем
. Если этот предел существует, то вычисляем
предел![[IMG]](http://corum.mephist.ru/tex/images/7c87d51921b591473446b239082dcfff.gif) .
.
Если и этот предел существует, то график имеет наклонную асимптоту![[IMG]](http://corum.mephist.ru/tex/images/b1bac797e12f46d64cf5ea67272789c2.gif) .
.Далее вычисляем производную:
![[IMG]](http://corum.mephist.ru/tex/images/58179155a8c34801d25bafb37ca36484.gif) .
.
Точки, в которых и числитель, и знаменатель обращаются в нуль, называются особыми.
Для построения графика ищем точки, в которых производные![[IMG]](http://corum.mephist.ru/tex/images/e7dc13797dad5af3cd517719af0dda71.gif) терпят разрыв или обращаются в нуль:
терпят разрыв или обращаются в нуль:
![[IMG]](http://corum.mephist.ru/tex/images/c31d92666cadaf2b1041b5a16ae01101.gif) . Эти точки задают промежутки монотонного изменения функции.
. Эти точки задают промежутки монотонного изменения функции.Напомним также, как вычисляется вторая производная:
![[IMG]](http://corum.mephist.ru/tex/images/11d530557a20490df0824a8fad459b2c.gif) .
.Лучше всего детали построения графиков параметрически заданных функций понимаются на конкретных примерах.
Функции, заданные в полярных координатах
Отдельно коснёмся построения графиков функций в полярных координатах. Напомним, что декартовы прямоугольные координаты связаны с полярными
посредством соотношений![[IMG]](http://corum.mephist.ru/tex/images/5fb401f020ab8a8ef2703054ba46560f.gif) . В плане построения графиков удобнее всего рассматривать функции, заданные
. В плане построения графиков удобнее всего рассматривать функции, заданные
уравнениями вида![[IMG]](http://corum.mephist.ru/tex/images/7bb6e7c7c9dfb62cdb3fd3b6fc28ef4a.gif) . Т.е. имеется зависимость расстояния точки от начала координат от полярного угла. Для построения графика
. Т.е. имеется зависимость расстояния точки от начала координат от полярного угла. Для построения графика
требуется исследовать эту зависимость. Особой специфики здесь нет.Замечание. Далее при построении графиков масштаб по осям абсцисс и ординат выбирался различным для удобства изображения.
Примеры
Пример 1.
Построить график функции![[IMG]](http://corum.mephist.ru/tex/images/af202d731dd3bb723ff7376cb0434b0c.gif) .
.Так как
![[IMG]](http://corum.mephist.ru/tex/images/0222bd2e9eaefd48c8f49342acdfaa6e.gif) , то график функции имеет горизонтальную асимптоту
, то график функции имеет горизонтальную асимптоту ![[IMG]](http://corum.mephist.ru/tex/images/d2d8a40d8006e4e4c599fac66209c267.gif) . Вертикальных и наклонных асимптот нет. Нуль функции
. Вертикальных и наклонных асимптот нет. Нуль функции ![[IMG]](http://corum.mephist.ru/tex/images/1567ccbc3aa038b2ecac14e445922a7d.gif) .
.Производная функции:
![[IMG]](http://corum.mephist.ru/tex/images/07f095f3b30b8d218b3b03ac5fd92eb9.gif) .
.
Стационарные точки![[IMG]](http://corum.mephist.ru/tex/images/823fcf9e64c4554c6f92bd7573d182db.gif) . По промежуткам знакопостоянства производной определяем промежутки монотонности функции:
. По промежуткам знакопостоянства производной определяем промежутки монотонности функции:
на интервалах![[IMG]](http://corum.mephist.ru/tex/images/444be50f4fe50267247ea3d6078a9612.gif) функция монотонно возрастает, на промежутке
функция монотонно возрастает, на промежутке ![[IMG]](http://corum.mephist.ru/tex/images/1389403c434535261d0399d3e4fbea22.gif) монотонно убывает.
монотонно убывает.
Следовательно, локальные максимумы![[IMG]](http://corum.mephist.ru/tex/images/2eba40d2d1a180b0fd62622c5fb3d566.gif) , локальный минимум
, локальный минимум ![[IMG]](http://corum.mephist.ru/tex/images/bf7feefd285bd46689926dcaccf8b22c.gif) .
.Вторая производная функции:
![[IMG]](http://corum.mephist.ru/tex/images/c46688d0297a142c028fa6279ac487f4.gif) .
.
Таким образом, точка![[IMG]](http://corum.mephist.ru/tex/images/98e830e7e322ae2b4f3c08626225d7ef.gif) – точки перегиба. Причём при
– точки перегиба. Причём при ![[IMG]](http://corum.mephist.ru/tex/images/88aef22b8c8155134c2b603c1d2d8b5a.gif)
функция вогнутая, а при![[IMG]](http://corum.mephist.ru/tex/images/ebbb8a3fdca90c9d680fe4095ef4d230.gif) функция выпуклая.
функция выпуклая.
Можно строить график.
![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_201.png)
Пример 2. График функции с наклонной асимптотой.
Построить график функции![[IMG]](http://corum.mephist.ru/tex/images/45f64cb1f8d133444db5886799879337.gif) .
.График имеет вертикальную асимптоту
![[IMG]](http://corum.mephist.ru/tex/images/df037215d1b8ed55f0a49751f4b95b8e.gif) .
.
Нули функции![[IMG]](http://corum.mephist.ru/tex/images/0cd81d1a8a4787342e5b65922a9264cd.gif) ; ось ординат кривая пересекает в точке
; ось ординат кривая пересекает в точке ![[IMG]](http://corum.mephist.ru/tex/images/a340557580734055e3abe47658d9950c.gif) .
.
Горизонтальных асимптот нет: на бесконечности функция стремится к бесконечности.
Ищем наклонные асимптоты:
![[IMG]](http://corum.mephist.ru/tex/images/1542582a8b0280f506b312bcf01d5108.gif) ,
,
т.е. асимптота![[IMG]](http://corum.mephist.ru/tex/images/fd11ef855093fa9c1318d033704dad77.gif) .
.Производная функции:
![[IMG]](http://corum.mephist.ru/tex/images/52ec941ee43f6061a06c3c37c52c0a94.gif) .
.
Стационарные точки![[IMG]](http://corum.mephist.ru/tex/images/ceae222b81be1faf22e940588273f60f.gif) . По промежуткам знакопостоянства производной определяем промежутки монотонности функции:
. По промежуткам знакопостоянства производной определяем промежутки монотонности функции:
на интервалах![[IMG]](http://corum.mephist.ru/tex/images/ba63d09f327a755e110e70cfc43968b5.gif) функция монотонно возрастает, на промежутке
функция монотонно возрастает, на промежутке ![[IMG]](http://corum.mephist.ru/tex/images/d2031fa0018a3805e13adbe23b6d0e35.gif) монотонно убывает.
монотонно убывает.
Следовательно, локальный максимум![[IMG]](http://corum.mephist.ru/tex/images/751361c9cfc86b41586cbcafd52329ac.gif) .
.Вторая производная функции:
![[IMG]](http://corum.mephist.ru/tex/images/41f12faeb41e7cfff7542203e56bcc45.gif) .
.
Таким образом, точка![[IMG]](http://corum.mephist.ru/tex/images/a340557580734055e3abe47658d9950c.gif) – точка перегиба. Левее неё функция выпуклая, правее – вогнутая. Информации достаточно для построения графика.
– точка перегиба. Левее неё функция выпуклая, правее – вогнутая. Информации достаточно для построения графика.
![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_3237.png)
Пример 3. График функции с точками возврата.
Построить график функции![[IMG]](http://corum.mephist.ru/tex/images/a1c8e26303dcab63d8531bd4ff6de67b.gif) .
.Нули функции
![[IMG]](http://corum.mephist.ru/tex/images/2445f87bd837de0a70be636bfea6dbc7.gif) . Горизонтальных асимптот нет: на бесконечности функция стремится к бесконечности. Вертикальных асимптот нет.
. Горизонтальных асимптот нет: на бесконечности функция стремится к бесконечности. Вертикальных асимптот нет.
Ищем наклонные асимптоты:
![[IMG]](http://corum.mephist.ru/tex/images/91e390a8b57d5cb8e729ccffae0a8c88.gif) ,
,
т.е. асимптота![[IMG]](http://corum.mephist.ru/tex/images/6ee824bf12a60259ac08f102bd86de6b.gif) .
.Производная функции:
![[IMG]](http://corum.mephist.ru/tex/images/04a486e050cf1c1a850a779b3d7fae4b.gif) .
.
Имеется стационарная точка![[IMG]](http://corum.mephist.ru/tex/images/11ff7b6f3a7bddd0d7340441e0fb6696.gif) и две критические точки
и две критические точки ![[IMG]](http://corum.mephist.ru/tex/images/2445f87bd837de0a70be636bfea6dbc7.gif) .
.
По промежуткам знакопостоянства производной определяем промежутки монотонности функции:
на интервалах![[IMG]](http://corum.mephist.ru/tex/images/ad8eb706726c1f1847bf4b662e45b0e8.gif) функция монотонно возрастает, на промежутке
функция монотонно возрастает, на промежутке ![[IMG]](http://corum.mephist.ru/tex/images/7117ae2ba79257f2819beacd3e55abde.gif) монотонно убывает.
монотонно убывает.
Следовательно, локальный максимум![[IMG]](http://corum.mephist.ru/tex/images/4a08d0a4f49b84f3a7b4014d5a766c8b.gif) , локальный минимум
, локальный минимум ![[IMG]](http://corum.mephist.ru/tex/images/bbabd76ac0b1eed0ea6fe6c0e617a324.gif) .
.Осторожность требуется при рассмотрении критических точек. В пределе при
![[IMG]](http://corum.mephist.ru/tex/images/db524aa87dd37b5368b4a57bcc91d535.gif) производная стремится к
производная стремится к ![[IMG]](http://corum.mephist.ru/tex/images/a5f2a912b5fd19da74188840a2201796.gif) независимо
независимо
от того, со стороны каких значений мы подходим к нулю: слева или справа. Поэтому в точке![[IMG]](http://corum.mephist.ru/tex/images/1567ccbc3aa038b2ecac14e445922a7d.gif) у графика вертикальная касательная.
у графика вертикальная касательная.
В пределе![[IMG]](http://corum.mephist.ru/tex/images/d4915c8be2386eebc04b644556d2e408.gif) производная тоже стремится к бесконечности, но слева она стремится к
производная тоже стремится к бесконечности, но слева она стремится к ![[IMG]](http://corum.mephist.ru/tex/images/e0bbdc41da4dbaf21bf4ca91c9257520.gif) , а справа – к
, а справа – к ![[IMG]](http://corum.mephist.ru/tex/images/a5f2a912b5fd19da74188840a2201796.gif) .
.
Таким образом, производная в этой точке не существует – это точка возврата.Вторая производная функции:
![[IMG]](http://corum.mephist.ru/tex/images/f6fa991f781a555c255856ec0f652f51.gif) .
.
Таким образом, точка![[IMG]](http://corum.mephist.ru/tex/images/a340557580734055e3abe47658d9950c.gif) – точка перегиба. Левее неё функция вогнутая, правее – выпуклая.
– точка перегиба. Левее неё функция вогнутая, правее – выпуклая.
Строим график.
![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_3009.png)
Пример 4. Построение графика функции в полярных координатах.
Построить кривую, заданную уравнением
![[IMG]](http://corum.mephist.ru/tex/images/e95b973c37d7825c5323d567e875630c.gif) .
.Самое разумное в данном случае – перейти к полярным координатам, тогда уравнение кривой примет вид
![[IMG]](http://corum.mephist.ru/tex/images/f49c38cd4c0e4fc1fb449f7edb1075e9.gif) .
.
Видно, что эта функция периодическая с главным периодом![[IMG]](http://corum.mephist.ru/tex/images/f1c3c82ecacef5ad48bbf83066497a64.gif) , поэтому достаточно исследовать функцию на отрезке
, поэтому достаточно исследовать функцию на отрезке ![[IMG]](http://corum.mephist.ru/tex/images/e4e3ced4e49bc56f840510d54d38fb11.gif) .
.
Вычисляем производную:
![[IMG]](http://corum.mephist.ru/tex/images/aa53bf978469ca933bef7fcb933f6ce8.gif) .
.
Критических точек у производной нет. Стационарных точек на рассматриваемом отрезке три:![[IMG]](http://corum.mephist.ru/tex/images/ba9a0fc926d6537e776ded252364fd83.gif) . При полярных углах
. При полярных углах
![[IMG]](http://corum.mephist.ru/tex/images/4751c4f41fdca198106e49bbc0d86e79.gif) производная положительна, т.е. модуль радиус-вектора возрастает, при углах
производная положительна, т.е. модуль радиус-вектора возрастает, при углах ![[IMG]](http://corum.mephist.ru/tex/images/d5939a05ba66ad3d620c6e5c740ad6c2.gif) – модуль радиус-вектора убывает.
– модуль радиус-вектора убывает.
Исследуем вторую производную:
![[IMG]](http://corum.mephist.ru/tex/images/58aa3679e5620c3d421828e4964a137e.gif) .
.
Вторая скобка числителя, очевидно, всегда положительна, как и знаменатель. А вот числитель может обращаться в нуль, причём
![[IMG]](http://corum.mephist.ru/tex/images/15b0a4099c412b45fdf90cfadb103615.gif) .
.
Понятно, что уравнение имеет два корня в рассматриваемом промежутке, причём они расположены симметрично относительно угла![[IMG]](http://corum.mephist.ru/tex/images/ef0796d7048ae9fb44b82cfb057f31db.gif) .
.
Таким образом, имеются две точки перегиба. Легко найти подстановкой во вторую производную значений полярного угла 0 и![[IMG]](http://corum.mephist.ru/tex/images/f1c3c82ecacef5ad48bbf83066497a64.gif) , что
, что
сначала кривая вогнутая, затем выпуклая, затем снова вогнутая.
Наконец, учтём, что![[IMG]](http://corum.mephist.ru/tex/images/8e1ff996e5e6a882bea5cbbf3399266b.gif) . Можно строить график.
. Можно строить график.
![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_1647.png)
Пример 5. Функция, заданная параметрически.
Построить кривую, заданную параметрически уравнениями
![[IMG]](http://corum.mephist.ru/tex/images/665ad2b55f99982f92283aba3b68fdc9.gif)
Построим графики зависимостей
![[IMG]](http://corum.mephist.ru/tex/images/82e27e9f819cc5bf21eff809c27ff248.gif) . Читателю рекомендуется проделать это в качестве упражнения.
. Читателю рекомендуется проделать это в качестве упражнения.
![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_5170.png)
На графике зависимости![[IMG]](http://corum.mephist.ru/tex/images/57610e4d141a1cbaf1c0d65b0b7ed1ff.gif) цветами выделены промежутки монотонности. Они соответствуют отдельным ветвям функции.
цветами выделены промежутки монотонности. Они соответствуют отдельным ветвям функции.
Аналогичным образом выделены части графика зависимости![[IMG]](http://corum.mephist.ru/tex/images/b99dac4d2bf0c2a38ab929d682d7b3ca.gif) . Ветви, выделенной красным цветом отвечает изменение параметра
. Ветви, выделенной красным цветом отвечает изменение параметра ![[IMG]](http://corum.mephist.ru/tex/images/30b2ab8dc1496d06b230a71d8962af5d.gif)
в пределах![[IMG]](http://corum.mephist.ru/tex/images/26cda3f3cead6431a1a0bbdd09a8fb38.gif) , выделенной синим цветом ветви отвечает
, выделенной синим цветом ветви отвечает ![[IMG]](http://corum.mephist.ru/tex/images/81badcd775cbd2f242a479b0b3c24a96.gif) , выделенной зелёным цветом отвечает
, выделенной зелёным цветом отвечает ![[IMG]](http://corum.mephist.ru/tex/images/a52c0784a4960fc48bcd8fb51cebddac.gif) .
.
Рассмотрим эти ветви отдельно. Предварительно для удобства приведём производные:
![[IMG]](http://corum.mephist.ru/tex/images/30fca77607fb2f061cb3133384d8353d.gif) .
.Начнём с ветви, для которой
![[IMG]](http://corum.mephist.ru/tex/images/81badcd775cbd2f242a479b0b3c24a96.gif) (синяя). Как видно из графика зависимости
(синяя). Как видно из графика зависимости ![[IMG]](http://corum.mephist.ru/tex/images/57610e4d141a1cbaf1c0d65b0b7ed1ff.gif) , переменная
, переменная ![[IMG]](http://corum.mephist.ru/tex/images/8725029ea89712eed8670bae64d30e47.gif) меняется в пределах от (-1)
меняется в пределах от (-1)
до 1. Переменная![[IMG]](http://corum.mephist.ru/tex/images/36a4dc9ccf2bdc09d800556724231fc6.gif) сначала возрастает, начиная с нуля, затем убывает до отрицательного значения, а потом снова возрастает, доходя
сначала возрастает, начиная с нуля, затем убывает до отрицательного значения, а потом снова возрастает, доходя
до нуля. Это поведение функция сохранит и на графике зависимости![[IMG]](http://corum.mephist.ru/tex/images/b858d74431ca1b2757d777b5b4b7b091.gif) . Нужно только найти точки локального максимума и минимума.
. Нужно только найти точки локального максимума и минимума.
Кроме того, вызывают интерес точки, отвечающие значениям параметра![[IMG]](http://corum.mephist.ru/tex/images/a247c1c5e17a5a9ad626c5ab030acf70.gif) : там производная
: там производная ![[IMG]](http://corum.mephist.ru/tex/images/6f77ede7e786e3a4906e9ab4fbc9af3c.gif) обращается в нуль.
обращается в нуль.
Производная![[IMG]](http://corum.mephist.ru/tex/images/92a39ad603a70736a2dacf4d350b7974.gif) при этом отлична от нуля. Следовательно, производная
при этом отлична от нуля. Следовательно, производная ![[IMG]](http://corum.mephist.ru/tex/images/a207210d1ccab3078b90ea382b2dc04c.gif) в точках
в точках ![[IMG]](http://corum.mephist.ru/tex/images/df9cdf28db1d67d5f5814885b05372f0.gif) бесконечна.
бесконечна.
Т.е. график имеет в этих точках вертикальные касательные.Ищем локальные экстремумы. Производная
![[IMG]](http://corum.mephist.ru/tex/images/92a39ad603a70736a2dacf4d350b7974.gif) обращается в нуль при
обращается в нуль при ![[IMG]](http://corum.mephist.ru/tex/images/c69930fce298ca3b7d102d582bf84016.gif) . Подставляя эти значения параметра
. Подставляя эти значения параметра
в функции![[IMG]](http://corum.mephist.ru/tex/images/8c377ad8100ed68ee9c0921ba5ea68a7.gif) , находим точку максимума
, находим точку максимума ![[IMG]](http://corum.mephist.ru/tex/images/121d9791523d66693e2e8dbfd4ea1ec8.gif) и точку минимума
и точку минимума ![[IMG]](http://corum.mephist.ru/tex/images/48a899021999c5c94b6a130d2350252a.gif) .
.Обратимся ко второй производной
![[IMG]](http://corum.mephist.ru/tex/images/d6e0696fc9a93af8f2964d8d5f61ceb2.gif) . Она обращается в нуль на рассматриваемом отрезке изменения параметра один раз –
. Она обращается в нуль на рассматриваемом отрезке изменения параметра один раз –
при![[IMG]](http://corum.mephist.ru/tex/images/852fbd92e65e2b3c6f5951528ab291f1.gif) . Это означает наличие в точке
. Это означает наличие в точке ![[IMG]](http://corum.mephist.ru/tex/images/bf7feefd285bd46689926dcaccf8b22c.gif) перегиба. Левее этой точки вторая производная отрицательна, а потому кривая выпуклая,
перегиба. Левее этой точки вторая производная отрицательна, а потому кривая выпуклая,
справа – кривая вогнута.Переходим к исследованию ветви, для которой
![[IMG]](http://corum.mephist.ru/tex/images/31a5f27da411b145a67a9ff3a4e3556f.gif) (красная). Очевидно наличие асимптоты
(красная). Очевидно наличие асимптоты ![[IMG]](http://corum.mephist.ru/tex/images/1567ccbc3aa038b2ecac14e445922a7d.gif) . Кроме того,
. Кроме того,
отметим, что с ростом параметра переменная![[IMG]](http://corum.mephist.ru/tex/images/8725029ea89712eed8670bae64d30e47.gif) монотонно приближается к (-1) , а переменная
монотонно приближается к (-1) , а переменная ![[IMG]](http://corum.mephist.ru/tex/images/36a4dc9ccf2bdc09d800556724231fc6.gif) монотонно растёт от
монотонно растёт от ![[IMG]](http://corum.mephist.ru/tex/images/e0bbdc41da4dbaf21bf4ca91c9257520.gif)
до нуля. Монотонность изменения переменной![[IMG]](http://corum.mephist.ru/tex/images/36a4dc9ccf2bdc09d800556724231fc6.gif) подтверждается отсутствием на рассматриваемом промежутке изменения параметра
подтверждается отсутствием на рассматриваемом промежутке изменения параметра
нулей у производной![[IMG]](http://corum.mephist.ru/tex/images/92a39ad603a70736a2dacf4d350b7974.gif) . Зато исследование второй производной показывает, что обращается в нуль вторая производная
. Зато исследование второй производной показывает, что обращается в нуль вторая производная ![[IMG]](http://corum.mephist.ru/tex/images/d6e0696fc9a93af8f2964d8d5f61ceb2.gif)
при![[IMG]](http://corum.mephist.ru/tex/images/e70a79de97999018cfe9348d42346a09.gif) . Отсюда следует, что точка
. Отсюда следует, что точка ![[IMG]](http://corum.mephist.ru/tex/images/f2c6dbb13b5d5e6e7aa2c127e4523652.gif) является точкой перегиба. Левее её кривая вогнутая, правее – выпуклая.
является точкой перегиба. Левее её кривая вогнутая, правее – выпуклая.Третья ветвь (зелёная) симметрична второй относительно начала координат. Проведённого исследования достаточно для построения кривой. Ниже
она изображена.
![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_2202.png)
Пример 6. Функция, заданная параметрически и имеющая точки самопересечения.
Построить кривую, заданную параметрически уравнениями
![[IMG]](http://corum.mephist.ru/tex/images/fde3fc2429c3222d12f5929a0ffa947f.gif)
Снова начнём с построения графиков зависимостей
![[IMG]](http://corum.mephist.ru/tex/images/82e27e9f819cc5bf21eff809c27ff248.gif) . Как видно, зависимость
. Как видно, зависимость ![[IMG]](http://corum.mephist.ru/tex/images/57610e4d141a1cbaf1c0d65b0b7ed1ff.gif) та же, что и в примере 5.
та же, что и в примере 5.
Поэтому график снова будет содержать три ветви, отвечающие тем же интервалам изменения параметра, что и в примере 5.
![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_5597.png)
Требующиеся производные:
![[IMG]](http://corum.mephist.ru/tex/images/00e729aa761dfe278750064ca8693b59.gif)
Снова начнём с “синей” ветви. В данном случае переменная
![[IMG]](http://corum.mephist.ru/tex/images/36a4dc9ccf2bdc09d800556724231fc6.gif) на данном промежутке изменения параметра монотонно убывает.
на данном промежутке изменения параметра монотонно убывает.
Снова в точках, отвечающих значениям параметра![[IMG]](http://corum.mephist.ru/tex/images/a247c1c5e17a5a9ad626c5ab030acf70.gif) производная
производная ![[IMG]](http://corum.mephist.ru/tex/images/a207210d1ccab3078b90ea382b2dc04c.gif) бесконечна: там производная
бесконечна: там производная ![[IMG]](http://corum.mephist.ru/tex/images/6f77ede7e786e3a4906e9ab4fbc9af3c.gif)
обращается в нуль, а производная![[IMG]](http://corum.mephist.ru/tex/images/92a39ad603a70736a2dacf4d350b7974.gif) при этом отлична от нуля. График имеет в этих точках вертикальные касательные.
при этом отлична от нуля. График имеет в этих точках вертикальные касательные.Переходим ко второй производной
![[IMG]](http://corum.mephist.ru/tex/images/d6e0696fc9a93af8f2964d8d5f61ceb2.gif) . Она обращается в нуль только в точке
. Она обращается в нуль только в точке ![[IMG]](http://corum.mephist.ru/tex/images/bf7feefd285bd46689926dcaccf8b22c.gif) . Это точка перегиба.
. Это точка перегиба.
Кстати, сразу отметим, что больше ни в одной точке эта производная в нуль не обращается, т.е. других точек перегиба нет. А рассматриваемая ветвь
слева от точки перегиба вогнута, а справа – выпукла.Интереснее поведение “красной” ветви. Функция имеет локальный экстремум в точке, соответствующей значению параметра
![[IMG]](http://corum.mephist.ru/tex/images/d0ad978a74acb076a75c53200504249c.gif) , т.е.
, т.е.
в точке![[IMG]](http://corum.mephist.ru/tex/images/b085cd233aaa9e2ca747f729cfa094a3.gif) . Знак производной
. Знак производной ![[IMG]](http://corum.mephist.ru/tex/images/7e234d9714881dddf73ce99e3aed8964.gif) или график зависимости
или график зависимости ![[IMG]](http://corum.mephist.ru/tex/images/b99dac4d2bf0c2a38ab929d682d7b3ca.gif) позволяет установить, что найденная точка
позволяет установить, что найденная точка
экстремума является точкой максимума: сначала функция возрастает и только потом начинает убывать, стремясь к асимптоте![[IMG]](http://corum.mephist.ru/tex/images/1567ccbc3aa038b2ecac14e445922a7d.gif) .
.
Так как область изменения аргумента![[IMG]](http://corum.mephist.ru/tex/images/8725029ea89712eed8670bae64d30e47.gif) перекрывается с областью изменения аргумента “синей” ветви, то в совокупности с характером монотонности
перекрывается с областью изменения аргумента “синей” ветви, то в совокупности с характером монотонности
“красной” ветви понятно, что кривая должна иметь самопересечение (т.н. двойную точку). Знак второй производной![[IMG]](http://corum.mephist.ru/tex/images/d6e0696fc9a93af8f2964d8d5f61ceb2.gif) показывает, что кривая
показывает, что кривая
должна быть выпуклая (напомним, что точек перегиба здесь быть не может, как мы выяснили выше).“Зелёная” ветвь симметрична “красной” относительно начала координат. Для построения графика осталось найти характерные точки: точки пересечения с осями
координат и координаты точек, где функция имеет бесконечную первую производную. Всего есть две точки пересечения кривой с осью абсцисс (не считая
того, что кривая проходит через начало координат):
![[IMG]](http://corum.mephist.ru/tex/images/f121a092a97bbda223597203c5264edc.gif) .
.
Бесконечная первая производная у функции в точках, отвечающих значениям параметра![[IMG]](http://corum.mephist.ru/tex/images/ffb87b77a1439161f4efb82ae97687d6.gif) , т.е. в точках
, т.е. в точках ![[IMG]](http://corum.mephist.ru/tex/images/30e37d06db04c4145c956795ad03a162.gif) .
.
Строим кривую.
![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_2940.png)
Пример 7. Функция, заданная параметрически и имеющая особые точки.
Построить кривую, заданную параметрически уравнениями
![[IMG]](http://corum.mephist.ru/tex/images/7355cde776a6ff40a0339dbbfd694b80.gif)
Опять начинаем с построения графиков зависимостей
![[IMG]](http://corum.mephist.ru/tex/images/82e27e9f819cc5bf21eff809c27ff248.gif) . Снова зависимость
. Снова зависимость ![[IMG]](http://corum.mephist.ru/tex/images/57610e4d141a1cbaf1c0d65b0b7ed1ff.gif) та же, что и в примере 5, т.е.
та же, что и в примере 5, т.е.
график снова содержит три ветви, отвечающие тем же интервалам изменения параметра, что и в примере 5.
![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_94.png)
Требующиеся производные:
![[IMG]](http://corum.mephist.ru/tex/images/43c29d8fd8bcb223f4d46fe070602f9b.gif) .
.Как и в двух последних примерах, начнём с ветви, отвечающей значениям параметра
![[IMG]](http://corum.mephist.ru/tex/images/81badcd775cbd2f242a479b0b3c24a96.gif) (“синяя” ветвь). Переменная
(“синяя” ветвь). Переменная ![[IMG]](http://corum.mephist.ru/tex/images/36a4dc9ccf2bdc09d800556724231fc6.gif) на данном
на данном
промежутке изменения параметра монотонно убывает. В точках, отвечающих значениям параметра![[IMG]](http://corum.mephist.ru/tex/images/a247c1c5e17a5a9ad626c5ab030acf70.gif) производные
производные ![[IMG]](http://corum.mephist.ru/tex/images/6f77ede7e786e3a4906e9ab4fbc9af3c.gif) и
и ![[IMG]](http://corum.mephist.ru/tex/images/92a39ad603a70736a2dacf4d350b7974.gif)
обращаются в нуль. Следовательно, это точки возврата кривой.
Их координаты![[IMG]](http://corum.mephist.ru/tex/images/19fde2c41e0a3b7e8e0607a72c24e9f6.gif) . График имеет в этих точках т.н. полукасательные. Дело в том, что формально производную
. График имеет в этих точках т.н. полукасательные. Дело в том, что формально производную ![[IMG]](http://corum.mephist.ru/tex/images/a207210d1ccab3078b90ea382b2dc04c.gif) можно вычислить:
можно вычислить:
![[IMG]](http://corum.mephist.ru/tex/images/a9eb64148050bc65eff9197659ffa94d.gif) .
.
Эта производная, как обычно задаёт угловой коэффициент “касательной”. Учитывая, что она должна проходить через точку возврата, находим
![[IMG]](http://corum.mephist.ru/tex/images/2e7303341d1054887c6d872cce92e8b8.gif) .
.Рассматриваемая ветвь имеет точку перегиба
![[IMG]](http://corum.mephist.ru/tex/images/bf7feefd285bd46689926dcaccf8b22c.gif) . Левее этой точки кривая вогнута, правее – выпукла. Других точек перегиба у кривой нет.
. Левее этой точки кривая вогнута, правее – выпукла. Других точек перегиба у кривой нет.Теперь “красная” ветвь. Переменная
![[IMG]](http://corum.mephist.ru/tex/images/36a4dc9ccf2bdc09d800556724231fc6.gif) монотонно убывает, кривая стремится к асимптоте
монотонно убывает, кривая стремится к асимптоте ![[IMG]](http://corum.mephist.ru/tex/images/1567ccbc3aa038b2ecac14e445922a7d.gif) . По знаку второй производной
. По знаку второй производной ![[IMG]](http://corum.mephist.ru/tex/images/d6e0696fc9a93af8f2964d8d5f61ceb2.gif)
устанавливаем, что эта ветвь всюду выпуклая.“Зелёная” ветвь симметрична “красной” относительно начала координат. Для построения графика определим точки пересечения кривой с осью абсцисс
(не считая прохождения кривой через начало координат):
![[IMG]](http://corum.mephist.ru/tex/images/82f96a2bddfd44e604e2c08145599496.gif) .
.
Строим кривую.
![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_2328.png)
-

Crystal
Корумчанин
Преподаватель МИФИФункция по-разному себя может вести на плюс бесконечности и на минус бесконечности. В изложении же это никак не отражено, что может привести к ошибкам в определении асимптот функций типа y = x * arctg(x).
-
Crystal, ты имеешь в виду, что при вычислении пределов для нахождения асимптот нужно отдельно рассматривать случаи
![[IMG]](http://corum.mephist.ru/tex/images/7362a61052368af8b1fcba2e4642aebd.gif) и
и ![[IMG]](http://corum.mephist.ru/tex/images/8d2a06ff80e12da9e0ca174c3e0ea6dd.gif) .
.
Да, это правильно, разумеется. Приведённый тобой пример это подтверждает. Но по-моему всегда считалось, что запись![[IMG]](http://corum.mephist.ru/tex/images/6edb46e3ad2cfa15dc7368290598e389.gif) не конкретизирует знак
не конкретизирует знак
бесконечности, а потому предполагает оба варианта. Поэтому и написал я так совершенно сознательно: ошибки, допускаемые по невнимательности
предупредить практически невозможно. Существуют и более “жёсткие” примеры, чем приведённый тобой. Я решил ограничиться тем, что сейчас есть.
Не знаю, имеет ли смысл отдельно прописывать случай разных асимптот.
Поделиться этой страницей