Как найти точки в которых производная паралельна

Как найти кол во точек в которых производная параллельна прямой

• +7 (953) 35-222-89
• Санкт-Петербург, Лиговский пр.52
• Kyziaha@gmail.com

Производная, часть II: геометрический смысл

Продолжение задач на производные для первой части ЕГЭ.

Геометрический смысл производной и ее применения для исследования функций.

Геометрический смысл производной

Про геометрический смысл написано много теории. Не буду вдаваться в вывод приращения функции, напомню основное для выполнения заданий:

Производная в точке x равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке, то есть это тангенс угла наклона к оси Х.

Возьмем сразу задание из ЕГЭ и начнем в нем разбираться:

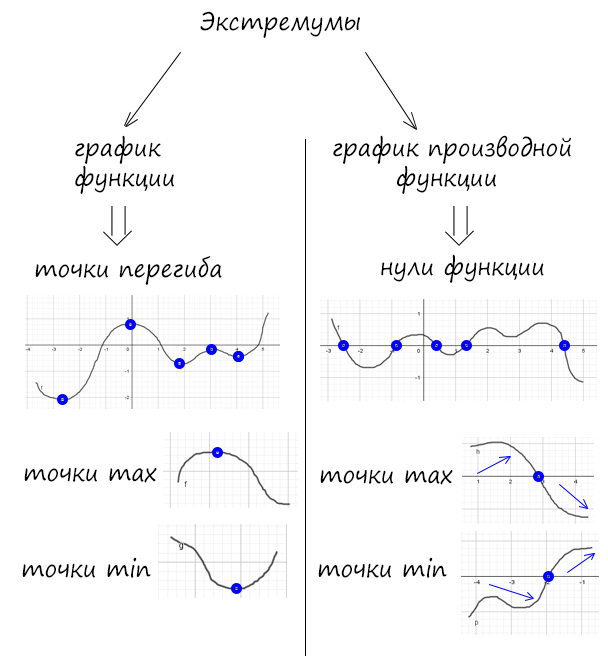
Задание №1. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Кто очень торопится и не хочет разбираться в объяснениях: стройте до любого такого треугольника (как показано ниже) и делите стоячую сторону (вертикальную) на лежащую (горизонтальную) и будет вам счастье, если про знак не забудите (если прямая убывает(→↓), то ответ должен быть с минусом, если прямая возрастает(→↑), то ответ должен быть положительный!)

Найти нужно угол между касательной и осью Х, назовем его α: проведем параллельную оси Х прямую в любом месте через касательную к графику, получим тот же угол.

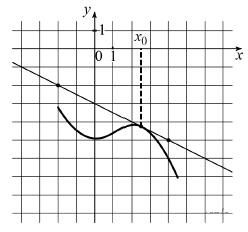
Лучше не брать точку х0, т.к. понадобится большая лупа для определения точных координат.

Взяв любой прямоугольный треугольник (на рисунке предложено 3 варианта), найдем tgα (углы, то равны, как соответственные), т.е. получим производную функции f(x) в точке x0. Почему же так?

Если мы проведем касательные в других точках x2, x1 и т.д. касательные будут другие.

Вернемся к 7 классу, чтобы построить прямую!

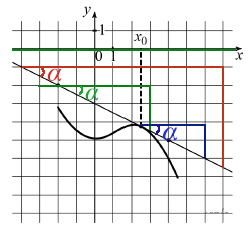
Уравнение прямой задается уравнением y = kx + b , где

k — наклон относительно оси Х.

b — расстояние между точкой пересечения с осью Y и началом координат.

Производная прямой, всегда одна и та же: y’ = k.

В какой бы точке на прямой мы не взяли производную, она будет неизменна.

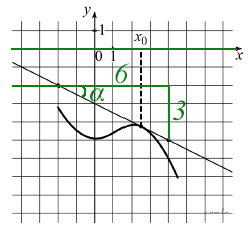
Поэтому, осталось только найти tgα (как было сказано выше: делим стоячую сторону на лежачую). Делим противолежащий катет на прилежащий, получаем, что k = 0,5. Однако, если график убывает, коэффициент отрицательный: k = −0,5.

Советую себя проверять вторым способом:
По двум точкам можно задать прямую. Найдем координаты двух любых точек. Например, (-2;-2) и (2;-4):

Подставим в уравнение y = kx + b вместо y и х координаты точек:

Решив эту систему, получим b = −3, k = −0,5

Вывод: Второй способ дольше, но в нем вы не забудете про знак.

Задание №2 . На рисунке изображён график производной функции f(x). На оси абсцисс отмечены восемь точек: x1, x2, x3, . x8. Сколько из этих точек лежит на промежутках возрастания функции f(x) ?

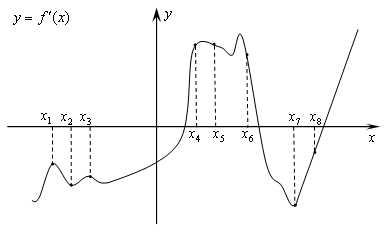
Если график функции убывает — производная отрицательна (верно и наоборот).

Если график функции возрастает — производная положительна (верно и наоборот).

Эти две фразы помогут вам решить большую часть задач.

Внимательно смотрите, рисунок производной вам дан или функции, а дальше выбирайте одну из двух фраз.

Построим схематично график функции. Т.к. нам дан график производной, то там, где она отрицательна, график функции убывает, где положительна — возрастает!

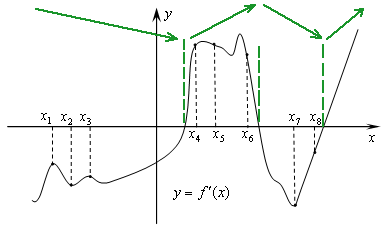
Получается, что 3 точки лежат на участках возрастания: x4; x5; x6.

Задание №3. Функция f(x) определена на промежутке (-6; 4). На рисунке изображен график ее производной . Найдите абсциссу точки, в которой функция принимает наибольшее значение.

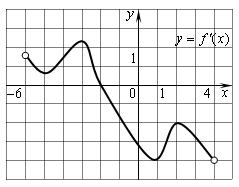
Советую всегда строить, как идет график функции, такими стрелочками или схематично со знаками (как в №4 и №5):

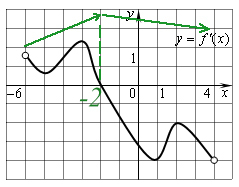
Очевидно, если график возрастает до −2, то максимальная точка и есть −2.

Задача №4. На рисунке изображён график функции f(x) и двенадцать точек на оси абсцисс: x1, x2, . x12. В скольких из этих точек производная функции отрицательна?

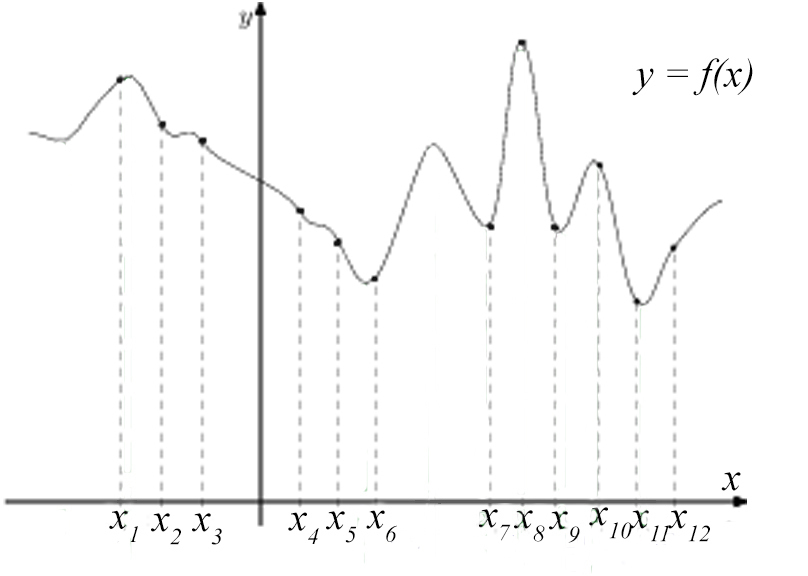
Задача обратная, дан график функции, нужно схематично построить, как будет выглядеть график производной функции, и посчитать, сколько точек будет лежать в отрицательном диапазоне.

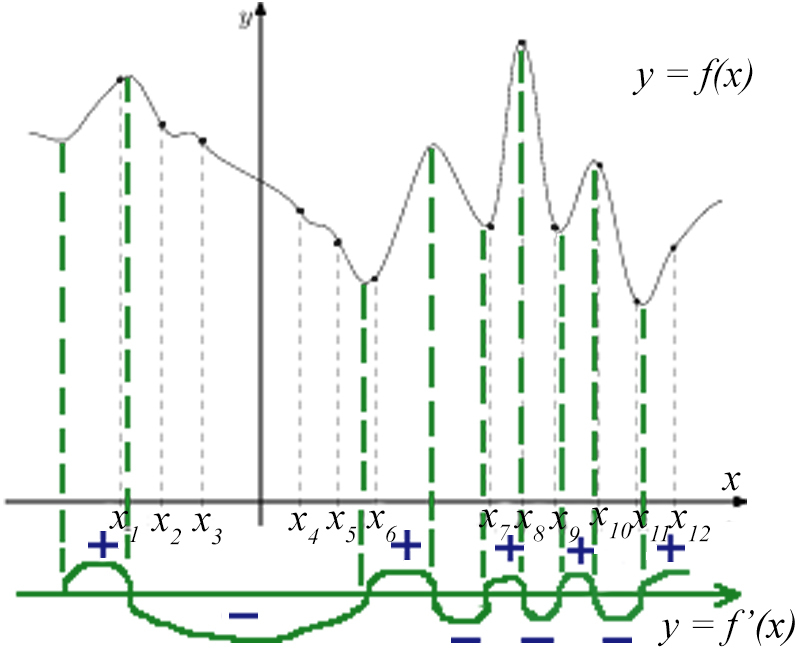
Положительные: x1, x6, x7, x12.

Отрицательные: x2, x3, x4, x5, x9, x10, x11.

Ответ: 7

Еще один вид заданий, когда спрашивается про какие-то страшные “экстремумы”? Что это такое вам найти не составит труда, я же поясню для графиков.

Задача №5. На рисунке изображен график производной функции f(x), определенной на интервале (-16; 6). Найдите количество точек экстремума функции f(x) на отрезке [-11; 5].

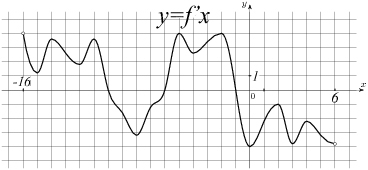Отметим промежуток от -11 до 5!

Обратим свои светлые очи на табличку: дан график производной функции => тогда экстремумы это точки пересечения с осью X.

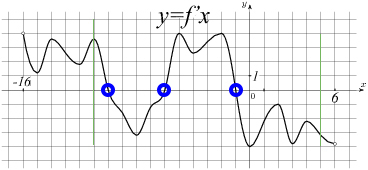
Задача №6. На рисунке изображен график производной функции f(x), определенной на интервале (-13; 9). Найдите количество точек максимума функции f(x) на отрезке [-12; 5].

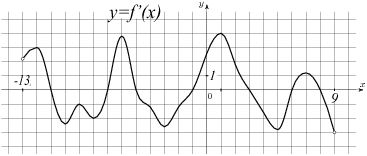Отметим промежуток от -12 до 5!

Можно одним глазом взглянуть в табличку, точка максимума – это экстремум, такой, что до него производная положительна (функция возрастает), а после него производная отрицательна (функция убывает). Такие точки обведены в кружочек.

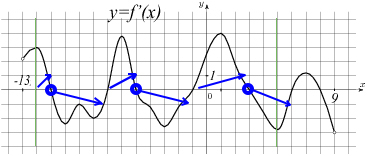
Стрелочками показано, как ведет себя график функции

Задача №7. На рисунке изображен график функции f(x),определенной на интервале (-7; 5). Найдите количество точек, в которых производная функции f(x) равна 0.

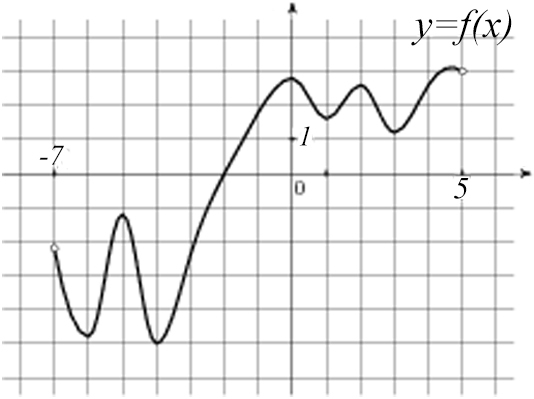
Можно посмотреть на выше приведенную табличку (производная равна нулю, значит это точки экстремума). А в даной задаче дан график функции, значит требуется найти количество точек перегиба !

А можно, как обычно : строим схематический график производной.

Производная равна нулю, когда график функций меняет свое направление (с возрастания на убывание и наоборот)

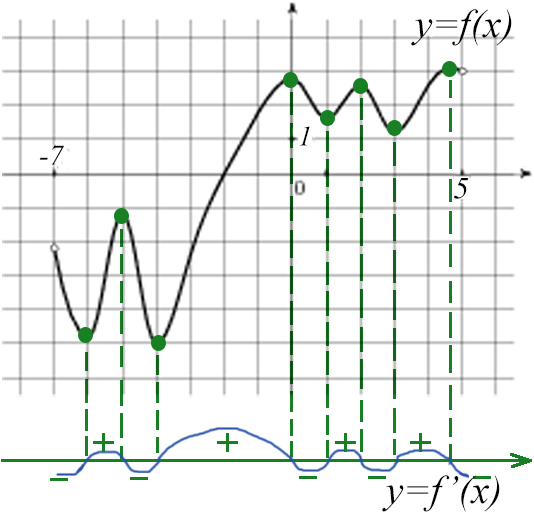
Задача №8. На рисунке изображен график производной функции f(x), определенной на интервале (-2; 10). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

Построим схематично график функции:

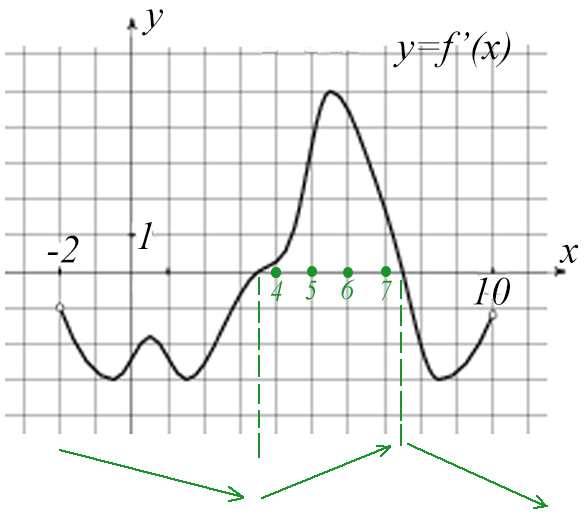
Там, где он возрастает, получаем 4 целые точки: 4 + 5 + 6 + 7 = 22.

Задача №9. На рисунке изображен график производной функции f(x), определенной на интервале (-6; 6). Найдите количество точек f(x), в которых касательная к графику функции параллельна прямой y = 2x + 13 или совпадает с ней.

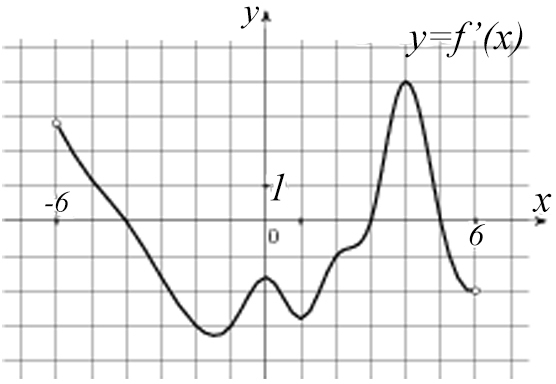
Нам дан график производной! Значит, и нашу касательную нужно «перевести» в производную.

Производная касательной: y’ = 2.

А теперь построим обе производные:

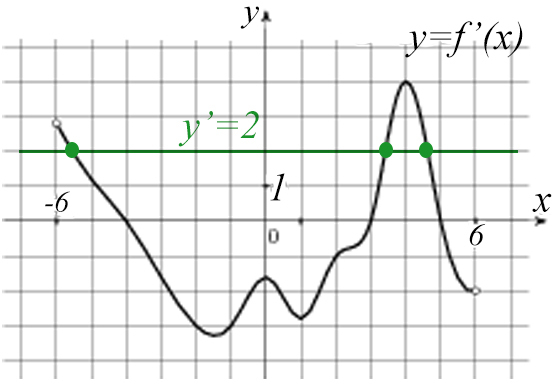Касательные пересекаются в трех точках, значит, наш ответ 3.

Задача №10. На рисунке изображен график функции f(x), и отмечены точки -2, 1, 2, 3. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

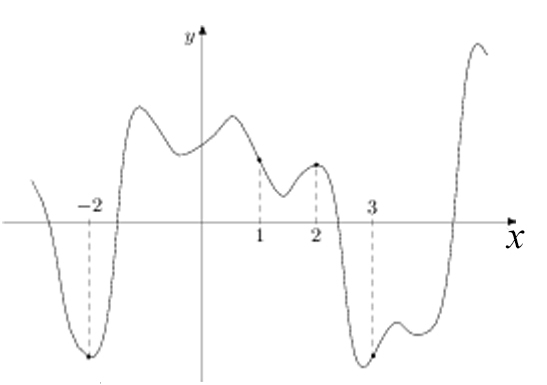
Задание чем-то похоже на первое: чтобы найти значение производной, нужно построить касательную к этому графику в точке и найти коэффициент k.

Если прямая убывает, k

Если прямая возрастает, k > 0.

Подумаем, как значение коэффициента отразится на наклоне прямой:

При k = 1 или k = − 1 график будет посередине между осями Х и У.

Чем ближе прямая к оси Х, тем ближе коэффициент k нулю.

Чем ближе прямая к оси Y, тем ближе коэффициент k к бесконечности.

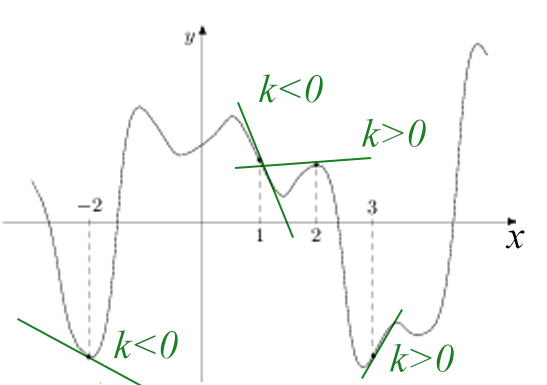
В точке -2 и 1 k именно там и будет наименьшее значение производной

Задание №11. Прямая является касательной y = 3x + 9 к графику функции y = x³ + x² + 2x + 8 . Найдите абсциссу точки касания.

Прямая будет касательной к графику, когда графики имеют общую точку, как и их производные. Приравняем уравнения графиков и их производные:

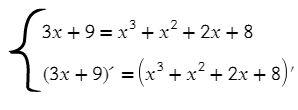Решив второе уравнение, получаем 2 точки. Чтобы проверить, какая из них подходит, подставляем в первое уравнение каждый из иксов. Подойдет только один.

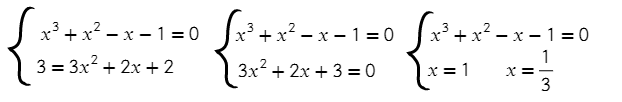
Кубическое уравнение совсем решать не хочется, а квадратное за милую душу.

Вот только, что записывать в ответ, если получится два “нормальных” ответа?

При подстановке икса (х) в первоначальные графики y = 3x + 9 и y = x³ + x² + 2x + 8 должен получиться один и тот же Y

Верно! Значит x=1 и будет ответом

Задание №12. Прямая y = − 5x − 6 является касательной к графику функции ax² + 5x − 5 . Найдите a .

Аналогично приравняем функции и их проивзодные:

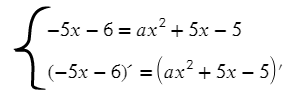
Решим эту систему относительно переменных a и x :

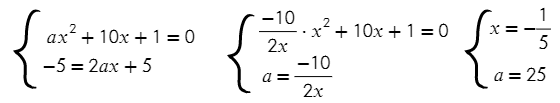Ответ: 25

Задание с производными считается одним из самых сложных в первой части ЕГЭ, однако, при небольшой доли внимательности и понимания вопроса у вас все получится, и вы поднимете процент выполнения этого задания!

Большинство заданий взято с сайтов ФИПИ и РЕШУ ЕГЭ.

Узнать ещё

Знание — сила. Познавательная информация

Производная равна нулю на графике функции

В №7 ЕГЭ несколько видов заданий, в который нужно по графику функции найти точки, в которых производная обращается в нуль.

Как найти, в каких точках производная равна нулю на графике функции?

В точках, в которых производная равна нулю, касательная к графику функции параллельна оси абсцисс.

Это могут быть точки экстремума (те из них, в которых производная существует):

Либо точки перегиба:

В окрестности точки экстремума график лежит по одну сторону от касательной, в окрестности точки перегиба — по разные стороны.

1)На рисунке изображён график функции y=f(x), определённой на интервале (−1; 11). Найдите корень уравнения f'(x)=0.

Касательная к графику функции y=f(x) параллельна оси абсцисс в точке x=3.

Следовательно, корнем уравнения f'(x)=0 является x=3.

2)На рисунке изображён график функции y=f(x), определённой на интервале (−4; 20). Найти количество решений уравнения f'(x)=0.

Касательная к графику параллельна оси абсцисс в четырёх точках.

Значит, уравнение f'(x)=0 имеет четыре решения.

3)На рисунке изображен график функции y=f(x), определенной на интервале (−4; 10) . Найдите количество точек, в которых производная функции f(x) равна 0.

Касательная к графику параллельна оси Ox в трёх точках.

Таким образом, производная функции f(x) равна 0 в трёх точках.

В этих примерах мы рассматривали график функции y=f(x)!

Задания, в которых надо определить в каких точках производная равна нулю на графике производной y=f'(x), решаются иначе!

Задание 6. Геометрический смысл производной

В задаче 6 дается график функции или производной, по которому требуется определить одну из следующих величин:

1. Значение производной в некоторой точке x₀,
2. Точки максимума или минимума (точки экстремума),
3. Интервалы возрастания и убывания функции (интервалы монотонности).

Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.

Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.

Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.

Вычисление значения производной. Метод двух точек

Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x₀, и требуется найти значение производной в этой точке, применяется следующий алгоритм:

1. Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x₁; y₁) и B (x₂; y₂). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
2. Зная координаты, легко вычислить приращение аргумента Δx = x₂ − x₁ и приращение функции Δy = y₂ − y₁.
3. Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.

Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.

Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

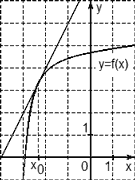
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x₂ − x₁ = −1 − (−3) = 2; Δy = y₂ − y₁ = 6 − 2 = 4.

Найдем значение производной: D = Δy/Δx = 4/2 = 2.

Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

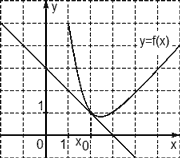
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x₂ − x₁ = 3 − 0 = 3; Δy = y₂ − y₁ = 0 − 3 = −3.

Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.

Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

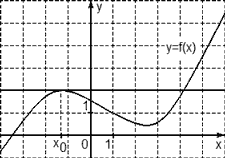
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x₂ − x₁ = 5 − 0 = 5; Δy = y₂ − y₁ = 2 − 2 = 0.

Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.

Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.

Вычисление точек максимума и минимума

Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:

1. Точка x₀ называется функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x₀) ≥ f(x).
2. Точка x₀ называется функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x₀) ≤ f(x).

Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:

1. Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
2. Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x₀ известно, что f’(x₀) ≠ 0, то возможны лишь два варианта: f’(x₀) ≥ 0 или f’(x₀) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
3. Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.

Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.

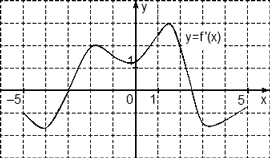
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:

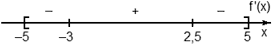
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.

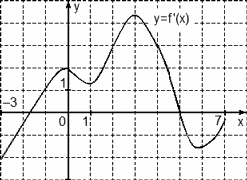
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:

Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].

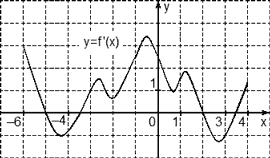
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:

На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.

Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.

Нахождение интервалов возрастания и убывания функции

В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:

1. Функция f(x) называется [a; b] если для любых двух точек x₁ и x₂ из этого отрезка верно утверждение: x₁ ≤ x₂ ⇒ f(x₁) ≤ f(x₂). Другими словами, чем больше значение аргумента, тем больше значение функции.
2. Функция f(x) называется [a; b] если для любых двух точек x₁ и x₂ из этого отрезка верно утверждение: x₁ ≤ x₂ ⇒ f(x₁) ≥ f(x₂). Т.е. большему значению аргумента соответствует меньшее значение функции.

Сформулируем достаточные условия возрастания и убывания:

1. Для того чтобы непрерывная функция f(x) возрастала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
2. Для того чтобы непрерывная функция f(x) убывала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.

Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:

1. Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
2. Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
3. Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.

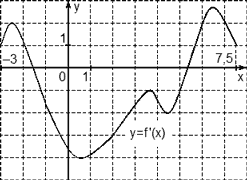
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:

Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

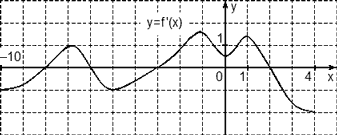
Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:

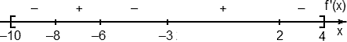
Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l₁ = − 6 − (−8) = 2;
l₂ = 2 − (−3) = 5.

Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l₂ = 5.

[spoiler title=”источники:”]

http://www.berdov.com/ege/derivative/summary/

[/spoiler]

Печать страницы

1

---

2

---

3

---

4

---

5

---

6

---

7

---

8

---

9

---

10

---

11

---

12

---

13

---

14

---

15

---

16

---

17

---

18

---

19

---

20

---

21

---

22

---

23

---

24

---

25

---

26

---

27

---

28

---

29

---

30

---

31

---

32

---

33

---

34

---

35

---

36

---

37

---

38

---

39

---

40

---

41

---

42

---

43

---

44

---

45

---

46

---

47

---

48

---

49

---

50

---

51

---

52

---

53

---

54

---

55

---

56

---

57

---

58

---

59

---

60

---

61

---

62

---

63

---

64

---

65

---

66

---

67

---

68

---

69

---

70

---

71

---

72

---

73

---

74

---

75

---

76

---

77

---

78

---

79

---

80

---

81

---

82

---

83

---

84

---

85

---

86

---

87

---

88

---

89

---

90

---

91

---

92

---

93

---

94

---

95

---

96

---

97

---

98

---

99

---

100

---

101

---

102

---

103

---

104

---

105

---

106

---

107

---

108

---

109

---

110

---

111

---

112

---

113

---

114

---

115

---

116

---

117

---

118

---

119

---

120

---

121

---

122

---

123

---

124

---

125

---

126

---

127

---

128

---

129

---

130

---

131

---

132

---

133

---

134

---

135

---

136

15 марта 2011

В задаче 6 дается график функции или производной, по которому требуется определить одну из следующих величин:

1. Значение производной в некоторой точке x₀,
2. Точки максимума или минимума (точки экстремума),
3. Интервалы возрастания и убывания функции (интервалы монотонности).

Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.

Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.

Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.

Вычисление значения производной. Метод двух точек

Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x₀, и требуется найти значение производной в этой точке, применяется следующий алгоритм:

1. Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x₁; y₁) и B (x₂; y₂). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
2. Зная координаты, легко вычислить приращение аргумента Δx = x₂ − x₁ и приращение функции Δy = y₂ − y₁.
3. Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.

Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.

Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x₂ − x₁ = −1 − (−3) = 2; Δy = y₂ − y₁ = 6 − 2 = 4.

Найдем значение производной: D = Δy/Δx = 4/2 = 2.

Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x₂ − x₁ = 3 − 0 = 3; Δy = y₂ − y₁ = 0 − 3 = −3.

Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.

Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x₂ − x₁ = 5 − 0 = 5; Δy = y₂ − y₁ = 2 − 2 = 0.

Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.

Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.

Вычисление точек максимума и минимума

Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:

1. Точка x₀ называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x₀) ≥ f(x).
2. Точка x₀ называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x₀) ≤ f(x).

Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:

1. Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
2. Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x₀ известно, что f’(x₀) ≠ 0, то возможны лишь два варианта: f’(x₀) ≥ 0 или f’(x₀) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
3. Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.

Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.

Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:

Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.

Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:

Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].

Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:

На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.

Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.

Нахождение интервалов возрастания и убывания функции

В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:

1. Функция f(x) называется возрастающей на отрезке [a; b] если для любых двух точек x₁ и x₂ из этого отрезка верно утверждение: x₁ ≤ x₂ ⇒ f(x₁) ≤ f(x₂). Другими словами, чем больше значение аргумента, тем больше значение функции.
2. Функция f(x) называется убывающей на отрезке [a; b] если для любых двух точек x₁ и x₂ из этого отрезка верно утверждение: x₁ ≤ x₂ ⇒ f(x₁) ≥ f(x₂). Т.е. большему значению аргумента соответствует меньшее значение функции.

Сформулируем достаточные условия возрастания и убывания:

1. Для того чтобы непрерывная функция f(x) возрастала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
2. Для того чтобы непрерывная функция f(x) убывала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.

Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:

1. Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
2. Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
3. Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.

Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:

Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:

Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l₁ = − 6 − (−8) = 2;
l₂ = 2 − (−3) = 5.

Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l₂ = 5.

Смотрите также:

1. ЕГЭ 2022, задание 6. Касательная к графику функции
2. ЕГЭ 2022, задание 6. Касательная к графику функции
3. Схема Бернулли. Примеры решения задач
4. Решение задач B6: №362—377
5. Четырехугольная пирамида: как найти координаты вершин
6. Нестандартная задача B2: студенты, гонорары и налоги

  Здравствуйте! Ударим по приближающемуся ЕГЭ качественной систематической подготовкой, и упорством в измельчении гранита науки!!! В конце  поста имеется конкурсная задача, будьте первым! В одной из статей данной рубрики мы с вами рассматривали задачи, в которых был дан график функции, и ставились различные вопросы, касающиеся экстремумов, промежутков возрастания (убывания) и прочие.

В этой статье рассмотрим задачи входящие в ЕГЭ по математике, в которых дан график производной функции, и ставятся следующие вопросы:

1. В какой точке заданного отрезка функция принимает наибольшее (или наименьшее) значение.

2. Найти количество точек максимума (или минимума) функции, принадлежащих заданному отрезку.

3. Найти количество точек экстремума функции, принадлежащих заданному отрезку.

4. Найти точку экстремума функции, принадлежащую заданному отрезку.

5. Найти промежутки возрастания (или убывания) функции и в ответе указать сумму целых точек, входящих в эти промежутки.

6. Найти промежутки возрастания (или убывания) функции. В ответе указать длину наибольшего из этих промежутков.

7. Найти количество точек, в которых касательная к графику функции параллельна прямой вида у = kx + b или совпадает с ней.

8. Найти абсциссу точки, в которой касательная к графику функции параллельна оси абсцисс или совпадает с ней.

Могут стоять и другие вопросы, но они не вызовут у вас затруднений, если вы поняли геометрический смысл производной и свойства производной для исследования функций (ссылки указаны на статьи, в которых представлена необходимая для решения информация, рекомендую повторить).

Основная информация (кратко):

1. Производная на интервалах возрастания имеет положительный знак.

Если производная в определённой точке из некоторого интервала имеет положительное значение,  то график функции на этом интервале возрастает.

2. На интервалах убывания производная имеет отрицательный знак.

Если производная в определённой точке из некоторого интервала имеет отрицательное значение,  то график функции на этом интервале убывает. 

3. Производная в точке х равна угловому коэффициенту касательной, проведённой к графику функции в этой же точке.

4. В точках экстремума (максимума-минимума) функции производная равна нулю. Касательная к графику функции в этой точке параллельна  оси ох.

Это нужно чётко уяснить и помнить!!!

Многих график производной «смущает». Некоторые по невнимательности принимают его за график самой функции. Поэтому в таких зданиях, где видите, что дан график, сразу же акцентируйте своё внимание в условии на том, что дано: график функции или  график производной функции?

Если это график производной функции, то относитесь к нему как бы к «отражению» самой функции, которое просто даёт вам информацию об этой функции.

Рассмотрим задание:

На рисунке изображен график у = f′(х) — производной функции  f(х), определенной на интервале (–2;21).

Ответим на следующие вопросы:

1. В какой точке отрезка [7;15] функция f(х) принимает наибольшее значение.

На заданном отрезке производная функции отрицательна, значит функция на этом отрезке убывает (она убывает от левой границы интервала к правой). Таким образом, наибольшее значение функции достигается на левой границе отрезка, т. е. в точке 7.

Ответ: 7

2. В какой точке отрезка [3;6] функция f(х) принимает наименьшее значение.

По данному графику производной можем сказать следующее. На заданном отрезке производная функции положительна, значит  функция на этом отрезке возрастает (она возрастает от левой границы интервала к правой). Таким образом, наименьшее значение функции достигается на левой границе отрезка, то есть в точке  х = 3.

Ответ: 3

3. Найдите количество точек максимума функции f(х), принадлежащих отрезку [0;20].

Точки максимума соответствуют точкам смены знака производной с положительного на отрицательный. Рассмотрим, где таким образом меняется знак.

На отрезке (3;6) производная положительна, на отрезке (6;16) отрицательна.

На отрезке (16;18) производная положительна, на отрезке (18;20) отрицательна.

Таким образом, на заданном отрезке [0;20] функция имеет две точки максимума х = 6 и  х = 18.

Ответ: 2

4. Найдите количество точек минимума функции f(х), принадлежащих отрезку [0;4].

Точки минимума соответствуют точкам смены знака производной с отрицательного на положительный.  У нас на  интервале (0;3) производная  отрицательна, на интервале (3;4) положительна.

Таким образом, на отрезке [0;4] функция имеет только одну точку минимума х = 3.

*Будьте внимательны при записи ответа – записывается количество точек, а не значение х, такую  ошибку можно допустит из-за невнимательности.

Ответ: 1

5. Найдите количество точек экстремума функции f(х), принадлежащих отрезку [0;20].

Обратите внимание, что необходимо найти количество точек экстремума (это и  точки максимума и точки минимума).

Точки экстремума соответствуют точкам смены знака производной (с положительного на отрицательный или наоборот). На данном в условии графике это нули функции. Производная обращается в нуль в точках 3, 6, 16, 18.

Таким образом, на отрезке [0;20] функция имеет 4 точки экстремума.

Ответ: 4

6. Найдите промежутки возрастания функции f(х). В ответе укажите сумму целых точек, входящих в эти промежутки.

Промежутки возрастания данной функции f(х) соответствуют промежуткам, на которых ее производная положительна, то есть интервалам (3;6) и (16;18). Обратите внимание, что границы интервала не входят в него (круглые скобки – границы не включены в интервал, квадратные – включены). Данные интервалы содержат целые точки 4, 5, 17. Их сумма равна: 4 + 5 + 17 = 26

Ответ: 26

7. Найдите промежутки убывания функции f(х) на заданном интервале. В ответе укажите сумму целых точек, входящих в эти промежутки.

Промежутки убывания функции f(х) соответствуют промежуткам, на которых производная функции отрицательна. В данной задаче это интервалы (–2;3), (6;16), (18;21).

Данные интервалы содержат следующие целые точки: –1, 0, 1, 2, 7, 8, 9, 10, 11, 12, 13, 14, 15, 19, 20. Их сумма равна:

 ( –1) + 0 + 1 + 2 + 7 + 8 + 9 + 10 +

+ 11 + 12 + 13 + 14 + 15 + 19 + 20  =  140

Ответ: 140

*Обращайте внимание в условии: включены ли границы в интервал или нет. Если границы будут включены, то и в рассматриваемых в процессе решения интервалах эти границы также необходимо учитывать.

8. Найдите промежутки возрастания функции f(х). В ответе укажите длину наибольшего из них.

Промежутки возрастания функции f(х) соответствуют промежуткам, на которых производная функции положительна. Мы уже указывали их: (3;6) и (16;18). Наибольшим из них  является интервал (3;6), его длина равна 3.

Ответ: 3

9. Найдите промежутки убывания функции f(х). В ответе укажите длину наибольшего из них.

Промежутки убывания функции f(х) соответствуют промежуткам, на которых производная функции отрицательна. Мы уже указывали их, это интервалы (–2;3), (6;16), (18;21), их длины соответственно равны 5, 10, 3.

Длина наибольшего равна 10.

Ответ: 10

10. Найдите количество точек, в которых касательная к графику функции f(х) параллельна прямой у = 2х + 3  или совпадает с ней.

Значение производной в точке касания равно угловому коэффициенту касательной. Так как касательная параллельна прямой у = 2х + 3 или совпадает с ней, то их угловые коэффициенты равны 2. Значит, необходимо найти количество точек, в которых у′(х₀) = 2. Геометрически это соответствует количеству точек пересечения графика производной с прямой  у = 2. На данном интервале таких точек 4.

Ответ: 4

11. Найдите точку экстремума функции f(х), принадлежащую отрезку [0;5].

Точка экстремума функции это такая точка, в которой её производная равна нулю, при чём в окрестности этой точки производная меняет знак (с положительного на отрицательный или наоборот). На отрезке [0;5] график производной пересекает ось абсцисс, производная меняет знак с отрицательного на положительный. Следовательно, точка х = 3 является точкой экстремума.

Ответ: 3

12. Найдите абсциссы точек, в которых касательные к графику у = f (x) параллельны оси абсцисс или совпадают с ней. В ответе укажите наибольшую из них.

Касательная к графику у = f (x) может быть параллельна оси абсцисс или совпадать с ней, только в точках, где производная равна нулю (это могут быть точки экстремума или стационарные точки, в окрестностях которых производная свой знак не меняет). По данному графику видно, что производная равна нулю в точках 3, 6, 16,18. Наибольшая равна 18.

Можно построить рассуждение таким образом:

Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна оси абсцисс или совпадает с ней, её угловой коэффициент равен 0  (действительно тангенс угла в ноль градусов равен нулю). Следовательно, мы ищем точку, в которой угловой коэффициент, равен нулю, а значит, и производная равна нулю. Производная равна нулю в той точке, в которой её график пересекает ось абсцисс, а это точки  3, 6, 16,18.

Ответ: 18

На рисунке изображен график у = f′(х) — производной функции f(х), определенной на интервале (–8;4). В какой точке отрезка [–7;–3] функция f(х) принимает наименьшее значение.

Посмотреть решение

На рисунке изображен график у = f′(х)  — производной функции f(х), определенной на интервале (–7;14). Найдите количество точек максимума функции f(х),  принадлежащих отрезку [–6;9].

Посмотреть решение

На рисунке изображен график у = f′(х)  — производной функции f(х), определенной на интервале (–18;6). Найдите количество точек минимума функции f(х),  принадлежащих отрезку [–13;1].

Посмотреть решение

На рисунке изображен график у = f′(х)   — производной функции f(х), определенной на интервале (–11; –11). Найдите количество точек экстремума функции f(х),  принадлежащих отрезку [–10; –10].

Посмотреть решение

На рисунке изображен график у = f′(х)   — производной функции f(х), определенной на интервале (–7;4). Найдите промежутки возрастания функции f(х). В ответе укажите сумму целых точек, входящих в эти промежутки.

Посмотреть решение

На рисунке изображен график у = f′(х) — производной функции f(х), определенной на интервале (–5;7). Найдите промежутки убывания функции f(х). В ответе укажите сумму целых точек, входящих в эти промежутки.

Посмотреть решение

На рисунке изображен график у = f′(х)   — производной функции f(х), определенной на интервале (–11;3). Найдите промежутки возрастания функции f(х). В ответе укажите длину наибольшего из них.

Посмотреть решение

На рисунке изображен график у = f′(х) — производной функции f(х), определенной на интервале (–2;12). Найдите промежутки убывания функции f(х). В ответе укажите длину наибольшего из них.

Посмотреть решение

На рисунке изображен график у = f′(х) — производной функции f(х), определенной на интервале (–10;2). Найдите количество точек, в которых касательная к графику функции f(х) параллельна прямой       у = –2х – 11 или совпадает с ней.

Посмотреть решение

На рисунке изображен график у = f′(х) — производной функции f(х), определенной на интервале (–4;8). Найдите точку экстремума функции f(х), принадлежащую отрезку [–2;6].

Посмотреть решение

На рисунке изображен график у = f′(х) — производной функции f(х). Найдите абсциссу точки, в которой касательная к графику у=f(х) параллельна прямой у = 2х – 2 или совпадает с ней.

Посмотреть решение

На рисунке изображен график  у = f′(х) — производной функции f(х). Найдите абсциссу точки, в которой касательная к графику у = f(х)  параллельна оси абсцисс или совпадает с ней.

Посмотреть решение

На этом всё. В данной рубрике мы продолжим рассматривать задачи, не пропустите!

Условие задачи то же (которую мы рассматривали). Найдите сумму трёх чисел:

1. Сумма квадратов экстремумов функции f (х).

2. Разность квадратов суммы точек максимума и суммы точек минимума функции f (х).

3. Количество касательных к f (х), параллельных прямой у = –3х + 5.

Первый, кто даст верный ответ, получит поощрительный приз – 150 рублей. Ответы пишите в комментариях. Если это ваш первый комментарий на блоге, то сразу он не появится, чуть позже (не беспокойтесь, время написания комментария регистрируется). 

Успеха вам!

С уважением, Александр Крутицих.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.