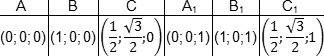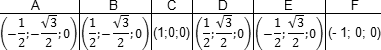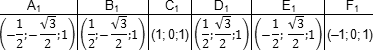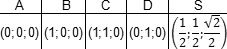Метод координат в пространстве
Для того, чтобы использовать метод координат, надо хорошо знать формулы. Их три:
Главная формула — косинус угла φ между векторами a = (x1; y1; z1) и b = (x2; y2; z2):
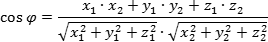
На первый взгляд, выглядит угрожающе, но достаточно немного практики — и все будет работать великолепно.
Задача. Найти косинус угла между векторами a = (4; 3; 0) и b = (0; 12; 5).
Решение. Поскольку координаты векторов нам даны, подставляем их в первую формулу:
Задача. Составить уравнение плоскости, проходящей через точки M = (2; 0; 1), N = (0; 1; 1) и K = (2; 1; 0), если известно, что она не проходит через начало координат.
Решение. Общее уравнение плоскости: Ax + By + Cz + D = 0, но, поскольку искомая плоскость не проходит через начало координат — точку (0; 0; 0) — то положим D = 1. Поскольку эта плоскость проходит через точки M, N и K, то координаты этих точек должны обращать уравнение в верное числовое равенство.
Подставим вместо x, y и z координаты точки M = (2; 0; 1). Имеем:
A · 2 + B · 0 + C · 1 + 1 = 0 ⇒ 2A + C + 1 = 0;
Аналогично, для точек N = (0; 1; 1) и K = (2; 1; 0) получим уравнения:
A · 0 + B · 1 + C · 1 + 1 = 0 ⇒ B + C + 1 = 0;
A · 2 + B · 1 + C · 0 + 1 = 0 ⇒ 2A + B + 1 = 0;
Итак, у нас есть три уравнения и три неизвестных. Составим и решим систему уравнений:
Получили, что уравнение плоскости имеет вид: − 0,25x − 0,5y − 0,5z + 1 = 0.
Задача. Плоскость задана уравнением 7x − 2y + 4z + 1 = 0. Найти координаты вектора, перпендикулярного данной плоскости.
Решение. Используя третью формулу, получаем n = (7; − 2; 4) — вот и все!
Вычисление координат векторов
А что, если в задаче нет векторов — есть только точки, лежащие на прямых, и требуется вычислить угол между этими прямыми? Все просто: зная координаты точек — начала и конца вектора — можно вычислить координаты самого вектора.
Чтобы найти координаты вектора, надо из координат его конца вычесть координаты начала.
Эта теорема одинаково работает и на плоскости, и в пространстве. Выражение «вычесть координаты» означает, что из координаты x одной точки вычитается координата x другой, затем то же самое надо сделать с координатами y и z. Вот несколько примеров:
Задача. В пространстве расположены три точки, заданные своими координатами: A = (1; 6; 3), B = (3; − 1; 7) и C = (− 4; 3; − 2). Найти координаты векторов AB, AC и BC.
Рассмотрим вектор AB: его начало находится в точке A, а конец — в точке B. Следовательно, чтобы найти его координаты, надо из координат точки B вычесть координаты точки A:
AB = (3 − 1; − 1 − 6; 7 − 3) = (2; − 7; 4).
Аналогично, начало вектора AC — все та же точка A, зато конец — точка C. Поэтому имеем:
AC = (− 4 − 1; 3 − 6; − 2 − 3) = (− 5; − 3; − 5).
Наконец, чтобы найти координаты вектора BC, надо из координат точки C вычесть координаты точки B:
BC = (− 4 − 3; 3 − (− 1); − 2 − 7) = (− 7; 4; − 9).
Ответ: AB = (2; − 7; 4); AC = (− 5; − 3; − 5); BC = (− 7; 4; − 9)
Обратите внимание на вычисление координат последнего вектора BC: очень многие ошибаются, когда работают с отрицательными числами. Это касается переменной y: у точки B координата y = − 1, а у точки C y = 3. Получаем именно 3 − (− 1) = 4, а не 3 − 1, как многие считают. Не допускайте таких глупых ошибок!
Вычисление направляющих векторов для прямых
Если вы внимательно прочитаете задачу C2, то с удивлением обнаружите, что никаких векторов там нет. Там только прямые да плоскости.
Для начала разберемся с прямыми. Здесь все просто: на любой прямой найдутся хотя бы две различные точки и, наоборот, любые две различные точки задают единственную прямую.
Кто-нибудь понял, что написано в предыдущем абзаце? Я и сам не понял, поэтому объясню проще: в задаче C2 прямые всегда задаются парой точек. Если ввести систему координат и рассмотреть вектор с началом и концом в этих точках, получим так называемый для прямой:
Зачем нужен этот вектор? Дело в том, что — это угол между их направляющими векторами. Таким образом, мы переходим от непонятных прямых к конкретным векторам, координаты которых легко считаются. Насколько легко? Взгляните на примеры:
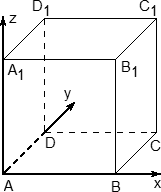
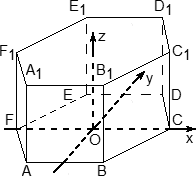
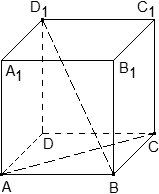
Задача. В кубе ABCDA1B1C1D1 проведены прямые AC и BD1. Найдите координаты направляющих векторов этих прямых.
Поскольку длина ребер куба в условии не указана, положим AB = 1. Введем систему координат с началом в точке A и осями x, y, z, направленными вдоль прямых AB, AD и AA1 соответственно. Единичный отрезок равен AB = 1.
Теперь найдем координаты направляющего вектора для прямой AC. Нам потребуются две точки: A = (0; 0; 0) и C = (1; 1; 0). Отсюда получаем координаты вектора AC = (1 − 0; 1 − 0; 0 − 0) = (1; 1; 0) — это и есть направляющий вектор.
Теперь разберемся с прямой BD1. На ней также есть две точки: B = (1; 0; 0) и D1 = (0; 1; 1). Получаем направляющий вектор BD1 = (0 − 1; 1 − 0; 1 − 0) = (− 1; 1; 1).
Ответ: AC = (1; 1; 0); BD1 = (− 1; 1; 1)
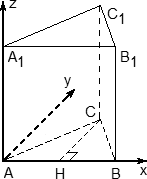
Задача. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, проведены прямые AB1 и AC1. Найдите координаты направляющих векторов этих прямых.
Введем систему координат: начало в точке A, ось x совпадает с AB, ось z совпадает с AA1, ось y образует с осью x плоскость OXY, которая совпадает с плоскостью ABC.
Для начала разберемся с прямой AB1. Тут все просто: у нас есть точки A = (0; 0; 0) и B1 = (1; 0; 1). Получаем направляющий вектор AB1 = (1 − 0; 0 − 0; 1 − 0) = (1; 0; 1).
Теперь найдем направляющий вектор для AC1. Все то же самое — единственное отличие в том, что у точки C1 иррациональные координаты. Итак, A = (0; 0; 0), поэтому имеем:
Небольшое, но очень важное замечание насчет последнего примера. Если начало вектора совпадает с началом координат, вычисления резко упрощаются: координаты вектора просто равны координатам конца. К сожалению, это верно лишь для векторов. Например, при работе с плоскостями присутствие на них начала координат только усложняет выкладки.
Вычисление нормальных векторов для плоскостей
Нормальные векторы — это не те векторы, у которых все в порядке, или которые чувствуют себя хорошо. По определению, нормальный вектор (нормаль) к плоскости — это вектор, перпендикулярный данной плоскости.
Другими словами, — это вектор, перпендикулярный любому вектору в данной плоскости. Наверняка вы встречали такое определение — правда, вместо векторов речь шла о прямых. Однако чуть выше было показано, что в задаче C2 можно оперировать любым удобным объектом — хоть прямой, хоть вектором.
Еще раз напомню, что всякая плоскость задается в пространстве уравнением Ax + By + Cz + D = 0, где A, B, C и D — некоторые коэффициенты. Не умаляя общности решения, можно полагать D = 1, если плоскость не проходит через начало координат, или D = 0, если все-таки проходит. В любом случае, координаты нормального вектора к этой плоскости равны n = (A; B; C).
Итак, плоскость тоже можно успешно заменить вектором — той самой нормалью. Всякая плоскость задается в пространстве тремя точками. Как найти уравнение плоскости (а следовательно — и нормали), мы уже обсуждали в самом начале статьи. Однако этот процесс у многих вызывает проблемы, поэтому приведу еще парочку примеров:
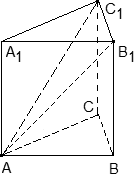
Задача. В кубе ABCDA1B1C1D1 проведено сечение A1BC1. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA1 соответственно.
Поскольку плоскость не проходит через начало координат, ее уравнение выглядит так: Ax + By + Cz + 1 = 0, т.е. коэффициент D = 1. Поскольку эта плоскость проходит через точки A1, B и C1, то координаты этих точек обращают уравнение плоскости в верное числовое равенство.
Подставим вместо x, y и z координаты точки A1 = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = − 1;
Аналогично, для точек B = (1; 0; 0) и C1 = (1; 1; 1) получим уравнения:
A · 1 + B · 0 + C · 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = − 1;
A · 1 + B · 1 + C · 1 + 1 = 0 ⇒ A + B + C + 1 = 0;
Но коэффициенты A = − 1 и C = − 1 нам уже известны, поэтому остается найти коэффициент B:
B = − 1 − A − C = − 1 + 1 + 1 = 1.
Получаем уравнение плоскости: − A + B − C + 1 = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; − 1).
Задача. В кубе ABCDA1B1C1D1 проведено сечение AA1C1C. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA1 соответственно.
В данном случае плоскость проходит через начало координат, поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz = 0. Поскольку плоскость проходит через точки A1 и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство.
Подставим вместо x, y и z координаты точки A1 = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;
Аналогично, для точки C = (1; 1; 0) получим уравнение:
A · 1 + B · 1 + C · 0 = 0 ⇒ A + B = 0 ⇒ A = − B;
Положим B = 1. Тогда A = − B = − 1, и уравнение всей плоскости имеет вид: − A + B = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; 0).
Вообще говоря, в приведенных задачах надо составлять систему уравнений и решать ее. Получится три уравнения и три переменных, но во втором случае одна из них будет свободной, т.е. принимать произвольные значения. Именно поэтому мы вправе положить B = 1 — без ущерба для общности решения и правильности ответа.
Координаты середины отрезка
Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.
Итак, пусть отрезок задан своими концами — точками A = (xa; ya; za) и B = (xb; yb; zb). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:
Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.
Задача. Единичный куб ABCDA1B1C1D1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA1 соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A1B1. Найдите координаты этой точки.
Поскольку точка K — середина отрезка A1B1, ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A1 = (0; 0; 1) и B1 = (1; 0; 1). Теперь найдем координаты точки K:
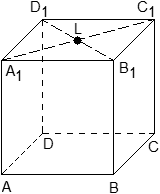
Задача. Единичный куб ABCDA1B1C1D1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA1 соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A1B1C1D1.
Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A1L = C1L, т.е. точка L — это середина отрезка A1C1. Но A1 = (0; 0; 1), C1 = (1; 1; 1), поэтому имеем:
Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и
.
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и
. Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и
:
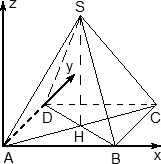
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму:
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и
, а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
То есть A + C + D = 0.
Аналогично для точки K:
Получили систему из трех уравнений:
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
Выразим C и B через A и подставим в третье уравнение:
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
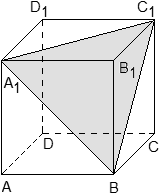
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать “параллелепипед”.
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор
.
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей),
— нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
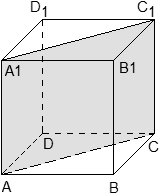
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD =
. Высота параллелепипеда AA1 =
. Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Метод координат в задачах типа С2.
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»
Сертификат и скидка на обучение каждому участнику
В ы б е р е м н а ч а л о к оо р д и н а т . П р о в е д е м т ри в з а и м н о п е р п е н д и к у л яр ны е о с и х , y и z . Выберем м а с ш т а б .
П о л у ч и л а с ь с и с т е м а к о о р д и н а т в т р е х м е р н о м п р о с т р а н с т в е .
К а ж д а я т о ч к а х а р а к т е р и з у е т с я т р е м я ч и с л а м и – к оо р д и н а т а м и п о x , y и z . З а п и с ь M ( − 1 ; 3 ; 2 ) о з н а ч а е т , ч т о к оо р д и н а т а т о ч к и M п о x ( а б с ц и сс а ) р а в н а − 1 , к оо р д и н а т а п о y ( о р д и н а т а ) р а в н а 3 , а к оо р д и н а т а п о z ( а пп л и к а т а ) р а в н а 2 .
В е к т о р ы в п р о с т р а н с т в е о п р е д е л яю т с я т а к ж е , к а к и н а п л о с к о с т и.
Э т о н а п р а в л е н ны е о т р е з к и, и м е ю щ и е н а ч а л о и к о н е ц . Т о л ь к о в п р о с т р а н с т в е в е к т о р з а д а е т с я т р е м я к оо р д и н а т а м и x , y и z :
ﺂ؟ 
Чтобы н а й т и к о о р д и н а т ы в е к т о р а , так же, как и на плоскости, и з к оо р д и н а т ы к о н ц а надо в ы ч есть к оо р д и н а т у н а ч а ла.
1.
2. 
Если точка M – середина отрезка AB , то ее координаты находятся по формуле:
3. 
4. 
 – сумма векторов.
– сумма векторов.
5. 
6. 
7. 
8. 
2. Введение системы координат.
Метод координат – это, конечно, очень хорошо, но в настоящих задачах C 2 никаких координат и векторов нет, поэтому их надо вводить.
Самое замечательное свойство заключается в том, что не имеет никакого значения как именно вводить систему координат. Если все вычисления будут правильными, то и ответ будет правильным.
2.1 Координаты куба.
Система координат вводится очень просто:
Начало координат – в точке A
Если ребро куба не указано, то принимаем его за единичный отрезок;
Ось x направляем по ребру АВ, у – по ребру А D , а ось z – по ребру AA 1 .
Теперь у каждой вершины куба есть координаты:
A (0; 0; 0), B (1; 0; 0), C (1; 1; 0), D (0; 1; 0),
2.2 Координаты правильной треугольной призмы
A (1; 0; 0), B 

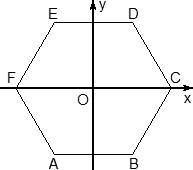
2.3 Координаты правильной шестиугольной призмы

2.4 Координаты правильной четырехугольной пирамиды
Введем систему координат с началом в точке А
Найдем координаты точки S . Рассмотрим треугольники ASH и ABH
AS = AB = 1 по условию;
Угол AHS = AHB = 90°, поскольку SH — высота, а AH ⊥ HB как диагонали квадрата;
Сторона AH — общая.
Следовательно, прямоугольные треугольники ASH и ABH равны по одному катету и гипотенузе. Значит, SH = BH = 0,5 · BD . Но BD — диагональ квадрата со стороной 1. Поэтому имеем:
Итак, координаты точки S :
Рассмотрим случай, если боковые ребра пирамиды не равны ребрам основания. В этом случае рассмотрим треугольник AHS :
Треугольник AHS — прямоугольный , причем гипотенуза AS — это одновременно и боковое ребро исходной пирамиды SABCD . Катет: AH = 0,5 · AC . Оставшийся катет SH найдем по теореме Пифагора . Это и будет координата z для точки S .
3. Матрицы и определители второго и третьего порядка.
Определение: Таблица, составленная из четырёх чисел 

Определение: Число ∆ называется определителем или детерминантом матрицы.
∆ =
Определитель третьего порядка можно вычислить так:
4. Метод координат в пространстве
4.1 Угол между прямыми.
Вычисление направляющих векторов для прямых.
В задаче С2 прямые всегда задаются парой точек. Если ввести систему координат и рассмотреть вектор с началом и концом в этих точках, получим направляющий вектор для прямой.
α -угол между прямыми
3.1 Угол между двумя прямыми – это угол между их направляющими векторами.
Задача 1 .
В единичном кубе ABCDA 1 B 1 C 1 D 1 найдите угол между прямыми AE и BF , где E – середина ребра A 1 B 1 , где Е – середина ребра А 1 В 1 а F – середина ребра B 1 C 1.
Решение (1 способ)
K – середина A 1 D 1 AK ║ BF угол KAE = φ
По теореме Пифагора
По теореме косинусов для ∆ AKE
KE ² = AE ² + AK ² – 2 * AE * AK * cos φ
cos φ =0,8 φ = arccos 0.8
Решение (2 способ)
С помощью векторов и координат легко найти угол между прямыми.
А если требуется найти угол между плоскостями или между прямой и плоскостью, то для этого нам понадобится уравнение плоскости в пространстве.
4.2 Плоскость в пространстве задается уравнением.
Ax + By + Cz + D =0,
где A , B и С – координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; -2; 0) и К (4; 1; 2)
Уравнение плоскости выглядит так:
Ax + By + Cz + D =0
Получим систему из трех уравнений:
В ней четыре неизвестных: A , B , С и D . Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило – простое вместо одной из переменных можно взять любое число, не равное нулю.
Решив систему, получим:
A =- 

Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на -3. Тогда коэффициенты станут целыми:
Вектор 
Если плоскость проходит через начало координат, то D =0 (так как D ≠0 не позволит получить верное числовое равенство).
Уравнение плоскости, проходящей, через заданную точку 
Уравнение плоскости можно составить и с помощью определителя третьего порядка :
Пусть имеем точки

Тогда уравнение плоскости, проходящей через эти три точки ,будет иметь вид:

4.3 Угол между плоскостями равен углу между нормалями к этим плоскостям:
cos φ =
При пересечении двух плоскостей образуется четыре угла . Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения – чтобы косинус угла был неотрицателен.
В кубе A B C D A 1 B 1 C 1 D 1 то ч к и E и F с середины ребер соответственно A 1 B 1 и
A 1 D 1 . Найдите косинус у г л а между плоскостями A E F и B D D 1 .
В и д н о , ч т о п л о с к о с т и A E F и B D D 1 пересекаются где-то вне куба . В классическом решении пришлось бы строить пересечения . Н о координатный м е т о д з н а ч и т е л ь н о в с ё у п р о щ а е т . Достаточно о т м е т и ть к оо р д и н а т ы н у ж н ы х т о ч е к и н а й ти у г о л м е ж д у н о р м а л я м и к п л о с к о с т я м A E F и B D D 1 .
A (0; 0; 0), C (1; 1; 0)
Сначала – нормаль к плоскости BDD 1 . Мы можем подставить координаты точек B , D и D 1 в уравнение плоскости и найти координаты вектора нормали. А можно увидеть нужную нормаль на чертеже. Ведь плоскость BDD 1 – это диагональное сечение куба. Вектор 
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF .
A 

Составим уравнение плоскости:
Уравнение плоскости AEF : 2 x +2 y – z =0
Нормаль к плоскости AEF : 
Найдем угол между плоскостями:
4.4 Угол между прямой и плоскостью

В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, найдите угол между прямой DE , где E -середина апофемы SF грани ASB грани и плоскостью ASC
OB – вектор нормали плоскости ASC
DE – направляющий вектор прямой
OB – 
DE – 


4.5 Расстояние от точки до плоскости

В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , все рёбра которой равны 1, найдите расстояние от точки E до прямой B 1 C 1 .
Решение (1 способ)
1) Рассмотрим Δ CDE :
по теореме косинусов:
СЕ 2 = 2 С D 2 – 2CD 2 cos120° = 2 + 2*1/2 = 3 =>
CE =
2) Рассмотрим ΔС 1 СЕ: он прямоугольный, т.к. С 1 С перпендикулярна плоскости нижнего основания => CC 1 перпендикулярна СЕ.
По теореме Пифагора:
С 1 Е 2 = ( 
3) Рассмотрим ΔBCE : он прямоугольный , т.к. 120° – 60°:2 = 90° (из Δ CDE )
ВЕ 2 = ( 
4) Рассмотрим ΔВВ 1 Е: он прямоугольный, т.к. ВВ 1 перпендикулярна ВЕ,
по теореме Пифагора:
В 1 Е 2 = В 1 В 2 + ВЕ 2 = 4 + 1 = 5, ВЕ =
С 1 Е = 2, С 1 В 1 = 1, В 1 Е = 

6) Искомое расстояние от точки Е до прямой В 1 С 1 – это длина С 1 Е = 2
1) Поместим призму в прямоугольную систему координат, расположив координатные оси, как показано на рисунке. СС 1 , СВ и СЕ попарно перпендикулярны, поэтому можно направить вдоль них координатные оси. Получаем координаты:
С 1 (0;0;1), Е ( 
2) Найдем координаты векторов С 1 В 1 и С 1 Е:
С 1 В 1 (0;1;0), С 1 Е ( 
3) Найдем косинус угла между С 1 В 1 и С 1 Е, используя скалярное произведение векторов С 1 В 1 и С 1 Е:
cosβ = 
4) С 1 Е = 
4.6 Расстояние между скрещивающимися прямыми
в пространстве — это длина их общего перпендикуляра. Общий перпендикуляр скрещивающихся прямых — отрезок с концами на этих прямых, перпендикулярный обеим этим прямым.
Если прямые в пространстве пересекаются, расстояние между ними считается равным 0.
Пусть есть не пересекающиеся в пространстве прямые a и b.
Построим плоскости α и β так, чтобы эти плоскости были параллельны, плоскость α содержала в себе прямую a , плоскость β содержала в себе прямую b .
Расстоянием между прямыми a и b будет расстояние между плоскостями α и β .
Александров А.Д. и др
. Геометрия для 10-11 классов: Учеб. пособие для учащихся школ и классов с углубленным изучением математики . Просвещение, 1992.
2. Ю.М.Нейман, Т.М. Королева, Е.Г. Маркарян .
Математика: ЕГЭ: Учебно-справочные материалы «Просвещение», 2011.
3 . Погорелов А.В.
Геометрия: Учеб. для 7-11 кл. сред. шк., 4-е изд. – М.: Просвещение, 1993.
ЕГЭ 2011. Математика. Задача С2. Геометрия. Стереометрия
. Под ред. А. Л. Семенова и И.В.Ященко. МЦНМО, 2011.
Нахождение углов между прямыми и плоскостями (координатно-векторный метод) . Математика в школе. – 2011. – №4.
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/vektory-v-prostranstve-i-metod-koordinat/
http://infourok.ru/metod_koordinat_v_zadachah_tipa_s2.-305542.htm
[/spoiler]
Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.
Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора:
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и
.
Сумма векторов:
Разность векторов:
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и
. Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и
:
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
:
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму.
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и
, а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
Для точки M:
То есть A + C + D = 0.
Для точки N:
Аналогично для точки K:
Получили систему из трех уравнений:
.
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
;
.
Выразим C и B через A и подставим в третье уравнение:
.
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Упростим систему:
.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать “параллелепипед”.
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Итак, AA1 = √3
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор
.
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей),
— нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD =
. Высота параллелепипеда AA1 =
. Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Векторы в пространстве и метод координат» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
Как найти координаты вершин куба в пространстве
Содержание
- 11 класс. Геометрия. Метод координат в пространстве. Прямоугольная система координат.
- Вопросы
- Поделись с друзьями
- Комментарии преподавателя
- 1. Введение
- 2. Координаты вектора
- Координаты куба
- Координаты трехгранной призмы
- Координаты шестигранной призмы
- Координаты четырехугольной пирамиды
11 класс. Геометрия. Метод координат в пространстве. Прямоугольная система координат.
- Оглавление
- Занятия
- Обсуждение
- О курсе
Вопросы
Задай свой вопрос по этому материалу!
Поделись с друзьями
Комментарии преподавателя
1. Введение
Если через точку О в пространстве мы проведем три перпендикулярные прямые, назовем их, выберем направление, обозначим единичные отрезки, то мы получим прямоугольную систему координат в пространстве. Оси координат называются так: Ох – ось абсцисс, Оy – ось ординат и Оz – ось аппликат. Вся система координат обозначается – Oxyz. Таким образом, появляются три координатные плоскости: Оxy, Оxz, Оyz.
Приведем пример построения точки В(4;3;5) в прямоугольной системе координат (см. Рис. 1).
Рис. 1. Построение точки B в пространстве
Первая координата точки B – 4, поэтому откладываем на Ox 4, проводим прямую параллельно оси Oy до пересечения с прямой, проходящей через у=3. Таким образом, мы получаем точку K. Эта точка лежит в плоскости Oxy и имеет координаты K(4;3;0). Теперь нужно провести прямую параллельно оси Oz. И прямую, которая проходит через точку с аппликатой 5 и параллельна диагонали параллелограмма в плоскости Oxy. На их пересечении мы получим искомую точку B.
Рассмотрим расположение точек, у которых одна или две координаты равны 0 (см. Рис. 2).
Например, точка A(3;-1;0). Нужно продолжить ось Oy влево до значения -1, найти точку 3 на оси Ox, и на пересечении линий, проходящих через эти значения, получаем точку А. Эта точка имеет аппликату 0, а значит, она лежит в плоскости Oxy.
Точка C(0;2;0) имеет абсциссу и аппликату 0 – не отмечаем. Ордината равна 2, значит точка C лежит только на оси Oy, которая является пересечением плоскостей Oxy и Oyz.
Чтобы отложить точку D(-4;0;3) продолжаем ось Ox назад за начало координат до точки -4. Теперь восстанавливаем из этой точки перпендикуляр – прямую, параллельную оси Oz до пересечения с прямой, параллельной оси Ox и проходящей через значение 3 на оси Oz. Получаем току D(-4;0;3). Так как ордината точки равна 0, значит точка D лежит в плоскости Oxz.
Следующая точка E(0;5;-3). Ордината точки 5, аппликата -3, проводим прямые проходящие через эти значения на соответствующих осях, и на их пересечении получаем точку E(0;5;-3). Эта точка имеет первую координату 0, значит она лежит в плоскости Oyz.
2. Координаты вектора
Начертим прямоугольную систему координат в пространстве Oxyz. Зададим в пространстве прямоугольную систему координат Oxyz. На каждой из положительных полуосей отложим от начала координат единичный вектор, т. е. вектор, длина которого равна единице. Обозначим единичный вектор оси абсцисс
Рис. 1. Разложение вектора по трем координатным векторам
Возьмем вектор
Коэффициенты этого разложения x, y и z называются координатами вектора в пространстве.
Рассмотрим правила, которые позволяют по координатам данных векторов найти координаты их суммы и разности, а также координаты произведения данного вектора на данное число.

2) Вычитание:
3) Умножение на число: 
Возьмем точку A(x1;y1;z1) и точку B(x2;y2;z2) (см. рис. 3). Представим вектор
Рассмотрим примеры, иллюстрирующие свойства векторов и их выражение через координаты. Возьмем векторы
Теперь умножаем число 3 на каждую координату в скобках, и то же самое делаем с 2:
У нас получилась сумма трех векторов, складываем их по изученному выше свойству:
Ответ:
Дано: Треугольная пирамида AOBC (см. рис. 4). Плоскости AOB, AOC и OCB – попарно перпендикулярны. OA=3, OB=7, OC=4; M — сер.AC; N — сер.OC; P – сер. CB.
Найти:
Решение: Введем прямоугольную систему координат Oxyz с началом отсчета в точке O. По условию обозначаем точки A, B и C на осях и середины ребер пирамиды – M, P и N. По рисунку находим координаты вершин пирамиды: A(3;0;0), B(0;7;0), C(0;0;4).
Так как координаты вектора 


Вектора
Метод координат — это, конечно, очень хорошо, но в настоящих задачах C2 никаких координат и векторов нет. Поэтому их придется вводить. Да-да, вот так взять и ввести: указать начало отсчета, единичный отрезок и направление осей x, y и z.
Самое замечательное свойство этого метода заключается в том, что не имеет никакого значения, как именно вводить систему координат. Если все вычисления будут правильными, то и ответ будет правильным.
Тем не менее, приведу некоторые рекомендации, как лучше ввести систему координат для самых часто встречающихся в задаче C2 многогранников. С указанием конкретных точек. Во всех случаях упор делается на минимизацию объема вычислений.
Координаты куба
Если в задаче C2 будет куб — считайте, что вам повезло. Это самый простой многогранник, все двугранные углы которого равны 90°.
Система координат также вводится очень просто:
- Начало координат — в точке A;
- Чаще всего ребро куба не указано, поэтому принимаем его за единичный отрезок;
- Ось x направляем по ребру AB, y — по ребру AD, а ось z — по ребру AA1.
Обратите внимание: ось z направляется вверх! После двумерной системы координат это несколько непривычно, но на самом деле очень логично.
Итак, теперь у каждой вершины куба есть координаты. Соберем их в таблицу — отдельно для нижней плоскости куба:
| Точка | A | B | C | D |
| Координаты | (0; 0; 0) | (1; 0; 0) | (1; 1; 0) | (0; 1; 0) |
| Точка | A1 | B1 | C1 | D1 |
| Координаты | (0; 0; 1) | (1; 0; 1) | (1; 1; 1) | (0; 1; 1) |
Несложно заметить, что точки верхней плоскости отличаются соответствующих точек нижней только координатой z. Например, B = (1; 0; 0), B1 = (1; 0; 1). Главное — не запутаться!
Координаты трехгранной призмы
Призма — это уже намного веселее. При правильном подходе достаточно знать координаты только нижнего основания — верхнее будет считаться автоматически.
В задачах C2 встречаются исключительно правильные трехгранные призмы (прямые призмы, в основании которых лежит правильный треугольник). Для них система координат вводится почти так же, как и для куба. Кстати, если кто не в курсе, куб — это тоже призма, только четырехгранная.
Итак, поехали! Вводим систему координат:
- Начало координат — в точке A;
- Сторону призмы принимаем за единичный отрезок, если иное не указано в условии задачи;
- Ось x направляем по ребру AB, z — по ребру AA1, а ось y расположим так, чтобы плоскость OXY совпадала с плоскостью основания ABC.
Здесь требуются некоторые пояснения. Дело в том, что ось y НЕ совпадает с ребром AC, как многие считают. А почему не совпадает? Подумайте сами: треугольник ABC — равносторонний, в нем все углы по 60°. А углы между осями координат должны быть по 90°, поэтому сверху картинка будет выглядеть так:
Надеюсь, теперь понятно, почему ось y не пойдет вдоль AC. Проведем в этом треугольнике высоту CH. Треугольник ACH — прямоугольный, причем AC = 1, поэтому AH = 1 · cos A = cos 60°; CH = 1 · sin A = sin 60°. Эти факты нужны для вычисления координат точки C.
Теперь взглянем на всю призму вместе с построенной системой координат:
Получаем следующие координаты точек:
Как видим, точки верхнего основания призмы снова отличаются от соответствующих точек нижнего лишь координатой z. Основная проблема — это точки C и C1. У них есть иррациональные координаты, которые надо просто запомнить. Ну, или понять, откуда они возникают.
Координаты шестигранной призмы
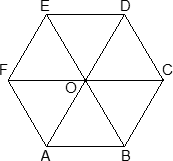
Шестигранная призма — это «клонированная» трехгранная. Можно понять, как это происходит, если взглянуть на нижнее основание — обозначим его ABCDEF. Проведем дополнительные построения: отрезки AD, BE и CF. Получилось шесть треугольников, каждый из которых (например, треугольник ABO) является основанием для трехгранной призмы.
Теперь введем собственно систему координат. Начало координат — точку O — поместим в центр симметрии шестиугольника ABCDEF. Ось x пойдет вдоль FC, а ось y — через середины отрезков AB и DE. Получим такую картинку:
Обратите внимание: начало координат НЕ совпадает с вершиной многогранника! На самом деле, при решении настоящих задач вы обнаружите, что это очень удобно, поскольку позволяет значительно уменьшить объем вычислений.
Осталось добавить ось z. По традиции, проводим ее перпендикулярно плоскости OXY и направляем вертикально вверх. Получим итоговую картинку:
Запишем теперь координаты точек. Предположим, что все ребра нашей правильной шестигранной призмы равны 1. Итак, координаты нижнего основания:
Координаты верхнего основания сдвинуты на единицу по оси z:
Координаты четырехугольной пирамиды
Пирамида — это вообще очень сурово. Мы разберем только самый простой случай — правильную четырехугольную пирамиду, все ребра которой равны единице. Однако в настоящих задачах C2 длины ребер могут отличаться, поэтому ниже приведена и общая схема вычисления координат.
Итак, правильная четырехугольная пирамида. Это такая же, как у Хеопса, только чуть поменьше. Обозначим ее SABCD, где S — вершина. Введем систему координат: начало в точке A, единичный отрезок AB = 1, ось x направим вдоль AB, ось y — вдоль AD, а ось z — вверх, перпендикулярно плоскости OXY. Для дальнейших вычислений нам потребуется высота SH — вот и построим ее. Получим следующую картинку:
Теперь найдем координаты точек. Для начала рассмотрим плоскость OXY. Здесь все просто: в основании лежит квадрат, его координаты известны. Проблемы возникают с точкой S. Поскольку SH — высота к плоскости OXY, точки S и H отличаются лишь координатой z. Собственно, длина отрезка SH — это и есть координата z для точки S, поскольку H = (0,5; 0,5; 0).
Заметим, что треугольники ABC и ASC равны по трем сторонам (AS = CS = AB = CB = 1, а сторона AC — общая). Следовательно, SH = BH. Но BH — половина диагонали квадрата ABCD, т.е. BH = AB · sin 45°. Получаем координаты всех точек:
Вот и все с координатами пирамиды. Но не с координатами вообще. Мы рассмотрели лишь самые распространенные многогранники, однако этих примеров достаточно, чтобы самостоятельно вычислить координаты любых других фигур. Поэтому можно приступать, собственно, к методам решения конкретных задач C2.
«>
Оценка статьи:
Загрузка…
Геометрия, 11 класс
Урок № 3. Координатный метод решения задач
Перечень вопросов, рассматриваемых в теме:
- специфика и преимущества решения задач в пространстве координатным методом;
- типы задач, решаемые координатным методом;
- этап решения задачи координатным методом;
- решение несложных задач методом координат.
Глоссарий по теме
Уравнение вида 
При этом вектор 

Вектор 


Основная литература:
Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб. для общеобразоват. Учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 163-170.
Потоскуев Е.В., Звавич Л. И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 353-260.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Работа по теме урока. Объяснение новой темы
Мы рассмотрели несложную задачу на применение метода координат в пространстве.
Векторы 


Рассмотрим этот метод более подробно.
Суть метода координат на плоскости и в пространстве заключается в следующем.
- Ввести систему координат удобным образом (исходя их свойств заданной фигуры)
- Записать условие задачи в координатах, определив во введенной системе координат координаты точек и/или векторов
- Используя алгебраические преобразования, решить задачу
- Интерпретировать полученный результат в соответствии с условием данной задачи
В рассмотренном нами примере, поскольку был дан куб, мы могли ввести систему координат с центром в любой его вершине.
В координатах удобно решать задачи, связанные с поиском расстояний и углов. Но для того чтобы его использовать, нужно знать некоторые формулы:
- Угол между прямыми
- Угол между прямой и плоскостью
- Угол между плоскостями
- Расстояние от точки до плоскости
- Расстояние от точки до прямой в пространстве
- Расстояние между скрещивающимися прямыми
Расстояние между параллельными плоскостями определяется как расстояние от точки, лежащей в одной плоскости, до другой плоскости.
Мы рассмотрим только первые четыре формулы.
Введем их.
Угол между прямыми
Если прямая задана двумя точками A и B, то известен направляющий вектор этой прямой 



Дальше ищется арккосинус от найденного числа. Заметим, что если косинус получился отрицательным, то это значит, что угол между векторами тупой. Поэтому мы берем модуль получившегося числа.
Фактически мы уже рассмотрели пример вычисления угла между прямыми в пространстве.
Угол между прямой и плоскостью
Сначала рассмотрим уравнение плоскости, проходящей через три точки.

Вам известно, что в пространстве плоскость задается уравнением, аналогичным тому, которое на плоскости задает прямую.
Если линейное уравнение вида 


Вам известно, что три точки в пространстве определяют единственную плоскость. Поэтому, если заданы три точки, то мы можем найти уравнение плоскости
Мы можем подставить координаты заданных точек в уравнение плоскости и решить систему из трех уравнений с тремя переменными:

В этой системе четыре неизвестных, однако, мы можем избавиться от одной, если разделим все уравнения на D:

Для изучения данного способа в 11 классе на базовом уровне введение понятий матрица, определитель матрицы не желателен, данные понятия не входят в базовый курс изучения геометрии.
Иногда эта система оказывается несложной. Но иногда бывает трудно ее решить, и тогда можно использовать следующую формулу:
Обозначение |M| означает определитель матрицы М.
В нашем случае матрица представляет собой таблицу 3х3 элемента. И определитель |M| вычисляется следующим образом:

Таким образом, уравнение плоскости будет записано так:

Пример 1:
Написать уравнение плоскости, проходящей через точки K(1; -2; 3), L (0; 1; 1), M (1; 0; 1).
Составим систему.

Решая ее, получим значения А, В и С: 

Ответ: 
Теперь запишем формулу угла между прямой и плоскостью.
Пусть дано уравнение плоскости: 

Тогда 
Пример 2:
Найдем угол между прямой и плоскостью. В качестве плоскости возьмем ту, уравнение которой мы только что написали:

Прямая проходит через точки Т(2; -1; 4) и Р(3; 2; 2).
Направляющий вектор прямой: 
Найдем синус угла между прямой и плоскостью:

Угол между прямой и плоскостью 
Ответ: 
Угол между плоскостями
Пусть:
уравнение первой плоскости:
уравнение второй плоскости:
Тогда 
Пример 3:
Найдем угол между плоскостями:


Найдем косинус угла между плоскостями:

Угол между плоскостями:
Ответ:
Расстояние от точки до плоскости
Пусть координаты точки: 

Тогда Расстояние от точки до плоскости вычисляется по формуле: 
Пример 4.
Найдем расстояние от точки М(4; 3; 4) до плоскости 

Теперь рассмотрим решение задачи координатным методом с использованием рассмотренных формул.
Пример 5.
АВС…D1 – куб с ребром 4. Найти расстояние от точки А до плоскости ЕКС (Е – середина D1C1, K – середина C1B1)
Введем систему координат с началом в вершине А так, как показано на рисунке:
Интересующие нас точки будут иметь координаты:
A(0; 0; 0), C(4; 4; 0), E(4; 2; 4), K(2; 4; 4).
Напишем уравнение плоскости ЕКС:

Решая ее, получим значения А, В, С и D: 
Уравнение плоскости имеет вид: 
Теперь найдем расстояние от точки А до плоскости ЕКС: 
Ответ: 
Рассмотрим задачу (№14 из варианта ЕГЭ).
В кубе ABC…D1 все рёбра равны 4. На его ребре BB1 отмечена точка K так, что KB = 3. Через точки K и C1 построена плоскость α, параллельная прямой BD1.
а) Докажите, что A1P : PB1 = 2 : 1, где P — точка пересечения плоскости α с ребром A1B1.
б) Найдите угол наклона плоскости α к плоскости грани BB1C1C.
Решение:
Переформулируем первый пункт этой задачи таким образом:
Проведем плоскость через точки Р, K и C1 и докажем, что она параллельна прямой BD1.
Введем систему координат так, как показано на рисунке:
Найдем координаты точек 
Р(

Напишем уравнение плоскости 


Решая ее, получим значения А, В, С и D: 

Теперь докажем, что плоскость 
Найдем угол между прямой BD1 и плоскостью 
Точки В и D1 имеют координаты: В (4; 0; 0), D1 (0; 4; 4).
Направляющий вектор прямой BD1 – это вектор 
Он имеет координаты 
Теперь найдем синус угла между вектором 


В этом случае нам не нужно считать знаменатель дроби. Так как числитель получился равен 0, то дробь равна 0, то есть синус угла между плоскостью и прямой равен 0, значит, плоскости параллельны или совпадают. Но, так как точка В, например, в плоскости, очевидно, не лежит, то плоскости параллельны.
Это значит, что плоскость, параллельная прямой BD1 и проходящая через точки 
Теперь рассмотри второй пункт задачи. Уравнение плоскости 
В(4; 0; 0). Поэтому она имеет уравнение 
То есть ее коэффициенты 
Найдем угол между плоскостями, используя формулу


Ответ: 
Координаты вектора
Вектор – отрезок, имеющий длину и указывающий направление.
На самом деле, понимать, что такое вектор для решения задач методом координат необязательно. Можно просто использовать это понятие, как необходимый инструмент для решения задач по стереометрии. Любое ребро или отрезок на нашей фигуре мы будем называть вектором.
Для того, чтобы определить координаты вектора, нужно из координат конечной точки вычесть координаты начальной точки. Пусть у нас есть две точки (Рис. 4) :
$$ т.А(x_A,y_A,z_A); $$
$$ т.B(x_B,y_B,z_B); $$
Тогда координаты вектора (vec{AB}) можно определить по формуле:
$$ vec{AB}={x_B-x_A,y_B-y_A,z_B-z_A}. $$
Скрещивающиеся прямые
И так, мы научились находить координаты точек, и при помощи них определять координаты векторов. Теперь познакомимся с формулой нахождения косинуса угла между скрещивающимися прямыми (векторами). Пусть даны два вектора:
$$ a={x_a,y_a,z_a};$$
$$ b={x_b,y_b,z_b}; $$
тогда угол (alpha) между ними находится по формуле:
$$ cos{alpha}=frac{x_a*x_b+y_a*y_b+z_a*z_b}{sqrt{{x_a}^2+{y_a}^2+{z_a}^2}*sqrt{{x_b}^2+{y_b}^2+{z_b}^2}}. $$
Уравнение плоскости
В задачах №14 (С2) ЕГЭ по профильной математике часто требуется найти угол между прямой и плоскостью и расстояние между скрещивающимися прямыми. Но для этого вы должны уметь выводить уравнение плоскости. В общем виде уравнение плоскости задается формулой:
$$ A*x+B*y+C*z+D=0,$$
где (A,B,C,D) – какие-то числа.
Если найти (A,B,C,D), то мы мы найдем уравнений плоскости. Плоскость однозначно задается тремя точками в пространстве, значит нужно найти координаты трех точек, лежащий в данной плоскости, а потом подставить их в общее уравнение плоскости.
Например, пусть даны три точки:
$$ K(x_K,y_K,z_K);,L(x_L,y_L,z_L);,P(x_P,y_P,z_P). $$
Подставим координаты точек в общее уравнение плоскости:
$$begin{cases} A*x_K+B*y_K+C*z_K+D=0,\ A*x_L+B*y_L+C*z_L+D=0, \ A*x_P+B*y_P+C*z_P+D=0.end{cases}$$
Получилась система из трех уравнений, но неизвестных 4: (A,B,C,D). Если наша плоскость не проходит через начало координат, то мы можем (D) приравнять (1), если же проходит, то (D=0). Объяснение этому простое: вы можете поделить каждое ваше уравнения на (D), от этого уравнение не изменится, но вместо (D) будет стоять (1), а остальные коэффициенты будут в (D) раз меньше.
Теперь у нас есть три уравнения и три неизвестные – можем решить систему:
Пример 3
Найти уравнение плоскости, проходящей через точки
$$ K(1;2;3);,P(0;1;0);,L(1;1;1). $$
Подставим координаты точек в уравнение плоскости (D=1):
$$begin{cases} A*1+B*2+C*3+1=0,\ A*0+B*1+C*0+1=0, \ A*1+B*1+C*1+1=0.end{cases}$$
$$begin{cases} A+2*B+3*C+1=0,\ B+1=0, \ A+B+C+1=0.end{cases}$$
$$begin{cases} A-2+3*C+1=0,\ B=-1, \ A=-C.end{cases}$$
$$begin{cases} A=-0.5,\ B=-1, \ C=0.5.end{cases}$$
Получаем искомое уравнение плоскости:
$$ -0.5x-y+0.5z+1=0.$$
Расстояние от точки до плоскости
Зная координаты некоторой точки (M(x_M;y_M;z_M)), легко найти расстояние до плоскости (Ax+By+Cz+D=0:)
$$ rho=frac{|A*x_M+B*y_M+C*z_M+D|}{sqrt{A^2+B^2+C^2}}. $$
Пример 4
Найдите расстояние от т. (H (1;2;0)) до плоскости, заданной уравнением
$$ 2*x+3*y-sqrt{2}*z+4=0.$$
Из уравнения плоскости сразу находим коэффициенты:
$$ A=2,,B=3,,C=-sqrt{2},,D=4.$$
Подставим их в формулу для нахождения расстояния от точки до плоскости.
$$ rho=frac{|2*1+3*2-sqrt{2}*0+4|}{sqrt{2^2+3^2+{-sqrt{2}}^2}}. $$
$$ rho=frac{12}{sqrt{16}}=3.$$
Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми – это расстояние от любой точки одной из прямых до параллельной ей плоскости, проходящей через вторую прямую.
Таким образом, если требуется найти расстояние между скрещивающимися прямыми, то нужно через одну из них провести плоскость параллельно второй прямой. Затем найти уравнение этой плоскости и по формуле расстояния от точки до плоскости найти расстояние между скрещивающимися прямыми. Точку на прямой можно выбрать произвольно (у которой легче всего найти координаты).
Пример 5
Рассмотрим задачу из досрочного ЕГЭ по математике 2018 года.
Дана правильная треугольная призма (ABCFDE), ребра которой равны 2. Точка (G) – середина ребра (CE).
- Докажите, что прямые (AD) и (BG) перпендикулярны.
- Найдите расстояние между прямыми (AD) и (BG).
Решение:
Решим задачу полностью методом координат.
Нарисуем рисунок и выберем декартову систему координат. (Рис 5).
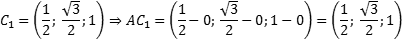
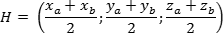
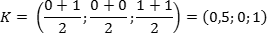



















 – сумма векторов.
– сумма векторов.



































































. Эти векторы сонаправлены с направлениями осей, имеют единичную длину и ортогональны – попарно перпендикулярны. Такие вектора называют <strong>координатными векторами</strong> или <strong>базисом.</strong></p>
<p style=)















. Зная координаты нужных точек, найдем координаты оставшихся векторов.</p>
<p style=)
$% куба до точки пересечения диагоналей грани $%BB_1C_1C$%.</li>
</ol>
<p>задан <strong>15 Мар ’15 11:56</strong> </p>
<p> melwentay <br />230 ● 6 ● 42 <br />95% принятых</p>
<p>Здесь не сказано, какая из вершин принята за начало координат а также не указан порядок выбора осей, что создаёт неоднозначность в ответах на некоторые из пунктов. Координаты вершин всегда имеют вид 000, 001, 010, 011, 100, 101, 110, 111 (пишу для простоты без скобок и промежуточных запятых). Для всего остального требуются уточнения, хотя там всё в принципе просто.</p>
<p>@falcao, начало координат-точка А. Оси x,y,z соответствуют ребрам AB, AD, AA1</p>
<p>Тогда все координаты непосредственно видны из рисунка: B(1;0;0), D(0;1;0), C(1;1;0), C1(1;1;1). Середина ребра соответствует полусумме координат: (1;1;1/2). В пункте 3 берётся середина грани, координаты (1;1/2;1/2). Расстояние до нуля — корень из суммы квадратов, то есть $%sqrt<3/2>=sqrt6/2$%.</p>
<div style=)