Как найти точку делящую вектор в отношении

Деление отрезка в заданном соотношении: координаты точки

Когда существуют условия деления отрезка в определенном отношении, необходимо уметь определять координаты точки, служащей разделителем. Выведем формулу для нахождения этих координат, поставив задачу на плоскости.

Определение координат точки, делящей отрезок в заданном отношении, на плоскости

Исходные данные: задана прямоугольная система координат O x y и две лежащие на ней, несовпадающие точки с заданными координатами A ( x A , y A ) и B ( x B , y B ) . А также задана точка С , делящая отрезок А В в отношении λ (некоторое положительное действительное число). Необходимо определить координаты точки С : x C и y C .

Перед тем, как приступить к решению поставленной задачи, немного раскроем смысл заданного условия: «точка С , делящая отрезок А В в отношении λ ». Во-первых, это выражение свидетельствует о том, что точка С лежит на отрезке А В (т.е. между точками А и В ). Во-вторых, понятно, что согласно заданному условию отношение длин отрезков А С и С В равно λ . Т.е. верно равенство:

В этом случае точка А – начало отрезка, точка В – конец отрезка. Если бы было задано, что точка С делит в заданном отношении отрезок В А , тогда верным было бы равенство: .

Ну и совсем очевидный факт, что если λ = 1 , то точка С является серединой отрезка А В .

Решим поставленную задачу при помощи векторов. Отобразим произвольно в некой прямоугольной системе координат точки А , В и точку С на отрезке А В . Построим радиус-векторы указанных точек, а также векторы A C → и C B → . Согласно условиям задачи, точка С делит отрезок А В в отношении λ .

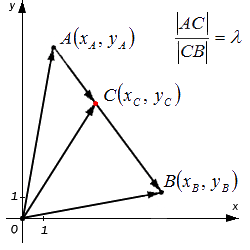
Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = ( x A , y A ) и O B → = ( x B , y B ) .

Определим координаты вектора : они будут равны координатам точки С , которые и требуется найти по условию задачи.

Используя операцию сложения векторов, запишем равенства: O C → = O A → + A C → O B → = O C → + C B → ⇔ C B → = O B → – O C →

По условию задачи точка С делит отрезок А В в отношении λ , т.е. верно равенство A C = λ · C B .

Векторы A C → и C B → лежат на одной прямой и являются сонаправленными. λ > 0 по условию задачи, тогда, согласно операции умножения вектора на число, получим: A C → = λ · C B → .

Преобразуем выражение, подставив в него : C B → = O B → – O C → .

A C → = λ · ( O B → – O C → ) .

Равенство O C → = O A → + A C → перепишем как O C → = O A → + λ · ( O B → – O C → ) .

Используя свойства операций над векторами, из последнего равенства следует: O C → = 1 1 + λ · ( O A → + λ · O B → ) .

Теперь нам остается непосредственно вычислить координаты вектора O C → = 1 1 + λ · O A → + λ · O B → .

Выполним необходимые действия над векторами O A → и O B → .

O A → = ( x A , y A ) и O B → = ( x B , y B ) , тогда O A → + λ · O B → = ( x A + λ · x B , y A + λ · y B ) .

Таким образом, O C → = 1 1 + λ · ( O A → + λ · O B → ) = ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ ) .

Резюмируя: координаты точки С , делящей отрезок А В в заданном отношении λ определяются по формулам : x C = x A + λ · x B 1 + λ и y C = у A + λ · y B 1 + λ .

Определение координат точки, делящей отрезок в заданном отношении, в пространстве

Исходные данные: прямоугольная система координат O x y z , точки с заданными координатами A ( x A , y A , z A ) и B ( x B , y B , z B ) .

Точка С делит отрезок А В в отношении λ . Необходимо определить координаты точки С .

Используем ту же схему рассуждений, что и в случае выше на плоскости, придем к равенству:

O C → = 1 1 + λ · ( O A → + λ · O B → )

Векторы и являются радиус-векторами точек А и В , а значит:

O A → = ( x A , y A , z A ) и O B → = ( x B , y B , z B ) , следовательно

O C → = 1 1 + λ · ( O A → + λ · O B → ) = ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ , z A + λ · z B 1 + λ )

Таким образом, точка С , делящая отрезок А В в пространстве в заданном отношении λ , имеет координаты: ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ , z A + λ · z B 1 + λ )

Рассмотрим теорию на конкретных примерах.

Исходные данные: точка С делит отрезок А В в отношении пять к трем. Координаты точек А и В заданы A ( 11 , 1 , 0 ) , B ( – 9 , 2 , – 4 ) .

Решение

По условию задачи λ = 5 3 . Применим полученные выше формулы и получим:

x A + λ · x B 1 + λ = 11 + 5 3 · ( – 9 ) 1 + 5 3 = – 3 2

y A + λ · y B 1 + λ = 1 + 5 3 · 2 1 + 5 3 = 13 8

z A + λ · z B 1 + λ = 0 + 5 3 · ( – 4 ) 1 + 5 3 = – 5 2

Ответ: C ( – 3 2 , 13 8 , – 5 2 )

Исходные данные: необходимо определить координаты центра тяжести треугольника А В С .

Заданы координаты его вершин: A ( 2 , 3 , 1 ) , B ( 4 , 1 , – 2 ) , C ( – 5 , – 4 , 8 )

Решение

Известно, что центром тяжести любого треугольника является точка пересечения его медиан (пусть это будет точка М ). Каждая из медиан делится точкой М в отношении 2 к 1 , считая от вершины. Исходя из этого, найдем ответ на поставленный вопрос.

Допустим, что А D – медиана треугольника А В С . Точка М – точка пересечения медиан, имеет координаты M ( x M , y M , z M ) и является центром тяжести треугольника. М , как точка пересечения медиан, делит отрезок А D в отношении 2 к 1 , т.е. λ = 2 .

Найдем координаты точки D . Так как A D – медиана, то точка D – середина отрезка В С . Тогда, используя формулу нахождения координат середины отрезка, получим:

x D = x B + x C 2 = 4 + ( – 5 ) 2 = – 1 2 y D = y B + y C 2 = 1 + ( – 4 ) 2 = – 3 2 z D = z B + z C 2 = – 2 + 8 2 = 3

Вычислим координаты точки М :

x M = x A + λ · x D 1 + λ = 2 + 2 · ( – 1 2 ) 1 + 2 = 1 3

y M = y A + λ · y D 1 + λ = 3 + 2 · ( – 3 2 ) 1 + 2 = 0

z M = z A + λ · z D 1 + λ = 1 + 2 · 3 1 + 2 = 7 3

Деление векторов в данном соотношении

Пусть вектор 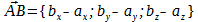задан координатами своего начала A(a_x; a_y; a_z) и конца B(b_x; b_y; b_z) и пусть точка C(c_x; c_y; c_z) расположена между точка A и B

пусть при этом известно соотношение длин векторов

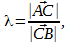
тогда координаты точки C(c_x; c_y; c_z) находятся по формулам

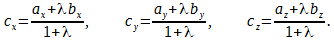
Примеры решения заданий по делению векторов и отрезков

Отрезок AB точками C(3, 4) и D(5, 6) разделён на три равные части. Найти координаты точек A и B.

Р е ш е н и е. Обозначим координаты точек A и B так: А(x1, y1), B(x1, y1). Для отрезка AD точка C является серединой, потому λ = AC / CD = 1 и по формулам деления отрезка в данном соотношении

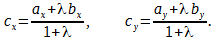
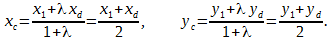
Подставим в последнее равенство координаты x_c, y_c, x_d, y_d:

3 = (x1 + 5)/2, 4 = (y1 + 6)/2,

откуда находим, x₁ = 1, y₁ = 2. Точка A имеет координаты A(1, 2).

Поскольку точка D есть середина отрезка CB, то x_d = (x_c + x₂)/2, или 5 = (3 + x₂)/2, отсюда x₂ = 7.

отсюда y₂ = 8. Получили B(7, 8).

О т в е т: A(1, 2), B(7, 8).

Даны вершины треугольника A(2, -4), B(4, -5) и C(-4, 7). Определить середины его сторон.

Р е ш е н и е. Воспользуемся формулой для определения середин сторон отрезка, при известных двух точках:

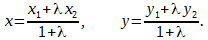
Поскольку отрезки делятся на равные части, то

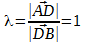
Тогда формула приобретает вид:

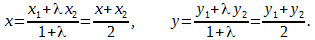
Координата x для отрезка AB равна (2+4)/2 = 3, координата y для отрезка AB равна (-4-5)/2 = -4,5.

Координата x для отрезка AC равна (2-4)/2 = -1, координата y для отрезка AC равна (-4+7)/2 = 1,5.

Координата x для отрезка BC равна (4-4)/2 = 0, координата y для отрезка BC равна (-5+7)/2 = 1.

О т в е т: искомые точки имеют координаты (3; -4,5), (-1; 1,5) и (0; 1).

Даны три вершины параллелограмма A(2, -4), B(4, -2), C(-2, 4). Определить четвёртую вершину D, противоположную B.

Р е ш е н и е. Найдём точку, в которой пересекаются диагонали параллелограмма.

Назовём точку пересечения диагоналей точкой E.

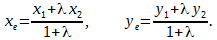
Поскольку этой точкой диагонали делятся на два равных отрезка

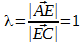
то формула приобретает вид:

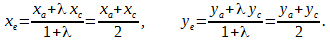
Найдём середину отрезка AC:

Итак, точка E имеет координаты (0, 0).

Данная точка также является серединой отрезка BD, поскольку это вторая диагональ параллелограмма. Тогда

подставим известные значения:

Теперь найдём вторую координату:

подставим известные значения:

Даны вершины треугольника A(2, 3); B(4, -10); C(-4, 1), определить длину его медианы, проведённой из вершины B.

Р е ш е н и е. Назовём точку пересечения медианы и стороны AC точкой D. Поскольку медиана делит сторону треугольника пополам, то воспользуемся формулой нахождения координат точки посередине отрезка:

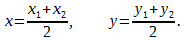
Точка D имеет координаты (-1, 2).

Воспользуемся формулой нахождения длины отрезка, когда известны координаты его крайних точек:

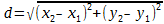
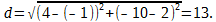
О т в е т: Длина медианы, проведённой из вершины B, равна 13.

Лекция Способы задания векторов. Деление отрезка в заданном отношении. Скалярное произведение двух векторов и его основные свойства.

1.4. Способы задания векторов

Вектор может быть задан следующими способами:

1. Координатами вектора

2 . Координатами начальной z

и конечной точек.

3. Модулем вектора и углами , M

которые он образует с координатными осями.

При этом значения

называются направляющими косинусами . O y

Между этими способами задания a _z

векторов существует определённая связь. a _x

Например, переход от (2) к (1) x a _y

осуществляется следующим образом :

т ак как , то z A

.

Переход от (3) к (1) и наоборот

осуществляется по формулам: B

x O y

1.5. Деление отрезка в заданном отношении

Р ассмотрим следующую задачу : даны две точки и . Требуется найти точку такую, что отно-шение z А

Построим векторы : М

Из условия коллинеарности векторов

и имеем В

Полученное равенство представим в

координатной форме х Оу

(1)

Замечание 1. Из формул (1) следует частный случай деления отрезка пополам

П ример 1. Треугольник задан координатами своих вершин Найти его центр тяжести . z В

Известно, что центр тяжести треугольника

лежит на пересечении его медиан и, если

точка К  середина стороны ВС , то по А М К

свойству медиан у

Определим вначале координаты х С

точки К :

далее по формулам (1) получим координаты точки М :

Тема 2: Скалярное произведение

2.1. Скалярное произведение двух векторов и его основные свойства

Определение. Скалярным произведением двух векторов и называется число, равное произведению модулей этих векторов на косинус угла между ними и обозначается

(2)

Замечание 2. Формулу (2) можно представить в другой форме

(3)

Рассмотрим механический смысл скалярного произведения. Если  постоянная сила, а  вектор перемещения, то  работа силы на перемещении

Из определения скалярного произведения следуют его свойства:

1.  скалярное произведение коммутативно.

2. , если векторы и перпендикулярны (ортогональны), или хотя бы один из них является нулевым вектором.

3.

Если воспользоваться замечанием 1 из лекции 4 и формулами (3), то легко доказать следующее свойство:

4.

Таким образом, операции со скалярным произведением аналогичны операциям с многочленами.

2.2. Скалярное произведение векторов, заданных координатами

Из определения и свойства (1) скалярного произведения следуют формулы : .

Аналогично получаем :

(4)

2.3. Длина вектора. Угол между двумя векторами.

По формулам (2) и (4) получаем

(5)

Из определения скалярного произведения и формул (4), (5) следует

(6)

(7)

Если в формуле (7) положить , то найдем

.

Аналогично можно получить выражения для оставшихся двух направ-ляющих косинусов

; . (8)

Замечание 3. Формулу (5) для модуля вектора можно было получить, исходя из геометрического смысла координат вектора, используя теоре-му Пифагора.

Замечание 4. Из выражений (8) для направляющих косинусов следует их основное свойство

Пример 2. Даны два вектора Найти их скалярное произведение и угол между ними.

По формулам (5) и (7) получаем

Пример 3*. Найти координаты единичного вектора, который перпенди-кулярен вектору и образует угол с вектором

Из свойства направляющих косинусов следует, что координаты еди-ничного вектора равны значениям соответствующих направляющих косинусов и поэтому из условия задачи получаем следующую систему уравнений

Из второго уравнения системы получаем Тогда из первого уравнения имеем . Если полученные выражения подставить в третье уравнение системы, то приходим к квадратному уравнению

Из этого уравнения и . Тогда окончательно нахо-дим два единичных вектора , удовлетворяющих условию задачи.

[spoiler title=”источники:”]

http://greleon.ru/vishmath/lekcii/175-lekciya-sposoby-zadaniya-vektorov-delenie-otrezka-v-zadannom-otnoshenii-skalyarnoe-proizvedenie-dvuh-vektorov-i-ego-osnovnye-svoystva.html

[/spoiler]

Опять с векторами!)

Пушистик:)

Гуру

(3662),
закрыт

13 лет назад

Даны точки
Требуется найти координаты точкиK(x,y),
делящей
отрезокMN
в отношении
Рассмотрим векторыЭти векторы коллинеарныИз векторной алгебры известно, что если
векторы коллинеарны, то соответствующие
координаты пропорциональны. Имеем:

(по условию).

Из этих уравнений
легко найти x
и y

(2.1.1)

Если
то точкаK
является серединой отрезка MN.
Формулы (2.1) примут вид:

(2.1.2)

Это формулы
координат середины отрезка.

Пример 1.
Найти
координаты
точки K,
делящей отрезок MN,
где M(-1,4)
и N(2,1),
в отношении 2 : 1.

Решение.
По условию
Подставим координаты точкиM
и N
в формулы (2.1.1). Имеем:

Точка K
имеет координаты: x=1,
y=2.

Ответ: K(1,2).

Пример 2.
Отрезок АВ разделен на три равные части.
Определить координаты точек деления,
если А(3,-2), В(6,4).

Решение.
Обозначим точки деления С и D.
Точка D
делит отрезок АВ в отно-

шении АD:DB
= 2. Координаты точки D
найдем по формулам (2.1.1).

Итак, D(5,2).

Координаты точки
С можно найти аналогично, взяв

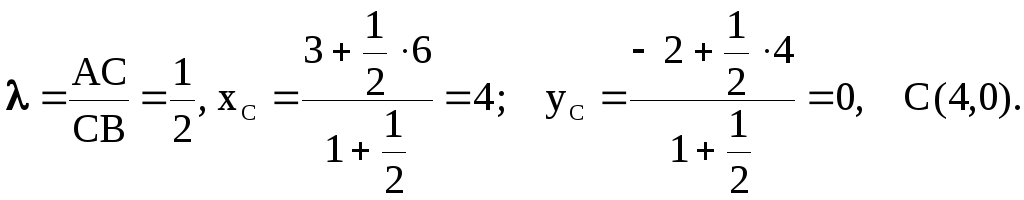
Существует другой
способ нахождения координат точки С.
Точка С является серединой отрезка АD.
По формулам (2.1.2) имеем

Ответ:
D(5,2)
; C(4,0).

Пример 3.
Найти точку пересечения медиан
треугольника АВС, где А(-1,3) ;

B(3,-2);
C(5,3).

Решение:
Пусть точка О – точка пересечения медиан
AM
и BN
треугольника ABC.
Точка М является серединой отрезка ВС.
По формулам (2.1.2) получим координаты
точки М:

Из школьного курса
планиметрии известно, что точка О делит
медиану АМ в отношении АО:ОМ = 2:1.
По формулам (2.1.1) получим

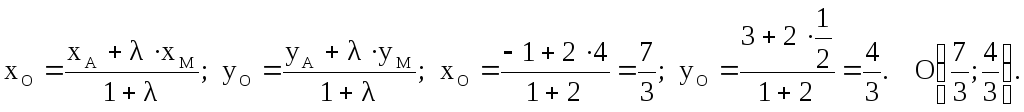
Ответ:
Точка пересечения медиан

Замечание: Точка
пересечения медиан треугольника является
его центром тяжести.

3. Прямая на плоскости.

3.1. Простейшей из
линий является прямая. Всякую прямую,
не параллельную оси ординат, можно
представить уравнением вида

,
(3.1.1)

где к есть тангенс
угла
образованного прямой с положительным
направлением оси абсцисс (ox).

Величину к называют
угловым
коэффициентом.
Величину b
– начальной
ординатой.

Если прямая
параллельна оси ox,
то
Уравнение прямой примет вид:y
= b
(3.1.2)

Если прямая
параллельна оси oy,
то
не существует. В этом случае уравнение
прямой будет иметь вид:x
= a
(3.1.3),
где а – абсцисса точки, через которую
проходит данная прямая ( точки пересечения
прямой с осью ox).

Пример 1.
Какую прямую представляет уравнение

Решение. Данное
уравнение задает прямую, у которой
Так какПоэтому данное уравнение представляет
прямую, проходящую через начало координат
(b
= 0) и образующую с осью ox
угол

Пример 2.
Написать
уравнение прямой, параллельной оси ox
и имеющей на-

чальную
ординату b
=
.

Решение: По
формуле (3.1.2) имеем y
=где

Итак, искомая
прямая задается уравнением

Ответ:

Пример 3.
Написать уравнение прямой, параллельной
оси oy
и проходящей

через точку
M(3,1).

Решение:
По формуле (3.1.3) уравнение прямой имеет
вид x
= a
, где а – абсцисса точки М. а = 3. Уравнение
прямой x
= 3.

Ответ:
x
= 3.

3.2. Уравнение
прямой по точке и угловому коэффициенту.

Пусть прямая
проходит через точку
и имеет угловой коэффициент к. Уравнение
такой прямой можно записать в виде
(3.1.1)гдеb
– неизвестная
величина. Так как прямая проходит через
точку,
то координаты точки удовлетворяют
уравнению (3.1.1). ИмеемОтсюда

Подставим значение
“b”
в уравнение (3.1.1), получим
–или

(3.2.1)

Полученное уравнение
называется уравнением прямой по точке
и угловому коэффициенту.

Пример 1.
Составить уравнение прямой, проходящей
через точку

и образующей с
положительным направлением оси ox
угол

Решение:
Так как
тоПрименив формулу (3.2.1), получимy-(-2)=-1(x-1)
y+2
= -x+1

y=-x-1.

Ответ:
y=-x-1.

Пример 2.
Составить
уравнение прямой, проходящей через
точку А(-3,4) и имеющей угловой коэффициент
к = 2.

Решение:
Применяем
формулу (3.2.1) y
– 4 = 2 (x+3)
y
– 4 = 2x
+ 6

y
= 2x
+
10.

Ответ:
y
= 2x
+ 10.

Пример 3.
Составить
уравнение прямой, проходящей через
точку М(-1, 2) параллельно оси ox.

Решение:
Если прямая параллельна оси ox,
то угол между прямой и положительным
направлением оси ox
равен нулю. Следовательно,
По формуле (3.2.1) получимy
– 2 = 0 (x
+ 1)

y
– 2 = 0

Ответ:
y
= 2.

3.3.Уравнение
прямой по точке и нормальному вектору.

Пусть прямая
проходит через точку
Поднормальным
вектором
понимают вектор, который перпендикулярен
данной прямой. Обозначим его
Возьмем на прямой произвольную точкуM(x,y)
и рассмотрим вектор
Используя векторную алгебру, найдем
координаты вектораВекторперпендикулярен вектору.Из векторной
алгебры известно, что скалярное
произведение этих векторов равно нулю.
Следовательно,

(3.3.1)

Полученное уравнение
называется уравнением
прямой по точке и нормальному вектору.
Преобразуем полученное уравнение:

Ax + By –
A– B=
0.Пусть
C = -A-B,тогда
получим:

Ax
+ By + C = 0 (3.3.2)

Уравнение (3.3.2)
называется общим
уравнением прямой.
Напомним, что коэффициенты А и В в
уравнении определяют координаты
нормального вектора

Рассмотрим общее
уравнение прямой подробнее.

1). Если А = 0, то
уравнение примет вид

By
+ C
= 0 ; y
= –Прямая параллельна осиox.
(3.1.2)

2). Если В = 0, то
уравнение примет вид:

Ax
+ C
= 0, x
= –
Прямая параллельна оси oy.
(3.1.3.)

3). Если С = 0, то
уравнение примет вид: Ax
+ By
= 0. y
= –

Прямая проходит через начало координат
и имеет угловой коэффициент k
= –
См. пример 1 пункт 3.1.

Из общего
уравнения прямой, если
можно найти угловой коэффициент к. Для
этого выразимy
из этого уравнения : Ax
+ By
+ C
= 0.

By = – Ax –
C ; y = ––Отсюда,

k
= –
(3.3.3)

Пример 1.
Прямая задана уравнением 3x
– 4y
+5 = 0. Найти координаты нормального
вектора.

Решение:
Координатами
нормального вектора
являются коэффициенты приx
и y
данного уравнения прямой. Имеем А = 3;
В = – 4.

Ответ:

Пример 2.
Составить уравнение прямой, проходящей
через точку М(2,-1) и имеющей нормальный
вектор

Решение:
Применяем
формулу (3.3.1). Имеем 0(x
– 2) + 2(y
+ 1) = 0

2y
+ 2 = 0

y
+ 1 = 0.

Ответ:
y
+ 1 = 0.

Пример 3.
Составить уравнение прямой, проходящей
через точку М(0; 1) перпендикулярно вектору

где А(-1; 2), В(1; -1).

Решение:
Найдем координаты вектора
–
(-1); -1-2);
(2;
-3).

Вектор является нормальным
векторомискомой
прямой. По формуле (3.3.1) имеем 2(x
– 0) -3(y
-1) = 0

2x
– 3y
+ 3 = 0.

Ответ:
2x
– 3y
+ 3 = 0.

3.4. Уравнение
прямой по точке и направляющему вектору.

Пусть прямая
проходит через точку
Направляющим векторомданной прямой называется вектор,
параллельный этой прямой. Пусть дан
векторВозьмем на прямой произвольную точкуM(x,y)
и рассмотрим вектор
Векторы
иколлинеарны,следовательно, их
соответствующие координаты пропорциональны.

(3.4.1)

Полученное уравнение
является уравнением прямой по
точке и направляющему вектору.

Пример 1.
Прямая задана
уравнением:

Написать координаты
направляющего вектора; найти координаты
точки, лежащей на прямой; составить
общее уравнение прямой.

Решение:
Направляющий
вектор
= (−1; 2). Точкумы получим, приравняв нулю числители
данного уравнения:x
+ 2 = 0

x
=−2; y
– 3 = 0

y
= 3.

Итак,
(−2; 3).

Общее уравнение
прямой получим по свойству пропорций:
(x+2)∙2
= (y−3)∙(−
1)

2x
+ 4 = −y
+ 3

2x
+ y
+ 1 = 0.

Ответ:
(−1;
2),
(−2;
3), 2x
+ y
+ 1 = 0.

Пример 2.
Составить
уравнение прямой по точке М(2,-5) и
направляющему вектору
(-2,4).

Решение:
Применяем
формулу
(3.4.1). Имеем:

4(x-2)
= -2(y+5)
4x
– 8 = – 2y
– 10

4x
+ 2y
+ 2 = 0

2x
+ y
+ 1 =0.

Ответ: 2x
+ y
+ 1 = 0.

Пример 3.
Через точку
С(- 2, 1) провести прямую, параллельную
вектору
где А(2,-1), В(3,4).

Решение:
Вектор можно взять за
направляющий вектор данной прямой. (3-2; 4-(-1)) = (1;
5). Применяем
формулу (3.4.1). Имеем:

5(x
+ 2) = y
– 1

5x
+ 10 = y
– 1

5x
– y
+ 11 = 0.

Ответ:
5x
– y
+11 = 0.

3.5. Уравнение
прямой, проходящей через две заданные
точки.

Известно, что
через две данные точки можно провести
единственную прямую. Пусть
прямая проходит через точкиЗа направляющий векторданной прямой можно взять вектор.

Составим уравнение
прямой по точке и направляющему
вектору

По формуле (3.4.1)
имеем:

(3.5.1)

Если
то прямая параллельна осиoy.
Ее уравнение имеет вид:

(3.5.2)

Если
то прямая параллельна осиox.
Ее уравнение :

y
=

(3.5.3)

Пример 1.
Составить уравнение прямой АВ, если
А(2,-1); В(1,3).

Решение:
Применяем
формулу (3.5.1):

4(x
– 2) = -(y
+ 1)
4x
+ y
– 7 = 0.

Ответ:
4x
+ y
– 7 = 0.

Пример 2.
Составить уравнение прямой, проходящей
через точки М(4,-2) и N(4,5).

Решение:
Так как

то по формуле (3.5.2) уравнение прямой
имеет вид:

x = 4.
Прямая
параллельна оси oy.

Пример 3. Дан
треугольник АВС, у которого А(1,2), В(4,3),
С(1,3). Составить уравнения его сторон.

Решение: 1)
Найдем уравнение стороны АВ. ПО формуле
(3.5.1) имеем:
x
– 1 = 3(y
– 2)
x
– 3y
+ 5 = 0.

2) Сторона ВС
находится по формуле (3.5.3), так как
y
= 3.

3) Уравнение стороны
АС выпишем по формуле (3.5.2), так как
x
= 1.

Ответ:
AB:
x
– 3y
+ 5 = 0; BC:
y
= 3; AC:
x
= 1.

Пример 4.
Даны вершины треугольника АВС А(- 1, 3),
В(3,-2), С(5,3). Составить уравнение медианы,
проведенной из вершины В.

Решение: Пусть
ВМ – медиана, тогда точка М является
серединой отрезка АС. По формулам (2.1.2)
имеем:

M(2,3).

Уравнение медианы
ВМ получим по формуле (3.5.1):

5(x-
3) = -(y
+2)

5x
+ y
– 13 = 0.

Ответ:
BM:
5x
+ y
– 13 = 0.

3.6. Уравнение
прямой в отрезках.

Если прямая отсекает
на осях отрезки а и b,
не равные нулю, то ее уравнение можно
записать в виде:
.
(3.6.1)

Такое уравнение
называется уравнением
в отрезках.
Рассмотрим это уравнение. Пусть x
= 0, тогда

Пусть y
= 0, тогда

Прямая проходит
через точки А(а,0) и B(0,b).

Пример.
Записать
уравнение прямой в отрезках. Построить
эту прямую.

3x
– 2y + 12 = 0.

Решение:
3x
– 2y
= – 12. Разделим обе части этого уравнения
на – 12. Получим:

a = – 4, b = 6.

Построим полученную
прямую. Для этого отложим на оси ox
a
= – 4, на оси oy

b
= 6 и соединим полученные точки.

3.7. Расстояние
от точки до прямой.

Пусть прямая
задана уравнением Ax
+ By
+ C
= 0. Найдем расстояние от точки
до этой прямой. Подрасстоянием
от точки до прямой понимают длину отрезкагде М – основание перпендикуляра,
опущенного из точкина данную прямую. Расстояниенаходим по формуле:

(3.7.1)

Пример. Найти
расстояние от точки
до прямой 3x
+ 4y
– 22 =0.

Решение: По
формуле (3.7.1) получим:

Ответ:
d
= 4.

Соседние файлы в предмете Математика

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

  03.03.20154.96 Кб8Содержание OneNote.onetoc2

• #

Когда существуют условия деления отрезка в определенном отношении, необходимо уметь определять координаты точки, служащей разделителем. Выведем формулу для нахождения этих координат, поставив задачу на плоскости.

Определение координат точки, делящей отрезок в заданном отношении, на плоскости

Исходные данные: задана прямоугольная система координат Oxy и две лежащие на ней, несовпадающие точки с заданными координатами A(xA,yA) и B(xB,yB) . А также задана точка С, делящая отрезок АВ в отношении λ (некоторое положительное действительное число). Необходимо определить координаты точки С: xC и yC .

Перед тем, как приступить к решению поставленной задачи, немного раскроем смысл заданного условия: «точка С, делящая отрезок АВ в отношении λ». Во-первых, это выражение свидетельствует о том, что точка С лежит на отрезке АВ (т.е. между точками А и В). Во-вторых, понятно, что согласно заданному условию отношение длин отрезков АС и СВ равно λ. Т.е. верно равенство:

ACCB=λ .

В этом случае точка А – начало отрезка, точка В – конец отрезка. Если бы было задано, что точка С делит в заданном отношении отрезок ВА, тогда верным было бы равенство: .

Ну и совсем очевидный факт, что если λ = 1, то точка С является серединой отрезка АВ.

Решим поставленную задачу при помощи векторов. Отобразим произвольно в некой прямоугольной системе координат точки А, В и точку С на отрезке АВ. Построим радиус-векторы указанных точек, а также векторы AC→ и CB→ . Согласно условиям задачи, точка С делит отрезок АВ в отношении λ.

Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: OA→=(xA, yA) и OB→= (xB , yB) .

Определим координаты вектора : они будут равны координатам точки С, которые и требуется найти по условию задачи.

Используя операцию сложения векторов, запишем равенства: OC→=OA→+AC→    OB→=OC→+CB→⇔CB→=OB→-OC→

По условию задачи точка С делит отрезок АВ в отношении λ, т.е. верно равенство AC=λ·CB .

Векторы AC→ и CB→ лежат на одной прямой и являются сонаправленными. λ > 0 по условию задачи, тогда, согласно операции умножения вектора на число, получим: AC →=λ·CB→ .

Преобразуем выражение, подставив в него : CB→=OB→-OC→ .

AC→=λ·(OB→-OC→) .

Равенство OC→=OA→+AC→ перепишем как OC→=OA→+λ·(OB→-OC→) .

Используя свойства операций над векторами, из последнего равенства следует: OC→=11+λ·(OA→+λ·OB→) .

Теперь нам остается непосредственно вычислить координаты вектора OC→=11+λ·OA→+λ·OB→ .

Выполним необходимые действия над векторами OA→ и OB→ .

OA →=(xA , yA) и OB→ = (xB , yB) , тогда OA→+λ·OB→ = (xA+λ·xB, yA+λ·yB) .

Таким образом, OC→=11+λ·(OA→+λ·OB→) = (xA+λ·xB1+λ , yA+λ·yB1+λ) .

Резюмируя: координаты точки С, делящей отрезок АВ в заданном отношении λ определяются по формулам : xC = xA+λ·xB1+λ и  yC=уA+λ·yB1+λ .

Определение координат точки, делящей отрезок в заданном отношении, в пространстве 

Исходные данные: прямоугольная система координат Oxyz, точки с заданными координатами A (xA , yA , zA) и B (xB , yB , zB) .

Точка С делит отрезок АВ в отношении λ. Необходимо определить координаты точки С.

Используем ту же схему рассуждений, что и в случае выше на плоскости, придем к равенству:

OC →=11+λ·(OA→+λ·OB→)

Векторы и являются радиус-векторами точек А и В, а значит:

OA→= (xA , yA , zA) и OB→=(xB , yB , zB), следовательно

OC→=11+λ·(OA→+λ·OB→) = (xA +λ·xB1+λ , yA +λ ·yB1+λ , zA + λ·zB1+λ)

Таким образом, точка С, делящая отрезок АВ в пространстве в заданном отношении λ, имеет координаты: (xA+λ·xB1+λ , yA+λ·yB1+λ , zA + λ·zB1+λ)

Рассмотрим теорию на конкретных примерах.

Когда существуют условия деления отрезка в определенном отношении, необходимо уметь определять координаты точки, служащей разделителем. Выведем формулу для нахождения этих координат, поставив задачу на плоскости.

Определение координат точки, делящей отрезок в заданном отношении, на плоскости

Исходные данные: задана прямоугольная система координат O x y и две лежащие на ней, несовпадающие точки с заданными координатами A ( x A , y A ) и B ( x B , y B ) . А также задана точка С , делящая отрезок А В в отношении λ (некоторое положительное действительное число). Необходимо определить координаты точки С : x C и y C .

Перед тем, как приступить к решению поставленной задачи, немного раскроем смысл заданного условия: «точка С , делящая отрезок А В в отношении λ ». Во-первых, это выражение свидетельствует о том, что точка С лежит на отрезке А В (т.е. между точками А и В ). Во-вторых, понятно, что согласно заданному условию отношение длин отрезков А С и С В равно λ . Т.е. верно равенство:

В этом случае точка А – начало отрезка, точка В – конец отрезка. Если бы было задано, что точка С делит в заданном отношении отрезок В А , тогда верным было бы равенство: .

Ну и совсем очевидный факт, что если λ = 1 , то точка С является серединой отрезка А В .

Решим поставленную задачу при помощи векторов. Отобразим произвольно в некой прямоугольной системе координат точки А , В и точку С на отрезке А В . Построим радиус-векторы указанных точек, а также векторы A C → и C B → . Согласно условиям задачи, точка С делит отрезок А В в отношении λ .

Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = ( x A , y A ) и O B → = ( x B , y B ) .

Определим координаты вектора : они будут равны координатам точки С , которые и требуется найти по условию задачи.

Используя операцию сложения векторов, запишем равенства: O C → = O A → + A C → O B → = O C → + C B → ⇔ C B → = O B → — O C →

По условию задачи точка С делит отрезок А В в отношении λ , т.е. верно равенство A C = λ · C B .

Векторы A C → и C B → лежат на одной прямой и являются сонаправленными. λ > 0 по условию задачи, тогда, согласно операции умножения вектора на число, получим: A C → = λ · C B → .

Преобразуем выражение, подставив в него : C B → = O B → — O C → .

A C → = λ · ( O B → — O C → ) .

Равенство O C → = O A → + A C → перепишем как O C → = O A → + λ · ( O B → — O C → ) .

Используя свойства операций над векторами, из последнего равенства следует: O C → = 1 1 + λ · ( O A → + λ · O B → ) .

Теперь нам остается непосредственно вычислить координаты вектора O C → = 1 1 + λ · O A → + λ · O B → .

Выполним необходимые действия над векторами O A → и O B → .

O A → = ( x A , y A ) и O B → = ( x B , y B ) , тогда O A → + λ · O B → = ( x A + λ · x B , y A + λ · y B ) .

Таким образом, O C → = 1 1 + λ · ( O A → + λ · O B → ) = ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ ) .

Резюмируя: координаты точки С , делящей отрезок А В в заданном отношении λ определяются по формулам : x C = x A + λ · x B 1 + λ и y C = у A + λ · y B 1 + λ .

Определение координат точки, делящей отрезок в заданном отношении, в пространстве

Исходные данные: прямоугольная система координат O x y z , точки с заданными координатами A ( x A , y A , z A ) и B ( x B , y B , z B ) .

Точка С делит отрезок А В в отношении λ . Необходимо определить координаты точки С .

Используем ту же схему рассуждений, что и в случае выше на плоскости, придем к равенству:

O C → = 1 1 + λ · ( O A → + λ · O B → )

Векторы и являются радиус-векторами точек А и В , а значит:

O A → = ( x A , y A , z A ) и O B → = ( x B , y B , z B ) , следовательно

O C → = 1 1 + λ · ( O A → + λ · O B → ) = ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ , z A + λ · z B 1 + λ )

Таким образом, точка С , делящая отрезок А В в пространстве в заданном отношении λ , имеет координаты: ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ , z A + λ · z B 1 + λ )

Рассмотрим теорию на конкретных примерах.

Исходные данные: точка С делит отрезок А В в отношении пять к трем. Координаты точек А и В заданы A ( 11 , 1 , 0 ) , B ( — 9 , 2 , — 4 ) .

Решение

По условию задачи λ = 5 3 . Применим полученные выше формулы и получим:

x A + λ · x B 1 + λ = 11 + 5 3 · ( — 9 ) 1 + 5 3 = — 3 2

y A + λ · y B 1 + λ = 1 + 5 3 · 2 1 + 5 3 = 13 8

z A + λ · z B 1 + λ = 0 + 5 3 · ( — 4 ) 1 + 5 3 = — 5 2

Ответ: C ( — 3 2 , 13 8 , — 5 2 )

Исходные данные: необходимо определить координаты центра тяжести треугольника А В С .

Заданы координаты его вершин: A ( 2 , 3 , 1 ) , B ( 4 , 1 , — 2 ) , C ( — 5 , — 4 , 8 )

Решение

Известно, что центром тяжести любого треугольника является точка пересечения его медиан (пусть это будет точка М ). Каждая из медиан делится точкой М в отношении 2 к 1 , считая от вершины. Исходя из этого, найдем ответ на поставленный вопрос.

Допустим, что А D – медиана треугольника А В С . Точка М – точка пересечения медиан, имеет координаты M ( x M , y M , z M ) и является центром тяжести треугольника. М , как точка пересечения медиан, делит отрезок А D в отношении 2 к 1 , т.е. λ = 2 .

Найдем координаты точки D . Так как A D – медиана, то точка D – середина отрезка В С . Тогда, используя формулу нахождения координат середины отрезка, получим:

x D = x B + x C 2 = 4 + ( — 5 ) 2 = — 1 2 y D = y B + y C 2 = 1 + ( — 4 ) 2 = — 3 2 z D = z B + z C 2 = — 2 + 8 2 = 3

Вычислим координаты точки М :

x M = x A + λ · x D 1 + λ = 2 + 2 · ( — 1 2 ) 1 + 2 = 1 3

y M = y A + λ · y D 1 + λ = 3 + 2 · ( — 3 2 ) 1 + 2 = 0

z M = z A + λ · z D 1 + λ = 1 + 2 · 3 1 + 2 = 7 3

§1. Система координат

1.1 Система координат на плоскости (пространство r2 )

Декартовая прямоугольная система координат на плоскости считается заданной, если заданы две взаимно перпендикулярные прямые (оси координат), начало отcчёта и единица масштаба.

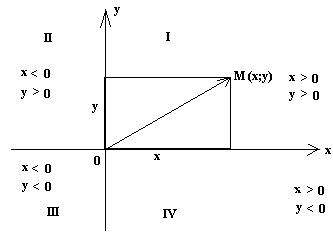рис.1

Горизонтальная ось — ось абсцисс, положительное направление оси — вправо.

Вертикальная ось, перпендикулярная к первой, называется осью ординат. Положительное направление — вверх.

Положение точки на плоскости определяется двумя числами — абсциссой и ординатой. Они называются координатами точки.

Координаты пишутся в круглых скобках рядом с названием точки, причем на первом месте в прямоугольной системе координат записывается абсцисса точки, а на втором — ее ордината. Например, если x-абсцисса точки, а y — ее ордината, то это записывается так: A(x;y). У точек, лежащих на оси абсцисс, ординаты равны нулю, а у точек, лежащих на оси ординат — абсциссы равны нулю. Абсцисса и ордината точки есть расстояния этой точки до осей ОY и ОХ соответственно, которым приписываются определённые знаки в зависимости от четверти, на которые оси координат делят всю координатную плоскость.

Четверти (квадранты) и знаки координат указаны на рисунке 1. Если соединить точку с началом координат, получим вектор 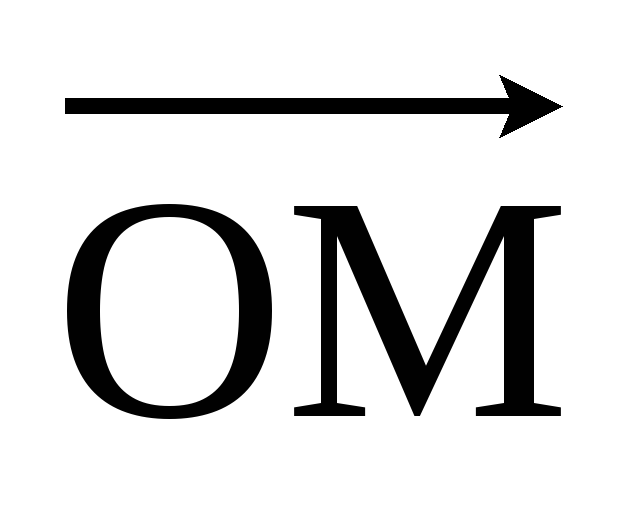, который называется радиусом — вектором точки М. Координаты радиуса — вектора совпадают с координатами точки.

1.2 Простейшие задачи аналитической геометрии Расстояние между двумя точками на плоскости

Пусть заданы две точки А(х₁;y₁) и B(x₂;y₂). Требуется найти расстояние АВ между ними.

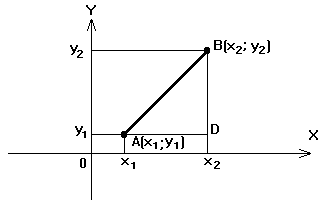Рис. 2

АВ=. (1.1)

Расстояние между двумя точками на плоскости равно корню квадратному из суммы квадратов разностей одноимённых координат.

Слагаемые в круглых скобках можно менять местами, т.к. каждая скобка возводится в квадрат.

Деление отрезка в данном отношении

Пусть А(х₁;у₁) и В(х₂;у₂) концы отрезка АВ. Точка С(х;у) делит отрезок АВ в отношении .

Требуется найти координаты точки С (рисунок 3).

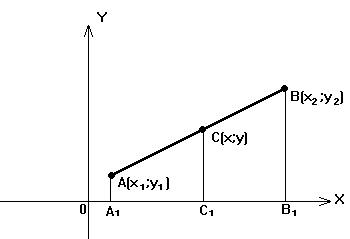Рис. 3

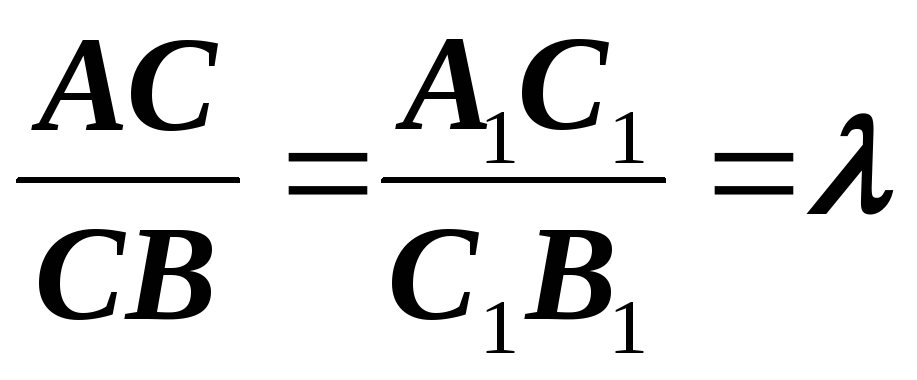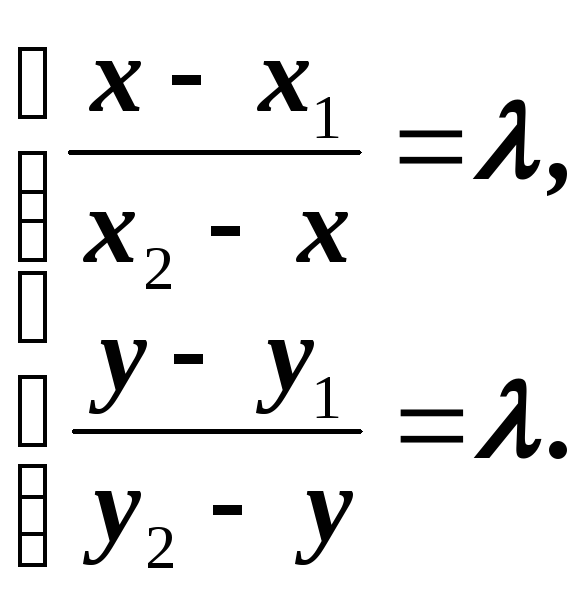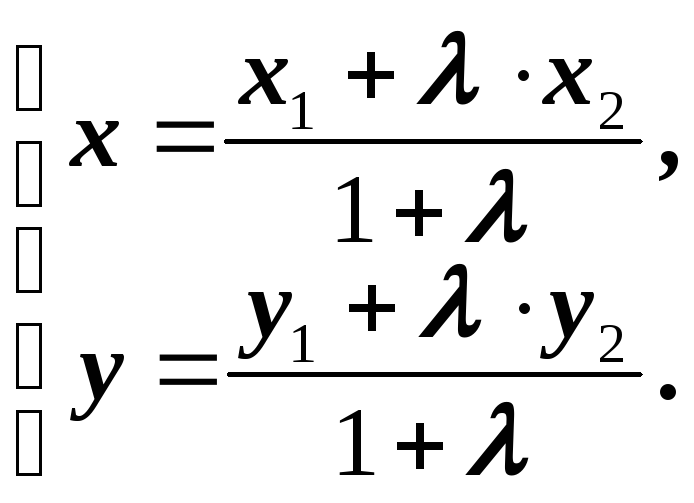Так как  ( на основе теоремы о пересечении отрезка параллельными прямыми) (1.2)(1.3)

Если разрешить уравнения (1.2) относительно Х и У получатся формулы (1.3). Если =1, то есть точкаС-середина АВ, и

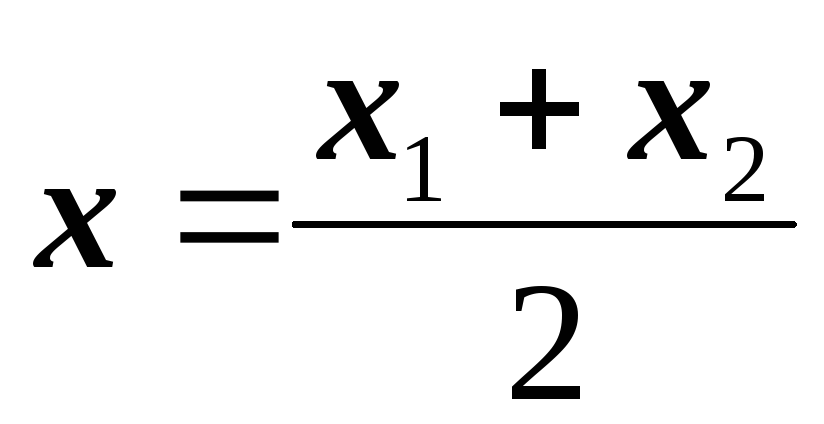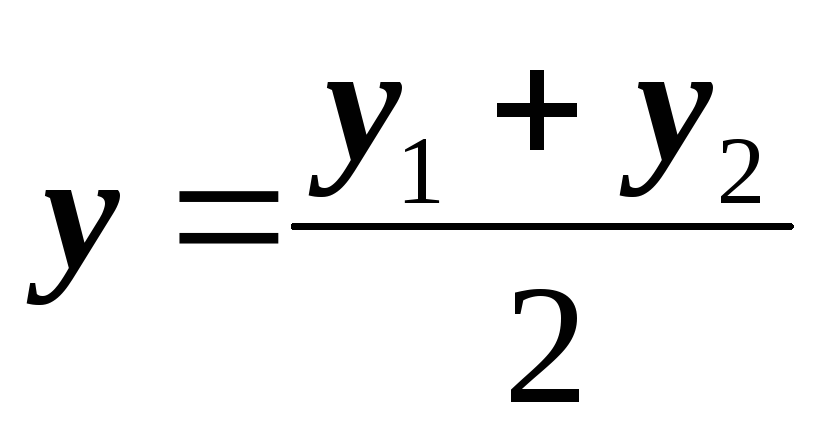; (1.4)

Замечание. Если точка С вне отрезка АВ — за концом отрезка, то — отрицательное число (рисунок 4).

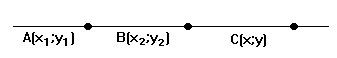Рис. 4

, т.к. направление отрезков АС и СВ — противоположны .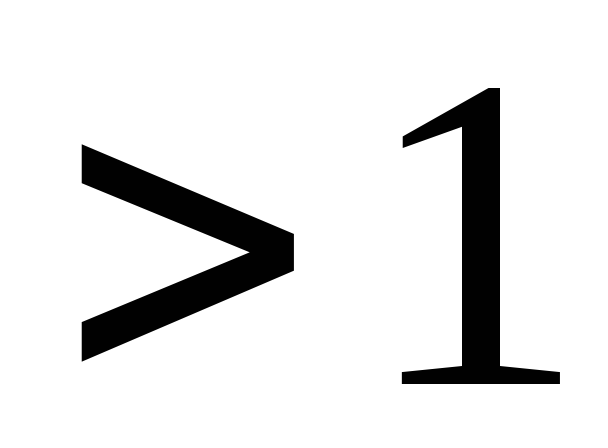

б) С — за началом отрезка (рисунок 5).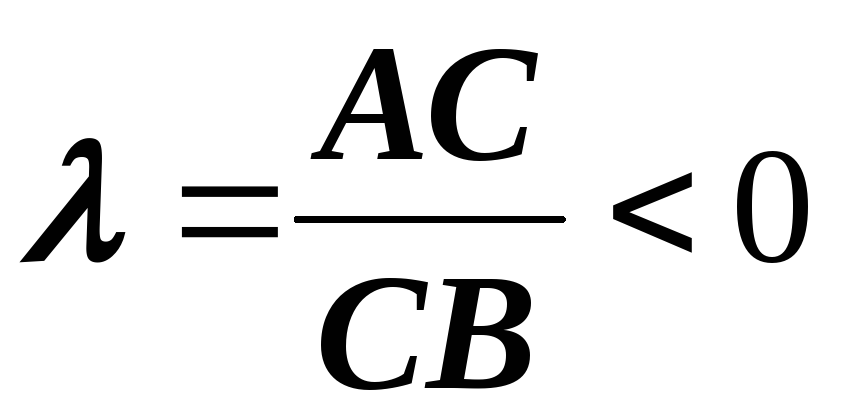и.

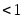Рис. 5

§2 Векторы.

Линейные операции с векторами

Проекция вектора на ось

Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы.

Действия над векторами в координатной форме.

1.Основные понятия

Опр.1 Величины, которые полностью определяются своими

численными значениями, называются скалярными.

Опр. 2 Вектором называется направленный прямолинейный отрезок.

Обозначается или 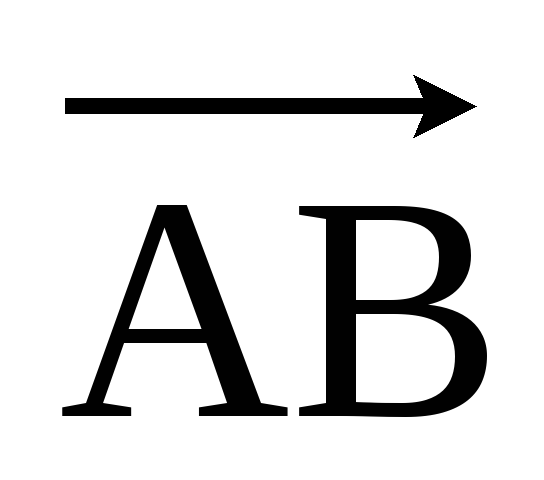. Вектор считается заданным, если известны его длина и направление.

Опр.3 Число, равное длине вектора, называется его модулем или длиной вектора.

Обозначается 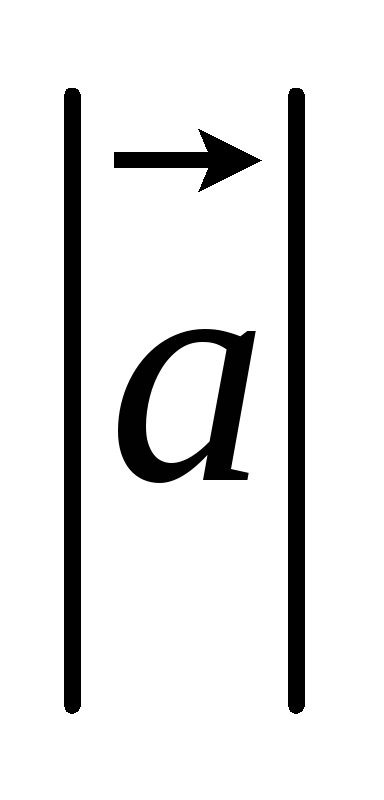или . Модуль может быть только положительным числом.

Векторы в пространстве свободны, т.е. начало его (точку приложения) можно поместить в любую точку пространства, при этом нужно сохранить длину и направление.

Опр.4 Вектор ВА называется противоположным Вектору АВ.

Опр 5 Вектор называется единичным (е), если длина его равна 1, а если его направление совпадает с направлением данного вектора, то он называется ортом вектора а.

Опр 6 Вектор называется нулевым, если совпадают координаты его

начальной и конечной точек.

Длина нулевого вектора равна нулю.

Опр 7 Векторы иназываютсяколлинеарными, если они лежат

на одной прямой или на параллельных прямых. .

Направления их могут быть одинаковыми или противоположными.

Опр. 8 Векторы иназываютсяравными, если они коллинеарные,

имеют одинаковую длину и направление().

Опр. 9 Векторы, лежащие в одной плоскости, называются

Nav view search

Navigation

Search

Деление отрезка в заданном отношении (векторный и координатный способы).

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Зная координаты точек $M_1(x_1, y_1, z_1)$ и $M_2(x_2, y_2, z_2)$ и отношение $lambda,$ в котором точка $M$ делит направленный отрезок $overline,$ найдем координаты точки $M.$

Пусть $O -$ начало координат. Обозначим $overline=r_1,$ $overline=r_2,$ $overline=r.$ Так как, $$overline=r-r_1, overline=r_2-r,$$ то $r-r_1=lambda(r_2-r),$ откуда (так как $lambda
eq -1$) $$r=frac<1+lambda>.$$ Полученная форма и дает решение задачи в векторной форме. Переходя в этой формуле к координатам, получим $$x=frac<1+lambda>, y=frac<1+lambda>, z=frac<1+lambda>.$$

Примеры.

2.57. Отрезок с концами в точках $A(3, -2)$ и $B(6, 4)$ разделен на три равные части. Найти координаты точек деления.

Решение.

Пусть $C(x_C, y_C)$ и $D(x_D, y_D) -$ точки, которые делят отрезок $AB$ на три равные части. Тогда $$lambda_1=frac=frac<1><2>;$$ $$x_C=frac<1+lambda_1>=frac<3+frac<1><2>cdot 6><1+frac<1><2>>=4;$$

Далее находим координаты точки $D:$

Ответ: $(4, 0)$ и $(5, 2).$

2.58. Определить координаты концов отрезка, который точками $C(2, 0, 2)$ и $D(5, -2, 0)$ разделен на три равные части.

Решение.

Пусть $A(x_A, y_A, z_A)$ и $B(x_B, y_B, z_B) -$ концы заданного отрезка.

Выпишем формулы для нахождения координат точки $C$ и подставим известные координаты:

Аналогичные равенства запишем для точки $D:$

Далее запишем полученные уравнения относительно $x_A, x_B;$ $y_A, y_B$ и $z_A, z_B$ попарно в виде систем и решим их:

Таким образом, получили координаты концов отрезка $A(-1, 2, 4)$ и $B(8, -4, -2).$

Ответ: $A(-1, 2, 4),$ $B(8, -4, -2).$