Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).


Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
– Производная положительна там, где функция возрастает.
– Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после – производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.
(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.
(- 9): функция возрастает, а потом убывает – максимум.
(-7): минимум.
(3): максимум.
Все вышесказанное можно обобщить следующими выводами:
– Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
– Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции (f'(x)).
- Найдите корни уравнения (f'(x)=0).
- Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
– если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
– если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
– если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:
(15x^4-60x^2=0) (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0) (x^2-4=0)
(x=±2)
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является (-2).
Ответ. (-2).
Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов
Скачать статью
Как найти точки минимума и максимума функции
Содержание:
-
Минимум и максимум функции
- Точка минимума, минимум функции
- Точка максимума, максимум функции
- Исследование функций на экстремумы
- Примеры задач
Минимум и максимум функции
Минимумом и максимумом функции, другими словами экстремумами, называют точки, в которых функция меняет характер монотонности (с возрастания на убывание и наоборот). Важно понимать, что экстремумы это не максимальные и минимальные значения функции. Обозначаются следующим образом:
- (y_{min}, y_{max}) — минимум, максимум функции или экстремумы;
- (x_{min}, x_{max}) — точки минимума, максимума функции;
- (y_{наиб}, y_{наим}) — наибольшее (максимальное), наименьшее (минимальное) значение функции.
Точка минимума, минимум функции
Точка минимума — такая точка (x_0), если у неё существует окрестность, для всех точек которой выполняется неравенство (f(x)geq f(x_0))
Минимум функции — значение функции в точке минимума (x_0)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Простыми словами, точка минимума — это та, где убывание функции меняется на возрастание.
Точка максимума, максимум функции
Точка максимума — такая точка (x_0), если у неё существует окрестность, для всех точек которой выполняется неравенство (f(x)leq f(x_0))
Максимум функции — значение функции в точке максимума (x_0)
Простыми словами, точка максимума — это та, где возрастание функции меняется на убывание.
Точки максимума и минимума на графике:
Исследование функций на экстремумы
Теорема. Если функция f(x) имеет экстремум в точке (x=x_0,) то в ней производная либо равна 0, либо не существует.
Алгоритм нахождения экстремумов с помощью производной:
-
Найти область определения функции — D(y).
-
Определить производную — f ‘(x).
-
Определить стационарные точки y = f(x), т.е. те, которые принадлежат D(y), f ‘(x) в них обращается в ноль, отыскать критические точки, в которых производной не существует (пример: (f^,(x)=frac1{2sqrt x}), производной не существует при x = 0).
-
Исследовать характер изменения функции f (x) и знак f ‘(x) в промежутках, на которые найденные критические точки делят область определения (при отрицательном знаке производной функция убывает, при положительном — возрастает).
-
Относительно каждой критической точки определить, является ли она точкой максимума, минимума (возрастание меняется на убывание — точка максимума, убывание на возрастание — минимума) или не является точкой экстремума (то есть, меняется ли знак производной при переходе через исследуемую точку).
-
Вычислить значения функции в точках экстремума.
Примеры задач
Задача 1
Исследовать на экстремумы функцию (f(x)=x^3-3x^2.)
Решение задачи по алгоритму:
1) (D(y): xin(-infty;+infty)), т.е. x — любое число.
2) Производная: (f'(x)=3x^2-6x) .
3) Из пункта 1 следует, что критических точек нет. Найдем стационарные:
Приравниваем f ‘(x) к 0, решаем квадратное уравнение (3x^2-6x=0), получаем (x_1=0),(;x_2=2.)
4) Отметим на горизонтальной оси координат точки 0 и 2. Подставим любое x из интервала ((-infty;0)) в f'(x), например, пусть x = -1, тогда (f'(x)=3{(-1)}^2-6(-1)=3+6=9). Получаем f ‘(x)>0, значит на исследуемом интервале f(x) возрастает. Аналогично рассмотрим оставшиеся интервалы. Итого, на отрезке (0;2) производная отрицательна, функция убывает, а на интервале ((2;+infty)) производная положительна, возрастает. Из этого следует, что x=0 – точка максимума, а x=2 – минимума.
5) Найдем значение экстремумов функции.
(f(0)=0-3times0=0)
(f(2)=2^3-3times2^2=8-12=-4)
Ответ: (x_{min}=2,;y_{min}=-4;;x_{max}=0,;y_{max}=0) или (0;0) – минимум функции, (2;-4) – максимум.
Задача 2
Найти промежутки монотонности функции (f(x)=frac x{x^2-4}).
1) (D(y): xinmathbb{R},;)кроме(;pm2)
2) (f'(x)=frac{1(x^2-4)-xtimes2x}{{(x^2-4)}^2}=-frac{x^2+4}{{(x^2-4)}^2})
3) Итак, как выяснилось в пункте 1, критические точки 2 и -2. Если мы приравняем f ‘(x) к 0, чтобы найти стационарные точки, то увидим, что уравнение не будет иметь корней. Значит, стационарных точек нет. Из этого следует, что функция монотонна на всей области определения. Проверим, возрастает она или убывает. Для этого решаем неравенство (-frac{x^2+4}{{(x^2-4)}^2}leq0) и получим, что неравенство верно при любом x, значит функция убывает.
Не забываем, что в ответе, указывая промежуток, обязательно нужно исключить критические точки -2 и 2 т.к. в них функция не определена.
Ответ: f(x) убывает на промежутке ((-infty;-2)cup(-2;2)cup(2;+infty)).
Задача 3
Докажите, что функция (f(x)=x^5+2x^3-4) возрастает на всех числовой прямой.
1) (D(y): xinmathbb{R}), значит критических точек нет.
2) (f'(x)=5x^4+6x)
3) Приравняем f'(x) к 0 и найдем корень: x = 0. Отметим 0 на числовой прямой и определим знак производной на промежутках ((-infty;0)) и ((0;+infty)). Получим, что производная положительна на обоих промежутках, следовательно функция возрастает на всей числовой прямой.
Утверждение доказано
7. Взаимосвязь функции и ее производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Связь производной с точками экстремума функции
В данных задачах речь идет о непрерывных функциях (простым языком, функция будет непрерывна на интервале, если ее график можно нарисовать на этом интервале, не отрывая ручку от листа).
(blacktriangleright) (color{royalblue}{text{Точки}}) (локального) (color{royalblue}{text{экстремума}}) функции – это точки (локального) максимума и минимума.
Окрестность – это интервал вокруг точки некоторого радиуса. Например, окрестностью точки (x=0) можно назвать интервал ((-1;1)), или ((-0,1;0,1)), или ((-0,0000001;0,0000001)) и т.д.
(blacktriangleright) (color{royalblue}{text{Точка}}) (color{royalblue}{text{максимума}}) (x_{max}) – такая внутренняя точка области определения функции, для которой выполнено: (f(x)leqslant
f(x_{max})) для любого (x) из некоторой окрестности точки (x_{max}).
То есть можно найти такую окрестность, что для любой точки из этой окрестности будет выполнено данное неравенство.
Заметим, что, например, если функция определена на отрезке ([0;2]), то все точки интервала ((0;2)) будут внутренними, а вот точки (0) и (2) – граничными (то есть не внутренними).
(blacktriangleright) (color{royalblue}{text{Точка}}) (color{royalblue}{text{минимума}}) (x_{min}) – такая внутренняя точка области определения функции, для которой выполнено: (f(x)geqslant
f(x_{min})) для любого (x) из некоторой окрестности точки (x_{min}).
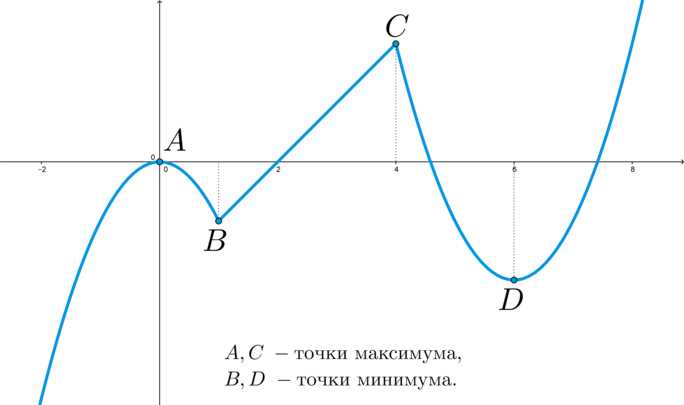
Например, для точки (C) за окрестность можно взять интервал ((3;5)) или даже ((2;6)), а можно совсем маленький — ((4-0,01;4+0,01)).

Следующие факты помогают искать точки экстремума функции.
(blacktriangleright) Если производная (f’) в точке (x) равна нулю и меняет свой знак слева направо с “(+)” на “(-)” , то эта точка является точкой максимума.
Заметим также, что если производная (f’) в точке (x) не существует и меняет свой знак слева направо с “(+)” на “(-)” (но (x) – внутренняя точка области определения функции (f,)!), то эта точка является точкой максимума.
Пример: в точке (A) производная равна нулю и эта точка является точкой максимума; в точке (C) производная не “равна нулю”, а не существует, при этом точка (C) также является точкой максимума.
(blacktriangleright) Если производная в точке (x) равна нулю и меняет свой знак слева направо с “(-)” на “(+)” , то эта точка является точкой минимума.
Также, если производная (f’) в точке (x) не существует и меняет свой знак слева направо с “(-)” на “(+)” (но (x) – внутренняя точка области определения функции (f,)!), то эта точка является точкой минимума.
(blacktriangleright) Заметим, что точки экстремума – это значение абсциссы (x).
(blacktriangleright) Заметим, что существует такое понятие, как критические точки — это все точки, в которых производная функции либо равна нулю, либо не существует.
Таким образом, только часть критических точек является точками экстремума.
Задание
1
#3107
Уровень задания: Равен ЕГЭ
На рисунке изображен график производной функции (f(x)), определенной на отрезке ([-10;37]). Найдите количество точек максимума функции (f(x)) на отрезке ([0;37]).
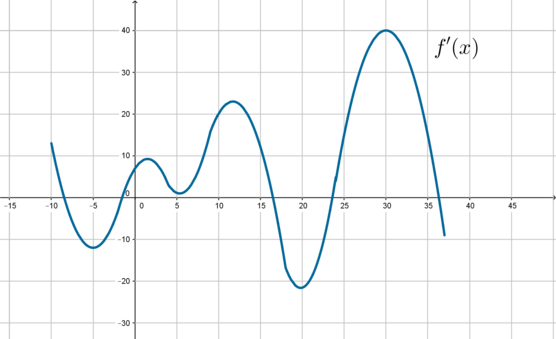
Точка максимума – значение (x), в котором производная меняет свой знак с “(+)” на “(-)”. Следовательно, в этой точке ее график пересекает ось абсцисс “сверху вниз” (если двигаться по рисунку слева направо). Отметим отрезок ([0;37]) и увидим, что таких точек 2:
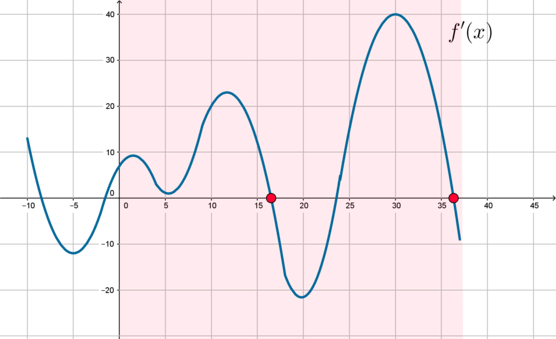
Ответ: 2
Задание
2
#2962
Уровень задания: Равен ЕГЭ
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-2,4; 8,7)). Найдите сумму точек экстремума этой функции на отрезке ([1;6]).
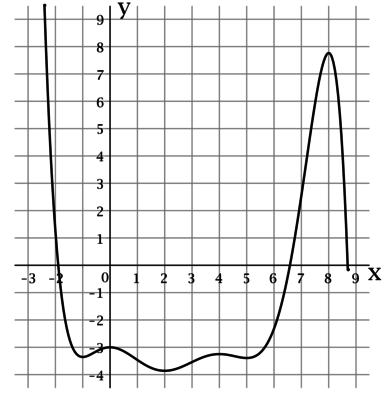
Так как на рисунке изображен график функции, то точки экстремума – это точки на графике, в которых функция меняется с возрастания на убывание или наоборот. Эти точки: (x=-1; 0; 2; 4; 5; 8.) Из них на отрезке ([1;6]) лежат только точки (2; 4; 5), следовательно, их сумма равна (2+4+5=11.)
Ответ: 11
Задание
3
#730
Уровень задания: Равен ЕГЭ
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-3; 8,5)). Найдите сумму точек экстремума этой функции.
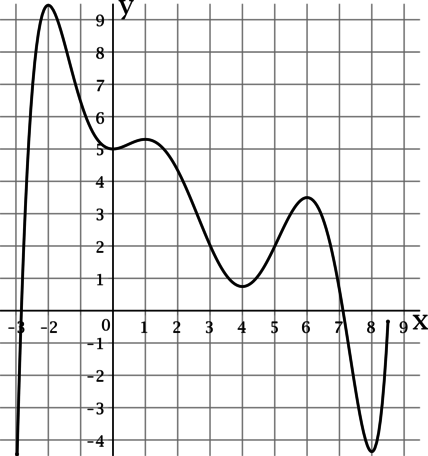
Точкой экстремума функции называется точка, в которой функция достигает локально минимальное или локально максимальное значение.
По рисунку можно определить, что функция (f(x)) достигает локально минимальные значения в точках (0), (4) и (8), а локально максимальные значения в точках (-2), (1) и (6). Таким образом, сумма точек экстремума этой функции равна (0 + 4 + 8 + (-2) + 1 + 6 = 17).
Ответ: 17
Задание
4
#731
Уровень задания: Равен ЕГЭ
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-2,4; 8,7)). Найдите сумму точек экстремума этой функции.
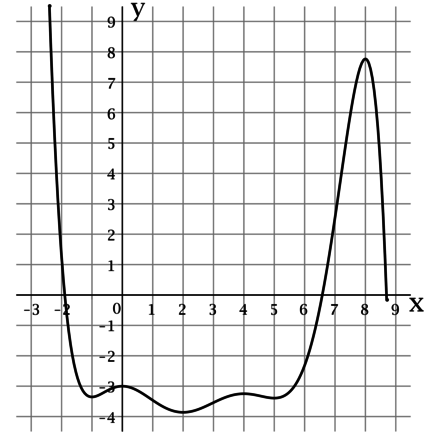
Точкой экстремума функции называется точка, в которой функция достигает локально минимальное или локально максимальное значение.
По рисунку можно определить, что функция (f(x)) достигает локально минимальные значения в точках (-1), (2) и (5), а локально максимальные значения в точках (0), (4) и (8). Таким образом, сумма точек экстремума этой функции равна (-1 + 2 + 5 + 0 + 4 + 8 = 18).
Ответ: 18
Задание
5
#732
Уровень задания: Равен ЕГЭ
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-3; 9)). Найдите произведение точек экстремума этой функции.
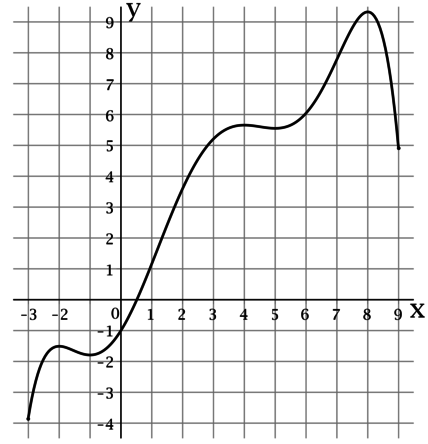
Точкой экстремума функции называется точка, в которой функция достигает локально минимальное или локально максимальное значение.
По рисунку можно определить, что функция (f(x)) достигает локально минимальные значения в точках (-1) и (5), а локально максимальные значения в точках (-2), (4) и (8). Таким образом, произведение точек экстремума этой функции равно ((-1)cdot 5cdot (-2)cdot 4cdot 8 = 320).
Ответ: 320
Задание
6
#733
Уровень задания: Равен ЕГЭ
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-2.8; 7.8)). Найдите произведение точек экстремума этой функции.
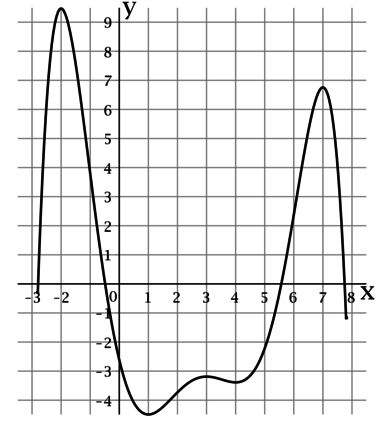
Точкой экстремума функции называется точка, в которой функция достигает локально минимальное или локально максимальное значение.
По рисунку можно определить, что функция (f(x)) достигает локально минимальные значения в точках (1) и (4), а локально максимальные значения в точках (-2), (3) и (7). Таким образом, произведение точек экстремума этой функции равно (1cdot 4cdot (-2)cdot 3cdot 7 = -168).
Ответ: -168
Задание
7
#734
Уровень задания: Равен ЕГЭ
На рисунке изображен график (y = f'(x)) – производной функции (y = f(x)), определенной на интервале ((-1; 8)). В какой точке отрезка ([2; 5]) функция (y = f(x)) принимает наибольшее значение?
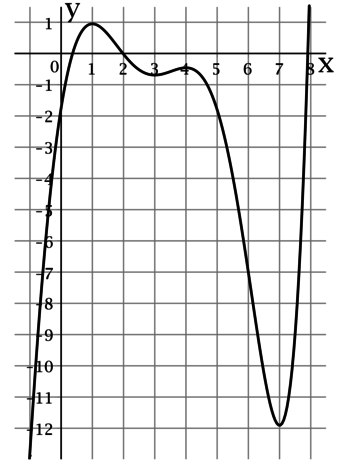
По рисунку можно определить, что функция (y = f'(x)) на отрезке ([2; 5]) принимает неположительные значения, при этом (f'(2) = 0). Так как на полуинтервале ((2; 5]) производная функции (f(x)) отрицательна, то сама функция (f(x)) на ((2; 5]) убывает, тогда (y = f(x)) на отрезке ([2; 5]) принимает наибольшее значение при (x = 2).
Ответ: 2
Итоговый экзамен по математике для выпускников 11-х классов обязательно включает задания на поиск точек максимума и минимума функциональных зависимостей. Их решение проводится аналитически – методом дифференцирования. Применение производной для исследования функции на экстремум сокращает время анализа и позволяет представить общий вид графика зависимости еще до выполнения построений.
Обучающий ресурс «Школково» позволит учащимся освежить в памяти главные моменты темы – уточнить теоретические знания и отработать их в решении ряда задач. Наш подход к обучению в отношении поиска точек экстремума функции через производную в типовых заданиях ЕГЭ основан на принципе глубокой взаимосвязи теории и практики. Сначала ученик читает правила «Теоретической справки», потом смотрит видео с объяснениями учителя, а затем работает с реальным педагогом. В процессе просмотра предлагаемых на сайте вебинаров можно задать интересующие вопросы и получить помощь в решении конкретных задач.
В разделе «Каталог» имеются подборки тематических заданий на нахождение точек экстремума функции с помощью производной, а также нахождения производной угла наклона касательной. Каждый пример содержит готовое решение и правильный ответ, с которыми можно ознакомиться после окончания самостоятельной работы. «Конструктор» примерных вариантов ЕГЭ позволит провести исследование экстремумов функций с помощью производных в ходе пробного выполнения экзаменационной работы.

УСТАЛ? Просто отдохни
Простой алгоритм нахождения экстремумов. Учимся находить с bugaga.net.ru.
- Находим производную функции
- Приравниваем эту производную к нулю
- Находим значения переменной получившегося выражения (значения переменной, при которых производная преобразуется в ноль)
- Разбиваем этими значениями координатную прямую на промежутки (при этом не нужно забывать о точках разрыва, которые также надо наносить на прямую), все эти точки называются точками «подозрительными» на экстремум
- Вычисляем, на каких из этих промежутков производная будет положительной, а на каких – отрицательной. Для этого нужно подставить значение из промежутка в производную.
Из точек, подозрительных на экстремум, надо найти именно экстремумы. Для этого смотрим на наши промежутки на координатной прямой. Если при прохождении через какую-то точку знак производной меняется с плюса на минус, то эта точка будет максимумом, а если с минуса на плюс, то минимумом.
Чтобы найти наибольшее и наименьшее значение функции, нужно вычислить значение функции на концах отрезка и в точках экстремума. Затем выбрать наибольшее и наименьшее значение.
https://bugaga.net.ru/ege/math/ekstremum.html bugaga.net.ru
Рассмотрим пример
![]()
Находим производную и приравниваем её к нулю:
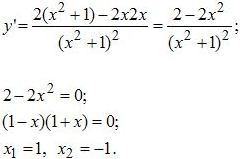
Полученные значения переменных наносим на
координатную прямую и высчитываем знак производной на каждом из промежутков. Ну
например, для первого возьмём -2,
тогда производная будет равна -0,24,
для второго возьмём 0, тогда
производная будет 2 , а для третьего возьмём 2, тогда производная будет -0,24. Проставляем соответствующие знаки.
![]()
Видим, что при прохождении через точку -1 производная меняет знак с минуса на плюс, то есть это будет точка минимума, а при прохождении через 1 – с плюса на минус, соответственно это точка максимума.
Смотрите также:
- Решение ЕГЭ по математике (часть B)
- Как найти экстремум (точки максимума и минимума) функции
- Формулы логарифмов
- Таблица со значениями синусов, косинусов
- Таблица производных
Еще больше материалов для подготовки к ЕГЭ
