Как найти точку фишера для проектов

Построить
профили NPV
всех четырех проектов, найти графически
и рассчитать аналитически точку Фишера.

Точка
Фишера – точка, которая дает одинаковую
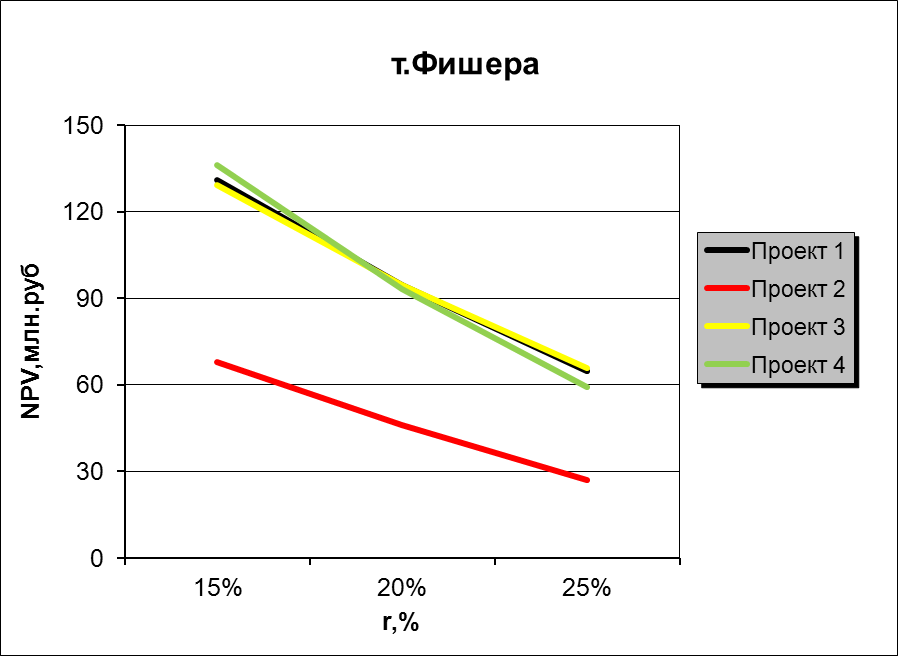
доходность для проектов. График
№1. Точка Фишера.

По
графику определяем два наиболее
предпочтительных
проекта – 2-ой и 3-ий и рассчитаем для них
точку Фишера аналитически.

Для
аналитического расчета точки Фишера
рассчитываются дисконтированные потоки
нового проекта ∆, как разница между
потоками 2 и 3 проектов (таблица №8).

Таблица
№ 8. Аналитический расчет точки Фишера.

NPV_15%
=
40/1.15-64/1.15^2-40/1.15^3+40/1.15^4+24/1.15^5+ +16/1.15^6 =
55,76679475
млн.
руб.

NPV_25%
= 40/1.25-64/1.25^2-40/1.25^3+40/1.25^4+24/1.25^5+ +16/1.25^6 =
103,8085938
млн.
руб.

IRR
= 15+((55,76679475*(25-15))/(55,76679475-103,8085938)
=
3,392026129%

4. Анализ безубыточности проекта.

По
результатам расчетов показателей
эффективности проектов и точки Фишера
предварительно выбираем наиболее
выгодный проект (проект 4), рассчитаем
для него точку безубыточности и построим
график безубыточности проекта.

Таблица
№9. Расчет параметров графика безубыточности
проекта 4.

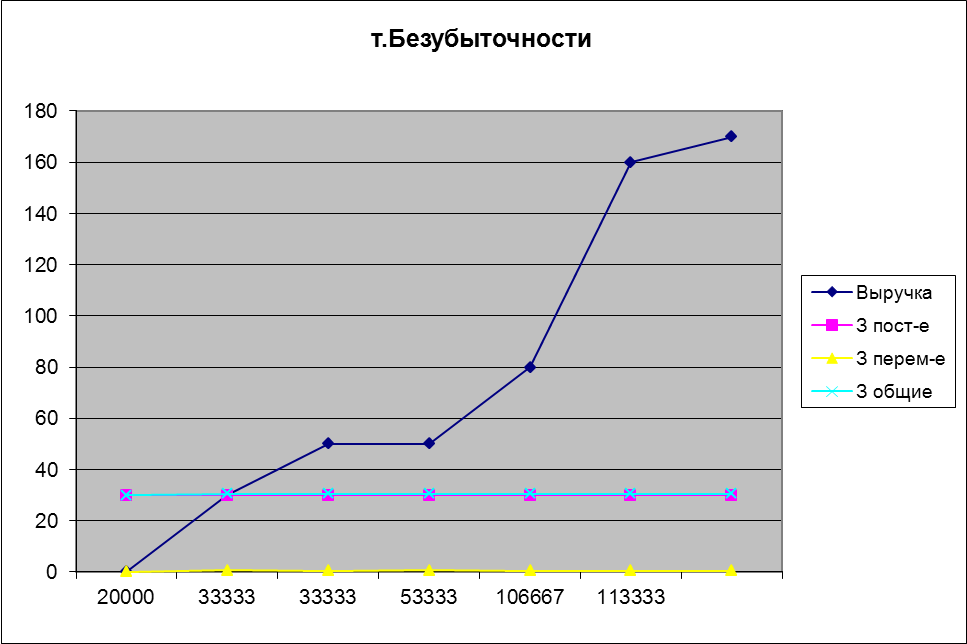
График
№2. Точка безубыточности проекта №4.

Тб
= Зпост / Ц – Зпер

Зпост
= 30 млн. руб.

Q
= 113333 т.ед.

Выр
= 170 млн. руб.

Ц
= Выручка/Q
= 1500 руб.

Тб
= З.пост./(Цена-∑
З.пер/Q)=30000000/(1500-510143,5105/113333)
= 20060

1. Оценка риска инвестиционных проектов.

Необходимо
оценить, насколько проекты являются
рискованными. Для этого используются
два метода: метод сценарного анализа и
метод анализа чувствительности

1. Метод
   сценарного анализа.

Метод
сценариев предполагает учет чувствительности
NPV
к изменению входящих переменных в рамках
разброса или вероятности возникновения
события. Определяем величину риска на
1 руб. NPV
для каждого рассматриваемого проекта.

Таблица
№ 10. Расчет денежных потоков при
пессимистическом варианте наступления
событий.

Таблица № 11. Расчет денежных потоков
при наиболее вероятном варианте
наступления событий.

Таблица № 12. Расчет денежных потоков
при оптимистическом варианте наступления
событий.

Таблица
№ 13. Расчет NPV для
пессимистического, наиболее вероятного
и оптимистического вариантов наступления
события.

Таблица
№ 13. Расчет среднеожидаемого NPV,
дисперсии и коэффициента вариации.

Коэффициент
вариации – показывает уровень риска
на 1 руб. дохода. Из расчетов следует,
что проект №4 имеет наименьший коэффициент
вариации, т.е. проект №4 менее рискован,
чем другие.

1. Метод
   анализа чувствительности.

Анализ
чувствительности показывает изменение
NPV,
при изменении одной из переменных,
формирующих NPV.
Степень влияния определяется по
чувствительности показателя при
отклонении его от базового значения.
Отклонения объема реализации и цены
капитала равны 5 и 10%.

Таблица
№ 14. Расчет NPV
при изменении объема реализации (Q)
и цены капитала (r)
для проекта №1.

Таблица
№ 15. Расчет NPV при изменении
объема реализации (Q) и
цены капитала (r) для
проекта №2.

Таблица
№ 16. Расчет NPV при изменении
объема реализации (Q) и
цены капитала (r) для
проекта №3.

Таблица
№ 16. Расчет NPV при изменении
объема реализации (Q) и
цены капитала (r) для
проекта №4.

График
№3. График чувствительности NPV
к
изменению объема реализации.

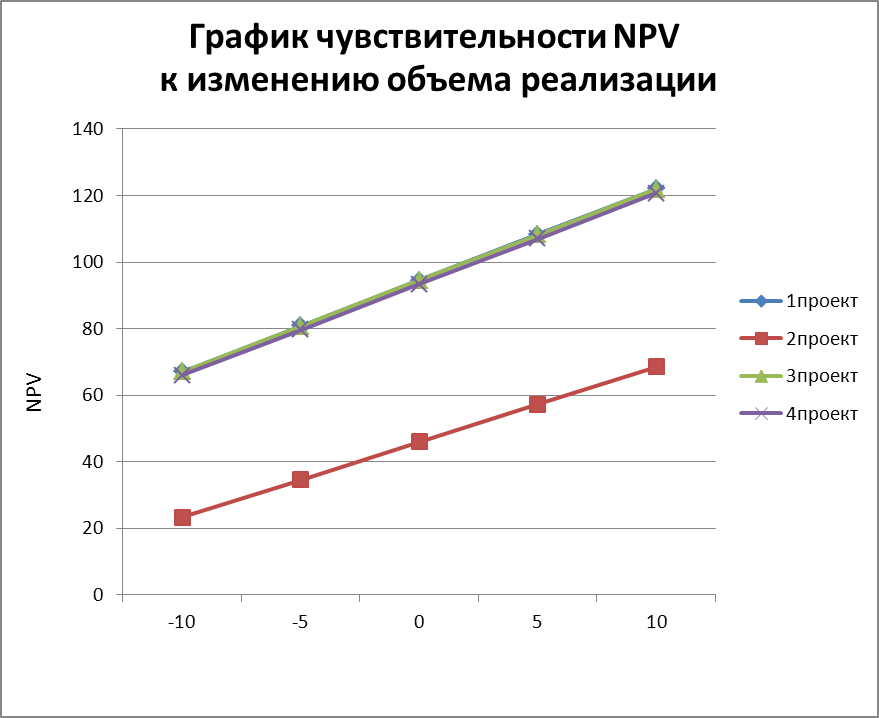
На
графике №3 наклон прямых проектов 2 и 3
практически одинаковый, что свидетельствует
о том, что чувствительность NPV
этих проектов к изменению объема
реализации одинакова. Наклон прямой
проекта 4 более крутой по сравнению с
проектами 1, 2 и 3, следовательно, наибольшей
чувствительностью обладает NPV
4 проекта и риск данного проекта больше
по сравнению с другими. Наклон прямой
проекта 1 более пологий и значит проект
1 менее рискованный, чем проекты 2 и 3.

График
№4. График чувствительности NPV
к
изменению цены капитала.

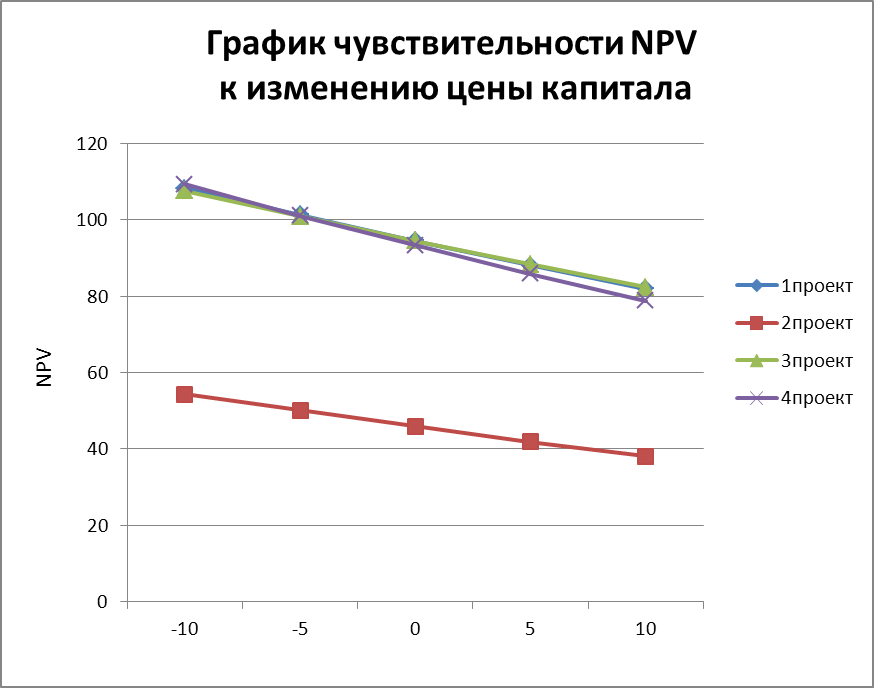
На
графике №4 видно, что наклон прямой
проекта 4 более крутой, а значит риск
данного проекта выше, чем у проектов 1,
2 и 3. Наклон прямых проектов 1 и 3 практически
одинаковый. Это говорит о том, что
чувствительность NPV
этих проектов к изменению цены капитала
примерно одинаковая. Наклон прямой
проекта 2 более пологий и значит
чувствительность проекта 2 ниже чем у
остальных проектов. Проект 2 менее
рискован, чем проекты 1, 3 и 4.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Рассмотрим два аспекта: независимые и альтернативные проекты.

1. Динамические показатели эффективности независимых проектов (NPV, IRR, PI) тесно взаимосвязаны и позволяют оценить их эффективность с разных сторон. Поэтому при отборе реальных инвестиционных проектов данные показатели следует рассматривать в комплексе.

Для единичного инвестиционного проекта, который может рассматриваться как единичное множество независимых проектов, показатели NPV, IRR, PI дают одинаковые рекомендации принять, или отвергнуть проект. То есть, проект приемлемый по одному показателю, будет приемлем и по другим. Это объясняется следующей взаимосвязью:

1. Как показали результаты многочисленных обследований практики принятия решений в области инвестиционного проектирования в условиях рынка, в анализе эффективности инвестиционных проектов наиболее часто применяются критерии NPV и IRR. Однако возможны ситуации, когда эти критерии противоречат друг другу, например, при оценке альтернативных (взаимоисключающих) проектов. Рассмотрим ряд ситуаций.

В сравнительном анализе альтернативных проектов критерий IRR можно использовать с известными оговорками. Так, если значение IRR для проекта А больше, чем для проекта В, то проект А в определенном смысле может рассматриваться как более предпочтительный, поскольку допускает бoльшую гибкость в варьировании источниками финансирования инвестиций, цена которых может существенно различаться. Однако такое преимущество носит весьма условный характер. Поскольку  IRR является относительным показателем, то на его основе невозможно сделать правильные выводы об альтернативных проектах с позиции их возможного вклада в увеличение капитала предприятия. Этот недостаток особенно четко проявляется, если проекты существенно различаются по величине денежных потоков.

При отборе альтернативных инвестиционных проектов, несмотря на отмеченную ранее взаимосвязь показателей NPV, IRR, и PI, возникает проблема ранжирования вариантов и выбора показателя ранжирования. Одной из причин данной проблемы можно считать то, что NPV – абсолютный показатель, а PI и IRR– относительные. Основными же причинами признают следующие:

• существуют различия в динамике будущих денежных поступлений;
• существуют различия в потребных суммах инвестиций.

Проблему ранжирования альтернативных проектов удобно рассмотреть на примере.

Пример.  Строительство для отопления микрорайона котельной предполагает альтернативное использование трёх видов топлива: угля, газа и мазута. Расчёт эффективности альтернативным проектом приведён в таблице 11.1. (норма дисконта 10%).

Таблица 11.1.

Из таблицы 11.1. видно, что по NPV предпочтительнее газовая схема, по PI- мазутная, а IRR- угольная.

Причины подобного разнобоя в оценках инвестиционных проектов проанализируем по кривым зависимостям  для газовой и угольной схем энергоснабжения котельной (рис.11.1), т.е. решение уравнений

Рисунок 11.1 – Иллюстрация нахождения точки Фишера

Выбор варианта по критерию наивысшей величины NPV  зависит преимущественно от того, какой уровень коэффициента дисконтирования при этом используется. В примере имеется точка пересечения Фишера при     11,45 % , при которой оба варианта имеют одинаковые значения NPV и являющаяся пограничной точкой, различающей ситуации предпочтения NPV i-х проектов.  При доходности на вложенный капитал больше чем    11,45 % преимущественно оказывается на стороне угля, а при меньшей  11,45 % – газовой схемы. Очевидно, что показатель IRR  не всегда позволяет выявить предпочтительный проект. Таким образом, использование критерия NPV предпочтительнее при сравнении альтернативных вариантов.

Пример. Проанализируем два альтернативных проекта. Цена авансированного капитала составляет 10 %. Исходные данные (в тыс. руб.) и результаты расчетов приведены в таблице 11.2.

Таблица 11.2 – Анализ проектов с различными  по величине денежными потоками

На первый взгляд, проект А является более предпочтительным, поскольку его IRR значительно превосходит IRR проекта В. Однако, если предприятие имеет возможность профинансировать проект В, следует принять именно его, так как вклад проекта B в увеличение капитала предприятия на порядок превосходит вклад проекта А.

1. Основной недостаток критерия NPV в том, что это абсолютный показатель, а потому он не дает представления о так называемом “резерве безопасности проекта”. Имеется в виду следующее: если допущены ошибки в прогнозах денежного потока (что совершенно не исключено особенно в отношении последних лет реализации проекта) или коэффициента дисконтирования, насколько велика опасность того, что проект, который ранее рассматривался как прибыльный, окажется убыточным?

Информацию о резерве безопасности проекта дают критерии IRR и РI. Так, при прочих равных условиях, чем больше IRR по сравнению с ценой авансированного капитала, тем больше резерв безопасности. Что касается критерия РI, то правило здесь таково: чем больше значение РI превосходит единицу, тем больше резерв безопасности. Иными словами, с позиции риска можно сравнивать два проекта по критериям IRR и РI, но нельзя – по критерию NPV. Рассмотрим следующую ситуацию.

Пример. Проект С имеет следующие прогнозные значения элементов денежного потока (млн.  долл.): -100, 20, 25, 40, 70. Требуется проанализировать целесообразность включения его в инвестиционный портфель при условии, что цена авансированного капитала 15 %.

Расчеты показывают, что проект приемлем, поскольку при  r = 15 %          NPVс  = 2,6 млн. долл. Хотя проект обеспечивает достаточно высокий прирост капитала предприятия, ситуация не так проста, как это представляется на первый взгляд. Поскольку значение  IRRc = 16,0 %, т.е. очень близко к прогнозируемой цене капитала, очевидно, что проект С является весьма рискованным. Если предположить, что в оценке прогнозируемой цены источника допущена ошибка и реальное ее значение может возрасти до 17 %, то мнение о проекте С меняется – его нельзя принять, так как NPVc = -2,3 млн. долл.

Данный пример показывает, что высокое значение NPV не всегда должно служить решающим аргументом при принятии решений инвестиционного характера, поскольку, во-первых, оно определяется масштабом проекта и, во-вторых, может быть сопряжено с достаточно высоким риском. Напротив, высокое значение IRR в ряде случаев указывает на наличие определенного резерва безопасности в отношении данного проекта.

1. Поскольку зависимость NPV от ставки дисконтирования r нелинейна, а значение NPV существенно зависит от r, причем степень этой зависимости различна и определяется динамикой элементов денежного потока, то NPV проектов не одинаково реагируют на изменение r.

Пример. Рассмотрим два независимых проекта (млн. руб.):

А: -200, 150,  80,   15,   15,   10;

B: -200,  20,    50,   50,   90,   110.

Требуется ранжировать их по степени приоритетности при условии, что цена источника финансирования весьма неопределенна и, предположительно, может варьировать в интервале от 5 % до 20 %. В таблице 11.3. приведены результаты расчетов для возможных ситуаций.

Таблица 11.3

Из приведенных расчетов видно, что проекты А и B неодинаково реагируют на изменение значения коэффициента дисконтирования: при переходе от 10 к 15 % NPV проекта В снижается на 98 %, тогда как NPV проекта А – на 52,6 %. Ясна и причина такой неодинаковости: проект А имеет убывающий денежный поток, а  В – нарастающий. Так как интенсивность возмещения инвестиций в проекте А существенно выше, чем в проекте В, то он в меньшей степени реагирует на негативное увеличение значения коэффициента дисконтирования. Что касается проектов типа В, то они являются более рискованными, о чем можно судить и по значению IRR.

1. Для проектов классического характера критерий IRR показывает лишь максимально допустимый уровень затрат по проекту. В частности, если цена инвестиций в оба альтернативных проекта меньше, чем значения IRR для них, выбор может быть сделан лишь с помощью дополнительных критериев. Более того, критерий IRR не позволяет различать ситуации, когда цена капитала меняется. Рассмотрим соответствующий пример.

Пример. В таблице 11.4.  приведены исходные данные по двум альтернативным проектам (в млн. руб.). Необходимо выбрать один из них при условии, что цена капитала, предназначенного для инвестирования, составляет    а) 5 %; б) 15 %.

Таблица 11.4.

Если исходить из критерия IRR, то оба проекта и в ситуации а), и в ситуации б) являются приемлемыми и равноправными. Но так ли это? Построим графики функции NPV = f (r) для обоих проектов (рисунок 11.2).

Рисунок 11.2 – Нахождение точки Фишера

Точка пересечения двух графиков (r = 9,82 %). Показывает значение коэффициента дисконтирования, при котором оба проекта имеют одинаковый NPV  и называется точкой Фишера (рис. 11.2). Она примечательна тем, что служит пограничной точкой, разделяющей ситуации, которые “улавливаются” критерием NPV и не “улавливаются” критерием IRR.

В данном примере критерий IRR не только не может расставить приоритеты между проектами, но и не показывает различия между ситуациями а) и б). Напротив, критерий NPV позволяет расставить приоритеты в любой ситуации. Более того, он показывает, что ситуации а) и б) принципиально различаются между собой. А именно, в случае (а) следует принять проект А, поскольку он имеет больший NPV, в случае б) следует отдать предпочтение проекту В. Отметим, что точка Фишера для потоков А и В может быть найдена как IRR приростного потока (А-В) или, что то же самое, (В – А).

1. Одним из существенных недостатков критерия IRR является то, что в отличие от критерия NPV он не обладает свойством аддитивности, т.е. для двух инвестиционных проектов А и В, которые могут быть осуществлены одновременно:

Пример. Проанализируем целесообразность инвестирования в проекты А, В, С при условии, что проекты В и С являются альтернативными, а проект А – независимым. Цена инвестированного капитала составляет 10%.

Исходя из условия примера необходимо проанализировать несколько сценариев:

а) целесообразность принятия каждого из проектов в отдельности (А, В или С);

б) целесообразность принятия комбинации проектов (А+В) и (А+С).

Результаты анализа приведены в таблице 11.5.

Таблица 11.5 – Анализ комбинации инвестиционных проектов (млн. руб.)

Из приведенных расчетов видно, что все три исходных проекта являются приемлемыми, поэтому необходимо проанализировать возможные их комбинации. По критерию IRR относительно лучшей является комбинация проектов А и С, однако такой вывод не вполне корректен, поскольку резерв безопасности в обоих случаях комбинаций весьма высок, но другая комбинация (А + В) дает большее возможное увеличение капитала компании.

1. В принципе не исключена ситуация, когда критерий IRR не с чем сравнивать. Например, нет основания использовать в анализе постоянную цену капитала. Если источник финансирования – банковская ссуда с фиксированной процентной ставкой, цена капитала не меняется, однако чаще всего проект финансируется из различных источников, поэтому для оценки используется средневзвешенная цена капитала фирмы, значение которой может варьировать в зависимости, в частности, от общеэкономической ситуации, текущих прибылей и т.п.
2. Критерий IRR совершенно непригоден для анализа неординарных инвестиционных потоков, то есть проектов с неординарным денежным потоком. В этом случае возникает как множественность значений IRR, так и неочевидность экономической интерпретации возникающих соотношений между показателем IRR и ценой капитала. Возможны также ситуации, когда положительного значения IRR попросту не существует.

Выходные данные:

ИНВЕСТИЦИОННОЕ ПРОЕКТИРОВАНИЕ: ОСНОВЫ ТЕОРИИ И ПРАКТИКИ / Москаленко А.П., Москаленко С.А., Ревунов Р.В., Вильдяева Н.И. //  Санкт-Петербург, Лань, 2018. (1-е, Новое)

Вернуться к оглавлению “Инвестиционное проектирование: основы теории и практики”

 Готовое решение: Заказ №10150

 Тип работы: Задача

Статус:  Выполнен (Зачтена преподавателем ВУЗа)

 Предмет: Экономика

 Дата выполнения: 14.11.2020

 Цена: 229 руб.

Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

Задача 7

Определите точку Фишера для двух инвестиционных проектов. Объясните значение т. Фишера. Постройте график. Точку Фишера найдите через разностный поток.

Решение:

Точка Фишера представляет собой точку пересечения графиков NPV двух сравниваемых проектов. Абсцисса точки Фишера является пограничной точкой, разделяющей ситуации, улавливаемые критерием NPV и не улавливаемые критерием IRR (имеется в виду ранжирование проектов по степени их предпочтительности). Если значение стоимости капитала находится справа от абсциссы точки Фишера, то критерии NPV и IRR дают одинаковые результаты при оценке альтернативных инвестиционных проектов, если слева, то критерии NPV и IRR противоречат друг другу.

Вычислим чистый дисконтированный доход:

где    CF_k – денежный поток за период k;

r – ставка дисконтирования;

IС_k – инвестиции за период k.

1) если NPV < 0, то в случае принятия проекта ценность компании уменьшится, т. е. владельцы компании понесут убыток;

2) если NPV = 0, то в случае принятия проекта ценность компании не изменится, т. е. благосостояние ее владельцев останется на прежнем уровне;

3) если NPV > 0, то в случае принятия проекта ценность компании, а следовательно, и благосостояние ее владельцев увеличится.

Пусть r₁=20%, r₂=24%, r₃=27%, r₄=30%, r₅=35%.

NPV1А=301+0,2+25(1+0,2)2+30(1+0,2)3-50=9,72 д.е.

NPV2А=301+0,24+25(1+0,24)2+30(1+0,24)3-50=6.19 д.е.

Инструкция