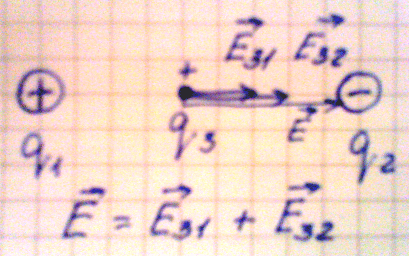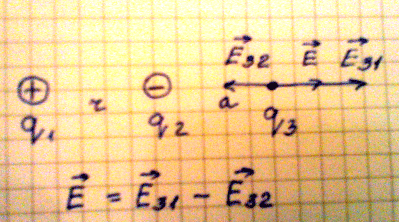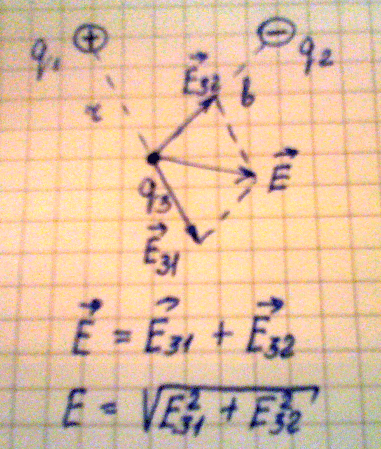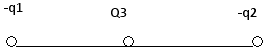Как найти точку где напряженность равна нулю

Напряженность электрического поля, созданного точечным зарядом, в данной точке равна

[ E = k cdot frac{left| q right|}{r^{2}}. ]

В любой точке пространства электрическое поле создано двумя зарядами q₁ и q₂. Результирующая напряженность полей в искомой точке будет равна

[ vec{E} = vec{E}_{A} + vec{E}_{B}, ]

где E_A, Е_B — напряженности полей, создаваемых зарядами q₁ (в точке А) и q₂ (в точке В) в этой точке. Очевидно, что Е = 0 только в той точке, в которой векторы Е_A и Е_B равны по модулю и противоположны по направлению.

Рассмотрим напряженность в точках на прямой, соединяющей заряды (рис. ).
В любой точке L на прямой слева от q₁ напряженность Е_L не равна 0, так как E_LA > E_LB (заряд в точке А больше по величине заряда в точке В, а расстояние меньше).
В любой точке C, расположенной между зарядами, напряженность Е_С не равна 0, т.к. векторы напряженностей E_CA  и E_CB направлены в одну сторону.
Таким образом, мы приходим к выводу, что искомая точка – это точка D, которая лежит на прямой, проходящей через данные заряды, справа от меньшего заряда q₂ на некотором расстоянии x от него. В этой точке E_DA = E_DB или

[ frac{k cdot left| q_{1} right|}{DA^{2}} =
frac{k cdot left| q_{2} right|}{DB^{2}}, ; ;
frac{left| q_{1} right|}{DA^{2}} = frac{left| q_{2} right|}{DB^{2}}, ; ;
frac{2q}{left( d + x right)^{2}} = frac{q}{x^{2}}, ]

2x² – (d + x)² = 0, x² – 2d⋅x – d² = 0.

Получили квадратное уравнение, корни которого равны

[ x = d cdot left( 1 pm sqrt{2} right). ]

Так как х > 0 (точка D лежит правее точки В), то

[ x = d cdot left( 1 + sqrt{2} right). ]

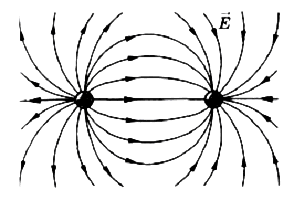
Где в системе из двух разноименных зарядов напряженность равна 0?

Напряженность – величина векторная, поэтому сумма векторов должна быть равна нулю.  Из этого следует, что векторы должны быть направлены встречно, а их модули равны.  Тогда очевидно, что если заряды одноименны, такая точка, где напряженность равна нулю, находится на оси между зарядами. Если заряды разноименные (разные по знаку) такая точка находится на продолжении оси, соединяющей заряды, как показано на рисунке выше. Конкретное местоположение этой точки зависит от величины каждого из зарядов и вот почему. Модуль вектора напряженности определяется по формуле:

$E=frac{q}{4pivarepsilon_0varepsilon R^2}$  

Тогда, исходя из изложенного принципа, что модули напряженности, создаваемой каждым из зарядов, равны, можем записать:

$frac{q_1}{4pivarepsilon_0varepsilon R_1^2}=frac{q_2}{4pivarepsilon_0varepsilon R_2^2}$  $               (1)

Обозначим расстояние между зарядами L, тогда расстояние искомой точки х, от второго заряда:

$R_2=L-R_1$               (2)

Подставим (2) в (1):

$frac{q_1}{R_1^2}=frac{q_2}{(L-R_1)^2}$             (3)

Решаем квадратное уравнение (3) и получаем:

$R_1=2q_1Lpmsqrt{frac{4q_1^2L^2-4(q_1-q_2)q_1L^2}{2(q_1-q_2)}}$

Ну, а если заряды разного знака, то (2) надо записать соответственно и далее алгоритм тот же.

«Практика
рождается из тесного

соединения
физики и математики»

Френсис
Бэкон

В
данной теме рассмотрим решение задач на напряженность поля.

Задача
1.
В некоторой точке поля на заряд 80 нКл действует сила 60 мкН. Найдите
напряженность поля в этой точке. Если в эту же точку поместить заряд 200 нКл,
то какая сила на него будет действовать?

ДАНО:	СИ	РЕШЕНИЕ Напряжённость электрического поля в данной точке равна отношению кулоновской силы, действующей на заряд, к величине этого заряда Тогда Если поместим другой заряд в эту же точку поля, то напряжённость в ней не изменится Тогда

Ответ:
Е = 667 Н/Кл; F = 150мкН.

Задача
2.
В вершинах квадрата со стороной 40 см находятся заряд q₁
(равный –2 нКл) и заряды q₂,
q₃,
q₄
(равные 4 нКл). Найдите
напряжённость поля в центре квадрата.

ДАНО:	СИ	РЕШЕНИЕ Поскольку модули положительных зарядов одинаковы, ясно, что напряжённости, создаваемые зарядами q2 и q4 компенсируют друг друга в центре квадрата. А вот векторы напряжённости зарядов q1 и q3 направлены одинаково, поскольку заряд q1 отрицательный, а q3 – положительный. Напряжённость электрического поля, создаваемого несколькими зарядами, определяется, исходя из принципа суперпозиции полей. Тогда в проекциях на ось Ох Напряженность поля создаваемая зарядом q определяется по формуле Расстояние от центра квадрата до заряда определяется по формуле Тогда напряженность поля создаваемая зарядами q1 и q3 равна Тогда по принципу суперпозиции полей

Ответ:
675 Н/Кл.

Задача
3.
. Напряжённость электрического поля на поверхности заряженного шара равна 20
кН/Кл. Найдите модуль силы, действующей на точечный заряд 20 нКл, находящийся
на расстоянии 80 см от центра шара. Заряд шара распределён равномерно и равен 3
мкКл.

ДАНО:	СИ	РЕШЕНИЕ Запишем формулу, по которой рассчитывается напряжённость заряженного шара В задаче дана напряженность поля на поверхности шара, то есть, при r = R. Это попадает под первый случай. Исходя из этого, можем выразить квадрат радиуса шара Получаем, что радиус шара больше расстояния между точечным зарядом и центром шара. Значит, для вычисления напряжённости в точке, где находится заряд q, нужно использовать вторую формулу. Сила, действующая на точечный заряд в данной точке поля, равна Тогда

Ответ:
276,8 мкН.

Задача
4.
Два точечных заряда 30 нКл и –20 нКл находятся на расстоянии 15 см друг от
друга. Найдите положение точки на прямой, проходящей через эти заряды, напряженность
поля в которой равна нулю.

ДАНО:	СИ	РЕШЕНИЕ Согласно принципу суперпозиции полей Напряжённость поля точечного заряда на произвольном расстоянии от него рассчитывается по формуле Рассмотрим линии напряжённости зарядов на этой прямой. Линии напряжённости направлены от положительного заряда. Также, линии напряжённости направлены к отрицательному заряду. Таким образом, можно убедилиться, что между зарядами q1 и q2, векторы напряжённости Е1 и Е2 сонаправлены, а, значит, точка, в которой напряжённость равна нулю, не может находится между зарядами. Она находится где-то за зарядом q2, где векторы напряжённости направлены в противоположные стороны. Тогда напряженности поля, создаваемые первым и вторым зарядами соответственно равны В проекциях на ось Ох Таким образом получили стандартное квадратное уравнение. Определяем дискриминант Тогда корни квадратного уравнения равны Т.к.

Ответ:
напряжённость поля будет равна нулю в точке, находящейся на расстоянии 16,2 см
от заряда q₁.

Цель урока: дать понятие напряжённости электрического поля и ее
определения в любой точке поля.

Задачи урока:

• формирование понятия напряжённости электрического поля; дать понятие о
  линиях напряжённости и графическое представление электрического поля;
• научить учащихся применять формулу E=kq/r² в решении
  несложных задач на расчёт напряжённости.

Электрическое поле – это особая форма материи, о существовании которой можно
судить только по ее действию. Экспериментально доказано, что существуют два рода
зарядов, вокруг которых существуют электрические поля, характеризующиеся
силовыми линиями.

Графически изображая поле, следует помнить, что линии напряженности
электрического поля:

1. нигде не пересекаются друг с другом;
2. имеют начало на положительном заряде (или в бесконечности) и конец на
   отрицательном (или в бесконечности), т. е. являются незамкнутыми линиями;
3. между зарядами нигде не прерываются.

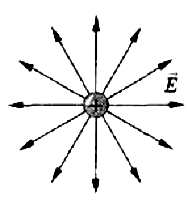
Рис.1

Силовые линии положительного заряда:

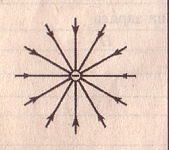
Рис.2

Силовые линии отрицательного заряда:

Рис.3

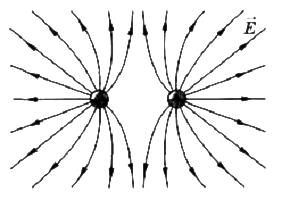
Силовые линии одноименных взаимодействующих зарядов:

Рис.4

Силовые линии разноименных взаимодействующих зарядов:

Рис.5

Силовой характеристикой электрического поля является напряженность, которая
обозначается буквой Е и имеет единицы измерения
или
.
Напряженность является векторной величиной, так как определяется отношением силы
Кулона к величине единичного положительного заряда

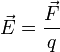
В результате преобразования формулы закона Кулона и формулы напряженности
имеем зависимость напряженности поля от расстояния, на котором она определяется
относительно данного заряда

где: k – коэффициент пропорциональности, значение которого зависит от
выбора единиц электрического заряда.

В системе СИ
Н·м²/Кл²,

где ε₀ – электрическая
постоянная, равная 8,85·10^-12 Кл²/Н·м²;

q – электрический заряд (Кл);

r – расстояние от заряда до точки в которой определяется напряженность.

Направление вектора напряженности совпадает с направлением силы Кулона.

Электрическое поле, напряженность которого одинакова во всех точках
пространства, называется однородным. В ограниченной области пространства
электрическое поле можно считать приблизительно однородным, если напряженность
поля внутри этой области меняется незначительно.

Общая напряженность поля нескольких взаимодействующих зарядов будет равна
геометрической сумме векторов напряженности, в чем и заключается принцип
суперпозиции полей:

Рассмотрим несколько случаев определения напряженности.

1. Пусть взаимодействуют два разноименных заряда. Поместим точечный
положительный заряд между ними, тогда в данной точке будут действовать два
вектора напряженности, направленные в одну сторону:

Е₃₁ – напряженность точечного заряда 3 со стороны заряда 1;

Е₃₂ – напряженность точечного заряда 3 со стороны заряда 2.

Согласно принципу суперпозиции полей общая напряженность поля в данной точке
равна геометрической сумме векторов напряженности Е₃₁ и Е₃₂.

Напряженность в данной точке определяется по формуле:

Е = kq₁/x² + kq₂/(r – x)²

где: r – расстояние между первым и вторым зарядом;

х – расстояние между первым и точечным зарядом.

Рис.6

2. Рассмотрим случай, когда необходимо найти напряженность в точке удаленной
на расстояние а от второго заряда. Если учесть, что поле первого заряда больше,
чем поле второго заряда, то напряженность в данной точке поля равна
геометрической разности напряженности Е₃₁ и Е₃₂.

Формула напряженности в данной точке равна:

Е = kq1/(r + a)² – kq₂/a²

Где: r – расстояние между взаимодействующими зарядами;

а – расстояние между вторым и точечным зарядом.

Рис.7

3. Рассмотрим пример, когда необходимо определить напряженность поля в
некоторой удаленности и от первого и от второго заряда, в данном случае на
расстоянии r от первого и на расстоянии bот второго заряда. Так как одноименные
заряды отталкиваются , а разноименные притягиваются, имеем два вектора
напряженности исходящие из одной точки, то для их сложения можно применить метод
противоположному углу параллелограмма будет являться суммарным вектором
напряженности. Алгебраическую сумму векторов находим из теоремы Пифагора:

Е = (Е₃₁² +Е₃₂²)^1/2

Следовательно:

Е = ((kq₁/r² )² + (kq₂/b²)²)^1/2

Рис.8

Исходя из данной работы, следует, что напряженность в любой точке поля можно
определить, зная величины взаимодействующих зарядов, расстояние от каждого
заряда до данной точки и электрическую постоянную.

4. Закрепление темы.

Проверочная работа.

Вариант № 1.

1. Продолжить фразу: “электростатика – это …

2. Продолжить фразу: электрическое поле – это ….

3. Как направлены силовые линии напряженности данного заряда?

4. Определить знаки зарядов:

5. Указать вектор напряженности.

6. Определить напряженность в точке В исходя из суперпозиции полей.

Своя оценка работы	Оценка работы другим учеником

Вариант № 2.

1. Продолжить фразу: “электростатика – это …

2. Продолжить фразу: напряженностью называется …

3. Как направлены силовые линии напряженности данного заряда?

4. Определить заряды.

5. Указать вектор напряженности.

6. Определить напряженность в точке В исходя из суперпозиции полей.

Своя оценка работы	Оценка работы другим учеником

Задачи на дом: