Как найти точку глобального минимума

8.3.1. Понятие глобального экстремума функции

Рассмотрим
функцию
,
которая задана на замкнутом множестве.
Точканазывается точкойглобального
максимума
или наибольшим
значением
функции на множестве
,
если
.

Если же
,
то точка
называется точкойглобального
минимума
или наименьшим
значением
функции на множестве
.

Точка
называется точкойглобального
экстремума
функции
на множестве,
если точкаявляется глобальным минимумом или
глобальным максимумом функциина множестве.

Если функция
непрерывна на замкнутом и ограниченном
множестве
,
то из теоремы Вейерштрасса следует,
что во множественайдутся точки глобального максимума
и минимума функции.

Точки глобального
экстремума функции могут быть внутренними
точками множества
или принадлежать границе множества.
Если точка глобального экстремума
является внутренней, то она является
локальным экстремумом функции.Отсюда
вытекает алгоритм отыскания глобальных
экстремумов функции
на множестве
:

1. Во множестве
найти все критические точки функции, а
также точки, в которых функция не
дифференцируема.

2. Найти все точки,
в которых функция может принимать
наибольшее и наименьшее значения на
границе множества
.

3. Вычислить
значения функции в точках, найденных в
пунктах 1 и 2.

4. Среди значений,
найденных в пункте 3, выбрать наибольшее
и наименьшее значения.

Примеры

1. Найти глобальный
экстремум функции
на множестве.

Решение.
Множество
является ограниченным, таки.
Из теоремы 4.9. вытекает, чтоявляется замкнутым множеством.
Следовательно функцияна множествеимеет глобальный минимум и максимум.
Множествопредставляет собой треугольник,
ограниченный осями координат и прямой(рис. 8.7).

Рис.8.7.

Найдем критические
точки функции
.
Так как

,
,

то функция
имеет единственную критическую точку,
которая принадлежит множеству.

Исследуем функцию
на отрезке
,.
Подставляяв выражение для функции, получим.
Функция принимает наименьшее и наибольшее
значение на концах отрезка и в критической
точке.
Отсюда следует, что на отрезке,функция принимает наименьшее и наибольшее
значение только в точках

,
и.

Исследуем функцию
на отрезке
,.
Подставляяв выражение для функции, получим.
Функция принимает наименьшее и наибольшее
значение на концах отрезка и в критической
точке.
Отсюда следует, что на отрезке,функция принимает наименьшее и наибольшее
значение только в точках

,
и.

Исследуем функцию
на отрезке
,.
Подставляяв выражение для функции, получим

.

Функция принимает
наименьшее и наибольшее значение на
концах отрезка и в критической точке
.
Отсюда следует, что на отрезке,функция принимает наименьшее и наибольшее
значение только в точках

,
и.

В таблице 8.1
приведены значения функции во всех
найденных точках.

Таблица
8.1

Из таблицы 8.1
следует, что
и—
точки соответственно глобального
минимума и максимума функция,
и

,
.
●

Задачи

Найти глобальные
экстремумы функции
на множестве.

1.
,.

2.
,.

3.
,.

4.
,.

5.
,.

Ответы

1.
,.

2.
,.

3.
,.

4.
,.

5.
,.
▲

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

4
МЕТОДЫ ПОИСКА ГЛОБАЛЬНОГО МИНИМУМА ОДНОМЕРНЫХ МНОГОЭКСТРЕМАЛЬНЫХ ФУНКЦИЙ

Некоторые методы решения многомерных задач оптимизации (если размерность
вектора варьируемых параметров X больше единицы, то детерминированная
задача оптимизации называется многопараметрической задачей оптимизации) требуют
решения одномерной задачи глобальной оптимизации (ставится задача отыскания
глобального минимума критерия оптимальности f(x)).

4.1
Метод перебора. Одномерный метод Монте-Карло

Рассматривается следующая одномерная задача условной глобальной
оптимизации (если задача оптимизации является задачей условной оптимизации и
отыскивается глобальный минимум критерия оптимальности f(x), то эта задача оптимизации называется задачей
глобальной условной оптимизации): найти минимум, вообще говоря,
многоэкстремальной функции f(x), определенной в замкнутой области допустимых значений D = [a;b]:

                                                             (4.1)

Алгоритм метода перебора

 

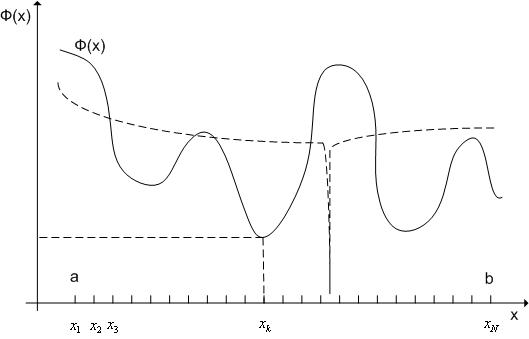Рис.
4.1. Иллюстрация метода перебора

Шаг 1. Покрываем интервал [a;b] некоторой сеткой с узлами .

Шаг 2. Производим испытание в точке ,
т.е. вычисляем значения  функции f(x) в этой точке.

Шаг 3. Полагаем r =
2.

Шаг 4. Производим испытание в точке x_r
и вычисляем значение f_r = f(x_r) функции f(x) в этой точке.

Шаг 5. Если , то
выполняем присваивания .

Шаг 6. Если r <
N, то выполняем присваивание r = r +
1 и переходим к шагу 4, иначе заканчиваем вычисления.

Шаг 7. Принимаем  в качестве приближенного
значения точки глобального минимума функции f(x) на интервале [a;b] или каким-либо из рассмотренных одномерных методов
локальной оптимизации организуем в окрестности точки  поиск локального минимума
этой функции.

При выборе количества узлов сетки  можно
исходить из требуемой точности решения  –
максимальный шаг сетки принять равным этой величине.

Замечание.
Метод перебора, как и любой другой метод глобальной оптимизации, при отсутствии
априорной информации о свойствах минимизируемой функции не гарантирует
нахождение глобального минимума (пунктирный график на рис. 4.1).

Алгоритм одномерного метода Монте-Карло

Шаг 1. Генерируем с помощью какого-либо программного генератора случайных
чисел, равномерно распределенных в интервале [a;b], случайное число .

Шаг 2. Производим испытание в точке  и
вычисляем значения  функции f(x) в этой точке.

Шаг 3. Полагаем r =
2.

Шаг 4. Аналогично шагу 1 генерируем случайное число .

Шаг 5. Производим испытание в точке  –
вычисляем значение f_r = f(x_r) функции f(x) в этой точке.

Шаг 6. Если , то выполняем
присваивания .

Шаг 7. Если r <
N, то выполняем присваивание r = r +
1 и переходим к шагу 4, иначе заканчиваем вычисления. Здесь N – количество испытаний.

Шаг 8. Принимаем  в качестве приближенного
значения точки глобального минимума функции f(x) на интервале [a;b] или каким-либо из рассмотренных одномерных методов
локальной оптимизации организуем в окрестности точки  поиск
локального минимума этой функции.

При достаточно большом N метода
гарантирует нахождение глобального минимума с высокой вероятностью.

4.2
Метод выделения интервалов унимодальности

Рассмотрим одномерную задачу условной глобальной оптимизации: найти
минимум одномерной многоэкстремальной функции f(x), определенной в замкнутой области допустимых значений D = [a;b] и имеющей в этой области конечное число минимумов
(4.1).

Метод выделения интервалов унимодальности функции f(x) требует априорного знания оценки d > 0 минимального расстояния между локальными
минимумами этой функции.

Алгоритм метода выделения интервалов унимодальности (рис.
4.2):

Шаг 1. Полагаем r =
1.

Шаг 2. Если функция f(x)
в точке a возрастает, то полагаем  и переходим к шагу 4.

Шаг 3. Если функция f(x)
в точке a убывает, то полагаем  и переходим к шагу 5.

 

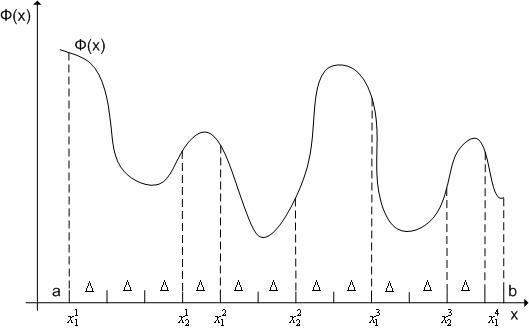
Рис. 4.2. К алгоритму метода выделения интервалов унимодальности

Шаг 4. Последовательно увеличивая х на величину  по формуле , находим первую точку , в которой функция f(x) убывает. Здесь и
далее  – величина в несколько раз меньшая
величины d.

Шаг 5. Последовательно увеличивая х на величину  по формуле , находим первую точку , в которой функция f(x) возрастает.

Шаг 6. В качестве r-го интервала
унимодальности принимаем интервал [].

Шаг 7. Если интервал [a;b] исчерпан, переходим шагу 8, иначе полагаем  и переходим к шагу 4.

Шаг 8. Положим, что общее количество найденных интервалов унимодальности
функции f(x)
равно N – 1. Каким-либо одномерным методом
локальной оптимизации находим локальный минимум функции f(x) в каждом из N – 1
интервалов унимодальности. Обозначим точки этих минимумов . Соответствующие значения функции f(x) обозначим . Добавим к точкам  точки  и
вычислим соответствующие значения функции f(x).

Шаг 9. Найдем минимальную из величин  и
соответствующее значение аргумента: .

Шаг 10. В качестве решения задачи глобальной оптимизации (4.1) примем
точку .

На рис. 4.2 интервалами унимодальности являются интервалы .

Для определения того, возрастает или убывает в данной точке функция f(x), может использоваться
ее первая разность в этой точке , где х – некоторая малая
величина. А именно, если   f_x > 0,
то функция возрастает в точке х; иначе – убывает. Заметим, что при этом
в каждой точке требуется выполнить дополнительное испытание функции f(x).

Если функция f(x)
непрерывно дифференцируема в интервале [a;b], то для определения того, возрастает или убывает в
данной точке эта функция, можно, очевидно, использовать значения первой
производной функции f(x)
в этой точке. А именно, если , то в точке x функция f(x) возрастает; в противном случае – убывает.

Замечание

Если априорная оценка d минимального
расстояния между локальными минимумами функции f(x) отсутствует, то никаких оснований полагать, что в
интервалах, выделенных с помощью рассмотренного алгоритма, функция f(x) является унимодальной
функцией. Пусть, например, функция f(x) на интервале [c;d] постоянна (рис. 4.3). Если к такой функции применить
алгоритм выделения интервалов унимодальности с любым >
0, то в качестве интервала унимодальности будет выделен интервал , на котором функция f(x) имеет бесконечное
количество минимумов, т.е. не является унимодальной функцией.

 

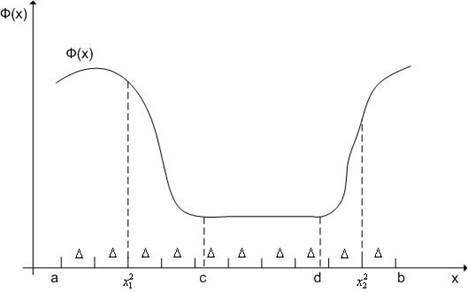
Рис.
4.3. Иллюстрация к замечанию

4.3
Метод аппроксимирующих моделей

Рассмотрим одномерную задачу условной глобальной оптимизации: найти
минимум одномерной мультимодальной функции f(x), определенной в замкнутой области допустимых значений D = [a;b] (4.1).

Алгоритм метода аппроксимирующих моделей:

 

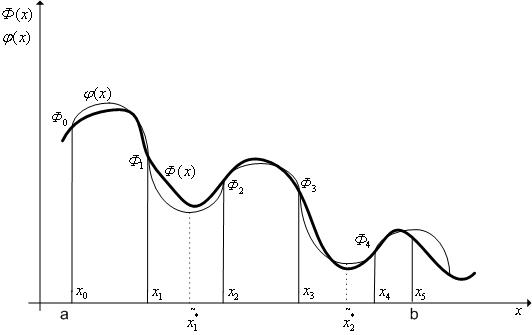
Рис.
4.4. Алгоритм метода аппроксимирующих моделей. N = 5

Шаг 1. Покрываем интервал [a;b] некоторой сеткой с узлами  и
производим испытания в точках , т.е. вычисляем
значения функции f(x)
в этих точках .

Шаг 2. Строим аппроксимирующую функцию ,
проходящую через точки . Эту функцию
принято называть математической моделью минимизируемой функции f(x) или модельной
функцией.

Шаг 3. Оцениваем адекватность построенной модели .
Для этого:

производим дополнительные испытания функции f(x) в некоторых точках;

вычисляем значения модельной функции  и
функции f(x) в
этих точках ;

вычисляем погрешность аппроксимации, например, .

Шаг 4. Если погрешность аппроксимации превышает заданную, то по
результатам всех предшествующих испытаний строим новую модельную функцию  и переходим к шагу 3.

Шаг 5. Определяем положение глобального минимума модельной функции , который или принимается в
качестве глобального минимума функции f(x), или уточняется с помощью какого-либо метода локальной
оптимизации.

            На
рис. 4.4  – точки локального минимума
модельной функции ; точка  – приближенное значение точки
глобального минимума функции f(x) на интервале [a;b].

В качестве модельных функций  чаще всего
используют полиномы и сплайны.

Рассмотрим использование в качестве модельной функции полиномов.

Аппроксимирующий полином Лагранжа

Будем искать аппроксимирующий полином в виде

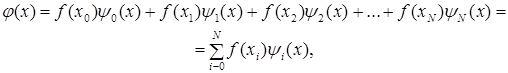   (4.2)

где  – неизвестные полиномы от х,
независящие от аппроксимируемой функции .

Из того условия, что модельная функция  должна
совпадать с аппроксимируемой функцией f(x) в узлах сетки ,
имеем систему из  N + 1
равенств:

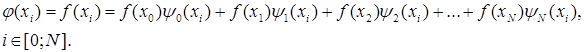(4.3)

Для выполнения равенств (4.3) полиномы ,
очевидно, должны удовлетворять условиям

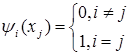                                                  (4.4)

или, другими
словами, полином , должен иметь в качестве
корней все числа , кроме числа x_j, а при x = x_j должен иметь значение, равное единице.

Условию (4.4) удовлетворяют только полиномы вида , где A
– неизвестная константа. Найдем эту константу из условия :

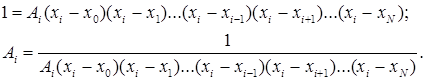
Таким образом,

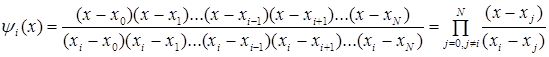    (4.5)

и искомый
аппроксимирующий полином определяют выражением

                                     (4.6)

Полином (4.6) называется аппроксимирующим полиномом Лагранжа.

Использование аппроксимирующего полинома Лагранжа (4.6) в качестве
модельной функции идейно очень просто, но обладает существенным недостатком.
Пусть после построения этого полинома на сетке  и
проверке его адекватности выясняется, что погрешность аппроксимации превышает заданную.
Тогда, в соответствии с рассмотренным выше алгоритмом метода, необходимо
построить новый полином Лагранжа на сетке, полученной объединением сеток , ,
что требует пересчета всех посчитанных ранее функций . От этого недостатка свободна
модификация аппроксимирующего полинома Лагранжа – аппроксимирующий полином
Ньютона.

После построения аппроксимирующего полинома возникает задача нахождения
стационарных точек функции . Поскольку
аппроксимирующий полином непрерывен и, по крайней мере, один раз непрерывно
дифференцируем, его стационарные точки удобно искать как нули первой
производной – т.е. как корни уравнения

Наибольшее и наименьшее значения функции.
Глобальные максимумы и минимумы

Краткая теория

---

Наибольшее значение
функции

 на
множестве

 называют глобальным максимумом, а ее
наименьшее значение – глобальным минимумом.

Чтобы найти глобальные
экстремумы функции

 на
отрезке

, на котором она непрерывна, надо: найти
критические точки, принадлежащие интервалу

, и вычислить значения функции в этих
точках; вычислить значения функции в граничных точках отрезка, то есть

 и

; из всех полученных значений выбрать
наименьшее и наибольшее.

Общая схема решения
прикладных задач такова:

Устанавливается
зависимость рассматриваемой величины

 от
некоторой независимой величины

 (обозначения, разумеется, могут быть другими).
Из условия задачи
определяется тот промежуток, в котором может изменяться аргумент

.
Когда величина

 представлена как функция аргумента

, к ней применяется теория экстремумов.

В прикладных задачах чаще
всего встречается случай, когда внутри рассматриваемого промежутка (отрезка,
полуинтервала или интервала) оказывается лишь одна критическая точка

. Если в этой точке непрерывная функция
имеет локальный максимум (минимум), то он является ее наибольшим (наименьшим)
значением.

Примеры решения задач

---

Задача 1

Определить наибольшее и
наименьшее значения функции

 на
отрезке

:

на отрезке

Решение

Найдем критические точки
этой функции, лежащие на отрезке 

.

Для этого найдем
производную функции:

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Приравняем производную к
нулю:

 -критическая
точка, лежащая на отрезке

Вычислим значение функции
в найденной точке и на концах отрезка:

Сравнивая полученные значения,
находим:

---

Задача 2

Найти наибольшее и
наименьшее значения функции

 на
отрезке

.

Решение

Найдем критические точки
этой функции, лежащие на отрезке 

.

Для этого найдем
производную функции:

Приравняем производную к
нулю и решим полученное уравнение:

Найденная
точка

 лежит в заданном интервале

Вычислим
значение функции в найденных точках и на концах отрезка:

Сравнивая полученные
значения, находим:

Экстре́мум (лат. extremum — крайнее) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).

Задачи нахождения экстремума возникают во всех областях человеческого знания: теория автоматического управления, проблемы экономики, биология, физика и т. д.^[1]

Определения[править | править код]

Пусть дана функция и  — внутренняя точка области определения Тогда

Если неравенства выше строгие, то называется точкой строгого локального или глобального максимума или минимума соответственно.

Значение функции называют соответственно (строгим) локальным или глобальным максимумом или минимумом. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума.

Замечание[править | править код]

Функция определённая на множестве может не иметь на нём ни одного локального или глобального экстремума. Например,

Необходимые условия существования локальных экстремумов[править | править код]

• Из леммы Ферма вытекает следующее^[2]:

Пусть точка является точкой экстремума функции , определенной в некоторой окрестности точки .

Тогда либо производная не существует, либо .

Эти условия не являются достаточными, так, функция может иметь нуль производной в точке, но эта точка может не быть точкой экстремума, а являться, скажем, точкой перегиба, как точка (0,0) у функции .

Достаточные условия существования локальных экстремумов[править | править код]

является точкой строгого локального максимума. А если

то является точкой строгого локального минимума.

Заметим, что при этом функция не обязательно дифференцируема в точке .

и

является точкой локального максимума. А если

и

то является точкой локального минимума.

Если чётно и , то  — точка локального максимума.
Если чётно и , то  — точка локального минимума.
Если нечётно, то экстремума нет.

См. также[править | править код]

• Критическая точка (математика)
• Методы оптимизации
• Условный экстремум

Примечания[править | править код]

Литература[править | править код]

• Пшеничный Б.Н. Необходимые условия экстремума. — М.: Наука, 1969. — 150 с.

Урок 52
§29. Оптимизация

По традиции обычно рассматривают задачу поиска минимума. Если нужно найти максимум, просто меняют знак функции: значение функции f(x) максимально там, где значение функции -f(x) минимально.

В математике различают локальный («местный») и глобальный («общий») минимум (рис. 5.18).

Локальный минимум — минимальное значение функции в окрестности некоторой точки.

Глобальный минимум — минимальное значение функции при заданных ограничениях.

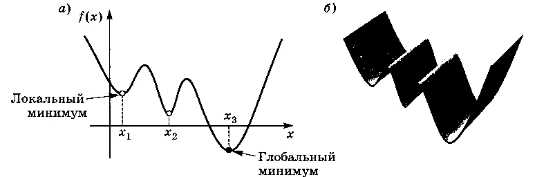
Рис. 5.18

Минимум в точке х₃ — глобальный, потому что здесь функция имеет наименьшее значение во всей рассматриваемой области.

Очевидно, что нас всегда интересует глобальный минимум. Однако большинство существующих методов оптимизации 1) предназначены именно для поиска локальных минимумов вблизи заданной начальной точки (начального приближения).

1) Для некоторых типов функций существуют методы глобальной оптимизации, но они сложны и выходят за рамки школьного курса.

Можно представить себе, что график функции — это срез поверхности, на которую устанавливается шарик в некоторой начальной точке (см. рис. 5.18, б); куда этот шарик скатится, такой минимум и будет найден.

Результат поиска локального минимума зависит от начального приближения.

Следующая страница Пример: оптимальная раскройка листа

Cкачать материалы урока

Как найти точку максимума функции?

Поиск точки максимума и минимума функции — довольно распространенная задача в математическом анализе. Иногда требуется экстремум. Многие думают, что под словом «экстремум» подразумевают наибольшее или наименьшее значение функции. Это не совсем верно. Значение может быть наибольшим или минимальным, но не являться экстремумом.

Глобальный и локальный максимум

Максимум бывает локальным или глобальным. Точка локального максимума — это аргумент, который при подстановке в f(x) даёт значение не меньше, чем в других точках из области около этого аргумента. Для глобального максимума эта область расширяется до всей области допустимых аргументов. Для минимума всё наоборот. Экстремум — это локальное экстремальное — минимальное или максимальное — значение.

Как правило, если математиков интересует глобально самое большое значение f(x), то в интервале, не на всей оси аргументов. Подобные задачи обычно сформулированы фразой «найдите точку максимума функции на отрезке». Здесь подразумевается, что надо выявить аргумент, при котором она не меньше, чем на всём остальном указанном отрезке. Поиск локального экстремума является одним из шагов решения такой задачи.

Дано y = f(x). Требуется определить пик функции на указанном отрезке. f(x) может достигать его в точке:

• экстремума, если она попадает в указанный отрезок,
• разрыва,
• ограничивающей заданный отрезок.

Исследование

Пик f(x) на отрезке или в интервале находится путём исследования данной функции. План исследования для нахождения максимума на отрезке (или интервале):

Найти область допустимых аргументов и пересечения этой области с областью исследования.
1. Выявить асимптоты. Они равны пределу при стремлении аргумента к точкам разрыва.
2. Определить первую производную и вычислить экстремальные точки и выяснить поведение функции в окрестности этих точек.
3. Рассчитать значение f(x) в точках, ограничивающих область исследования.
4. Сравнить экстремум со значением функции в точках разрыва и на концах интервала. Определить среди них наибольшее.

Теперь подробно разберем каждый шаг и рассмотрим некоторые примеры.

Область допустимых аргументов

Область допустимых аргументов — это те x, при подстановке которых в f(x) она не престаёт существовать.Область допустимых аргументов ещё называют областью определения. Например, y = x^2 определена на всей оси аргументов. А y = 1/x определена для всех аргументов, кроме x = 0.

Найти пересечение области допустимых аргументов и исследуемого отрезка (интервала) требуется для того, чтобы исключить из рассмотрения ту часть интервала, где функция не определена. Например, требуется найти минимум y = 1/x на отрезке от -2 до 2. На самом деле требуется исследовать два полуинтервала от -2 до 0 и от 0 до 2, так как уравнение у = 1/0 не имеет решения.

Асимптоты

Асимптота — это такая прямая, к которой функция тянется, но не дотягивается. Если f(x) существует на всей числовой прямой и неразрывна на ней, то вертикальной асимптоты у неё нет. Если же она разрывна, то точка разрыва является вертикальной асимптотой. Для y = 1/x асимптота задаётся уравнением x = 0. Эта функция тянется к нулю по оси аргументов, но дотянется до него, только устремившись в бесконечность.

Если на исследуемом отрезке имеется вертикальная асимптота, около которой функция стремится в бесконечность с плюсом, то пик f(x) на здесь не определяется. А если бы определялся, то аргумент, при котором достигается максимум, совпал бы с точкой пересечения асимптоты и оси аргументов.

Производная и экстремумы

Производная — это предел изменения функции при стремящемся к нулю изменении аргумента. Что это значит? Возьмём небольшой участок из области допустимых аргументов и посмотрим как изменится здесь f(x), а потом уменьшим этот участок до бесконечно малого размера, в этом случае f(x) станет изменяться так же, как и некая более простая функция, которая именуется производной.

Значение производной в определенной показывает под каким углом проходит касательная к функции в выбранной точке. Отрицательное значение говорит о том, что функция здесь убывает. Аналогично положительная производная говорит о возрастании f(x). Отсюда появляются два условия.

1) Производная в точке экстремума либо нулевая, либо неопределенная. Это условие необходимое, но недостаточно. Продифференцируем y = x^3, получим уравнение производной: y = 3*x^2. Подставим в последнее уравнение аргумент «0», и производная обратится в нуль. Однако, это не экстремум для y = x^3. У неё не может быть экстремумов, она убывает на всей оси аргументов.

2) Достаточно, чтобы при пересечении точки экстремума у производной менялся знак. То есть, до максимума f(x) растёт, а после максимума она убывает — производная была положительной, а стала отрицательной.

После того как аргументы для локального максимума были найдены их надо подставить в исходное уравнение и получить максимальное значение f(x).

Концы интервала и сравнение результатов

При поиске максимума на отрезке необходимо проверить значение на концах отрезка. Например, для y = 1/x на отрезке [1; 7] максимум будет в точке x = 1. Даже если внутри отрезка есть локальный максимум, нет никакой гарантии, что значение на одном из концов отрезка не будет больше этого максимума.

Теперь необходимо сравнить значения в точках разрыва (если f(x) здесь не стремится в бесконечность), на концах исследуемого интервала и экстремум функции. Наибольшее из этих значений и будет максимумом функции на заданном участке прямой.

Для задачи с формулировкой «Найдите точку минимума функции» необходимо выбрать наименьшее из локальных минимумов и значений на концах интервала и в точках разрыва.

Локальные и глобальные экстремумы

В задачах математического программирования обычно разыскивается экстремум (максимум или минимум) целевой функции при некоторых ограничениях на значения ее переменных, которые записываются в виде системы уравнений и неравенств.

Точка называется локальным минимумом , если существует число такое, что для любой точки x из сколь угодно малой окрестности точки :

Аналогично определяется локальный максимум функции в точке.

В чем отличие локального минимума от глобального? Глобальный минимум – это точка x*, в которой целевая функция принимает значение не большее, чем в любой допустимой точке. Локальный минимум – это точка x*, в которой целевая функция принимает значение не большее, чем в любой достаточно «близкой» к x* допустимой точке.

Всегда можно легко перейти от задачи на максимум к задаче на минимум , и наоборот.

При этом решения этих двух задач достигаются в одной и той же точке, а значения целевых функций противоположны (см. рис. )

Рис.1. Переход от задачи на максимум к задаче на минимум

В некоторых случаях существование решения ЗМП гарантирует следующая теорема:

Теорема Вейерштрасса (TW). Если допустимое множество X замкнуто, ограничено и непусто, а целевая функция F(x) непрерывна на Х, то она достигает и наибольшего и наименьшего значения на этом множестве.

Обратите внимание на то, что невыполнение условий TW оставляет вопрос о существовании решения ЗМП открытым.

ПРИМЕР 1. Проиллюстрируем применение TW к следующим задачам:

? а) Допустимое множество задачи открыто и неограничено, что делает невозможным применение TW. Тем не менее целевая функция рассматриваемой ЗМП имеет глобальный минимум в точке .

b) Функция непрерывна на ограниченном, замкнутом множестве. Это означает, что в силу TWна рассматриваемом промежутке целевая функция задачи достигает своего наибольшего и наименьшего значения.

c) Допустимое множество задачи замкнуто и ограничено, однако целевая функция терпит разрыв на данном промежутке в точке , и TWв данном случае неприменима. Целевая функция данной ЗМП не имеет глобального минимума и максимума. ?