Как найти точку максимума функции дробь

Сайты, меню, вход, новости

ЕГЭ профильный уровень. №11 Степенные, иррациональные и дробные функции. Задача 53admin2023-03-22T18:53:09+03:00

Задача 53. Найдите точку максимума функции    (y = frac{{16}}{x} + x + 3)

Область определения функции: (x in ,,left( { — infty ;0} right) cup left( {0;infty } right).)

Найдём производную заданной функции:

(y’ = ,frac{{{{16}^prime } cdot x — 16 cdot x’}}{{{x^2}}} + x’ + 3′ = frac{{0 cdot x — 16}}{{{x^2}}} + 1 =  — frac{{16}}{{{x^2}}} + 1)

Найдём нули производной:

(1 — frac{{16}}{{{x^2}}} = 0,,,,,,,, Leftrightarrow ,,,,,,,,,{x^2} = 16,,,,,,,, Leftrightarrow ,,,,,{x_1} =  — 4,,,,,,,{x_2} = 4.)

Определим знаки производной и её поведение:

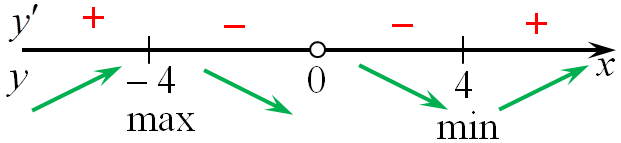
Следовательно, точка максимума  (x =  — 4.)

Ответ:  –4.

Рациональная функция. В этой статье мы рассмотрим несколько примеров. Требуется определить точки максимума или минимума. Ранее уже были рассмотрены подобные задания с логарифмами, тригонометрическими и степенными функциями.

Рекомендую повторить теорию, необходимую для решения, в том числе приоизводные элементарных функций и правила дифференцирования.

Алгоритм нахождения точек максимума (минимума) функции:

1. Вычисляем производную функции.

2. Приравниваем её к нулю, решаем уравнение.

3. Полученные корни отмечаем на числовой прямой. 

*Также на ней отмечаем точки, в которых производная не существует. Получим интервалы возрастания (убывания) функции.

4. Определяем знаки производной на этих интервалах (подставляя произвольные значения из полученных интервалов в производную).

Рассмотрим задания:

77471. Найдите точку максимума функции

Найдём производную данной функции:

Найдем нули производной:

Определим знаки производной функции, подставляя значения из интервалов в найденную производную, и изобразим на рисунке поведение функции. На числовой прямой, кроме найденных корней, так же отмечаем точку в которой производная не существует, для данной функции это точка х = 0 (в ней функция прерывается):

В точке х = – 4  функция меняет знак с положительного на отрицательный, значит это искомая точка максимума.

Ответ: – 4

77500. Най­ди­те точку мак­си­му­ма функ­ции

Найдём производную данной функции:

Найдем нули производной:

*В данном случае производная существует при всех значениях  х.

Отметим на числовой прямой точки х₁ = –17 и х₂ = 17.  Определим знаки производной функции на интервалах, подставляя значения из них в найденную производную:

В точке х = –17 функция меняет знак с положительного на отрицательный,  значит это искомая точка максимума.

Ответ: – 17

77501. Най­ди­те точку ми­ни­му­ма функ­ции

Найдём производную данной функции:

Найдем нули производной:

*В данном случае производная существует при всех значениях  х.

Отметим на числовой прямой точки х₁ = –1 и х₂ = 1.  Определим знаки производной функции на интервалах, подставляя значения из них в найденную производную:

В точке х = 1 функция меняет знак с отрицательного на положительный,  значит это искомая точка минимума.

Ответ: 1

129871. Най­ди­те точку мак­си­му­ма функ­ции

Ответ: 18

129901. Най­ди­те точку ми­ни­му­ма функ­ции

Ответ: –26

132697. Най­ди­те точку мак­си­му­ма функ­ции

Ответ: 3

132727.  Най­ди­те точку ми­ни­му­ма функ­ции

Ответ: 14

Посмотреть решение

Посмотреть решение

Посмотреть решение

В будущем рассмотрим задания с дробно-рациональными функциями, где требуется найти наибольшее (наименьшее) значение на интервале, не пропустите!

Успеха Вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Найти точку минимума можно, выполнив 6 простых шагов.

1) Найдем первую производную.

2) Приравняем ее к нулю и найдем значения х, при которых производная обращается в ноль.

3) На координатной прямой отмечаем иксы, которые получились, и точки разрыва, если таковые имеются.

4) В получившихся промежутках выбираем любое число и подставляем его в ПРОИЗВОДНУЮ!!! Определяем знак получившегося результата.

5) На координатной прямой отмечаем знаками “+” и “-” в зависимости от того, что получилось в пункте 4. Расставляем стрелочки. Если в промежутке стоит плюс, значит стрелочка смотрит вверх, если минус – вниз.

6) По стрелочкам определяем какая точка будет точкой максимума, а какая – точкой минимума. Точка максимума – сверху, точка минимума – снизу.

Начнем-с.

Ищем производную от функции.

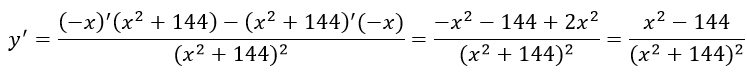
Приравниваем ее к 0 и решаем уравнение относительно х.

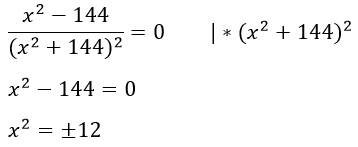
На числовой прямой отмечаем точки -12 и 12, в получившихся промежутках выбираем числа. Я выбрала -20, 0 и 20.

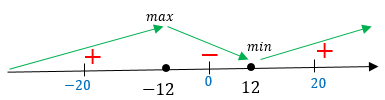
Выбранные числа подставляем в производную, прикидываем знак результата.

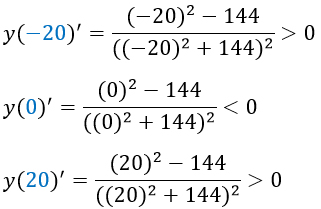
Там, где у меня получились положительные результаты, на чертеже я поставила плюсики, а там, где отрицательный результат, – минусик.

Расставляем стрелочки и видим, что точка максимума у нас равна -12.

Ответ: -12.

Наибольшее значение функции 

Наменьшее значение функции 

Точки max 

Точки min

---

Как говорил крестный отец: «Ничего личного». Только производные!

Статью Как посчитать производные? надеюсь, ты изучил, без этого дальше будет проблематично.

12 задание по статистике считается достаточно трудным, а все потому, что ребята не прочитали эту статью (joke). В большинстве случаев виной всему невнимательность.

12 задание бывает двух видов:

1. Найти точку максимума / минимума (просят найти значения «x»).
2. Найти наибольшее / наименьшее значение функции (просят найти значения «y»).

Как же действовать в этих случаях?

Найти точку максимума / минимума

1. Взять производную от предложенной функции.
2. Приравнять ее к нулю.
3. Найденный или найденные «х» и будут являться точками минимума или максимума.
4. Определить с помощью метода интервалов знаки и выбрать, какая точка нужна в задании.

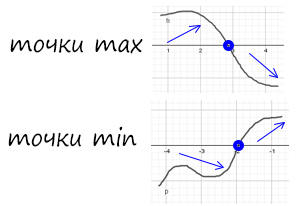
Задания с ЕГЭ: 

Найдите точку максимума функции 

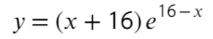
• Берем производную:

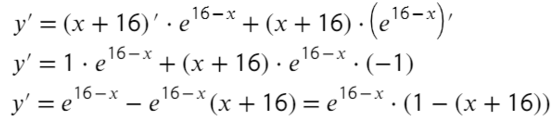
• Приравняем ее к нулю:
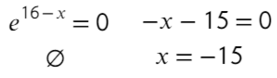
• Получили одно значение икса, для нахождения знаков подставим −20 слева от корня и 0 справа от корня в преобразованную производную (последняя строчка с преобразованием):

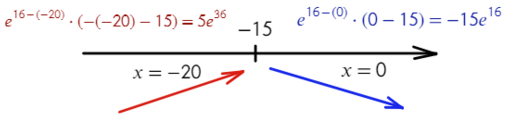
Все верно, сначала функция возрастает, затем убывает — это точка максимума!
Ответ: −15

Найдите точку минимума функции

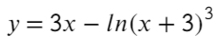
• Преобразуем и возьмем производную: 

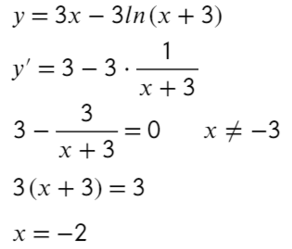
• Получается один корень «−2», однако не стоит забывать о «−3», она тоже будет влиять на изменение знака.

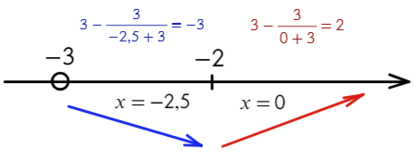
• Отлично! Сначала функция убывает, затем возрасает — это точка минимума!

Ответ: −2

Найти наибольшее / наименьшее значение функции

1. Взять производную от предложенной функции.
   
2. Приравнять ее к нулю.
   
3. Найденный «х» и будет являться точкой минимума или максимума.
   
4. Определить с помощью метода интервала знаки и выбрать, какая точка нужна в задании.
5. В таких заданиях всегда задается промежуток: иксы, найденные в пункте 3, должны входить в данный промежуток.
6. Подставить в первоначальное уравнение полученную точку максимума или минимума, получаем наибольшее или наименьшее значение функции. 

Задания с ЕГЭ: 

Найдите наибольшее значение функции на отрезке [−4; −1] 

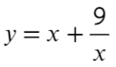
• Преобразуем и возьмем производную: 
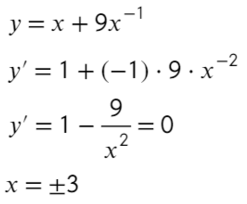
• «3» не вдходит в промежуток [−4; −1]. Значит, остается проверить «−3» — это точка максимума?

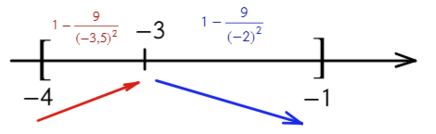
• Подходит, сначала функция возрастает, затем убывает — это точка максимума, и в ней будет наибольшее значение функции. Остается только подставить в первоначальную функцию:

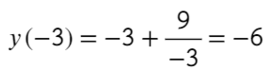
Ответ: −6

Найдите наибольшее значение функции на отрезке [0; 1,5π]

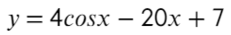
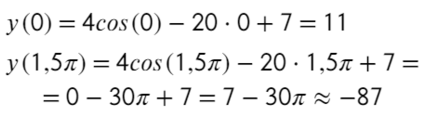
• Наибольшее значение функции равно «11» при точке максимума (на этом отрезке) «0».

Ответ: 11

Выводы:

1. 70% ошибок заключается в том, что ребята не запоминают, что в ответ на наибольшее/наименьшее значение функции нужно написать «y», а на точку максимума/минимума написать «х».
2. Нет решения у производной при нахождении значений функции? Не беда, подставляй крайние точки промежутка!
3. Ответ всегда может быть записан в виде числа или десятичной дроби. Нет? Тогда перерешивай пример.
4. В большинстве заданий будет получаться одна точка и наша лень проверять максимум или минимум будет оправдана. Получили одну точку — можно смело писать в ответ.
5. А вот с поиском значения функции так поступать не стоит! Проверяйте, что это нужная точка, иначе крайние значения промежутка могут оказаться больше или меньше.

Будь в курсе новых статеек, видео и легкого математического юмора.